Estimating Reference Evapotranspiration using Data Mining Prediction

Models and Feature Selection

Hinessa Dantas Caminha

, Ticiana Coelho da Silva

, Atslands Rego da Rocha

and S´ılvio Carlos R. Vieira Lima

Federal University of Cear´a, Campus de Quixad´a, Quixad´a, CE, Brazil

Federal University of Cear´a, Campus do Pici, Fortaleza, CE, Brazil

INOVAGRI Institute, Av. Santos Dumont 3131-A, Fortaleza, CE, Brazil

Keywords:

Data Mining, Irrigated Agriculture, M5P, Linear Regression.

Abstract:

Since the irrigated agriculture is the most water-consuming sector in Brazil, it is a challenge to use water

in a sustainable way. Evapotranspiration is the combination process of transferring moisture from the earth

to the atmosphere by evaporation and transpiration from plants. By estimating this rate of loss, farmers can

efﬁciently manage the crop water requirement and how much water is available. In this work, we propose

prediction models, which can estimate the evapotranspiration based on climatic data collected by an automatic

meteorological station. Climatic data are multidimensional, therefore by reducing the data dimensionality,

then irrelevant, redundant or non-signiﬁcant data can be removed from the results. In this way, we consider in

the proposed solution to apply feature selection techniques before generating the prediction model. Thus, we

can estimate the reference evapotranspiration according to the collected climatic variables. The experiments

results concluded that models with high accuracy can be generated by M5’ algorithm with feature selection

techniques.

1 INTRODUCTION

Reducing poverty and the food insecurity are cru-

cial. Irrigated agriculture plays an important role in

this goal to be achieved, by ensuring innovative ap-

proaches that lead to increased productivity and pro-

vide sustainable solutions (fao, 2015). According to

(inf, 2015), irrigation is responsible for 72% of water

consumed in Brazil. While other sectors are expand-

ing such as water supply, industry, manufacturing and

the environment itself, the need for water resources

grows as well. Therefore, the agriculture sector must

be responsible for reviewing and adjusting its meth-

ods according to the amount of water available to use

(Garces-Restrepo et al., 2007).

Irrigation management aims at proposing tech-

niques to increase the water preservation and the en-

ergy resources without reducing the economic pro-

duction of the crop. This can be done based on how

much water is required to cultivate as well as the soil

characteristics and the soil capacity to retain water.

Among the several current techniques, we can men-

tion the technique of climate monitoring, which con-

sists of the use of weather stations to provide cli-

matic data and estimate the water consumption of

the crop. Such estimation is computed by using the

evapotranspiration concept. According to (Frizzone

et al., 2013), the evapotranspiration (ET) means the

simultaneous occurrence of evaporation and transpi-

ration on the vegetation. Its rate is usually described

in millimeters (mm) for a given unit of time (which

can be an hour, day, decade, month or even an entire

year) and it expresses the amount of water lost from a

cropped surface in units of water depth (Allen et al.,

1998). In order to compute the crop water require-

ment, which refers to the amount of water that needs

to be supplied, it is performed an estimation based on

the reference evapotranspiration (ET

) and the crop

coefﬁcient (K

) (Frizzone et al., 2013). This approach

x ET

) provides a simple, convenient and repro-

ducible way to estimate the evapotranspiration (ET)

from a variety of crops and climatic conditions (Allen

et al., 1998).

The only factors affecting ET

are climatic param-

eters. Consequently, ET

is a climatic parameter, and

it can be computed from the weather data. ET

ex-

presses the evaporating power of the atmosphere at a

particular location and time of the year and it does not

272

Caminha, H., Silva, T., Rocha, A. and Lima, S.

Estimating Reference Evapotranspiration using Data Mining Prediction Models and Feature Selection.

DOI: 10.5220/0006327202720279

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 272-279

ISBN: 978-989-758-247-9

consider the crop characteristics and soil factors. The

FAO Penman-Monteith method (Allen et al., 1998)

is recommended as the sole method for determining

. However, their use is complex and requires that

all climate variables be present. In this way, several

procedures have been developed for estimating miss-

ing climatic parameters.

Climatic data can also be analyzed by data min-

ing techniques. Data mining refers to the applica-

tion of techniques and algorithms for recognizing pat-

terns and models about the data being able to gen-

erate knowledge. There exist several papers which

analyze meteorological and climatic data, such as

(Xavier et al., 2016), (Hendrawan and Murase, 2011),

(Rahimikhoob, 2014) and (Sawalkarand Dixit, 2015).

We aim to analyze these data as well by using data

mining. In this paper, we aim to answer the follow-

ing research question: Is it possible to estimate refer-

ence evapotranspiration without loss of accuracy re-

gardless of the availability of all variables? To solve

this problem, we use a dataset with historical series,

generated by a weather station in the UFC Quixad´a,

Cear´a, Brazil. The prediction models were created

by using the data mining technique M5’ proposed on

(Wang and Witten, 1996). M5’ created more than one

function to calculate the reference evapotranspiration,

and it speciﬁcally refers to the crops present in the

environments where the climatic data were collected.

Another example of such techniques to generate pre-

diction models is Regression, which learns a function

that maps a data item to a real-valued prediction vari-

able (Fayyad et al., 1996). In this work, we apply

linear regression models as well to estimate the refer-

ence evapotranspiration based on climatic data.

However, the data collected from weather stations

can be inaccurate or missing due to several reasons

such as sensor failure, calibration problems, wireless

transmission loss or environmental noise. Moreover,

we can also highlight the existence of missing val-

ues due to the problems with data storage or datalog-

ger power failures. In order to overcome these prob-

lems, feature selection techniques can help to handle

the ﬂuctuating, inaccuracy or imprecision of the sen-

sor readings in a proper way and avoid that a wrong

decision would be made.

We may notice that related papers proposed mod-

els usually applied to calculate the reference evap-

otranspiration and the models are not composed of

all attributes of climatic data. Moreover, as climatic

data are multidimensional, by reducing the number

of attributes so that irrelevant, redundant or non-

signiﬁcant data might be removed from results (Liu

and Yu, 2005), we can save computation time in the

analysis of these data as well.

Data pre-processing is a signiﬁcant step in the

knowledge discovery process since quality decisions

must be based on quality data. The Feature Selection

is one of the data reduction techniques, which the goal

is to ﬁnd a minimum set of attributes such that the re-

sulting probability distribution of the data classes is as

close as possible to the original distribution obtained

using all attributes (Karegowda et al., 2010).

In this way, we propose to apply feature selec-

tion before generating the prediction model for ref-

erence evapotranspiration (ET

). In this paper, the

model to predict the reference evapotranspiration was

generated by using the attributes selected. Our so-

lution generated two models, one by applying M5’

algorithm and another one by applying linear regres-

sion. We have performed many experiments in or-

der to compare the models generated with the origi-

nal data (without feature selection) and with feature

selection in order to discover which one results in a

more accurate model.

The remaining of this paper is structured as fol-

lows. Section 2 reports our solution and Section

3 presents the performed experiments. Section 4

presents the related works. Finally, Section 5, we

draw conclusions and propose future works.

2 METHODOLOGY

We aim at discovering a model to predict the ET

value for the collected data of a weather station. To

achieve this goal, we used an adaptation of the KDD

(standing for Knowledge Discovery in Databases)

process described in (Fayyad et al., 1996) to drive our

methodology. The next subsections correspond to the

steps of the process and how they were executed.

2.1 Data Collection

The ﬁrst stage consists to collect climatic data gen-

erated by the weather station. They are related to the

climatic conditions monitored by the station in the pe-

riod from 16th of June to 19th of October of 2016 at

the city of Quixad´a, Cear´a, Brazil. The data collec-

tion were performed through a serial connection with

the data logger of the station provided by software

PC200W (pc2, 2016). The dataset was stored in CSV

ﬁles.

The original dataset contains 3191 numeric type

tuples, no missing values and it is composed of the

attributes described in Table 1.

Estimating Reference Evapotranspiration using Data Mining Prediction Models and Feature Selection

273

Table 1: Attributes present in the dataset.

Attributes

Timestamp

Precipitation (mm)

Wind Speed

Solar radiation (total and average)

Temperature (maximum and minimum)

Relative air humidity (min, max and average)

Air temperature (min, max and average)

Atmospheric pressure (min, max and average)

2.2 Pre-processing

Data pre-processing refers to collecting, clean, and

persist the data in a ﬁle or table for future analysis.

In this step, the instances which have a non-standard

value for any of the attributes are removed from the

dataset. We call these instances outliers, and they can

affect the accuracy of the prediction model. In or-

der to discover the outliers, for each attribute of the

dataset, we studied how ET

varies with each attribute

presented in Table 1.

Figures 1 and 2 show the variation of the ET

value versus the average of solar radiation and the

maximum air temperature, respectively. By plotting,

we could ﬁnd the outliers tuples that should be re-

moved from the dataset.

Based on our study, we remove the instances con-

taining the values presented in Table 2. After the data

pre-processing, the number of instances in the dataset

reduced to 1120.

Table 2: Removed instances.

Precipitation > 1 Maximum atmospheric pressure

> 625.000

Medium solar radiation >

25.4809

Total solar radiation > 6000000

Minimum temperature > 23.4105 Medium relative humidity >

99.8006

Wind speed > 4 Maximum temperature >

24.8820

Minimum air temperature < 1 Minimum air temperature >

36.692

Maximum air temperature < 1 Minimum air temperature >

37.965

Minimum relative air humidity >

87.062

Maximum relative air humidity >

95.5

2.3 Feature Selection

In this step, after the data pre-processing, the fea-

ture selection algorithms were performed. For this

0 5000 10000 15000 20000

0.00 0.10 0.20

Medium solar radiation

ET0

Figure 1: Variation of the medium solar radiation versus

value.

0 10000 20000 30000

0.00 0.10 0.20

Maximum air temperature

ET0

Figure 2: Variation of the maximum air temperature versus

value.

purpose, we use the WEKA framework (Hall et al.,

2009). The cross-validation method with ten folds

was used to deﬁne the training and test sets.

We experimented only the ﬁlter approach by ap-

plying the CFS algorithm (Hall, 2000). The CFS is

a simple ﬁlter algorithm that ranks feature subsets

according to a correlation based heuristic evaluation

function. The bias of the evaluationfunction is toward

subsets that contain features that are highly correlated

with the class and uncorrelated with each other. Ir-

relevant features should be ignored because they will

have low correlation with the class (Hall, 1999). We

evaluated all search algorithms present in WEKA and

that were compatible with CFS. However, the Best

First, Exhaustive Search Genetic Search, and Random

Search algorithms achieved the best accuracy when

generating the predictive models.

In Table 3, the correlation coefﬁcients generated

by the models can be observed using the attributes se-

lected by each search algorithm. Table 4 shows which

attributes were selected by each algorithm.

2.4 Prediction Model

We created the prediction models by applying the

linear regression and M5P algorithms, both imple-

mented in the WEKA tool. In order to create the mod-

els, we split the dataset into 70% for training and 30%

for testing.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

274

Table 3: Correlation for the generated models by applying

different search algorithms.

Algorithm M5P Linear Regression

CFS + Greedy Stepwise 0.988 0.9511

CFS + Linear Forward 0.988 0.9511

CFS + Subset Size Forward Selection 0.988 0.9511

CFS + Scatter Search VL 0.9881 0.9511

Table 4: Selected Attributes.

Algorithm Selected Attributes

CFS + Best First Minimum atmospheric pressure

Maximum air temperature

Wind speed

Medium solar radiation

CFS + Exhaustive Search Minimum atmospheric pressure

Minimum air temperature

Medium air temperature

Wind speed

Medium solar radiation

CFS + Genetic Search Minimum atmospheric pressure

Minimum air temperature

Maximum air temperature

Medium air temperature

Wind speed

Medium solar radiation

CFS + Random Search Minimum atmospheric pressure

Maximum temperature

Medium air temperature

Wind speed

Medium solar radiation

Each algorithm produced its particular model us-

ing the attributes taken as input. Thus, we generated

ﬁve distinct models, one of which was created from

all the attributes of the dataset and the others models

were generated only from the attributes selected by

the feature selection algorithms. These models and

their comparisons are presented in the following sec-

tion.

3 EXPERIMENTS AND RESULTS

In these experiments, we have used two main algo-

rithms that generate prediction models: M5P and Lin-

ear Regression. Table 5 presents the correlation of

the models generated by M5P and Linear Regression.

Both methods generated models with feature selec-

tion as a previous step, as well as without any feature

selection step. All in all, according to the correlations

reported, the prediction models exhibit a high correla-

tion between the predicted value for ET

and the real

value by using the test dataset.

We avoid presenting all the prediction models

generated through these experiments due to lack of

space. In this way, we have chosen to present the

prediction model with the highest correlation gener-

ated by M5P and Linear Regression, in addition us-

ing feature selection as a previous step. According

to Table 5, the highest correlation for both algorithms

with feature selection occurred when we applied CFS

+ Random Search. We prefer to present those models

with the selected attributes since models without fea-

ture selection the decision tree generated by M5P is

too long and complex.

In what follows, ﬁrst we report the attributes cho-

sen by the feature selection method (CFS + Random

Search) and then the Tables 6 and 7 show the model

generated by M5P. Notice that each line of the table

corresponds to an equation and its respective condi-

tion. Moreover, Table 8 presents the prediction model

discovered by Linear Regression, however by apply-

ing at ﬁrst the feature selection method (CFS + Ran-

dom Search).

• MaxT = Maximum temperature

• WSpeed = Wind speed

• AvgAirT = Medium air temperature

• AvgSRad = Medium solar radiation

• MinAtP = Minimum atmospheric pressure

In order to validate the prediction models, we per-

formed a linear regression, by using the R statistical

language, to measure the accuracy of the real value

and the predicted value of ET

for 100 random tu-

ples of the testing set. This is done by generating the

coefﬁcient R

and a function that relates the two val-

ues. The coefﬁcient of determination, also called R

gives some information about the goodness of ﬁt of a

model. In regression, the R

coefﬁcient of determina-

tion is a statistical measure of how well the regression

line approximates the real data points. The coefﬁcient

of determination ranges from 0 to 1. An R

of 1 indi-

cates that the regression line perfectly ﬁts the data.

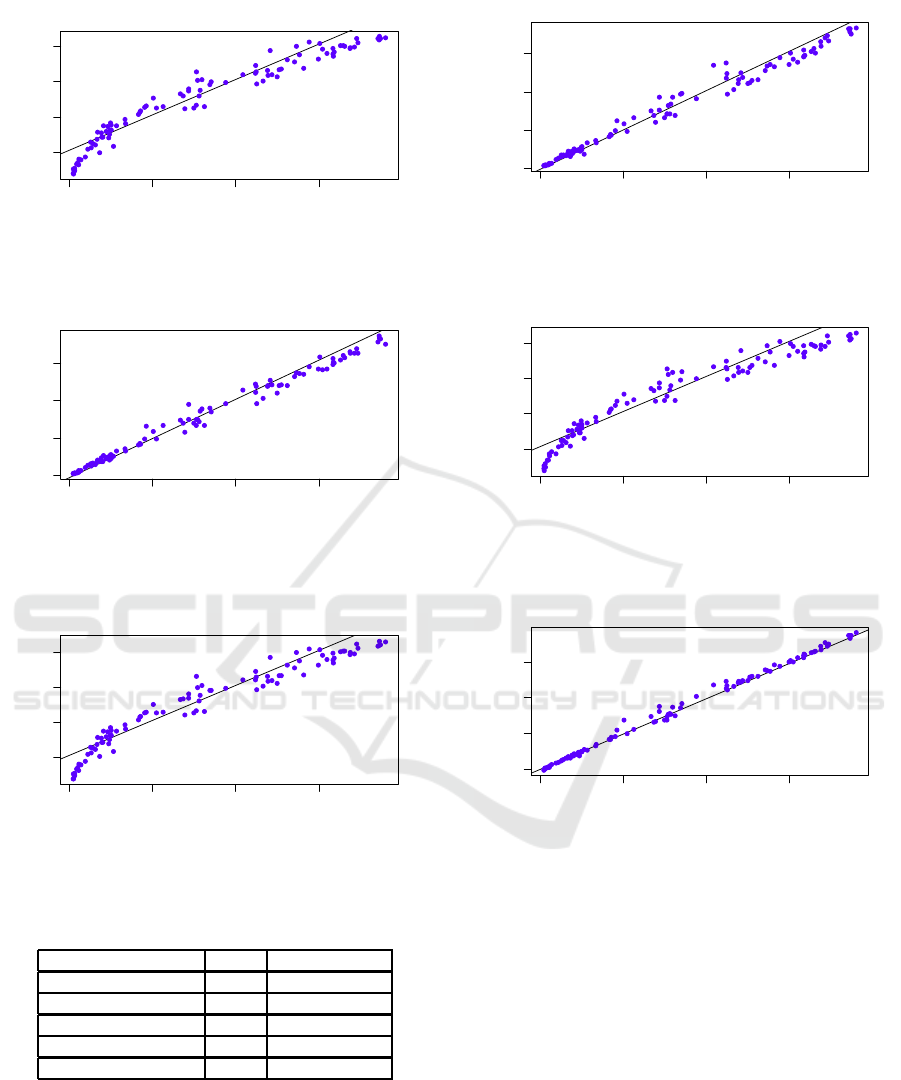
In what follows (Figures 3, 4, 5, 6, 7, 8, 9, 10, 11,

and 12), we show for each prediction model gener-

ated in these experiments, the plotting of the predicted

value of ET

and the real value for 100 tuples chosen

randomly from the testing dataset. We also report in

Table 9, the R

value for each plotting.

According to Table 9, the best models are gen-

erated by the M5P method, as already expected by

Table 5: Correlation for the generated models.

Algorithm M5P Linear Regression

CFS + BestFirst 0.988 0.9511

CFS + Exhaustive Search 0.9897 0.9536

CFS + Genetic Search 0.9899 0.9536

CFS + Random Search 0.9963 0.9653

Without feature selection 0.9969 0.9659

Estimating Reference Evapotranspiration using Data Mining Prediction Models and Feature Selection

275

Table 6: Equations generated by applying M5P with CFS +

Random Search.

Condition Equation

AvgAirT <= 26.4 and WSpeed

<= 0.784

et0 = -0.0022 * MaxT + 0.002 *

AvgAirT + 0.0145 * WSpeed +

0.0024 * AvgSRad - 0.0115

WSpeed > 0.784 and AvgAirT

<= 24.718 and AvgSRad <=

6.249

et0 = -0.0057 * MaxT + 0.0054

* AvgAirT + 0.0097 * WSpeed +

0.001 * AvgSRad - 0.0088

AvgSRad > 6.249 et0 = -0.0103 * MinAtP - 0.0064

* MaxT + 0.0035 * AvgAirT +

0.0156 * WSpeed + 0.0052 *

AvgSRad + 6.1857

AvgAirT > 24.718 and AvgSRad

<= 6.963

et0 = -0.0069 * MaxT + 0.0065

* AvgAirT + 0.0138 * WSpeed +

0.0031 * AvgSRad - 0.0293

AvgSRad > 6.963 et0 = -0.0068 * MaxT + 0.0086

* AvgAirT + 0.0187 * WSpeed +

0.0023 * AvgSRad - 0.0787

AvgAirT > 26.4 and AvgSRad

<= 6.122 and AvgAirT <=

29.416

et0 = -0.0043 * MaxT + 0.0071

* AvgAirT + 0.0275 * WSpeed -

0.0024 * AvgSRad - 0.0932

AvgAirT > 29.416 and WSpeed

<= 0.822

et0 = -0.0021 * MaxT + 0.0044

* AvgAirT + 0.0617 * WSpeed +

0.0004 * AvgSRad - 0.1006

WSpeed <= 1.433 and AvgAirT

<= 32.715

et0 = -0.002 * MaxT + 0.009 *

AvgAirT + 0.0521 * WSpeed +

0.0004 * AvgSRad - 0.2454

AvgAirT > 32.715 et0 = -0.0023 * MaxT + 0.0083

* AvgAirT + 0.0602 * WSpeed +

0.0004 * AvgSRad - 0.2245

WSpeed > 1.433 and AvgAirT

<= 31.746

et0 = -0.0034 * MaxT + 0.0108

* AvgAirT + 0.0393 * WSpeed +

0.0004 * AvgSRad - 0.2582

AvgAirT > 31.746 et0 = -0.0041 * MaxT + 0.012 *

AvgAirT + 0.0551 * WSpeed -

0.0031 * AvgSRad - 0.294

AvgSRad > 6.122 and AvgAirT

<= 30.43 and WSpeed <= 1.851

et0 = -0.0062 * MaxT + 0.0074

* AvgAirT + 0.0407 * WSpeed +

0.002 * AvgSRad - 0.0994

WSpeed > 1.851 and MaxT <=

20.49

et0 = -0.0071 * MaxT + 0.0091

* AvgAirT + 0.0403 * WSpeed +

0.0016 * AvgSRad - 0.1248

MaxT > 20.49 et0 = -0.0067 * MaxT + 0.0089

* AvgAirT + 0.0357 * WSpeed +

0.0041 * AvgSRad - 0.1412

WSpeed <= 1.92 and WSpeed

<= 1.356

et0 = 0.003 * MinAtP - 0.0029

* MaxT + 0.0061 * AvgAirT +

0.0679 * WSpeed + 0.0008 *

AvgSRad - 1.9219

comparing the correlation of the models presented in

Table 5.

The approach proposed in this paper, the estima-

tion of ET

was performed for the collected climatic

variables of a weather station. We also applied a fea-

ture selection to reduce the dimensionality of the cli-

matic data. You can easily see in these experiments,

even with feature selection processing, the prediction

Table 7: Equations generated by applying M5P with CFS +

Random Search.

Condition Equation

WSpeed > 1.356 et0 = 0.0078 * MinAtP - 0.0041

* MaxT + 0.0068 * AvgAirT +

0.0643 * WSpeed + 0.0014 *

AvgSRad - 4.8287

AvgAirT <= 32.648 and WSpeed

<= 2.264

et0 = 0.0031 * MinAtP - 0.0066

* MaxT + 0.009 * AvgAirT +

0.0497 * WSpeed + 0.001 *

AvgSRad - 1.9765

WSpeed > 2.264 et0 = 0.0025 * MinAtP - 0.0065

* MaxT + 0.0103 * AvgAirT +

0.0499 * WSpeed + 0.0009 *

AvgSRad - 1.659

AvgAirT > 32.648 and WSpeed

<= 2.376

et0 = 0.0015 * MinAtP - 0.005

* MaxT + 0.0077 * AvgAirT +

0.0643 * WSpeed + 0.0015 *

AvgSRad - 1.0391

WSpeed > 2.376 et0 = 0.0018 * MinAtP - 0.0058

* MaxT + 0.0086 * AvgAirT +

0.0635 * WSpeed + 0.0018 *

AvgSRad - 1.2602

Table 8: Prediction Model generated by the Linear Regres-

sion with CFS + Random Search.

Linear Regres-

sion

et0 = -0.006 * MaxT

+ 0.0057 * AvgAirT

+ 0.0289 * WSpeed +

0.0055 * AvgSRad +

-0.0601

0.00 0.05 0.10 0.15

Weather Station

M5P: Feature Selection

R−squared: 0.989

Figure 3: Correlation between the estimated ET0 by M5P +

GeneticSearch and the weather station.

models achieved a high correlation degree between

the estimated ET

and its real value for the testing

dataset. So, it is worth reducing the data dimensional-

ity since the prediction models for ET

still have high

accuracy.

4 RELATED WORK

The use of predictive models to estimate the crop wa-

ter requirement has been studied by several authors

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

276

0.00 0.05 0.10 0.15

Weather Station

Linear Regression: Feature Selection

R−squared: 0.9302

Figure 4: Correlation between the estimated ET0 by Linear

Regression + GeneticSearch and the weather station.

0.00 0.05 0.10 0.15

Weather Station

M5P: Feature Selection

R−squared: 0.989

Figure 5: Correlation between the estimated ET0 by M5P +

ExhaustiveSearch and the weather station.

0.00 0.05 0.10 0.15

Weather Station

Linear Regression: Feature Selection

R−squared: 0.9308

Figure 6: Correlation between the estimated ET0 by Linear

Regression + ExhaustiveSearch and the weather station.

Table 9: Coefﬁcient of determination (R

Algorithm M5P Linear Regression

CFS + Genetic Search 0.989 0.9302

CFS + Exhaustive Search 0.989 0.9308

CFS + BestFirst 0.9821 0.9262

CFS + RandomSearch 0.9957 0.9618

Without feature selection 0.9972 0.9666

and approached in different ways.

The paper (Hendrawan and Murase, 2011) pro-

poses irrigation system based on machine vision. The

system presents a predictive model which is used to

determine the amount of water required for the plants

with respect to its respective texture. In this way, the

stress caused by water was observed in a sunagoke

0.00 0.05 0.10 0.15

Weather Station

M5P: Feature Selection

R−squared: 0.9821

Figure 7: Correlation between the estimated ET0 by M5P +

BestFirst and the weather station.

0.00 0.05 0.10 0.15

Weather Station

Linear Regression: Feature Selection

R−squared: 0.9262

Figure 8: Correlation between the estimated ET0 by Linear

Regression + BestFirst and the weather station.

0.00 0.05 0.10 0.15

Weather Station

M5P: Feature Selection

R−squared: 0.9957

Figure 9: Correlation between the estimated ET0 by M5P +

RandomSearch and the weather station.

moss crop. Such observation was executed from pho-

tos and their respective color conversions. The au-

thors applied several algorithms of feature selection,

and the textures selected by each algorithm were used

as input to the classiﬁer Back-Propagation Neural

Network. The study concluded the textures chosen by

the feature selection algorithms created accurate pre-

dictive models. Similar to (Hendrawan and Murase,

2011), our work proposes to use feature selection in

order to create a prediction model based on the set of

selected attributes. However, our proposal uses such

approach to estimate the reference evapotranspiration.

In (Xavier et al., 2016), the authors proposed a life

cycle model in data science to answer the question:

Can a simple approach be found to estimate poten-

Estimating Reference Evapotranspiration using Data Mining Prediction Models and Feature Selection

277

0.00 0.05 0.10 0.15

Weather Station

Linear Regression: Feature Selection

R−squared: 0.9618

Figure 10: Correlation between the estimated ET0 by Lin-

ear Regression + RandomSearch and the weather station.

0.00 0.05 0.10 0.15

Weather Station

M5P without Feature Selection

R−squared: 0.9972

Figure 11: Correlation between the estimated ET0 by M5P

without feature selection and the weather station.

0.00 0.05 0.10 0.15

0.00 0.10

Weather Station

Linear Regression without Feature Selection

R−squared: 0.9666

Figure 12: Correlation between the estimated ET0 by Lin-

ear Regression without feature selection and the weather

station.

tial evapotranspiration with an acceptable accuracy?

The experiments were performed by using historical

series (provided by INMET) of 263 meteorological

stations distributed in several cities of Brazil. The

authors used the M5P to create the models. To val-

idate the results, the authors compared the errors of

the models created by the M5P algorithm to the errors

generated using the Penman-Monteith model imple-

mented by R. They also examined the correlations of

the models. At the end of their study, they concluded

the models found out have a good accuracy and were

simpler than the Penman-Monteith method. Our pro-

posal also used the M5P to create predictive models.

However, we did not estimate the potential evapotran-

spiration. Moreover, we used different attribute selec-

tion algorithms for dimensionality reduction.

In (Sawalkar and Dixit, 2015), the authors ob-

tained meteorological data collected from the three

meteorological stations of United States of Geo-

logical Survey (USGS), Florida USA. For each

dataset, they calculate the evapotranspiration param-

eter (daily and monthly) using both the Penman-

Monteith method and the M5 decision trees. The

authors compared these models with their respective

correlation coefﬁcients and associated errors. They

concluded the models generated by M5 algorithm es-

timated the evapotranspiration more accurately than

the Penman-Monteith method. Similarly, our pro-

posal used an algorithm based on M5 trees (M5P) to

create the prediction models. However, our proposal

differentiates by using feature selection algorithms for

dimensionality reduction.

In (Rahimikhoob, 2014), the authors created mod-

els to estimate the reference evapotranspiration by

using the M5 algorithm and also an artiﬁcial neural

network (ANN). They performed experiments using

data collected from four meteorological stations in-

stalled in the Sistan and Baluchestan provinces, Iran.

Based on the results, the authors concluded the ac-

curacy value of the model created by the M5 algo-

rithm was approximate to that of the model created by

ANN network. Moreover, they concluded the models

had a high degree of correlation with the data used.

Similar to (Rahimikhoob, 2014), our proposal created

prediction models using two different approaches to

estimate reference evapotranspiration. However, we

used Linear Regression as the second approach and

performed feature selection for data reduction.

5 CONCLUSIONS

In this paper, we aim at studying how to predict the

reference evapotranspiration value by using climatic

data. Moreover, these data are multidimensional and

might be not trivial to use a prediction model with

many attributes. Our solution applies feature selec-

tion methods in order to reduce the data dimensional-

ity and then investigate prediction models more accu-

rate. According to the results concerning the correla-

tions of the models, we can highlight that among the

four algorithms used (BestFirst, Random Search, Ex-

haustive Search, Genetic Search), the Random Search

selected the best set of attributes since it generates

the model with the highest correlation. Moreover,

M5P generated better models than traditional linear

regression. Since the Penman-Monteith method is

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

278

too complex, the approach and the models reported

in this work could be very useful for farmers and

agronomists to estimate the evapotranspiration refer-

ence in locations with similar climatic conditions to

the city of Quixad´a. Moreover, other methods us-

ing data mining predictivemodels could be developed

based on the results introduced in this paper. As future

works, we aim to validate and improve our proposed

models for other datasets from other meteorological

stations.

REFERENCES

(2015). Irrigation Sector Reform. FAO. Corporative Web-

site.

(2015). Relat´orio de Conjuntura dos Recursos H´ıdricos no

Brasil 2014. Agˆencia Nacional de

Aguas.

(2016). PC200W 4.4.2. Campbell Scientiﬁc, Inc. Corpora-

tive Website.

Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.

(1998). Crop evapotranspiration-guidelines for com-

puting crop water requirements-fao irrigation and

drainage paper 56. Fao, Rome, 300(9):D05109.

Fayyad, U., Piatetsky-Shapiro, G., and Smyth, P.

(1996). From data mining to knowledge discovery in

databases. AI magazine, 17(3):37.

Frizzone, J. A., de Souza, F., and Lima, S. C. R. V. (2013).

Manejo da irrigac¸˜ao: Quando, Quanto e Como Irri-

gar. INOVAGRI.

Garces-Restrepo, C., Vermillion, D., and Muoz, G. (2007).

Irrigation management transfer: Worldwide efforts

and results.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: an update. ACM SIGKDD explorations

newsletter, 11(1):10–18.

Hall, M. A. (1999). Correlation-based feature selection

for machine learning. PhD thesis, The University of

Waikato.

Hall, M. A. (2000). Correlation-based feature selection of

discrete and numeric class machine learning.

Hendrawan, Y. and Murase, H. (2011). Neural-intelligent

water drops algorithm to select relevant textural fea-

tures for developing precision irrigation system using

machine vision. Computers and Electronics in Agri-

culture, 77(2):214–228.

Karegowda, A. G., Manjunath, A., and Jayaram, M. (2010).

Comparative study of attribute selection using gain ra-

tio and correlation based feature selection. Interna-

tional Journal of Information Technology and Knowl-

edge Management, 2(2):271–277.

Liu, H. and Yu, L. (2005). Toward integrating feature

selection algorithms for classiﬁcation and clustering.

IEEE Transactions on knowledge and data engineer-

ing, 17(4):491–502.

Rahimikhoob, A. (2014). Comparison between m5 model

tree and neural networks for estimating reference

evapotranspiration in an arid environment. Water re-

sources management, 28(3):657–669.

Sawalkar, N. and Dixit, P. (2015). Evapotranspiration mod-

eling using m5 model tree.

Wang, Y. and Witten, I. H. (1996). Induction of model trees

for predicting continuous classes. Working paper se-

ries.

Xavier, F., Tanaka, A. K., and Amorim, F. A. B. (2016).

Application of data science techniques in evapotran-

spiration estimation.

Estimating Reference Evapotranspiration using Data Mining Prediction Models and Feature Selection

279