
Multi-agent Coordination using Reinforcement Learning
with a Relay Agent
Wiem Zemzem and Moncef Tagina
COSMOS Laboratory, National School of Computer Science, University of Manouba, Tunis, Tunisia
Keywords:
Distributed Reinforcement Learning, A Cooperative Action Selection Strategy, A Relay Agent, Unknown and
Stationary Environments.
Abstract:
This paper focuses on distributed reinforcement learning in cooperative multi-agent systems, where several
simultaneously and independently acting agents have to perform a common foraging task. To do that, a
novel cooperative action selection strategy and a new kind of agents, called ”relay agent”, are proposed.
The conducted simulation tests indicate that our proposals improve coordination between learners and are
extremely efficient in terms of cooperation in large, unknown and stationary environments.
1 INTRODUCTION
Reinforcement learning (RL) negotiates the problem
of how an agent can learn by interacting with its en-
vironment and observing the results of these inter-
actions. It is an important technique for automatic
learning in uncertain environments. Though it has
been applied to many domains widely, the multiagent
case has not been investigated thoroughly. This is due
to the difficulty of applying the theory of the single-
agent RL to the multi-agent case and it becomes much
harder when dealing with more complex problems,
like cooperative learning in distributed systems (Par-
talas et al., 2008). It’s the main focus of the current
paper: we aim to coordinate a group of autonomous
agents in order to perform a cooperative foraging task
in a distributed manner.
Many existing works dealing with distributed co-
operative systems use independent learners (ILs).
These learners are called independent since they learn
independently from each other without taking into ac-
count the behaviors of the other agents (Torrey and
Taylor, 2012). They hence bring the benefit of a state
space size independent of the number of agents but
suffers from the lack of multi-agent coordination. A
direct communication between ILs is, therefore, use-
ful in order to ensure knowledge sharing and transfer
among them.
As examples, the policy averaging (PA) method
(Tan, 1997) and the experience counting (EC) method
(Cunningham and Cao, 2012) are proposed as shar-
ing strategies that are adopted by all agents in the en-
vironment. Results show that these sharing methods
expedite learning and outperform independent learn-
ing methods. However, they assume that each agent
knows how many other agents are in the environ-
ment and has enough memory to store the informa-
tion learned by each of them. In real situations where
agents are robots and take on a physical form, these
assumptions may prove to be unrealistic. In addition
to that, at each learning iteration, all state/action pairs
are evaluated and updated after querying other agents
for their entire Qtables and, at the end of each step, all
agents will have the same stored data. Again, these
updates and information exchange are computation-
ally intensive, especially in the case of a large number
of agents and/or a large size of the environment.
Another method, called D-DCM-MultiQ (Guo
and Meng, 2010), seems to be more interesting than
these latter. By this approach, each agent stores a
simple QTable, like a single-agent system, and at
each learning step, it only updates the current ex-
perimented state/action pair using its own informa-
tion in addition to those of its local neighbors. The
multi-agent cooperation is then ensured with a lit-
tle amount of stored and exchanged data. However,
this method suffers from some limitations, namely the
non-continuous spread of the goal’s reward causing
the blockage of learning and even the no completion
of the assigned task. Our previous work, presented
in (Zemzem and Tagina, 2015), deals with the same
problem but in non stationary environments. The pro-
posed approach sort previous knowledge according
to the moment of its last modifications and uses the
Zemzem, W., Tagina, M. and Tagina, M.
Multi-agent Coordination using Reinforcement Learning with a Relay Agent.
DOI: 10.5220/0006327305370545
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 537-545
ISBN: 978-989-758-247-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
537

information of the next state instead of the current
one, which increases the amount of stored informa-
tion and needs additional calculations. Using our pre-
vious approach, a satisfactory result was approved in
the case of dynamic environments. However, a sim-
pler and less costly approach can be adopted when
dealing with only stationary environments: this is the
objective of the current paper.
Several propositions have been made in the
present manuscript in order to overcome the short-
comings of the D-DCM-MultiQ method and improve
multi-agent learning in large, stationary and unknown
environments. The main contributions of this paper
are presented in the following points:
• In order to overcome the limitations of the D-
DCM-MultiQ method, the action selection strat-
egy is not only based on the own information
of the learner, but also on the information of its
neighbors which increases the efficiency of the
choice. In this regard, a new cooperative action
selection strategy is proposed and evaluated. This
proposed method is derived from the ε-greedy
policy (Coggan, 2004). Using this latter, no mem-
orization of exploration specific data is required,
which makes it particularly interesting for very
large or even continuous state-spaces.
• As the communication between agents is local, an
agent can trap between two states (one state in-
side the communication range of the neighboring
agent and another state outside its communication
range). To this end, a second form of agent, called
”relay agent”, is designed to ameliorate the co-
operation between learning agents by storing all
learners’ information. When choosing the next
action to perform, each learning agent should es-
pecially exploit the relay’s backups if it is within
its neighborhood.
• To ensure an efficient learning regardless of the
environment size and the communication range,
the relay agent must move randomly during the
whole learning phase in order to cover different
regions of the environment over time and ensure
the resolution of bottleneck situations in a timely
manner.
• A particular update of the relay’s knowledge is
suggested in order to optimize the size of the
stored data; for each state/action pair, the relay
agent stores only the most promising value of all
neighbors’ information related to this pair, instead
of saving all learners’ information. As a result, the
relay retains a single Qvalue for each state/action
pair, like a learning agent.
The rest of the paper is organized as follows.
Problem statement is described in Section 2. In Sec-
tion 3, the D-DCM-Multi-Q approach is presented
and briefly reviewed. Section 4 is dedicated to present
our suggestions for improvement. Several experi-
ences are conducted in Section 5 showing the effi-
ciency of our proposals. Some concluding remarks
and future works are discussed in Section 6.
2 PROBLEM STATEMENT
The learning problem is a cooperative foraging task in
a large, stationary and two-dimensional discrete envi-
ronment. As in (Guo and Meng, 2010) and (Zemzem
and Tagina, 2015), agents can perform four actions:
”left”, ”right”, ”up” and ”down” and their decisions
are only based on the interaction with the environ-
ment as well as the interaction with local neighbors. It
is assumed that all agents are initially in the nest, and
each agent can locate itself using its on-board sensors
such as encoders and can detect the target or obstacles
using sonar sensors. Each agent has limited onboard
communication range and can share its state informa-
tion with its neighbors that are within its communica-
tion range.
The foraging task may be abstractly viewed as a
sequence of two alternating tasks for each agent:
• Start from the nest and reach the food source (For-
aging Phase). In this case, the learning method is
applied.
• Start from the food source, laden with food, and
reach the nest (Ferrying Phase). Every time one
agent finds the food source, it will wait for other
agents to reach the target (Waiting Phase). Once
all the agents find the food source, they start a
collective transport phase. As agents must follow
the same path, they select the shortest path among
all agents’ foraging paths (Zemzem and Tagina,
2015).
To provide agents with distributed RL, we use a
model close to Markov Decision Processes (MDPs).
It is a tuple of (n,S, A, T, R), where n is the number of
agent’s neighbors. S is a set of states which is defined
as S = [s
1
, .., s
m
], where m is the number of states each
of which is identified by the coordinates (x, y). A is a
set of actions available to an agent which is defined as
A = [a
1
, .., a
p
]. R : S× A −→ r is the reward function
for an agent and T is a state transition function (T is
a probability distribution over S) (Bruno C. Da Silva,
Eduardo W. Basso, Ana L. C. Bazzan, 2006).
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
538

3 A REVIEW OF THE
D-DCM-MultiQ METHOD
D-DCM-MultiQ is a distributed reinforcement learn-
ing method for multi-agent cooperation (Guo and
Meng, 2010). To update its Q-value at a state s
i
, the
i
th
agent uses its own Q-value at that state as well as
the Q-values of its neighboring agents at the next state
s’
i
(see Eq.1).
Q
k+1,i
(s
i
, a
i
) = (1− α
k
)Q
k,i
(s
i
, a
i
) + α
k
∗
R
k,i
(s
i
, a
i
) +
γ
N
N
∑
j=1
max
a
j
Q
k, j
s
′
i
, a
j
!
(1)
As noted in (Guo and Meng, 2010), Q
k+1,i
(s
i
, a
i
)
represents the new Q-value of the i
th
agent after exe-
cuting action a
i
at state s
i
and receiving the immediate
reward R
k,i
(s
i
, a
i
). α is the learning rate, γ is the de-
caying factor and N is the neighbors’ number of the
i
th
agent.
As to the action selection strategy, the Boltz-
mann policy (Coggan, 2004) was applied in (Guo and
Meng, 2010). At any state s, action a is selected ac-
cording to the following probability:
e
Q(s,a)
T
∑
a
e
Q(s,a)
T
(2)
where T, called temperature, decreases over time
according to the rule of T =
T0
b+1
. b is the number of
tasks being finished by an agent.
According to Eq.1, the experiences of neighboring
agents is incorporated into the Q-value of the i
th
agent
through a weighted linear combination of their state
values. So, each agent can learn from the previous
experiences of its neighbors. However, these incor-
poration isn’t always advantageous. In the contrary,
the following problems can occur when applying the
D-DCM-MultiQ method:
• Impossible cooperation in the case of obstacle
avoidance scenario: If an agent A
1
hits an ob-
stacle and gets a penalty, it saves this experience
into its state value. When the same scenario oc-
curs to another agent A
2
and agent A
1
is within its
neighborhood, A
2
can’t profit from the previous
experience of its neighbor to avoid that obstacle
since the multi-agent cooperation is only available
when updating a state-action pair (s, a). However,
according to the RL concept, this update is only
occurring after experiencing the action a in the
state s. A
2
could take advantage of prior knowl-
edge of its neighbor A
1
if the cooperation was in-
corporated in the choice of the next action to per-
form, but this was not the case of the Boltzmann
policy.
• Blockage of learning: By exploiting the knowl-
edge of its neighbors when updating each state/
action pair, an agent can spread promising in-
formation (related to the food source) to inter-
mediate states even before detecting the target.
This will lead to a non-continuous spread of the
goal’s reward from the food source to the nest
area. The agent can then trap between two inter-
mediate states because only its own information
is used when choosing the next action to perform.
As the Boltzmann temperature decreases, the ex-
ploration rate also decreases and the opportunity
to reach the target becomes increasingly difficult.
This blockage is indeed due to an insufficient co-
ordination between agents. Increasing exploration
can solve these situations but prevents the system
from constantly taking the best solution after con-
vergence.
In the next section, we will present our sug-
gestions to overcome these impasses, especially the
proposition of a cooperative action selection strategy
and the introduction of a new form of agent, called
”relay agent”, to improve the information exchange
between learners.
4 OUR PROPOSALS FOR
IMPROVING MULTI-AGENT
COORDINATION
When using the Qvalues of all existing agents in
the neighborhood, some of these values may be not
promising before the convergence of the learning al-
gorithm. For a better backward propagation of the
goal’s reward, a useful update of the Qvalue can be
obtained by using only the information of the agent
having the highest Qvalue in the next state. In this
case, equation (1) becomes:
Q
k+1,i
(s
i
, a
i
) = (1− α
k
)Q
k,i
(s
i
, a
i
) + α
k
∗
(R
k,i
(s
i
, a
i
) + γmax
a
′
(max
j
Q
k, j
s
′
i
, a
′
)) (3)
where agent j refers to agent i or one of its neigh-
bors.
Multi-agent Coordination using Reinforcement Learning with a Relay Agent
539

4.1 First Proposal: A Cooperative
Action Selection Strategy
To ensure that each agent gets the most out of its
neighborhood information, one possible solution is to
exploit this information in the action choice in addi-
tion to when updating the state/action values. Thus,
each agent chooses the next action to perform based
on its own information as well as the information of
its neighbors.
As a result, a new cooperative action selection
strategy, called CG-LRVS (Cooperative Greedy pol-
icy based on Least Recently Visited States), is pro-
posed. It’s defined by Eq.4.
action
CG−LRVS
=
argmax
a
Q
∗
(s, a) with probability ε
argmax
a
Q
∗
(s, a) and
leadingtotheleast
recentlyvisitedstate with probability (1− ε)
(4)
where
|Q
∗
(s, a) | = max
rob
|Q
rob
(s, a)| (5)
and rob refers to each agent in the communication
range, including the agent itself.
For each pair (s, a), max
rob
|Q
rob
(s, a)| refers to
the largest absolute value of Q(s, a) of all agents in
the neighborhood. Once the agent selects the most re-
liable Qvalue of each available action in the current
state s (Q
∗
(s, a
1
), ..., Q
∗
(s, a
p
)) by using the absolute
value and exploiting the information of all its neigh-
borhood, it then applies the Boltzmann policy to se-
lect an action among all available ones.
The absolute value is particularly considered in or-
der to determine the action leading to an obstacle that
has already been tested by at least one agent. Thereby,
this obstacle can be avoided without being really ex-
perimented, which makes possible the cooperation in
the case of obstacle avoidance scenarios. The follow-
ing scenario is presented for further explanation:
Consider that a penalty of −90 is received by an
agent if it hits an obstacle and (s
i
, a
i
) is a state/action
pair leading to a collision. At time step t, an
agent R
1
is in the state s
i
and has a neighboring
agent R
2
; If the transition (s
i
, a
i
) is already exper-
imented by R
1
(Q
R1
(s
i
, a
i
) = −90) and not yet by
R
2
(Q
R2
(s
i
, a
i
) = 0). Without using absolute val-
ues, max
a
(Q
R1
(s
i
, a
i
), Q
R2
(s
i
, a
i
)) = max
a
(−90, 0) =
0. As a result, R
1
can choose the action a
i
and
make a bad decision in spite of its previous knowl-
edge. On the contrary, by using the absolute
value, max
rob
(|Q
R1
(s
i
, a
i
)|, |Q
R2
(s
i
, a
i
)|)= max
rob
(| −
90|, |0|) = 90. R
1
will consider that the transition
(s
i
, a
i
) has a value of −90 (Q
∗
((s
i
, a
i
) = −90). The
probabilityassigned to this transition, using the Boltz-
mann policy, will be lower than some other transitions
(s
i
, b). Consequently, R
1
will avoid this obstacle and
chooses a more trusted action in that state.
The same scenario will take place if this transition
is already experimented by R
2
(Q
R2
(s
i
, a
i
) = −90)
and not yet by R
1
(Q
R1
(s
i
, a
i
) = 0): By exploiting the
knowledge of R
2
, R
1
will avoid the obstacle without
the need to experiment it before.
Finally, as explained in our previous work
(Zemzem and Tagina, 2015), exploiting least recently
visited states accelerates learning since it encourages
the agent to visit new and distant areas. This exploita-
tion is possible using a new table Anc : S 7→ N storing
the last visit of each visited state. Anc(s) = t means
that the last visit of the state s was occurred at the
learning iteration t. Each agent i saves one table Anc
and updates it as follows:
For each pair (s,a) ∈ S × A: Anc(s, a) = Anc
j
(s, a),
where j refers to the same agent or one of its neigh-
bors having the largest value of Anc(s, a) (see Eq.6).
j = argmax
agent
(Anc
agent
i
(s, a), Anc
neighbor
i
1
(s, a),
..., Anc
neighbor
i
n
(s, a)) (6)
4.2 Limits of Cooperative Action
Selection Strategies
Because of the limited communication range, each
agent can’t take advantage of promising information
of another agent unless it is within its neighborhood.
As a result, even by using cooperativeaction selection
strategy, the blockage still occur in the limits of the
communication range and can’t be solved if the other
agent is waiting at the food source. Other blocking
situations can occur during intermediate episodes (not
the first one) after the propagationof the goal’s reward
to several non-consecutive states. In that case, all
learning agents can trap between intermediate states
before reaching the target and remain at this situation
since no other agent can help them. Fig. 1 illustrates
this scenario. In this example, the communication
range is set to 3.
4.3 Second Proposal: Adding a ”Relay”
Agent
Our objective is to solve the problem of blockage
while maintaining the same properties of the D-DCM-
MultiQ approach namely, a model-free method and a
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
540

Figure 1: Failings of the first proposal.
local communication range. To this end, we propose
to use a ”relay” agent storing the Qvalues functions
of all learning agents. Whenever a learning agent is
in the neighborhood of the relay agent, it transmits
its new function values to this relay agent. Thus, the
relay updates its old knowledge. Conversely, when
choosing the next action to perform, each learning
agent exploits, in preference, the information of the
relay if it is in its neighborhood. Otherwise, it uses the
knowledge of the neighboring learners. In the worst
case, if the neighborhoodis empty, the agent uses only
its own function values Q. Thus, by adding a ”relay”
agent, a learning agent can take advantage of promis-
ing information from another agent not necessarily in
its communication range. The same procedure is ap-
plied when updating the table Q and the table Anc (in
Eq. 3 and Eq6, j refers to the relay else neighboring
learners and in the worst case to the agent itself).
By this way, the blockage will be solved only in
the area inside the communication range of the relay.
As the relay’s communication is also limited, fixing
the relay in a specific position is not promising; a
learning agent may be trapped between several states
that are not all covered by the relay nor by other learn-
ers. A better alternative is that, at each learning step,
the relay moves randomly and communicates with its
neighboring learners to update its stored information.
Using a moving relay, the blockage will be solved
whatever the size of the environment, the communi-
cation range and the number of learning agents. This
will be further explained in the experimental Section.
To avoid the storage of the Qtables of all learn-
ers, a reduction in the size of the relay’s informa-
tion is possible by retaining a single Qvalue for each
state/action pair, like a learning agent. For each pair
(s, a) ∈ S × A, the update of Q by the relay is then as
follows: Q(s, a) = Q
j
(s, a), where j refers to the relay
or one of the neighboring learners having the largest
absolute value of Q(s, a) (see Eq. 7).
j = argmax
r
(|Q
relay
(s, a)|, |Q
neighbor
1
(s, a)|, ...,
|Q
neighbor
n
(s, a)|) (7)
4.4 Algorithms’ Summary
Fig. 2 describes the learning procedure. Compared
to D-DCM-MultiQ, the novelty is in using the CG-
LRVS policy (Eq.4) for the action choice, the up-
date of the Q-value using only the information of the
agent having the highest Q-value in the next state
(Eq. 3), in addition to a slight modification in the ex-
ecution of learning steps so that the learner uses the
same neighboring information to update the last expe-
rienced state/action pair as well as to choose the next
action to perform.
Figure 2: The pseudo code of the learner’s behavior.
The relay agent doesn’t use a learning approach.
Fig. 3 describes how it acts at each learning step.
Multi-agent Coordination using Reinforcement Learning with a Relay Agent
541

Figure 3: The pseudo code of the relay’s behavior.
5 EXPERIMENTS AND ANALYSIS
In this Section, we will evaluate the impact of our pro-
posals on distributed multi-agent decision-making.
As described earlier, the testing scenario is a coopera-
tive foragingtask with a static target. We aimto evalu-
ate the performance of our learning method in a wide
unknown environment. While the experiences done
in (Guo and Meng, 2010) are restricted to a 10 × 10
grid world, several experiences will be conducted in
what follows with varying the environment size, the
limit of the communication and the number of learn-
ing agents. The largest tested environnement contains
61 × 61 cells. It is then more than 37 times larger
than the environment which is considered in (Guo and
Meng, 2010).
The testing environment is simulated using Sim-
bad, a Java 3d robot simulator (Hugues and Bredeche,
2006). A 30× 30 grid world is shown in Fig. 4. The
cell, called the nest, is the starting position. A ball,
situated at the bottom right corner, refers to the food.
The maze is surrounded by walls and contains obsta-
cles.
For all performed experiments, the Q-value of
each agent is setup to be zero initially. The explo-
ration rate is defined as ε = 0.5. γ and α are de-
fined as 0.9 for all agents. The neighborhood range
is set at
Grid
Width
3
for each agent. This means that two
agents can communicate when the distance between
them is less than
Grid
Width
3
cells (using the Manhattan
distance). It is assumed that agents can localize them-
selves within the grid map but they don’t know where
the target and obstacles are. The action set for each
agent are defined as ”up”, ”right”, ”down” and ”left”.
Since it is a grid-based environment, we define the
actual position of the agent as its state variable. We
assume that every grid is large enough to contain sev-
eral agents at the same time. These parameter settings
and assumptions are used in (Guo and Meng, 2010) to
evaluate the D-DCM-MultiQ algorithm. Note that all
conducted experiences in the rest of the paper contain
only one relay which moves randomly and the size of
the multi-agent system corresponds to the number of
learning agents.
Figure 4: A 30× 30 grid world.
Finally, as we deal with a large state space, sev-
eral experiences have been made while varying the
goal’s reward and the best reward distribution is then
adopted. It is defined as follows: r = 0 for regular ac-
tions, r = −90 for actions resulting collision with ob-
stacles and r = 18000 for actions leading to the food
source.
5.1 Result 1: The Impact of
Cooperative Action Selection on the
Learning Performance
In this Section, the proposed CG-LRVS policy (Eq. 4)
is evaluated. For that, two systems of three learning
agents are compared with varying the number and na-
ture of agents that cooperate when selecting actions in
each system:
• 1
st
system using a cooperative action selection
procedure (the agent exploits the relay’s informa-
tion if it’s within its neighborhood else all oth-
ers neighboring learners’ information and in the
worst case, only its own information) and a coop-
erative update of Q (Eq. 3).
• 2
nd
system using a cooperativeupdate of Q (Eq. 3)
but without a cooperative action selection proce-
dure (the agent uses only its own information).
As described earlier, a minimum of cooperation
in the action selection policy must be satisfied in
order to avoid blocking situations and allow the
completion of the foraging task. For that, we keep
only one situation of cooperation between agents:
it’s when the relay and the learner are in the same
cell.
As shown in Fig. 5-a, learning is accelerated
through cooperative decisions. By exploiting more
knowledge in the choice of the next action to perform,
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
542
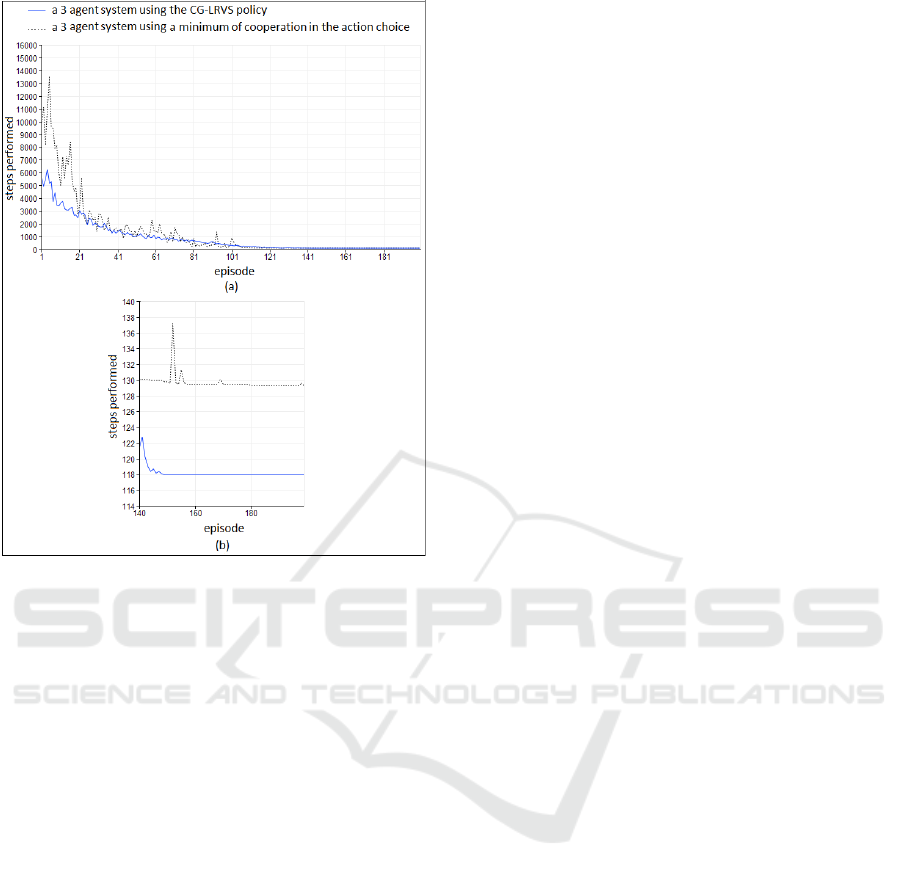
Figure 5: The average number of time steps needed on each
episode over time, with varying the level of cooperation dur-
ing the selection of actions (average of thirty experiences).
the chance to detect the food source at the earliest pos-
sible opportunity is increased and the length of learn-
ing episodes is therefore reduced. Moreover, com-
paring the learning curves in Fig. 5-b, the constructed
path is less efficient when decreasing the cooperation
level between agents: the agent doesn’t benefit from
other neighbors’ knowledge to optimize its own path.
That’s why the agents’ trajectories are often different
and haven’t the same length.
5.2 Result 2: The Impact of Modifying
the Size of the Environment, the
Number of Learning Agents and the
Communication Range on the
Learning Performance
It is of interest to understand the impact of modifying
the size of the environment, the number of learning
agents as well as the range of communication on our
proposed learning method. Specifically, we intend to
determine how the learning performance evolves in
addition to how the communication frequency is af-
fected.
To do that, several experiments are carried out
with varying the aforementioned elements. In each
experiment, results are calculated over 30 runs. The
reward is defined as {−90, 0, 18000}.
The communication frequency measures how of-
ten information are transferred from one agent to an-
other. For each agent (relay and learner), the commu-
nication frequency (resp. Com-Freq-Relay and Com-
Freq-Learner) increases by 1 communication unit af-
ter receiving information from another agent. The
communication frequency of the entire system (Com-
Freq-System) is calculated by summing up the com-
munication frequency of all its agents.
We note that the communication frequency is only
recorded during the foraging phase. From the be-
ginning of learning, the relay moves randomly and
exchanges information with its neighboring learners.
Once the food source is reached by all learners and the
ferrying phase is started. Learning agents no longer
communicate with the relay. This latter remains mo-
tionless and stops communicating with its neighbors
until it is interrogated by one learning agent, which
means the beginning of a new foraging phase.
5.2.1 Learning Performance
Table. 1 records the conducted experiments, the num-
ber of episodes and the average number of time steps
required for the convergence of the system in each
studied case.
It can be seen that, regardless of the size of the
environment and the limit of the communication, the
number of episodes and time steps needed before
finding the optimal solution is decreased by increas-
ing the number of agents. Learning is also accelerated
by increasing the communication range; In the case of
the 30 × 30 grid world and with the same number of
agents, learning is expedited by raising the value of
the communication range. The same holds true for
the 61× 61 grid world.
5.2.2 Impact of Increasing the Communication
Range on the Communication Frequency
In this section, we aim to study the impact of increas-
ing the communication range on the communication
frequency. For that, two systems of several agents are
tested:
• In the 1
st
system, a 30 × 30 grid world is consid-
ered with varying the communication range from
5 to 10. The results are shown in Fig. 6.
• In the 2
nd
system, a 61× 61 grid world is consid-
ered with varying the communication range from
10 to 20. The results are shown in Fig. 7.
After increasing the communication range (to 10
in the 1
st
system and to 20 in the 2
nd
one), we note
Multi-agent Coordination using Reinforcement Learning with a Relay Agent
543
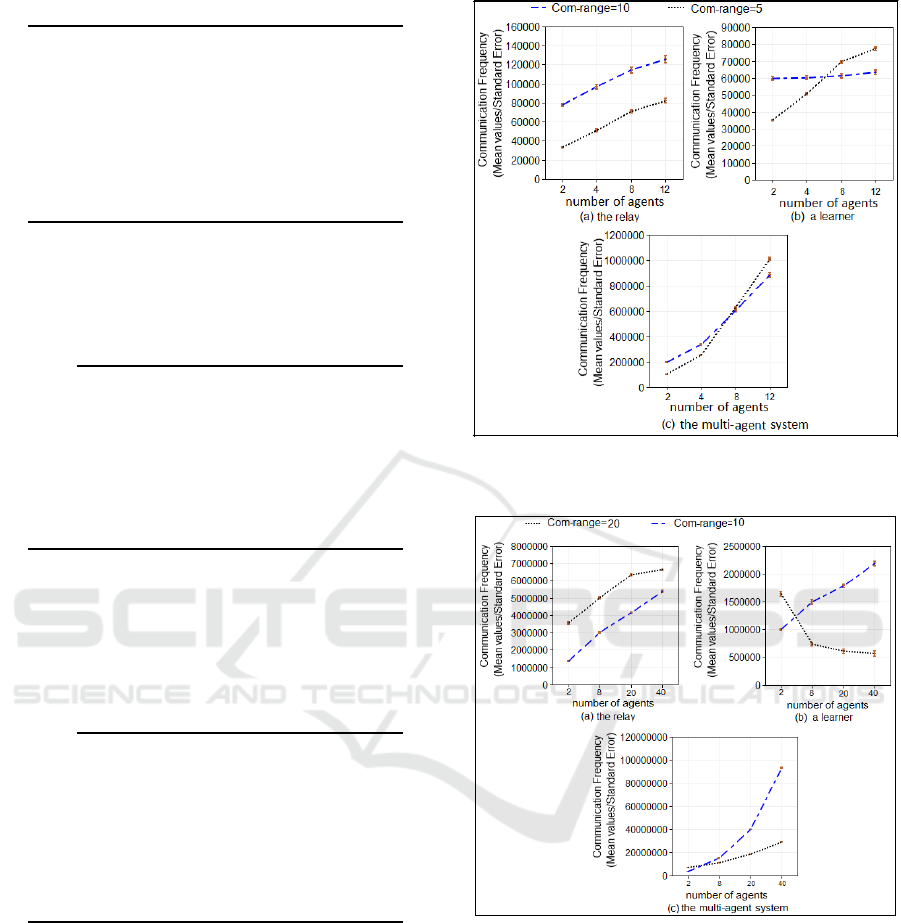
Table 1: This caption has one line so it is centered.
Marge
Com-
mu-
ni-
ca-
tion
Grid
Size
Num-
ber
of
learn-
ing
agents
Episodes
neces-
sary
for
con-
ver-
gence
Average
number of
time steps
needed for
convergence
(Mean val-
ues/Standard
error)
5
10× 10
2 24
3858.533±
88.33
4 14
2392.566±
60.611
8 8
1446.666±
41.632
30× 30
2 246
270440.566±
4141.963
4 158
208745.233±
3597.89
8 102
155556.566±
3473.187
12 74
122650.233±
2753.296
10
30× 30
2 189
215807.9±
3796.626
4 94
133714.566±
2745.421
8 54
79230.833±
1648.466
12 35
59355.966±
1352.006
61× 61
2 468
3.995·10
6
±
22891.716
8 208
2.314·10
6
±
18597.436
20 108
1.38· 10
6
±
13473.187
40 71
0.898·10
6
±
10298.942
that, in both cases, the difference between Com-Freq-
Relay and Com-Freq-learner becomes much greater
and that Com-Freq-Relay increases significantly by
extending the number of agents, contrary to Com-
Freq-learner which increases much smaller in the 1
st
system (Fig. 6-a and Fig. 6-b) and even decreases in
the 2
nd
one (Fig. 7-a and Fig. 7-b).
According to Fig. 6-b, we can see that in the case
of a 30 × 30 grid world, the increase of Com-freq-
learner is much smaller with Com-range=10 than that
with Com-range=5. Moreover, when the number of
learning agents exceeds 7, Com-Freq-Learner using
Com-range=10 is less than that using Com-range=5.
Figure 6: The impact of increasing the range of commu-
nication in the communication frequency (average of thirty
experiences in a 30× 30 grid world).
Figure 7: The impact of increasing the communication
range in the communication frequency (average of thirty ex-
periences in a 61× 61 grid world).
As a result, the communicationfrequencyof the entire
system is also decreased while the learning is accel-
erated. Fig. 6-c illustrates this result; if number-of-
agents> 7:
Com-Freq-Sys(Com-range=10)<Com-Freq-
Sys(Com-range=5)
The same holds true for the 61 × 61 grid world.
According to Fig. 7, we can see that with Com-
range=20, Com-Freq-Learnerdecreases by increasing
the number of learners. This is because the commu-
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
544

nication with the relay is more favored which makes
the cooperation more efficient. As a result, when the
number of learning agents exceeds 4, the communica-
tion frequency of the entire system is also decreased
while the learning is speeded up.
This justifies again why our method outperforms
those storing all agents’ Qtables by each learner, as
EC (Cunningham and Cao, 2012) and PA (Tan, 1997).
Using these latter methods, each learning agent com-
municates with all its neighbors which will always
lead to the increase of Com-Freq-Sys. The gain made
by our proposed method is not limited to the commu-
nication frequency but other savings in memory and
computation are also ensured due to the decrease of
information saved and updated by each learner.
6 CONCLUSION AND FUTURE
WORKS
In this paper,a new distributed RL method for cooper-
ative multi-agent systems is proposed. Its is based on
a cooperative action selection policy and a relay agent
that accelerate learning and ensure a good multi-agent
coordination. However, to ensure an effective shar-
ing of information, this method ignores collisions be-
tween agents. We expect to further improve our work
by eliminating this restrictive assumption and trying
more complex scenarios. Possible test cases include
stochastic mazes (rather than deterministic mazes),
several targets, as well as continuous state spaces.
Real-world applications are usually characterized by
these complex elements.
ACKNOWLEDGEMENTS
This research received no specific grant from any
funding agency in the public, commercial or not-for-
profit sectors.
REFERENCES
Bruno C. Da Silva, Eduardo W. Basso, Ana L. C. Bazzan,
P. M. E. (2006). Dealing with non-stationary environ-
ments using context detection. In the 23rd Interna-
tional Conference on Machine Learning, pages 217–
224. ACM Press.
Coggan, M. (2004). Exploration and exploitation in re-
inforcement learning. Research supervised by Prof.
Doina Precup, CRA-W DMP Project at McGill Uni-
versity.
Cunningham, B. and Cao, Y. (2012). Non-reciprocating
Sharing Methods in Cooperative Q-Learning Environ-
ments. In 2012 IEEE/WIC/ACMInternational Confer-
ences on Web Intelligence and Intelligent Agent Tech-
nology, pages 212–219. IEEE.
Guo, H. and Meng, Y. (2010). Distributed Reinforcement
Learning for Coordinate Multi-Robot Foraging. Jour-
nal of Intelligent and Robotic Systems, 60(3-4):531–
551.
Hugues, L. and Bredeche, N. (2006). Simbad: An Au-
tonomous Robot Simulation Package for Education
and Research. In International Conference on Simula-
tion of Adaptive Behavior, volume 4095, pages 831–
842. Springer Berlin Heidelberg.
Partalas, I., Feneris, I., and Vlahavas, I. (2008). A hy-
brid multiagent reinforcement learning approach us-
ing strategies and fusion. International Journal on
Artificial Intelligence Tools, 17(05):945–962.
Tan, M. (1997). Multi-agent reinforcement learning: in-
dependent vs. cooperative agents. In the tenth inter-
national conference on machine learning, pages 330–
337. Morgan Kaufmann Publishers Inc.
Torrey, L. and Taylor, M. E. (2012). Help an agent out:
Student/teacher learning in sequential decision tasks.
In Proceedings of the Adaptive and Learning Agents
Workshop 2012, ALA 2012 - Held in Conjunction with
the 11th International Conference on Autonomous
Agents and Multiagent Systems, AAMAS 2012, pages
41–48.
Zemzem, W. and Tagina, M. (2015). Cooperative multi-
agent learning in a large dynamic environment. In
Lecture Notes in Computer Science, chapter MDAI,
pages 155–166. Springer.
Multi-agent Coordination using Reinforcement Learning with a Relay Agent
545
