
Weaknesses of Ant System for the Distributed Job Shop Scheduling
Problem
Imen Chaouch
1,2
, Olfa Belkahla Driss
1,3
and Khaled Ghedira
1,4
1
COSMOS Laboratory, Universit
´
e de la Manouba, La Manouba, Tunisia
2
Ecole Nationale des Sciences de l’Informatique, Universit
´
e de la Manouba, La Manouba, Tunisia
3
Ecole Sup
´
erieure de Commerce de Tunis, Universit
´
e de la Manouba, La Manouba, Tunisia
4
Institut Sup
´
erieur de Gestion de Tunis, Universit
´
e de Tunis, Tunis, Tunisia
Keywords:
Ant System, Distributed, Job Shop, Makespan, Scheduling, Multi-factory.
Abstract:
Globalization has opened up huge opportunities for the plant and industrial investors. The problem of single
plant is now more generalised, namely, multi factory problem. This paper deals with the problem of Distributed
Job shop Scheduling in multi-factories. The problem solving process consists of finding an effective way to
assign jobs to factories then, to generate a good operation schedule. To make this, an Ant System algorithm
is implemented. Several numerical experiments are conducted to evaluate the performance of the Ant System
algorithm applied to the Distributed Job shop Scheduling, and the results show the shortcoming of the standard
Ant System algorithm compared to developed algorithms in the literature.
1 INTRODUCTION
The manufacturing industry has undergone an impor-
tant evolution these recent years due to the trend of
globalisation. Owing to this evolution, there have
been significant changes in the structure of produc-
tion plants. Industrial companies are increasingly
merging to distributed ones and thus, the structure
of their shops changes from simple configurations to
distributed ones. This system enables firms to in-
crease their competitiveness and responsiveness in the
global markets (Karimi and Davoudpour, 2017). Dis-
tributed workshops are becoming a popular thematic
to study in the field of scheduling problems : Dis-
tributed Flow shop ( (Naderi and Ruiz, 2010), (Gao
and Chen, 2011), (Bargaoui et al., 2016), etc.), Dis-
tributed Job shop ( (Jia et al., 2007), (Naderi and
Azab, 2015), etc.).
In this paper, we focus on the Distributed Job shop
Scheduling Problem (DJSP), which can be considered
as an extension of the simple Job shop Scheduling
Problem (JSP). It can be treated as a set of f fac-
tories, which are geographically distributed in dif-
ferent areas. Each factory contains m machines on
which certain number of jobs have to be processed. A
generic representation can be seen in figure.1. Dis-
tributed Scheduling problems in multi-factory pro-
duction are much more complicated than classical
scheduling problems (Chung et al., 2009) since two
decisions have to be taken: allocating jobs to suitable
factories and sequencing the operations on machines
so that yield a feasible schedule aiming to minimize
one or more predefined performance criteria.
In this work, we seek to minimize the maxi-
mum completion time (makespan, denoted as C
max
)
of DJSP, which is the maximum makespan among all
factories using an Ant System algorithm.
(Garey et al., 1976) proved that the JSP is strongly
NP-hard. Hence, the DJSP is ordinarily NP-hard and
the case of the simple JSP can be obtained when f =
1.
In this paper, we focus our attention on the DJSP
in multi-factories assuming that all factories are iden-
tical due to the complexity of the problem in such a
system. The rest of the paper is organized as follows.
Section 2 gives the specifications of the DJSP. Then a
short literature review of the limited existing literature
on DJSP is provided. Section 3 proposes an effective
way to assign jobs to factories and sketches the pro-
posed Ant System algorithm. Section 4 conducts the
numerical experiments. Finally, Section 5 concludes
the paper and suggests few future research directions.
574
Chaouch, I., Driss, O. and Ghedira, K.
Weaknesses of Ant System for the Distributed Job Shop Scheduling Problem.
DOI: 10.5220/0006332405740581
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 574-581
ISBN: 978-989-758-247-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

2 PROBLEM STATEMENT AND
STATE-OF-THE-ART
Scheduling problems have become a popular issue for
researchers and industrialists in the last three decades,
particularly the JSP since it is one of the most difficult
tasks. (Colorni et al., 1994), (Dell’Amico and Tru-
bian, 1993), (Adams et al., 1988) and (Davis, 1985)
are pioneer researches in the literature that dealt with
the JSP. Recently, the JSP has evolved from the simple
configuration with one factory to the Distributed one
and becomes increasingly, one of the most important
issues to raise.
The DJSP can be stated as follows: a set J =
{
j
1
... j
n
}
of independent jobs, each of which consists of an or-
dered set of operations. Each operation must be exe-
cuted on a specific machine from a set M =
{
i
1
...i
m
}
of machines geographically distributed on f identi-
cal factories. The main objective of the problem is
to find an optimal scheduling minimizing a speci-
fied criterion which is generally time related such as
makespan, maximum tardiness or total tardiness. In
our case, we are aiming to minimize the maximum
completion time (makespan) among all factories.
There are various constraints on both jobs and ma-
chines. The DJSP entails the following assumptions:
• All jobs are independent and available for pro-
cessing at time 0 and all machines are continu-
ously available.
• Once a job is assigned to a factory it cannot be
transferred to another factory as the remaining op-
erations must be completed in the same plant.
• All factories are able to process all jobs.
• There are no precedence constraints among the
operations of different jobs.
• Each operation needs to be processed during an
uninterrupted time of a fixed processing period
and a given machine.
• A job can be processed by at most one machine at
a time and a machine can process at most one job
at a time.
• It is assumed that a job does not visit the same
machine twice and neither the release times nor
due dates are specified.
• Setup times of machines and transit times between
operations are negligible.
The following example will make the idea clear
about the representation of the problem. Consider a
DJSP with f = 2, n = 6 and m = 2. The processing
time matrix is shown in table 1. A feasible Gantt chart
of this problem is shown in figure 2. Makespan in fac-
tory 1 is 17 and makespan in factory 2 is 15, leading to
the conclusion that the makespan of this DJSP is equal
to the maximum makespan between the two factories,
which is 17.
Table 1: Processing time matrix.
Job Machine Processing Route
1 2
1 4 7 {1,2}
2 6 6 {2,1}
3 5 6 {2,1}
4 6 4 {1,2}
5 3 5 {2,1}
6 4 4 {2,1}
Researchers are beginning to study the DJSP re-
cently. We can find Jia et al. (Jia et al., 2002) which
have studied the DJSP and proposed a Genetic Al-
gorithm (GA) approach in order to facilitate collabo-
ration between geographically distributed plants. In
their next paper, to solve the same problem in a multi-
factory network, authors in (Jia et al., 2003) presented
a Modified Genetic Algorithm (MGA) in which two-
step encoding method was used to encode the factory
candidates and to affect jobs and operations. Later
(Jia et al., 2007), they refined their previous approach
and proposed a GA integrated with Gantt Chart (GC)
to derive the factory combination and schedule.
Recently, the problem of DJS have been math-
ematically formulated by Naderi and Azab (Naderi
and Azab, 2014) with two different Mixed Inte-
ger Linear Programming models (MILP). In addi-
tion, three well-known heuristics were first adapted
to the problem; these are Shortest Processing Time
first (SPT), Longest Processing Time first (LPT) and
Longest Remaining Processing Time (LRPT). Then,
three Greedy Heuristics have been deployed (GH1,
GH2 and GH3). In their next paper (Naderi and Azab,
2015), authors have differently treated the problem.
Different forms of a developed simulated annealing
have been designed and implemented and to further
improve the algorithm, two additional mechanisms of
local search and restart phase were designed. The al-
gorithm has been hybridized as well with a greedy
heuristic.
Weaknesses of Ant System for the Distributed Job Shop Scheduling Problem
575

Figure 1: An outline of a typical Distributed Scheduling problem. f factories with m machines, on which jobs have to be
processed.
Figure 2: Gantt Chart of the Distributed Job shop Schedul-
ing Problem.
3 THE PROPOSED ANT SYSTEM
ALGORITHM
3.1 Job-factory Assignment
A crucial step in solving the DJS problem is the
allocation of jobs to suitable factory. The objective
is to partition jobs into factories so as to equilibrate
the workload in different factories. In our approach,
we use the job-facility assignment rule introduced in
(Naderi and Azab, 2014). As first step, the workload
on each machine is separately calculated using the
following rule (1), which is defined for each job j on
each machine i as follows:
workload( j, i) =
∑
k∈R
j,i
p
j,k
!
+ p
j,i
∀
i, j
(1)
Where R
j,i
is the set of all machines preceding
machine i in the processing of job j and P
j,i
is the
processing time of job j on machine i.
The Workload of each operation is calculated and
regarding the total workloads, the jobs are ranked in
descending order, from highest workload to the low-
est ones. Suppose that we have f factories. The n first
jobs are assigned to factories
{
1...n
}
, respectively.
The workload of machines on different factories be-
comes equal to those of the assigned jobs and the
maximum workload in the f factories is determined.
To assign the next job, the maximum workload is
calculated if the job is assigned to a factory. All the
possibilities should be enumerated and the workload
is calculated at each time. Then, the job is assigned
to the factory with minimum of the maximum work-
load. The procedure repeats for subsequent jobs until
all jobs are assigned. To better illustrate this concept,
it is applied to the previous example with 2 factories,
6 jobs and 2 machines (Table 1). The Workload of
each operation is shown in Table 2.
Table 2: The workload of the example.
Job Machine Total Rank
1 2
1 4 11 15 4
2 12 6 18 1
3 11 6 17 2
4 6 10 16 3
5 8 5 13 5
6 8 4 12 6
Regarding the total workloads, the jobs are ranked
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
576
(2, 3, 4, 1, 5, 6). The two first jobs (jobs 2 and 3) are
assigned to factories 1 and 2, respectively. The work-
load of machines 1 and 2 on the first factory becomes
12 and 6, respectively. The workload of machines 1
and 2 on the second factory becomes 11 and 6, re-
spectively. Thus, the maximum workload in factories
1 and 2 are 12 and 11, respectively. To assign the next
job (job 4), the maximum workload is calculated. If
job 4 is assigned to factory 1, the workloads become
18 and 16 while if it is assigned to factory 2, we have
workloads of 17 and 16. The maximum workload of
factories 1 and 2 are 18 and 17, respectively. There-
fore, job 4 is assigned to factory 2. The procedure
repeats for subsequent jobs.
This method proved to be efficient to well equilibrate
workloads in different factories.
3.2 Ant System Applied to the DJSP
Once all jobs are affected to their corresponding fac-
tory, they need to be sequenced. To do this, Ant Sys-
tem algorithm is applied. It is important to mention
that this is the first time that the Ant System algo-
rithm is applied to DJSP since the thematic areas is
recent. As the name suggests, ant algorithms have
been inspired by the behavior of real ant colonies, in
particular, by their collective foraging behaviour. The
first Ant Colony System (ACS) was introduced by
Dorigo’s Ph.D. (Dorigo, 1992), which is called Ant
System (AS). The basic idea in AS is to imitate the
cooperative behavior of real ants to solve optimiza-
tion problems (Talbi, 2009). In the nature, ants are
able to find the shortest path between a food source
and their nest according to their collective behaviour.
During their move, they lay down a chemical trail
(pheromone) on the ground, which guides other ants
towards best path. In DJSP, the aim is to find the best
path giving the minimum makespan among all pos-
sible paths. The flowchart for the AS and the EAS
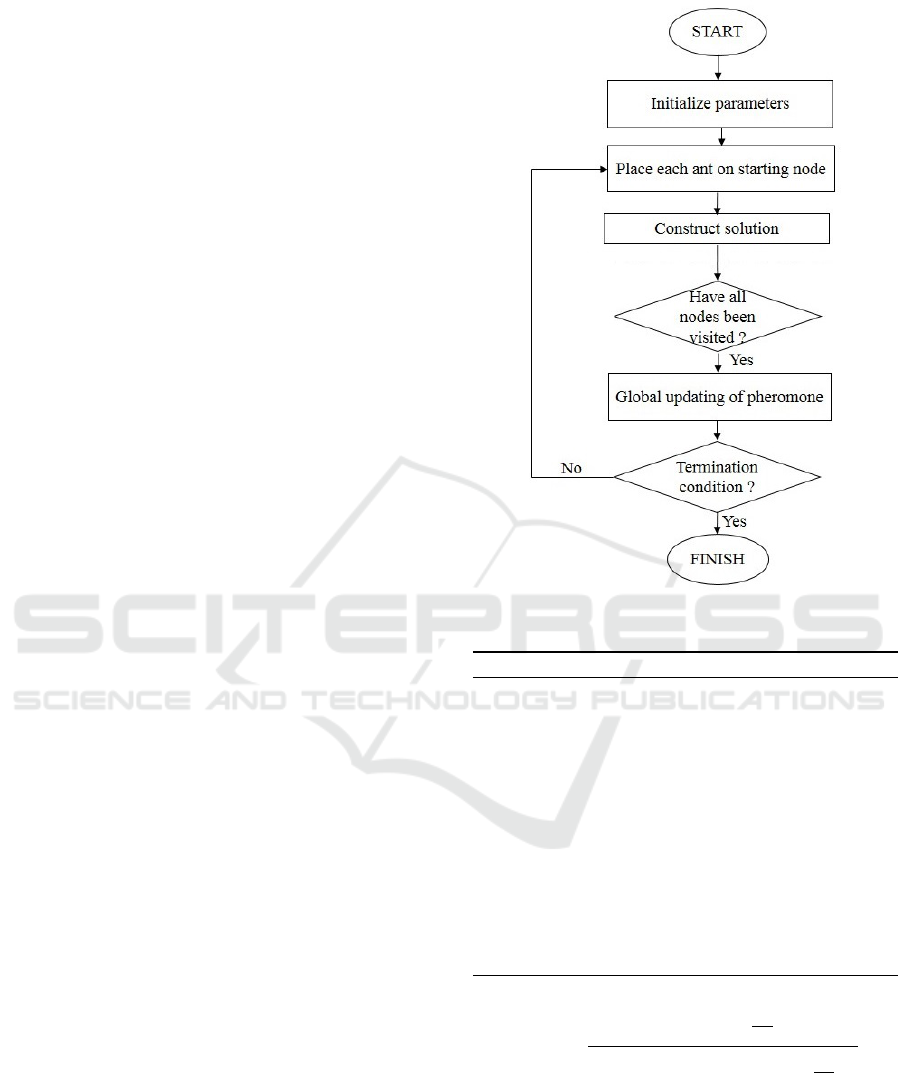
algorithms can be defined in Figure 3.
The algorithm below presents the generic ant al-
gorithm. The metaheuristic consists of a parameter
initialization step and mainly two algorithmic proce-
dures which are repeated until a stopping criteria is
reached, a maximum number of iterations in our case.
Constructing Solutions by Ants
The first procedure consists of a probabilistic con-
struction of solutions by all the ants according to the
State Transition Rule (2). The probability for an ant
to choose its next node is directed by both the amount
of pheromone on the route and heuristic distance from
its current location to the next one.
Figure 3: AS chart.
Algorithm 1: Ant System pseudocode.
Begin
Set parameters, initialize pheromone trails
While Stopping criterion not satisfied do
Position each ant in a starting node
Repeat
For each ant do
Choose next node by applying the state transition rule
End for
Until every ant has built a solution
Update best solution
Apply Global updating of pheromone
End While
End.
p(i, j)(t) =
[τ
i, j
(t)]
α
×
h
1
d
i, j
i
β
∑
j∈AllowedNodes
[τ
i, j
(t)]
α
×
h
1
d
i, j
i
β
(2)
with
• τ
i, j
quantity on pheromone between the node
i
and
node
j
• d
i, j
heuristic distance between node
i
and node
j
.
In our case, d
i, j
is the processing time of the oper-
ation.
Weaknesses of Ant System for the Distributed Job Shop Scheduling Problem
577

• p
i, j
probability to branch from node
i
to node
j
• The parameters α and β tune the relative impor-
tance in probability of the amount of pheromone
versus the heuristic distance.
Artificial ants can be considered as stochastic greedy
procedures that construct a solution in a probabilistic
manner by adding solution components to partial ones
until a complete solution is derived (Talbi, 2009).
In the general AS, the set of next operations for an
ant in node
i
to visit is all those not visited. Which is
not the case in the DJSP, choosing the next operation
should respect the operation precedence constraints.
Therefore, for each transition from a node
i
to node
j
,
the ant has to build its Allowed List containing the
operation that can visit.
Updating Pheromone
Once all ants generate a solution, the second pro-
cedure is applied which consist of updating the
pheromone trail using an updating rule (3).
τ
i, j
(t + n) = ρ × τ
i, j
(t) + ρ × ∆τ
i, j
(t + n) (3)
∆τ
i, j
(t + n) =
Q
BestC
max
ant
(4)
where:
ρ : evaporation coefficient ∈ [0, 1]
Q : Constant
The pheromone updating rule is applied in two
phases:
• An evaporation phase where a fraction of the
pheromone evaporates and decreases automati-
cally, so as to diversify the search procedure into
larger solution spaces.
• a reinforcement phase where each ant deposits an
amount of pheromone which is proportional to the
generated solutions
4 NUMERICAL EXPERIMENTS
Experimental results are conducted over two phases.
First, the developed AS algorithm is tested on the
classic FT03 (Fisher and Thompson, 1963) with f =
1, leading us to the case of the simple Job shop Prob-
lem. This phase shows that our solution is not only
relevant for the DJSP but also for the simple case
when f = 1, leading to the simple JSP. Then, some
experiments were conducted on well-known bench-
marks with different level of f proposed by (Fisher
and Thompson, 1963) and (Lawrence, 1984). In the
second phase, 80 instances of Taillard benchmark for
job shop (Taillard, 1993) are tested with different lev-
els of f ( f = 2, 3, 4, 5), summing up 320 instances and
compared with other algorithms in the literature. The
results described in the following sections have been
obtained on a personal computer with 3.4 GHz Intel
Core i7 and 8 GB of RAM memory.
4.1 Small Instances
4.1.1 Traditional Scheduling Problem
If there is one factory, the DJSP becomes a traditional
JSP. Our proposed algorithm is able to deal with the
traditional JSP because each job has the information
of selected factory ID, and this ID is always fixed and
set to 1. In other words, the total number of factories
is 1, that means that all jobs are affected to the same
factory and the job-factory assignment procedure is
omitted.
We apply here our algorithm on the instance FT03
(3 jobs, 3 machines) proposed by (Fisher and Thomp-
son, 1963) to measure the effectiveness of the pro-
posed algorithm for the traditional JSP (table 3) As
seen in figure 4, makespan obtained by the proposed
AS algorithm is 12 units which is the optimal value
obtained in the literature.
Table 3: Processing time matrix of the FT03.
Job Machine Processing Route
1 2 3
1 3 5 2 {2,3,1}
2 2 4 1 {1,2,3}
3 1 3 4 {1,3,2}
Figure 4: The resultant schedule of the encoded solution of
FT03 with f=1.
4.1.2 Distributed Scheduling Problem
To test the performance of the AS applied to the
DJSP on small instances, well-known benchmarks are
used with different level of f ((Fisher and Thomp-
son, 1963) and (Lawrence, 1984) ). Table 4 sum-
marizes the results obtained by our AS applied to
small instances. Unfortunately, there is no studies
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
578

in the literature using (Fisher and Thompson, 1963)
and (Lawrence, 1984) for the DJSP. For this purpose,
we have been content to cite our obtained results for
small instances without comparison with previous re-
searches. As we can see from table 4, AS is performs
well when the number of factories increases.
Table 4: Obtained C
max
of small instances using AS for
DJSP.
n m f = 2 f = 3 f = 4 f = 5
ft03 3 3 10 10 - -
ft06 6 6 48 47 47 47
ft10 10 10 1053 839 727 655
ft20 20 5 1254 986 789 667
la01 10 5 688 446 459 413
la02 10 5 628 456 394 394
la03 10 5 516 380 356 356
la04 10 5 527 397 421 370
la05 10 5 550 380 380 380
4.2 Large Instances
To test the performance of the AS applied to the DJSP
on large instances, we use those of Taillard bench-
mark for job shops (Taillard, 1993). This bench-
mark includes 8 combinations for n and m, and 10
instances for each combination. It sums up to 80
instances. Each instance is solved by different lev-
els of f ( f = 2, 3, 4, 5); thus, there are 320 instances.
First, the AS parameters are tuning and the best re-
sults are obtained with the parameters initialized as
α = 0.2, β = 0.8, ρ = 0.7, the number of iterations is
fixed at 2000. Table 5 shows the average RPD ob-
tained for the proposed AS applied to large instances.
For each instance, these results are calculated with the
maximum makespan among all factories. The perfor-
mance measure used in this research is Relative Per-
centage Deviation (RPD). It can be calculated as fol-
lows:
RPD =
Alg −Min
Min
× 100 (5)
where
• Alg is the makespan obtained by any of the algo-
rithm
• Min is the lowest makespan obtained for a given
instance.
Results are compared with six available algorithms,
GH3 proposed in (Naderi and Azab, 2014), SA, HAS,
Table 5: The RPD of the AS on large instances with differ-
ent level of f .
Instances 2 f 3 f 4 f 5 f Average
n m
15 15 75 39 4.3 -4.4 28
20 15 119 45 19 13 49
20 145 79 35 18 69
30 15 147 71 28 10 64
20 198 112 61 33 101
50 15 163 92 48 16 79
20 278 127 92 59 139
100 20 418 149 96 52 178
Table 6: The RPD of the AS compared with other algo-
rithms.
n m Algorithms
AS HSA SA GSA GA GH3
15 15 28 0.42 0.34 0.79 2.35 5.37
20 15 49 0.76 0.92 2.06 3.85 9.69
20 69 0.2 0.31 1.30 6.36 8.79
30 15 64 0.4 1.35 2.65 6.07 11.73
20 101 0.14 0.95 2.00 9.09 13.97
50 15 79 1.68 3.42 3.45 10.17 20.46
20 139 0.12 3.19 2.44 12.81 19.40
100 20 178 0.00 6.89 8.52 20.77 61.09
Average 88.46 0.46 2.17 2.90 8.93 18.81
GSA in (Naderi and Azab, 2015) and genetic algo-
rithm (GA) in (Jia et al., 2007). We should mention
that the RPD values of the SA, HAS, GSA and GA
are calculated by taken the best value given by the
algorithms as optimal value. In their paper, (Naderi
and Azab, 2015) didn’t mention the value of the ob-
tained makespan, that is why we consider the optimal
of (Taillard, 1993). Table 6 shows the results averaged
by the combinations of (n, m).
As we can see from table 6, AS provides worst re-
sults among the tested algorithms with average RPD
of 88, 46.
The reason for these poor results may be explained
by the fact that there is no local search included to
improve ant’s solutions or to guide the ants when ex-
ploring their space.
Figure 5 shows the average RPD of the tested al-
Weaknesses of Ant System for the Distributed Job Shop Scheduling Problem
579
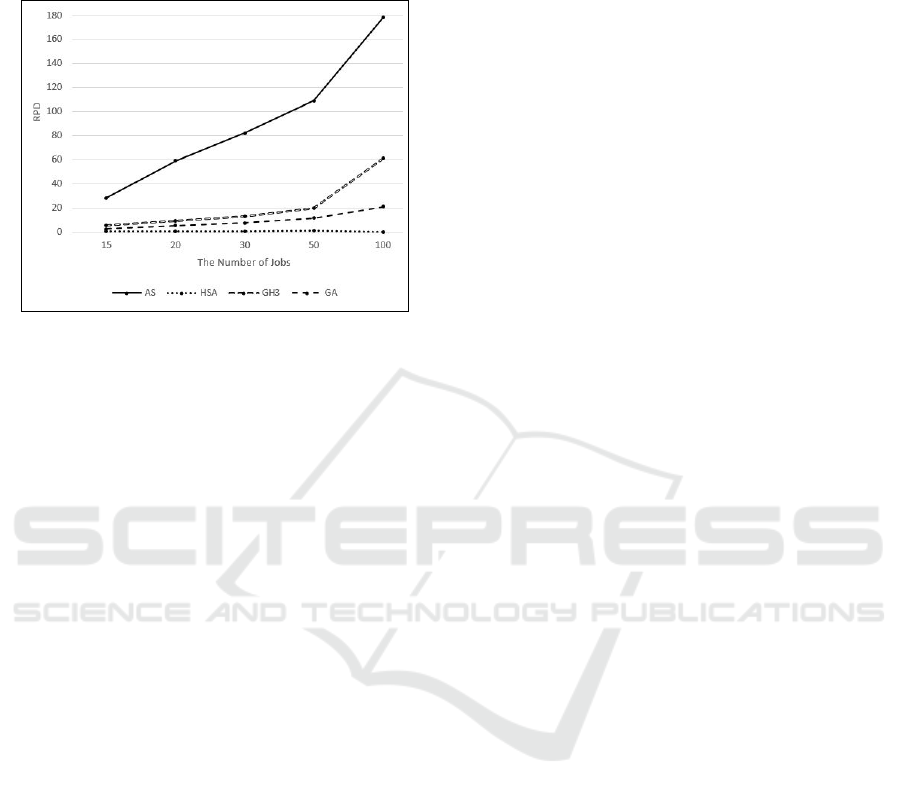
gorithms versus the number of jobs. It is interesting
to see that the Average RPD for almost all algorithms
increases with the number of jobs being increased.
Figure 5: The average RPD of the tested algorithms versus
the number of jobs.
Some initial results for small instances were en-
couraging and have shown the viability of the ap-
proach. However, for larger instances AS gives a very
poor solution quality compared to state-of-the-art al-
gorithms. This is due to randomized character of the
AS algorithm which makes probabilistic decisions in
the construction of the solution. In the literature, re-
searchers presented various improvements over AS. A
first improvement on the initial form of AS, is the Eli-
tist Strategy for Ant System, introduced in (Dorigo,
1992) and (Dorigo et al., 1996) where only the best-
so-far solution is used to update the pheromone trails
and the idea is to enhance the promising search space.
Other improvements were presented such as rank-
based Ant System (AS
rank
) (Bullnheimer et al., 1997),
it can be considered as an extension of the elitist
strategy. Ants are sorted according to the quality of
their solutions and the amount of pheromone that each
ant deposits on the trails decreases according to its
rank. Meanwhile, the best-so-far ant still deposits
pheromone at each iteration.
MAX – MIN Ant System (MMAS) (St
¨
utzle,
1998; St
¨
utzle and Hoos, 1997; St
¨
utzle and Hoos,
2000) is another improvements of AS. MMAS intro-
duces upper and lower bounds to the values of the
pheromone trails, as well as a different initialization
of their values. All trails are maintained inside an in-
terval bounded [τ
min
, τ
max
] in order to avoid stagnation
caused by exploring best solutions.
There are others extensions of AS, for exam-
ple Ant Colony System (ACS) by Dorigo and
Gambardella (Dorigo and Gambardella, 1997a;
Dorigo and Gambardella, 1997b; Gambardella and
Dorigo, 1996),Approximate Non-deterministic Tree
Search (ANTS) by Maniezzo (Maniezzo, 1999) and
population-based ACO (P-ACO) by Guntsch and
Middendorf (Cagnoni et al., 2002)
It will be interesting to apply different AS forms
in order to see the influence of the improvements on
DJSP.
5 CONCLUSION AND
PERSPECTIVES
In this work, we have applied the Ant System algo-
rithm for the first time to solve the Distributed Job
shop Scheduling Problem with makespan minimiza-
tion criterion. The algorithm is compared with other
algorithms in literature. Despite of the fact that AS
succeeded in solving small instances of DJSP, results
are very poor for large instances and show that the
standard AS is not competitive at all comparing to
other methods.
For future work, it will be interesting to in-
vestigate on the different variations of Ant System,
namely Elitist ant system (EAS), Max-Min Ant Sys-
tem (MMAS), etc. and maybe the integration of local
search leads to a possible improvement of the results.
Also, we can study the problem aiming to optimize
other objectives. And finally, we can consider the case
of a DJSP with non identical factories. Because some-
where, considering that the factories are the same, can
be an idealization to the real problem, since it is rarely
the case.
REFERENCES
Adams, J., Balas, E., and Zawack, D. (1988). The shifting
bottleneck procedure for job shop scheduling. Man-
agement science, 34(3):391–401.
Bargaoui, H., Belkahla Driss, O., and Gh
´
edira, K. (2016).
Minimizing makespan in multi-factory flow shop
problem using a chemical reaction metaheuristic. In
IEEE Congress on Evolutionary Computation, At Van-
couver, Canada, pages 2919–2929.
Bullnheimer, B., Hartl, R. F., and Strauss, C. (1997). A new
rank based version of the ant system. a computational
study.
Cagnoni, S., Gottlieb, J., Hart, E., Middendorf, M., and
Raidl, G. R. (2002). Applications of Evolutionary
Computing: EvoWorkshops 2002: EvoCOP, EvoIASP,
EvoSTIM/EvoPLAN Kinsale, Ireland, April 3-4, 2002.
Proceedings, volume 2279. Springer Science & Busi-
ness Media.
Chung, S. H., Lau, H. C., Ho, G. T., and Ip, W. (2009). Op-
timization of system reliability in multi-factory pro-
duction networks by maintenance approach. Expert
Systems with Applications, 36(6):10188–10196.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
580

Colorni, A., Dorigo, M., Maniezzo, V., and Trubian, M.
(1994). Ant system for job-shop scheduling. Belgian
Journal of Operations Research, Statistics and Com-
puter Science, 34(1):39–53.
Davis, L. (1985). Job shop scheduling with genetic algo-
rithms. In Proceedings of an international conference
on genetic algorithms and their applications, volume
140. Carnegie-Mellon University Pittsburgh, PA.
Dell’Amico, M. and Trubian, M. (1993). Applying tabu
search to the job-shop scheduling problem. Annals of
Operations Research, 41(3):231–252.
Dorigo, M. (1992). Optimization, learning and natural al-
gorithms. Ph. D. Thesis, Politecnico di Milano, Italy.
Dorigo, M. and Gambardella, L. M. (1997a). Ant colonies
for the travelling salesman problem. BioSystems,
43(2):73–81.
Dorigo, M. and Gambardella, L. M. (1997b). Ant colony
system: a cooperative learning approach to the travel-
ing salesman problem. IEEE Transactions on evolu-
tionary computation, 1(1):53–66.
Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant sys-
tem: optimization by a colony of cooperating agents.
IEEE Transactions on Systems, Man, and Cybernet-
ics, Part B (Cybernetics), 26(1):29–41.
Fisher, H. and Thompson, G. L. (1963). Probabilistic learn-
ing combinations of local job-shop scheduling rules.
Industrial scheduling, 3(2):225–251.
Gambardella, L. M. and Dorigo, M. (1996). Solving sym-
metric and asymmetric tsps by ant colonies. In In-
ternational conference on evolutionary computation,
pages 622–627.
Gao, J. and Chen, R. (2011). A hybrid genetic algorithm for
the distributed permutation flowshop scheduling prob-
lem. International Journal of Computational Intelli-
gence Systems, 4(4):497–508.
Garey, M. R., Johnson, D. S., and Sethi, R. (1976).
The complexity of flowshop and jobshop scheduling.
Mathematics of operations research, 1(2):117–129.
Jia, H., Fuh, J. Y., Nee, A. Y., and Zhang, Y. (2002). Web-
based multi-functional scheduling system for a dis-
tributed manufacturing environment. Concurrent En-
gineering, 10(1):27–39.
Jia, H., Fuh, J. Y., Nee, A. Y., and Zhang, Y. (2007). In-
tegration of genetic algorithm and gantt chart for job
shop scheduling in distributed manufacturing systems.
Computers & Industrial Engineering, 53(2):313–320.
Jia, H., Nee, A. Y., Fuh, J. Y., and Zhang, Y. (2003). A
modified genetic algorithm for distributed scheduling
problems. Journal of Intelligent Manufacturing, 14(3-
4):351–362.
Karimi, N. and Davoudpour, H. (2017). A knowledge-based
approach for multi-factory production systems. Com-
puters & Operations Research, 77:72–85.
Lawrence, S. (1984). Resource constrained project
scheduling: an experimental investigation of heuristic
scheduling techniques (supplement). Graduate School
of Industrial Administration.
Maniezzo, V. (1999). Exact and approximate nondeter-
ministic tree-search procedures for the quadratic as-
signment problem. INFORMS journal on computing,
11(4):358–369.
Naderi, B. and Azab, A. (2014). Modeling and heuristics for
scheduling of distributed job shops. Expert Systems
with Applications, 41(17):7754–7763.
Naderi, B. and Azab, A. (2015). An improved model and
novel simulated annealing for distributed job shop
problems. The International Journal of Advanced
Manufacturing Technology, pages 1–11.
Naderi, B. and Ruiz, R. (2010). The distributed permutation
flowshop scheduling problem. Computers & Opera-
tions Research, 37(4):754–768.
St
¨
utzle, T. (1998). Local search algorithms for combina-
torial problems. Darmstadt University of Technology
PhD Thesis, 20.
St
¨
utzle, T. and Hoos, H. (1997). Max-min ant system and
local search for the traveling salesman problem. In
Evolutionary Computation, 1997., IEEE International
Conference on, pages 309–314. IEEE.
St
¨
utzle, T. and Hoos, H. (2000). Max–min ant system. Fu-
ture generation computer systems, 16(8):889–914.
Taillard, E. (1993). Benchmarks for basic scheduling prob-
lems. European Journal of Operational Research,
64(2):278–285.
Talbi, E.-G. (2009). Metaheuristics: from design to imple-
mentation, volume 74. John Wiley & Sons.
Weaknesses of Ant System for the Distributed Job Shop Scheduling Problem
581
