An Accurate Tax Fraud Classiﬁer with Feature Selection based on

Complex Network Node Centrality Measure

Tales Matos, Jos

e Antonio F. de Macedo, Jos

e Maria Monteiro and Francesco Lettich

Federal University of Cear

a, Campus do Pici, Fortaleza, Brazil

Keywords:

Fraud Detection, Data Mining, Tax Evasion, Feature Selection.

Abstract:

Fiscal evasion represents a very serious issue in many developing countries. In this context, tax fraud detection

constitutes a challenging problem, since fraudsters change frequently their behaviors to circumvent existing

laws and devise new kinds of frauds. Detecting such changes proves to be challenging, since traditional

classiﬁers fail to select features that exhibit frequent variations. In this paper we provide two contributions

that try to tackle effectively the tax fraud detection problem: ﬁrst, we introduce a novel feature selection

algorithm, based on complex network techniques, that is able to capture key fraud indicators – over time, this

kind of indicators turn out to be more stable than new fraud indicators. Secondly, we propose a classiﬁer

that leverages the aforementioned algorithm to accurately detect tax frauds. In order to prove the validity of

our contributions we provide an experimental evaluation, where we use real-world datasets, obtained from the

State Treasury Ofﬁce of Cear

a (SEFAZ-CE), Brazil, to show how our method is able to outperform, in terms

of F

scores achieved, the state-of-the-art available in the literature.

1 INTRODUCTION

Fiscal evasion represents a very serious issue for the

economy of developing countries. Although institu-

tions often undertake initiatives to collect meaning-

ful taxpayer information, thus trying to reduce ﬁscal

evasion, the level of tax frauds remains high – for in-

stance, the level of tax evasion in Brazil is of about

US$ 143 billions (Sonegometro, 2016). On the posi-

tive side, the continuous collection of more and more

taxpayer data opens up to new kinds of opportunities,

since it allows the creation of increasingly effective

approaches that are able to mitigate tax evasion.

In this work, we consider a real-world scenario in-

volving the State Treasury Ofﬁce of Cear

a (SEFAZ-

CE, Brazil), the agency in charge of supervising over

200,000 active contributors in the state of Cear

Brazil. Although SEFAZ-CE maintains a large

dataset containing a plethora of information, its en-

forcement team struggles to perform thorough inspec-

tions on taxpayers accounts. Indeed, the inspection

process involves countless fraud indicators, thus re-

quiring burdensome amounts of time and being po-

tentially subject to human errors. In this paper, we

aim to ease this kind of tasks by introducing novel

algorithmic tools.

We start by posing ourselves four key questions:

what are the behavioral patterns behind fraud indi-

cators? Are there some kind of correlations among

fraud indicators? Which are the most relevant fraud

indicators? How can we assess the risk that some tax-

payer commits a fraud?

In this paper we try to answer these questions by

introducing a new method for predicting potential tax

frauds. The method is structured in four phases, and

relies on data mining, statistical analysis, and dimen-

sionality reduction techniques. During the ﬁrst phase,

our approach analyzes the frequency of individual

attributes, as well as the frequency associated with

combinations of attributes, trying also to understand

whether attributes exhibit some kind of statistical dis-

tribution over time. By virtue of these information,

in the second phase our method infers the dimensions

that are the most relevant for taxpayer classiﬁcation.

Subsequently, in the third phase our approach vali-

dates the hypothesis of using the centrality measure

to select key indicators, while in the ﬁnal phase it out-

puts a list that reports the fraud risk associated with

each taxpayer. Overall, our proposal signiﬁcantly im-

proves the approach presented in (Matos et al., 2015),

in that it uses complex network techniques to pick

up key indicators that can help to accurately identify

frauds.

In the experimental evaluation we show how our

Matos, T., Macedo, J., Monteiro, J. and Lettich, F.

An Accurate Tax Fraud Classiﬁer with Feature Selection based on Complex Network Node Centrality Measure.

DOI: 10.5220/0006335501450151

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 145-151

ISBN: 978-989-758-247-9

145

algorithm is able to achieve equivalent, or better,

scores with respect to the algorithm proposed in

(Matos et al., 2015) – the improvement is equal to

about 54% when considering the dataset introduced

in this work, while comparable F

scores are achieved

when considering the dataset introduced in (Matos

et al., 2015). In the same evaluation we also show

how our method is able to achieve better F

scores –

the improvement is up to 47% when considering the

dataset introduced in this work – with respect to an

SVM

-based approach (Shavers et al., 2006).

The paper is structured as follows: Section 2

presents the related work. Section 3 presents the case

study that we consider in this work. Section 4 presents

our proposal. Section 5 presents the experimental set-

ting, while Section 6 presents the experimental evalu-

ation. Finally, Section 7 draws the ﬁnal conclusions.

2 RELATED WORK

(Glancy and Yadav, 2011) proposes a quantitative

model to detect fraudulent ﬁnancial reports. The goal

of the model is to detect attempts to conceal informa-

tion, or report incorrect information, in annual ﬁlings

presented to the US Securities and Exchange Com-

mission (SEC). In order to achieve this, the authors

analyze all the information contained within a textual

document by means of techniques based on the Sin-

gular Value Decomposition (SVD).

(Ngai et al., 2011) presents a review of the litera-

ture – along with a classiﬁcation scheme – concerning

the application of data mining techniques to detect ﬁ-

nancial frauds. The ﬁndings clearly show that data

mining techniques have been applied extensively to

detect insurance frauds, although corporate and credit

card frauds have also attracted a great deal of attention

in recent years. In general, the review shows that the

main data mining techniques used in the literature are

based on logistic models, neural networks, Bayesian

belief networks, and decision trees.

(Bhattacharyya et al., 2011) evaluates two ap-

proaches, both relying on the usage of support vector

machines, random forests techniques and logistic re-

gression, as part of an attempt to better detect credit

card frauds. In this study, the authors consider real-

world data concerning international credit card trans-

actions.

(Ravisankar et al., 2011) considers data mining

techniques, such as Multilayer Feed Forward Neural

Network (MLFF), Support Vector Machines (SVM),

Genetic Programming (GP), Group Method of Data

The acronym stands for support vector machine.

Handling (GMDH), Logistic Regression (LR), and

Probabilistic Neural Network (PNN), to identify com-

panies that commit ﬁnancial statement frauds. Cou-

pled with these techniques, the authors consider also

the usage of feature selection techniques. The exper-

imental evaluation, which considers a dataset involv-

ing 202 Chinese companies, shows how PNN is the

clear winner when feature selection is not used, while

GP and PNN emerge as winners in the opposite case.

(Kirkos et al., 2007) explores the effectiveness of

data mining classiﬁcation techniques to detect compa-

nies that issue fraudulent ﬁnancial statements (FFS),

and deals with the identiﬁcation of factors associated

with FFSs. More precisely, the study investigates

the usefulness of decision trees, neural networks and

Bayesian belief networks; in the end, the authors re-

port that Bayesian Belief Networks emerge as win-

ners.

anchez et al., 2009) proposes the use of associ-

ation rules to extract behavior patterns from unlaw-

ful transactions observed in transactional credit card

databases. In turn, this knowledge is exploited to de-

tect and prevent frauds.

(Li et al., 2012) employs Bayesian classiﬁcation

and association rules to identify signs of fraudulent

accounts and patterns of fraudulent transactions; de-

tection rules are created according to identiﬁed signs,

and used to devise a system able to detect fraudulent

accounts. By means of an empirical veriﬁcation, the

authors show their solution can successfully identify

fraudulent accounts in early stages, as well as provide

useful information to ﬁnancial institutions.

(Phua et al., 2010) presents a survey that catego-

rizes, compares, and summarizes the literature related

to automated fraud detection. More precisely, the sur-

vey covers a set of works published between 2000 and

2010, and discusses the main methods and techniques

used to detect frauds automatically, along with their

shortcomings.

(Fanning and Cogger, 1998) uses a Neural Net-

work to devise a fraud detection model. The input

vector consists of ﬁnancial ratios and qualitative vari-

ables. In the experimental evaluation, the authors

compare the performance of their model with stan-

dard statistical methods, such as linear and quadratic

discriminant analysis, and logistic regression. Over-

all, the authors claim that their model is more effec-

tive at detecting frauds than its competitors.

(Abbott et al., 2000) uses statistical regression

analysis to examine if the use of independent audit

committees (such as independent managers that meet

at least twice per year) within companies can miti-

gate the likelihood of frauds. Indeed, the paper con-

cludes that when this happens, ﬁrms are less likely to

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

146

be sanctioned for fraudulent or misleading reporting.

3 CASE STUDY

In this section we present a case study that concerns

the data collected by the Treasury State of Cear

(SEFAZ-CE), Brazil, which is responsible for collect-

ing taxes within the state of Cear

a. This case study

will serve us as a basis to represent the problem we

want to tackle, thanks to the volume and nature of the

data provided by the agency.

One of the goals of this study is to analyze tax-

payer fraud indicators to identify relevant key indi-

cators (main features) that may characterize potential

tax frauds. Indeed, the data to be analyzed may be

possibly huge, and may contain many different kinds

of information – just to name a few examples, ac-

counting data, goods inventory, sales data, legal data,

etc. A proper interpretation of fraud indicators is of

paramount importance to guide tax auditors during

the process of identifying irregular behaviors. In-

deed, without the aid of algorithmic tools, auditors

must usually resort to thorough and complex analyses

which, in turn, make the task of detecting frauds time

consuming and error prone.

3.1 Tax Fraud Indicator Dataset

Data provided by SEFAZ-CE were extracted from 8

applications, summing up to 72 million of records.

We selected taxpayers data collected during a period

ranging from 2009 to 2011, which corresponds to the

current audit period. We used fourteen fraud indica-

tors, all identiﬁed by expert tax auditors. From a ﬁ-

nancial point of view, these indicators are of key im-

portance, since they correspond to the largest amount

of money that can be recovered from fraudulent trans-

actions. Each fraud indicator is determined by a tax

auditor after analyzing information issued by taxpay-

ers, such as tax documents, records of the movement

of goods at the border of the state of Cear

a, and tax-

payer sales data. Due to conﬁdentiality reasons, we

anonymized the indicators by means of letters and

numbers; more speciﬁcally, to anonymize taxpayers

data a sequential ID is assigned to each taxpayer,

while each fraud indicator – fourteen in total – is re-

named by means of the symbols A, B, C, D, E, F, G,

H, I, J, K, L, M, and N. Data from 2009 and 2010 have

the same indicators (A, B, C, D, E, F, G, H, I, J, K, L,

M and N), while data from 2011, despite having the

same number of indicators, is characterized by differ-

ent kinds of indicators, namely X1, X2, X3, X4, X5,

X6, X7, X8, X9, X10, X11, X12, X13, X14; this is

Figure 1: Frequency of tax fraud indicators for the years

2009, 2010 and 2011.

due to the fact that indicators frequently change from

year from year, since fraudster tend to search alterna-

tive ways to avoid paying taxes.

As shown in the section detailing our tax fraud de-

tection method (Section 4), frequent variations affect

fraud indicators (features) year by year: this calls for

an algorithm that is able to automatically identify key

indicators. This, in turn, helps to better characterize

tax fraudsters, thus improving the quality of the re-

sults returned by a predictive model. Indeed, we high-

light that this is one of the main contributions charac-

terizing this paper, thus differentiating our work with

respect to (Matos et al., 2015).

An Accurate Tax Fraud Classiﬁer with Feature Selection based on Complex Network Node Centrality Measure

147

3.2 Tax Fraud Matrices

Three matrices were constructed for the years 2009,

2010, and 2011. Each matrix relates to taxpay-

ers (rows) and their corresponding fraud indicators

(columns). Each indicator uses a binary representa-

tion, where 1 (one) indicates the presence of fraud,

while 0 (zero) the absence. The matrix for data re-

lated to 2009 has 11,386 rows and 14 columns, the

one for 2010 possesses 12,424 rows and 14 columns,

while the one from 2011 contains 10,627 rows and 14

columns. Taxpayers who did not present any evidence

of fraud were excluded, since they were considered

outliers.

3.3 Data Overview

Figure 1 presents three histograms, detailing the fre-

quency of fraud indicator frequencies collected for the

years 2009, 2010 and 2011 respectively. In 2009,

10,789 (95%) out of 11,386 taxpayers have at least

one type of fraud evidence, while 597 (5%) of tax-

payers do not present any evidence. In 2010, 11,989

(96%) out of 12,424 taxpayers exhibit at least one

type of fraud evidence, while 435 (4%) do not present

any kind of anomaly. Overall, we report that the fre-

quency of the vast majority of fraud indicators in-

creased from 2009 to 2010, thus indicating that tax

evasion represents a very relevant problem that needs

to be addressed.

4 TAX FRAUD DETECTION

METHOD

In this section we present a detailed description

of TAXFRAUDDETECTOR, our tax fraud detection

method. The main goal of TAXFRAUDDETECTOR is

to compute the risk that a taxpayer has to commit a

fraud. TAXFRAUDDETECTOR takes in input four pa-

rameters, i.e., a tax fraud matrix, S, and three thresh-

olds, supp, con f , and li f t representing, respectively,

the support, condifence, and lift thresholds used by

the Apriori algorithm (Agrawal et al., 1994) leveraged

within our approach; in this context, we remind that

the value given to li f t determines the ﬁnal set of asso-

ciation rules deemed relevant by TAXFRAUDDETEC-

TOR, hence highlighting its important role. Algorithm

1 presents the pseudocode.

TAXFRAUDDETECTOR starts by processing the

tax fraud matrix S by means of Apriori (line 2, func-

tion KeyRules): this has the purpose of identifying rel-

evant association rules that, in turn, allow to focus on

the most relevant fraud indicators (function KeyRules,

Algorithm 1: TAXFRAUDDETECTOR.

Input :

• S, the data matrix.

• supp, the support threshold to be used with Apriori.

• con f , the conﬁdence threshold to be used with Apriori.

• li f t, the lift threshold to be used with Apriori.

1 begin

2 kRules ← KeyRules(S, supp, con f , li f t)

3 KeyIndicators ← KFind(kRules)

4 S

← Subset(S, KeyIndicators)

5 return DimRedSVD(S

)

Algorithm 2: KeyRules(S, supp, con f , li f t).

1 begin

2 RuleSet ←

3 AP ← Apriori(S, supp, con f )

4 foreach ap ∈ AP do

5 if (Li f t(ap) ≥ li f t) then

6 RuleSet ← RuleSet ∪ {ap}

7 return RuleSet

Algorithm 2, line 5). We note that this is the main

difference our method exhibits with respect to (Matos

et al., 2015), since the latter performs the selection of

key determinants by means of inference rules. Subse-

quently, association rules are used to generate a graph

(we call it fraud graph) and discover the key fraud

indicators (line 3, function KFind). Key indicators

are ﬁnally used to ﬁlter out from S irrelevant indica-

tors, thus obtaining a modiﬁed data matrix S

(line 4,

function Subset). The algorithm concludes by reduc-

ing the dimensionality of key indicators, by means of

an SVD-based algorithm (Golub and Reinsch, 1970),

to a single dimension (line 5, function DimRedSVD):

this generates a list of scalars, each one representing

the degree of fraud risk associated with a taxpayer.

Algorithm 3: KFind(kRules).

1 begin

2 KeyIndicator ←

3 G ← graph where each sequence of indicators appearing in

kRules is a vertex v ∈ V , while each association rule ar ∈ kRules

represents an edge e ∈ E

4 foreach v ∈ G do

5 v

Degree

← v

I nDegree

+ v

OutDegree

6 foreach v ∈ G do

7 if v

Degree

> (AV GDegree(G)+ 3 · ST DevDegree(G)) then

8 KeyIndicator ← KeyIndicator ∪ {v}

9 return KeyIndicator

Before concluding this section we spend two

words on KFind (Algorithm 3). KFind takes in in-

put a set of association rules, i.e., kRules: ﬁrst, from

kRules it generates a graph, G = (V, E), that repre-

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

148

sents relationships among fraud indicators (line 3).

The graph is built as follows: each vertex represents

a sequence of fraud indicators, while each edge rep-

resents an association rule – for example, the exis-

tence of an association rule (ABC → D) ∈ kRules im-

plies that {ABC, D} ∈ V and (ABC, D) ∈ E. Finally,

KFind selects the nodes having degree (i.e., in-degree

plus out-degree) greater than three times the standard

deviation characterizing G’s degree distribution – in

other words, we exploit the 3-sigma conﬁdence inter-

val (Montgomery, 2007; Bland and Altman, 1996).

5 EXPERIMENTAL SETTING

In the following we present the experimental setting

used to conduct the experiments reported in Section

5.1 Methodology

In order to conduct the experimental evaluation

we applied the following methodology: ﬁrst, from

the dataset provided by SEFAZ-CE (introduced in

Section 3) we picked up 120 contributors having

the highest values in the ranking list computed by

TAXFRAUDDETECTOR – as such, this list represents

the group of people that, according to our method,

have the highest chance to be fraudsters. Next, from

the same dataset we picked up 50 contributors hav-

ing the lowest values, thus representing the group of

people that, according to our method, have the lowest

chance to be fraudsters.

Subsequently, we provided the two lists to two

experienced tax auditors, who conducted a thorough

analysis to check the correctness of TAXFRAUDDE-

TECTOR’s results and create a ground truth. From

the analysis, they concluded that out of 120 people

making up the ﬁrst group, 85 were indeed fraudsters,

while out of 50 people making up the second group,

23 were honest taxpayers.

To estimate the accuracy of the classiﬁcation

methods when employing selected features, we use

the k-fold cross-validation technique; more speciﬁ-

cally, we rely on the 10-fold cross-validation as it

tends to provide less biased estimations (Kohavi et al.,

1995).

5.2 Measures

In order to assess the quality of the results returned

by TAXFRAUDDETECTOR and its competitors, we

resort to well-established metrics commonly used in

data mining to evaluate the quality of a classiﬁer (Tan

Table 1: Confusion matrix, with positive and negative clas-

siﬁcation.

Classiﬁcation Correct Not Correct

Fraudsters 85 (TP) 35 (FP)

Not fraudsters 7 (FN) 23 (TN)

Table 2: Statistical measures used to assess the quality of

the results returned by classiﬁers.

Measure Deﬁnition

Accuracy A =

T P+T N

Precision P =

T P

T P+FP

Recall R =

T P

T P+FN

Score F =

2·R·P

R+P

et al., 2005). In the following we brieﬂy introduce

them.

Given a set of N taxpayers, we can evaluate the

results of a classiﬁer by constructing an integer con-

fusion matrix; in order to do this, we ﬁrst have to de-

ﬁne the following types of outcomes when consider-

ing any result:

• A True Positive (TP) result occurs when a fraud-

ster is correctly classiﬁed as such.

• A False Positive (FP) result occurs when an hon-

est contributor is classiﬁed as a fraudster.

• A False Negative (FN) result occurs when a fraud-

ster is not classiﬁed as such.

• A True Negative (TN) result occurs when a honest

contributor is classiﬁed as honest.

Accordingly, we arranged the ﬁgures returned by

the auditors’ evaluation into a confusion matrix (Ta-

ble 1), which in turn allows to easily derive statistical

measures that are commonly used to assess the quality

of a classiﬁer (Table 2).

5.3 Competitors

In the experimental evaluation we compare the fol-

lowing methods:

• TAXFRAUDDETECTOR.

• The method proposed in (Matos et al., 2015),

which is also the current state-of-the-art in the lit-

erature.

• An SVM-based approach that uses indicators (as

features) previously selected by TAXFRAUDDE-

TECTOR.

• An SVM-based approach that uses indicators pre-

viously selected in (Matos et al., 2015).

• An SVM-based approach that does not recur to

any kind of feature selection.

An Accurate Tax Fraud Classiﬁer with Feature Selection based on Complex Network Node Centrality Measure

149

We included an SVM-based classiﬁer mainly for two

reasons: ﬁrst, to analyze how it performs with re-

spect to our method; secondly, to understand whether

TAXFRAUDDETECTOR can be used as a tool to im-

prove the performance of approaches based on ma-

chine learning techniques. Finally, we report that the

SVM classiﬁer used in this work is based on the radial

basis function kernel.

5.4 Run-time Parameters

When executing TAXFRAUDDETECTOR we provide

the following parameters: supp = 0.6, con f = 0.6

and li f t = 1.05. We report that these values were cho-

sen according to the opinions provided by SEFAZ-CE

business experts.

When executing the algorithm from (Matos et al.,

2015), we provided the same set of parameters that

were used in their paper.

Finally, the SVM-based approach relies on the

SVM package available in R (David Meyer, 2017; R

Core Team, 2016); the following parameters are pro-

vided at execution time: kernel = ”radial”, gamma =

0.01, cost = 10. We report that the values given to

gamma and cost were picked up after trying out dif-

ferent values, with gamma varied in the [10

−6

, 10

−1

]

range and cost varied in the [10

, 10

] range.

6 EXPERIMENTAL EVALUATION

In this section we assess the quality of the results

achieved by TAXFRAUDDETECTOR and its competi-

tors by means of the measures deﬁned in Table 2, and

according to the data reported in the confusion matrix

(Table 1).

The experiments relates to the results achieved

when considering the dataset covering the year 2011.

Table 3 shows the results. From the results, we no-

tice that TAXFRAUDDETECTOR is able to achieve

the best classiﬁcation quality, with an F

score

equal to 77%, thus indicating that our approach is

able to detect potential fraudsters more effectively

than our competitors. Another observation is that

TAXFRAUDDETECTOR shows better results than the

SVM-based classiﬁer, and that the latter is able to im-

prove its classiﬁcation quality considerably once it is

combined with our approach (or, to a lesser degree,

with (Matos et al., 2015)). Finally, we report that re-

sults related to data covering the years 2009 and 2010

exhibit similar results (we omit them for brevity).

In general, we deem that the results show how fea-

ture selection, coupled with centrality measure (Boc-

caletti et al., 2006), is able to considerably improve

Figure 2: Degree distribution for the years 2010 and 2011.

The X-axis is associated with the degree, while the Y-axis is

associated with the occurrences of vertices having a given

degree.

the classiﬁcation of fraudsters, either for TAXFRAUD-

DETECTOR, (Matos et al., 2015), or SVM. As such,

we believe that centrality measure is an adequate fea-

ture for classiﬁcation, since graphs generated during

the classiﬁcation process have a degree distribution

that behaves according to the power law (Figure 2).

7 CONCLUSIONS

In this paper we proposed a new method to determine

the risk that taxpayers have to commit tax frauds. The

method extends and improves (Matos et al., 2015) in

that it uses a new technique to discover key indicators

of frauds by resorting to the centrality measure over a

graph of indicators: this implicitly captures relation-

ships between key fraud indicators.

On the one hand, we claim that previous methods

fail to perform accurate predictions since they can-

not cope effectively with changes that affect indica-

tors over time. On the other hand, our technique relies

on the observation that, once we are able to capture re-

lationships between indicators, this allows to ﬁnd out

the most relevant ones. Moreover, the degree distri-

bution of a graph of indicators behaves according to a

power law, which in turn suggests that key indicators

retain their importance regardless of the scale used to

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

150

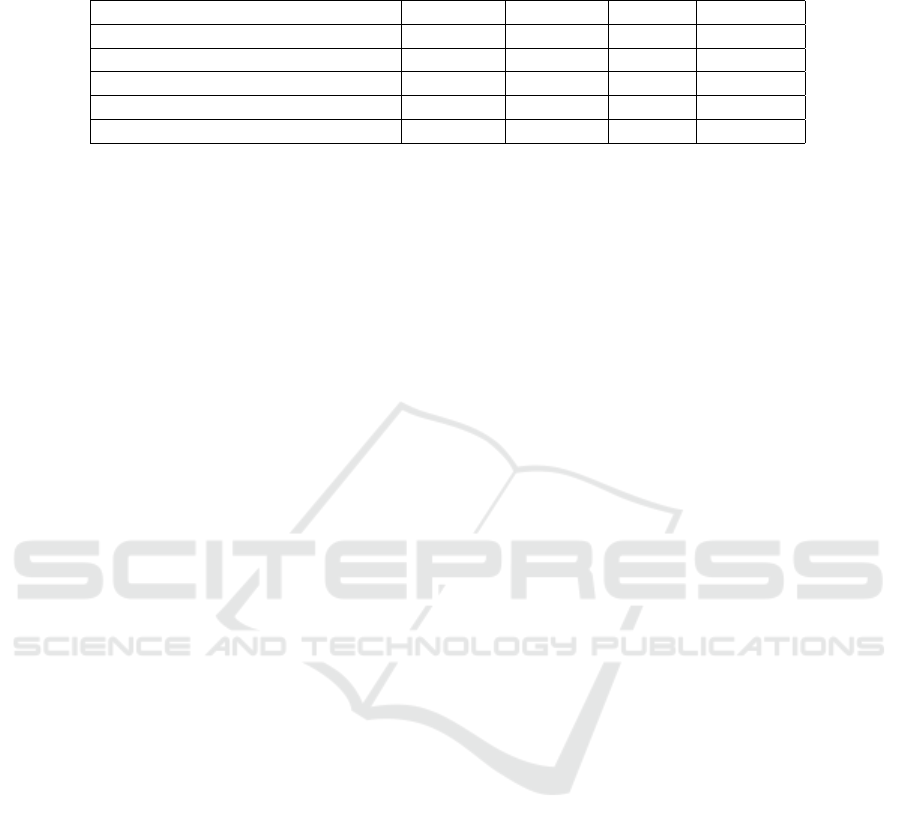
Table 3: Assessment of the quality of the results returned by TAXFRAUDDETECTOR and its competitors when analyzing the

SEFAZ-CE 2011 dataset.

Method Accuracy Precision Recall F

Score

TAXFRAUDDETECTOR 81.33% 78.14% 76.08% 77.0962%

(Matos et al., 2015) 51.27% 48.94% 51.11% 50.0014%

SVM using TAXFRAUDDETECTOR 56.26% 53.12% 47.23% 50.0021%

SVM using (Matos et al., 2015) 33.42% 30.07% 39.13% 34.0069%

SVM 87.49% 45.09% 8.22% 13.9112%

analyze them. As such, this scenario represents a typ-

ical complex network, hence a proper analysis of the

underlying topology can offer useful insights into the

network properties.

In the experimental evaluation we show that our

approach achieves F

scores of about 54% greater

than (Matos et al., 2015) when considering the dataset

introduced by this work, while it maintains equivalent

scores when considering the dataset introduced in

(Matos et al., 2015). Furthermore, we show that our

method is able to improve F

scores of about 47%

with respect to an SVM-based approach, when con-

sidering the dataset introduced in this work.

As a future line of research, we are considering the

application of other metrics over graph determinants

to further improve the feature selection process; ﬁ-

nally, we plan to explore more issues related to graph

topology, which in turn have the potential to improve

the accuracy of fraud detection.

REFERENCES

Abbott, L. J., Park, Y., and Parker, S. (2000). The effects of

audit committee activity and independence on corpo-

rate fraud. Managerial Finance, 26(11):55–68.

Agrawal, R., Srikant, R., et al. (1994). Fast algorithms for

mining association rules. In Proc. 20th int. conf. very

large data bases, VLDB, volume 1215, pages 487–

499.

Bhattacharyya, S., Jha, S., Tharakunnel, K., and West-

land, J. C. (2011). Data mining for credit card fraud:

A comparative study. Decision Support Systems,

50(3):602–613.

Bland, J. M. and Altman, D. G. (1996). Statistics notes:

measurement error. Bmj, 313(7059):744.

Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and

Hwang, D.-U. (2006). Complex networks: Structure

and dynamics. Physics reports, 424(4):175–308.

David Meyer (2017). Support Vector Machines. FH Tech-

nikum Wien, Austria.

Fanning, K. M. and Cogger, K. O. (1998). Neural network

detection of management fraud using published ﬁnan-

cial data. International Journal of Intelligent Systems

in Accounting, Finance & Management, 7(1):21–41.

Glancy, F. H. and Yadav, S. B. (2011). A computational

model for ﬁnancial reporting fraud detection. Deci-

sion Support Systems, 50(3):595–601.

Golub, G. H. and Reinsch, C. (1970). Singular value de-

composition and least squares solutions. Numerische

mathematik, 14(5):403–420.

Kirkos, E., Spathis, C., and Manolopoulos, Y. (2007). Data

mining techniques for the detection of fraudulent ﬁ-

nancial statements. Expert systems with applications,

32(4):995–1003.

Kohavi, R. et al. (1995). A study of cross-validation and

bootstrap for accuracy estimation and model selection.

In Ijcai, volume 14, pages 1137–1145.

Li, S.-H., Yen, D. C., Lu, W.-H., and Wang, C. (2012).

Identifying the signs of fraudulent accounts using data

mining techniques. Computers in Human Behavior,

28(3):1002–1013.

Matos, T., de Macedo, J. A. F., and Monteiro, J. M. (2015).

An empirical method for discovering tax fraudsters: A

real case study of brazilian ﬁscal evasion. In Proceed-

ings of the 19th International Database Engineering

& Applications Symposium, pages 41–48. ACM.

Montgomery, D. C. (2007). Introduction to statistical qual-

ity control. John Wiley & Sons.

Ngai, E., Hu, Y., Wong, Y., Chen, Y., and Sun, X. (2011).

The application of data mining techniques in ﬁnan-

cial fraud detection: A classiﬁcation framework and

an academic review of literature. Decision Support

Systems, 50(3):559–569.

Phua, C., Lee, V., Smith, K., and Gayler, R. (2010). A

comprehensive survey of data mining-based fraud de-

tection research. arXiv preprint arXiv:1009.6119.

R Core Team (2016). R: A Language and Environment for

Statistical Computing - version 0.99.903. R Founda-

tion for Statistical Computing, Vienna, Austria.

Ravisankar, P., Ravi, V., Rao, G. R., and Bose, I. (2011).

Detection of ﬁnancial statement fraud and feature se-

lection using data mining techniques. Decision Sup-

port Systems, 50(2):491–500.

anchez, D., Vila, M., Cerda, L., and Serrano, J.-M. (2009).

Association rules applied to credit card fraud detec-

tion. Expert Systems with Applications, 36(2):3630–

3640.

Shavers, C., Li, R., and Lebby, G. (2006). An svm-based

approach to face detection. In 2006 Proceeding of

the Thirty-Eighth Southeastern Symposium on System

Theory, pages 362–366. IEEE.

Sonegometro (2016 (Retrieved December 14,

2016)). Tax Evasion in Brazil. http://

www.quantocustaobrasil.com.br.

Tan, P.-N., Steinbach, M., and Kumar, V. (2005). Introduc-

tion to Data Mining, (First Edition). Addison-Wesley

Longman Publishing Co., Inc., Boston, MA, USA.

An Accurate Tax Fraud Classiﬁer with Feature Selection based on Complex Network Node Centrality Measure

151