DOTSIM

A Simulation-based Optimization Methodology for the Optimal Duplication

Sequence on Freight Transportation Systems

Heygon Araujo and Samyr Vale

Department of Computer Science, Federal University of Maranh

ao - UFMA, Sao Lu

ıs, Maranh

ao, Brazil

Keywords:

Optimization, Transportation Systems, Methodology, Simulation, Railways.

Abstract:

The deﬁnition of the best sequence on route duplication of freight systems consists on a complex NP-hard

problem. There exists a huge variety of meta-heuristics (MH) capable of generating satisfactory solutions.

However, it is fastidious to know which MH will produce the best solution for a Duplication Sequencing

Problem (DSP). There not exists a methodology to structure, plan and control algorithms and processes in

modeling the various MH applied to ﬁnd the best solution in this type of problems. This paper proposes

a process development methodology which guides to evaluate the best duplication sequence comparing the

MH’s performance with existing approaches such as linear analytical method (LAM). The potential of this

methodology is demonstrated by a case study in railway systems.

1 INTRODUCTION

Rail transportation is one of the most efﬁcient trans-

portation ways due to its capacities to freight and pas-

sengers at low costs comparing with road transporta-

tion. The growth of its support infrastructure is com-

plex as much as its importance.

The duplication sequence problem (DSP) is des-

cribed as a set of single segments or routes in a trans-

portation system, the link between these routes (usu-

ally duplicated where vehicles can park) called cros-

sing loops, and the travel cost between the connected

crossing loops. The best solution for a DSP is the se-

quence which has lower cost, besides that all routes

should be duplicated one at a time. For most of DSP

problems the search for the best solution is relevantly

hard. A problem with 10 single routes has about 3.5

x 10

feasible solutions. An exhaustive search runned

by a computer with capacity to process 1 billion solu-

tions per second would ﬁnd the best solution in about

four years.

For this kind of problem, a satisfactory solution,

close to an optimal one, may be obtained by meta-

heuristics (MHs). MHs are optimization methods ba-

sed in robust strategies to avoid optimal local soluti-

ons (Gendreau and Potvin, 2010). Different MHs pro-

vide satisfactory solutions for different instances from

PSD, however, how to select the most promising for

an speciﬁc DSP? It involves a typical selection pro-

blem algorithm (Rice, 1976). According to the theo-

rem ”No free Lunch” (Wolpert and Macready, 1997)

always selecting the same algorithm does not produce

satisfactory results. On the other hand, by processing

all available algorithms for the desired instance and

after select the best solution would be relevantly ex-

pensive. A computational methodology could provide

a comprehensive framework for MHs management in-

cluding to plan, run, schedule, control and analyse

different algorithms and results on the duplication se-

quence problems. To the best of our knowledge, there

is no methodology available which describes how to

conduct a feasibility way to ﬁnd the best solution in

DSP problems. This paper proposes a methodology

based on simulation and optimization techniques to

identify satisfactory solutions for a determined DSP

problem, comparing the performance between diffe-

rent MHs in order to ﬁnd which is the more promising

over different instances. The remaining of this paper

is organized as follows: section 2 describes the DSP

problem. Section 3, presents a brief literature review

of Railway Capacity Concepts, Simulation and Opti-

mization approaches in transportation systems. Three

varieties of algorithms are discussed based on the se-

arching space model. Section 4 presents and explains

the methodology; in section 5, a mathematical mo-

deling is depicted; a case study based in railway sys-

tems is reported in section 6. Section 7 gives conclu-

sions and ﬁnal remarks.

Araujo, H. and Vale, S.

DOTSIM - A Simulation-based Optimization Methodology for the Optimal Duplication Sequence on Freight Transportation Systems.

DOI: 10.5220/0006337404590466

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 2, pages 459-466

ISBN: 978-989-758-248-6

459

2 DUPLICATION SEQUENCE

PROBLEM IN

TRANSPORTATION

SYSTEMS - DSP

For most of the DSP problems the exhaustive search

for the best solution requires complex modeling and

hard computational efforts. A problem with 10 sin-

gle routes has about 3.5 x 10

viable solutions. An

exhaustive search processed by a computer with ca-

pacity to process 1 billion solutions per second would

ﬁnd the best one in about four years. Certainly,

an analyst will not spend all this time to deﬁne the

best duplication sequence for a transportation system

which needs investments in its infrastructure.

Figure 1: A Rail Transportation System with two single seg-

ments and three crossing loops.

DSP basically consists on deﬁning the best pri-

ority duplication sequence in transportation systems

that still have single routes or segments (as depicted

in ﬁgure 1) and that is experiencing a need to incre-

ase its transportation capacity to support an increase

in demand. Moreover, in DSP all single routes should

be duplicated and the priority of each route must be

deﬁned. The complexity of a DSP increases exponen-

tially according to the amount of singles segments as

showed in ﬁgure 2.

We can also observe in ﬁgure 2 an example of pri-

ority for a system with N=5 single segments. The

priority deﬁned is shown by the arrow, in other words,

the ”S1” is going to be the ﬁrst segment duplicated,

and the last will be the ”S5”. In additional, for each

route selected to duplicate, there are N-1 more possi-

bilities. That is the reason for DSP become a permuta-

tion problem. For system with 5 segments, we would

have a search space with 5! or 120 viable solutions.

Figure 2: Feasible Solutions for a railway with 5 singles

segments/routes.

Each segment has a cost which can be represen-

ted by a variety of variables which depend on the ob-

jective of the transport route analyst, e.g, investment

costs, capacity costs, or the average between them,

etc.

There are a variety of applications in the real

world that are modeled through the DSP, such as

freight and passenger in onshore transportation sy-

stems, e.g. railways, LRVs (Light Rail Vehicles),

highways, roads, subway etc.

3 RAILWAY CAPACITY

CONCEPTS

3.1 Simulation

(Pegden et al., 1995) presents a more complete de-

ﬁnition, covering the entire simulation process. He

mentions that ”simulation is the process of designing

a computer model of a real system and conducting

experiments with this model in order to understand

their behavior and/or evaluate strategies for their ope-

ration.” As noted, the mentioned author considers that

simulation as a larger process, including not only the

construction of the template, but also all the following

experimental method, searching excessively: (i) To

describe the system behaviour, (ii) To build theories

and hypotheses considering the observations made,

(iii) To provide a base model for future behaviour pre-

dictions, that means, the effects produced by changes

in the system or employed in methods over its opera-

tion.

There are a variety of simulation software which

can measure the cost for feasible solutions to DSP

problems such as GPSS, JSL, Arena, ProModel, Si-

mul8 and FlexSim among more than sixty commer-

cial simulators.

In this research, a framework and open source

software called the Java Simulation Library (JSL) is

used as a simulation environment. The JSL has been

used in a number of researches and educational set-

tings; however, its implementation has not been fully

described in the literature except through its many ap-

plications (Rossetti, 2008).

This paper uses a simulation model as an objective

function in the search for optimal solutions. The key

indicator deﬁned by the analyst is collected in the si-

mulation model which should be maximized or mini-

mized. Detailed information about the infrastructure

(e.g. rail segments capacities, disturbances, preven-

tive maintenance, number of trains, headway, etc) are

necessaries to specify the input data for the simulation

model.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

460

3.2 Optimization Approach

Simulation-Optimization and its applications in

railways: Simulation-based optimization stands for

a programming problem (usually a stochastic one)

whose objective function is evaluated by means of an

experimental simulation. Due to the complexity and

the stochasticity considered within the simulation, the

objective function is (i) usually subject to several le-

vels of random noise, (ii) not necessarily differenti-

able, and (iii) expensive to evaluate from the com-

putational standpoint. It is intuitive that simulation

optimization problems can be intractable if the op-

timization problem has a large number of variables

and/or the simulation involves many parameters and

many interactions to be described. The mathemati-

cal formalization and the computational complexity

of optimizing via simulation is clearly described in

(Fu, 1994; Fu, 2002).

In the ﬁeld of railway systems, simulation-based

optimization has been used to face different problems

regarding the design of both train operations and in-

frastructure. A method for robust timetabling is intro-

duced by (Kroon et al., 2008) which adopts a stochas-

tic optimization model to allocate time supplements

and buffer times in a timetable in order to make it ro-

bust against stochastic disturbances during real ope-

rations.

It is important to emphasize that this work treats

the duplication railway sequence as a classic problem

of permutation considering as an NP-hard problem in

combinatorial optimization. (Kang et al., 2014) men-

tions that the MHs more used to similar permutation

problems, such as the Travelling Salesman Problem

(TSP) are: Tabu-Search (TS), Greedy Randomized

Adaptive Search Procedure (GRASP), Simulated An-

nealing (SA), genetic Algorithm (GA), and Colony

Optimization Algorithm (COA).

3.3 Optimization Approach for DSP in

Railways

In this paper, three approaches were explored:

Genetic Algorithm: Genetic techniques were cho-

sen because of their suitability in optimizing non-

polynomial (NP) complete problems. GAs have alre-

ady been used for symbolic layout, (Fourman, 1985),

and work scheduling (Davis, 1985).

Chromosomes were constructed in which each

gene represents the segment to be duplicated in chro-

nological order. Connected with each chromosome

is a ﬁtness represented by the amount of discharged

trains which is collected from the simulation model.

The method use a population of chromosomes, each

chromosome is tested and a ﬁtness is evaluated. A

new population of chromosomes is bred from the cur-

rent population, with the parents chosen on a ﬁtness

basis.

Each generation was evaluated in the following

manner: it is created an initial population which is

randomly generated with one hundred duplication rail

sequences. Then each member of the population is

then evaluated and a ﬁtness for that individual is si-

mulated.

In the selection stage the current population is im-

proved discarding the bad designs and only keep the

best individuals in the population. The basic idea was

ﬁtter individuals were selected for next generations.

During crossover new individuals or duplication se-

quences were created by combining aspects of our

selected individuals. This ’combining aspects’ is to

cross two individuals and create two new sons who

combine part of the chromosome from their parents.

The goal is that this aspect combination between indi-

viduals create an even ’ﬁtter’ offspring which will in-

herit the best traits from each of their parents. To add

a little bit randomness into our population’s genetics

it was implemented a mutation state which typically

random swaps were done to individuals genome. Now

we provide our next generation and we can start again

until a termination condition.

Tabu-Search: The tabu search (TS) is a determi-

nistic metaheuristic based on local search (Glover,

1986), which makes extensive use of memory for gui-

ding the search. Basic elements of a tabu search are

the concepts of move and tabu list, which restrict the

set of solutions to explore. From the incumbent solu-

tion, non-tabu moves deﬁne a set of solutions, called

the neighborhood of the incumbent solution. At each

step, the best solution in this set is chosen as the new

incumbent solution. Then, some attributes of the for-

mer incumbent are stored in a tabu list (TL), used by

the algorithm to avoid being trapped in local optima

and to avoid re-visiting the same solution. The moves

in the tabu list are forbidden as long as these are in

the list, unless an aspiration criterion is satisﬁed. The

tabu list length can remain constant or be dynamically

modiﬁed during the search.

Simulated Annealing: SA has been adopted wi-

dely to solve engineering problems,e.g., trains plat-

form problem (Kang et al., 2014), transit network op-

timization problem (Zhao and Zeng, 2006), and bott-

leneck routing problem at railway stations (Wu et al.,

2012), etc. The SA starts from an initial solution at

a high temperature, and makes a number of changes

DOTSIM - A Simulation-based Optimization Methodology for the Optimal Duplication Sequence on Freight Transportation Systems

461

according to annealing schedules. For any two itera-

tions, there are two objective values marked as few

and fold, and the difference between the objective va-

lues (∆f - fnew - fold) is calculated.If ∆f¡= 0, then

the new solution is accepted with probability ρ-1. Ot-

herwise, it is accepted with a small probability ρm,

ρ-exp(-∆f/T), where T is the current annealing tem-

perature (Kang et al., 2014). As the cooling proceeds

to the set frozen point, the algorithm terminates.

4 DOTSIM METHODOLOGY

In this paper, we propose the DOTSIM methodology

to aid ﬁnding solutions with high quality in dupli-

cation sequencing problem in complex transportation

systems. Our methodology has the following charac-

teristics:

(i) We assume that the methodology can be ap-

plied for any onshore freight and passengers trans-

portation system such as: railways, LRVs (Light Rail

Vehicles), highways, roads, public transportation (e.g.

subway), etc, that is experiencing a need to increase

its capacity of transport so as to support an increase

in demand.

(ii) The objective function is strictly a simulation

model inside a optimization loop.

(iii) Our methodology is meant for both resear-

chers and practitioners and those users having a ba-

sic knowledge of simulation and optimization techni-

ques.

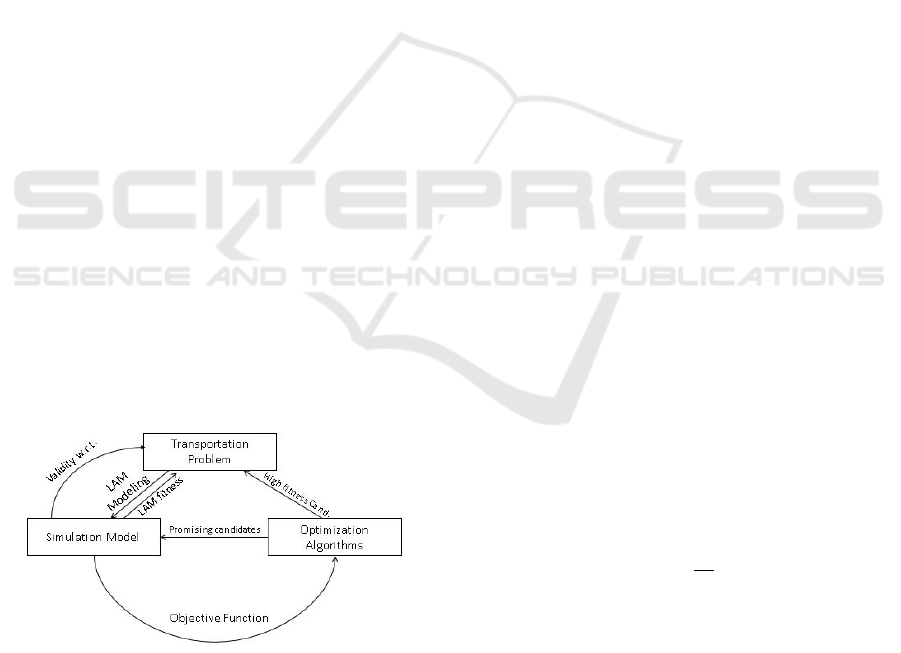
We distinguish the relationships among simula-

tion model, deﬁnition of the problem, optimization

techniques and linear analytical method (LAM) in ﬁ-

gure 3.

Figure 3: Simulation model, deﬁnition of the problem, op-

timization techniques and LAM.

A transportation problem is a transportation sy-

stem (real or proposed) that can be modeled. A simu-

lation model is a casual model of infrastructure of the

transportation system; this model may have determi-

nistic or stochastic variables as inputs. It tests dupli-

cation sequence candidates coming from the optimi-

zation algorithms and the own transportation system

through the LAM and works as an objective function.

The optimization algorithms are the MHs which will

choose promising candidates to the simulation mo-

del and receive feedbacks with the candidate’s ﬁtness.

Candidates with high quality ﬁtness are ranked by the

MHs and compared with a LAM with is measured

by the Simulation Model. Validation is a key part of

the methodology because it conﬁrms that the model

works in accordance with the analyst’s objective. Fi-

gure 3 shows that validation of a simulation model re-

lates to the transportation system, where w.r.t. stands

for ’with respect to’ (for validation of simulation mo-

dels see (de Freitas Filho, 2001)).

5 MATHEMATICAL MODELING

A railroad train analyses the capacity of the railway

line by measuring the practical and theoretical capa-

city of the rail network. The theoretical capacity is

considered as the maximum limit to the number of

trains that can simultaneously navigate a particular

stretch, also known as a theoretical maximum capa-

city.

The theoretical maximum capacity is characteri-

zed by the temporal spacing between trains, which

depends on the commercial speed of each train, travel

times and resources offered by signaling and existing

licensing systems.

In the case of simple line, the interval between

trains is proportional to the distance between consecu-

tive intersection of deviations away from the one that

can be counted among axes of stations, or between a

starting signal consecutive patios (when there is ap-

propriate signaling system, or when you can compute

the blocking times of simple line).

The maximum theoretical capacity can be equated

by the following mathematical expression:

C =

(1)

The C means capacity in number of trains/day and

the T means Travel time between shifts , round trip

(”headway”).

The value of the capacity is inversely proportional

to the travel times between shifts (equation 1). The

lower capacity snippets generate critical sections or

bottlenecks that determine the ﬂow capacity of the en-

tire line.

Trafﬁc or ﬂow capacity of a rail section is deﬁ-

ned by the number of trains which may move within a

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

462

given time interval (BRINA, 1982). The author indi-

cates two possibilities of calculation , one through the

actual graphic movement of trains and analytically by

Colson method , according to equation 2.

For this method, (BRINA, 1982) indicates the

need to use a factor that differentiates the rail accor-

ding to its efﬁciency, ranging from 60% to 80%, ter-

med ”K” factor. Addition of (BRINA, 1982), (Kraft,

1982) mentions that this K factor can vary between

60% and 75%. (Krueger et al., 2000) quoted in (Bar-

ros, 2013), cites that this parameter, the value of the

factor K, is the capacity that can be permanently pro-

vided under normal operating conditions and is ap-

proximately 2/3 of the theoretical capacity.

However , (Krueger et al., 2000) quoted in (Bar-

ros, 2013), uses three different deﬁnitions to classify

the types of capacity in evaluating the performance of

a railway system, unlike Brina, as follows: theoretical

capacity, practical and used.

The theoretical capacity is deﬁned by (Krueger

et al., 2000) cited (Barros, 2013) as the number of

trains that travel on a route in a given set period of

time, under ideal conditions, characterized by a vir-

tual scenario in which the trains have movement con-

stant with minimum headway between them. This

parameter expresses the maximum trafﬁc capacity,

whereas the movement of the trains is homogeneous

throughout the day, they are spaced evenly and no in-

terruptions in the system. To be a value obtained by

empirical formula and does not consider the effects

of trafﬁc variation and operations is impossible to be

practiced in real conditions.

The practical capacity is the number of boundary

units that can move on the railway line with a certain

level of reliability. A factor reﬂecting the conditions

of circulation of different types of trains with distinct

priorities, according to the accumulated trafﬁc and ot-

her system conditions, it is a more realistic measure

of capacity. How is the speciﬁc combination of in-

frastructure, trafﬁc and operations to move the maxi-

mum amount of products with a level of service and

predetermined reliability is the most signiﬁcant media

capacity of the rail system. (Krueger et al., 2000)

The following mathematical formula that expres-

ses the above deﬁnition:

C = k ∗

24 − T m

T s + T d

(2)

In this case the Tm means time allowed for the

maintenance of permanent way, Ts rise time or loa-

ding transit, Td fall time or unloading transit and K a

operational efﬁciency factor.

Table 1: SUBSCRIPTS AND PARAMETERS.

Symbol Deﬁnition

C Trafﬁc of ﬂow capacity of a rail section

Tm Time allowed for the maintenance of

permanent way

Ts Rise time or loading transit

Td Fall time or unloading transit

K Operational efﬁciency factor

6 CASE STUDY: DEFINING BEST

DUPLICATION SEQUENCE OF

SINGLE-TRACK RAILWAYS IN

ORDER TO INCREASE

CAPACITY OF

TRANSPORTATION

Companies have used LAMs to obtain optimal solu-

tions for railways duplication strategy. In this met-

hod, the single-track segments that are prioritized in

an ’optimal’ sequencing. That sequence is the one

which has the lowest ratio between practical capacity

(trains/day) and demand (also trains/day). In the case

shown in table 2 there is a clear imbalance in the ca-

pacities of segments (column 2), which in practice is

very common to happen because different altimetry

proﬁles pathway, communities near the railway, brid-

ges, viaducts etc.

Table 2: Practical Capacity versus Segment’s Demand

(trains/day).

Segment Practical

Capacity

Demand Balance

0-1 10.0 3.0 7

1-2 12.0 8.5 3.5

2-3 5.0 2.0 3

3-4 20.0 5.0 15

4-5 8.0 4.0 4

Given the results of table 3, the best strategy for

doubling this railway would be:

For the above example with 5 single-track seg-

ments, it is possible to evaluate a combination of 5!

different layouts or 120 possibilities. This complex-

ity tends to increase in railways with large distances.

For example, for a railway with 10 segments is pos-

sible to evaluate a combination of almost four million

different duplication sequences.

It is common practice in companies ﬁnd difﬁculty

to duplicate a lot of single-track segments in a short

DOTSIM - A Simulation-based Optimization Methodology for the Optimal Duplication Sequence on Freight Transportation Systems

463

Table 3: Optimal Duplication Sequence by analytical met-

hod.

Segment Priority

0-1 4

1-2 2

2-3 1

3-4 5

4-5 3

space of time, as this often conﬂicts with hand limi-

tations of skilled labor, large equipment etc. Also the

investments are very aggressive with values that ﬂuc-

tuate between 1.5 and 3.5 million dollars per kilome-

ter of railway line built.

In an attempt to avoid processing a problem with

this level of complexity with linear analytical met-

hods, the DOTSIM is applied in order to identify the

optimal solution to increase the capacity of a single-

track railway.

6.1 Modeling the Problem in JSL

In this paper an ”own-built” model has been used to

have a ﬂexible simulation environment that can be

effectively interfaced with mathematical tool-boxes

for white-box optimization, this means to be ﬂexible

enough to implement optimization algorithms and to

be adapted to the own needs of the user.

The framework used to model the railway is the

JSL. For introduction of modeling a passing loop of

JSL, was adopted a generic, hypothetical example.

Entities (trains) coming into the system and make the

discharge point of control or join a queue if it is busy.

In this problem we have to study a system which

transports a product from the loading point to the un-

loading point, with N passing loops or rail-houses

(RH) following the premises of times and movements

of the logistic system. The values of headway invol-

ved in the computational process were obtained rand-

omly according to speciﬁc route and operating cha-

racteristics as well as happens in dynamics complica-

ted systems or heavy-haul railways.

For all instances was adopted a saturation condi-

tion or heavy trafﬁc in the system. For each duplica-

tion was adopted a period of 7 days. In order to ensure

statistical conﬁdence level was deﬁned an amount of

10 replications, based on a tolerance of at least 90%

through of the observation of the moving average ﬁt-

ness, a simulation model output.

The model was developed in JSL generically re-

presenting railways with up to N segments. In other

simulation languages, this is a similar concept to ope-

ning a model building window (creating a model) and

dragging and dropping simulation constructs into the

model (Rossetti, 2008). Figure 4 presents the model

for the railway system proposed. The class ’ferrovia’

represents the entire system and can hold instances of

segments.

Figure 4: Java code based on JSL for a railway model.

Stochastic disturbances were implemented in the

JSL model by using a random routine creating events

that make the segments unavailable or failed (also

randomly). We deﬁned to the railway system stu-

died in this work, random distributions to represent

the time between failures and deterministic time for

the duration of the failure.

The JSL administer inputs data in the three follo-

wing different interacting modules:

- Infrastructure module: Input data required by

this module concern to tracks capacity (single or du-

plicated) as well as the railway duplication strategy

setting up the order of each segment.

- Rolling stock module: Rail vehicles have been

represented in this model by deﬁning the amount of

trains which are in the closed rail system.

- Timetable module: Import and export times be-

tween stations or passing loops with or without train

stop, stay times inside the load and unload points, are

all input data of this module.

The conception of the JSL rail model is based on

(Ara

ujo, 2013) which uses licensing rules, a set of ru-

les and procedures to ensure the safe movement of

trains.

6.2 Results

Results obtained for each instance are considered as

the average of simulation results over the 10 different

disturbed scenarios, or replications. The duplication

sequence problem has been solved for all the scena-

rios, considering a comparison with the LAM for this

problem.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

464

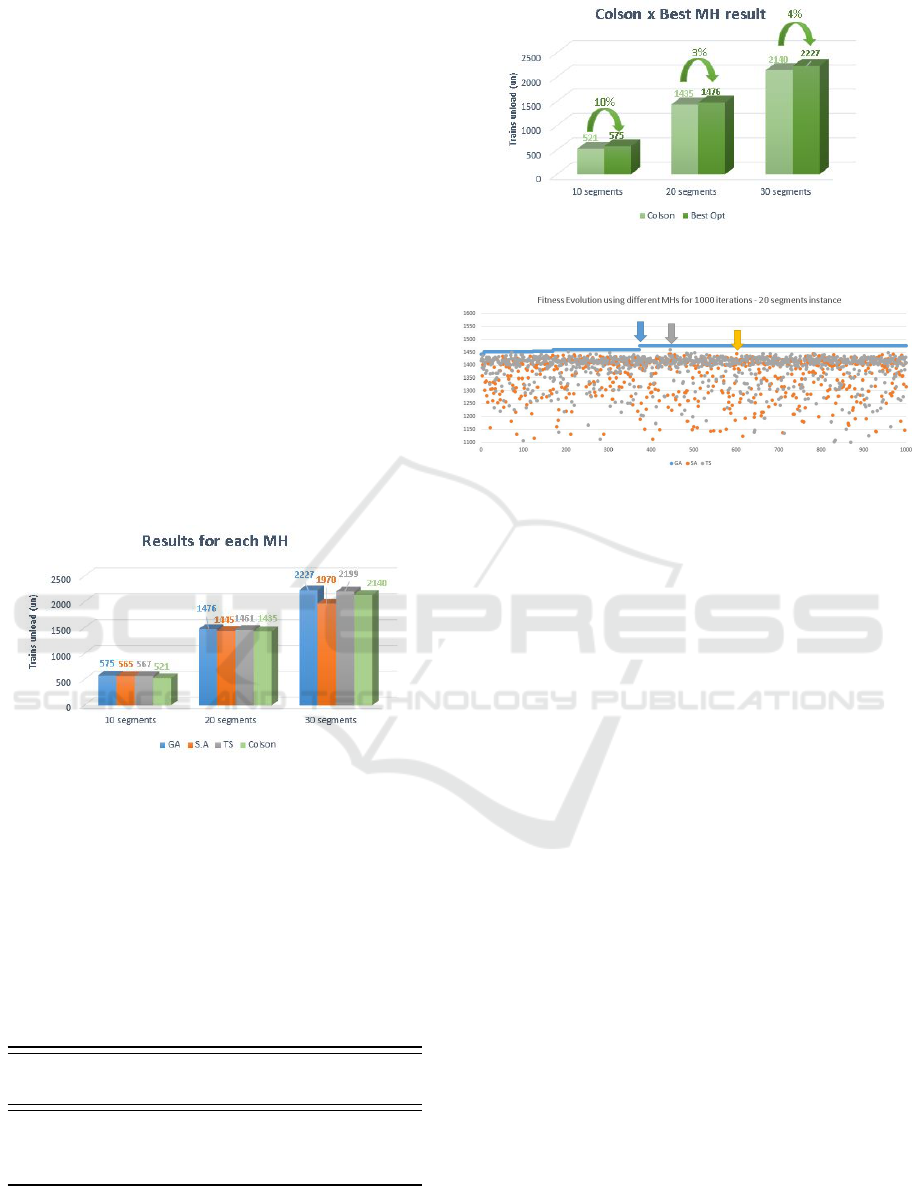
In ﬁgures 5 and 6 are shown the evolution curves

of the three MHs for 1000 iterations or generations

in the case of GA. It is possible to achieve a gain of

10% in the ﬁrst instance. Furthermore, it is possible

to observe a decrease of this gain according to the in-

crease of the amount of segments. This probably hap-

pens because the search space increases exponentially

with more single-tracks in the problem as said in the

section 5.

Figure 5 reports the results for each MH in the 3

instances. The genetic algorithm achieves the best re-

sults unanimously for all the scenarios. We can also

analyze that the best result for the GA is achieved with

almost 400 iterations and after that we see just a con-

stant behavior (Fig. 7); in the ﬁgure 7 the blue line

refers to the GA, orange line to SA and gray line to

Tabu-Search.The tabu-search algorithm waits a little

more to achieve its best result as well as the simulated

annealing algorithm. This behavior is also observed

in the other instances, with another conclusion which

it indicates that the SA moves more away of the best

candidates.

Figure 5: Ranking of Meta Heuristics for the railway dupli-

cation sequencing problem.

Another advantage for the GA is the computing

time as shown in the table 4. The SA spent less time

than the GA and Tabu-search but do not achieve the

best candidate comparing with the LAM. The tabu-

search spent a huge computing time to explore the se-

arch space specially in the 30-segments railway sce-

nario.

Table 4: Computing times to solve the optimization pro-

blem (hours).

MH 10 seg-

ments

20 seg-

ments

30 seg-

ments

G.A. 3.7 16.5 40

S.A. 0.2 0.5 1.5

Tabu Search 10.3 45.4 140

Figure 6: Comparison between best MH result and the

LAM (Colson).

Figure 7: Fitness Evolution using different MHs for 1000

iterations - 20 instance segments.

7 CONCLUSIONS

Practitioners strongly need to increase the capacity le-

vel of freight transportation systems in order to meet

growing levels in passengers and freight demand. To

achieve this objective, to duplicate the routes of the

system is sometimes necessary. Duplication sequen-

cing problems are NP-hard optimization problems.

Up to now both in practice and in scientiﬁc literature,

companies and existing approaches have used analy-

tical linear methods for a problem which is naturally

complex and non-linear.

To solve this problem a simulation-based optimi-

zation methodology is presented which guides sear-

ching the optimal duplication sequence on routes of

freight transportation systems.

A case study with different instances for railways

is presented with the application of three MHs. The

objective of this study is ﬁnding satisfactory soluti-

ons compared with analytical linear methods, which

is relevant because it can help railway companies to

minimize costs and to increase railway productivities.

Furthermore, the duplication strategy in a whole rail-

way can be deﬁned by considering only a single opti-

mization problem.

Results of models in different instances with N

single segments and stochastic factors which maxi-

mize the number of unloaded trains during the con-

struction period and which are also robust with re-

spect to random operation disturbances show the abi-

DOTSIM - A Simulation-based Optimization Methodology for the Optimal Duplication Sequence on Freight Transportation Systems

465

lity of DOTSIM to search global optimal solutions for

supporting duplication strategies in railways.

A comparison with analytical method underlined

that the proposed method strongly increases the rail-

way capacity and consequently decreases investment

costs.

Further research will be addressed to evaluate

more instances, more complex disturbances that can

inﬂuence the integrated system, such as several load

and unload points, exchange points etc.

ACKNOWLEDGEMENTS

This research is supported by FAPEMA.

REFERENCES

Ara

ujo, H. F. H. (2013). Utilizac¸

ao de ferramentas de

simulac¸

ao para analise de capacidade e dimensiona-

mento material rodante da efc.

Barros, J. (2013). Avaliac¸

ao dos principais m

etodos

anal

ıticos de c

alculo de capacidade de tr

afego utiliza-

dos em ferrovia nacional e internacional. PhD thesis,

Dissertac¸

ao de Mestrado–UFMG, Minas Gerais.

BRINA, H. L. (1982). Estradas de ferro, volume i e ii. Rio

de Janeiro, LTC: Livros T

ecnicos e Cient

ıﬁcos Editora

SA.

Davis, L. (1985). Job shop scheduling with genetic algo-

rithms. In Proceedings of an international conference

on genetic algorithms and their applications, volume

140. Carnegie-Mellon University Pittsburgh, PA.

de Freitas Filho, P. J. (2001). Introduc¸

a modelagem e

simulac¸

ao de sistemas: com aplicac¸

oes em Arena. Vi-

sual Books.

Fourman, M. P. (1985). Compaction of symbolic layout

using genetic algorithms. In Proceedings of the 1st

international conference on genetic algorithms, pages

141–153. L. Erlbaum Associates Inc.

Fu, M. C. (1994). Optimization via simulation: A review.

Annals of Operations Research, 53(1):199–247.

Fu, M. C. (2002). Optimization for simulation: The-

ory vs. practice. INFORMS Journal on Computing,

14(3):192–215.

Gendreau, M. and Potvin, J.-Y. (2010). Handbook of meta-

heuristics, volume 2. Springer.

Glover, F. (1986). Future paths for integer programming

and links to artiﬁcial intelligence. Computers & ope-

rations research, 13(5):533–549.

Kang, L., Zhu, X., Wu, J., Sun, H., Siriya, S., and Kanok-

vate, T. (2014). Departure time optimization of last

trains in subway networks: mean-variance model and

gsa algorithm. Journal of Computing in Civil Engi-

neering, 29(6):04014081.

Kraft, E. R. (1982). Jam capacity of single track rail lines.

In Proceedings of the Transportation Research Forum,

volume 23.

Kroon, L., Mar

oti, G., Helmrich, M. R., Vromans, M., and

Dekker, R. (2008). Stochastic improvement of cyclic

railway timetables. Transportation Research Part B:

Methodological, 42(6):553–570.

Krueger, H., Vaillancourt, E., Drummie, A. M., Vucko, S. J.,

and Bekavac, J. (2000). Simulation within the railroad

environment. In Proceedings of the 32nd conference

on Winter simulation, pages 1191–1200. Society for

Computer Simulation International.

Pegden, C. D., Sadowski, R. P., and Shannon, R. E. (1995).

Introduction to simulation using SIMAN. McGraw-

Hill, Inc.

Rice, J. R. (1976). The algorithm selection problem. Ad-

vances in computers, 15:65–118.

Rossetti, M. D. (2008). Java simulation library (jsl): an

open-source object-oriented library for discrete-event

simulation in java. International Journal of Simula-

tion and Process Modelling, 4(1):69–87.

Wolpert, D. H. and Macready, W. G. (1997). No free lunch

theorems for optimization. IEEE transactions on evo-

lutionary computation, 1(1):67–82.

Wu, J., Kang, L., Sun, H., and Jia, X. (2012). Track allo-

cation optimization in railway station: mean-variance

model and case study. Journal of Transportation En-

gineering, 139(5):540–547.

Zhao, F. and Zeng, X. (2006). Simulated annealing–genetic

algorithm for transit network optimization. Journal of

Computing in Civil Engineering, 20(1):57–68.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

466