fgssjoin: A GPU-based Algorithm for Set Similarity Joins

Rafael D. Quirino, Sidney R. Junior, Leonardo A. Ribeiro and Wellington S. Martins

Instituto de Informatica, Universidade Federal de Goias (UFG), Alameda Palmeiras, Quadra D, Campus Samambaia,

CEP 74001-970, Goiania, Goias, Brazil

Keywords:

Advanced Query Processing, High Performance Computing, Parallel Set Similarity Join, GPU.

Abstract:

Set similarity join is a core operation for text data integration, cleaning and mining. Most state-of-the-art

solutions rely on inherently sequential, CPU-based algorithms. In this paper we propose a parallel algorithm

for the set similarity join problem, harnessing the power of GPU systems through ﬁltering techniques and

divide-and-conquer strategies that scales well with data size. Experiments show substantial speedups over the

fastest algorithms in literature.

1 INTRODUCTION

In the last few decades there have been substantial

improvements in database systems, in part due to its

commercial importance, usefulness and extensive tes-

ting throughout the years. And yet, managing com-

plex data objects in these systems remains a chal-

lenge. In fact, many operations which are ﬁne for

simple objects are often ineffective for complex ones.

A good example is equality tests. They are ubiquitou-

sly used in database management operations, but of-

ten cannot capture the subtle relations between com-

plex objects, which highlights the need for similarity

calculations on such data.

Set similarity join is the operation of retrieving all

pairs of data objects (represented by sets of features)

from some data collection, for which the result of a

similarity function is not less than a given threshold.

The problem has attracted growing attention over the

years (Sarawagi and Kirpal, 2004; Chaudhuri et al.,

2006; Bayardo et al., 2007; Vernica et al., 2010; Xiao

et al., 2011; Ribeiro and H

arder, 2011; Wang et al.,

2012; Cruz et al., 2016), as volume and complexity

of data increase in the current Big Data era. It is both

an important operation by itself, and a crucial step for

more advanced data processing tasks, including inte-

gration (Doan et al., 2012), cleaning (Chaudhuri et al.,

2006), and data mining (Leskovec et al., 2014).

Assessing the exact similarity between complex

objects, particularly for joins where all pairs of ob-

jects must be compared, is often expensive, even for

state-of-the-art algorithms. In the case of textual

data, the infamous curse of dimensionality becomes

very apparent, since text data representations are of-

ten sparse and high-dimensional. Set-based simila-

rity functions are very attractive in this context be-

cause predicates involving such functions can be equi-

valently expressed as a set overlap constraint. As a

result, set similarity join is reduced to the problem of

identifying set pairs with enough overlap.

In this scenario, it becomes clear that parallel so-

lutions are welcome. Today, virtually all processors

support parallelism through the use of multiple cores.

Multi-core processing is a growing trend in the indu-

stry, and it has been followed by the so-called many-

core architectures like GPUs (graphical cards used

for general purpose computing). Many-core proces-

sors, also known as accelerators, have a large number

of processing units — hundreds or thousands — but in

the form of slower and simpler cores. Recent develop-

ments and the affordability of GPUs have made them

attractive to scientists in many areas. GPUs are de-

signed for massive multi-threaded parallelism and are

inherently energy-efﬁcient because they are optimi-

zed for throughput and performance per watt. Howe-

ver, GPUs have a different architecture and memory

organization from traditional CPUs. Therefore, con-

siderable parallelism (tens of thousands of threads)

and an adequate use of its hardware resources are nee-

ded to fully exploit its capabilities. This fact imposes

some constraints in terms of designing appropriate al-

gorithms and new implementation approaches.

In this paper we present a ﬁne-grained parallel al-

gorithm for the set similarity join problem and a GPU-

based implementation of this algorithm that allows

the usage of state-of-the-art preﬁx ﬁltering techni-

152

Quirino, R., Junior, S., Ribeiro, L. and Martins, W.

fgssjoin: A GPU-based Algorithm for Set Similar ity Joins.

DOI: 10.5220/0006339001520161

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 152-161

ISBN: 978-989-758-247-9

ques. The proposed parallel algorithm is based on

a divide-and-conquer strategy and partitioning of the

data set in blocks in such a way that all blocks are

indexed and queried against all others, following an

index-ﬁlter-verify cycle. This strategy ensures that

any data set can be processed regardless of the GPU

memory available. It also allows the skipping of some

blocks from being queried against others for which no

match could be generated. The main contributions of

this paper are:

• A parallel algorithm for the set similarity join pro-

blem.

• A GPU-based implementation of the proposed al-

gorithm.

• Extensive experimental work with standard data-

sets.

The remainder of this paper is organized as fol-

lows. Section 2 covers related work. Section 3 deﬁ-

nes the set similarity join problem and introduces im-

portant concepts. Section 4 presents an overview of

the architecture and programming model of a GPU.

Section 5 describes our solution. Section 7 presents

the experimental evaluation, while Section 8 conclu-

des the paper.

2 RELATED WORK

There have been many research on sequential set si-

milarity joins algorithms (Sarawagi and Kirpal, 2004;

Chaudhuri et al., 2006; Arasu et al., 2006; Bayardo

et al., 2007; Xiao et al., 2011; Ribeiro and H

arder,

2011; Wang et al., 2012). An experimental evalua-

tion of several state-of-the-art set similarity join al-

gorithms is presented by Mann et al. (Mann et al.,

2016). The ﬁltering-and-veriﬁcation framework is

prevalently adopted by such algorithms: ﬁrst, various

ﬁltering schemes are used to prune set pairs that can-

not meet the threshold; the actual similarity compu-

tation is then performed on each of the remaining set

pairs and those deemed as similar are sent to the out-

put. Popular ﬁltering schemes are length-based ﬁlter

(Sarawagi and Kirpal, 2004; Arasu et al., 2006), pre-

ﬁx ﬁlter (Sarawagi and Kirpal, 2004; Chaudhuri et al.,

2006; Ribeiro and H

arder, 2011; Wang et al., 2012),

and positional ﬁlter (Xiao et al., 2011). Veriﬁcation

can be optimized by employing a merge-like proce-

dure that stops earlier on set pairs that do not satisfy

the similarity constraint. Our proposed algorithm ex-

ploits all those optimization on many-core architectu-

res.

Approximate set similarity joins resort to data re-

duction techniques to speed up processing time. The

most popular technique in this context is Locality

Sensitive Hashing (LSH) (Indyk and Motwani, 1998),

which is based on hashing functions that are approx-

imately similarity-preserving. However, LSH-based

algorithms may miss valid output pairs. In contrast,

our approach always produces an exact result.

Another popular type of string similarity join em-

ploys constraints based on the edit distance, which is

deﬁned by the minimum number of character-editing

operations — insertion, deletion, and substitution —

to make two strings equal. As one can derive set

overlap bounds from the edit distance (Gravano et al.,

2001), the ﬁltering phase of our proposal can be rea-

dily used to reduce the number of distance computa-

tions (edit distance also lends itself to efﬁcient GPU

implementation (Chac

on et al., 2014)).

Lieberman et al. (Lieberman et al., 2008) presen-

ted a parallel similarity join algorithm for distance

functions of the Minkowski family (e.g,. Euclidean

distance). The algorithm ﬁrst maps the smaller input

dataset to a set of space-ﬁlling curves and then per-

forms interval searches for each point in the other da-

taset in parallel. The overall performance of the algo-

rithm drastically decreases as the number of dimen-

sions increases (see Figure 5b in (Lieberman et al.,

2008)) because every additional dimension requires

the construction of a new space-ﬁlling curve. Thus,

this approach can be prohibitively expensive on text

data, whose representation typically involves several

thousands of dimensions.

Cruz et al. (Cruz et al., 2016) proposes an approx-

imate set similarity join algorithm designed for GPU.

The Jaccard similarity between two sets is estimated

using MinHash (Broder et al., 1998), an LSH scheme

for Jaccard. MinHash can be orthogonally combined

with our algorithm to reduce set size and, thus, obtain

greater scalability.

To the best of our knowledge, the gSSJoin al-

gorithm, proposed by Ribeiro-Junior et al. (Junior

et al., 2016), is the only existing GPU-based algo-

rithm for exact set similarity join. Similarly to our

approach, gSSJoin ﬁrst builds an inverted index be-

fore performing similarity computations. However,

gSSJoin does not employ any ﬁltering technique to re-

duce the comparison space. We compare our proposal

with gSSJoin in Section 7.

Finally, recent work proposed to perform set si-

milarity joins on the MapReduce framework (Vernica

et al., 2010; Deng et al., 2014). We plan to investigate

the integration of fgssjoin into a distributed platform

to accelerate local computation in future work.

fgssjoin: A GPU-based Algorithm for Set Similarity Joins

153

3 BACKGROUND

In this section, we provide background on set simila-

rity join concepts and techniques.

3.1 Mapping Text Data to Sets

In order to express text data as sets of features, we use

the notion of q-grams, which are tokens obtained by

”sliding” a window of size q over the characters of a

given string. For example, if we have two strings s

”Computation” and s

= ”Compilation”, we have the

following 2-gram sets:

x = {Co, om, mp, pu, ut, ta, at,ti, io, on}

y = {Co, om, mp, pi, il, la, at, ti, io, on}

Applying the Jaccard similarity function (JS) to

the strings above yields:

JS(x, y) =

x ∩ y

x ∪ y

10 + 10 − 7

∼

0, 538.

3.2 Problem Deﬁnition, Basic Concepts,

and Optmization Techniques

Deﬁnition 1. (Set Similarity Join). Let U be a uni-

verse of features, C be a set collection where every

set consists of a number of features from U, Sim(x, y)

be a similarity function that maps two sets from C to

a number in [0, 1] and γ be a number in [0, 1] (called

threshold). Set similarity join is the operation of de-

ﬁning the set S of all pairs of sets from C, for which

Sim(x, y) ≥ γ.

We focus on a general class of set similarity

functions, for which the similarity predicate can be

equivalently represented as a set overlap constraint.

Speciﬁcally, we express the original similarity pre-

dicate in terms of an overlap lower bound (overlap

bound, for short) (Chaudhuri et al., 2006).

Deﬁnition 2. (Overlap Bound). Let x and y be sets

of features, Sim be a set similarity function, and γ be

a similarity threshold. The overlap bound between x

and y relative to Sim, denoted by overlap(x, y)

, is a

function that maps γ and the sizes of x and y to a real

value, s.t. Sim(x, y) ≥ γ ⇔

x ∩ y

≥ overlap(x, y).

This way, the similarity join problem can be re-

duced to a set overlap problem, in which we need to

obtain all pairs (x, y) whose overlap is not less than

overlap(x, y). The set overlap formulation enables

the derivation of size bounds. Intuitively, observe that

x ∩ y

≤

whenever

≥

, i.e., set overlap and

For ease of notation, the threshold γ is omitted in the

deﬁnitions of this section.

thus similarity are trivially bounded by

. Exploi-

ting the similarity function deﬁnition, it is possible to

derive tighter bounds allowing immediate pruning of

candidate pairs whose sizes are incompatible accor-

ding to the given threshold.

Deﬁnition 3. (Size Bounds). Let x be a set of featu-

res, Sim be a set similarity function, and γ be a simi-

larity threshold. The size bounds of x relative to Sim

are functions, denoted by minsize(x) and maxsize(x),

that maps γ and the size of x to a real value, s.t. ∀y, if

Sim(x, y) ≥ γ then minsize(x) ≤

≤ maxsize(x).

Therefore, given a set x we can safely ignore

all sets whose size do not fall within the interval

[minsize(x), maxsize(x)], because they can not match

with x according to the given threshold. Table 1 shows

the overlap and size bounds of three of the most wi-

dely used similarity functions: Jaccard, Dice, and Co-

sine (Arasu et al., 2006; Sarawagi and Kirpal, 2004;

Xiao et al., 2011; Li et al., 2008; Xiao et al., 2009).

If we ensure that all sets in the collection have its

features under the same total order O, we can combine

overlap and size bounds to prune even more the com-

parison space through the preﬁx ﬁltering technique.

The idea is to derive a new overlap constraint to be ap-

plied only to subsets of the original sets. For any two

sets x and y, under the order O, if

x ∩ y

≥ α then the

subsets consisting of the ﬁrst

−α + 1 elements of x

and the ﬁrst

−α + 1 elements of y must share at le-

ast one element (Chaudhuri et al., 2006; Sarawagi and

Kirpal, 2004). These subsets are called preﬁx ﬁltering

subsets and will be denoted by pre f (x). The exact

preﬁx size is determined by overlap(x, y), but it de-

pends on each matching pair. Given a set x, the ques-

tion is how to determine

pre f (x)

such that it sufﬁces

to identify all matches of x. Clearly, we have to take

the largest preﬁx in relation to all y. The preﬁx for-

mulation given above tell us that the preﬁx size is in-

versely proportional to overlap(x, y), and the former

increases monotonically with y. Therefore,

pre f (x)

is largest when

is smallest. The smallest possible

size of y, such that the overlap constraint can be satis-

ﬁed, is minsize(x).

Deﬁnition 4. (Max-preﬁx). Let x be a set of featu-

res. The max-preﬁx of x, denoted by maxpre f (x), is its

smallest preﬁx needed for identifying ∀y that

x ∩ y

≥

overlap(x, y).

maxpre f (x)

− dminsize(x)e +1.

We can also impose an order in the whole col-

lection. If we sort C by its sets sizes we can gua-

rantee that x is only matched with y if

≥

. In this

case the size of pre f (x) can be reduced. Instead of

using maxpre f (x) we can obtain a shorter preﬁx by

using overlap(x, x) to calculate the preﬁx size (Bay-

ardo et al., 2007; Xiao et al., 2011; Xiao et al., 2009).

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

154

Table 1: Set similarity functions.

Function Deﬁnition overlap(x,y) [minsize(x),maxsize(x)]

Jaccard

x ∩ y

x ∪ y

1 + γ

(

)





Dice

x ∩ y

γ(

)



2 − γ

(2 − γ)



Cosine

x ∩ y





Deﬁnition 5. (Mid-preﬁx). Let x be a set of fea-

tures. The mid-preﬁx of x, denoted by mid pre f (x),

is its smallest preﬁx needed for identifying ∀y ≥ x

that

x ∩ y

≥ overlap(x, y).

mid pre f (x)

−

doverlap(x, x)e + 1.

Further optimization is possible. We can sort each

set by its features frequencies in the collection, in in-

creasing order, which precipitates the least frequent

ones to the preﬁxes, thus ﬁltering out even more pairs

(since less frequent ones are likely to have fewer ma-

tches). We can also exploit the positional information

between common features in two sets, under the same

order, to verify if the remaining features in both sets

are enough to meet the given threshold (Xiao et al.,

2011).

4 GPU ARCHITECTURE AND

PROGRAMMING MODEL

In this section we provide a brief description of a

modern GPU architecture and its corresponding pro-

gramming model. We refer the reader to (Kirk and

Hwu, 2010) for more details on the GPU architecture

and its programming model.

Graphics processing units (GPUs) are specialized

architectures originally designed as special-purpose

co-processors for dedicated graphics rendering. Due

to the high computation power and improved pro-

grammability, they have recently become a powerful

accelerator for general purpose computing (GPGPU).

GPUs can be regarded as massively parallel proces-

sors with approximately ten times the computation

power and memory bandwidth of CPUs. Moreover,

the computational performance of GPUs is improving

at a rate higher than that of CPUs and at an exceptio-

nally high performance-to-cost ratio.

A GPU can be considered as a Multiple SIMD

(Single Instruction Multiple Data) processor, as de-

picted in ﬁgure 1. Each SIMD unit is known as a stre-

aming multiprocessor (SM) and contains streaming

processor (SP) cores, although different vendors and

development frameworks may use different terms (in

this paper we are using the terms from the CUDA

development framework). At any given clock cycle,

each SP executes the same instruction, but operates on

different data. The GPU supports thousands of light-

weight concurrent threads and, unlike the CPU thre-

ads, the overhead of creation and switching between

threads is negligible. The threads on each SM are or-

ganized into thread groups (blocks) that share com-

putation resources such as registers. A thread block

is divided into multiple schedule units, called warps,

that are dynamically scheduled on the SM. Because of

the SIMD nature of the SP’s execution units, if threads

in a schedule unit must perform different operations,

such as going through branches, these operations will

be executed serially as opposed to in parallel. Addi-

tionally, if a thread stalls on a memory operation, the

entire warp will be stalled until the memory access

is done. In this case the SM scheduler selects anot-

her ready warp and switches to that one. The GPU

global memory is typically measured in gigabytes of

capacity. It is an off-chip memory and has both a high

bandwidth and a high access latency. To hide the high

latency of this memory, it is important to have more

threads than the number of SPs and to have threads in

a warp accessing consecutive memory addresses that

can be easily coalesced. The GPU also provides a fast

on-chip shared memory which is accessible by all SPs

of an SM. The size of this memory is small but it has a

low latency and it can be used as a software-controlled

cache. Moving data from the CPU to the GPU and

vice versa is done through a PCIExpress connection.

The GPU programming model requires that part

of the application runs on the CPU while the

computationally-intensive part is accelerated by the

GPU. The programmer has to modify his application

to take the compute-intensive kernels and map them

fgssjoin: A GPU-based Algorithm for Set Similarity Joins

155

Global&Memory&

SM&

SP& SP& SP& SP&

Shared&Memory&&

...

SM&

SP& SP& SP& SP&

Shared&Memory&&

CPU&

PCIe 16x

GPU

Main&Memory&

Figure 1: GPU architecture.

to the GPU. The general ﬂow for a program consists

of the following. First the program running on the

CPU allocates memory on the GPU and copies data

to this area. Then the GPU code (kernel function) is

started on the GPU. The kernel executes its code in

parallel on the GPU and then the results can be co-

pied back to the CPU main memory. A new iteration

can take place or the CPU program can deallocate me-

mory on the GPU and terminate.

The GPU programming model exposes paralle-

lism through the data-parallel SPMD (Single Program

Multiple Data) kernel function. During implemen-

tation, the programmer can conﬁgure the number of

threads to be used. Threads execute data parallel com-

putations of the kernel and are organized in groups

called thread blocks. Thread blocks are further orga-

nized into a grid structure. When a kernel is laun-

ched, the blocks within a grid are distributed on idle

SMs. Threads of a block are divided into warps, the

schedule unit used by the SMs, leaving for the GPU

to decide in which order and when to execute each

warp. Threads that belong to different blocks cannot

communicate explicitly and have to rely on the global

memory to share their results. Threads within a thread

block are executed by the SPs of a single SM and can

communicate through the SM shared memory. Furt-

hermore, each thread inside a block has its own regis-

ters and private local memory and uses a global thread

block index, and a local thread index within a thread

block, to uniquely identify its data.

5 PARALLEL SIMILARITY JOIN

In this section we present our parallel algorithm to

solve the set similarity join problem with preﬁx ﬁl-

tering techniques. We describe the three key phases,

indexing, ﬁltering and veriﬁcation, and also our block

partitioning strategy.

Term Collection

E (entries)

Count number of terms

count

Compute preﬁx sum

index

invertedIndex

Point to 1

position

Figure 2: Creating the inverted index.

5.1 Indexing Phase

In state-of-the-art algorithms, the inverted index lists

are created during the ﬁltering process, which makes

them inherently sequential algorithms: sets are se-

quentially probed against the index and the state of

the lists in one iteration depends on their state in the

previous iteration. To go around this problem we need

to create the entire inverted index statically before the

ﬁltering phase, as show in ﬁgure 2. In this way we

can perform probes independently, because the index

is always complete. Hence, we need an efﬁcient pa-

rallel algorithm to create the inverted index. For this

purpose, we need to concatenate all features from all

sets in a unique array we call E. Let e ∈ E be an en-

try that contains three ﬁelds: the set it belongs to, a

feature and its positional information. So, the sets are

reduced to an array of tuples (s

, f

, p

). This will be

important in the positional ﬁltering step of the ﬁlte-

ring algorithm. When creating the entries for the in-

verted index algorithm we only add mid-preﬁx featu-

res to the array E. The concepts described in Section

2 allows us to use only max-preﬁx features from the

sets to probe against mid-preﬁx features in the index,

if we guarantee that matches will only occur between

bigger probing sets and smaller indexed sets. Then,

we calculate a count array, which counts the occur-

rence of each feature, and then perform a preﬁx sum

on it to obtain the starting indexes of each feature list

in the inverted index. Algorithm 1 shows the paral-

lel strategy used to create the whole inverted index in

memory. Note that V represents our dictionary (voca-

bulary).

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

156

Algorithm 1: DataIndexing(E).

input : Array of entries E[ 0 . . |E| − 1 ].

output: count, index, invertedIndex.

1 array of integers count[ 0 . . |V | − 1 ];

2 array of integers index[0. . |V | − 1 ];

3 invertedIndex[0. . |E | − 1 ]

4 Initialize count array with zeros;

5 Count the occurrences of each token, in parallel, on the input and

accumulates in count.

6 Perform an exclusive parallel preﬁx sum on count and store the

result in index.

7 forall t ∈ E, in parallel do

8 Copy t to invertedIndex, according to index and update index.

9 end

10 Return the arrays: count, index, and invertedIndex.

Algorithm 2: Filtering.

input : The collection of sets S, the inverted index I, the array

of buckets b, a threshold τ

output: The candidate pairs

1 Initialize b with zeros;

2 for each set x in S, in parallel do

3 for each feature f in x’s maxpreﬁx do

4 for each set y in f ’s inverted list do

5 if x.id < y.id then

6 if |y| < minsize(x) then

7 b[x.id][y.id] = −∞;

8 break;

9 else

10 if b[x.id][y.id] ≥ 0 then

11 rem = min(|x| − x. f pos, |y| − y. f pos);

12 ps = b[x.id][y.id];

13 m = overlap(x, y); /*τ omitted*/

15 if ps + 1 + rem < m then

16 b[x.id][y.id] = −∞;

17 else

18 b[x.id][y.id]+= 1;

19 end

20 end

21 end

22 end

23 end

24 end

25 end

5.2 Filtering Phase

With the entire inverted index stored in memory, we

can set each processor to perform one probe (process

one set) against the index, using only max-preﬁx fe-

atures from the set. One problem is how to accu-

mulate the scores (intersections) between all pairs of

sets. Since we can potentially have all set pairs being

candidates (specially for lower thresholds), we need

”buckets” for all possible pairs of sets in the col-

lection. So, we create an n x n matrix called b (the

buckets to contain the partial scores), where n is the

number of sets in our collection). It will contain the

partial intersection (partial scores) between probed

and indexed sets, because only parts of the sets (the

preﬁxes) are used in the process in this stage. After

performing the ﬁltering phase, we need to compact

the content of the scores table to obtain only the po-

sitive scores, i.e., the candidate pairs. So we create

an additional n x n array, the compacted buckets ar-

ray. After the compaction, this array will contain the

indexes of the scores in the table which are positive.

In order to reduce memory requirements (n x n array)

we partition the data collection in blocks and, thus we

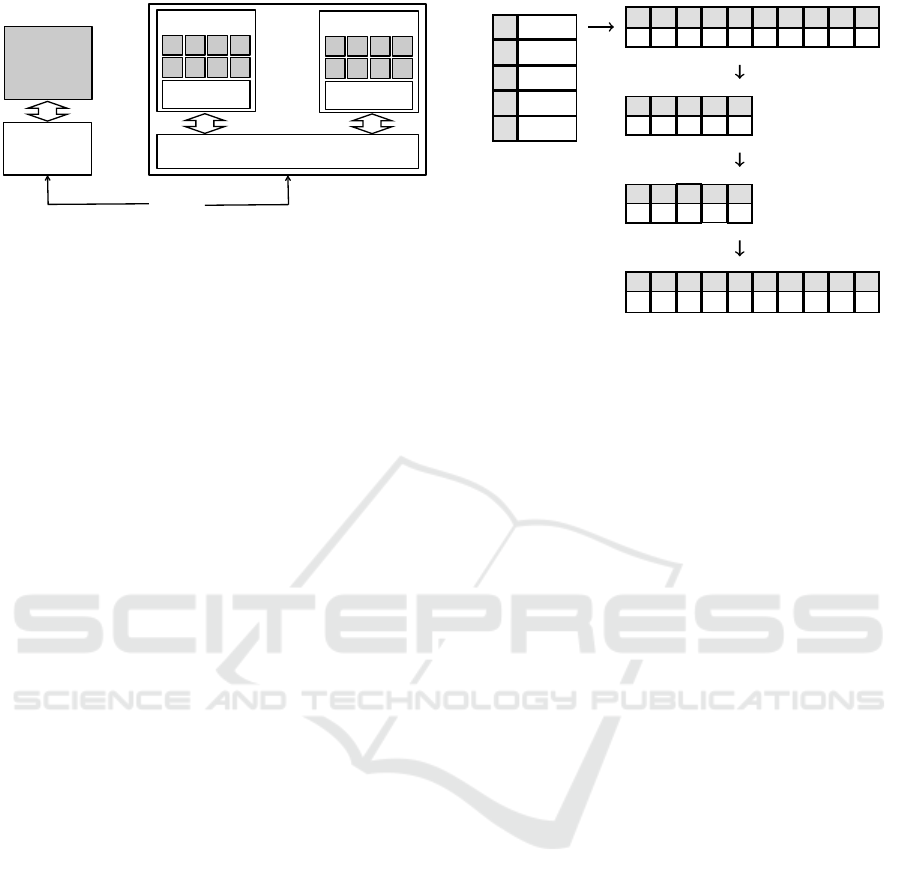
are be able to process collections of any size. Figure

3 illustrates the state of the memory after the ﬁltering

phase. Note that each row in the ﬁrst matrix in the

ﬁgure represents a set being queried against the index

while each column represents an indexed set.

Figure 3: Memory after the ﬁltering phase, with inverted

index, sets, the array b (buckets) of partial scores and its

corresponding array of compacted buckets (with the indexes

to the elements in b that have positive values), respectively.

Since we have ﬁve sets in this example, our tables are 5x5.

The numbers in the ﬁrst table are the partial scores after the

ﬁltering phase. Negative (−1) numbers represents −∞. The

second table is the compacted version of the ﬁrst; its values

(the absolute indexes of the selected elements from the ﬁrst

table) represent the candidate pairs and are provided to the

veriﬁcation phase.

Algorithm 2 is similar to state-of-the-art ﬁltering

based algorithms in literature, but here it is execu-

ted by each GPU processor (core) for one probing

set. From now on we will refer to a set being pro-

bed against the index as a query, and to a set in the

index as a source (because they generate the index).

For each query, the ﬁltering algorithm has two loops,

one to iterate on the max-preﬁx features of the query,

and one to consult the sources in the inverted list cor-

responding to each feature. Then we test if the query

id is smaller than the source id, i.e., we will only ma-

tch set x with set y if x.id < y.id. This test avoids

processing the same pair twice as well as ensures that

query sets are bigger than the sources, since the whole

collection is sorted in decreasing set cardinality order.

When we obtain a match we test if the source is smal-

ler than the query minsize. If it is, we can stop ite-

rating on the current inverted index list, because each

fgssjoin: A GPU-based Algorithm for Set Similarity Joins

157

list is also sorted in decreasing order of set cardina-

lity. Finally, only for pairs (buckets in partial scores)

not marked with −∞, we test if the remaining featu-

res are enough to meet the threshold; note that x. f pos

is the positional information of the current feature in

set x. If they are, we accumulate the score, if not we

mark them with −∞, so that they will not be consi-

dered anymore. In the end, array b will contain mar-

ked buckets, 0 buckets and positive ones, the former

being compacted (their absolute indexes) in the array

compacted buckets (cb for short). The compacted in-

dexes represent the pairs, since the bidimensional in-

dexes of the matrix (which represents the ids of query

and source sets) can be calculated from the absolute

index. It is the resulting candidate pairs list, which

will be passed to the next phase, veriﬁcation.

5.3 Veriﬁcation Phase

The veriﬁcation phase, which ultimately produces the

ﬁnal result, can be trivially processed in parallel. It

simply consists in performing the remaining score

calculation on each candidate pair to verify if there

is enough overlap to qualify them as a match. This

can easily be done in parallel, by making each pro-

cessor perform veriﬁcation on one candidate pair. We

can use the partial score to reduce a bit the overlap

calculations. By comparing the last feature from the

preﬁxes of the two sets in a candidate pair, we can

start the overlap calculation in the position of the fe-

ature with the smaller id in its own set, and in the

beginning with the other, with the initial value being

the partial score of the candidate pair, since any ma-

tch with preﬁx features in this set was already calcu-

lated in the ﬁltering phase. In each step of the overlap

calculation we also test if the remaining features are

enough to meet the threshold, marking those which

are not. Those not marked by this process form the

result set, the similar pairs according to the threshold

and the similarity function.

5.4 Block Partitioning and

Optimization

The need for quadratic arrays in the ﬁltering phase

sets a limit for the size of the databases we can

process. In order to solve this problem we need to

partition our search space into blocks that ﬁt into the

memory requirements. But then we must process this

blocks in such a way that all sets are matched against

each other. To achieve this we proceed similarly in

the ﬁltering phase, but we index the set’s preﬁxes of

one block, and use all the others before it to query

Algorithm 3: Veri f ication.

input : The array of buckets b with partial scores, the array of

compacted buckets cb with the indexes of the

candidate buckets (with positive scores), the array of

features f of each set and a threshold τ

output: The similar pairs list L

1 Initialize a list L;

2 for each index idx in cb, in parallel do

3 x, y = calc indexes(idx); /*x.id < y.id*/

4 m = overlap(x, y);

5 score = b[x.id][s.id];

6 f 1 = f [x.id][|maxpre f (x)|];

7 f 2 = f [y.id][|mid pre f (y)|];

8 p1, p2 = 0;

9 if f 1 < f 2 then

10 p1 = |maxpre f (x)|;

11 else

12 p2 = |mid pre f (y)|;

13 end

14 while p1 < |x| and p2 < |y| do

15 f 1 = f [x][p1]; f 2 = f [y][p2];

16 if (p1 == |x| − 1 and f 1 < f 2) or

(p2 == |y| − 1 and f 2 < f 1) then

17 break;

18 end

19 if f 1 == f 2 then

20 score+ = 1; p1+ = 1; p2+ = 1;

21 else

22 s = f 1 < f 2 ? x : y; p = f 1 < f 2 ? p1 : p2;

23 rem = |s| − p;

24 if rem + score < m then

25 break;

26 else

27 p+ = 1;

28 end

29 end

30 if score ≥ m then

31 include pair (x,y) in L;

32 end

33 end

34 end

its index. In this way we create an index-ﬁlter-verify

cycle with the blocks, gradually aggregating the re-

sults, which can be ﬂushed to the disk if approaching

memory limit. By using the previous blocks as que-

ries, as shown in ﬁgure 4, we ensure that only big-

ger sets are queried against smaller ones in the index,

since the collection is sorted in decreasing cardinality

order. This fact also allows us to skip some blocks

from being queried against others for which its ﬁrst

set’s maxsize is smaller than the query block’s last

set. In these cases it is guaranteed that no match could

be yield from the two blocks. This signiﬁcantly im-

proves performance for higher thresholds. Another

consequence of block partitioning is the possibility of

running in distributed memory systems, since we can

process each probe/index block pair in one node in

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

158

parallel, executing its own index-ﬁlter-verify calcula-

tions.

Figure 4: Illustration of the block processing scheme.

6 GPU IMPLEMENTATION

The GPU implementation consists of three main ker-

nels (functions that executes in the GPU), plus other

smaller kernels responsible for common parallel tasks

used by the main ones, like parallel counting and pre-

ﬁx sum in the inverted index creation and compaction

in the ﬁltering phase.

The three main kernels are scheduled by the block

processing function, that partitions the dataset into

blocks and executes the block processing scheme, as

shown in ﬁgure 4 where ”Query” means ﬁlter against

the index and verify the selected candidates. The

block processing scheme executes the index-ﬁlter-

verify cycle by calling their three associtated kernels.

The kernel responsible for the creation of the in-

verted index is simple, very like algorithm 1. It is

composed of three smaller kernels responsible for its

steps: parallel counting, parallel preﬁx sum and pa-

rallel building of the index according to the count and

preﬁx sum arrays.

For the ﬁltering algorithm, we create a single ar-

ray in the GPU memory, the partial scores array, with

a number of elements equals to the square of the num-

ber of sets in one block (the number of all possible

pairs for the block). We only allocate it once, and

reuse it for each ﬁltering execution, to save the al-

location time. We also allocate only once a com-

pacted buckets array, of the same size of the par-

tial scores, to contain the result of the compaction.

Of course these arrays must be cleaned (set to 0) at

each execution of the ﬁlter-verify algorithms in the

block processing scheme. The number of sets per

block must be chosen in such a way that two times

its squared value times the data type size used in par-

tial scores and compacted buckets is less than the me-

mory available in the GPU.

After the ﬁltering kernel is executed, it ﬁlls the

partial

scores array, and the compaction kernel can be

called to ﬁll the compacted buckets array, as shown in

ﬁgure 3. The result of the compaction is the absolute

indexes of the positive elements in partial scores. The

indexes represent the pairs, since they can be derived

from the absolute index. These indexes, i.e. the can-

didate pairs, as well as the partial scores are passed to

the veriﬁcation kernel. It will calculate the intersecti-

ons (the ﬁnal scores) between the candidate pairs, al-

ways checking if there is still enough features in the

sets to meet the minimum overlap, according to the

chosen similarity function (jaccard in our implemen-

tation). The pairs that pass the veriﬁcation algorithm

are pushed into a list, that is periodically ﬂushed to

the output ﬁle, where the actual similarity values are

calculated.

We used a ﬁxed number of thread blocks and of

threads per block, which depends on to the speciﬁc

GPU used. In order to ensure maximum utilization

of the device, we used a technique called persistent

threads. This technique allows one thread to be reu-

sed, processing more than one data element when the

number of elements to process is bigger than the num-

ber of threads sent to execution.

7 EXPERIMENTAL EVALUATION

7.1 Experimental Setup

We tested two reference sequential algorithms, all-

pairs (Bayardo et al., 2007) and ppjoin (Xiao et al.,

2011), as well as a massively parallel algorithm

gssjoin (Junior et al., 2016) and our parallel ﬁlter-

based algorithm fgssjoin.

Our experiments were executed on a machine

equipped with two Intel Xeon E5-2620, each with 6

processing cores (12 threads in hyper-threading) and

20MB of cache memory, 16GB of RAM memory and

4 Nvidia GTX Titan Black, each with 2880 proces-

sing cores and 6GB of memory, although we only

used one GTX Titan Black for our parallel implemen-

tation.

We used two standard databases: DBLP (a col-

lection of computer science article titles and authors),

with 100k registers, and IMDB (a collection of movie

titles, TV shows, etc), with 300k registers, which are

popular datasets in set similarity joins related work.

We pre-processed the data sets, removing accents and

punctuation, and setting all characters to lowercase.

Both datasets were q-tokenized with 2-grams and 3-

grams. We conducted our experiments varying the

threshold values from 0.5 to 0.9, in 0.1 increments.

Our baseline comparison algorithms were executed

on the Xeon processor, except gssjoin, which was also

executed on the Gtx Titan Black.

fgssjoin: A GPU-based Algorithm for Set Similarity Joins

159

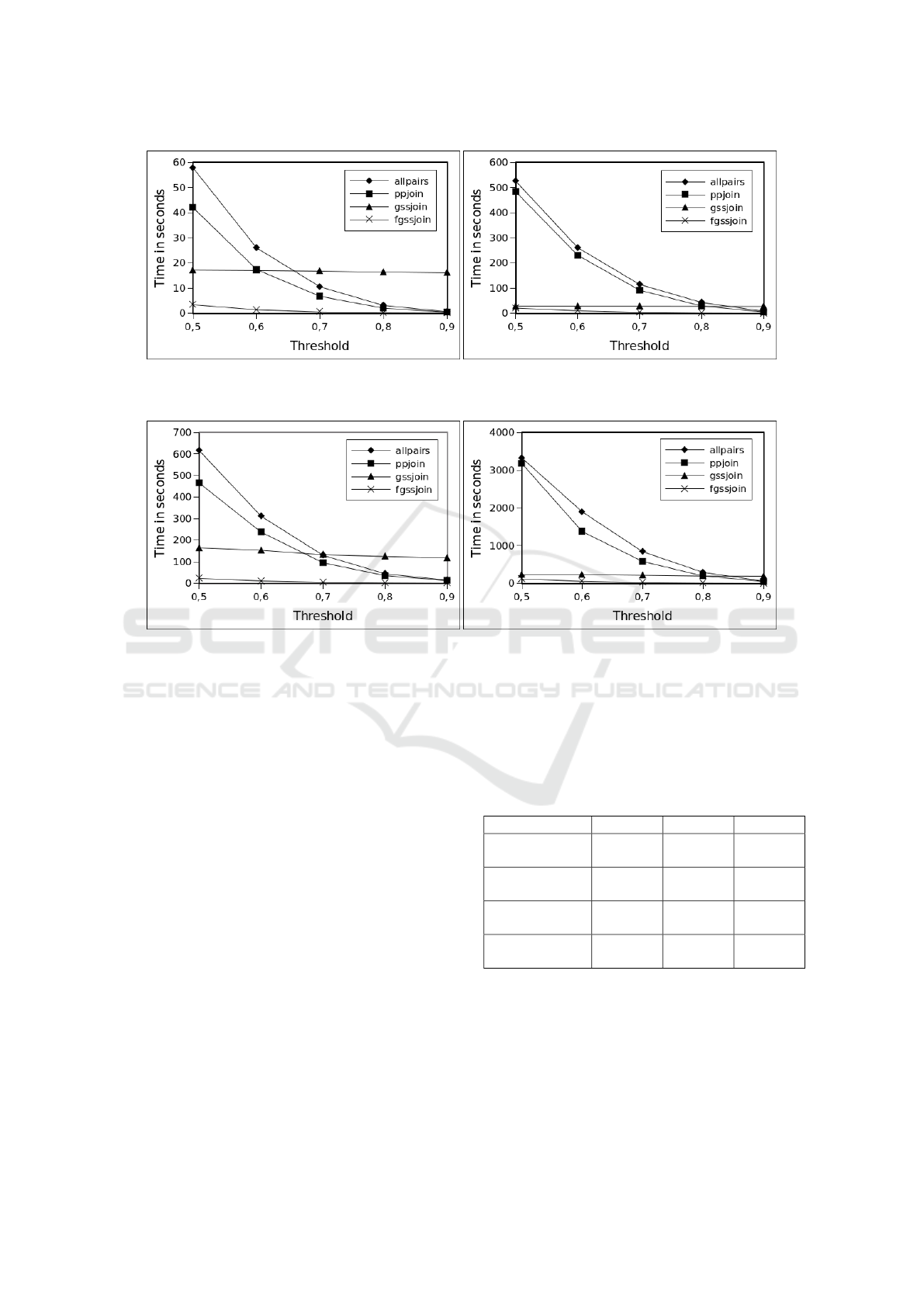
(a) DBLP 100k, 3-gram tokens (b) DBLP 100k, 2-gram tokens

Figure 5: Execution times for DBLP dataset, 100k registers, with 2-gram and 3-gram tokens.

(a) IMDB 300k, 3-gram tokens (b) IMDB 300k, 2-gram tokens

Figure 6: Execution times for IMDB dataset, 300k registers, with 2-gram and 3-gram tokens.

7.2 Performance Analysis

We report execution runtimes with varying threshold

values. Figure 5 shows the execution times obtai-

ned as we increase the threshold from 0.5 up to 0.9.

As can be seen, our algorithm achieved considerable

speedups of up to 25x faster than the leading sequen-

tial algorithm in literature. The best speedups were

achieved when the datasets were tokenized with 2-

grams. Of course the ﬁner grained 2-grams requi-

res more computational power, since there are fe-

wer combinations of 2 characters and this leads to

more matches and more candidate pairs in the ﬁlte-

ring phase, consequently raising the load for the veri-

fying phase. Also, we expect our algorithm to become

even better as the size of the dataset grows. One ca-

veat is that our algorithm relies on positional ﬁltering,

which is inherently sequential. Although it is very

efﬁcient in lowering the number of candidate pairs in

the ﬁltering phase, it imposes difﬁculties for some key

optimization in many-core architectures. For exam-

ple, it reduces memory coalescing, and hinders a hig-

her degree of parallelism, e.g., parallelizing the tokens

among processing units, instead of whole queries, in

the ﬁltering phase. Table 2 shows the best speedups

achieved on each dataset over the 3 other algorithms

used in experiments; the corresponding threshold va-

lue is shown in parentheses.

Table 2: Best speedups of fgssjoin over the other algorithms

on each dataset, with corresponding threshold values.

Dataset ppjoin allpairs gssjoin

DBLP, 2-gram

24.6x

(0.8)

36.6x

(0.8)

108.3x

(0.9)

DBLP, 3-gram

12.4x

(0.5)

17.1x

(0.5)

132.7x

(0.9)

IMDB, 2-gram

27.6x

(0.6)

38.5x

(0.6)

98.0x

(0.9)

IMDB, 3-gram

21.0x

(0.8)

27.5x

(0.8)

127.1x

(0.9)

8 CONCLUSIONS AND FUTURE

WORK

In this paper we presented a parallel algorithm, as

well as a GPU-based implementation to solve the set

similarity join problem, with considerable speedups

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

160

in relation to the state-of-the-art algorithms in lite-

rature. Our experiments, with standard datasets, re-

vealed good speedups, with a scalable behavior as we

increase the size of the datasets. Besides the good re-

sults in this paper, many improvements can be done.

We did not explore some speciﬁc optimization in re-

lation to the many-core architectures, like the use of

the so called shared memory in CUDA or local me-

mory in OpenCL (both are parallel development fra-

meworks), as well as memory coalescing. One ob-

servation in this research is the inherently sequential

nature of positional ﬁltering techniques, which hin-

ders a higher level of parallelism. We plan, in future

work, to remove the positional ﬁltering techniques

from our ﬁltering phase, and increase the degree of

parallelism by assigning one processing core to each

token, instead of each set, to make possible coalesced

memory accesses, hoping that the gain with the higher

degree of parallelism compensates the loss in ﬁltering

capacity. We also plan to make use of shared/local

memory as a way to increase locality and, hence,

achieve greater speedups. Finally, we plan to imple-

ment a multi-GPU version (to run on GPU clusters)

and process bigger datasets.

REFERENCES

Arasu, A., Ganti, V., and Kaushik, R. (2006). Efﬁcient exact

set-similarity joins. In Proceedings of the 32nd inter-

national conference on Very large data bases, pages

918–929. VLDB Endowment.

Bayardo, R. J., Ma, Y., and Srikant, R. (2007). Scaling up

All Pairs Similarity Search. In WWW, pages 131–140.

Broder, A. Z., Charikar, M., Frieze, A. M., and Mitzenma-

cher, M. (1998). Min-Wise Independent Permutations

(Extended Abstract). In STOC, pages 327–336.

Chac

on, A., Marco-Sola, S., Espinosa, A., Ribeca, P., and

Moure, J. C. (2014). Thread-cooperative, Bit-parallel

Computation of Levenshtein Distance on GPU. In

ICS, pages 103–112.

Chaudhuri, S., Ganti, V., and Kaushik, R. (2006). A primi-

tive operator for similarity joins in data cleaning. In

ICDE, page 5.

Cruz, M. S. H., Kozawa, Y., Amagasa, T., and Kitagawa, H.

(2016). Accelerating set similarity joins using gpus.

TLDKS, 28:1–22.

Deng, D., Li, G., Hao, S., Wang, J., and Feng, J. (2014).

MassJoin: A Mapreduce-based Method for Scalable

String Similarity Joins. In ICDE, pages 340–351.

Doan, A., Halevy, A. Y., and Ives, Z. G. (2012). Principles

of Data Integration. Morgan Kaufmann.

Gravano, L., Ipeirotis, P. G., Jagadish, H. V., Koudas, N.,

Muthukrishnan, S., and Srivastava, D. (2001). Ap-

proximate string joins in a database (almost) for free.

In VLDB, pages 491–500.

Indyk, P. and Motwani, R. (1998). Approximate Nearest

Neighbors: Towards Removing the Curse of Dimensi-

onality. In STOC, pages 604–613.

Junior, S. R., Quirino, R. D., Ribeiro, L. A., and Martins,

W. S. (2016). gssjoin: a gpu-based set similarity join

algorithm. In SBBD, pages 64–75.

Kirk, D. B. and Hwu, W.-m. W. (2010). Programming

Massively Parallel Processors: A Hands-on Appro-

ach. Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA, 1st edition.

Leskovec, J., Rajaraman, A., and Ullman, J. D. (2014). Mi-

ning of Massive Datasets, 2nd Ed. Cambridge Univer-

sity Press.

Li, C., Lu, J., and Lu, Y. (2008). Efﬁcient Merging and Fil-

tering Algorithms for Approximate String Searches.

In ICDE, pages 257–266.

Lieberman, M. D., Sankaranarayanan, J., and Samet, H.

(2008). A Fast Similarity Join Algorithm Using

Graphics Processing Units. In ICDE, pages 1111–

1120.

Mann, W., Augsten, N., and Bouros, P. (2016). An Em-

pirical Evaluation of Set Similarity Join Techniques.

PVLDB, 9(9):636–647.

Ribeiro, L. A. and H

arder, T. (2011). Generalizing Preﬁx

Filtering to Improve Set Similarity Joins. Information

Systems, 36(1):62–78.

Sarawagi, S. and Kirpal, A. (2004). Efﬁcient Set Joins on

Similarity Predicates. In SIGMOD, pages 743–754.

Vernica, R., Carey, M. J., and Li, C. (2010). Efﬁcient Pa-

rallel Set-similarity Joins using MapReduce. In SIG-

MOD, pages 495–506.

Wang, J., Li, G., and Feng, J. (2012). Can We Beat the Pre-

ﬁx Filtering?: An Adaptive Framework for Similarity

Join and Search. In SIGMOD, pages 85–96.

Xiao, C., Wang, W., Lin, X., and Shang, H. (2009). Top-

k set similarity joins. In 2009 IEEE 25th Internatio-

nal Conference on Data Engineering, pages 916–927.

IEEE.

Xiao, C., Wang, W., Lin, X., Yu, J. X., and Wang, G.

(2011). Efﬁcient Similarity Joins for Near-duplicate

Detection. TODS, 36(3):15.

fgssjoin: A GPU-based Algorithm for Set Similarity Joins

161