Extensions, Analysis and Experimental Assessment of a Probabilistic

Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

Alfredo Cuzzocrea

1,2

, Francesco Folino

, Massimo Guarascio

and Luigi Pontieri

ICAR-CNR, Via Pietro Bucci 7/11C, I-87036, Rende (CS), Italy

DIA Department, University of Trieste, I-34127, Trieste, Italy

Keywords:

Business Process Intelligence, Classiﬁcation, Deviance Detection.

Abstract:

The problem of discovering an effective Deviance Detection Model (DDM) out of log data, has been attracting

increasing attention in recent years in the very active research areas of Business Process Intelligence (BPI) and

of Process Mining. Such a model can be used to assess whether novel instances of the business process are

deviant or not, which is a hot topic in many application scenarios such as cybersecurity and fraud detection.

This paper extends a previous proposal where an innovative ensemble-learning framework for mining business

process deviances was introduced, hinging on multi-view learning scheme. Speciﬁcally, we introduce here an

alternative meta-learning method for probabilistically combining the predictions of different base DDMs. The

entire learning method is embedded into a conceptual system architecture that is meant to support the detection

and analysis of deviances in a Business Process Management scenario. We also discuss a wide and compre-

hensive experimental analysis of the proposed approach and of a state-of-the-art DDM discovery solution. The

experimental ﬁndings conﬁrm the ﬂexibility, reliability and effectiveness of the proposed deviance detection

approach, and the improvement gained over its previous version.

1 INTRODUCTION

Business Process Intelligence (BPI) and Process Min-

ing are active areas of research, which enjoy many

relevant real-life applications.

A recent thread of research in this area concerns

the problem of detecting deviant instances of a busi-

ness process (a.k.a. “deviance mining”), i.e. in-

stances that deviate from normal outcomes (Suriadi

et al., 2013; Bose and van der Aalst, 2013; Nguyen

et al., 2014; Lo et al., 2009; Cuzzocrea et al., 2015).

This problem is relevant in many application scenar-

ios such as cybersecurity and fraud detection, and so

forth. Essentially, the problem has been rephrased in

the literature as a binary classiﬁcation problem, where

the class of all deviant process instances is to be dis-

criminated from the one gathering all the other (nor-

mal) instances of the process under analysis. This

problem has been faced by inducing a suitable clas-

siﬁcation model (named hereinafter Deviance Detec-

tion Model, or DDM for short), out of some ﬂat repre-

sentation of a historical log of process traces (labelled

each as either deviant or normal). Such a model can

be then applied to any new instance of the process to

estimate whether it is a deviance or not.

In our opinion, the current literature in the ﬁeld

has not fully addressed a series ofissues that are likely

to arise in many real application scenarios. We dis-

cuss them in the following.

I1 First of all, most of the deviance mining ap-

proaches (including, in particular, (Bose and

van der Aalst, 2013; Swinnen et al., 2011; Nguyen

et al., 2014)) rely on training a single DDM from

a propositional view of the given log, where each

trace is encoded into a ﬁxed-length form by pro-

jecting the associated sequence of log events onto

some given set of behavioral patterns (such as

the individual activities, maximal repeats, or tan-

dem repeats used in (Bose and van der Aalst,

2013; Nguyen et al., 2014) and the experiments

discussed in Section 5). As shown in (Nguyen

et al., 2014) using multiple heterogenous kinds

of pattern can lead to higher classiﬁcation accu-

racy. However, mixing all heterogeneous patterns

into a single view is likely to produce a high-

dimensional, sparse and redundant representation

162

Cuzzocrea, A., Folino, F., Guarascio, M. and Pontieri, L.

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business Process Instances.

DOI: 10.5220/0006340001620173

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 162-173

ISBN: 978-989-758-247-9

!"#$%&'

()&*

+,)-).#/

01-

2&#"3,&4

5#6&'701-7

()&*6

!"#$%&

("#$%&)'*+

/",

- ("#$%&)'*+

,*,

,*1

.*,

.*1

/",*,

/",*1

/*,

/*1

8#6&7

91'&/6

8#:&6)#.

;1<5).&,

/",

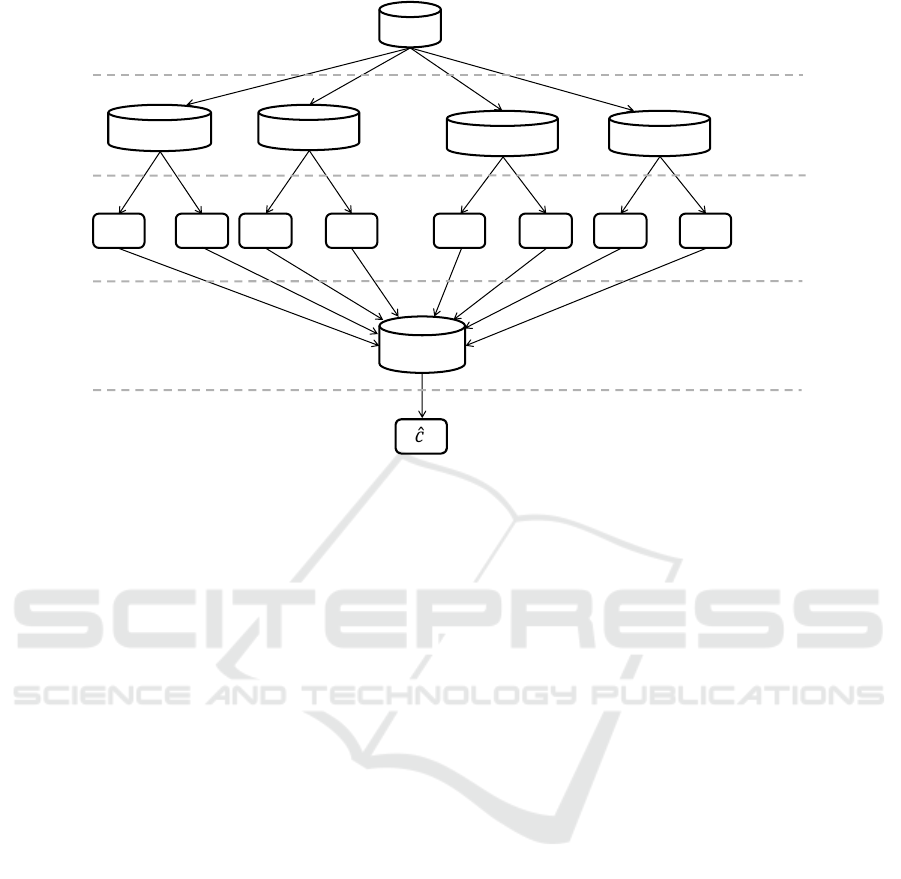
Figure 1: Conceptual data-processing ﬂow of the proposed approach: original data, transformed data and discovered DDMs.

of the training instances. This calls for adopting

some multi-view learning strategy (like the one

proposed in (Cuzzocrea et al., 2015)), capable of

exploiting different complementary views of the

given traces.

I2 In many real-life applications, analyzing a pre-

sumably deviant case is an expensive task. If

equipping the detected deviant instances with a

deviance probability score, this task could be fo-

cused on more suspicious instances. This capa-

bility could allow to use deviance prediction tools

more ﬂexibly and more effectively in real BPM

systems.

I3 Deviance mining analyses must be often car-

ried out in situations where the deviant in-

stances are far less than normal ones. This

is a case of “class imbalance” (Japkowicz and

Stephen, 1997), which constitutes a challenge for

most classiﬁer induction approaches, conceived

to maximize the overall accuracy without paying

special attention to the minority (i.e. deviant, in

our case) instances.

Some of these issues have been faced in a pre-

vious work of ours (Cuzzocrea et al., 2015), where

an ensemble-learning approach was proposed that ex-

ploits multi-view learning to solve the deviance min-

ing problem. This approach is summarized pictorially

in Figure 1. Basically, a number, say n, of comple-

mentary feature-based views of the given log L are

produced, which provide each a vector-space encod-

ing of both context properties and behavioral patterns

of the traces in L. Two layers of deviation-detection

models are induced from these views: (i) a collec-

tion of base models (learnt by applying k different

classiﬁer-induction methods to one of the n views

above), and (ii) a meta model, which integrates the

predictions of the base models into a “high-order” de-

viance forecast. As explained in (Cuzzocrea et al.,

2015), the latter model deals with heterogeneous be-

havioral patterns at a higher level of abstraction, so

effectively addressing the issue I1.

In order to deal with situations where deviant in-

stances are far less than normal ones (issue I3), the

learning procedure can be made integrate a resam-

pling mechanism, in order to reduce the level of class

imbalance.

In this paper, we provide three novel and sig-

niﬁcant contributions over (Cuzzocrea et al., 2015),

namely:

• two alternative Bayesian meta-learning methods

for probabilistically combining the predictions of

different base DDMs;

• a conceptual system architecture supporting the

detection and analysis of deviances in a Business

Process Management scenario; and

• a wide and comprehensive experimental analysis

of algorithm

HO-DDM-mine

and of a state-of-the-

art method (Nguyen et al., 2014).

More speciﬁcally, in our current approach the

meta-learning task can take advantage of (a cus-

tomized version of) one of the following meth-

ods for the induction of probabilistic classiﬁers:

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

163

AODE (Webb et al., 2005) or HNB (Zhang et al.,

2005). Notably, both these methods relax the as-

sumption of attribute independence that underlies

Na¨ıve Bayes models —this assumption hardly holds,

indeed, in our DDM learning setting, where sev-

eral activities/patterns are likely to be correlated one

another— with negligible additional costs in terms of

computation time. This allows to associate any new

process instance with a reliable estimate of the prob-

ability that it is deviant, thus addressing the delicate

issue I2.

The results of our empirical analysis conﬁrmed

the ﬂexibility, reliability and effectiveness of the pro-

posed deviance detection approach, and the improve-

ment gained over its previous version.

The rest of the paper is organized as follows. Sec-

tion 2 introduces some basic concepts and notation on

the speciﬁc kinds of Bayesian classiﬁers that are used

in our approach to accomplish the meta-learning sub-

task. The speciﬁc kind of overall DDM (named High-

Order Deviance Detection Model, short

HO-DDM

) that

is eventually returned by our approach is illustrated in

Section 3. Section 4 then presents a conceptual sys-

tem architecture for the detection and analysis of de-

viant process instances, in a BPM scenario, summa-

rizes the induction algorithm for extracting a

HO-DDM

out a given set of historical log traces. After dis-

cussing, in Section 5, the results of the experimental

activities that we have conducted on a real case study,

we draw a few concluding remarks in Section 6.

2 PRELIMINARIES: BAYESIAN

MODELS

As explained before, we want to probabilistically

classify a process trace as either deviant or not, in or-

der to equip the trace with a measure of conﬁdence in

the fact that it is really a deviance. In order to do this

in a scalable way, we resort to two extensions of the

popular Na¨ıve Bayes method. Before presenting these

methods in details, let us introduce some basic con-

cepts and notation concerning Bayesian classiﬁers, in

general, and Na¨ıve Bayes models, in particular.

In general, Bayesian classiﬁers combine a priori

knowledge of the classes with new evidence gath-

ered from data. Let us consider an instance space

with m+ 1 nominal attributes X

,...,X

,Y, such that

m ∈ N, and a class attribute Y encoding the class

label (if known) of any instance. For any attribute

Z ∈ {X

,...,X

,Y}, let dom(Z) be the associated do-

main, and let dom(Y) = {c

,...,c

}. Given an in-

stance x = hx

,...,x

i, where x

is the value observed

for attribute X

, the classiﬁcation problem amounts to

estimating the class label y ∈ dom(Y) for x, based

on some suitable classiﬁcation model, previously ex-

tracted from (already classiﬁed) training instances.

In a hard classiﬁcation setting, a Bayesian

classiﬁer computes P(y|x) for each class

y ∈ dom(Y), and assigns x to the class associ-

ated with the with the highest probability, i.e.,

∗

= argmax

y∈dom(Y)

(P(y|x)). Clearly, P(y|x) =

P(y,x)/P(x) and argmax

y∈dom(Y)

(P(y|x)) =

argmax

y∈dom(Y)

P(y,x). As P(y, x) = P(y) · P(x|y),

this hard classiﬁcation task amounts to ﬁnding

∗

∈ dom(Y) such that: y

∗

= argmax

y∈dom(Y)

(P(y) ·

P(x|y)).

For a fully probabilistic classiﬁcation, every class

membership probability can be estimated as:

P(y|x) ≈

P(y,x)

∑

′

∈dom(Y)

P(y

′

,x)

P(y,x)

∑

′

∈dom(Y)

P(y

′

) · P(x|y

′

)

(1)

While the prior probability P(y) can be derived

from the sample frequencies in the training set, one

should estimate the conditional probability P(x|y). In

Na¨ıve Bayes (NB) classiﬁers the latter task is accom-

plished by assuming that all the attributes are condi-

tionally independent of one another, given the class

label y. Under this hypothesis, for each y ∈ dom(Y),

it is P(y,x) = P(y) ·

∏

i=1

P(x

|y). Thus, the instance

x is assigned to the class y

∗

∈ dom(Y) such that

∗

= argmax

y∈dom(Y)

(P(y) ·

∏

i=1

P(x

|y)). Any “soft”

class membershipprobability P(y|x) can be computed

in a similar way.

NB classiﬁers work well in a wide range of ap-

plications (Langley et al., 1992). However, in cer-

tain settings (like the one considered in this work),

the attribute independence assumption is inappropri-

ate. Many efforts have been made in the literature to

relax such an assumption, without making the proba-

bility distribution too complex and hard to induce. We

next brieﬂy illustrate two popular extensions of NB

classiﬁers, namely AODE and HNB, which are both

used in the current implementation of our approach.

2.1 AODE

One-dependence estimators (ODEs) (Sahami, 1996)

generalize NBs by allowing each attribute to depend

on one other attribute besides the class. A subclass of

ODEs are SPODEs (Keogh and Pazzani, 2002; Ying

et al., 2007), where all the attributes can only depend

on a single common one, the super-parent (in addition

to the class). For example, for a SPODE with super-

parent X

, P(y,x) is computed as follows:

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

164

P(y,x) =P(y,x

) · P(x|y,x

) =

P(y,x

) ·

∏

i=1

P(x

|y,x

)

SPODEs are typically combined into a sort of

ensemble, in order to reduce the classiﬁcation vari-

ance and ensure higher accuracy (Webb et al., 2005).

Clearly, if the data instances feature m attributes, at

most m different SPODEs can be combined. The dif-

ferent SPODE models in such an ensemble are usu-

ally merged by computing an overall probability esti-

mate for P(y, x) as a linear combination of the prob-

ability estimates returned by all of these “base” mod-

els:

P(y,x) =

∑

j=1

· P

(y,x) =

∑

j=1

· P(y,x

) ·

∏

i=1

P(x

|y,x

) (2)

where P

(y,x) is the estimate of j-th SPODE for x,

and w

is the weight given to the same SPODE.

The Averaged One-Dependence Estimators

(AODE) (Webb et al., 2005) method adopts a simple

combination strategy, which only considers the

super-parents that appear in the training dataset

more than a minimum support threshold h ∈ N, and

assigns uniform weights to all of their corresponding

SPODEs. Hereinafter, we simply keep ﬁxex h = 1

—notice that the same choice has been made in the

experiments described in Section 5. According to this

strategy, P(y, x) is eventually estimated as follows:

P(y,x) =

∑

j∈S

P(y,x

) ·

∏

i=1

P(x

|y,x

)

|S |

(3)

where S is the subset of values x

that occur at least h

times in the training set (and w

is ﬁxed to 1/|S | for

all x

in S ).

In order to estimate, for each tuple x ∈ X and

each possible class label y ∈ dom(Y), the probabil-

ity P(y|x), one can simply normalize the numerator

in Eq. 3 over all the classes as follows:

P(y|x) =

P(y,x)

∑

′

∈Y

P(y

′

,x)

∑

j∈S

P(y,x

) ·

∏

i=1

P(x

|y,x

)

∑

′

∈dom(Y)

∑

j∈S

P(y

′

) ·

∏

i=1

P(x

′

)

(4)

2.2 Hidden Na

ıve Bayes

The basic assumption underlying a SPODE is that

each attribute can only depend on another one (i.e.

the super-parent), even though several other attributes

might actually inﬂuence the former. This assump-

tion is mitigated by averaging different SPODEs. By

contrast, in the Hidden Na

ıve Bayes (HNB for short)

model, each attribute x

is assumed to be possibly in-

ﬂuenced by a artiﬁcial “hidden” parent attribute, cap-

turing the inﬂuence that all other attributes may have

on x

. In other words, each attribute x

is allowed to

depend on a hidden parent x

(∀i = 1,...,m), in addi-

tion to the class y. Therefore, the probability P(y,x)

computed by an HNB can be written as:

P(y,x) = P(y) ·

∏

i=1

P(x

|y,x

) =

P(y) ·

∏

i=1

∑

j=1, j6=i

· P(x

|y,x

)

(5)

where

∑

j=1

i, j

= 1.

Clearly, the hidden parent x

for x

is deﬁned as

a mixture of the weighted inﬂuences from all other

attributes.

A key point in the construction of an HNB is

the deﬁnition of the weights w

i, j

(for any i, j in

{1,...,m}). In the approach proposed in (Zhang

et al., 2005), any weight w

i, j

is computed on the ba-

sis of the Conditional Mutual Information I

|y)

between x

and x

, which is deﬁned as follows:

|y) =

∑

P(x

,y) · log

P(x

|y)

P(x

|y)P(x

|y)

(6)

More speciﬁcally, for any i, j ∈ {1,...,m}, it is:

i, j

|y)

∑

j=1, j6=i

|y)

(7)

The posterior class-membership probability

P(y|x), for each tuple x ∈ X and each possible class

y ∈ dom(Y), can be simply obtained as follows:

P(y|x) =

P(y,x)

P(x)

P(y,x)

∑

′

∈dom(Y)

P(y

′

,x)

P(y) ·

∏

i=1



∑

j=1, j6=i

· P(x

|y,x

)



∑

′

∈dom(Y)



P(y

′

) ·

∏

i=1



∑

j=1, j6=i

· P(x

′

)



(8)

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

165

3 HIGH-ORDER DEVIANCE

DETECTION MODELS

Our approach to the discovery of an

HO-DDM

relies on

training multiple base learners on different feature-

based views of a given log L. According to the

processing ﬂow depicted in Figure 1, the approach

founds on training multiple base learners on n differ-

ent feature-based views of L, produced each accord-

ing to a different list of behavioral patterns (like those

used in (Bose and van der Aalst, 2013; Nguyen et al.,

2014; Cuzzocrea et al., 2015), and in our experimen-

tation).

Let P

,...,P

these pattern lists and f-

View(L,P

),...,f-View(L,P

) be the feature-based

views of L that are obtained by encoding the traces in

L according to the patterns in P

,...,P

, respectively.

More precisely, for each P

and each τ ∈ L, the view

f-View(L,P

) contains a tuple f -View(τ,P

) that

encodes all the context data of τ and the projection of

τ onto the patterns of P

. In particular, the correlation

between τ and each pattern p

∈ P

is computed as the

number of times that p

occurs in τ. Further details

can be found in (Cuzzocrea et al., 2015)

By applying k different learning algorithms to all

of these views, a list CL of r = n× k “base” DDMs is

obtained. These multi-view base classiﬁers are made

undergo a stacking-oriented meta-learning scheme, in

order to integrate all of them into a single higher-level

probabilistic DDM.

For the sake of notation, let PL be a list, of the

same length as CL, of pattern lists such that PL[q] is

the speciﬁc list of patterns that was used to train the

model CL[q], for any q ∈ {1,...,r}.

Then the meta-learning task is performed on a

meta-view s-View(L,CL,PL) of log L that stores, for

each trace τ ∈ L, a tuple s-View(τ,CL,PL) having

the same class label as τ, and featuring (as input

attributes) both the predictions of all the DDMs in

CL and the case/context attributes of τ. From s-

View(L,CL,PL) a probabilistic meta-classiﬁer (one

among HNB (Zhang et al., 2005) and AODE (Webb

et al., 2005)) is eventually induced, which can com-

bine the predictions of all of the base DDMs in CL.

The ﬁnal result of this learning procedure is a

multi-view deviance detection model, named High-

Order Deviation Detection Model (

HO-DDM

), which is

formally deﬁned below.

Deﬁnition 1 (HO-DDM) Let L be a log over some

proper trace universe T , and PROP(T ) be the space

With regard to the the labelling scheme of Figure 1 (and

assuming that the base DDMs appear inCL in the same left-

to-right order as in the ﬁgure), it is CL[q] = c

i, j

iff q = (i −

1) × k + j and PL[q] = P

iff i = ⌊(q− 1)/k⌋ + 1.

of all the data attributes that are associated with the

traces of T . Then, a High-Order Deviance Detec-

tion Model (

HO-DDM

) for L is a triple of the form

H = hCL,PL, ˆci, where: (i) PL is a list of r pat-

tern lists, for some r ∈ N; (ii) CL is a list of r

(base) DDMs such that, for each i ∈ {1,...,r}, CL[i]

is a DDM, learnt by using f-View(L,PL[i]) as train-

ing set, encoding a function of the form CL[i] :

PROP(T ) × R

→ {0,1}, which maps the proposi-

tional representation f-View(τ,PL[i]) of any trace τ ∈

T to a class label in {0,1}; and (iii) ˆc : PROP(T ) ×

{0,1}

→ [0, 1] is a (meta) classiﬁer providing an es-

timate for the probability that any trace τ in T is de-

viant, based on its (“stacking-oriented”) representa-

tion s-View(τ,CL,PL). 

In the current implementation of our approach, the

predictions of all the discovered base DDMs in CL

are combined using a probabilistic classiﬁer ˆc, com-

puted by applying one of the two Bayesian learning

methods described in the previous section. When a

novel trace τ is to be classiﬁed, each base model CL[i]

in the ensemble is applied to the vector-space repre-

sentation f-View(τ,PL[i]) of τ (produced according to

the same list PL[i] of patterns that was used to induce

CL[i]). The predictions made of the models in CL are

then combined into a single prediction by ˆc. Specif-

ically, by providing the latter model with a proposi-

tional view of τ mixing the original data properties of

τ (stored in prop(τ)) and the predictions assigned to

τ by the base models, the deviance probability score

ˆc(τ) is eventually returned as output. A simple way

to classify τ as deviant is to check whether ˆc(τ) > 0.5

—in this case to τ is assigned the label “1”. For the

sake of ﬂexibility, we allow for ﬁxing a lower de-

viance probability threshold γ ∈ (0,1), so that any τ

is deemed as deviant if and only if ˆc(τ) > γ.

4 DEVIANCE MINING AND

ANALYSIS FRAMEWORK:

ARCHITECTURE AND

IMPLEMENTATION

Figure 2 illustrates a conceptual system architecture

supporting the detection and analysis of deviant pro-

cess instances. Such a system, following a multi-

layer structure, is meant to handle the whole ﬂow of

log-based process analysis, from the discovery of an

HO-DDM

out of historical (labeled) log data, to the de-

tection of new deviant process instance, and the in-

spection and analysis of both the discovered mod-

els and detected deviances. The system is composed

of four different layers: Data/Model Repository, De-

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

166

!"#$%&& '()()* +,-%.,/

!"#

"$%&'()*

$%&'

(()&

*+,(()&

+(,

-./0

+(,

-./0

+(,

-./0

$%-'&.%/ 0"12./'3

)'4%,!'%3/./#

$%&'5(()

!'%3/./#

!"#

63"7'&&./#

('8.%/7'

9/&:'74."/

)";'<5

=8%<>%4."/

?;8%/7';5

)"/.4"3./#

0&%"12)-%"3,$%

!"#"$%&'()*+(,&-.#&/0

!(1."23( %.2.24

%&'()$!(1."23( 52")0-.-*

Figure 2: System Architecture for

HO-DDM-mine

viance Mining, Model/Deviance Analysis, and User

Interface.

Essentially, the bottommost layer is responsible

for storing both historical process logs and differ-

ent kinds of views (namely f-Views and s-Views) ex-

tracted from them, as well as the different kinds of

models that compose our

HO-DDM

s. All the process

mining and preprocessing methods implemented in

the Deviance Mining layer are meant to support the

induction of an HO-DDM out of historical log traces,

annotated each with a boolean deviance ﬂag. The dis-

covery of a

HO-DDM

from a given log L can be accom-

plished with the algorithm

HO-DDM-mine

proposed in

(Cuzzocrea et al., 2015), which is summarized in the

following. Basically, the algorithm follows a two-

phase computation strategy. In the ﬁrst phase, a num-

ber of base classiﬁers are discovered by applying a

given set of inductive learning methods to different

views of L, obtained each by projecting the traces in

L onto a different space of features. In the second

phase, all of these base classiﬁers are combined into

a single DDM, based on a meta-learning (stacking)

procedure.

In more detail, the algorithm iterates over the fol-

lowing main steps:

1. Preliminary to the extraction of the patterns, in

case log L is imbalanced, it can be made undergo

an oversampling procedure, where each deviant

trace in L is simply duplicated a certain number

of times.

2. For each pattern family speciﬁed by the ana-

lyst (e.g., individual activities, tandem repeats,

maximal repeats (Bose and van der Aalst, 2013;

Nguyen et al., 2014; Cuzzocrea et al., 2015)),

a list of relevant patterns of that family are ex-

tracted from L. The patterns that can be gener-

ated for each family are selected according to a

frequency-based strategy, where the patterns with

a high enough frequency in the log (or the q top

frequent ones) are kept.

3. For each pattern list P of those that have been

extracted in the previous step, the feature-based

view f-View(L,P) is materialized, and used as

training set for discovering different base DDMs

(using a different base learning algorithm for in-

ducing each of the latter). As a result, a list CL of

base DDMs is obtained, and an associated list PL

of pattern lists (such that PL[i] is the pattern list

used to train CL[i], for any position i in CL).

4. The discovered DDMs in CL are then com-

bined into a single overall meta-classiﬁer using

a stacking strategy. To this end, the “stacked”

view s-View(L,CL,PL) is computed, and a meta-

classiﬁer ˆc is induced from it, by applying one

of the two alternative probabilistic learning meth-

ods (e.g., our customized versions of the methods

AODE or HNB described in Section 2). The dis-

covered combiner must be able to compute, for

any “stacked” tuple x ∈ X, an estimate ˆc(x) of x’s

deviance probability (i.e. ˆc(x) ≈ P(Y = 1|x)) ac-

cording to Eq. 4 or 8 This can be done efﬁciently

by pre-computinga number of sufﬁcient statistics,

as described later on in this section.

All the discovered DDMs (be them base mod-

els or HO-DDMs) are made available to the

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

167

Model/Deviance Analysis Layer, which can produce

a series of evaluation measures, like those used in

our experimentations to quantitatively assess the va-

lidity of our approach. The Advanced Monitoring

module offers deviance-oriented runtime-support ser-

vices, which mainly consist in the notiﬁcation of alert

messages and in the suggestion of possible counter-

measures to be possibly undertaken when a deviant

process instance is detected. Finally, the Deviance In-

spection module is meant to allow the analyst to in-

spect and study single process instances detected as

(mostly) deviant, and try to understand the causes of

their abnormal behavior.

Details on the discovery of a HO-DDM: statistics

underlying the Bayesian combiners. As explained

previously, the Bayesian combiner ˆc in any

HO-DDM

(cf. Def. 1) must return, for each “stacked” tuple

x ∈ X, an estimate ˆc(x) of x’s deviance probability

(i.e. ˆc(x) ≈ P(Y = 1|x)) according to Eq. 4 or 8.

Such an estimate is computed on the basis of the

following (precomputed) statistics, which are all de-

rived from s-View(L,CL,PL) for all i, j ∈ {1,...,m},

∈ dom(X

), and x

∈ dom(X

), and constitute the

backbone of the combiner model ˆc:

• n

is the number of values for attribute X

;

• D (resp. N) is the number of deviant (resp. nor-

mal) tuples in s-View(L,CL,PL);

• D

(resp. N

) is the number of deviant (resp. nor-

mal) tuples in s-View(L,CL,PL) that feature the

value x

• D

(resp. N

) is the number of deviant (resp. nor-

mal) tuples in s-View(L,CL, PL) that feature both

values x

and x

• K is the number of tuples in s-View(L,CL,PL) (all

having a known value of the deviance label),

• K

is the number of tuples in s-View(L,CL,PL) for

which the value of attribute X

is known,

• K

is the number of tuples in s-View(L,CL, PL)

for which the values of both attributes X

and X

are known. 

Notice that the counters above are sufﬁcient to

estimate every base probability of the form P(y),

P(y,x

) and P(y,x

). The latter, in turn, can be

exploited to estimate every probability of the form

P(x

|y) and P(x

|y,x

) —for each values x

and x

of the attributes X

and X

(with the former play-

ing as super-parent), for i, j ∈ {1,...,m} and y ∈

{0,1}— that are needed to compute P(y|x) according

to Eq. 4 and 8. To make the estimation more robust,

these base probabilities are computed by using the

Laplace estimation method (Webb et al., 2005; Zhang

et al., 2005), as speciﬁed in the following: P(Y =

1) =

D+1

K+2

; P(Y = 1,x

) =

+2·n

; P(Y = 1,x

) =

+2·n

·n

; P(Y = 0) =

N+1

K+2

; P(Y = 0, x

) =

+2·n

;

P(Y = 0, x

) =

+2·n

·n

; P(x

|Y = 1) = P(Y =

1,x

)/P(Y = 1); P(x

|Y = 0) = P(Y = 0,x

)/P(Y =

0); P(x

|Y = 1,x

) = P(Y = 1,x

)/P(Y = 1,x

);

P(x

|Y = 0, x

) = P(Y = 0, x

)/P(Y = 0, x

5 EXPERIMENTAL ANALYSIS

The capability of our approach to effectively recog-

nize deviant behaviors has been assessed by conduct-

ing a series of tests on a real-life log, storing infor-

mation on the clinical pathways of gynecologic can-

cer patients within a Dutch hospital. This log was

made available as a benchmark dataset for the 2011

BPI Challenge (van Dongen, 2011). Details on these

datasets, omitted here for the sake of space, can be

found in (Cuzzocrea et al., 2015).

Different evaluation metrics exist in the literature

for testing the effectiveness of classiﬁcation models

in the presence of a rare class. Carefully choosing

these metrics is important since the usage of metrics

that do not adequately account for the rarity of the

minority class may easily lead to overestimating the

accuracy of a classiﬁer. Speciﬁcally, we used four

metrics widely used over imbalanced data, i.e. area

under the ROC curve (AUC) (Bradley, 1997), the G-

mean (Kubat et al., 1997), Precision (P), and Recall

(R) (Buckland and Gey, 1994).

5.1 Settings

Testing our approach requires two key settings: (1)

the kind of patterns used to project the log traces onto

a vector space, and (2) the classiﬁer-induction meth-

ods employed to derive, from such a feature-based

representation of the traces, the base and combined

models that compose the overall

HO-DDM

As concerns the former point, as a ﬁrst family of

behavioral patterns, denoted by

(i.e. individual ac-

tivities), we simply considered all the process activi-

ties in their own. In this case, for any trace, we regard

each activity, say a, as an additional (pattern-oriented)

feature of the trace, storing the number of times that a

occurs in the trace. In order to produce more sophis-

ticated representations of traces’ behaviors, we also

considered (as done in (Bose and van der Aalst, 2013;

Nguyen et al., 2014)) all the sequence-based patterns

possibly capturing control-ﬂow constructs (e.g., sub-

processes, loops, and parallelism) ruling the behav-

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

168

Table 1: Prediction results obtained on the BPIC11

log when using different conﬁgurations of the (single DDM) competitor

method (Nguyen et al., 2014). All the values were computed by averaging the results of 5 trials, performed according to a 5

fold cross-validation scheme. For each metrics, the best outcome is reported in bold.

Alg. Patterns AUC G-Mean R P AvgRank AvgRank 5%

IBk

{

IA.AMR

} 0.771±0.019 0.538±0.049 0.321±0.062 0.458±0.106 9.00 2.75

{

IA.ATR

} 0.782±0.024 0.566±0.062 0.362±0.092 0.476±0.108 4.25 1.50

{

IA.MR

} 0.779±0.020 0.538±0.050 0.321±0.062 0.456±0.097 8.25 2.75

{

IA.TR

} 0.772±0.028 0.545±0.111 0.351±0.151 0.411±0.076 9.00 2.25

{

} 0.798±0.034 0.597±0.043 0.397±0.072 0.493±0.084 1.75 1.00

ANN

{

IA.AMR

} 0.787±0.023 0.451±0.066 0.222±0.076 0.468±0.146 8.75 3.75

{

IA.ATR

} 0.780±0.020 0.470±0.124 0.261±0.172 0.409±0.144 10.50 3.50

{

IA.MR

} 0.777±0.026 0.523±0.201 0.360±0.271 0.412±0.082 8.75 2.25

{

IA.TR

} 0.795±0.038 0.512±0.182 0.339±0.227 0.417±0.049 8.00 2.75

{

} 0.779±0.037 0.426±0.032 0.198±0.028 0.359±0.107 12.75 4.75

J48

{

IA.AMR

} 0.740±0.066 0.587±0.099 0.397±0.139 0.459±0.082 6.50 1.50

{

IA.ATR

} 0.768±0.019 0.570±0.098 0.378±0.134 0.425±0.070 7.00 1.75

{

IA.MR

} 0.746±0.069 0.599±0.090 0.412±0.128 0.459±0.086 5.00 1.50

{

IA.TR

} 0.706±0.062 0.458±0.100 0.244±0.105 0.370±0.091 13.75 4.50

{

} 0.757±0.044 0.561±0.103 0.359±0.138 0.496±0.042 6.50 2.00

MAX 0.798±0.034 0.599±0.090 0.412±0.128 0.496±0.042 1.75 1.00

ior of the analyzed process: tandem repeats (

), al-

phabet tandem repeats (

ATR

), maximal repeats (

and alphabet maximal repeats (

AMR

). When comput-

ing the f-View representation of a trace, we turned

each of these patterns as a non negative integer at-

tribute, storing the number of times the respective pat-

tern occurred in the trace.

Similarly to (Nguyen et al., 2014), we considered

the following heterogenous families of patterns: (i)

{

}, i.e. individual activities used alone (produc-

ing a bag-of-activity representation of traces’ struc-

ture); (ii) {

IA,TR

}, i.e. the combination of individual

activities and of tandem repeats; (iii) {

IA,ATR

}, i.e.

individual activities combined with alphabet tandem

repeats; (iv) {

IA,MR

}, i.e. individual activities plus

maximal repeats; (v) {

IA,AMR

}, i.e. individual activi-

ties plus alphabet maximal repeats.

For each pattern family, we used only a selection

of those patterns that most frequently occur in the

log (namely, 100 patterns of type {

} and 250 pat-

terns for each other pattern family). In addition, when

HO-DDM-mine

exploited the re-sampling to mitigate

the skewness in the log, all the deviant (i.e. positive)

traces in it were duplicated until a deviant-normal ra-

tio of approximately 1:2 is reached.

As to the induction of base DDMs, we resorted

to the following methods: the decision-tree learn-

ing method J48 (Quinlan, 1993); the k-NN procedure

IBk (with k = 10); the multi-layer perception method

(named hereinafter ANN) (Zhang, 2000); the LibSVM

Support-Vector-Machines classiﬁer (Cortes and Vap-

nik, 1995) with an RDF kernel; and the rule-base clas-

siﬁer JRip (Witten and Frank, 2005).

For the induction of a probabilistic combiner

model, we tested two alternative settings of algorithm

HO-DDM-mine

: one using an AODE-based classiﬁer,

and the other using an HNB-based classiﬁer.

5.2 Test Results

A First Look a the Competitor’s Results. Since

the approach in (Nguyen et al., 2014) consists in ap-

plying each learning method to each distinct view of

the log (generated according to one of the pattern fam-

ilies described in the previous subsection), it produces

the 15 independent DDM models shown in Table 1

—namely, J48

{IA}

, ..., J48

{IA+AMR}

, IBk

{IA}

, ...,

IBk

{IA+AMR}

, ANN

{IA}

, ..., ANN

{IA+AMR}

—which

should be compared with the ones discovered by our

approach. However, it is easy to notice that the out-

comes in Table 1 are almost all very close to one an-

other, and no one single DDM can be clearly declared

winning over its competitors in all the quality metrics

simultaneously. For instance, the AUC value for the

IBK

{IA}

model is 0.798, while that for ANN

{IA+TR}

0.795 —this difference of less than 5% in their val-

ues reveals that they are practically equivalents to one

another in terms of AUC performances. The same

holds for the G-Mean of J48

{IA+MR}

(0.599), which

is very close again to that of IBk

{IA}

(0.597). Simi-

lar considerations can be easily spotted as well for the

remaining metrics. In such a situation, choosing the

most suitable competitor to run against

HO-DDM-mine

is not a straightforward task.

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

169

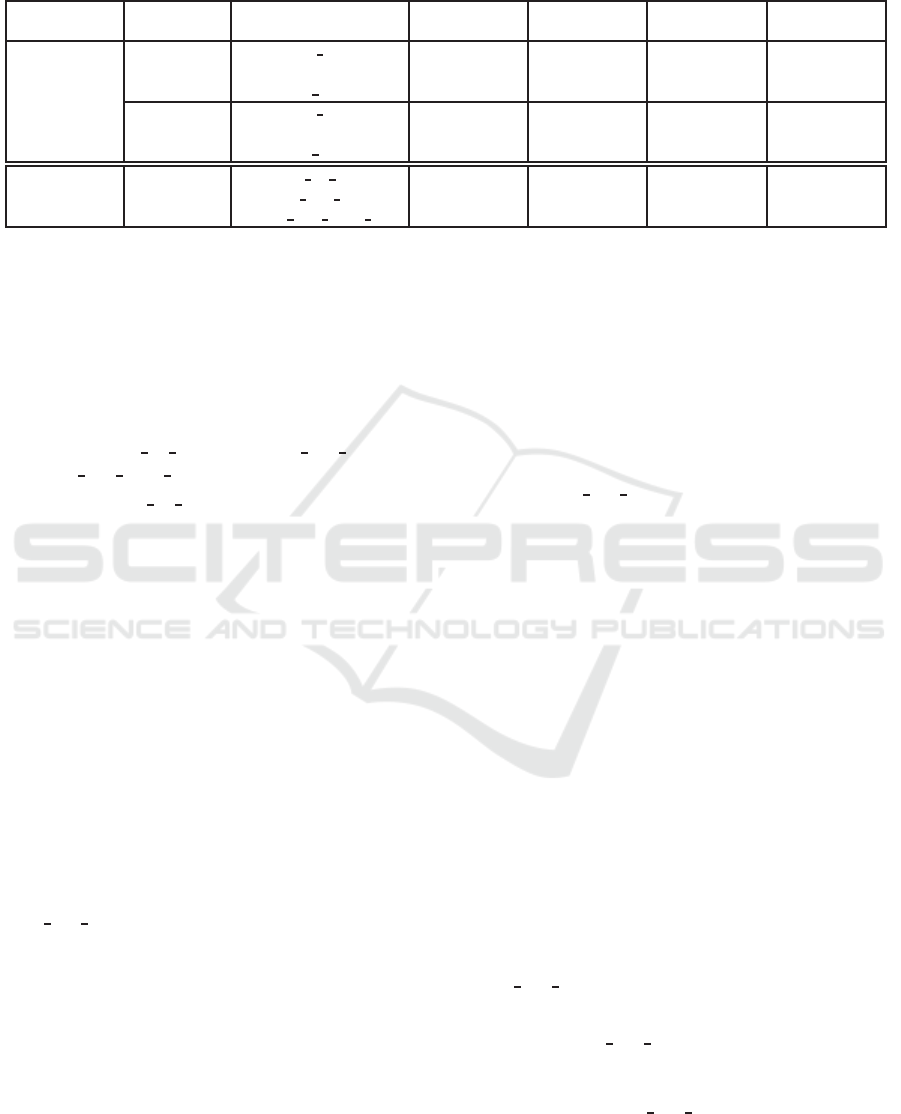
Table 2: Prediction results on the BPIC11

log by

HO-DDM-mine

and selected conﬁgurations of the competitor

method (Nguyen et al., 2014). All the values were computed by averaging the results of 5 trials, performed according to

a 5 fold cross-validation scheme. For each metrics, the best outcome is reported in bold.

Method

Bayesian

Combiner

Setting AUC G-Mean Recall Precision

Ours

HNB

RES+MORE LEARNERS

0.857±0.051 0.740±0.018 0.606±0.041 0.745±0.047

RES

0.822±0.040 0.726±0.030 0.592±0.059 0.717±0.044

NO RES

0.817±0.024 0.652±0.035 0.477±0.055 0.505±0.077

AODE

RES+MORE LEARNERS

0.853±0.053 0.736±0.022 0.598±0.042 0.742±0.049

RES

0.819±0.044 0.722±0.047 0.584±0.080 0.715±0.047

NO RES

0.813±0.026 0.648±0.039 0.469±0.056 0.502±0.082

(Nguyen et

al., 2014)

BEST OF BEST

0.798±0.034 0.599±0.090 0.412±0.128 0.496±0.042

BEST AVG RANK

0.798±0.034 0.597±0.043 0.397±0.072 0.493±0.084

BEST AVG RANK 5%

0.798±0.034 0.597±0.043 0.397±0.072 0.493±0.084

Summarizing the Competitor’s Achievements. In

order to enable an easier comparison of our approach

to the alternative settings of the competitor approach

presented above, we devised a method for summa-

rizing the performances of the latter. More pre-

cisely, we deﬁned three different criteria for choos-

ing the best achievement of the competitor ap-

proach: (i)

BEST OF BEST

, (ii)

BEST AVG RANK

, and

(iii)

BEST AVG RANK 5%

As to the

BEST OF BEST

row, it simply reports, for

each evaluation method, the best value (i.e. the max-

imum) obtained by all of the different conﬁgurations

of the approach in (Nguyen et al., 2014) in each sin-

gle metric. To make clear which values are chosen,

the best outcome in each column (i.e. performance

metric) of Table 1 have been marked in bold. For the

reader’ convenience, these values are also explicitly

reported in the row with the MAX label at the bottom

of the same table. Clearly, it is important to point out

that this row provides an overestimated evaluation of

the competitor approach, which may not correspond

to any actual conﬁguration of it. In a sense, this row

is a sort of upper bound for the performance of all the

considered conﬁgurations of the competitor.

Thus, in order to provide a more realistic (yet

concise) term of comparison, we deﬁned a sec-

ond criterion for a further competitor, denoted by

BEST AVG RANK

, aiming at meaningfully aggregating

all the results obtained with the approach of (Nguyen

et al., 2014) and reported in Table 1. The way this

competitor is actually determined is explained in the

following.

Let C be the set of all DDM models discovered

by the tested methods, and M = {AUC,G-Mean, R, P}

be the set of metrics considered in our evaluation set-

ting. For any model c ∈ C and any metrics m ∈ M,

let score(c,m) be the value returned by evaluating m

against c. Based on these values, we ranked the mod-

els in C over each metrics. More clearly, rank(c,m) =

1 (resp. rank(c,m) = k) iff c is the best (k-th best) per-

former according to metrics m. Considering all met-

rics equally important for assessing the quality of a

DDM, we computed an overall average ranking score

for each model c ∈ C as follows:

AvgRank(c) = .25× (rank(c, AUC)+

+ rank(c,G− Mean) + rank(c,R) + rank(c,P))

The

BEST AVG RANK

model, selected among all

the other models discovered by (using different con-

ﬁgurations of) the approach of (Nguyen et al., 2014),

is the one reaching the highest value of the overall

ranking score AvgRank.

Example 1. Let us consider the model IBK

{IA}

, dis-

covered with method IBk on individual-activities fea-

tures (i.e., by using only the family

of patterns)

According to the values in Table 1, it can be easily

noted that rank(IBK

{IA}

,AUC) = 1 since IBK

{IA}

scored higher than any other model on the AUC met-

ric (i.e. it achieved the maximum score over the AUC

column). By converse, rank(IBK

{IA}

,G-Mean) = 2,

since IBK

{IA}

is the second best performer accord-

ing to the G-Mean metric —the same holds also for

the metrics R and P. As a ﬁnal result, we obtain

the overall rank-oriented score AvgRank(IBK

{IA}

) =

.25 × (1 + 2 + 2 + 2) = 0.25 × 7 = 1.75. According

to this ranking criterion, the model returned by IBk

on the

-based log view is deemed as the best re-

sult of the approach in (Nguyen et al., 2014), namely

BEST AVG RANK

, with an average rank of 1.75. 

For the sake of comparison, the row of Table 2

marked as

BEST AVG RANK

reports the quality mea-

sures receivedby this model, as a second term of com-

parison for our approach.

The way the

BEST AVG RANK

competitor has been

computed might be susceptible to criticisms due

to numeric approximation problems possibly plagu-

ing very close values. Indeed, it may happen that

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

170

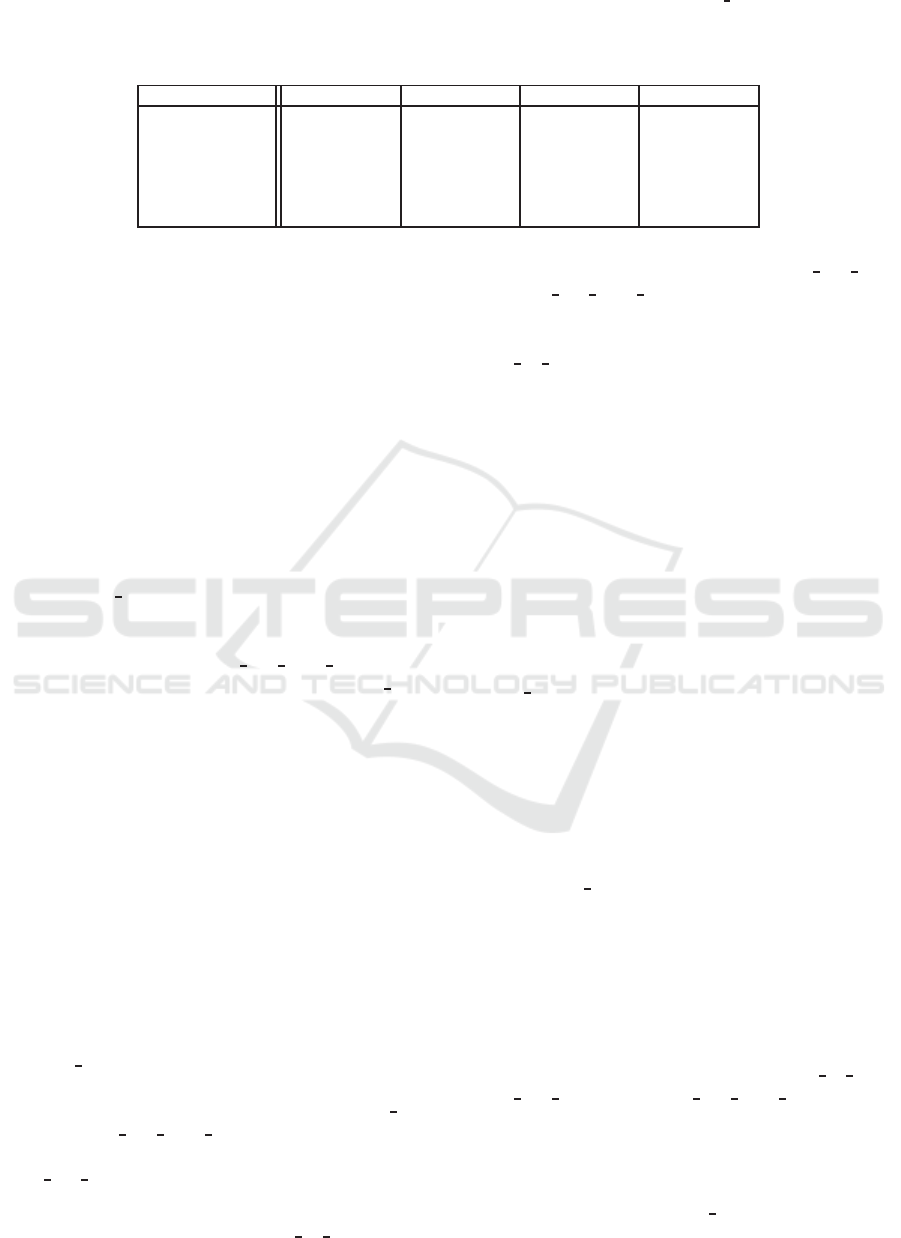
Table 3: Prediction results on the BPIC11

log by

HO-DDM-mine

(in the conﬁguration

RES+MORE LEARNERS

) when using

different learning algorithms (as an alternative to our

AODE

-based and

HNB

-based Bayesian meta-classiﬁers) for the discovery

of a combiner model. All the values were computed by averaging the results of 5 trials, performed according to a 5 fold

cross-validation scheme. For each metrics, the best outcome is reported in bold.

Meta-algorithm AUC G-Mean R P

HNB

0.857±0.051 0.740±0.018 0.606±0.041 0.745±0.047

AODE

0.853±0.053 0.736±0.022 0.598±0.042 0.742±0.049

AdaBoostM1

0.811±0.056 0.719±0.039 0.579±0.057 0.710±0.070

J48

0.748±0.057 0.724±0.048 0.584±0.065 0.718±0.071

JRip

0.715±0.029 0.693±0.033 0.543±0.040 0.676±0.061

Logistic

0.789±0.052 0.712±0.033 0.570±0.049 0.696±0.042

two models have performance scores so much close

among them (i.e. under a certain approximation

threshold z) that could be retained unfair assign-

ing them different ranks. In order to preventively

cope with such potential concerns, we considered a

third evaluation strategy accounting as equivalent two

models c1,c2 ∈ C w.r.t. a given metric m ∈ M if the

difference between their values falls below a speciﬁed

threshold z. More formally, this can be stated as in the

following:

rank(c1,m) = rank(c2, m) iff

|m(c1) − m(c2)| ≤ z× min(m(c1),m(c2))

As a consequence of the deﬁnition above, a new

rank AvgRank

z% can be easily deﬁned. Speciﬁcally,

in our setting we considered as a reasonable approxi-

mation a threshold of 5% (i.e. z = .05), and then we

selected the competitor

BEST AVG RANK 5%

(cf. last

row of Table 2) according to the index AvgRank

5%.

Example 2. Let us focus again on the IBk

model, and let z = .05 be the threshold value

used for alleviating the numeric approximation prob-

lem in our calculus. Based on Table 1, it re-

sults that rank(IBK

{IA}

,AUC) = 1, as IBK

{IA}

per-

forms better than any other approach over the

metric AUC. However, under this new threshold-

based setting, rank(IBK

{IA}

,G-Mean) = 1, although

the best performer w.r.t. the metric G-Mean

J48

{IA,MR}

. Indeed,

IBK

{IA}

and

J48

{IA,MR}

are ranked equally due to the fact that |G-

Mean(IBK

{IA}

) − G-Mean(J48

{IA,MR}

)| = |0.597 −

0.599| = .002 ≤ .05 × min(0.597,0.599) = .05 ×

0.597 = .03. Similar considerations apply for

metrics R and P. Therefore, we have that

AvgRank

5%(IBK

{IA}

) = .25 × (1 + 1 + 1 + 1) =

0.25 × 4 = 1.00. As a consequence,

IBK

{IA}

is the

best performer according to criterion AvgRank

5%,

i.e. the

BEST AVG RANK 5%

model. Please, notice

that, by pure chance, it incidentally coincides with the

BEST AVG RANK

model. 

Clearly, by the way it is computed, the perfor-

mances of our competitor in its

BEST OF BEST

setting

are always better than that in both the

BEST AVG RANK

and

BEST AVG RANK 5%

ones. Therefore, the com-

parative analysis carried out in the following is

focused on the (“optimistic” for the competitor)

BEST OF BEST

scenario.

Comparing HO-DDM-mine’s Results with the Best

Ones of the Competitor. Table 2 reports the results

obtained by algorithm

HO-DDM-mine

, compared with

those of the proposed in (Nguyen et al., 2014). For the

sake of comparison, we used the same families of pat-

terns and the same (or a slightly wider) set of classiﬁ-

cation methods as in (Nguyen et al., 2014), and turned

the probabilistic classiﬁcations of

HO-DDM-mine

into

deterministic ones, using a ﬁxed deviance threshold

γ = 0.5.

Speciﬁcally, as far as concerns

HO-DDM-mine

, we

tested three different conﬁgurations of it:

•

NO RES

, where no resampling procedure is applied

to the transformed log (in order to reduce the class

imbalance ratio), and the same set of (base) induc-

tive learning methods as in (Nguyen et al., 2014)

(namely J48, IBk, ANN) are used;

•

RES

, using our basic oversampling scheme and the

same battery of base classiﬁers as in the previous

conﬁguration (and in (Nguyen et al., 2014));

•

RES+MORE LEARNERS

, which uses the same over-

sampling setting as in conﬁguration

RES

, while

exploiting the classiﬁer-induction methods imple-

mented in our prototype system (i.e. J48, IBk,

ANN, LibSVM, JRip).

The three bottommost rows in the table report, as

a term of comparison, the best scores obtained by

all the settings of the competitor, and computed ac-

cording to the three criteria (namely,

BEST OF BEST

BEST AVG RANK

, and

BEST AVG RANK 5%

) explained

in the previous paragraph.

From the ﬁgures in Table 2, we can draw several

interesting observations. First of all,

HO-DDM-mine

(irrespective of the kind of probabilistic combiner

adopted), even in the basic

NO RES

conﬁguration, per-

forms always better (over all the quality metrics) than

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

171

the competitor (Nguyen et al., 2014), whatever con-

ﬁguration is used for the latter. This conﬁrms the va-

lidity of using an ensemble-learning approach to the

deviance detection problem. In particular, it is worth

noticing that when allowed to induce an HNB com-

biner, algorithm

HO-DDM-mine

achieves better perfor-

mances than its AODE-based version, despite the lat-

ter method make use of an ensemble of SPODEs (see

Section 2.1) while HNB only adopts a single Bayesian

model. This likely descends from the capability of

HNB to effectively capture the inherent dependencies

between the attributes in our s-View representation.

Performing a ﬁner grain analysis, we can notice

that the gain achieved by the HNB-based version of

HO-DDM-mine

over the approach in (Nguyen et al.,

2014) in its basic conﬁguration without resampling

becomes even more marked when using a basic over-

sampling procedure (i.e. in the

RES

conﬁguration).

Speciﬁcally, even though the increment in terms of

AUC is moderate (3.00%), we can observe a signif-

icant improvement for the metric G-Mean (21.20%),

and a noticeable 44.56% (resp. 43.69%) achievement

in terms of precision (resp. recall).

Further improvement is obtained by our approach

(still equipped with HNB) when letting it use both the

oversampling procedure and a broader range of base

classiﬁers (i.e. conﬁguration

RES+MORE LEARNERS

)

—actually, we only extended the learning methods

used by our competitor with the insertion of LibSVM

and JRip. Indeed, in this case, a gain of 7.39% (resp.

23.54%, 50.20%, 47.09%) is obtained in terms of

AUC (resp. G-Mean, precision, recall) w.r.t. the over-

estimated

BEST OF BEST

conﬁguration.

Notably, a similar trend in the results can be found

for the version of

HO-DDM-mine

adopting AODE as

combiner, and then it does not require any further sup-

plementary discussion.

In summary, it seems that the combination of

an oversampling method with our ensemble-learning

strategy helps obtain higher improvements (w.r.t. the

competitor supervised deviance-detection approach)

than exploiting a wider range of base classiﬁers.

Beneﬁts of using Bayesian Combiners. In a fur-

ther series of tests, we considered some variants of

algorithm

HO-DDM-mine

where we tried the follow-

ing meta-learning methods (for inducing the com-

biner model ˆc of any

HO-DDM

) as an alternative to its

native Bayesian classiﬁers:

AdaBoostM1

J48

JRip

Logistic

. The results of this experimentation are

reported in Table 3. It is clear that both kinds of

Bayesian combiner allow to achieve superior perfor-

mances, over all the quality metrics, than these alter-

native methods. This is likely due to their capabil-

ity of obtaining accurate and robust estimates of the

class membership probability, despite the high degree

of dependence between the attributes in the stacked

view given as input to it.

6 CONCLUSION

In this paper, we have extended a previous proposal

where an innovative ensemble-learning framework

for mining business process deviances that exploits

multi-view learning has been provided. Relevant con-

tributions, which clearly conﬁrm the ﬂexibility, the re-

liability and the effectiveness of the general deviance

detection framework, respectively, have been intro-

duced and experimentally assessed via a wide and

comprehensive experimental campaign. Notice that

our multi-view learning approach is neatly different

from many others in the literature that do not follow

an ensemble-based scheme (such as, e.g., (Blum and

Mitchell, 1998; Nigam and Ghani, 2000; Wang and

Zhou, 2010)), and somewhat rely on the fact that the

different data views are (more or less) conditionally

independent of one another given the label —an as-

sumption that does not hold in the setting considered

in this work, where the views are likely to feature high

levels of redundancy and of inter-dependence.

As future work, we mainly plan to investigate

on the combination of our ensemble learning ap-

proach with log-oriented clustering methods (like

those in (Folino et al., 2014; Bose and van der Aalst,

2010)), as well as to apply the framework to real-life

projects, in order to derivenewtest-beds, newrequire-

ments, and new solutions. Also, to provide effective-

ness, we aim at studying the integration of intelligent

data processing techniques (e.g., (Cuzzocrea and Ma-

trangolo, 2004; Cuzzocrea, 2006; Cuzzocrea et al.,

2009)).

REFERENCES

Bose, R.P.J.C., van der Aalst, W.M.P.: Discovering sig-

nature patterns from event logs. In: IEEE Symp.

on Computational Intelligence and Data Mining

(CIDM’13), pp. 111–118 (2013)

Bradley, A.P.: The use of the area under the roc curve in

the evaluation of machine learning algorithms. Pattern

Recognition 30(7), 1145–1159 (1997)

Buckland, M., Gey, F.: The relationship between recall and

precision. Journal of the American Society for Infor-

mation Science 45(1), pp. 12–19 (1994)

Cortes, C., Vapnik, V.: Support-vector networks. Machine

learning 20(3), pp. 273–297 (1995)

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

172

Cuzzocrea, A.: Accuracy Control in Compressed Mul-

tidimensional Data Cubes for Quality of Answer-

based OLAP Tools. In: Proc. of IEEE SSDBM 2006,

pp. 301–310, 2006

Cuzzocrea, A., Folino, F., Guarascio, M., Pontieri, L.: A

Multi-view Learning Approach to the Discovery of

Deviant Process Instances. In: Proc. of CoopIS 2015,

pp. 146–165, 2015

Cuzzocrea, A., Furfaro, F., Sacc`a, D.: Enabling OLAP in

mobile environments via intelligent data cube com-

pression techniques. Journal of Intelligent Information

Systems (33)(2), pp. 95–143 (2009)

Cuzzocrea, A., Matrangolo, U.: Analytical Synopses for

Approximate Query Answering in OLAP Environ-

ments. In: Proc. of DEXA 2004, pp. 359–370, 2004

van Dongen, B.:

http://dx.doi.org/10.4121/

uuid:d9769f3d-0ab0-4fb8-803b-0d1120ffcf54

van Dongen et al.: The ProM framework: A new era in

process mining tool support. In: Proc. of 26th 10th

Int. Conf. on Applications and Theory of Petri Nets

(ICATPN’05), pp. 444–454 (2005)

Frank, E., Hall, M.A., Holmes, G., Kirkby, R., Pfahringer,

B.: Weka - a machine learning workbench for data

mining. In: The Data Mining and Knowledge Discov-

ery Handbook, pp. 1305–1314 (2005)

Japkowicz, N., Stephen, S.: The class imbalance problem:

A systematic study. Intelligent Data Analysis 6(5), pp.

429–449 (2002)

Kubat, M., Holte, R., Matwin, S.: Learning when negative

examples abound. In: Proc. of 9th Europ. Conf. on

Machine Learning (ECML’97), pp. 146–153 (1997)

Langley P., Iba W., Thompson K.: An analysis of Bayesian

classiﬁers. In: Proc. of 10th Nat. Conf. on Artiﬁcial

intelligence (AAAI’92), pp. 223–228 (1992)

Lo, D., Cheng, H., Han, J., Khoo, S.C., Sun, C.: Classiﬁca-

tion of software behaviors for failure detection: A dis-

criminative pattern mining approach. In: Proc. of 15th

Int. Conf. on Knowledge Discovery and Data Mining

(KDD’09), pp. 557–566 (2009)

Nguyen, H., Dumas, M., Rosa, M.L., Maggi, F.M., Suriadi,

S.: Mining business process deviance: A quest for ac-

curacy. In: Proc. of 2014 Int. Conf. On the Move to

Meaningful Internet Systems (OTM’14), pp. 436–445

(2014)

Quinlan, J.R.: C4.5: programs for machine learning. Mor-

gan Kaufmann Publishers Inc., San Francisco, CA,

USA (1993)

Folino, F., Guarascio, M., Pontieri, L.: Mining predic-

tive process models out of low-level multidimensional

logs. In: Proc. of 26th Int. Conf. on Advanced Infor-

mation Systems Engineering (CAISE’14), pp. 533–

547 (2014)

Blum A. and Mitchell T.: Combining labeled and unlabeled

data with co-training. In: Proc. of the 11th Conf. on

Computational Learning Theory (COLT’98), pp. 92–

100 (1998)

Nigam K., Ghani R.: Analyzing the effectiveness and ap-

plicability of co-training. In: Proc. of the 9th Int.

Conf. on Information and Knowledge Management

(CIKM’00), pp. 86–93 (2000)

Wang W., Zhou Z.H.: A new analysis of co-training. In:

Proc. of the 27th Int. Conf. on Machine Learning

(ICML’10), pages 1135–1142, 2010.

Domingos P., Pazzani M.J.: Beyond Independence: Condi-

tions for the Optimality of the Simple Bayesian Clas-

siﬁer. In: Proc. 13th Int. Conf. on Machine Learning

(ICML’96). pp.105–112 (1996)

Domingos P., Pazzani M.J.: On the Optimality of the Sim-

ple Bayesian Classiﬁer under Zero-One Loss. Ma-

chine Learning 29, pp.103–130 (1997)

Keogh E.J., Pazzani M.J.: Learning the Structure of Aug-

mented Bayesian Classiﬁers. Int. J. Artiﬁcial Intelli-

gence Tools, 11(40), pp. 587–601 (2002)

Ying Y. et al.: To Select or To Weigh: A Comparative Study

of Linear Combination Schemes for SuperParent-

One-Dependence Estimators. IEEE Transactions on

Knowledge and Data Engineering, 19(12), pp.1652–

1665 (2007)

Bose, R.P.J.C., van der Aalst, W.M.P.: Trace clustering

based on conserved patterns: Towards achieving bet-

ter process models. In: Proc. of Business Process

Management Workshops (BPI’10), vol. 43, pp. 170–

181 (2010)

Sahami M.: Learning Limited Dependence Bayesian Clas-

siﬁers. In: Proc. 2nd ACM SIGKDD of Int. Conf.

Knowledge Discovery and Data Mining (KDD’96),

pp. 334–338 (1996)

Suriadi S., Chun O., van der Aalst W.M.P., ter Hofstede

A.H.M. : Root Cause Analysis with Enriched Process

Logs. In: Business Process Management Workshops

2012, pages 174–186, 2013.

Swinnen, J., Depaire, B., Jans, M.J., Vanhoof, K.: A pro-

cess deviation analysis - A case study. In: Proc. of

2011 Business Process Management Workshops, pp.

87–98 (2011)

Webb G.I., Boughton J., Wang Z. Not So Naive Bayes:

Aggregating One-Dependence Estimators. Machine

Learning, 58(1), pp. 5–24 (2005)

Zhang, G.P.: Neural networks for classiﬁcation: a survey.

Systems, Man, and Cybernetics, Part C: Applications

and Reviews, IEEE Transactions on 30(4), pp. 451–

462 (2000)

Zhang, H., Jiang, L., Su, J.: Hidden naive bayes. In: Proc

of AAAI, pp. 919–924 (2005)

Witten, I.H., Frank, E.: Data Mining: Practical Machine

Learning Tools and Techniques, Second Edition (Mor-

gan Kaufmann Series in Data Management Systems).

Morgan Kaufmann Publishers Inc. (2005)

Extensions, Analysis and Experimental Assessment of a Probabilistic Ensemble-learning Framework for Detecting Deviances in Business

Process Instances

173