From Temporal Models to Property-based Testing

Nasser Alzahrani, Maria Spichkova and Jan Olaf Blech

RMIT University, Melbourne, Australia

Keywords:

Formal Methods, Property based Testing.

Abstract:

This paper presents a framework to apply property-based testing (PBT) on top of temporal formal models.

The aim of this work is to help software engineers to understand temporal models that are presented formally

and to make use of the advantages of formal methods: the core time-based constructs of a formal method are

schematically translated to the BeSpaceD extension of the Scala programming language. This allows us to

have an executable Scala code that corresponds to the formal model, as well as to perform PBT of the models

functionality. To model temporal properties of the systems, in the current work we focus on two formal

languages, TLA+ and Focus

1 INTRODUCTION

Safety-critical systems, e.g., in the automotive dom-

ain (K

uhnel and Spichkova, 2007), become more and

more software-intensive with every year. While spe-

cifying such systems, a precise formal model, i.e.,

a mathematical model at some level of abstraction,

might be essential to eliminate ambiguity and to de-

tect possible errors early in the software development

life-cycle (SDL). Also, in most cases the system pro-

perties have to be analysed in relation to the time,

thus, veriﬁcation/testing of the temporal aspects is

crucial.

To achieve the integration of formal models into

SDL, the development process should be human-

oriented. Thus, aspects of human factors engineering

should be taken into account, cf. (Spichkova et al.,

2015). Moreover, using Formal Methods (FMs) can

be beneﬁcial while developing not only safety-critical

systems, but also web services, cf. (Newcombe et al.,

2015). FMs were successfully applied to design and

analyse systems since many years, cf. (Bowen and

Hinchey, 1995; Yu et al., 1999). Despite all the ad-

vantages of FMs, software engineers are not keen to

include them into the software development process.

This problem was discussed 15-20 years ago, e.g.,

in (Hinchey, 2003). This problem is still unsolved

now. Lack of readability and usability is one of the

reasons for very limited use of FMs in industrial pro-

jects (Zamansky et al., 2016). However, in some cases

even simply implementable improvements can make

an FM more readable and understandable, cf. (Spi-

chkova, 2012).

In many cases, FMs require huge amount of trai-

ning, as they use a very speciﬁc syntax that is unrea-

dable for novices. In general, testing approaches are

perceived by practitioners as more appropriate for a

real-life development process. However, they are usu-

ally comfortable with concepts from property-based

testing (PBT), which require a little bit of mathema-

tical thinking. PBT approach allows to use randomly

generated test cases based on properties to test sys-

tems against their speciﬁcations.

To led programmers in formulating and testing

properties of programs, Claessen and Hughes intro-

duced a tool named QuickCheck that is focusing on

Haskell programming language. They demonstrated

that QuickCheck allowed them to discover hundreds

of bugs, e.g., DropBox ﬁle sharing service (Claessen

and Hughes, 2011; Hughes, 2010). In its ﬁrst edition,

QuickCheck was proposed as a testing framework for

testing only functional programs. However, recent de-

velopment in the area of PBT incorporates the state-

fulness of systems. That provides functionality for the

testing of state-ful systems as well as for testing pro-

grams written in imperative languages, e.g., C (Ger-

des et al., 2015; Hughes, 2010).

We propose to apply PBT on top of temporal for-

mal models. This might help software engineers to

understand temporal formal models (which describe

the state of a system in every discrete time point), as

the FM constructs will be expressed in terms of sy-

stem code. This might contribute to the understanda-

bility of FMs indirectly, and allow software engineers

Alzahrani, N., Spichkova, M. and Blech, J.

From Temporal Models to Property-based Testing.

DOI: 10.5220/0006340302410246

In Proceedings of the 12th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2017), pages 241-246

ISBN: 978-989-758-250-9

241

to make use of the advantages of FMs. To achieve

this goal, we suggest to translate the core time-based

constructs of an FM to the BeSpaceD extension of the

Scala programming language, speciﬁed in (Blech and

Schmidt, 2014). This allows us to have an executable

Scala code that corresponds to the formal model, as

well as to perform PBT of the models functionality.

To model temporal properties of the systems, in the

current work we focus on two formal languages, Tem-

poral logic of actions (TLA+) and FOCUS

. TLA+

combines temporal logic with a logic of actions, and

is used to describe behaviours of concurrent systems,

cf. (Lamport, 1994; Lamport, 1993). FOCUS

is a

formal language providing concise but easily under-

standable speciﬁcations that is focused on timing and

spatial aspects of the system behaviour (Spichkova

et al., 2014; Spichkova, 2007).

To implement the proposed ideas, we selected

Scala programming language, as on the PBT level

this allows us to apply an extension to ScalaCheck

library. Early ideas of this approach was presented

at Software Technologies: Applications and Founda-

tions Conference, cf. (Alzahrani et al., 2016). In this

paper we go further and discuss the developed fra-

mework and how it can be applies to TLA+ and FO-

CUS

. This approach is based on a completed Minor

Master Thesis of the ﬁrst author.

2 PROPOSED FRAMEWORK

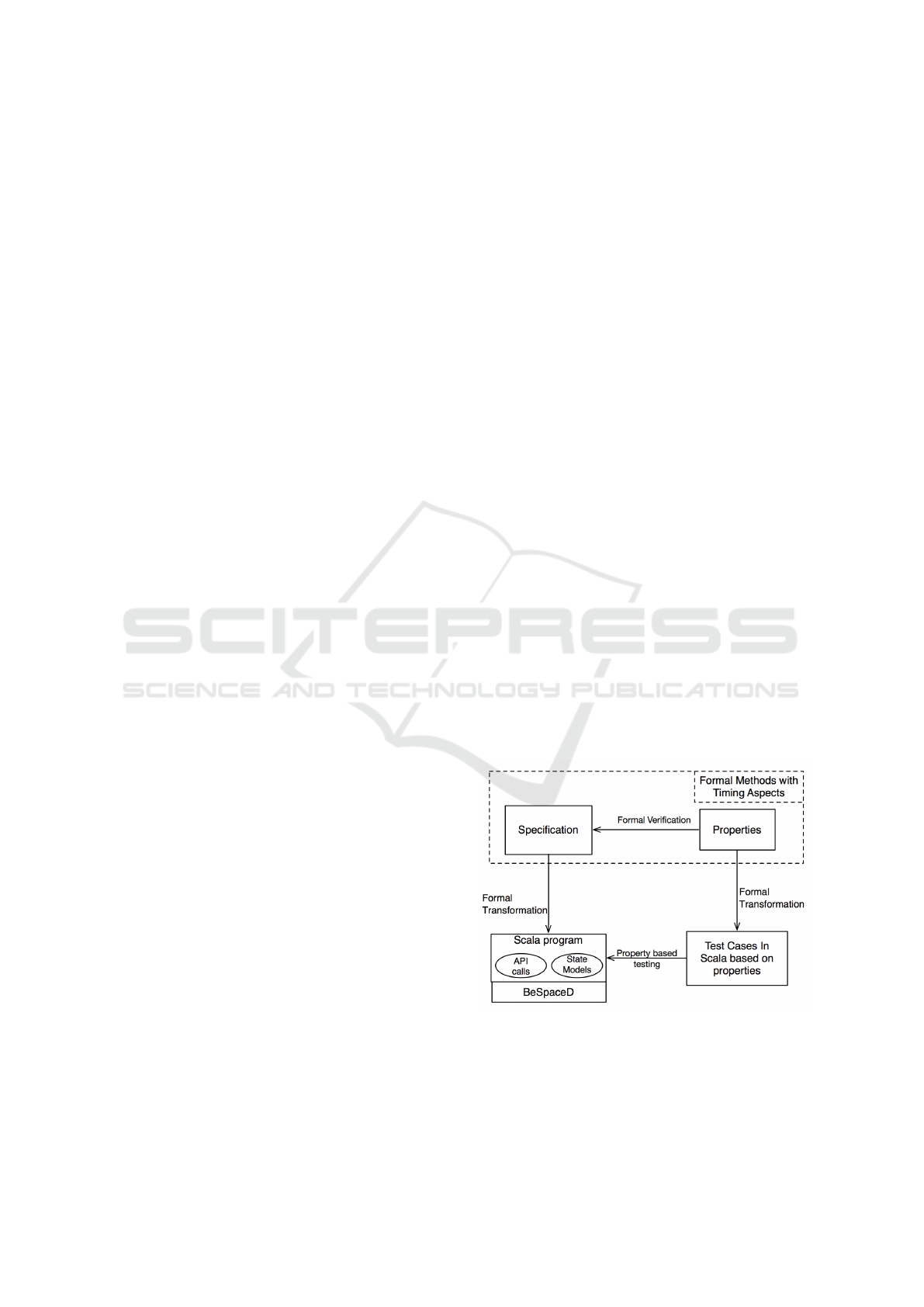
Figure 1 depicts the proposed framework that will al-

low for combining FMs with PBT. The general idea

is to start with specifying the system using human-

oriented modelling techniques based on FMs. After

the speciﬁcation phase, the software of the system

under test is designed according to the speciﬁcation.

The framework will then generate random test cases

to exercise and verify that the system runs according

to the speciﬁcation. If a test fails, it will be the judg-

ment of the engineer to decide whether the errors were

in the system software or in the speciﬁcation formu-

las for which the system was not correctly speciﬁed.

If the test passes without any errors, the system under

test meets the speciﬁcation.

The FM speciﬁcation gets translated to host pro-

gramming language (Scala in this case). These spe-

ciﬁcation gets formal veriﬁcation depending on the

ﬂavour of FM being used. For example, in case of

TLA+, the TLA+ model checker (TLC) is used to

check the speciﬁcation. On the other hand, in case of

FOCUS

, the theorem prover Isabelle/HOL via the

framework Focus on Isabelle is used to verify sys-

tems speciﬁcation, cf. (Nipkow et al., 2002) and (Spi-

chkova, 2007).

The workﬂow within the proposed framework in-

cludes the following steps:

• To create an (informal) requirements speciﬁcation

of the system;

• To transform the informal speciﬁcation to a for-

mal speciﬁcation (model) of the system, using

TLA+ or FOCUS

;

• To verify formal model, using TLA+ model chec-

ker or Isabelle/HOL theorem prover, respectively;

• To translate the formal model to Scala using the

provided translation schema;

• To add the speciﬁed in Scala model to the exten-

ded ScalaCheck library;

• To check the extended ScalaCheck library against

the behaviour generated by FM speciﬁcation.

In this section, we show the applicability of the

proposed framework to TLA+ and FOCUS

. The

goal is to demonstrate how the proposed framework

can be applied to many types of FMs with similar

syntax. Each subsection presents systematic informal

program transformation schemas. Using these sche-

mas makes transforming FM formulas to any hosting

language, Scala in this case, an easy mechanical task.

We start by analysing TLA+ syntax and semantics.

After that, we show the design and model the API

for the TLA+ ﬂavour. After that, we show the desig-

ned API and the testing it using small example (One

Bit Block). Similar process applied to FOCUS

, sho-

wing the analysis of FOCUS

syntax and semantics.

Restricting FOCUS

to it’s major parts that is related

to temporal properties.

Figure 1: Proposed Framework.

2.1 Application to TLA+

TLA provides a toolbox which includes an integra-

ted development environment (IDE) for the TLA+.

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

242

The IDE allows create and edit speciﬁcations, it also

shows parsing errors and can be used to turn TLA+

model checker. To decrease the cognitive load of the

developer and tester, it also includes an error trace

viewer and explorer: these components provide a

structured view of the states, illustrate how the sta-

tes/values are changed at each step, and allow to run

the TLA+ proof system.

A TLA formula such as Init ∧ [Next]v speciﬁes

the initial states and the allowed transitions of a sy-

stem. It allows for transitions that do not change the

value of v. This kind of transitions is called stuttering

transitions. Most TLA system speciﬁcations are of

the form Init ∧ [Next]

∧ L. The semantics of such

formulas are shown in Table 1. Table 2 shows logic

operators in TLA+ and their mappings in Scala, many

of the logical operators in Scala are provided by Be-

SpaceD.

Table 1: Semantics of TLA formula.

Init State formula describing the initial state(s)

Next Action formula formalizing the transition rela-

tion – usually a disjunction A1 ∨ .. ∨ An of pos-

sible actions (events) Ai

L Temporal formula asserting liveness conditions

Table 2: Operator mapping from TLA+ to Scala.

TLA+ Scala

/\ AND

\/ OR

⇒ IMPLIES

TRUE TRUE

FALSE FALSE

BOOLEAN Boolean

{

T RU E, FALSE

}

List(TRUE, FALSE)

≤ lessThanEq

≥ greaterThanEq

> greaterThan

< lessThan

 lessThanEqNot

≮ lessThanNot

 greaterThanEqNot

≯ greaterThanNot

∈ IN

x == e deﬁned(x, e)

x = e assign(x, e)

∀x ∈ S : p for {x ← S; if p} yield x

∃x ∈ S : p exists(x, S, p)

CHOOSE x ∈ S choose(x, List(S))

In TLA+, a representation of an abstraction of a sy-

stem is modelled using the standard model. The Stan-

dard Model states that an abstract system is described

as a collection of behaviours, each representing a pos-

sible execution of the system, where a behaviour is a

sequence of states and a state is an assignment of va-

lues to variables. In this model, an event (step) is the

transition from one state to the next in a behaviour.

For example, In one-bit clock, formulas are deﬁned

as follows:

VARIABLE b

Init == (b = 0) \/ (b = 1)

Next == \/ /\ b = 0

/\ b’ = 1

\/ /\ b = 1

/\ b’ = 0

These two TLA+ statements deﬁne Init and Next to

be two formulas. Therefore, referencing init or Next

is completely equivalent to typing ((b = 0) \/ (b = 1)).

The equality symbol = (typed ==) is read is deﬁned

to equal. To transform these formulas into a host pro-

gramming language, it is necessary to capture the es-

sential aspects of the formula to be transformed, i.e.,

to create a translation schema. Each transformation

step will consist of two elements: one to capture the

TLA+ formula and one to capture the corresponding

programming language function. The two schemata

together can then be used to do the transformation.

The TLA+ elements for the above formulas:

f1 == p \/ q

f2 == \/ /\ p

/\ q

\/ /\ q

/\ p

That is, f1 represent Init, f2 represent Next, p repre-

sent (b=0), q represent (b=1) respectively. According

to the translation schema, the translation of one bit

clock from TLA+ to Scala is as follows:

val b: TLAVariable = TLAVariable(IN(List(0, 1)))

val init: TLAInit = OR(defined(b,0), defined(b,1))

val next: TLANext = {

while(true) {

if defined(b, 0)

return assign(b, 1)

else

return assign(b, 0)

}

2.2 Application to FOCUS

The FOCUS

language was inspired by Focus, a fra-

mework for formal speciﬁcation and development of

interactive systems. In both languages, speciﬁcations

are based on the notion of streams, cf. (Broy and

Stølen, 2001). The syntax of FOCUS

is particularly

devoted to specify spatial (S) and timing (T) aspects in

a comprehensible fashion, which is the reason to ex-

tend the name of the language by ST: FOCUS

stream

is a mapping from natural numbers to lists of mes-

sages within the corresponding time intervals. Table

3 shows a partial mappings between FOCUS

basic

operators and their Scala representations.

From Temporal Models to Property-based Testing

243

Table 3: Operator mapping from FOCUS

to Scala.

FOCUS

Scala

/\ AND

\/ OR

→ IMPLIES

TRUE TRUE

FALSE FALSE

BOOLEAN Boolean

≤ lessThanEq

≥ greaterThanEq

> greaterThan

< lessThan

 lessThanEqNot

≮ lessThanNot

 greaterThanEqNot

≯ greaterThanNot

∈ IN

x == e deﬁned(x, e)

x = e assign(x, e)

∀x ∈ S : p for {x ← S; if p} yield x

∃x ∈ S : p exists(x, S, p)

hi List()

, . . . , a

i a

to a

Figure 2: FOCUS

Speciﬁcation of Steam Boiler Controller

(Spichkova, 2016).

The FOCUS

speciﬁcation layout is based on

human factor analysis within formal methods (Spi-

chkova, 2012; Spichkova, 2013). Figure 2 provides an

example on how a FOCUS

speciﬁcation looks like.

The in and out sections of FOCUS

speciﬁcations

are used to specify input and output streams of the

corresponding types. local and init sections include

local variables and initial values, respectively. FO-

CUS

requires using assumption-guarantee templa-

tes, to avoid the omission of unnecessary assumptions

about the system‘s environment. The keyword asm

lists the assumption that the speciﬁed component ex-

pect from its environment, e.g., the assumption ts(s)

would mean that the input stream s should contain ex-

actly one message per time interval. The component

behaviour that should be guaranteed in the case all

assumptions are fulﬁlled, is then described in the spe-

ciﬁcation section gar.

3 DISCUSSION AND

EVALUATION

Let us use the steam soiler (Broy and Stølen, 2001)

example to discuss the applicability of the develo-

ped framework. We selected this example as it (1)

is simple-enough to introduce it shortly, (2) is well-

known example for analysing FMs, (3) includes most

of the functionalities of the proposed framework.

For this example, we start by given the TLA+ and

FOCUS

speciﬁcation which gets translated to Scala

programming language before feeding the translated

speciﬁcation to the proposed framework. The trans-

lation correctness is veriﬁed manually by checking

the behaviour that is generated by the tools develo-

ped and used to generate systems behaviours with the

behaviour generated by the actual TLA model chec-

ker (TLC). We follow the informal deﬁnition of the

example provided in (Spichkova, 2016): The steam

boiler has a water tank, which contains a number of

gallons of water, and a pump, which adds 10 gallons

of water per time unit to its water tank, if the pump

is on. At most 10 gallons of water are consumed per

time unit by the steam production, if the pump is off.

The steam boiler has a sensor that measures the water

level. Initially, the water level is 500 gallons, and the

pump is off. In each time interval the system outputs

it current water level in gallons and this level should

always be between 200 and 800 gallons.

The system consists of three logical components:

SteamBoiler, Converter, and Controller. The speciﬁ-

cation Controller as shown in Figure 2 describes the

controller component of the system. The controller

role is to switch the steam boiler pump on and off. In

addition, it knows the current state of the pump. The

behaviour of this component is asynchronous to keep

the number of control signals as small as possible.

Figure 3 shows TLA+ speciﬁcation of the Steam

Boiler controller. Unlike FOCUS

, TLA+ is weakly

typed. Therefore, it uses a convention to indicated

types of variables using TypeOK keyword as shown

in the speciﬁcation.

To check the framework, we provided two imple-

mentation for the steam boiler system, correct (wrt.

the given FOCUS

and TLA+ speciﬁcation) and in-

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

244

Figure 3: TLA+ speciﬁcation of the Steam Boiler controller.

correct one (having mistakes wrt. the given speciﬁ-

cation). For instance, in the case when the system

is speciﬁed to have its current water level be bet-

ween 200 and 800 gallons, the wrong implementa-

tion does not satisfy this property and instead have

the the current level below 200 and above 800. The

wrong example also include the failure of the pump

to turn on or off. Table 4 shows number of invoca-

tions for every API call in each test run. Both trans-

lated TLA+ and FOCUS

speciﬁcations have similar

numbers since the schematic translation from TLA+

and FOCUS

to Scala is similar in both cases. The

extended ScalaCheck implementation that we develo-

ped does not shrink the test case to generate minimal

failing test cases (which would make the code easier

to debug). The future work will include the shrinking

behaviour that is inspired by QuickCheck library.

Table 5 contrast the performance of permutations

and PBT test runs between the schematic translation

of TLA+ and FOCUS

. There are no observable dif-

ferences between the performance of TLA+ and FO-

CUS

in almost all of the phases of the workﬂow.

This is expected since both TLA+ and FOCUS

has

similar syntax and the translation is similar in most

cases. For the same reason, there is no considerable

difference between lines of code after translation from

TLA+ to Scala which was 70 lines of code and the

translation from FOCUS

to Scala was 75 lines. All

tests were carried out on two machines:

Intel Core i5 2.6 GHz, RAM 8 GB

Intel Core-i7 360QM 2.0 GHz, RAM 4GB

To evaluate the performance of the scripts using to

support the framework, we used a number of further

Table 4: Number of API Invocations in test cases.

API Code TLA+ FOCUS

startSystem() 1 1

endSystem() 1 1

pumpDidOpen() 27 27

openPump() 11 11

pumpDidClose() 17 17

closePump() 47 47

waterLevelDidChange(amount: Int) 21 21

checkWaterLevel() 20 20

controlSignalDidChange(val: Int) 26 26

Table 5: Translated TLA+ and FOCUS

statistics (time in

seconds).

TLA+ FOCUS

API permutations 10-11 10-11

Behaviour Generating 7-8 7-8

Single Test run 0.5 0.5

Total Test run time 100 test cases 23-25 23-25

problems commonly used in the TLA+ community:

• One Bit Clock simply alternates between 0 and 1.

Such a clock is used to control any modern com-

puter. Its times being displayed as the voltage on

a wire. Therefore, there are only two states; the 0

state and the 1 state.

• The DieHard problem from the movieDie Hard 3,

the heroes had to solve the problem of obtaining

exactly 4 gallons of water using a 5 gallon jug, a

3 gallon jug, and a water faucet.

• Euclid‘s algorithm for computing the greatest

common divisor of two positive integers.

• Therac-25, a radiation therapy machine used in

curing cancer, led to deaths and serious injuries

of patients which received thousand times the nor-

mal dose of radiation (Miller, 1987; Leveson and

Turner, 1993). The causes of these accidents were

software failures as well as problems with the sy-

stem interface. The machine included VT-100

terminal which controlled the PDP-11 computer,

where the sequence of user actions leading to the

accidents was as follows: user selects 25 MeV

photon mode, enters cursor up, select 25 MeV

Electron mode, previous commands have to take

place in eight seconds.

Table 6 shows the statistics on the applied behaviour

generator. Diameter column is the number of states in

the longest path of the graph in which no state appears

twice. States Found column is the total number of

states it examined in the ﬁrst step of the algorithm or

as successor states in the second step. Distinct States

column is the number of states that form the set of

nodes of the graph. For instance, in case of One Bit

Clock, model checker found two distinct states.

From Temporal Models to Property-based Testing

245

Table 6: Behaviour Generator Statistics.

Example Diameter State Found Distinct States

DieHard 9 97 16

One Bit Clock 1 4 2

Euclid Algorithm 3 22 8

Therac25 9 97 16

4 CONCLUSION

We have presented our framework for application of

the property-based testing (PBT) concepts on top of

temporal formal models. This allows us to have an

executable Scala code that corresponds to the for-

mal model, as well as to perform PBT of the mo-

dels functionality. The framework is aiming on re-

duction of the impedance mismatch between formal

methods and practitioners through the combining of

formal methods with property-based testing. We in-

troduced the core ideas on how the framework can be

applied to particular formal languages, such as TLA+

and Focus

REFERENCES

Alzahrani, N., Spichkova, M., and Blech, J. O. (2016).

Spatio-Temporal Models for Formal Analysis and

Property-Based Testing, pages 196–206. Springer.

Blech, J. O. and Schmidt, H. (2014). BeSpaceD: Towards

a tool framework and methodology for the speciﬁca-

tion and veriﬁcation of spatial behavior of distributed

software component systems. CoRR.

Bowen, J. P. and Hinchey, M. G. (1995). Seven more myths

of formal methods. IEEE software, 12(4):34.

Broy, M. and Stølen, K. (2001). Speciﬁcation and Develop-

ment of Interactive Systems: Focus on Streams, Inter-

faces, and Reﬁnement. Springer.

Claessen, K. and Hughes, J. (2011). QuickCheck: A lig-

htweight tool for random testing of haskell programs.

SIGPLAN Not., 46(4):53–64.

Gerdes, A., Hughes, J., Smallbone, N., and Wang, M.

(2015). Linking unit tests and properties. In SIGPLAN

Workshop, pages 19–26. ACM.

Hinchey, M. G. (2003). Confessions of a formal methodist.

In Safety Critical Systems and Software, pages 17–20.

ACS.

Hughes, J. (2010). Software testing with quickcheck. In

Central European Functional Programming School,

pages 183–223. Springer.

uhnel, C. and Spichkova, M. (2007). Fault-tolerant com-

munication for distributed embedded systems. In Soft-

ware Engineering of Fault Tolerance Systems, vo-

lume 19, page 175. World Scientiﬁc Publishing.

Lamport, L. (1993). Hybrid systems in TLA+. In Gros-

sman, R. L., Nerode, A., Ravn, A. P., and Rischel, H.,

editors, Hybrid Systems, number 736 in LNCS, pages

77–102. Springer.

Lamport, L. (1994). The temporal logic of actions.

16(3):872–923.

Leveson, N. G. and Turner, C. S. (1993). An investigation

of the therac-25 accidents. Computer, 26(7):18–41.

Miller, E. (1987). The Therac-25 Experience. In Conf. State

Radiation Control Program Directors.

Newcombe, C., Rath, T., Zhang, F., Munteanu, B., Brooker,

M., and Deardeuff, M. (2015). How Amazon Web

Services Uses Formal Methods. CACM, 58(4):66–73.

Nipkow, T., Paulson, L. C., and Wenzel, M. (2002). Isa-

belle/HOL: a proof assistant for higher-order logic,

volume 2283. Springer Science & Business Media.

Spichkova, M. (2007). Speciﬁcation and seamless veriﬁca-

tion of embedded real-time systems: FOCUS on Isa-

belle. PhD thesis, Technical University Munich.

Spichkova, M. (2012). Human Factors of Formal Methods.

In IADIS Interfaces and Human Computer Interaction

2012.

Spichkova, M. (2013). Design of formal languages and in-

terfaces: “Formal” does not mean “unreadable”. IGI

Global.

Spichkova, M. (2016). Spatio-temporal features of

Focus

. CoRR.

Spichkova, M., Blech, J. O., Herrmann, P., and Schmidt,

H. W. (2014). Modeling Spatial Aspects of Safety-

Critical Systems with Focus

. In MoDeVVa, pages

49–58.

Spichkova, M., Liu, H., Laali, M., and Schmidt, H. W.

(2015). Human factors in software reliability engi-

neering. Workshop on Applications of Human Error

Research to Improve Software Engineering.

Yu, Y., Manolios, P., and Lamport, L. (1999). Model

checking tla+ speciﬁcations. In Correct Hardware

Design and Veriﬁcation Methods, pages 54–66. Sprin-

ger.

Zamansky, A., Rodriguez-Navas, G., Adams, M., and Spi-

chkova, M. (2016). Formal methods in collaborative

projects. In 11th International Conference on Evalu-

ation of Novel Approaches to Software Engineering.

IEEE.

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

246