Assured Reinforcement Learning for Safety-critical Applications
George Mason
1
, Radu Calinescu
1
, Daniel Kudenko
1
and Alec Banks
2
1
Department of Computer Science, University of York, Deramore Lane, York, U.K.
2
Defence Science and Technology Laboratory, Salisbury, U.K.
1 RESEARCH PROBLEM
Reinforcement learning (RL) is a branch of machine
learning used to solve sequential decision making
problems. This is achieved by using an autonomous
agent to explore an initially unknown problem envi-
ronment in order to learn a set of actions (known as an
optimal policy) to perform in the environment’s states
that will return the maximum possible expected re-
ward from the system (Wiering and Otterlo, 2012).
Despite RL having successes in areas such as
robotics (Kober et al., 2013) and gaming (Szita, 2012)
it has had little appeal in the domain of safety-critical
applications. This is because RL has no inherent guar-
antees that a learned solution will satisfy safety, legal
or regulatory requirements. This limitation has pre-
vented RL from being adopted in areas such as health-
care, business or legal systems, where behaviours by
the agent can be dangerous to itself, other systems or
humans. Furthermore, the agent may learn a set of
behaviours that are unpredictable or unfamiliar to hu-
man operators, therefore making the system difficult
to trust even if its operation may ultimately prove cor-
rect.
In recent years there has been growing interest in
this limitation with research emerging with the aim
to resolving it (Garc
´
ıa and Fern
´
andez, 2015). How-
ever, current approaches are still largely theoretical,
suffer from scalability issues, have difficulty in ex-
pressing non-trivial safety properties, or are unable to
offer firm guarantees that their RL solutions will sat-
isfy specific requirements.
The root of the problem lies in how objectives are
expressed in RL. Objectives are specified through a
reward function that returns a numerical “reward” to
the RL learning agent according to how beneficial an
action it performs in a system state is to achieving its
objectives. Those actions that will cause the agent
to complete an objective will yield rewards that are
greater than those actions that do not. The problem
with this mechanism is that it can be infeasible to
express complex requirements using rewards alone.
Furthermore, it can necessitate introducing more de-
tails into the underlying RL environment, which will
exacerbate the state-space explosion problem that af-
fects RL (Garc
´
ıa and Fern
´
andez, 2015) and therefore
will significantly reduce the rate of learning. When
objectives conflict with each other, there is the ad-
ditional issue of how to assign a reward function to
simultaneously reward the agent and punish it. The
nature of RL is to maximize a reward (or minimize a
cost), so traditional RL is inherently unable to find a
solution that lies in the middle of these two extremes.
A further problem of this learning approach is that
since the agent is motivated solely through accumu-
lating as much reward as possible it can learn a solu-
tion that, despite being optimal with respect to max-
imizing reward acquisition, may not follow conven-
tional human behaviours. Unfamiliar, “quirky” be-
haviours by the system further reduce its appeal in
scenarios where it is crucial that the system can be
trusted (Lange et al., 2012).
This project aims to address the problem of how
to develop assurances that an RL system will a) find a
solution that can guarantee to satisfy a wide range of
safety requirements, and b) learn solutions that can be
trusted to conform to conventional behaviours of the
domain where the system is deployed.
2 OUTLINE OF OBJECTIVES
Research towards safe RL faces two common prob-
lems. First, complex safety properties are often diffi-
cult to express using a reward function. Second, that
RL solutions have firm guarantees to satisfy specific
safety requirements, as opposed to a solution that is
“generally safer” than the one learned by traditional
RL.
The overarching aim of our project is to address
these limitations by developing a generic approach for
assured reinforcement learning (ARL) that achieves
two key objectives:
1. ARL should support the specification and reali-
sation of a broad range of complex requirements
(including constraints and optimisation objectives
Mason, G., Calinescu, R., Kudenko, D. and Banks, A.
Assured Reinforcement Learning for Safety-critical Applications.
In Doctoral Consortium (DCAART 2017), pages 9-16
9

(1) provide
High-level problem
model (abstract Markov
decision process)
(2) drive
Quantitative
verification
Selected safe abstract
policy (abstract MDP
policy)
(3) generates
(4) informs
(5) select
Reinforcement
learning
(6) constrains
Safe reinforcement
learning policy
(7) produces
Stage 1: Abstract policy generation
Stage 2: Safe reinforcement learning
AI engineer,
domain expert
Pareto front of safe
abstract policies
Constraints & optimisation
objectives (safety, cost,
reliability, rewards, etc.)
(8) updates
Figure 1: The envisaged approach for assured reinforcement learning.
for the RL solution) without impacting the size of
the underlying model.
2. ARL solutions should be guaranteed to sat-
isfy requirements within pre-specified probability
boundaries and execution costs.
The envisaged two-stage operation of our ARL
approach is depicted in Figure 1. In Stage 1, termed
abstract policy generation, we propose the use of an
abstract Markov decision process (AMDP) (Marthi,
2007; Li et al., 2006; Sutton et al., 1999) to model a
high-level representation of the RL problem. Also,
a set of safety constraints and optimisation objec-
tives are specified using probabilistic computation
tree logic (PCTL) (Hansson and Jonsson, 1994), an
expressive temporal logic that allows complex prop-
erties of Markov decision processes to be formu-
lated as concise formulae. Devising the AMDP and
the PCTL-encoded constraints and optimisation crite-
ria for the RL problem requires both domain knowl-
edge and AI expertise. Accordingly, teams compris-
ing both an AI engineer and a domain expert pro-
vide (1) these inputs for the first ARL stage. The
problem AMDP and constraints/optimisation criteria
are then used to drive (2) the search for safe AMDP
policies using quantitative verification (QV), a vari-
ant of model checking for the analysis and verifica-
tion of stochastic models (Kwiatkowska et al., 2007).
By exploring different areas of the AMDP parameter
spaces, QV generates (3) a set of abstract policies for
the AMDP, with the policies that are verified as satis-
fying all the constraints organised into a Pareto front.
This Pareto front captures the safe abstract policies
that are Pareto optimal with respect to the optimisa-
tion criteria, and can therefore be used to inform (4)
the users’ selection (5) of a suitable safe abstract pol-
icy.
In Stage 2 of ARL, termed safe reinforcement
learning, the selected safe abstract policy is translated
into a set of safety rules that constrains (6) the RL
agent’s exploration to low-level states and actions that
map to the high-level states and actions of the AMDP
known to be safe. As a result, the RL agent produces
(7) a safe reinforcement learning policy, i.e. an RL
policy that when followed will have equal safety lev-
els to those verified for the abstract policy, thus meet-
ing the safety requirements.
The two-stage ARL approach described above
makes two important assumptions: i) the AMDP
model will contain all necessary information for ab-
stract safe policies to fully apply to the low-level RL
model, and ii) this information will accurately reflect
the RL model. Should one or both of these assump-
tions not be satisfied, e.g. because the initial knowl-
edge is incomplete or the parameters of the system
change during runtime, then an abstract policy may
not necessarily provide the levels of safety that it was
verified to give. This necessitates a means of be-
ing able to detect inaccuracies in the AMDP model
and to then find an alternate safe abstract policy for
it. We therefore intend to extend the basic ARL
approach to incorporate knowledge revision of the
AMDP (Efthymiadis and Kudenko, 2015; Calinescu
et al., 2011), with the RL agent identifying discrepan-
cies between the safe abstract policy and the explored
environment and updating (8) the AMDP accordingly.
DCAART 2017 - Doctoral Consortium on Agents and Artificial Intelligence
10

3 STATE OF THE ART
Research into safe RL is scant but has had growing in-
terest in recent years. Existing approaches generally
fall in to one of two categories (Garc
´
ıa and Fern
´
andez,
2015). The first looks into modifying how the accu-
mulation of rewards is optimised. The second focuses
on adjusting the strategies employed by the agent to
explore the environment.
3.1 Preliminaries
RL uses a Markov decision process (MDP) as its un-
deryling framework. Formally an MDP is a tuple
(S, A, T, R), where: S is a finite set of states; A is a
finite set of actions; T : S×A×S → [0, 1] is a state
transition function such that for any s, s
0
∈ S and any
action a ∈ A that is allowed in state s, T (s, a, s
0
) gives
the probability of transitioning to state s
0
when per-
forming action a in state s; and R : S×A×S → R is
a reward function such that R(s, a, s
0
) = r is the re-
ward received by the agent when action a performed
in state s leads to state s
0
(Wiering and Otterlo, 2012).
Supplemental to this definition are policies, de-
noted π. A policy is a mapping of states to actions
such that for each state s ∈ S there is a corresponding
action a ∈ A. The notion of solving an MDP is to find
a policy that when followed will return the maximum
possible expected reward from the MDP environment,
such a policy is optimal and is denoted π
∗
. MDPs can
be solved using dynamic or linear programming, how-
ever, when the transition and/or reward functions are
initially unknown RL is used.
RL uses an autonomous agent to explore the MDP
environment to learn about its dynamics and where-
abouts of rewards contained within it. This explo-
ration is initially through the arbitrary selections of
actions in states and over time the agent encounters
rewards in the environment. Knowledge of these re-
wards is retained in the form of Q-values, a state-
action pair Q(s, a) that specifies the utility of perform-
ing action a in state s. In subsequent learning episodes
the agent can then reuse this information by selecting
the action in a state which has the highest utility value.
These Q-values are updated each time the agent revis-
its the state according to an update function such as Q-
learning (Watkins and Dayan, 1992). Given sufficient
learning episodes the agent will converge to accurate
(i.e. unchanging) utility values, when this eventuality
is reached the agent has learned an optimal solution.
3.2 Optimisation Strategies
An intuitive approach for safe RL is to give a negati-
ve reward (i.e. a cost) to the agent if it performs ac-
tions which lead to the agent entering states which
are denoted as unsafe. However, this simplistic ap-
proach suffers from several limitations. Firstly, it re-
quires knowing a priori exactly which states of the RL
environment are unsafe which may not be possible.
Secondly, assigning a cost of suitable magnitude is
not always obvious and requires trial and error to de-
termine, especially if safety objectives conflicts with
mission objectives. Finally, often it can be difficult
to define complex safety requirements in the reward
function and may necessitate significantly expanding
the state space of the model to accommodate the prop-
erties.
Therefore, instead of focussing on how to define
rewards for unsafe behaviours, various approaches
have been proposed that consider the criterion for how
the accumulation of rewards is optimised.
Ultimately we desire the agent to accumulate as
much reward as possible for achieving mission objec-
tives, but if the agent’s behaviour means it enter states
where it cannot achieve the objectives then it will not
acquire these rewards. Even though on average the
learned solution may receive the highest reward pos-
sible from the system, the variance of this reward in-
dicates how risky the solution is. I.e., if the agent
regularly receives a low reward for not achieving all
mission objectives then the solution is not one that
is particularly reliable. Therefore, redefining how the
agent optimises its reward accumulation is one avenue
of safe RL approaches.
One method is to optimise a policy so that no ac-
tions are irreversible, i.e. no actions can be done
which the agent cannot recover from and are thus safe.
Such an example is (Moldovan and Abbeel, 2012)
where a set of ergodic policies are identified and the
agent optimises over them. Whilst this approach guar-
antees that a solution will never lead to the agent be-
ing unsafe, the solution is often excessively far from
being optimal. Despite the fact that significant re-
wards could be gained at very low risk, since the risk
is not zero the rewards are not considered.
The worst-case criterion (Heger, 1994) optimises
a solution so that the worst possible outcome when
following it offers the maximum reward from the sys-
tem relative to all other possible solutions’ worst pos-
sible outcomes. This approach ensures that a solu-
tion will guarantee a minimum level of return will al-
ways be achieved, however, solutions typically yield
significantly lower returns than an optimal solution
would. Even though the probability of a worst-case
scenario occurring may be very low, this optimisa-
tion approach will disregard potentially large future
rewards.
Assured Reinforcement Learning for Safety-critical Applications
11

A similar approach is the risk-sensitive criterion
(Mihatsch and Neuneier, 2002) which uses a param-
eter to specify what amount of variability of return
is permissible. This parameter can be tuned so that
a solution is optimised to avoid variability or seek it.
Through this approach a solution can be found that
satisfies the level of risk that the user is comfortable
with. However, as with the worst-case criterion, low
variability can be produce solutions that are far from
optimal.
3.3 Exploration Strategies
An alternative to modifying how the agent’s solutions
are optimised is to modify how the agent actually ex-
plores the environment. Traditionally, an RL agent
starts with no knowledge of the environment and must
initially explore it randomly. This can lead to the
agent finding solutions which traverse unsafe states.
To ameliorate this problem, the exploration strategy
of the agent can be influenced so that it has some
knowledge of which states to transition to and which
to avoid.
The Lyapunov design (Perkins and Barto, 2003)
uses control Lyapunov functions to measure the dis-
tance from a safe system state to a failure (unsafe)
state. By constricting the set of actions to only ones
that cause the system to descend on a control Lya-
punov function, i.e. towards a stable equilibrium, safe
RL can achieved. However, finding appropriate Lya-
punov functions is often a difficult task and are be-
spoke for every problem scenario.
The Policy Improvement through Safe Rein-
forcement Learning (PI-SRL) algorithm (Garc
´
ıa and
Fern
´
andez, 2012) is a two-stage process where the
first stage has a predefined safe baseline policy that
is assumed to be suboptimal and the second stage is
to learn. The approach differs from policy iteration
as it uses two new components, a risk function to de-
termine the risk of a particular state and a baseline
behaviour which can be used when in states of risk.
However, in areas where there is no area of risk and
only a discrete change from safe to unsafe states the
algorithm can still result in failure.
Another approach is to use a series of demonstra-
tions to aid the agent discover an initial solution (Ar-
gall et al., 2009) for the problem. This initial so-
lution provides a basis for the agent so that it need
not explore unnecessary or unsafe states. The so-
lution derived from demonstrations will typically be
sub-optimal so the agent uses it only as guidance and
optimises it using traditional RL techniques. This
approach is limited, though, by the fact that it is
not always feasible to provide a safe demonstration
for every possible scenario. In such an eventuality
the agent must rely on conventional exploration tech-
niques, falling back to the problem of the agent un-
knowingly exploring dangerous states.
4 METHODOLOGY
To achieve our project objectives we have decom-
posed the research work into the following tasks.
1. Review existing literature on safe RL to learn the
current state of research and the limitations of ex-
isting approaches. Specifically, we aimed to iden-
tify limitations of existing RL solutions in order
to determine the trajectory of our research.
2. Form a theoretical method as a potential solution
for the identified limitations.
3. Implement the theoretical method as an actual ap-
plication. This can be done in an interleaving
fashion with task 2.
4. Evaluate the method using at least two qualita-
tively different case studies taken from bench-
mark RL experiments and real-world applications.
Evaluation will focus on how well safety levels
have been assured using our method compared to
traditional RL.
5. Extend the approach to accommodate incorrect
knowledge contained in the initial high-level
problem model. Information that is different in
the RL model can be relayed back to the high-
level model and an updated solution is generated.
6. Further evaluate the full framework for scalability
and generality by expanding existing case studies
and develop new ones.
To implement the RL experiments we will be
using the York Reinforcement Learning Library
(YORLL)
1
, which supports a wide range of environ-
ments and learning algorithms. To perform QV we
will use the PRISM model checker (Kwiatkowska
et al., 2011), which supports the verification of
reward-extended PCTL properties for MDPs. QV and
PRISM have been successfully used to analyse simi-
lar models of systems ranging from cloud infrastruc-
ture (Calinescu et al., 2012) and service-based sys-
tems (Calinescu et al., 2013) to unmanned vehicles
(Gerasimou et al., 2014), and thus we expect them to
also work well for ARL.
The evaluation of our ARL approach will focus
on how closely the learned RL policy adheres to the
1
YORLL is programmed in Java and is developed by
the University of York. It is free to download from
http://www.cs.york.ac.uk/rl/software.php
DCAART 2017 - Doctoral Consortium on Agents and Artificial Intelligence
12

safety requirements, relative to a control experiment
using traditional RL. Validating the policies can be
done empirically by running the learned safe RL pol-
icy and comparing the outcome to the safety levels
of the selected high-level policy. Given the stochas-
tic nature typical of RL experiments it is necessary to
run the safe RL policy numerous times to obtain an
average result (Arcuri and Briand, 2011).
5 EXPECTED OUTCOME
The expected outcome of our project is a general
framework to provide an assured RL solution that will
satisfy a broad range of safety requirements. Our
novel approach will mitigate the existing limitation
in safe RL research that safety cannot be guaranteed
to fulfil specific safety requirements. By using QV to
provably verify the properties of solution constraints
our assured RL framework will guarantee to satisfy
safety requirements.
We intend that the framework can be used across
multiple domains and will support large-scale scenar-
ios. The framework will require a set of requirements
expressed using PCTL as well as a high-level model
of the problem scenario. The end result will be a set
of rules specifying which actions the agent should, or
should not, perform in specific states of the RL model.
The outcome being that the RL agent will learn a so-
lution such that it will behave in a way that is guar-
anteed not to violate safety requirements whilst also
being optimal subject to the contraints.
Our framework will contribute to the ongoing re-
search into safe RL. Specifically, our approach will al-
leviate the recurring limitation that safety assurances
can not be guaranteed, or when guarantees are given
they are at an undesirably large detriment to optimal-
ity of the solution.
6 STAGE OF THE RESEARCH
So far, steps (1)–(7) of the approach shown in Figure 1
have been developed and evaluated. Preliminary work
on these steps is summarised in (Mason et al., 2016),
and the formalisation of this part of the approach and
experimental results of its evaluation are presented in
(Mason et al., 2017). Our current work is towards de-
veloping the knowledge-revision algorithm for updat-
ing the AMDP as discussed in Section 2 and shown
by step (8) from Figure 1.
6.1 Completed Work
For our high-level model we use an AMDP, which is
an abstract version of the low-level RL MDP. AMDPs
differ to conventional MDPs by being significantly
smaller in terms of their state space and action set
(Marthi, 2007). To achieve this, superfluous states of
the MDP are ignored and similar states conflated, only
those states with significant features, such as those
containing rewards, are retained (Li et al., 2006). The
low-level action set can be abstracted so that instead
of requiring a series of individual actions to enter the
next state of interest, high-level options are used in-
stead (Sutton et al., 1999). These options replace the
actions with single transitions between states. The
end AMDP has several orders of magnitude fewer
states than the RL MDP, and can be formally analysed
using QV. This allows the rapid verification of can-
didate high-level policies against the PCTL-encoded
problem requirements.
An algorithm has been developed to automate the
process of generating and verifying abstract policies
and assembling a Pareto-front of those policies that
were verified as being safe; this algorithm is presented
in (Mason et al., 2017). To generate candidate ab-
stract policies, the algorithm can utilize a range of
search techniques, including hill climbing, genetic al-
gorithms, e.g. (Gerasimou et al., 2015), or a simple
random search. As different search techniques can
perform better than others for certain types of prob-
lem scenarios, experiments are planned to identify
suitable techniques for different classes of RL prob-
lems (e.g., planning and navigation).
We have evaluated the method in two qualitatively
different case studies. The first case study is based on
the benchmark RL flag-collection experiment (Dear-
den et al., 1998) which we have extended by intro-
ducing the risk of the agent being captured. Details
of this case study are given below. The second case
study is based on an assisted living system for demen-
tia patients (Boger et al., 2006). In this experiment an
autonomous agent must give voice prompts to a de-
mentia sufferer to instruct them on what task to do
next when undertaking the activity of washing their
hands. The system learns what style of voice prompt
is most appealing to the patient, considering the vol-
ume of the prompt, the gender of the voice and the
explicitness of the instructions. This system must not
overload the patient with prompts as this can become
stressful for them; conversely the agent must mini-
mize the necessity of summoning a carer to intervene
should the patient not progress effectively.
The environment for the guarded flag-collection
case study is shown in Figure 2; the objective in this
benchmark RL experiment is to learn a route through
Assured Reinforcement Learning for Safety-critical Applications
13

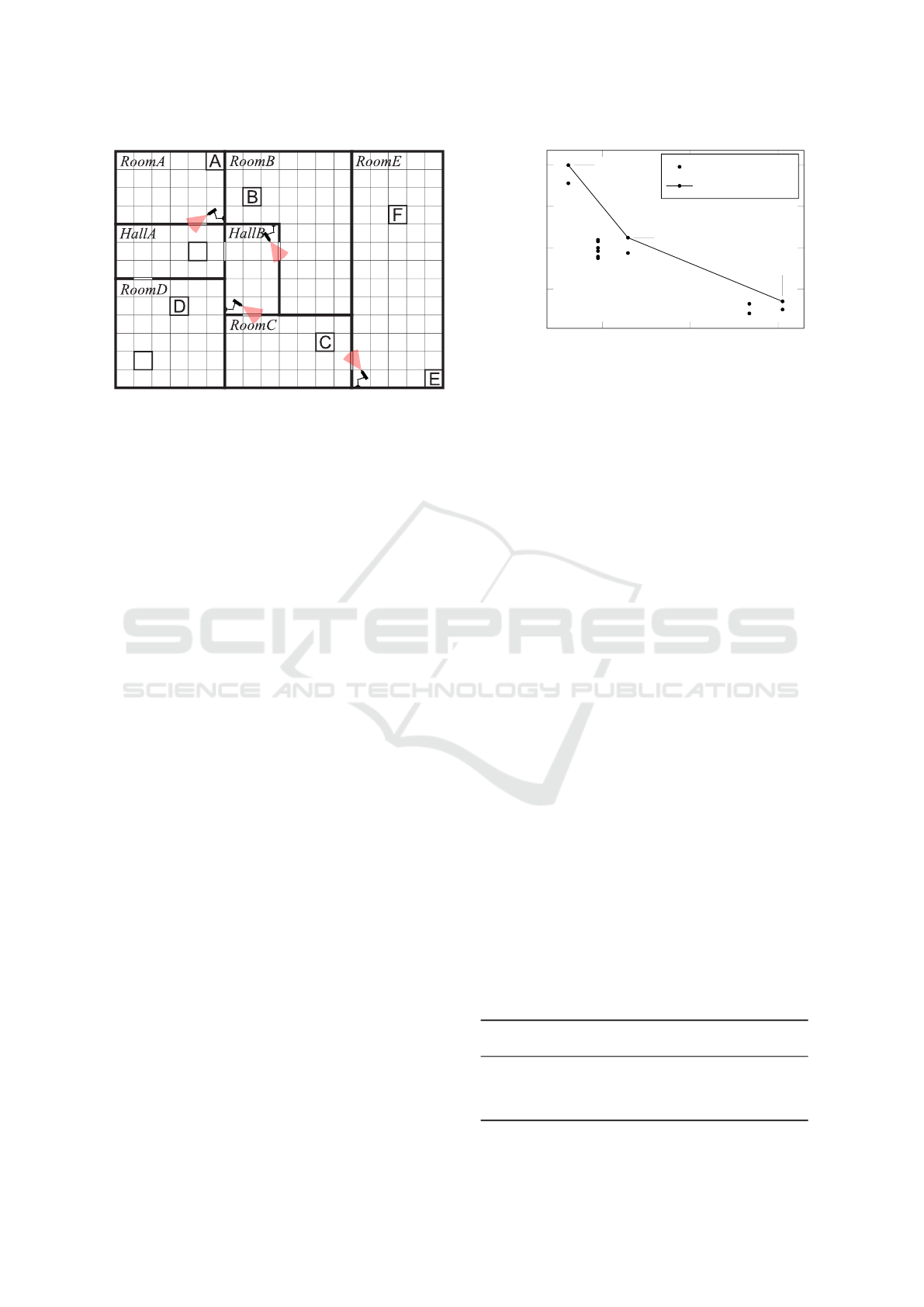
Start
Goal
Figure 2: The layout of the guarded flag collection environ-
ment. The areas of risk are illustrated by security cameras
which with a certain probability can detect the agent as it
traverses the doorways.
the environment to collect the flags A-F. In our case
study we have augmented the environment with secu-
rity cameras which can detect the agent as it passes
through certain doorways. Detection of the agent re-
sults in its capture and the experiment ending in fail-
ure, regardless of any flags already collected.
Each of the cameras has a different probability of
detecting the agent. Therefore, along with the origi-
nal optimisation objective to maximize the number of
flags collected we also have the conflicting safety ob-
jective of minimizing the probability that the agent is
captured. For our case study we specify the following
constraints:
C
1
The agent should reach the ‘goal’ area with pro-
bability at least 0.75.
C
2
The agent should cumulate more than two flags
before it reaches the ‘goal’ area.
Furthermore, we aim to maximise:
O
1
The probability that the agent reaches the ‘goal’.
O
2
The number of collected flags.
After constructing an AMDP for the problem we
used QV to identify a set of abstract policies that sat-
isfy the constraints C
1
and C
2
. From these safe poli-
cies we identified a Pareto front, i.e. a “front” of poli-
cies whose expected reward and probability of reach-
ing ‘goal’ cannot be both bettered by any other safe
policy. These safe policies and their associated Pareto
front are shown in Figure 3.
From this Pareto front three policies were selected
to be used for safe ARL; these are labelled A, B and
C on the Pareto front. These safe policies were trans-
lated into safe RL rules for ARL. The results of the
evaluation of the learned ARL policies are presented
in Table 1 alongside a baseline experiment using tra-
ditional RL, which we carried out in order to establish
0.8
0.85
0.9
3
3.5
4
4.5
A
B
C
Probability of reaching ‘goal’
Expected reward
Abstract policy
Pareto-front
Figure 3: Plot of abstract policies that satisfy the safety con-
straints C
1
and C
2
, and the Pareto front of safe policies A,
B and C.
the effects of ARL.
In both case studies our approach was successful
at satisfying the safety requirements (Mason et al.,
2017). Furthermore, the learned policy matched the
specific safety results that were verified for the high-
level safe policy. From these results we show that our
approach can achieve the levels of safety that were
required.
6.2 Ongoing Work
Currently, research is progressing with development
on a knowledge-revision algorithm as discussed in
Section 2. An algorithm is being formulated where an
RL agent first attempts ARL using what is presumed
to be a suitable abstract policy. Should the agent dis-
cover that the policy is not viable (e.g. the abstract
policy dictates the RL agent should perform an ac-
tion in a state where the action is not available), then
knowledge of the error is fed back to the AMDP and
a revised model is constructed.
Work is currently focussing on a means of recy-
cling redundant abstract policies where possible, thus
significantly reducing the verification effort required
to update the Pareto front of safe abstract policies.
Since it is often the case that there are only minor dif-
ferences between the initial, incorrect AMDP model
Table 1: The results for safe abstract policies A, B and C
when used for ARL along with a baseline, traditional RL
experiment for the guarded flag-collection (results averaged
over 5 independent experiments).
Abstract
Policy
Probability of
Reaching ‘goal’
Standard
Error
Expected
Reward
Standard
Error
None 0.72 0.0073 4.01 0.031
A 0.9 0.0012 2.85 0.0029
B 0.81 0.0019 3.62 0.0037
C 0.78 0.0012 4.5 0.0041
DCAART 2017 - Doctoral Consortium on Agents and Artificial Intelligence
14

and the corrected model, we envisage that the abstract
policies for the two models will be similar. Therefore,
it is intuitively not necessary to generate an entirely
different abstract policy. Since it is time consuming
to generate policies as well as to verify them, we aim
to reuse those elements of the initial abstract policy
that still match the abstract model.
To evaluate the algorithm, a series of experiments
will be conducted using extensions of the two case
studies described in the previous section. For each
case study we will produce a series of RL environ-
ments where the environment is uniquely different
from that of the initial AMDP. We will then deter-
mine if on average the knowledge revision algorithm
is faster at finding a new safe abstract policy than if
an AI engineer were to manually inspect the initial
RL model, reconstruct the high-level model, and gen-
erate safe abstract policies from scratch.
6.3 Future Work
Future work will involve more in depth analysis of
the framework’s performance. This includes evalu-
ation of how long it takes for a safe solution to be
learned and the processing overheads incurred. Ad-
ditionally, further experiments will be conducted by
expanding the existing case studies to establish how
well the framework will scale, also, new case studies
will be developed for different domains to determine
the range of scenarios which the technique can be ap-
plied to.
ACKNOWLEDGEMENTS
This paper presents research sponsored by the UK
MOD. The information contained in it should not be
interpreted as representing the views of the UK MOD,
nor should it be assumed it reflects any current or fu-
ture UK MOD policy.
REFERENCES
Arcuri, A. and Briand, L. (2011). A practical guide for us-
ing statistical tests to assess randomized algorithms in
software engineering. In 33rd Intl. Conf. Software En-
gineering, pages 1–10.
Argall, B. D., Chernova, S., Veloso, M., et al. (2009). A
survey of robot learning from demonstration. Robotics
and Autonomous Systems, 57(5):469–483.
Boger, J., Hoey, J., Poupart, P., et al. (2006). A planning
system based on markov decision processes to guide
people with dementia through activities of daily liv-
ing. IEEE Transactions on Information Technology in
Biomedicine, 10(2):323–333.
Calinescu, R., Johnson, K., and Rafiq, Y. (2011). Using ob-
servation ageing to improve Markovian model learn-
ing in QoS engineering. In 2nd Intl. Conf. Perfor-
mance Engineering, pages 505–510.
Calinescu, R., Johnson, K., and Rafiq, Y. (2013). Devel-
oping self-verifying service-based systems. In 28th
IEEE/ACM Intl. Conf. Automated Software Engineer-
ing, pages 734–737.
Calinescu, R., Kikuchi, S., and Johnson, K. (2012). Compo-
sitional reverification of probabilistic safety properties
for large-scale complex IT systems. In Large-Scale
Complex IT Systems. Development, Operation and
Management, pages 303–329. Springer Berlin Heidel-
berg.
Dearden, R., Friedman, N., and Russell, S. (1998).
Bayesian Q-learning. In 15th National Conference on
Artificial Intelligence, pages 761–768.
Efthymiadis, K. and Kudenko, D. (2015). Knowledge revi-
sion for reinforcement learning with abstract MDPs.
In 14th Intl. Conf. Autonomous Agents and Multiagent
Systems, pages 763–770.
Garc
´
ıa, J. and Fern
´
andez, F. (2012). Safe exploration
of state and action spaces in reinforcement learning.
Journal of Artifical Intelligence Research, 45(1):515–
564.
Garc
´
ıa, J. and Fern
´
andez, F. (2015). A comprehensive sur-
vey on safe reinforcement learning. Journal of Ma-
chine Learning Research, 16(1):1437–1480.
Gerasimou, S., Calinescu, R., and Banks, A. (2014). Effi-
cient runtime quantitative verification using caching,
lookahead, and nearly-optimal reconfiguration. In 9th
International Symposium on Software Engineering for
Adaptive and Self-Managing Systems, pages 115–124.
Gerasimou, S., Tamburrelli, G., and Calinescu, R. (2015).
Search-based synthesis of probabilistic models for
quality-of-service software engineering. In 30th
IEEE/ACM Intl. Conf. Automated Software Engineer-
ing, pages 319–330.
Hansson, H. and Jonsson, B. (1994). A logic for reasoning
about time and reliability. Formal Aspects of Comput-
ing, 6(5):512–535.
Heger, M. (1994). Consideration of risk in reinforcement
learning. In 11th Intl. Conf. Machine Learning, pages
105–111.
Kober, J., Bagnell, J. A., and Peters, J. (2013). Reinforce-
ment learning in robotics: A survey. International
Journal of Robotics Research, 32(11):1238–1274.
Kwiatkowska, M., Norman, G., and Parker, D. (2007).
Stochastic model checking. In 7th Intl. Conf. Formal
Methods for Performance Evaluation, volume 4486,
pages 220–270.
Kwiatkowska, M., Norman, G., and Parker, D. (2011).
PRISM 4.0: Verification of probabilistic real-time sys-
tems. In 23rd Intl. Conf. Computer Aided Verification,
volume 6806, pages 585–591.
Lange, D. S., Verbancsics, P., Gutzwiller, R. S., et al.
(2012). Command and control of teams of au-
Assured Reinforcement Learning for Safety-critical Applications
15

tonomous systems. In Large-Scale Complex IT
Systems. Development, Operation and Management,
pages 81–93. Springer Berlin Heidelberg.
Li, L., Walsh, T. J., and Littman, M. L. (2006). Towards a
unified theory of state abstraction for MDPs. In 9th In-
ternational Symposium on Artificial Intelligence and
Mathematics, pages 531–539.
Marthi, B. (2007). Automatic shaping and decomposition of
reward functions. In 24th Intl. Conf. Machine learn-
ing, pages 601–608.
Mason, G., Calinescu, R., Kudenko, D., and Banks, A.
(2016). Combining reinforcement learning and quan-
titative verification for agent policy assurance. In 6th
Intl. Workshop on Combinations of Intelligent Meth-
ods and Applications, pages 45–52.
Mason, G., Calinescu, R., Kudenko, D., and Banks, A.
(2017). Assured reinforcement learning with formally
verified abstract policies. In 9th International Confer-
ence on Agents and Artificial Intelligence. To appear.
Mihatsch, O. and Neuneier, R. (2002). Risk-sensitive re-
inforcement learning. Machine Learning, 49(2):267–
290.
Moldovan, T. M. and Abbeel, P. (2012). Safe exploration
in Markov decision processes. In 29th Intl. Conf. Ma-
chine Learning, pages 1711–1718.
Perkins, T. J. and Barto, A. G. (2003). Lyapunov design
for safe reinforcement learning. Journal of Machine
Learning Research, 3(1):803–832.
Sutton, R. S., Precup, D., and Singh, S. (1999). Between
MDPs and semi-MDPs: A framework for temporal
abstraction in reinforcement learning. Artificial Intel-
ligence, 112(1-2):181–211.
Szita, I. (2012). Reinforcement learning in games. In Rein-
forcement Learning: State-of-the-art, pages 539–577.
Springer-Verlag Berlin Heidelberg.
Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-
chine Learning, 8(3):279–292.
Wiering, M. and Otterlo, M. (2012). Reinforcement learn-
ing and markov decision processes. In Reinforcement
Learning: State-of-the-art, pages 3–42. Springer-
Verlag Berlin Heidelberg.
DCAART 2017 - Doctoral Consortium on Agents and Artificial Intelligence
16