Langrangian Relaxation of Multi Level Capacitated Lot Sizing
Problem with Consideration of Lead Time
Hanaa Razki and Ahmed Moussa
Laboratory of InformationTechnologies and Communication, ENSA,University Abdelmalek Essaâdi, Tanger, Morroco
Keyword: Tactical Planning, Multi Level Capacitated Lot Sizing Problem, Lagrangian Relaxation.
Abstract: Tactical planning consists to develop production plans by determining the quantities of products
manufactured by period to best meet customer demand at lower costs. This issue has been widely
discussed, according to two criteria: multi level and single level planning. The concept of multi level
reflects well the manufacturing structure. For this, we propose in this work a new mathematical model of lot
sizing finite capacity (Multi Level Capacitated Lot Sizing Problem) based on Lagrangian relaxation
optimization approach. Comparisons of this new model with traditional one demonstrate the efficiency of
this new approach as well in simulated case as real situations. The generated production plans are optimal
with 68% -98% compared to classical models.
1 INTRODUCTION
We are always looking for a relatively effective
solution that can help increase the level of
performance of production systems. This problem of
planning and scheduling production with limited
capacity resources reflects setup times, waiting and
production as well as different costs of production.
The formulations of the Big Bucket model (BB)
as Capacitated Lot Sizing Problem (CLSP) are
considered as a reference model for addressing the
plan generation of problematic production manager
in a single site environment (Comelli et al. 2008),
the Multi Level Capacitated Lot Sizing Problem
(MLCLSP), is recognized as a reference model and
deals with Manufacturing Resources Planning (MRP
and MRPII) issues, can be found in the literature for
some studies this problem (Almeder et al.2011,
Berretta et al.2005, Chen &Chu2003). If single site
issues have been extensively studied in the literature
(Nascimento et al.2010) point to the lack of a
reference model for multi site issues. This model
only determines the production quantities and
periods, regardless of the actual production sequence
of commands within a period of time. This type of
modeling has the advantage that it allows flexible
sequencing orders in a period, a significant cost
calculation. For small-Bucket models (SB) are
known, the Continuous Setup Lot Sizing Problem
(PRSP) and the Proportional Lot Sizing and
Scheduling Problem (PLSP).
The problem Multi Level Capacitated Lot Sizing
Problem (MLCLSP) is one of the most difficult
optimization problems known in the production. It
arises in any company that uses the sequential
approach to planning MRP. The approach was based
on the control of quantities on demand, compliance
with the BOM structure and the level of stock.
Consideration of production capacity and
product classifications pushed the authors to
consider the multiplicity of production resources
(Buschkuhl et al.2008), and we will find models of
mono or multi resource. Multi resource models
enable more accurate modeling of the operating
range of the various products and better estimate the
capacity of the production system. (Bel 1998)
demonstrated that to find feasible solutions for
MLCLSP is NP-complete, and when there are
considered setup time. Therefore, the proposed
Lagrangian heuristics include a feasibility strategy to
find feasible solutions from the penalization of the
constraints of the problem.
Most of the models and algorithms proposed
MLCLSP (Tempelmeier et al.2008) rely on one of
two possibilities: either the lead time is neglected,
and the lead time is taken into account, there is at
least one period for each component, forcing the
transit time (the number of periods) of finished
12
Razki, H. and Moussa, A.
Langrangian Relaxation of Multi Level Capacitated Lot Sizing Problem with Consideration of Lead Time.
In Doctoral Consortium (DCORES 2017), pages 12-19

products to be at least equal to the number of levels
of the BOM.
According to studies, the hypothesis of zero lead
time leads to plans that are not feasible, and the
lower level of scheduling problem is infeasible. On
the other side, if the lead time is positive, it usually
results in significant amounts of work in process,
causing subsequently increase the number of levels
in the nomenclature. This problem has been studied
by different researchers (Buschkühl et al.2010).
A recent study on the different model
formulations and solution methods for MLCSP is in
(Almeder et al.2014), the authors proposed two
models: one is batching and the other is streaming
lot. Computations indicate clearly that the solutions
obtained by MLCLSP are infeasible, and the lead
time excessive work in process from 15% to 60%
increase in the overall cost, they deployed the
algorithms Benders (Almeder et al.2014) variant
with a sanctions significant contribution to improve
the computational effort to find satisfactory
solutions.
The main contributions of our study are as follows:
We show that the solutions obtained with lead time
are feasible. We propose a linear programming
formulation integer. Regarding the approach of the
Lagrangian relaxation is to relax capacity constraints
while penalizing their violation in the objective
function, our experiences show that calculation
variant polarization capacity constraints give the
best solution of the problem. The comparison with
traditional models, we demonstrate the ability of this
new approach with more realistic results (68% -98
%).
In Section 2, we propose the new formulations of
the MLCLSP problem with major constraints. In
Section 3, we present our optimization approach to
problem solving with the new formulation of the
model, and in section 4, we apply the standard
reference instances and we compare the results with
those of classical MLCLSP.
2 PLANNING MODEL GENERIC
2.1 Classic Models
In supply chain management, support for the
medium term decision can be considered in the
construction of a solution (such a plan) it is to build
and generate a solution. The generative of this
approach is shown in Figure 1 (Sambasivan et
al.2002).
Figure 1: Generative approach (Sambasivan et al.2002).
Production management, where the models were
more widely used, the approach described above
concerning the planning model. We use planning
model into an optical performance evaluation to
build an optimal plan.
In this article, we present the classical model of
MLCLSP planning aims to generate a production
plan that minimizes the sum of setup costs and
inventory costs, while respecting the constraints of
stock and capacity.
The objective function of MLCLSP model is as
follows:
Min∑
N
i=1
∑
T
t=1
(C
i
.Y
it
+H
i
.I
it
) (1)
Under the constraints:
I
it+1
=I
it
+X
i(t-li)
-∑
N
j=1
a
ij
*X
jt
- D
it
i,t (2)
∑
N
i=1
P
i
*X
it
≤ C
t
i,t (3)
X
it
≤ G*Y
it
i,t (4)
I
it
≥0 , X
it
≥0 i,t (5)
Y
it
ϵ{0,1} i,t (6)
Model parameters:
i : Product
t: Period
P
i
: Time to produce a unit of product i
C
i
: Cost of setup of product i
D
it
: Demand for the product i at time t (external)
G: Arbitrarily large number (e.g., total demand or
maximum capacity)
H
i
: The cost of stock of product i
C
t
: The available capacity (time) at time t
l
i
: Lead time of item i (non negative integer
corresponding to the number of periods)
a
ij
: Amount of product i to produce a unit of product
j (gozinto-factor).
Decision variables:
I
it
: Stock level of product at the end of period t
X
it
: Quantity of product i in period t
Langrangian Relaxation of Multi Level Capacitated Lot Sizing Problem with Consideration of Lead Time
13

1 if the product and manufactured in the
period
0 no production
The objective function (1) minimizes the total
cost involved in the production plan, namely the
costs of production and storage, as well as fixed
setup costs, inventory costs. Constraint (2) expresses
the conservation of flux across the horizon with the
stress of lead time. Constraint (3) expresses the fact
that the plan that we would calculate to be finite
capacity. Indeed, for the realization of a plan, we
have an amount of resources that will be consumed
by the production of one or more references. Total
consumption should be less than the available
capacity. Constraint (4) to model the following
condition: if the setup of production, while the
quantity produced must not exceed an upper bound
of the output G. This represents the minimum
between the maximum amount of the reference can
be produced and the total demand on the horizon [t,
.., T]. Constraint (5) means that X
it
and I
it
variables
are continuous no negative for any reference i, for
each period t. The last constraint (6) expresses the
fact that Y
it
is a binary variable for any reference i in
each period t.
Many researchers are studying this model,
assume that the lead time is negligible, to the effect
that the predecessors and successors could be
produced in the same period ( l = 0 for all i ). The
MLCLSP is a model BB and the periods are
supposed to cover the long time intervals with a
number of production batches, so it would result in
significant amounts of work in production. If we
assume that the lead time is positive for at least one
period ( l = 1 for all i ) , we deliver the requested
quantity respecting the delivery time , There is
always in practice, there is always the possibility of
use of overtime to make production in our model the
objective function (1) does not account for
additional fabrication.
To verify the model, the example of Table 1
represents a lot sizing problem in 2 periods, 4
products and unconstrained capacity, Figure 2 shows
the structure of the nomenclature (Almeder et al.
2014).
Table 1: Data example.
Product
D
i1
D
i2
H
i
C
i
P
i
1
3
0
3
5
0.1
2
0
2
2
5
0.1
3
0
0
2
5
0.1
4
0
0
1
5
0.1
Figure 2: Example of nomenclature.
Figure 3: Limitation of the Multi Level Capacitated Lot
Sizing Problem.
The configuration presented in Figure 3 provides
the solution of the classical model, if we assume that
the lead time is negligible, and no setup change to
produce the product 4 , but with this solution we do
not respond to the objective function to optimize the
cost of the stock.
With this plan in Figure 4, we produce only the
amount requested for each period, for example in the
period 1 we produce an amount of 3 units of
product 4, we change the setup to produce product 3
and subsequently the product 1, which results in a
delay in customer demand level for product 1
because production will end in period 2. So with this
solution we are not optimizing the cost of setup and
customer demand.
Y
it
1
4
3
2
t
t
t
t
Period1
Period2
5units of Product 4
2units of Product 2
3units of Product 3
3units of Product 1
Setting stock
Product
Period2
DCORES 2017 - DOCTORAL CONSORTIUM
14

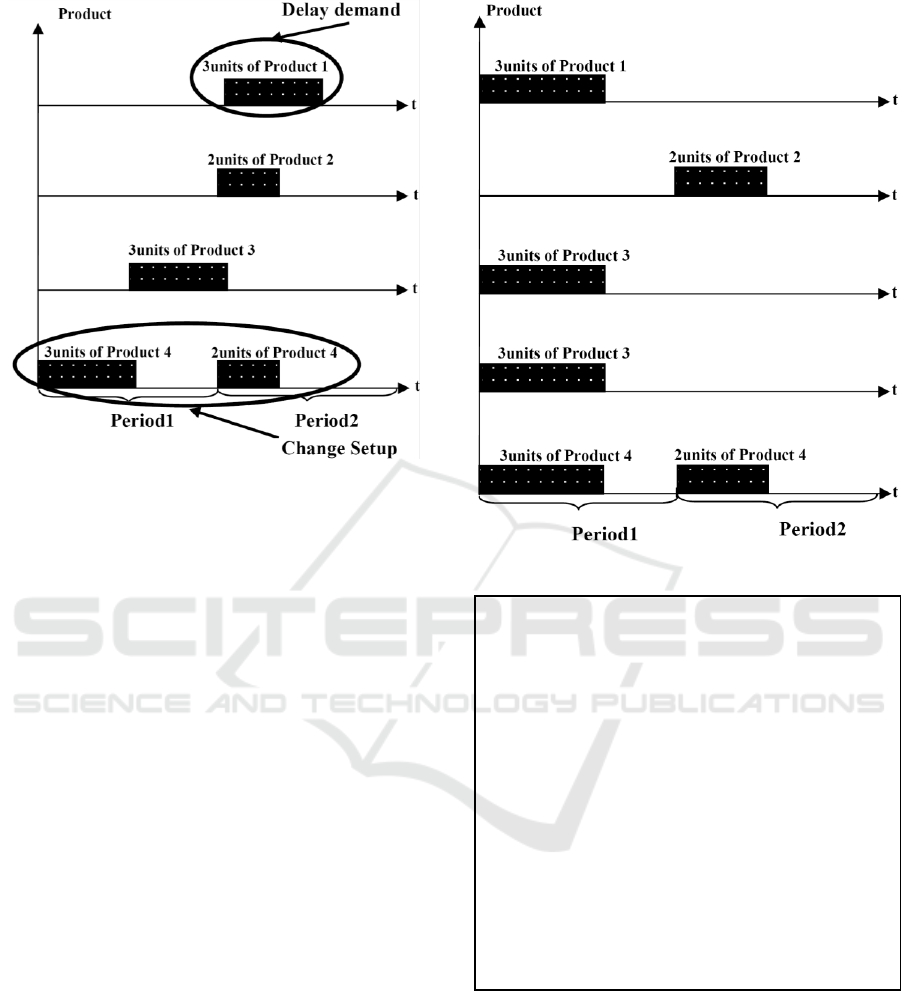
Figure 4: Limitation of the Multi Level Capacitated Lot
Sizing Problem.
2.2 Proposed Model
If we consider the two plans proposed above, we
notice that the constraint that violates our
optimization objective function is the constraint of
stock (2), so we propose a new formulation which
provides an optimal solution for our model, applying
the product of the net principle need i at time t, we
produce the necessary need in period t, and our
formulation we consider a lead time period to meet
customer delivery time.
The proposed new constraint:
I
it+1
= D
it
-I
it
-X
i(t-li)
i,t (7)
This plan in Figure 5, allows us to produce our
net needs at time t, if we take our example, our net
need for the period 1 of the finished product 1 is 3
units, so for the produce we must have 3 units of
subsets 3 and 4, with this solution we gain at the cost
of stock, the same principle to produce the finished
product 2.
We implemented the proposed model in CPLEX
12.2 (User’s Guide Standard Version Including
CPLEX Directives.2010), to see if our new
formulation is optimized for our objective function.
After the simulation, results are optimized with a
target of 40.
Figure 5: Verification of our new formulation.
Figure 6: Simulation results with CPLEX Solver.
3 OPTIMIZITION METHOD
3.1 Lagrangian Relaxation
The Lagrange relaxation technique has been the
subject of several studies (Fisher, M 2004) and was
raised in the problems of integration of production.
// solution (optimal) with objective 40
plan[1][1]=
<fabrication:1,production:3,stock:0>
plan[1][2]=
<fabrication:1,production:0,stock:0>
plan[2][1]=
<fabrication:1,production:0,stock:0>
plan[2][2]=
<fabrication:1,production:0,stock:0>
plan[3][1]=
<fabrication:1,production:0,stock:0>
plan[3][2]=
<fabrication:1,production:0,stock:0>
plan[4][1]=
<fabrication:1,production:0,stock:0>
plan[4][2]=
<fabrication:1,production:0,stock:0>
Langrangian Relaxation of Multi Level Capacitated Lot Sizing Problem with Consideration of Lead Time
15

This method can be used to approximate solutions,
seek a lower bound (ZLB) of the problem or to
obtain more optimal solutions. (Wu et al.2013)
developed a strategy for finding upper bounds
(ZUB) on the relaxation using Lagrangian for a lot
sizing problem with multiple products. A
metaheuristic was proposed in (Toledo et al.2014) to
resolve an extension of CLSP with to carry over.
(Nascimento et al.2010) proposed a strategy that
incorporates a genetic algorithm with a linear
program to find approximate solutions to a lot sizing
level problem and scheduling.
The approach of the Lagrangian relaxation is to
relax a subset of constraints while penalizing their
violation in the objective function by associating a
Lagrangian multiplier λit.
As shown in section 2, our new formulation of
MLCLSP model allows us to achieve an optimal
plan, but draws the MLCLSP is a BB model and
periods are supposed to cover long intervals with
several production batches, so it would lead to a
significant production capacity, and our equation (3)
expresses that our plan must be calculated with finite
capacity. That is why the approach of the
Lagrangian relaxation will be based on the
penalization of capacity constraints. (Berretta et
al.2005) presented a heuristic based on the
Lagrangian relaxation of the capacity constraints of
the mathematical formulation. To find a lower
bound (ZLB) for the problem.
Our news formulation of the objective function
is:
Min∑
N
i=1
∑
T
t=1
(C
i
.Y
it
+H
i
.I
it
) +
∑
N
i=1
∑
T
t=1
λ
it
(C
t
-∑
N
i=1
P
i
*X
it
) (8)
Under the constraints:
I
it+1
= D
it
-I
it
-X
i(t-li)
i,t
(9)
X
it
≤ G*Y
it
i,t (10)
I
it
≥0 , X
it
≥0 i,t (11)
Y
it
ϵ{0,1} i,t (12)
(Sambasivan et al.2005) points out three main
approaches in his study: the sub-gradient method
and the multiplier λ
it
adjustment method. This last
and according to (Fisher, M 2004) proved to be too
costly compared to the sub-gradient method.
Although the adjustment method has a high
potential, exceeding the sub-gradient method in
some case studies, but the sub-gradient is the most
used to determine the Lagrange multipliers tool.
So to solve this dual problem, the method chosen
is the sub-gradient. The sub-gradient algorithm
introduced in (8). It updates iteratively multipliers:
λ
it
= max {0; λ
it
+TG
i
) i,t (13)
T is the step of the iteration method, and G
i
is the
difference between the time required to produce all
units of product i in period t and the capacity limit in
period t, calculated in Equation (14):
G
i
= C
t
-∑
N
i=1
P
i
*X
it
i,t (14)
It is necessary to initialize the values T and λ
it
for
each iteration. The step T is important to optimize
our solution.
The choice of the step size T, is of importance
for the convergence of the sub-gradient method for
the optimal solution. Thus, the T update is given by
the equation below:
T =π (ZUB-ZLB)/G
i
² (15)
Figure 4 shows the algorithm of the principle of our
approach.
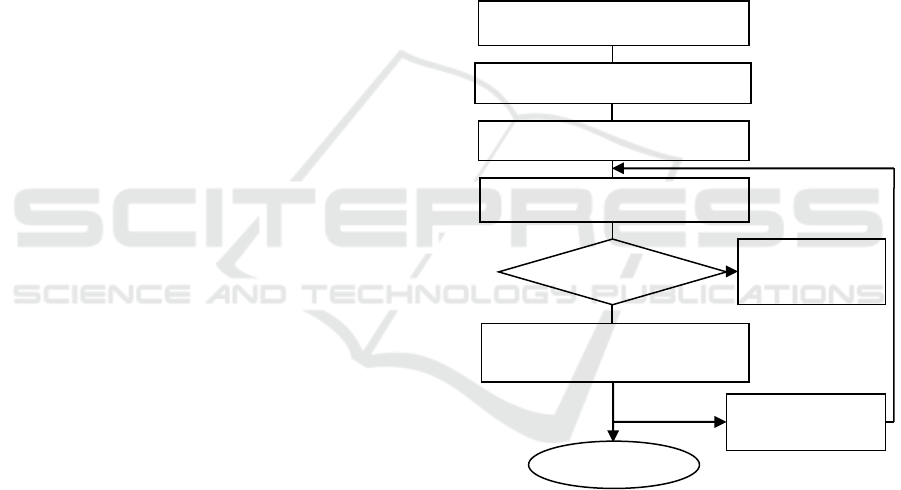
Figure 7: Flowchart of the principle of our approach.
To ensure the convergence of the method, the
solutions at each iteration step means that the T
tends to 0. According to the equation (15) T depends
the upper bound (ZUB) and the lower bound (ZLB),
if no lower bound is found to iterate , so the solution
is infeasible. (Almeder,C.2010) most BB models
provide the best lower bound.
Following algorithm shows a pseudo code of our
approach to feasibility of the solution:
Data: Approximate dual solution
Result: Either a heuristic solution for
the primal problem or infeasible
solution
Fin
Initialize π & λ
it
Calculate Subgradient
Calculate step T
Lagrangian problem solver
ZLB found
Update λ
it
λ
it
=max(0 ; λ
it
+TG
i
)
Infeasible
solution
Yes
Increment
iteration
No
DCORES 2017 - DOCTORAL CONSORTIUM
16

Repeat
Initialize arrays and variables used in
the loop that follows
Initialize π ]0; 2]
Initialize λit values
Executes Lower Bound and Upper Bound
model
Calc sub-gradient G
i
= Ct-∑P
i
*X
it
Calc T = π(ZUB−ZLB)/G
i
²
Solve the model to get the Upper
Bound
Update λ
it
to pass it as input data to
Lower Bound model in next iteration
End loop
4 SIMULATION
The optimal solution of the lot sizing problem
presented in Table 3 is obtained using Lagrangian
relaxation. The results are obtained by the linear
programming solver integer CPLEX 12.2 (User’s
Guide Standard Version Including CPLEX
Directives.2010).
All tests were implemented in C ++ and run on a
PC with 4G HP Core i5 processor.
4.1 Test Instances
We have carried out tests on a series of instances of
(C.Almeder et al.2014). The characteristics of bodies
are described in Table 2.
Table 2: Instances of C.Almeder et al. (2014).
Class
Instances
Periods
Products
A
1500
4
10
B
600
4
10
C
599
16
40
D
573
16
40
4.2 Analysis of Proposed Method
The model MLCLSP feasibility problem is to
consider a minimum period of lead time. As
mentioned previously this period may cause
amounts of work in production, then a substantial
increase in the stock.
(C.Almeder et al.2014) demonstrated the
infeasibility of the MLCLSP problem by running the
model with conventional test instances without
synchronization with a period of lead time. With a
run time limit of 10 minutes for CPLEX.
This document puts the Lagrangian strategies for
the upper and lower bounds of good quality for cases
tested and shows that our proposed approach will
guarantee us an optimal solution for the proposed
production plans with consideration of one period of
lead time.
Table 3 presents results obtained by CPLEX
Solver and table 4 presents the resulting solutions
for our approach, the columns show the lower bound
greater than the percentage of optimality GAP =
(ZUB- ZLB) / ZUB for each test class to improve
our cost model by considering a period of lead time.
Table 3: Simulation with CPLEX Solver.
Class
(Instance)
CPLEX
GAP
Time
A(1500)
14%
30s
B(600)
35,25%
9s
C(599)
infeasible
_
D(573)
infeasible
_
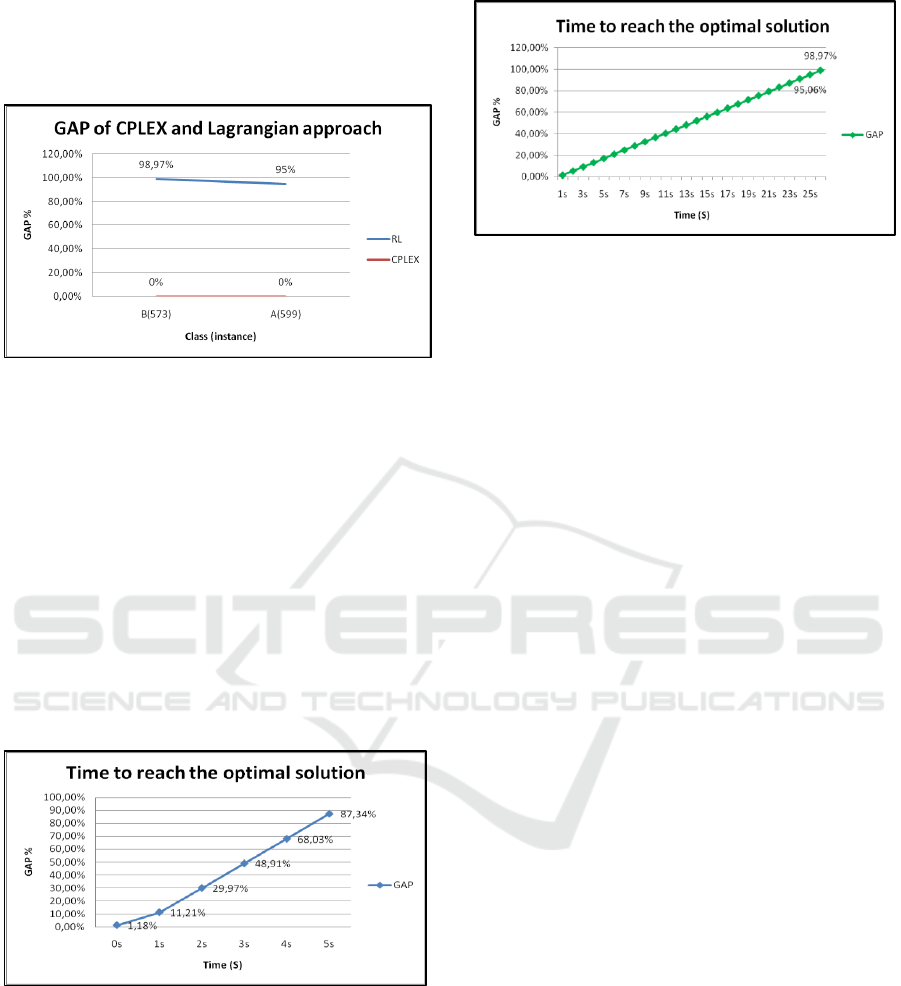
Table 4: Simulation with Lagrangian approach.
Class
(Instance)
RL
ZUB
ZLB
GAP
Time
A(1500)
205,5
26
87,34%
5s
B(600)
206,5
66
68,03%
6s
C(599)
16363
808
95%
25s
D(573)
16362
168
98,97%
26s
Table 4 presents the best values of the proposed
method of MLCLSP. So with the relaxation of
Lagrangian approach, we find optimal solutions with
87.34% for Class A, 68.03% for Class B, 95% for
Class C and 98.97% for Class D.
Table 3 shows that the solutions implemented in
CPLEX, are optimal with 14% for Class A and
35.25% for Class B, but for Class C and Class D
solutions are infeasible.
Figure 8: Results obtained for SB.
This graph shows that with the Lagrangian approach
we obtain the best optimal solutions for the model
Langrangian Relaxation of Multi Level Capacitated Lot Sizing Problem with Consideration of Lead Time
17

SB, even if we increase the instance. On the other
hand, we observe that the results obtained with the
CPLEX solver are lower and decrease with the
increase of the instance.
Figure 9: Results obtained for BB.
On this graph, we show that for the model BB
our plan remains optimal with the Lagrangian
approach, but for CPLEX Solver the solution is
infeasible.
So we show with our new formulation, BB or SB
model is optimized, resulting in a clear cost estimate
from stock and production and in parallel we are
responding to the constraint of important quantities
of production work, which request the use of
overtime to make up for production.
Comparing the results with those obtained by the
classical MLCLSP, we realize a 4.5% increase to
that produced by the Benders algorithms proposed
by (C.Almeder et al.2014).
Figure 10: The trend for SB.
The Proposed formulation we guarantee an
optimal solution after less 5s for SB and less than
25s for BB. The penalization of capacity constraint
provides lower bound to optimize our objective
function even if we consider the lead time. Figures
10 and 11, we show the improvement of the
objective value of the best solution for the cases
studied. Trends show that the improvement is
achieved in the initial iterations.
Figure 11: The trend for BB.
5 CONCLUSION
This paper presented a new formulation and solution
for the multi level capacitated lot sizing problem
(MLCLSP) with considering one period of lead time
that requires an important quantity of production
work requesting thus the use of overtime to make up
for production.
Besides, the proposed optimization method of
our problem was Lagrangian relaxation based on the
penalization capacity constraints. The performance
on several classes with different instances generated
was compared with the CPLEX Solver, and the
results show the efficiency of 68% to 98.97%. It
should be noted that the proposed model is more
suitable with the production constraints of planning.
We also remember that this approach is now under
implementation for real situations.
REFERENCES
Comelli, M., M. Gourgand et D. Lemoine, 2008. A review
of tactical planning models, Journal of Systems
Science and Systems Engineering, Vol.17(2), pp 204-
229.
Almeder,C.,&Almada-Lobo,B.(2011). Synchronization of
scarce resources for a parallel machine lot sizing
problem. International Journal of Production Research,
49(24),7315–7335.
Berretta, R., Franca, P., Armentano, V., 2005.
Metaheuristic approaches for the multilevel resource-
constraint lot-sizing problem with setup and lead
times. Asia - Pacific Journal of Operational Research
22 (2), 261–286.
Chen, H. et Chu, C. (2003). A lagrangian relaxation
approach for supply chain planning with order/ setup
costs and capacity constraints, Journal of System
Science and Systems Engineering.
Nascimento, M. C. V., M. C. G. Resende, and F. M. B.
Toledo (2010). GRASP with path-relinking for the
DCORES 2017 - DOCTORAL CONSORTIUM
18

multi-plant capacitated lot sizing problem. European
Journal of Operational Research 200, 747–754.
Buschkuhl, L., F. Sahling, S. Helber, and H. Tempelmeier
(2008). Dynamic capacitated lot sizing a classification
and review of the literature on \big bucket" problems.
[Bel 1998] Bel G., Aide à la conception et à la conduite de
systèmes à événements discrets : Application aux
systèmes de production, Habilitation à diriger des
recherches, Université Paul Sabatier, Toulouse, Mai
1998.
Tempelmeier, H., Buschkühl, L., 2008. Dynamic multi-
machine lotsizing and sequencing with simultaneous
scheduling of a common setup resource. International
Journal of Production Economics 113, 401–412.
Buschkühl, L., Sahling, F., Helber, S., Tempelmeier, H.,
2010. Dynamic capacitated lot-sizing problems: a
classification and review of solution approaches. OR
Spectrum 32, 231–261.
C. Almeder, R.Traxler al. 2014, Lead time considerations
for the multi-level capacitated lot-sizing problem,
European Journal of Operational Research 000 (2014)
1–12.
Sambasivan, M. and C. P. Schimidt (2002). A heuristic
procedure for solving multi-plant, multi-item, multi-
period capacited lot-sizing problems. Asia Pacific
Journal of Operational Research 19, 87–105.
IBM ILOG AMPL, Version 12.2. User’s Guide Standard
(Command-line) Version Including CPLEX
Directives. May 2010.
Fisher, M. L. (2004). The lagrangian relaxation method for
solving integer programming problems. Management
science 50 (12 supplement), 1861–1871.
Wu, T., C. Zhang, Z. Liang, and S. C. Leung (2013). A
lagrangian relaxation-based method and models
evaluation for multi-level lot sizing problems with
backorders. Computers & Operations Research 40,
1852–1863.
Toledo, C. F. M., L. de Oliveira, R. de Freitas Pereira, P.
M. Fran¸ca, and R. Morabito (2014). A genetic
algorithm/mathematical programming approach to
solve a two-level soft drink production problem.
Computers &Operations Research 48, 40–52.
Nascimento, M. C. V., M. C. G. Resende, and F. M. B.
Toledo (2010). GRASP with path-relinking for the
multi-plant capacitated lot sizing problem. European
Journal of Operational Research 200, 747–754.
Berretta, R., Franca, P., Armentano, V., 2005.
Metaheuristic approaches for the multilevel resource-
constraint lot-sizing problem with setup and lead
times. Asia - Pacific Journal of Operational Research
22 (2), 261–286.
Sambasivan, M. and S. Yahya (2005). A lagrangean-based
heuristic for multi-plant, multi-item, multi-period
capacitated lot-sizing problems with inter-plant
transfers. Computers and Operations Research 32,
537–555.
Almeder,C.(2010). A hybrid optimization approach
formulation level capacitated lot sizing problems.
European Journal of Operational Research, 200,599–
606
Langrangian Relaxation of Multi Level Capacitated Lot Sizing Problem with Consideration of Lead Time
19