Predicting the Stability of Large-scale Distributed Stream Processing

Systems on the Cloud

Tri Minh Truong, Aaron Harwood and Richard O. Sinnott

University of Melbourne, Melbourne, Australia

Keywords:

Stability, Resource Estimates, Stream Processing Systems.

Abstract:

Large-scale topology-based stream processing systems are non-trivial to build and deploy. They require un-

derstanding of the performance, cost of deployment and considerations of potential downtime. Our work

considers stability as a primary characteristic of these systems. By stability, we mean that unstable systems

exhibit large-spikes in latency and can drop throughput frequently or unpredictably. Such instabilities can be

due to variations of workloads or underlying hardware platforms that are often difﬁcult to predict. To under-

stand and tackle this for large-scale stream processing systems, we apply queueing theory and simulate the

results through a series of experiments on the Cloud.

1 INTRODUCTION

Stream processing is becoming increasingly impor-

tant to information and business processes. Real-time

information needs arise from almost all sectors. Many

applications are built for competitive advantages such

as ﬁnancial trading systems or customers services.

Other applications are used to monitor real-time traf-

ﬁc or security attacks e.g preventing real-time fraud.

Major online service providers are looking at trends

so that they can serve suitable items to on-line cus-

tomers as they click through web pages. The chal-

lenge with stream processing is the very high vol-

ume and processing demands of real-time data and

the need for very low latency.

Further distributed systems research is required

to meet the challenges placed upon the new genera-

tion of big data stream processing systems (Hu et al.,

2014; Krempl et al., 2014). We call such systems,

simply, big systems. It is no longer sufﬁcient for such

big systems to process data in batches, as is usually

assumed in high performance computing. Data must

be processed online and in real-time. The real-time

results from such big systems must be available to the

users and the users must be able to interact with the

processing in real-time.

A core challenge of stream processing is to adapt

to dynamic conﬁguration of the underlying infrastruc-

ture in the presence of bursty trafﬁc. The rise of a new

breed of general-purpose frameworks for stream pro-

cessing with simple programming APIs allows users

to create massive distributed systems that hide the

complexity of scaling out and fault-tolerance (Toshni-

wal et al., 2014; Kulkarni et al., 2015; Zaharia et al.,

2010). (Heinze et al., 2014a) points out that this gen-

eration of data streaming systems are driving the de-

sign of cloud-based stream processing.

While there are many research works proposed to

dynamically scale stream processing systems such as

(Heinze et al., 2014c; Gedik et al., 2014; Heinze et al.,

2014b; Lohrmann et al., 2015), they are not straight-

forward to deploy, even to Cloud environments. The

problem lies with resource estimation. Thus, resource

estimates are only discussed as a result of scaling op-

erator parallelism, e.g where acquiring or releasing

resources is needed. Scaling increases or decreases

the waiting time for services. There has not been any

approaches that explicitly solve resource estimation

problems in terms of stability.

Resource estimation is especially difﬁcult due to

different stream processing queries with various data

streams and ﬂuctuating workloads. It is in this aspect

that our research is most concerned. From a queueing

theory perspective, every ﬁnite buffering system has a

non-zero probability that the buffer will become full.

As such, resource estimates have a direct connection

to stability prediction. The question is how to gauge

the cost to pay for such stability.

Truong, T., Harwood, A. and Sinnott, R.

Predicting the Stability of Large-scale Distributed Stream Processing Systems on the Cloud.

DOI: 10.5220/0006357606030610

In Proceedings of the 7th International Conference on Cloud Computing and Services Science (CLOSER 2017), pages 575-582

ISBN: 978-989-758-243-1

575

1.1 Contributions

This paper proposes a strategy to estimate resources

required for stream processing systems by applying

queueing theory to predict the stability of such sys-

tems. The goal is to achieve an appropriate utilised

level for effective use with minimum resources and

at the same time provide processing stability under

heavy workload. The contributions of this paper in-

clude:

• We apply queueing theory to provide a model for

understanding and for predicting stability, and

• A reliable resource estimation technique through

simple performance metrics based on measure-

ment and monitoring which can be adapted to

many topology-based stream processing frame-

works and Cloud environments.

1.2 Related Work

Related work such as (Pietzuch et al., 2006; Cardellini

et al., 2015; Eidenbenz and Locher, 2016; Chatzis-

tergiou and Viglas, 2014) focus on efﬁcient operator

placement which determines, within a set of available

distributed computing nodes, the nodes that should

host and execute each operator. These works pro-

pose adaptivity strategies to optimize the Quality of

Service of stream processing systems at deployment

based on assumptions of knowledge of the resource

requirements. In real world scenarios, such assump-

tions are not realistic and can lead to sub-optimal uti-

lization of available resources.

Many existing works on elasticity propose the use

of metrics such as the congestion index, throughput,

CPU, latency or network usage, etc. (Heinze et al.,

2015) implemented stream processing system elas-

ticity. An optimization algorithm proposed in this

work was used to ﬁnd the parameter conﬁguration

based on setting of six parameters for the scaling

strategy, which (1) minimized the monetary cost and

(2) ensured a good quality of service. Recent work

(Jamshidi and Casale, 2016) proposed an auto-tuning

algorithm that leveraged Gaussian Processes to ﬁnd

optimal conﬁgurations given a limited budget of ex-

periments.

(Aniello et al., 2013) propose schedulers used to

deploy a topology in tuning Storm (Toshniwal et al.,

2014) performance. This solution focused on adap-

tively placing and migrating tasks at runtime based on

statistics such as where to place tasks that exchange

comparably large amounts of data. Recently, Heron

(Kulkarni et al., 2015) has improved Storm's con-

gestion handling mechanism by using back-pressure

approaches however elasticity is not explicitly ad-

dressed.

The Stela system (Xu et al., 2016) does not change

running topologies because it is considered intrusive

to the applications. When the user requests a scale-

out with a given number of new machines Stela then

decides which operators to give more resources to,

by increasing their parallelism based on an Expected

Throughput Percentage metric. Stela ﬁrst identiﬁes

these operators that are congested based on their in-

put, processing and output rates. It relies on the Con-

gestionRate parameter to control the sensitivity of the

algorithm.

Recent work (Lohrmann et al., 2015) proposed an

elasticity model that provides latency guarantees by

tuning task-wise parallelism level in a ﬁxed size clus-

ter.

Our work is orthogonal to these works (Xu et al.,

2016; Lohrmann et al., 2015; Jamshidi and Casale,

2016) and achieves these metrics and statistics based

on analysis in terms of stability which can be incor-

porated to improve resource utilization at runtime.

2 BACKGROUND

First generation big system architectures are “batch-

based”, for example Apache Hadoop (Zikopoulos

et al., 2011) and Apache Spark (Zaharia et al., 2010)

and many such research and development projects

that ultimately became Apache Software Foundation

projects. These use map-reduce like processing on

batches of data (Dean and Ghemawat, 2008; Condie

et al., 2010). The concept of a data stream is not

necessarily maintained in such approaches. These

architectures have progressed to include the con-

cept of micro-batching, to better handle data in real-

time. Second generation big system architectures are

“topology-based”, for example Apache Storm (Tosh-

niwal et al., 2014), Apache Samza (Kleppmann and

Kreps, 2015), Aurora (Abadi et al., 2003) and Yahoo!

S4 (Neumeyer et al., 2010). In such approaches, pro-

cessing is decomposed into components and the data

stream concept is maintained between components.

In this research we focus on topology-based archi-

tectures which arguably have the strongest research

focus in stream-based distributed systems today.

2.1 Topology-based Stream Processing

Background

Topology-based stream processing platforms repre-

sent processing components, which we call operators,

as nodes in a directed graph, where the edges repre-

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

576

sent the ﬂow of tuples in the stream between operators

(see Figure 1). Apache Storm is arguably the most

widely used topology-based stream processing plat-

form today. Operators that have no incoming edges

are called sources (Spouts in Apache Storm) and they

produce tuples. A source typically receives data from

a big data provider, e.g. Twitter, where each “tweet”

is transformed into a tuple within the system. Oper-

ators with no outgoing edges are called sinks (usu-

ally a database) and they remove tuples from the sys-

tem. Operators with both inputs and outputs generally

transform the incoming tuple stream from one tuple

type to another. Operators may receive multiple input

streams of differing tuple types and produce multiple

output streams of differing tuple types.

Database

Publish/

User

Interface

Twitter

Google

Facebook

Topology−based stream processing system

Figure 1: Conventional view of the role of a topology based

stream processing system. We use triangles to represent

sources, hollow circles for operators and solid dots as sinks.

The role of a topology-based platform is to allow

programmers to deﬁne the operators and the topology

needed and then to transparently map this to some un-

derlying hardware in such a way that programmers

see only that operators receive tuples and emit them.

A good platform will transparently provide a reliable

and efﬁcient sub-communication system, thereby re-

moving such details from the programmer. Further-

more, to be competitive, the platform will provide a

means to scale up, whereby multiple instances of an

operator can be transparently used by the platform to

increase the throughput of stream processing (see Fig-

ure 2).

2.2 Queueing Theory model

We use queueing theory to model our stream pro-

cessing system. In particular, each component of the

topology can be considered as a queueing system.

Some notations are necessary for the discussion. Let

random variable t be the time interval between the ar-

rival times of 2 successive tuples and let u be the pro-

cessing/service time of a tuple, which is assumed to

be independently and identically distributed for all ar-

rival times.

One fundamental measure of queueing system

performance is the trafﬁc intensity a which can be

given as:

a =

E(u)

E(t)

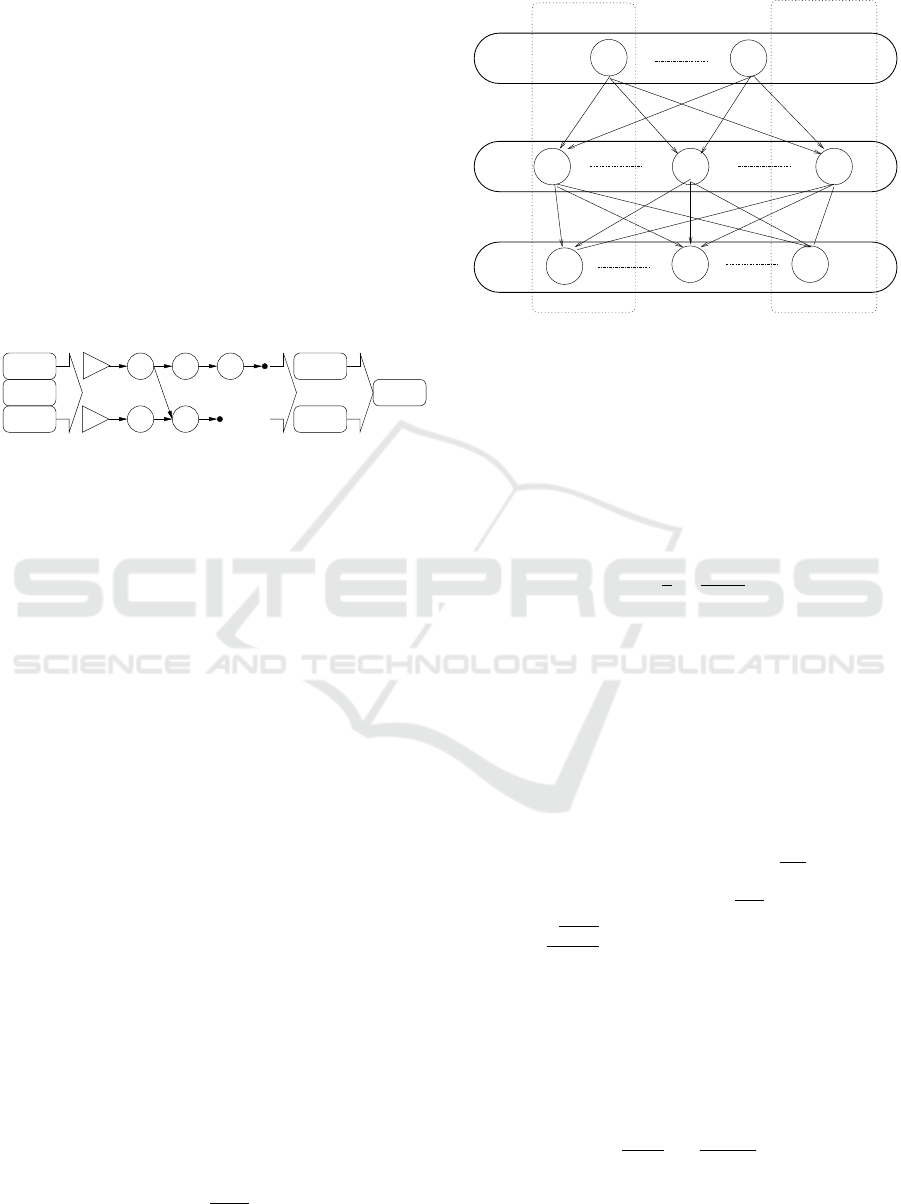
Worker 1

Parallelism of operators for maximum througput

Element

Sink

Worker N

Process

Source

Figure 2: Multiple instances of an operator are used to in-

crease the throughput of stream processing. Instances are

shown as circles and instances of the same operator are

grouped together in horizontal box. Arrows represent com-

munications. Note that the source is also considered as

an operator with no incoming communications. Workers

are actual machines. Resource estimates are based on how

many resources should be acquired for the stream process-

ing applications.

For c identical servers, the quantity

ρ =

E(u)

cE(t)

is the server utilization and represents the average

fraction of time that each server is busy (assuming the

trafﬁc is evenly distributed to the servers). Thus, the

trafﬁc intensity a is a measure of the required number

of servers and a measure of congestion (ρ).

In our approach, the number of servers is trans-

lated into the number of instances required to remove

congestion with ρ → 1 and a →c.

Furthermore, we can consider each instance to be

a single-server G/G/1 queueing system. Thus letting:

• λ be the mean arrival rate (i.e λ =

E(t)

• µ be the service rate (i.e µ =

E(u)

), and

• c

√

Var(x)

E(x)

be the coefﬁcient of variation of x ∈

{

t,u

}

Under heavy trafﬁc for a queueing system where

ρ = a = λ/µ and ρ → 1, Kingman’s approximation

(Kingman, 1961) states that the expected (mean or av-

erage) steady state time a tuple spends in the queue is

given as:



1 −ρ



+ c



E(u) (1)

As a result, we can estimate the latency (waiting

time + processing time) for the average tuple and the

Predicting the Stability of Large-scale Distributed Stream Processing Systems on the Cloud

577

buffer size needed in each instance in order to avoid

back-pressure (congestion).

3 METHODOLOGY

3.1 Stable Resource Estimation

Techniques

The basic principle behind scalable stream process-

ing platforms is the notion of operators that consume

one or more data streams, process received tuples

and continuously output results in the form of data

streams. Taking advantage of topology-based archi-

tectures to address the problem of resource estima-

tion, we propose the following strategy based on this

observation: the topology provides a means to scale

up whereby multiple instances of an operator can be

transparently used by the platform to increase the

throughput of stream processing.

To start estimating, we start with each operator

having 1 instance which is given 1 CPU as the basic

unit for execution. From the Heron design (Kulkarni

et al., 2015), each instance is mapped to an execu-

tor which is run inside a Java Virtual Machine as a

single thread. Thus in order to fully utilize the CPU

resources, more instances can be added starting with

the spout operator. When the point of back-pressure

occurs i.e there are too many spout operator instances

vs. bolt operator instances, we can proﬁle the ex-

pected performance of the given topology.

In case of back-pressure, the operator which

causes the back-pressure will be given more instances

in order to speed up the ﬂow. Another challenge is

when the throughput of stream processing increases.

We argue that as long as the throughput is increasing,

the process of adding instances should continue. The

rate of back-pressure is a percentage of time which

the system spends on dealing with back-pressure. For

example, if every period of 60 seconds, the time spent

on back-pressure is 40 seconds, then on average, the

system rate of back-pressure is approximately 66%.

In practice, the back-pressure rate is proportional to

the data dropping rate. In essence, this process min-

imizes the rate of back-pressure and achieves higher

throughput given a set of resources.

Our approach is similar to (Gedik et al., 2014)

which makes use of 2 locally computed metrics: con-

gestion and throughput. Based on such information, a

control algorithm reactively adapts the parallelism of

local operators to workload changes.

At the same time, increasing parallelism may re-

sult in better throughput but only to a certain point

as the effects of load can exacerbate back-pressure.

However, even if load is under-utilized, back-pressure

can simply arise by chance. This depends on the sta-

bility of the conﬁguration.

It is in this aspect that the balance of performance

and cost needs to be optimised. Through combining

empirical results such as tuple processing time distri-

bution into an analytical framework such as queuing

theory, we are able to measure the expected proba-

bility of back-pressure. As a result, we can provide

guarantees of data delivery/processing and achieve

the desired throughput with minimal back-pressure

rate probability. Furthermore, the analysis of CPU

memory in terms of queue sizes can also be modelled.

Utilising baseline performance, we can give ap-

proximate estimates of the resource requirements

needed to achieve the required throughput for stream

processing systems.

3.2 Predicting Stability

Queueing theory typically deals with system perfor-

mance in a steady-state. That is, most queueing mod-

els assume that the system has been operating with the

same arrival rate, average service time and other char-

acteristics for a sufﬁciently long period that the prob-

abilistic behaviour of performance measures such as

queue length and customer delay is independent of

when the system is actually observed. Without mea-

surement data, it is not possible to predict stability.

In a stable and fully utilised queueing system

where no signiﬁcant overheads exist, the queue time

will approximate to the execution time. If the queue

time is more than the execution time, it means the

trafﬁc is low. In such scenarios, we can increase the

throughput until the queue time is around the same as

the execution time.

The execution time gives information in terms

of system load. If more processes are scheduled

under given resource constraints, increased context-

switching overheads will occur especially when the

number of processes exceeds the underlying CPU re-

sources. For queue times which are larger than exe-

cution times, this does not necessarily mean that the

trafﬁc is low, but rather it is an indication of the over-

heads of context switching. In this case, increasing

the throughput might exacerbate the problem.

A stable system requires that the execution time

is less than the inter-arrival time so that the queueing

system is stable. While the data items inter-arrival

rates can be measured directly, it is harder to mea-

sure the maximum processing rate of all component

instances. In the case where the execution time or pro-

cess rate is less than the arrival rate, the system will

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

578

Table 1: Performance measurement data at runtime.

Symbol Description

Measured by online normal estimator

the execute time is the time

from start of processing for

each tuple to the end of the

processing

E(u

e,i

),Var(u

e,i

) the mean and variance of the

execute time at component i

the queue time is the mea-

surement of time difference

between the start of every

such processing

E(u

q,i

),Var(u

q,i

) the mean and variance of the

queue time at component i

the data inter-arrival time

E(t

),Var(t

) the mean and variance of the

data items inter-arrival time

for component i

Derived using the above measurements

E(t

)

the mean arrival rate for

component i

q,i

E(u

q,i

)

the service rate including

queue time for component i

e,i

E(u

e,i

)

the processing rate for com-

ponent i

e,i

the optimal trafﬁc intensity

where queue management

cost is negligible for compo-

nent i

√

Var(x)

E(x)

the coefﬁcient of variation of

x ∈



q,i



expect to have increased waiting times. The queue

time in this scenario (u

∗

) reﬂects the total time to ex-

ecute each tuple and includes the execution time and

overheads due to queue management.

3.2.1 Queueing theory in action

For a given set of resources, our approach is to in-

crease the inter-arrival rate by increasing the spout

processes when the queue time is greater than the exe-

cution time. As the queue time decreases with respect

to the execution time under the same resource con-

straints, the system throughput will increase and ex-

hibit higher CPU loads. When no reduction in queue

time occurs at each i

bolt component, the system is

fully utilised i.e as ρ → 1 and this is u

∗

q,i

It is widely known in queueing theory that the

higher the average utilization level, the longer the wait

times. However, it is important to note that this re-

lationship is nonlinear. Unless average utilization is

strictly less than 100%, the system will be unstable

and the queue will continue to grow. Thus, under typ-

ical trafﬁc conditions, we have

E(u

q,i

) = E(u

∗

q,i

) ×e

q,i

where e

q,i

≥ 1 is an excess coefﬁcient.

As given in equation (1), the utilization ρ gives

estimates of the expected waiting time in the queue

for tuples and the average delay approaches inﬁnity as

the utilization approaches one at u

∗

q,i

. The higher the

degree of variability in the system, the worse the de-

lays for the same utilization level. Thus, excess CPUs

have to be provided to maintain stability using e

q,i

the excess coefﬁcient.

If all workers are homogeneous, the quantity a

gives an indication of the number of required servers

or ρ =

cµ

< 1.

In heterogeneous environments, these goals can be

harder to achieve. Assuming effective load-balancing

among parallel instances, the workload is expected to

spread evenly and thus, E(u

q,i

) will be the minimum

queue time of all instances of the i

component.

In heterogeneous environments, the performance

metrics are not necessarily useful because the ma-

chine that runs an instance may happen to have slower

CPU speed than others. Moreover, it is noted that

getting the right measurements is not easy because

they can be machine-dependent. If the conﬁgurations

were calculated based on the slowest machine perfor-

mance, the ‘real’ utilization would be a lot lower be-

cause other machines are capable of faster processing.

However, due to the nature of heterogeneity, conﬁg-

uration using the fastest CPU will result in instabil-

ity at runtime. As shown in later results, instability

will signiﬁcantly penalize throughput of stream pro-

cessing. It is also known that queueing systems have

economies of scale, e.g the smaller the system, the

longer the delays will be for a given utilization level.

Our approach is to over schedule the processes over

heterogeneous resources to exploit the randomness in

spreading out data streams over all resources as well

as scaling up the queueing system.

In so doing, we observe both inter-arrival stabil-

ity and queue time stability. Inter-arrival rate stabil-

ity means that the system keeps up with increases in

throughput. Whereas, queue time stability means that

the context-switching overheads due to over schedul-

ing are not signiﬁcant. The goal is to achieve a queue

time state where the resources are fully utilised for ef-

fective throughput and at the same time support inter-

arrival stability.

Predicting the Stability of Large-scale Distributed Stream Processing Systems on the Cloud

579

Table 2: Host Types and Capacity.

VCPUs Disk RAM Location

Instance 1 2 70 GB 8 GB Melbourne

Instance 2 2 70 GB 8 GB Melbourne

Instance 3 2 70 GB 8 GB Melbourne

Instance 4 4 70 GB 16 GB Melbourne

Instance 5 4 70 GB 16 GB Melbourne

Instance 6 16 70 GB 64 GB Melbourne

Total 30 280 GB 120 GB Melbourne

4 EXPERIMENTS

4.1 Setup

While there are a number of topology-based plat-

forms, in our work we chose Heron (which extends

Apache Storm) due to its popular streaming APIs that

have been adopted by the research community and

their ability to analyse the performance of individual

operators.

This work was based on a single availability

zone and carried out on the Big Systems Research

Group’s 200 node NeCTAR (NeCTAR, 2016) allo-

cation. NeCTAR has a 10Gb backbone and associ-

ated interconnects, hence delays due to networking

congestion are not a factor. However for larger scale

streams with network buffering issues, then such fac-

tors would have to be considered as part of the queue-

ing system/algorithms.

4.2 Preliminary Results

We use a simple topology called ExclamationTopol-

ogy. This topology comes within the Apache Storm

distribution as a topology for testing purposes. The

topology has one spout type and one bolt type ar-

ranged into 2 levels. The logic of the spout randomly

emits one word from a pre-deﬁned set of words. The

logic of the bolt is to append 3 exclamation marks at

the end of each tuple it receives and emits it to the

next level (if there is one).

In combination with back-pressure information,

each instance provides performance data without

modifying the stream processing platform. Each

spout will periodically be sampled using estimators

to get the time between emits. This is a measurement

of the inter-arrival rate where the tuple is injected into

later bolts. Similarly, at each bolt, we periodically

sample the execution time and queue time. As with

emits in spouts, bolt emits also give measurement of

inter-arrival rates for the tuples which ﬂow to later

bolts.

In Figure 3, we observe that the throughput in-

Table 3: Parameters.

Mean (ns) Standard Deviation

Utilization Low High Stable

Spout emit t

e,1

4000 2000 150000

Bolt 1 exec u

e,1

1200 1500 15000

Bolt 1 queue u

q,1

7000 2500 200000

Bolt 1 emit t

e,2

7000 2500 200000

Bolt 2 exec u

e,2

300 500 1500

Bolt 2 queue u

q,2

8000 3200 250000

creases by adjusting the level of parallelism of differ-

ent components based on measurement metrics and

back-pressure monitoring. The measurement results

in Table 3 are collected by stepping through a num-

ber of conﬁgurations. Starting with topology con-

ﬁguration 1-1-1 where each component’s parallelism

is 1 and each component is given 1 CPU. From this

conﬁguration, we obtain the throughput of 7 million

tuples per second (MT/s) consistently and no back-

pressure is detected. We start increasing spout com-

ponent parallelism to 2 and achieve throughput of 7

MT/s as shown for topology 2-1-1 in Figure 3. This

is due to the back-pressure of bolt 1. As shown in

Table 3, the bolt 1 execution time (u

e,1

= 1500) is

lower than the spout emit rate (t

e,1

= 2000) but the to-

tal queue time of bolt 1 (u

∗

q,1

= 2500), which includes

queue management overheads. Thus, in order to have

stability, the utilization (ρ =

cµ

< 1) must be strictly

adhered to. Thus, back-pressure is expected for this

conﬁguration at bolt 1 speciﬁcally.

On the other hand, the conﬁguration topology of

1-2-1 in which bolt 1 has a parallelism of 2 shows that

the throughput is signiﬁcantly increased since the uti-

lization ρ =

cµ

∗

q,1

×2

2500

2000×2

< 1. Furthermore,

the conﬁguration of 2-2-1 does not gain the same

throughput as compared to 1-2-1. In this conﬁgura-

tion, the back-pressure is detected at bolt 2 and it is

predictable because the bolt 2 queue time u

∗

q,2

= 3200

whereas the inter-arrival rate for bolt 2 is t

e,2

= 2500

under high utilization. As soon as we increase paral-

lelism at bolt 2 to conﬁguration 2-2-2, the throughput

is increased again as shown.

Figure 4 illustrates that over-scheduling does not

signiﬁcantly increase throughput when the CPU re-

sources are under high load. When we increase the

parallelism of each component, the throughput can

only be as high as a stable conﬁguration given the

same resources. More importantly, it is noted that sta-

bility is very signiﬁcant for throughput. Even over-

scheduling does not penalize the throughput as much

as unstable conﬁguration provision. As shown in Fig-

ure 4, topology 3-2-2 can only achieve a throughput

of 30 MT/s whereas topology 3-3-2 has a through-

put above 36 MT/s and topology 2-2-2 has throughput

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

580

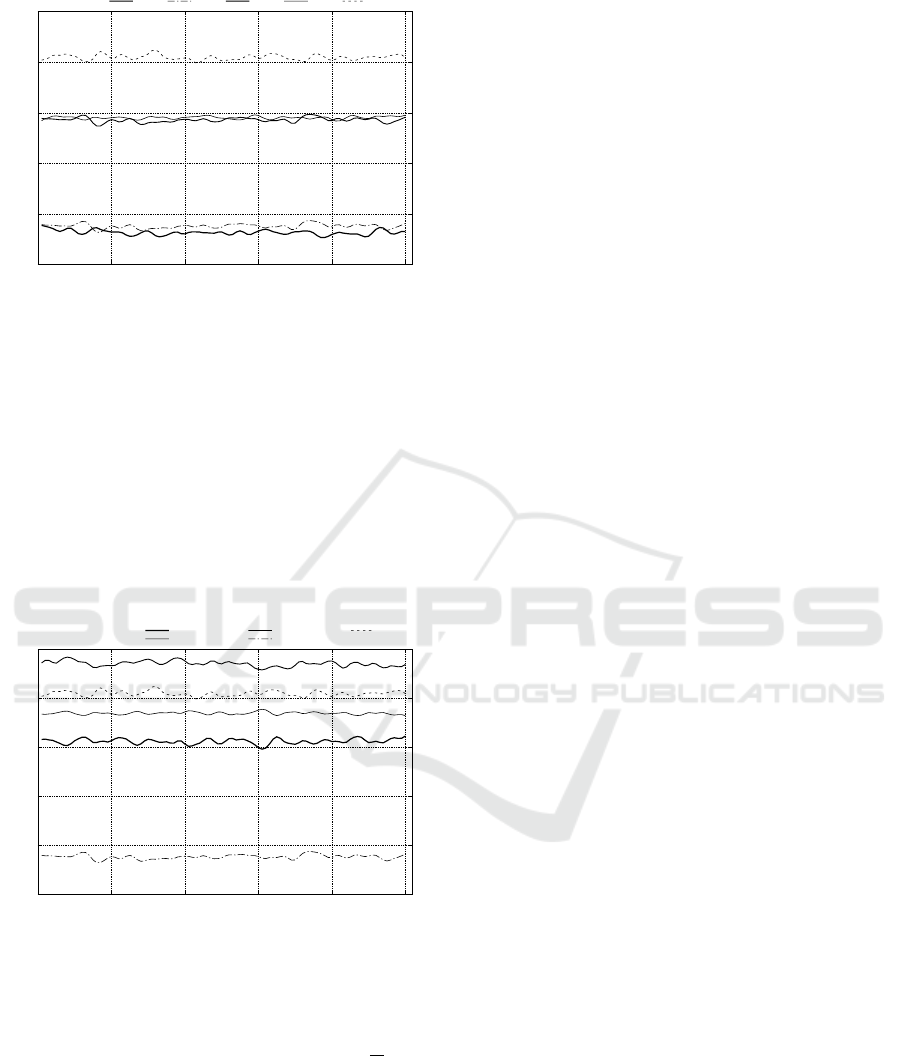
0 20 40 60 80 100

Throughput (M/s)

Run Time (m)

1-1-1

2-1-1 1-2-1 2-2-1 2-2-2

Figure 3: The throughput increases by adjusting the level of

parallelism of different components based on measurement

metrics and back-pressure monitoring. Each topology con-

ﬁguration is referred to by the number of instances at spout

and bolts iteratively, e.g, 1-2-1 indicates topology conﬁgu-

ration of 1 spout instance, 2 instances for bolt level 1 and 1

instance of bolt level 2.

well above this level. Increasing resources for unsta-

ble conﬁgurations such as 3-3-2 only gains marginal

throughput beneﬁts. Speciﬁcally, it is shown in Figure

4 that when we use 4 CPUs and 6 CPUs to run topol-

ogy 2-2-2 and 3-3-2 respectively, the throughputs are

42 MT/s and 48 MT/s.

0 20 40 60 80 100

Throughput (M/s)

Run Time (m)

3-2-2

3-3-2

3-3-2 (6 cpus)

2-1-1

2-2-2

Figure 4: Throughput increase with performance metrics.

After obtaining the measurement data in Table 3,

we want to scale this topology to make use of more

CPUs and different machine types as shown in Ta-

ble 2. Following the previous equation ρ =

cµ

< 1,

we identify conﬁguration 5-7-10 as a stable conﬁgura-

tion. The results have several important implications.

First, we use 19 CPUs to run 22 processes which il-

lustrates that we have over-scheduled processes over

available resources to achieve higher utilization. Sec-

ond, we monitor for back-pressure to show that the

conﬁguration is in fact stable even for heterogeneous

environments. Third, to ensure that we have conﬁ-

dence in the measurements, we run the topology three

times. The ﬁrst two times have a higher throughput

of 70 MT/s and no back-pressure, whilst for the third

run, the throughput drastically reduces to 35 MT/s due

to back-pressure.

5 CONCLUSIONS

Back-pressure rates are essential to identify stream

processing systems that are under-performing. This

has signiﬁcant implications on cost-efﬁciency to

users. Furthermore, once back-pressure happens, the

latency of stream processing is dominated by the time

for buffers to clear up. As such, preventing bottle-

necks in such environments is mandatory for system

performance. With our approach, stable conﬁgura-

tions provide effective throughput while minimizing

resource consumption. This offers an opportunity to

address the issues of resource provisioning and par-

allelization in performance-oriented contexts. This is

especially important to public pay-as-you-go Cloud

environments.

6 FUTURE WORK

There are several extensions to this work including

cost efﬁciency and application and infrastructure dy-

namism. With regard to cost efﬁciency, it is important

to users that the monetary cost of using Cloud-based

infrastructure is balanced with the actual system per-

formance. This includes many aspects of stream pro-

cessing applications. In future work, we shall con-

sider cost models that take into account service level

agreements and include more comprehensive models

for optimising throughput and cost. This includes the

richness of Cloud costing approaches, e.g spot prices

and VM reservation etc.

Any stream processing system expects to have

varying workloads throughout long running execu-

tions. In a normal situation, the workload may be in

some range which can be estimated based on previ-

ous experience. Changes in workload can arbitrarily

happen however and may be a result of either a tem-

porary outage or permanent increase/decrease in per-

formance. For temporary outages and especially in

short periods of time, this should not result in any sig-

niﬁcant changes of resources other than memory for

buffering imbalances. For other cases, it may be de-

sirable that a more general approach supporting ser-

vice level agreements (SLAs) is proposed in order to

guarantee that the required QoS is actually achieved

(Lohrmann et al., 2015; Heinze et al., 2014b; Xu

Predicting the Stability of Large-scale Distributed Stream Processing Systems on the Cloud

581

et al., 2016).

REFERENCES

Abadi, D. J., Carney, D., C¸ etintemel, U., Cherniack, M.,

Convey, C., Lee, S., Stonebraker, M., Tatbul, N., and

Zdonik, S. (2003). Aurora: a new model and ar-

chitecture for data stream management. The VLDB

JournalThe International Journal on Very Large Data

Bases, 12(2):120–139.

Aniello, L., Baldoni, R., and Querzoni, L. (2013). Adaptive

online scheduling in storm. In Proceedings of the 7th

ACM international conference on Distributed event-

based systems, pages 207–218. ACM.

Cardellini, V., Grassi, V., Lo Presti, F., and Nardelli, M.

(2015). Distributed qos-aware scheduling in storm. In

Proceedings of the 9th ACM International Conference

on Distributed Event-Based Systems, pages 344–347.

ACM.

Chatzistergiou, A. and Viglas, S. D. (2014). Fast heuristics

for near-optimal task allocation in data stream pro-

cessing over clusters. In Proceedings of the 23rd ACM

International Conference on Conference on Informa-

tion and Knowledge Management, pages 1579–1588.

ACM.

Condie, T., Conway, N., Alvaro, P., Hellerstein, J. M.,

Elmeleegy, K., and Sears, R. (2010). Mapreduce on-

line. In Nsdi, volume 10, page 20.

Dean, J. and Ghemawat, S. (2008). Mapreduce: simpliﬁed

data processing on large clusters. Communications of

the ACM, 51(1):107–113.

Eidenbenz, R. and Locher, T. (2016). Task allocation

for distributed stream processing. arXiv preprint

arXiv:1601.06060.

Gedik, B., Schneider, S., Hirzel, M., and Wu, K.-L. (2014).

Elastic scaling for data stream processing. IEEE

Transactions on Parallel and Distributed Systems,

25(6):1447–1463.

Heinze, T., Aniello, L., Querzoni, L., and Jerzak, Z.

(2014a). Cloud-based data stream processing. In

Proceedings of the 8th ACM International Conference

on Distributed Event-Based Systems, pages 238–245.

ACM.

Heinze, T., Jerzak, Z., Hackenbroich, G., and Fetzer, C.

(2014b). Latency-aware elastic scaling for distributed

data stream processing systems. In Proceedings of

the 8th ACM International Conference on Distributed

Event-Based Systems, pages 13–22. ACM.

Heinze, T., Pappalardo, V., Jerzak, Z., and Fetzer, C.

(2014c). Auto-scaling techniques for elastic data

stream processing. In Data Engineering Workshops

(ICDEW), 2014 IEEE 30th International Conference

on, pages 296–302. IEEE.

Heinze, T., Roediger, L., Meister, A., Ji, Y., Jerzak, Z., and

Fetzer, C. (2015). Online parameter optimization for

elastic data stream processing. In Proceedings of the

Sixth ACM Symposium on Cloud Computing, pages

276–287. ACM.

Hu, H., Wen, Y., Chua, T.-S., and Li, X. (2014). Toward

scalable systems for big data analytics: A technology

tutorial. IEEE Access, 2:652–687.

Jamshidi, P. and Casale, G. (2016). An uncertainty-aware

approach to optimal conﬁguration of stream process-

ing systems. In Modeling, Analysis and Simulation

of Computer and Telecommunication Systems (MAS-

COTS), 2016 IEEE 24th International Symposium on,

pages 39–48. IEEE.

Kingman, J. (1961). The single server queue in heavy traf-

ﬁc. In Mathematical Proceedings of the Cambridge

Philosophical Society, volume 57, pages 902–904.

Cambridge Univ Press.

Kleppmann, M. and Kreps, J. (2015). Kafka, samza and

the unix philosophy of distributed data. IEEE Data

Engineering Bulletin.

Krempl, G.,

Zliobaite, I., Brzezi

nski, D., H

ullermeier, E.,

Last, M., Lemaire, V., Noack, T., Shaker, A., Sievi,

S., Spiliopoulou, M., et al. (2014). Open challenges

for data stream mining research. ACM SIGKDD ex-

plorations newsletter, 16(1):1–10.

Kulkarni, S., Bhagat, N., Fu, M., Kedigehalli, V., Kellogg,

C., Mittal, S., Patel, J. M., Ramasamy, K., and Taneja,

S. (2015). Twitter heron: Stream processing at scale.

In Proceedings of the 2015 ACM SIGMOD Interna-

tional Conference on Management of Data, pages

239–250. ACM.

Lohrmann, B., Janacik, P., and Kao, O. (2015). Elas-

tic stream processing with latency guarantees. In

Distributed Computing Systems (ICDCS), 2015 IEEE

35th International Conference on, pages 399–410.

IEEE.

NeCTAR (2016). The National e-Research Collaboration

Tools and Resources project. https://nectar.org.

au/.

Neumeyer, L., Robbins, B., Nair, A., and Kesari, A. (2010).

S4: Distributed stream computing platform. In 2010

IEEE International Conference on Data Mining Work-

shops, pages 170–177. IEEE.

Pietzuch, P., Ledlie, J., Shneidman, J., Roussopoulos, M.,

Welsh, M., and Seltzer, M. (2006). Network-aware

operator placement for stream-processing systems. In

22nd International Conference on Data Engineering

(ICDE’06), pages 49–49. IEEE.

Toshniwal, A., Taneja, S., Shukla, A., Ramasamy, K., Pa-

tel, J. M., Kulkarni, S., Jackson, J., Gade, K., Fu, M.,

Donham, J., et al. (2014). Storm@ twitter. In Proceed-

ings of the 2014 ACM SIGMOD international confer-

ence on Management of data, pages 147–156. ACM.

Xu, L., Peng, B., and Gupta, I. (2016). Stela: Enabling

stream processing systems to scale-in and scale-out

on-demand. In IEEE International Conference on

Cloud Engineering (IC2E).

Zaharia, M., Chowdhury, M., Franklin, M. J., Shenker, S.,

and Stoica, I. (2010). Spark: cluster computing with

working sets. HotCloud, 10:10–10.

Zikopoulos, P., Eaton, C., et al. (2011). Understanding

big data: Analytics for enterprise class hadoop and

streaming data. McGraw-Hill Osborne Media.

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

582