A Virtual Environment to Support Classroom Face-to-Face Teaching
of Engineering Courses
Ana Paula Ladeira
1
, Juliana Capanema Ferreira Mendonca
1
, Osmar Ventura Gomes
1
,
Celso Peixoto Garcia
2
and Bráulio Roberto Gonçalves Marinho Couto
3
1
Instituto Politécnico (IPOLI), Centro Universitário UNA, Av. Professor Mário Werneck, 1685, Belo Horizonte, Brazil
2
UNISOCIESC Educação e Tecnologia, Rua Albano Schmidt, 3333, Joinville, Brazil
3
Instituto de Engenharia e Tecnologia (IET), Centro Universitário de Belo Horizonte - UniBH,
Av. Professor Mário Werneck, 1685, Belo Horizonte, Brazil
Keywords: Online Tool, Higher Education, Computer Assisted Learning.
Abstract: The objective of our study is to answer three questions: a) How to build a low cost online teaching tool to
support face-to-face classrooms of introductory engineering disciplines? b) What is the effectiveness of the
use of virtual environment in promoting learning? c) Does the number of accesses by the students onto the
virtual environment increases their grades and reduces their failure in introductory engineering disciplines?
The online teaching tool was developed in Moodle environment, being composed by three components for
each discipline: a) video lectures, b) video lessons explaining how to solve proposed exercises, c) a list of
unsolved exercises. To evaluate the effectiveness of the virtual environment we collected data during Jan-
Dec/2016, amongst engineer students. The main predictor variable, the number of access to the online
support tool, was firstly evaluated in univariate analysis. Multiple linear regression was used to assess how
the outcome of “final grade” were influenced by all predictors variables together, in a multivariate way. The
number of accesses by the students onto the virtual environment increases their grades and reduces their
failure in introductory engineering disciplines, especially for General Chemistry, Differential Calculus,
Physics Electricity and Algorithms.
1 INTRODUCTION
Any country that intends to be serious about
building a strong economy and be successful
through the 21th century must produce hundreds of
thousands of engineers during the next decade. How
can we get there if the majority of students give up
their bachelor courses right after beginning? The
first two years of engineering are hard and, in
essence, do not inspire any student! Actually, high-
performing students frequently cite uninspiring
introductory courses as a factor in their choice to
quit (PCAST, 2012). In this paper we present a
virtual environment to support face-to-face teaching
in introductory disciplines of engineering courses.
Many initiatives to improve the first years of
engineering education and courses other than
engineering have been developed recently
(Greenhalgh, 2001). Most initiatives proposed lately
are based on computer supported tools and active
learning methods as case studies, problem-based
learning, problem sets in groups, concept mapping,
peer instruction, analytical challenge before lecture,
computer simulations and games dynamics (Saxe,
Braddy, Bailer, 2015; Sim, 2015; Boada, Soler,
Prados, Poch, 2004). Success of active teaching
practices and intelligent tutoring system has been
validated (Roll, Aleven, McLaren, Koedinger,
2011). For example, students in traditional lecture
courses are twice as likely to leave engineering and
three times as likely to drop out of college entirely
compared with students taught using active learning
techniques. Besides, students in a face-to-face class
that used active learning methods learned twice as
much as those taught in a traditional class, as
measured by test results (PCAST, 2012).
Unfortunately, in spite of all evidences in favor
of active learning methods, we have not yet achieved
to broadly apply such teaching practice to
engineering courses. Some isolated initiatives are
underway in a private higher education institution
from Brazil, with about ten thousand engineering
Ladeira, A., Mendonca, J., Gomes, O., Garcia, C. and Couto, B.
A Virtual Environment to Support Classroom Face-to-Face Teaching of Engineering Courses.
DOI: 10.5220/0006358904990504
In Proceedings of the 9th International Conference on Computer Supported Education (CSEDU 2017) - Volume 1, pages 499-504
ISBN: 978-989-758-239-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
499

students. However, the majority of our students are
enrolled in traditional lecture courses. In fact, this is
the reality of most engineering courses in Brazil and
in other countries as well. Face-to-face engineering
courses still need support environment to help
students to improve their learning processes in such
classrooms.
The objective of our study is to answer three
questions: a) How to build a low cost online
teaching/learning tool to support face-to-face
classrooms of introductory engineering disciplines?
b) What is the effectiveness of the use of virtual
environment in promoting learning? c) The number
of accesses by the students onto the virtual
environment increases their grades and reduces their
failure in introductory engineering disciplines?
2 METHODS
The online teaching tool to support face-to-face
classrooms was developed in Moodle environment
(https://moodle.org/). The objective was to build an
online tutoring system based on the idea of passive
tutoring, understood as a way of self-regulated
learning. For each discipline involved, chosen
among those introductory to engineering, an
asynchronous learning course was developed, free
and not obligatory (Haslam, 2014). Students were
encouraged to access the environment that is
available through the Internet, 24 hours a day, 7 days
a week, being composed by three components:
a) video lectures with the theories of the
discipline,
b) video lessons that explain how to solve a
representative list of exercises from the
discipline, one video for each exercise
chosen,
c) a list of unsolved exercises.
The way in which the Moodle was introduced to
the students was not directly integrated with the
face-to-face teaching. Actually, we made a kind of
marketing using email to introduce the environment
to all students and professors. To evaluate the
effectiveness of the virtual environment in
promoting learning, we collected data during
January and December, 2016, amongst engineer
students in a private university from Belo Horizonte,
Brazil. Two outcome variables were chosen for
analysis: the final grade of the student, varying from
zero to 100 points, and a categorical variable, the
final result in the discipline (approved versus not-
approved). Predictors or independent variables
evaluated: the number of accesses by students onto
the specific online discipline environment, varying
from zero to “n” accesses, student age (years),
student gender (male versus female), percentage of
missed face-to-face class, from a specific discipline
(0 to 100%), number of disciplines per semester,
varying from one to “k” disciplines, course schedule
or course shift (day versus night), and type of high
school background of the student before he enters
university (private school versus public school). If
the discipline involved had one or more online class,
the type of course (face-to-face versus distance
learning), was analyzed as a categorical variable
also. The main predictor variable, the number of
access to the online support tool, was firstly
evaluated in univariate analysis by Mann-Whitney
two-sample test. Multiple linear regression was used
to assess how the outcome “final grade” were
influenced by all predictors variables together, in a
multivariate way (Altman, 1991). All analysis were
done by bilateral statistical hypothesis testing with a
significance level of 5% ( = 0.05).
3 RESULTS
Presently, the virtual environment developed allows
support for seven disciplines: Geometry, General
chemistry, Differential calculus, Physics
(mechanics), Algorithms, Integral calculus, and
Physics (electricity). It is available for all students
and professors after user authentication in the link
www.una.br. Data from January to December 2016,
during two academic semesters, were used to
investigate the effectiveness of the online supporting
tool. We gathered information about all students that
participated at least in one class of any of the seven
disciplines elected, during the first or the second
semester or both. A total of 3,056 different students
could use the environment in one year. The cost for
teachers to the implementation of the educational
resources was about EUR 1,000 per discipline,
totaling €7,000 which gives a cost of €2.30 per
student. It was necessary about four months to
produce all materials. After that, there is almost no
cost to maintain the services. The number of
students per discipline varied from 1,170 in Physics
(mechanics) to 657 in General chemistry (Table 1).
Students’ behavior in regarding to the access of the
virtual tool varied greatly among the disciplines:
standard deviation was much higher than its
respective mean from all seven disciplines (Table 1).
Despite all the campaign encouraging students to use
the environment, the majority did not access the
CSEDU 2017 - 9th International Conference on Computer Supported Education
500

online tool anytime during both semesters. Actually,
for all disciplines the majority of student did not
access the virtual tool anytime. Percentage for each
discipline of students that did not use the online tool
are: 63% (Geometry), 64% (Differential calculus),
65% (Physics electricity), 70% (Integral calculus),
71% (General chemistry), 74% (Physics mechanics),
and 75% (Algorithms).
Table 1: Number of access by each discipline during 2016
(n - total of students, mean access and standard deviation):
results present very high variability in this predictor,
suggesting students that behave completely different in
terms of use of the virtual environment.
Discipline n Mean Std Dev
Physics (mechanics) 1,170 4.4 10.9
General chemistry 657 5.8 14.4
Integral calculus 1052 6.0 16.3
Algorithms 710 6.1 17.3
Physics (electricity) 828 13.7 30.4
Differential calculus 828 13.8 30.5
Geometry 835 14.7 36.1
Note: standard deviation quantify the variability of the
number of access by each discipline. Standard deviation
higher than the mean indicates that the data are spread out
over a wider range of values.
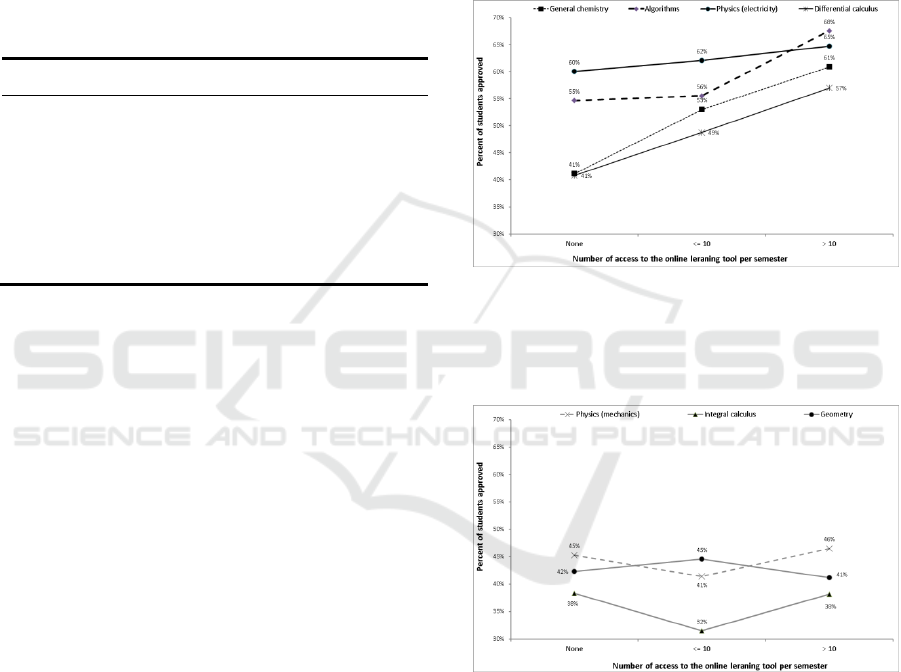
Figure 1 and 2 represent graphical analysis of the
profile of access to the virtual environment as a
protective factor against failure in each discipline.
From the seven disciplines, four suggest good
effectiveness of the online tool and three showed
unsuccessful. In a univariate analysis (Table 2),
access for Physics (electricity) it was not
significantly associated with the student’s success.
Tables 3.1 to 3.7 contain multivariate analysis
for the seven disciplines. By using this analysis we
can evaluate the joined effects of all predictors as
possible protective factors, that rising the students’
final grade, and risk factors, which decrease the final
grade of each discipline. Similar to other studies
(Senior, 2008), the most important risk factor for all
the seven face-to-face classes is the percentage of
missed classes. Surprisingly, when night course shift
was significantly associated with final grade, it was
identified as a protective factor for failure on
Physics mechanics (Table 3.4), Differential calculus
(Table 3.6) and Algorithms (Table 3.7).
The more disciplines to which a student attends
along the semester, the better tends to be their final
grades in Geometry (Table 3.2), Physics mechanics
(Table 3.4), Integral calculus (Table 3.5), and
Algorithms (Table 3.7). To attend more disciplines
during a semester seems to force the student to
dedicate more to achieve success during that
semester! The virtual environment is a significantly
support system for classroom face-to-face teaching
of four disciplines: General chemistry (Table 3.1),
Physics electricity Table 3.3), Differential calculus
(Table 3.6) and Algorithms (Table 3.7).
Unfortunately, the online support tool did not work
very well on three distinct situations: Geometry
(Table 3.2), Physics mechanics (Table 3.4) and
Integral calculus (Table 3.5).
Figure 1: Results of the profile of number of access and
rate of approval in each discipline suggest effectiveness of
the environment to prevent failure in General chemistry,
Differential calculus, Algorithms, and Physics
(electricity).
Figure 2: Three disciplines seem to be not affected by the
number of access to the online tool: rate of approval in
Integral calculus, Physics (mechanics) and Geometry were
constant, independently of the use of the virtual
environment.
A Virtual Environment to Support Classroom Face-to-Face Teaching of Engineering Courses
501

Table 2: Impact of number of access to the online tool by
each discipline against the outcome “final result”
(approved versus not approved): in a univariate analysis,
this predictor was significantly protective factor against
failure in three disciplines (General chemistry, Algorithms
and Differential calculus).
Discipline
Final
result:
approved
?
N Mean s
p
value
Physics
mechanics
No 644 4 11 0.916
Yes 526 4 11
General
chemistry
No 355 4 12 <0.01
Yes 302 7 17
Integral
calculus
No 659 6 15 0.474
Yes 393 7 18
Algorithms No 307 4 12 0.029
Yes 403 8 20
Physics
electricity
No 319 11 25 0.128
Yes 509 15 33
Differential
calculus
No 448 9 23 <
0.01
Yes 380 19 37
Geometry No 482 13 35 0.611
Yes 353 17 38
Obs.: s = standard deviation.
p value by Mann-Whitney two-sample test
p value < 0.05 = statistically significantly results.
Table 3.1: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
General chemistry. Number of access to the virtual
environment and number of disciplines per semester are
significantly protective factors, raising final grade of
General chemistry. Student’s age and, mainly, the
percentage of face-to-face missed classes are significantly
risk factors for the final grade.
Predictor b s.e.
p
value
Constant 60.81 5.2
Chemistry: #accesses 0.21 0.1 0.000
High school in private school 0.49 1.9 0.801
#disciplines per semester 2.77 0.6 0.000
Age (years) -0.35 0.1 0.013
Gender = female -0.97 1.7 0.577
Night course -2.99 1.8 0.105
Missed classes (%) -206 11.1 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
Table 3.2: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Geometry. Number of access to the virtual environment
does not affect the students’ final grade. Number of
disciplines per semester and private high school are
significantly protective factors, raising final grade of
Geometry. Student’s age and, mainly, the percentage of
face-to-face missed classes are significantly risk factors
for the final grade.
Predictor
b s.e.
p
value
Constant
64.15 4.4
Geometry: #accesses
0.03 0.0 0.111
High school in private school
3.56 1.6 0.025
#disciplines per semester
1.49 0.6 0.013
Age (years)
-0.26 0.1 0.044
Gender = female
0.56 1.5 0.702
Night course
2.59 1.7 0.125
Missed classes (%)
-116 3.9 0.000
Obs.: b = regression coefficients;
s.e. = standard error.
Table 3.3: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Physics (electricity). Number of access to the virtual
environment is a significantly protective factor, raising
final grade of Physics electricity. Only the percentage of
face-to-face missed classes is a significantly risk factor for
the final grade.
Predictor b s.e.
p
value
Constant 74.77 4.3
Physics electricity: #accesses 0.04 0.0 0.017
High school in private school 1.65 1.3 0.212
#disciplines per semester 0.24 0.5 0.633
Age (years) -0.19 0.1 0.118
Gender = female 0.27 1.2 0.814
Night course -2.92 1.6 0.068
Missed classes (%) -134 8.1 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
Besides using the access to the online tool as a
predictor for the student final grade, we collected
data from six more variables that were used to build
the multiple linear regression models. Coefficients
of determination (R
2
) were calculated for the linear
models. Low value of R
2
indicates poor model. All
seven models built did not properly predict future
values of any final grade (Table 4): R
2
varied from
CSEDU 2017 - 9th International Conference on Computer Supported Education
502

26% to 52%. This result strongly suggests that is
necessary to find more predictors in an attempt to fit
the final grade data.
Table 3.4: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Physics (mechanics). Number of access to the virtual
environment does not affect the students’ final grade.
Number of disciplines per semester and, surprisingly,
night shift course are significantly protective factors,
raising final grade of Physics mechanics. Only the
percentage of face-to-face missed classes is a significantly
risk factor for the final grade.
Predictor b s.e.
p
value
Constant 49.86 4.1
Physics mechanics: #accesses 0.08 0.1 0.163
High school in private school 2.00 1.5 0.170
#disciplines per semester 3.75 0.5 0.000
Age (years) -0.22 0.1 0.071
Gender = female -0.45 1.3 0.738
Night course 3.18 1.5 0.040
Missed classes (%) -131 5.8 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
Table 3.5: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Integral calculus. Number of access to the virtual
environment does not influence the students’ final grade.
Only the number of disciplines per semester is a
significantly protective factor, raising the final grade of
Integral calculus. The percentage of face-to-face missed
classes is significantly risk factor for the final grade.
Predictor b s.e.
p
value
Constant 41.48 4.74
Integral calculus: #accesses 0.05 0.04 0.305
High school in private school -1.39 1.69 0.412
#disciplines per semester 3.65 0.61 0.000
Age (years) -0.04 0.13 0.766
Gender = female 1.55 1.58 0.326
Night course -0.78 1.71 0.649
Missed classes (%) -90 4.61 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
Table 3.6: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Differential calculus. Number of access to the virtual
environment and, surprisingly, night shift course are
significantly protective factors, raising final grade of
Differential calculus. Student’s age and, mainly, the
percentage of face-to-face missed classes are significantly
risk factor for the final grade.
Predictor b s.e.
p
value
Constant 63.06 4.93
Differential calculus: #access 0.07 0.02 0.008
High school in private school 2.26 1.89 0.231
#disciplines per semester 0.63 0.54 0.249
Age (years) -0.33 0.13 0.013
Gender = female 1.15 1.63 0.480
Night course 4.53 1.60 0.005
Missed classes (%) -103 4.81 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
Table 3.7: Multiple linear regression model for
multivariate analysis of the influence of all predictors
together onto the outcome “final grade”: analysis of
Algorithms. Number of access to the virtual environment,
number of disciplines per semester and, surprisingly, night
shift course are significantly protective factors, raising
final grade of Algorithms. Student’s age and, mainly, the
percentage of face-to-face missed classes are significantly
risk factor for the final grade. When the course is offered
as a distance learning class is also a risk factor for the final
grade of Algorithms, reducing students’ grade.
Predictor b s.e.
p
value
Constant 44.40 6.75
Algorithms: #accesses 0.17 0.06 0.006
Distance education course -17,6 3,80 0,000
High school in private school 1.98 2.29 0.388
#disciplines per semester 5.02 0.71 0.000
Age (years) -0.34 0.17 0.050
Gender = female -2.65 2.15 0.219
Night course 6.873 3.47 0.048
Missed classes (%) -220 17.27 0.000
Obs.: b = regression coefficients; s.e. = standard error.
p value < 0.05 = statistically significantly results.
A Virtual Environment to Support Classroom Face-to-Face Teaching of Engineering Courses
503

Table 4: Goodness-of-fit of the multiple linear regression
models: statistic R
2
, that assess crudely how well the
model fits data overall, is poor for the seven models.
Discipline & Regression model R
2
Geometry 52%
General chemistry 45%
Differential calculus 41%
Physics (mechanics) 33%
Algorithms 32%
Integral calculus 32%
Physics (electricity) 26%
4 CONCLUSIONS
Regarding the questions presented in this paper, we
can promptly answer that is possible to build an
effective low cost online teaching/learning tool to
support face-to-face classrooms of introductory
engineering disciplines. The number of accesses by
the students onto the virtual environment increases
their grades and reduces their failure in introductory
engineering disciplines, especially for General
chemistry, Differential calculus, Physics electricity
and Algorithms. Unfortunately, the online tool does
not support students of Geometry, Physics
mechanics nor Integral calculus. For these
disciplines, we understand that it is necessary to
reformulate its online contents, i.e., we need to
review all video lectures and the video lessons that
explain how to solve exercises, specifically for these
three disciplines. The main conclusion of this paper
refers to the fact that it is really possible to use an
online education support system in a way that
students from face-to-face classes can improve their
chances of success in introductory disciplines of
engineering.
ACKNOWLEDGEMENTS
The authors are very thankful to all professors that
developed each disciplines’ content in the virtual
tutoring environment: Naísses Lima (Algorithms),
Paloma Campos (Differential calculus), Rodnei
Marques (Integral calculus), Sérgio Vieira (Physics
electricity), Alexandra Maia (Geometry), Gisele
Mendes (General chemistry), and Marina Valentin
(Physics mechanics).
REFERENCES
Altman, D.G., 1991. Practical statistics for medical
research. Chapman & Hall, 610p.
Boada, I., Soler, J., Prados, F., Poch, J. 2004. A
teaching/learning support tool for introductory
programming courses. In the Proceedings of the Fifth
International Conference on Information Technology
Based Higher Education and Training. ITHET, 604-
609. Retrieved from http://www.academia.edu/
2952178/A_teaching_learning_support_tool_for_intro
ductory_programming_courses.
Greenhalgh, T., 2001. Computer assisted learning in
undergraduate medical education. BMJ, 322:40.
Retrieved from http://www.bmj.com/content/322/
7277/40.
Haslam, J., 2014. Synchronous vs. Asynchronous Classes.
eLearners. Retrieved from https://
www.elearners.com/education-resources/degrees-and-
programs/synchronous-vs-asynchronous-classes/
PCAST - President’s Council of Advisors on Science and
Technology, 2012. Engage to Excel: Producing One
Million Additional College Graduates with Degrees in
Science, Technology, Engineering, and Mathematics.
Washington, DC: White House Office of Science and
Technology Policy. Retrieved from https://
www.whitehouse.gov/sites/default/files/microsites/ost
p/fact_sheet_final.pdf.
Roll, I., Aleven, V., McLaren, B. M., Koedinger, K. R.,
2011. Improving students’ help-seeking skills using
metacognitive feedback in an intelligent tutoring
system. Learning and Instruction, 21(2), 267-280.
Retrieved from http://www.cs.cmu.edu/afs/
cs.cmu.edu/Web/People/bmclaren/pubs/RollEtAl-
ImprovingHelpSeekingWithITS-LandI2011.pdf.
Saxe, K., Braddy, L., Bailer, J., et al., 2015. A common
vision for undergraduate mathematical sciences
programs in 2025. Mathematics Association of
America. Retrieved from http://www.maa.org/sites/
default/files/pdf/CommonVisionFinal.pdf.
Senior, B.A., 2008. Correlation between absences and
final grades in a college course. Proceedings of the
44th Annual Conference of the Associated Schools of
Construction, Auburn, Alabam. Retrieved from
http://ascpro0.ascweb.org/archives/cd/2008/paper/CE
UE275002008.pdf.
Sim, T.Y., 2015. Exploration on the impact of online
supported methods for novice programmers. e-
Learning e-Management and e-Services (IC3e) 2015
IEEE Conference. 158-162. Retrieved from
http://ieeexplore.ieee.org/abstract/document/7403505/
CSEDU 2017 - 9th International Conference on Computer Supported Education
504