
From Group-by to Accumulation: Data Aggregation Revisited
Alexandr Savinov
Bosch Software Innovations GmbH, Stuttgarterstr. 130, 71332 Waiblingen, Germany
Keywords: Data Processing, Grouping and Aggregation, Data Accumulation, Concept-oriented Model.
Abstract: Most of the currently existing query languages and data processing frameworks rely on one or another form
of the group-by operation for data aggregation. In this paper, we critically analyze properties of this
operation and describe its major drawbacks. We also describe an alternative approach to data aggregation
based on accumulate functions and demonstrate how it can solve these problems. Based on this analysis, we
argue that accumulate functions should be preferred to group-by as the main operation for data aggregation.
1 INTRODUCTION
1.1 Data Aggregation
If we ignore how data is organized in a data
management system, then data processing of any
kind can be reduced to computing new data values
from the existing or previously computed values by
applying some operations. These data processing
operations can be broken into two major categories.
Operations from the first category (which can be
referred to as horizontal operations) process data
values stored in individual elements like tuples,
objects, documents or records which can be directly
accessed from the source data element. Therefore,
these operations are used for relatively simple
record-level transformations as opposed to
transformations based on subsets of records
described below. The possibility to access all the
necessary arguments of such an operation is based
on some mechanism of connectivity. The dominant
approach to connectivity relies on the relational join
operation but other models and frameworks use
references or links. The result of such operations is
always computed from one or more attribute values
of related elements (but not subsets). A typical
example is computing the amount for an order item
given its price and quantity attributes:
SELECTi.price*i.quantityASamount
FROMOrderItemsASi
A horizontal operation can be formally
represented as a function of single-valued
arguments. In the above example, such a function
can be written as the expression
amount(i)=i.price*i.quantity. Here the
output value is computed as a product of two input
values which are accessed via attributes of this same
record. In more complex cases, the arguments of the
operation could be accessed using intermediate
records but they still would be single values rather
than subsets. For example, if the item price is stored
in another table then this expression could be written
as follows:
amount(i)=i.product.price*
i.quantity
. Most of the difficulties of this simple
and natural approach are due to the connectivity
mechanism which is responsible for providing
access to related elements and data values (dot
notation in the above example). In particular, the use
of relational join makes it especially difficult
(Savinov, 2016a) to directly apply such functional
representation for computing new data values.
Operations from the second category (also
referred to as vertical or aggregate operations)
process data values stored in subsets of elements by
aggregating multiple input values into one output
value. These subsets, normally called groups, are
represented and produced by the mechanism of
grouping which defines how elements belong to one
group depending on their properties. Grouping is as
important for vertical operations as connectivity is
for horizontal operations because they both
determines what elements will be processed and how
these elements will be accessed. The dominant
approach to grouping assumes that all records
having the same value of some attribute(s) belong to
one group. For example, the total amount of one
370
Savinov, A.
From Group-by to Accumulation: Data Aggregation Revisited.
DOI: 10.5220/0006359803700379
In Proceedings of the 2nd International Conference on Internet of Things, Big Data and Security (IoTBDS 2017), pages 370-379
ISBN: 978-989-758-245-5
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

order consisting of a number of order items can be
computed using the following SQL query:
SELECTSUM(i.amount)AStotal
FROMOrderItemsASi
GROUPBYi.order//Groupdefinition
A vertical (aggregation) operation can also be
formally represented as a function. However, this
function takes set-valued arguments rather than
single values in the case of horizontal operations.
For example, in the above example this function is
written as the following expression:
total(group)=SUM(group) where group is a
subset of order items from the
OrderItems table
belonging to one order. Vertical operations are used
for complex data processing and analysis. They are
traditionally more difficult to understand and use
than horizontal operations, and most of the
difficulties are due to the grouping mechanism and
user-defined aggregate functions.
1.2 Related Work
Relational algebra (Codd, 1970) is intended for
manipulating relations, that is, it provides operations
which take relations as input and produce a new
relation as output. This formalism does not provide
dedicated means for data aggregation just because it
belongs to a set-oriented approach where the main
unit is that of a set rather than a value. In particular,
it is not obvious how to define and manipulate
dynamically defined groups of tuples, that is, subsets
which depend on values in other tuples.
Theoretically, it could be done by introducing nested
relations, complex objects and relation-valued
attributes (see e.g. Abiteboul et al., 1989) but any
such modification makes the model significantly
more complicated and actually quite different from
the original relational approach.
Since aggregation is obviously a highly
important operation, these functions were introduced
in early relational DBMSs and its support was added
to SQL (Database Languages|SQL, 2003) in the
form of a dedicated group-by operator. Importantly,
group-by is not a formal part of the relational model
but rather is a construct of a query language that
supports this model but can also support other data
models. In other words, group-by is not a specific
feature of the relational model and actually does not
rely on its main principles. In particular, it has been
successfully implemented in many other models,
query languages, database management systems and
data processing frameworks. Nowadays, in the
absence of other approaches, group-by is not merely
a formal operation but rather a dominant pattern of
thought for the concept of data aggregation.
An alternative approach to aggregation is based
on using correlated queries where the inner query is
parameterized by a value provided by the outer
query. This parameter is interpreted as a group
identifier so that the outer query iterates through all
the groups while the inner query iterates through the
group members by aggregating all of them into one
value. Yet, this approach still needs the group-by
operator but it is interesting from the conceptual
point of view because it better separates different
aspects used during data aggregation.
Aggregation is also a crucial part of the map-
reduce data processing paradigm (Dean and
Ghemawat, 2004) where map is a horizontal
operation and reduce is a vertical operation. Its main
advantage is that it allows for almost arbitrarily
complex data processing scenarios due to the
complete control over data aggregation and the
natively supported mechanism of user-defined
aggregations. Yet, map-reduce is much closer to
programming than to data processing because
manual loops are required with direct access to the
data being processed.
Aggregation is an integral part of many other
data processing frameworks like pandas (McKinney,
2010; McKinney, 2011), R or Spark SQL (
Armbrust
et al., 2015
) which rely on data frames as the primary
data structure. One of their specific features is that
they provide a separate operation for grouping
elements of a data frame so that different aggregate
functions can be then applied to these groups as a
next operation. This approach is also closer to
programming models rather than to data models
because user-defined aggregations still require direct
access to and explicit loops through the group
elements.
1.3 Goals and Contribution
This paper is devoted to the problem of data
aggregation. We discuss this mechanism at logical
level of data representation and processing, and not
physical level where numerous implementations and
optimization techniques exist taking into account
various hardware architectures and network
properties. The main mechanism for data
aggregation which has been dominating among other
approaches for dozens of years is the group-by
operation. Yet, despite its wide adoption, this
operation has some serious conceptual drawbacks. In
particular, group-by does not naturally fit into the
relational (set-oriented) setting and looks more like a
From Group-by to Accumulation: Data Aggregation Revisited
371

technical operator mixing various concerns and
artificially attached to this rigor formalism. Group-
by does not clearly separate such aspects as
grouping (breaking a set into subsets) and
aggregation (reducing a subset to one value). Also, it
does not provide a principled mechanism for user-
defined aggregations without support from the
system level. The latter drawback – having no
support for user-defined aggregate functions at
logical level – makes this operation almost useless
for complex data transformations and analytics. In
other words, a data model without user-defined
aggregations cannot be viewed as a complete
general-purpose model. At least two fixes are
possible and widely used in practice to overcome
this problem. providing some support directly from
the system or introducing explicit loops over the
group elements for data aggregation. However, the
former approach will turn the model into a physical
one and the latter approach will turn it into a
programming model. Therefore, the both currently
existing general solutions are not acceptable if we
want to have aggregation as an integral part of the
logical model without any hooks to the physical
level or extensions in the form of programming
language constructs.
These significant drawbacks of group-by
motivated us to rethink this mechanism and search
for alternative approaches to data aggregation. As a
possible solution to the existing problems of the
group-by operation, we propose a new alternative
approach based on accumulate functions which does
not have these drawbacks and provides some
significant benefits. The main idea behind this new
approach is that an accumulate function
incrementally updates the current aggregate as
opposed to applying an aggregate function to a
whole group by returning the final aggregate.
The standard approach to aggregation (Fig. 1a)
means that we iterate through all the groups in the
main loop, retrieve group members (facts) for each
of them and then pass them as a subset to the
aggregate function which returns a single value
treated as the aggregate for this group. In the case of
accumulate functions (Fig. 1b), we iterate through
all the facts to be aggregated (not groups), pass each
individual fact to the accumulate function (not a
subset of facts) which updates the aggregate for the
group element this fact belongs to.
The main benefit of accumulate functions is that
they significantly simplify the task of describing
data aggregation operations by clearly separating
different concerns and factoring aggregation out into
one small (accumulate) function. It does not require
any support from the physical level of the model and
uses only what is available at the logical level. It
also fixes the problem of user-defined aggregations
because accumulate functions do not loop through
any subset but rather their purpose is to update the
current aggregate using a new fact. In other words,
describing the logic of aggregation is as easy as
writing a normal arithmetic expression for defining
new calculated columns.
Figure 1: Aggregation (a) vs. accumulation (b).
The use of accumulate functions requires
switching from the set-oriented paradigm to the
function-oriented paradigm where a model is
represented as a number of functions and data
operations are described as function definitions (or
expressions). We do not explicitly define such a
function-oriented approach in this paper but
familiarity with major principles of the functional
data model (Kerschberg and Pacheco, 1976; Sibley
and Kerschberg, 1977) could help in understanding
how accumulation works. Accumulate functions
have been implemented in the DataCommandr
system (Savinov, 2016b) which uses the concept-
oriented data model (Savinov, 2016c).
The paper has the following layout. In Section 2
we critically analyze properties of group-by by
emphasizing some of its fundamental drawbacks in
the context of data processing. Section 3 describes
an alternative approach to data aggregation by
introducing the mechanism of accumulate functions
and discusses its advantages. Section 5 makes
concluding remarks by summarizing drawbacks of
group-by and advantages of accumulation.
2 “WHO IS TO BLAME?”
GROUP-BY
2.1 What is in a Group-By? Four
Operations
Group-by operation takes one table, called fact table,
as input and produces one table, called group table,
as its output. One of the attributes of the fact table
the values of which are aggregated is referred to as a
Facts
Grou
p
s
MAINLOOP
Facts
Grou
p
s
a=a+f.m
a=SUM(g)
a) b)
Accumulatefunction
updatesaggregate
Aggregatefunction
computesaggregate
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
372

measure. One attribute of the group table is
computed during aggregation. For example, if
OrderItems is a table consisting of order items
(facts) each belonging to some order (group) then
the group-by operator could be used to produce a list
of all orders with large total amount computed from
only cheap order items:
SELECTorder,SUM(amount)AStotal 1
FROMOrderItems 2
WHEREprice<10.0 3
GROUPBYorder 4
HAVINGtotal>1000.0 5
Here we select only facts (order items from the
OrderItems table) with low price (line 3). GROUPBY
clause specifies that all facts from
OrdreItems
having the same
order attribute belong to one group
(line 4). Once the facts have been filtered and
grouped, the third step is to aggregate them. It is
done by defining a new attribute in the
SELECT
clause as the standard
SUM aggregate function
(line 1). Finally, the set of groups is filtered by
selecting only orders with large total amount
(line 5).
Although group-by looks like one operation, it is
actually a sequence of four components (Fig. 2)
described below.
Input filter specifies criteria for selecting facts
to be processed by group-by. These criteria are
specified in the
WHERE clause precisely as it is done
in
SELECT queries. All records which do not satisfy
these criteria are ignored during aggregation. In the
above example (line3), we selected only cheap order
items.
Grouping criteria provide conditions which
determine a group each fact belongs to. In group-by,
it is assumed that all facts that have identical values
for the attributes listed after
GROUPBY are assigned
to one group. Implicitly, this means that each unique
combination of values of the grouping attributes
represents one group. In our example (line 4), all
order items having identical
order attribute belong
to one group. The grouping component is
responsible for the generation of the output table by
instantiating its elements and in this sense it is an
operation on sets because it takes a filtered input set
and produced an output set.
Aggregate function converts measure values of
all facts of one group to a single value which is then
assigned to the aggregate attribute of the group table.
An aggregate function is specified as a new attribute
definition in the
SELECT clause and a measure is
specified as its argument. Thus the aggregation
component is responsible for the generation of a new
attribute and hence it is a column operation rather
than a set operation. After executing this component,
a new column storing aggregates for each group will
be appended to the group table generated on the
previous step.
Output filter is applied to the group table after
aggregation and selects only groups which satisfy
the criteria provided in the
HAVING clause. In the
previous example (line 5), we select only groups
with the total amount greater than 1000.0.
Figure 2: Constituents of the group-by operation.
Two of the four constituents of the group-by
operation are filtering: the input fact table is filtered
using
WHERE clause and the output group table is
filtered using
HAVING clause. There is no clear
reason why these two filters have been made integral
part of the group-by operation. Theoretically, it
could increase performance but a good query
optimizer should not have any problems in
producing the same query execution plan given input
and output filters as separate operations. We treat
such integration of input and output filters into
group-by as one of its drawbacks because the
operation becomes conceptually heavier and queries
are getting more difficult to write and understand.
Yet, in contrast to other drawbacks described below,
it does not have significant consequences because
these filters are essentially independent of the
grouping component and the aggregation
component, and therefore this drawback can be
easily eliminated by simply not using these filters. In
other words, removing the input and output filter
steps from group-by will make this operation only
better without any losses (except for maybe systems
with no query optimization).
2.2 Grouping is Projection
Grouping operation is applied to a fact table and
produces a new group table. Grouping criteria are
specified using the common value semantics which
means that facts having identical values for some
attributes are considered related elements. In the
case of group-by, they are considered members of
one group which is (implicitly) identified by these
values. In (Savinov, 2016a), we argued that the
common value semantics is rather inappropriate for
describing connectivity. It is also not very
convenient for describing the group membership
Input
Filter
Grouping
Aggregation
Output
Filter
New
Table
New
Attribute
Select
Grou
p
s
Select
Facts
From Group-by to Accumulation: Data Aggregation Revisited
373

relation. In particular, grouping criteria are a cross-
cutting concern because each query has to repeat
these conditions even if they are the same. It is
difficult to modularize grouping definitions so that
they can be reused in different queries. If we change
the way groups are defined, then we need to update
all queries. It is also difficult to specify grouping
criteria using complex relationships derived from
other data. For example, what if we want to group
order items around their production place which
however is derived from the data in other tables? A
conceptually alternative approach to grouping
consists in introducing some kind of ‘member_of’
relation for facts which determines a group each fact
belongs to (Section 3.2).
How facts can be grouped is only one aspect of
the grouping mechanism in group-by. A more
serious problem is that conceptually, grouping as an
operation has nothing to do with aggregation. In
particular, it might well make sense to define one
grouping to be used in many different aggregations
or to apply one aggregation to many different
groupings.
Just as for input-output filters, relational algebra
already has such an operation. Indeed, grouping is
essentially equivalent to the relational project where
the result is a set of all distinct tuples composed of
the specified attributes. Thus group-by provides its
own internal version of relational project instead of
reusing project as an independent operation that can
be freely combined with aggregation and other
operators.
In fact, grouping (as relational project) operation
is not needed at all if the group table already exists.
For example, if the database has already both the
OrderItems fact table and the Orders group table
then all groups as elements of the
Orders table
already exist and hence there is no need to do
grouping at all. Yet, group-by does not allow us to
skip the grouping step because it is an inherent part
of group-by. The groups in this case will be built for
each query execution with no possibility to reuse an
already existing group table. For example, if we
want to compute several aggregations for orders then
it would be natural to reuse the existing
Orders table
or to produce it once and add the necessary columns
with aggregates. Yet, in the case of group-by, each
aggregated column will be produced along with the
whole group table and all these individually
generated group tables need to be joined if we want
to have all aggregates in one output table.
Inclusion of grouping into group-by operator has
the same consequences as including input-output
filters into group-by. It is not possible to reuse one
grouping operation for different aggregations which
makes query writing more difficult and limits
possibilities of optimization when translating such
queries. However, in contrast to input-output filters
which can be simply ignored or replaced by pre- or
post- filters, grouping operation cannot be easily
removed from group-by. The reason is that its
parameters are needed in the aggregation operation
and hence it is the aggregation component that has to
be changed.
2.3 No User-defined Aggregate
Functions
Complex data processing and analysis can hardly be
done without custom aggregations performed by
user-defined aggregate function as opposed to
having only a limited set of standard functions like
SUM. The standard group-by conception does not
support user-defined aggregate functions and it is
one of its biggest limitations. Yet, the problem is
even worse because this mechanism is difficult to
introduce without breaking some major principles of
the relational model.
There are two major approaches to solving the
problem of user-defined aggregate functions both of
them being widely used in practice. The first
approach introduces user-defined aggregate
functions as extensions of the physical level of the
system. They could be provided as external libraries
which rely on this system API by essentially
extending the set of standard functions. Once such a
new aggregate function has been added, for
example, by registering or linking its library, its
name will be recognized by the query parser. This
approach is used by many database management
systems but we do not consider it in this paper
because it does not change the principles of data
aggregation at logical level of the model. In other
words, at the logical level, the model and group-by
still do not support custom aggregations and any
system has its own support for these functions.
In the second approach, user-defined aggregate
functions are provided at the level of the query
language or the corresponding standard API. The
most widespread technique consists in providing a
possibility to define a normal function which gets a
collection of elements or values as input and returns
a single value as output. In particular, this simple
and natural approach is the core stone of the map-
reduce data processing paradigm where such
functions are responsible for the reduce part of the
data processing flow. For example, assume that we
want to aggregate items for each order by using a
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
374

custom aggregate function which finds a weighted
total (as opposed to a simple sum) by multiplying
each order item amount by some factor which
depends on this amount. The function iterates
through all the group elements provided in the input
collection and applies the necessary weight to each
amount before updating the aggregate stored in the
local variable:
DOUBLEweightedTotal(OrderItemsgroup) (1)
{
DOUBLEout=0.0;//Aggregate
FOR(factINgroup)//Explicitloop
IF(fact.amount<100)
out+=fact.amount*1.0;
ELSE
out+=fact.amount*0.5;
RETURNout;//Finalvalue
}
One problem with this approach is that it is
actually not data processing anymore but rather a
programming technique. In data modeling and data
processing, in contrast to programming, the goal is
to avoid explicit loops with intermediate state and
direct access to the subset elements. A query writer
is supposed to provide only criteria and options for
data operations at the level of one element
(instance). How the elements are iterated should not
be defined in the query but rather is part of the
system level (DBMS). This approach does not
conform to general criteria for data modeling and
data processing because such aggregate functions
have to explicitly loop through the subset by
maintaining an intermediate state between iterations
in order to compute the aggregate. Essentially, the
use of such type of user-defined aggregate functions,
for instance in map-reduce, means switching to
programming. Since such user-defined aggregate
functions have a form of an arbitrary program, they
cannot be easily integrated into a global query
execution plan and have to be executed precisely as
they are written.
Another problem with such user-defined
aggregate functions is that they can be quite
inefficient at run time for the following reasons:
The system has to generate all the groups in an
explicit form to pass them to the aggregate
function. The problem is that there can be a huge
number of such (small) groups or some groups
could be very large (comparable with the
complete data set).
Computation of aggregates could be inefficient
because it cannot be optimized for smaller and
larger groups. Essentially, the user-provided
code needs direct access to the data managed by
the system which makes the task of physical data
organization more difficult.
Global optimization of different parts of a data
flow can be difficult because they are written
using non-compatible techniques and belong to
different paradigms, for example, high level
relational queries, custom reduce functions, and
grouping provided by the system. For example,
we could imagine the situation where a user-
defined aggregate function needs not only data
from this group but also data that results from
some query by accessing other collections in this
database.
Currently there are many sophisticated techniques
that make data aggregation by means of user-defined
aggregate function much more efficient especially
taking into account properties of one or another
underlying platform or data management system like
Apache Hadoop or Spark (Zaharia et al., 2012).
However, most of these approaches are being
developed at physical level of the data processing
system without any changes to the way aggregation
is done at logical level and hence they treat
aggregation as an extension rather than an integral
part of the model. In this context, the goal is to get
rid of explicit groups and explicit looping through
these groups.
3 “WHAT IS TO BE DONE?”
ACCUMULATION
3.1 What is in an Accumulation?
Column Definition
Accumulation is an alternative approach to data
aggregation which is based on the functional data
modeling paradigm as opposed to the set-oriented
paradigm. The main difference is that an aggregated
attribute is directly defined as a function which gets
a single fact and knows only how to update the
current value of the aggregate. It is referred to as an
accumulate function because it is unaware of the
whole group and does not know how to compute the
final aggregate but rather knows only how to
accumulate an individual fact into the intermediate
aggregate.
To illustrate this difference, let us show how the
standard
SUM aggregate function can be equivalently
defined as an accumulate function. Instead of
looping through the group elements by returning the
final aggregate as a sum of its values within one
From Group-by to Accumulation: Data Aggregation Revisited
375
procedure, we can only update the intermediate sum
and return it:
SUM(OrderItemsfact,DOUBLEout){
RETURNout+fact.amount;
}
Here the current value is passed in the out argument
of the
SUM accumulate function. Alternatively, the
current value could be found from the fact:
SUM(OrderItemsfact){
Ordergroup=fact.order;
DOUBLEout=group.total;
RETURNout+fact.amount;
}
Another variation of this approach is to directly
update the value stored in the group table instead of
returning it:
SUM(OrderItemsfact){
fact.order.total+=fact.amount;
}
All the three modifications are conceptually
equivalent because the only operation they do is
modifying some intermediate aggregate using a new
fact. The database engine loops through all the facts
in the
OrderItems table and passes each individual
element to the accumulate function along with the
current output of this same function for the group.
This function updates the received output by adding
the amount stored in the fact and returns the updated
sum. This updated sum will be passed to this same
method next time it is called for another fact of this
same group. Here we also assume that either the
system or the accumulate method itself can
determine the group each fact belongs to.
Importantly, an accumulate function is
essentially a column definition. Its name is the
column name. Its (output value) type is the column
type specifying what kind of data this column stores.
Note that calculated columns are defined in the same
way. For example, we could define a new calculated
column as a function of two attributes:
DOUBLEdiscount(Ordero){ (2)
RETURNo.total+o.customer.bonus;
}
The same could be written as a query:
CREATECOLUMNDOUBLE (3)
o.discount=o.total+o.customer.bonus
TABLEOrdersaso
The main difference of accumulated columns
from normal calculated columns is that they use a
different (fact) table to compute its output. Hence,
they need an additional parameter with the fact table
name. For example, a column with the total amount
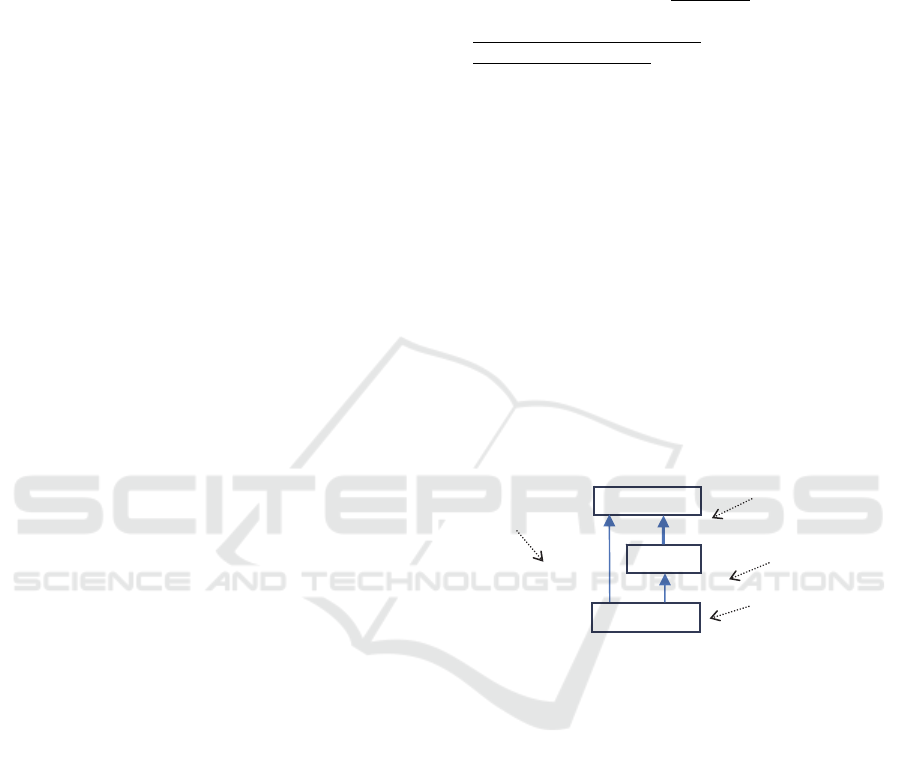
for all orders could be defined as follows (Fig. 3):
CREATECOLUMNDOUBLE (4)
o.total=o.total+i.amount
TABLEOrderso
FACTTABLEOrderItemsi
GROUPPATHi.order
In addition to the DOUBLE column type, we
specify its name as a function name (
total).
Actually, it can be any function that returns a double
value and is defined elsewhere or in-line (like the
SUM accumulate function). The TABLE keyword is
followed by the table name this column belongs to.
In this example, we define a new accumulated
column for the
Orders table. The FACT TABLE
keyword is the most important one because it
changes the way this column is computed. It says
that the
total() function will be evaluated for each
element of the
OrderItems table rather than for the
Orders table where this column is defined. Without
this keyword, it will be evaluated for each element
of the
Orders table and will be a normal calculated
column like
i.price*i.quantityASamount from
Section 1.1.
Figure 3: Structure of the accumulation.
This generic approach has several minor design
alternatives which do not change its essence but can
change its flexibility and performance under certain
conditions. The alternatives depend on which part –
the query or accumulate function – is responsible for
and aware of the following aspects:
Grouping – how to determine a group element
the current fact belongs to. In the above example,
we assumed that grouping is specified at the
level of the query in the
GROUP PATH clause. In
the next subsection we will discuss other
alternatives and properties of the grouping
mechanism.
Measures – what attributes of the facts have to be
aggregated. In our examples, we assumed that an
accumulate function gets a fact as an element
(tuple). Other alternatives and properties of user-
OrderItems
Orders
Double
GROUPPATH
amount
FACTTABLE
total=out+amount
order
accumulatecolumn
measure
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
376

defined accumulate functions are discussed in
Section 3.3.
3.2 Grouping is Membership Relation
The mechanism of accumulation does not use a
separate grouping step based on the relational
project operation as it is done in group-by. Instead,
accumulation relies on the group relation between
the fact table and the group table. The main task of
the group relation is to determine a group each
individual fact belongs to and it can be any function
from the group table to the fact table. For example,
if we want to view orders as groups consisting from
order items then the
order attribute of the
OrderItems table will represent a group relation.
Given an order item, we can always get its group as
output of this attribute. Importantly, we do not
perform projection or computation of some new
table (although formally it can be done) because
relational project is not used in the accumulation
mechanism.
Since a group relation is a normal function, we
do not introduce a new mechanism but simply use a
new semantics of links (Savinov, 2016a,
Section 3.1): a link points to an element (group) this
element (fact) belongs to. One advantage of this
approach is that grouping is actually defined at the
level of the whole model and the existing group
relations can be reused in aggregations as well as
other operations like project. Moreover, a group
relation can be an arbitrary function which actually
computes its output so that groups are derived
dynamically during computations. It is always
possible to provide custom or user-defined groups
instead of using only table attributes for representing
the group relation.
Another property of this grouping mechanism is
that both the fact table and the group table are
assumed to already exist, that is, no new table results
from the accumulation. If the group table does not
exist, then it has to be created. In particular, it can be
produced from the fact table by using projection
along the group relation.
One design alternative in the context of group
relation is whether it is provided in the query itself
or encoded into the accumulate function. If the
group (relation) path is specified at the level of the
query (like
GROUPPATH in query (4)) then the query
engine will use it to retrieve a group for each fact,
get the current aggregate for this group element and
pass this value to the accumulate function which will
return an updated aggregate for this group. Here we
explicitly declare the group relation at the level of
the query and then the engine uses it for aggregation.
An alternative approach is where all these steps are
performed by the accumulate function itself and
hence the group relation is not declared – it is simply
part of the logic of each accumulate function. Query
(4) can be rewritten without an explicit group path
which instead is used in the accumulate function:
CREATECOLUMNDOUBLE
o.total=i.order.total+i.amount
TABLEOrderso
FACTTABLEOrderItemsi
GROUPPATHi.order//Notused
This query knows only that the total function has
to be evaluated for each element in the
OrderItems
table and hence an accumulate function will take
only one parameter – an element of the fact table.
However, the accumulate function has to determine
the group and also retrieve its current aggregate
(underlined fragment in this example). Such queries
are somewhat simpler and this approach could be
more flexible in some situations. However, it is
necessary to understand that such accumulate
functions mix two concerns, grouping and
aggregation. Also, the system could define groups
for the facts more efficiently by applying the
necessary optimizations which is not possible if
grouping is done by the accumulate function.
3.3 User-defined Accumulate Functions
In group-by, user-defined aggregate functions are
either not supported or require writing an explicit
loop by getting a collection of elements as a
parameter. In contrast, an accumulate function
processes one instance rather than a collection by
receiving a single (fact) element as input and
returning a single (updated) value as output. For
example, if we want to compute weighted total then
instead of the aggregate function (1) in Section 2.3
we can write the following accumulate function:
DOUBLEweightedTotal(OrderItemsfact){
IF(fact.amount<100)
RETURNout+fact.amount*1.0;
ELSE
RETURNout+fact.amount*0.5;
}
This function receives the current value via the out
argument (or using the function name) and updates it
by adding the measure
amount weighted by some
factor depending on its value. Thus this function
updates its previous output by assuming that it will
be called many times for each element of one group.
From Group-by to Accumulation: Data Aggregation Revisited
377

Accumulate functions define new columns using
function operations rather than new sets using set
operations. Therefore, they can be easily used to
define new columns very similar to how calculated
columns are defined. For the same reason,
accumulate functions cannot be directly used in a
conventional data flow graph where nodes are sets
and edges are set operations. Actually, the attempt to
make aggregation integral part of a set algebra is
precisely why the group-by is so conceptually
eclectic and looks more like an artificial addition to
some framework than an independent formal
operation. And treating aggregation as a column
definition is precisely why accumulate functions are
so simple and natural.
An accumulate function can be viewed as an
aggregate function where both the loop and the local
variable with the current aggregate are factored out
of the procedure. The accumulate function itself
defines only the body of this loop without any
intermediate state. This makes the whole approach
not only conceptually simpler but also potentially
more efficient because organizing and optimizing
various processing loops is precisely what a database
engine is intended for.
Our examples assume that an accumulate
function gets one fact element as a parameter. This
fact is then used to update the current output. In this
case, the measure is not explicitly declared at the
query level and it is not known which property of
the fact will be actually used to update the current
aggregate. Thus this approach does not limit
aggregation by only one measure attribute. It is
possible to use other attributes, functions or other
data elements that can be accessed from this fact
element. For example, we could compute the total
for each order by using order item price and quantity
directly from the accumulate function:
CREATECOLUMNDOUBLE
o.total=o.total+i.price*i.quantity
TABLEOrderso
FACTTABLEOrderItemsi
GROUPPATHi.order
Here we essentially use two measure attributes for
updating the aggregate: price and quantity.
An alternative approach is to explicitly declare
one measure in the query so that the query engine
will retrieve or compute its value and pass it to the
accumulate function as an argument:
CREATECOLUMNDOUBLE
o.total=o.total+measure
TABLEOrderso
FACTTABLEOrderItemsi
GROUPPATHi.order
MEASUREi.price*i.quantity
Here the measure keyword denotes the value that
has to be used to update the current aggregate and is
used instead of the whole fact reference. This
approach is less flexible from the point of view of
aggregation but provides more possibilities for query
optimization because the engine knows more about
what data the accumulate function will use.
It is important to understand that the semantics of
accumulate functions is different from that of
aggregate functions. If we want it to be equivalent to
an aggregate function implemented by explicitly
looping through a group then it has to satisfy certain
formal criteria. First, the result has to be independent
of the order of updates and hence this operation has
to obey the commutative law: ܾܽൌܾܽ.
Second, to be able to apply updates to partial results,
an accumulate function has to obey the associative
law:
ሺ
ܾܽ
ሻ
ܿൌܽሺܾܿሻ.
Implementing the traditional logic of aggregation
using accumulate functions is easy for some
functions like
SUM or MAX but it can be unobvious for
other functions. For example, computing an average
value is reduced to defining two accumulate
functions,
SUM and COUNT, while the result is a new
calculated function dividing the sum by the count for
each row. Expressing the logic of aggregation using
accumulate functions can be rather tricky, for
example, if we want to compute a median value.
However, it is necessary to understand that the
conventional aggregate functions will always be
more expressive and more flexible just because we
essentially get full control over the computation
process. Yet, we do not treat it as a drawback
because it as a natural (and typical) limitation caused
by delegating some functionality (loop organization
and optimization) to the system.
Accumulate functions are used to define columns
and hence they cannot be easily integrated into a set-
oriented model or data processing system. A data
model with accumulate functions has to support
functions and function operations. In other words,
the conventional approach to data processing
consists in defining a graph where nodes are sets and
edges are set operations. In contrast, accumulate
functions require a model where nodes can be
functions (columns) and edges are function
operations. In such a model, every function is
defined in terms of other functions and evaluating a
function means finding its output values given
output values of the functions it depends on.
Apparently, this approach cardinally differs from the
set-oriented paradigm. The principles of such a
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
378

model were described in (Savinov, 2016c) and
implemented in the DataCommandr system
(Savinov, 2016b).
4 CONCLUSIONS
Although group-by is a powerful data processing
operator, it has the following conceptual drawbacks:
Group-by is an eclectic mixture of several quite
different operations rather than one operator
Grouping in group-by is essentially the relational
project operation which conceptually has nothing
to do with aggregation
Group-by does not inherently support user-
defined aggregate functions without explicit
loops and without system support
We also proposed and analyzed an alternative
mechanism to data aggregation based on accumulate
(update) functions which provides the following
benefits:
The complete logic of aggregation is
modularized in one accumulate function which
defines a column in terms of other columns
Accumulation uses group membership relation
(which is also a function) and does not involve
relational project
Accumulation inherently supports user-defined
functions because it is a functional approach
which is based on column operations rather than
set operations
Taking into account these properties we argue that
the mechanism of accumulation should be preferred
to group-by as the main aggregation operation in
data models and data processing frameworks.
However, it belongs to the functional data modeling
paradigm which is based on defining and
manipulating functions rather than sets. Formal
integration of the functional and set-oriented
approaches including set operations as well as
(horizontal and vertical) column operations will be
our focus for future research.
REFERENCES
Abiteboul, S., Fischer, P.C., Schek, H.-J., 1989. Nested
Relations and Complex Objects in Databases (LNCS).
Springer, Berlin.
Armbrust, M., Xin, R.S., Lian, C., Huai, Y., Liu, D.,
Bradley, J.K., Meng, X., Kaftan, T., Franklin, M.J.,
Ghodsi, A., Zaharia, M., 2015. Spark SQL: Relational
Data Processing in Spark. In SIGMOD 2015.
Codd, E., 1970. A Relational Model for Large Shared
Data Banks. Communications of the ACM, 13(6), 377–
387.
Database Languages|SQL, ISO/IEC 9075-*:2003, 2003.
Dean, J, Ghemawat, S., 2004. MapReduce: Simplified
data processing on large clusters. OSDI'04, 137–150.
Kerschberg, L., Pacheco, J.E.S., 1976. A Functional Data
Base Model. Report No. 2/1976, Departamento de
Informatica, Pontificia Universidade Catolica - Rio de
Janeiro, Brazil.
McKinney, W., 2010. Data Structures for Statistical
Computing in Python. In Proc. 9th Python in Science
Conference (SciPy 2010), 51–56.
McKinney, W., 2011. pandas: a Foundational Python
Library for Data Analysis and Statistics. In Proc.
PyHPC 2011.
Savinov, A., 2016a. Joins vs. Links or Relational Join
Considered Harmful. Internet of Things and Big Data
(IoTBD’2016), 362–368
Savinov, A., 2016b. DataCommandr: Column-Oriented
Data Integration, Transformation and Analysis.
Internet of Things and Big Data (IoTBD’2016), 339–
347.
Savinov, A., 2016c. Concept-oriented model: The
functional view. arXiv preprint arXiv:1606.02237
[cs.DB] 2016 https://arxiv.org/abs/1606.02237
Sibley, E.H., Kerschberg, L., 1977. Data architecture and
data model considerations. In Proceedings of the
AFIPS Joint Computer Conferences, 85–96.
Zaharia, M., Chowdhury, M., Das, T., Dave, A., Ma, J.,
McCauley, M., Franklin, M.J., Shenker, S., Stoica, I.,
2012. Resilient Distributed Datasets: A Fault-Tolerant
Abstraction for In-Memory Cluster Computing. NSDI
2012.
From Group-by to Accumulation: Data Aggregation Revisited
379
