
Probing Complexity with Epidemics: A New Reactive Immunization
Strategy
E. Alfinito
1
, M. Beccaria
2
, A. Fachechi
3
and G. Macorini
4
1
Dipartimento di Ingegneria dell’Innovazione, Universit
`
a del Salento, Campus Ecotekne, 73100 Lecce, Italy
2,3,4
Dipartimento di Matematica e Fisica E. De Giorgi, Universit
`
a del Salento & INFN, Via Arnesano, 73100 Lecce, Italy
Keywords:
Epidemic Models, Reactive Immunization, Complex Networks.
Abstract:
Epidemic evolution on complex networks strongly depends on their topology and the infection dynamical
properties, as highly connected nodes and individuals exposed to the contagion have competing roles in the
disease spreading. In this spirit, we propose a new immunization strategy exploiting the knowledge of network
geometry and dynamical information about the spreading infection. The flexibility and effectiveness of the
proposed scheme are successfully tested with numerical simulations on a wide set of complex networks.
1 INTRODUCTION
Epidemic processes and the related immunization
problem is a very hot topic in statistical mechanics of
complex networks (Pastor-Satorras et al., 2015). The
central issue in the realization of an effective vacci-
nation program is in fact the identification of the most
relevant features in the infection spreading. This is in
general a highly non-trivial problem, so that novel im-
munization programs, looking at some particular as-
pects of the complex system, have been realized. Ac-
cording to their application and the required knowl-
edge about the system, immunization programs can
be roughly classified in two opposite approaches. The
first one is the preventive case, which aims to make
the healthy network stronger against future epidemic
events by using (global or local) information about
its topology. This is the case of Targeted Immuniza-
tion (TI) (Pastor-Satorras and Vespignani, 2002), Ac-
quaintance Immunization (AI) (Cohen et al., 2003)
as well as their variations and refinements (Stauffer
and Barbosa, 2006; Hu and Tang, 2012). On the
other hand, the reactive approach is designed for deal-
ing with an already spreading infection. In this case,
topological knowledge and information about the epi-
demic state can be combined so that a dynamical reac-
tion can be carried out, see for example (Ruan et al.,
2012; Altarelli et al., 2014; Liu et al., 2014; Perra
et al., 2012; Yan et al., 2014; Pereira and Young,
2015). A paradigmatic example of this approach is
the so-called High-Risk Immunization (HR) (Nian
and Wang, 2010), in which only individuals interact-
ing with infected nodes are vaccinated. In some real
situations, only the reactive setting is possible, for ex-
ample to control unexpected disease outbreaks or, in
a technological context, to fight malware diffusion.
In such situations, a good control of epidemic con-
tagion needs a fast intervention, so it is more conve-
nient to have an immunization program working well
on the largest possible set of networks. Unfortunately,
known immunization strategies have been usually de-
signed to work in very specific settings. We propose
a new immunization strategy which generalizes TI in
order to take into account the presence of an already
propagating epidemic. Our claim is that the most rel-
evant individuals in the epidemic diffusion have to
be identified according to a clever balance between
network topological features and the epidemic state
at the vaccination time. We test the effectiveness of
our protocol with a Monte Carlo implementation of
SIR model (Kermack and McKendrick, 1927; May
and Anderson, 1979) and extensively compare it with
standard immunization strategies on a variety of com-
plex (theoretical and real) networks.
2 THEORETICAL BACKGROUND
2.1 Implementation of SIR Model
In the SIR model (Kermack and McKendrick, 1927),
individuals are classified according to their condition
in susceptible (S), infected (I) and recovered (R). Epi-
116
Alfinito, E., Beccaria, M., Fachechi, A. and Macorini, G.
Probing Complexity with Epidemics: A New Reactive Immunization Strategy.
DOI: 10.5220/0006361301160123
In Proceedings of the 2nd International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2017), pages 116-123
ISBN: 978-989-758-244-8
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

demic dynamics is therefore represented by the tran-
sitions S → I and I → R. In our implementation of
SIR model, the initial condition is a single infected
node (patient zero) in the network. At each step, an
infected individual is randomly selected and recov-
ers with probability p
SIR
. If this is not the case, one
of its susceptible neighbors is randomly chosen and
gets infected. The immunization takes place as a re-
action to the epidemic spreading when a given frac-
tion f (the epidemic threshold) of the total population
is infected. In the procedure, the fraction g of indi-
viduals to be vaccinated is selected according to some
score assigned to each node, which results in a prior-
ity list for the nodes to be vaccinated. The spreading
algorithm goes on as long as infected individuals are
present. Once the system reaches its final state, we
consider the final density d
R
of recovered individuals
as a measure of total number of individuals involved
in the epidemic. Clearly, an immunization strategy is
effective if it significantly reduces the density d
R
by
immunizing a relatively small fraction d
V
of the pop-
ulation. Since the evolution of the system is stochas-
tic, we perform a large number of simulations and the
effectiveness of a given strategy is measured in terms
of the averages hd
R
i and hd
V
i.
2.2 A New Immunization Strategy
Motivated by the issues discussed in the introduction,
we propose a local refinement of TI. Specifically, our
score takes into account both static knowledge of the
network geometry and dynamical information about
the epidemics, and it is given by
s
i
= d
i
+
∑
j∈N
i
β
δ
j,I
(d
j
)
1/2
+ γ
δ
j,S
d
i
d
i
− d
j
d
i
+ d
j
. (1)
Here, N
i
is the i-th node neighborhood, d
i
its con-
nectivity degree and δ
j,I
and δ
j,S
are Kronecker deltas
selecting respectively infected or susceptible nodes.
Finally, β and γ are tunable free parameters. Clearly,
the β-term favors the vaccination of nodes near the
epidemic front, where the factor (d
j
)
−1/2
is justified
by the fact that less connected neighbors constitute
bottlenecks for the epidemic spreading. The γ-term is
a further improvement based on the leverage central-
ity (Joyce et al., 2010).
2.3 Standard Immunization Strategies
In our numerical tests, we extensively compare our
proposal with the following standard immunization
strategies, suitably modified in the reactive setting:
• Targeted Immunization (TI). Originally de-
signed for scale-free networks, this scheme se-
lects nodes to be immunized among the suscep-
tible ones according to their degree.
• Acquaintance Immunization (AI). In this case,
random neighbors of randomly selected nodes are
vaccinated (if susceptible). This is a degree-based
vaccination strategy using only local information
about the network.
• High Risk Immunization (HR). Nodes to be im-
munized are chosen among the susceptible neigh-
bors of infected nodes.
3 COMPLEX NETWORKS
In this section, we briefly describe the networks we
considered as background for the epidemic spreading.
They range from the standard theoretical cases to a
collection of real world systems.
3.1 Theoretical Networks
In the first class, we consider the Barab
`
asi-Albert
(Albert and Barab
´
asi, 2002; Bornholdt and Schuster,
2006) and the Watts-Strogatz (Albert and Barab
´
asi,
2002; Bornholdt and Schuster, 2006; Watts and Stro-
gatz, 1998) models, which are respectively the proto-
types of scale-free and small-world graphs. We de-
note with BA[Q] the Barab
`
asi-Albert graph obtained
adding Q new links at each step of the growth algo-
rithm. On the other hand, we indicate as WS[Q] the
Watts-Strogatz graph obtained starting with a regu-
lar network with each node connected to 2Q adja-
cent sites. The rewiring probability in constructing
WS graphs is denoted by θ. In this paper, we con-
sider BA[2] and WS[2] networks with two different
rewiring probabilities θ = 0.1,0.5 for the WS case.
Since some real networks are believed to be approxi-
mately or locally scale-free, we also propose two vari-
ants of Barab
`
asi-Albert model. The first one is re-
alized starting with a BA graph and then randomly
rewiring R of its links. This variant can be thought as
a model that interpolates, depending on R , between
the pure scale-free networks and the completely ran-
dom graphs. We start with a BA[2] network and con-
sider R = 500, 1000,2000 rewiring events. The sec-
ond variant is realized starting with a network with
N nodes equally distributed in m BA centers. The
centers are then further randomly connected adding
new links between individuals in different clusters. In
this case, we start with m = 5,10,20 BA clusters with
N = 5000 total nodes and add k = 100,500,2000 new
edges.
Probing Complexity with Epidemics: A New Reactive Immunization Strategy
117

Table 1: Some common graph metrics for the real networks considered in the MC simulations: in the four columns we report
the mean value, variance, maximum and minimum for the degree, vertex eccentricity, closeness centrality and betweenness
centrality.
CA-HepTh-pruned Degree Eccentricity Clos. centr. Bet. centr.
mean 5.74809 12.5302 0.171894 21357.1
variance 41.7448 1.07741 0.000597495 3.32398×10
9
max 65. 18. 0.247167 1.15586×10
6
min 1. 10. 0.0813124 0.
p2p-Gnutella08 Degree Eccentricity Clos. centr. Bet. centr.
mean 6.5966 7.16003 0.218169 11471.8
variance 72.9622 0.423737 0.000621478 4.16777×10
8
max 97. 9. 0.295973 305191.
min 1. 6. 0.147952 0.
AA Degree Eccentricity Clos. centr. Bet. centr.
mean 4.74715 8.01616 0.227506 1836.35
variance 77.3613 0.857017 0.00110411 7.90946×10
7
max 145. 11. 0.35615 213598.
min 1. 6. 0.13556 0.
Internet AS Degree Eccentricity Clos. centr. Bet. centr.
mean 4.18991 7.15294 0.282169 14661.
variance 1095.36 0.359583 0.00163744 6.53432×10
10
max 2389. 10. 0.474276 2.03136×10
7
min 1. 5. 0.141305 0.
ProteinYeast Degree Eccentricity Clos. centr. Bet. centr.
mean 2.73388 13.275 0.150965 4234.31
variance 12.2956 1.68203 0.000581309 1.38406×10
8
max 56. 19. 0.234773 225922.
min 1. 11. 0.0791633 0.
3.2 Real Networks
Finally, the set of real networks we consider in this
paper is the following:
1. Internet AS, 11174 nodes, 23408 links. Undi-
rected unweighted Internet Network
1
(Colizza
et al., 2006) at the Autonomous System level.
Nodes represent Internet service providers and
links connections between them. Data were
collected by the Oregon Route Views Project
(http://www.routeviews.org/) in May 2001.
2. AA, 1057 nodes, 2502 links. Interactions between
metabolites of E. coli during the metabolic cycle
2
(Jeong et al., 2000). We consider the AA case.
3. CA-HepTh-pruned, 8638 nodes, 24836 links.
Arxiv HEP-TH (High Energy Physics - Theory)
collaboration network
3
from the e-print arXiv. A
paper is represented as a completely connected
subgraph in which nodes are its authors.
4. p2p-Gnutella08, 6300 nodes, 20776 links. Se-
quence of snapshots of the Gnutella file sharing
1
https://sites.google.com/site/cxnets/research222
2
http://www3.nd.edu/ networks/resources/metabolic/
3
http://snap.stanford.edu/data/ca-HepTh.html
network from August 2002.
4
Nodes are hosts of
Gnutella network and links connections between
them.
5. ProteinYeast, 1870 nodes, 2350 links. Protein In-
teraction Network
5
(Jeong et al., 2001).
Further information about the collection of real net-
works can be found in Table 1, in which some stan-
dard metrics are reported.
4 RESULTS
The discussion of our results is focused on the abil-
ity of the various immunization strategies to reduce
the epidemic prevalence hd
R
i as function of the vacci-
nated fraction of the population. In particular we use
the 50% and 25% of the original (i.e. without vac-
cination) prevalence as references (horizontal dotted
lines in the plots).
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
118
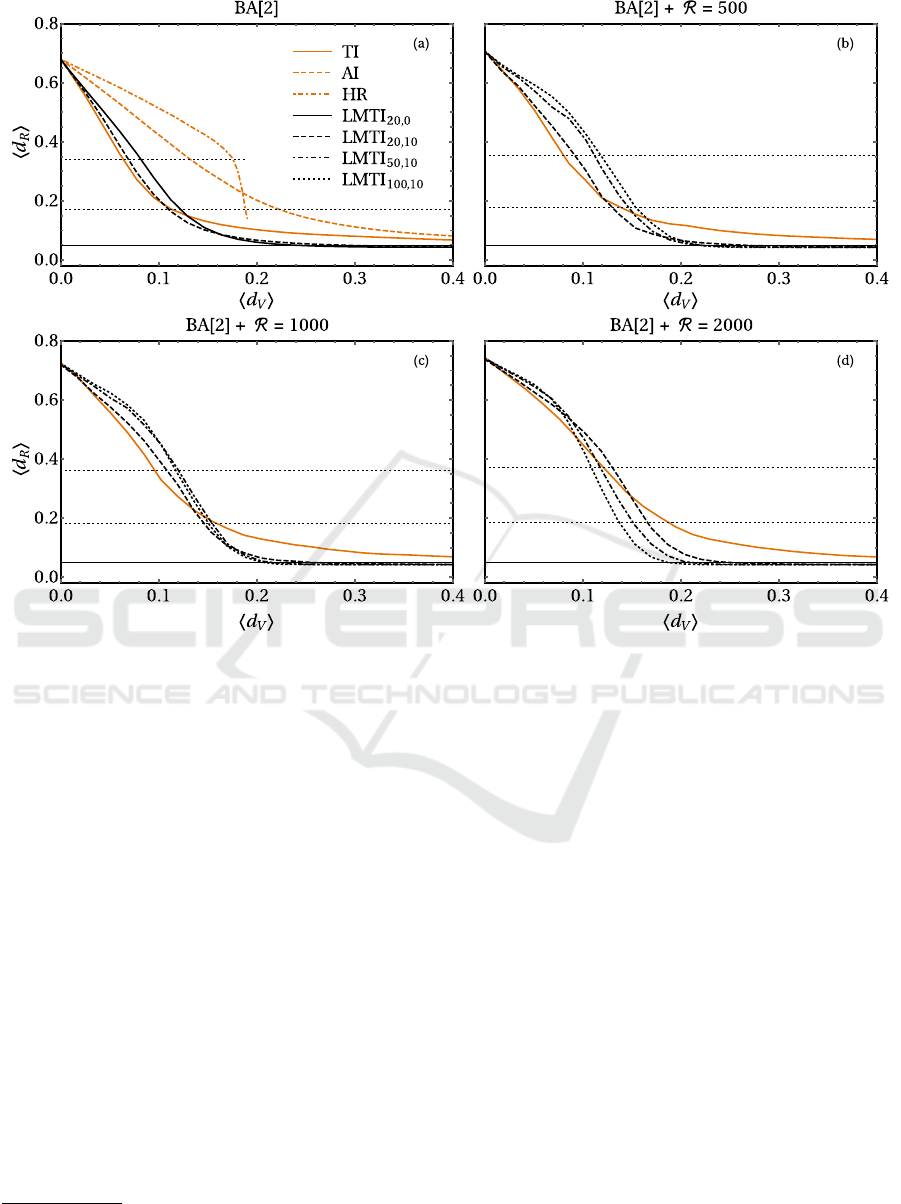
Figure 1: Results for various immunization strategies for randomly rewired BA[2] networks with N = 1000 nodes and
R = 0 (pure BA case, a), 500 (b), 1000 (c), 2000 (d) rewiring events. The LMTI scheme is compared to TI, AI and HR strate-
gies for the pure BA case, while various choice of β and γ are compared with TI only for non zero R . The horizontal solid line
is the epidemic threshold f = 0.05, while the horizontal dotted lines are 25% and 50% of the mean final density of recovered
without any vaccination.
4.1 Barab
´
asi-Albert Setting
Let us first consider the pure BA case, see panel (a) in
Fig. 1. Degree-based immunizations are clearly the
most effective ones in this setting. In particular, the
reduction of the epidemic prevalence by 50% is bet-
ter accomplished with TI. Besides, our strategy (with
the best choice β = 20 and γ = 10) has similar perfor-
mances at low hd
V
i. If we want to cut the prevalence
down to the 25%, TI and LMTI are almost identical,
but the latter is most advisable to further reduce the
epidemic strength. The results for partially random-
ized BAs are collected in panels (b), (c) and (d) of
Fig. 1. Here, we compare LMTI for different choices
of β and γ only with TI, as they are the best perform-
ers in the original setting. The first visible feature is
the gradual worsening of the TI performances for in-
creasing R . This behavior has a simple explanation:
4
http://snap.stanford.edu/data/p2p-Gnutella08.html
5
http://www3.nd.edu/ networks/resources/protein/bo.dat.gz
the random rewiring procedure works in opposite di-
rection with respect to the preferential attachment of
the BA growth algorithm, and the role of big spread-
ers in the original setting is here gradually downsized.
In this setup, the importance of local terms in (1) can
be better appreciated and immunization of the indi-
viduals close to the epidemic front becomes more and
more important in controlling the outbreak.
Another interesting result holds for the randomly
connected BAs, see Fig. 2. In this setting, the reduc-
tion to the 50% of the epidemic prevalence is generi-
cally best suited with TI, while the cutting to the 25%
is roughly equivalent for the two strategies (consid-
ering the best choice β = 20 and γ = 10 for LMTI).
However, LMTI always allows to stop the epidemic
for a sufficiently large vaccinated fraction (which in-
crease for higher k). TI generally appears more effec-
tive than LMTI for low values of hd
V
i. This can be
explained noticing that for increasing k with fixed m
or increasing m with fixed k, the connection of each
node with individuals belonging to other BA centers
Probing Complexity with Epidemics: A New Reactive Immunization Strategy
119

Figure 2: Results for various immunization strategies for randomly connected BA[2] clusters with N = 5000 total
nodes. The number of BA centers is m = 5 (a,b,c), 10 (d,e,f), 20 (g,h,i), each with k = 100, 500,2000 new links. and
R = 0 (pure BA case, a), 500 (b), 1000 (c), 2000 (d) rewiring events. The LMTI scheme is compared to TI only. The hor-
izontal solid line is the epidemic threshold f = 0.05, while the horizontal dotted lines are 25% and 50% of the mean final
density of recovered without any vaccination.
acquires more and more importance. Thus, it is more
likely that the epidemic spreads on the whole network
rather than to be localized in the initial cluster, there-
fore acquiring an extended front. In this case it is
convenient to adopt a non-local immunization strat-
egy, unless there is a sufficient vaccinations availabil-
ity to surround the infection. Finally, an interesting
aspect is that choices with higher β are more effec-
tive in stopping the epidemic as the network becomes
highly connected and clustered. This is clear from
Fig. 2 for k = 2000, where LMTI with the choice
β = 100 and γ = 10 allows to stop the epidemic for
hd
V
i = 0.25 in networks with m = 5 centers and for
hd
V
i = 0.20 for m = 20 initial clusters.
4.2 Watts-Strogatz Setting
Fig. 3 collects the results for Watts-Strogatz net-
works. They are radically different than the BA set-
ting. As a consequence of absence of hubs, a pure TI
is indeed a poor strategy in WS graphs. On the other
hand, our score shows a much better adaptability. The
presence of the local terms is fundamental in reducing
the epidemic prevalence, giving to the LMTI curves a
profile with a rapid fall-off. The only strategy giving
comparable results for small θ is HR, which was the
worst performer for BA. Moreover, HR performances
are highly sensitive to the θ value and dramatically
worsen for θ = 0.5. An interesting aspect of our strat-
egy is the role of the leverage term. In fact, for WS
network keeping a residual regular structure (θ = 0.1),
the γ-term is totally ineffective. Moreover, it becomes
even deleterious for highly randomized WS (θ = 0.5).
The choice β = 20 and γ = 0 is by far the best per-
former in all WS settings, always allowing to stop
the epidemic with a relatively low vaccinations (note
that all the other immunization strategies fail in doing
this).
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
120
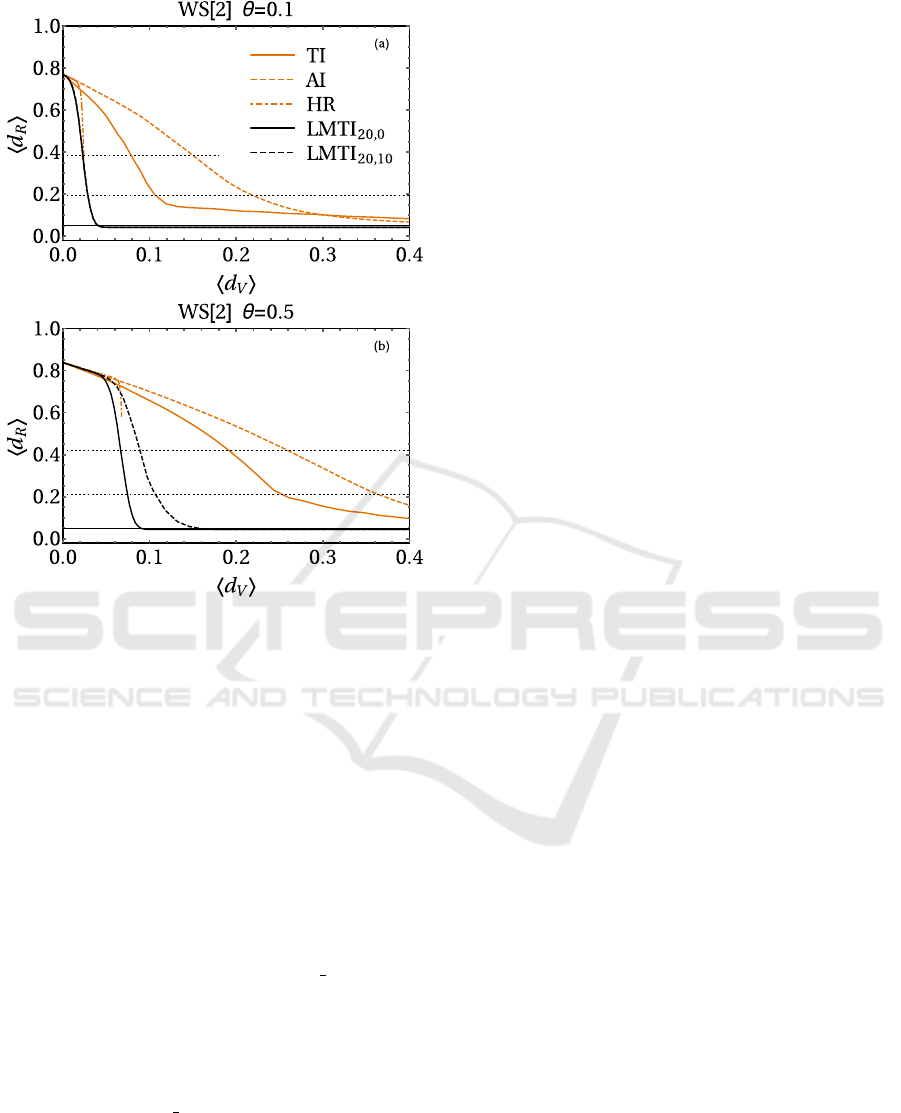
Figure 3: Results for various immunization strate-
gies for WS[2] networks with N = 1000 nodes and
θ = 0.1 (a), 0.5 (b). The LMTI scheme is compared to TI,
AI and HR strategies. The horizontal solid line is the epi-
demic threshold f = 0.05, while the horizontal dotted lines
are 25% and 50% of the mean final density of recovered
without any vaccination.
4.3 Real Networks
Fig. 4 collects the results for real networks. As a gen-
eral result, TI and LMTI are the most indicated strate-
gies for reducing the epidemic prevalence by 50%
(LMTI can cut it to the 25% with a slightly larger
vaccinated fraction). Moreover, HR generally works
worse than AI in all real networks we considered.
It is interesting to note that Internet AS and Pro-
teinYeast networks show a great structural resistance
to epidemic outbreaks. Even without any vaccina-
tion, the average size of an epidemic remains rela-
tively small (less than the 30% of the total popula-
tion). According to the k-shell decomposition (Seid-
man, 1983), Internet AS and ProteinYeast networks
have a relatively small center and a large periphery,
as the first two shells k = 1, 2 account for a very large
fraction of the nodes (respectively the 78% and the
86% of the entire population). ProteinYeast is also
the network with smallest mean degree and highest
vertex eccentricity. In these networks, the eradication
of the epidemic is particularly simple (with LMTI,
this can be done respectively with hd
V
i ∼ 0.15 and
hd
V
i ∼ 0.05). The other networks are much more ex-
posed to the risk of a pandemic outbreak. In fact,
without vaccination the typical size of the epidemic
involves more than the 60% of the population. In
p2p-Gnutella08 and CA-HepTh-pruned networks,
the results for the TI and LMTI with β = 20 are
almost the same, while in both cases the HR strat-
egy fails even in significantly reducing the epidemic
prevalence. It is interesting to note that in the p2p-
Gnutella08 network the AI is particularly efficient,
with performances similar to TI or LMTI for small
values of hd
V
i. With reference to Table 1, this net-
work presents the higher mean degree and the lowest
mean vertex eccentricity, suggesting that it is highly
and uniformly connected. As a consequence, in this
network it is very difficult to control the epidemic
spreading. Finally, results for AA network show again
that TI and LMTI are almost equivalent for small
values of hd
V
i, with the second one doing better for
slightly larger values of the vaccinated fraction.
5 CONCLUSION AND
DISCUSSION
In this work, we proposed a novel reactive immuniza-
tion strategy. It is based on a local modification of
TI protocol which aims to actively take into account
the presence of a propagating epidemic and use it as
a source of information to trigger an optimized vacci-
nation response. We numerically compared our pro-
posal with other standard immunization strategies and
proved that it is a very efficient choice in every case
we considered. Moreover, it always allows to stop the
epidemic with a relatively small vaccinated fraction.
Our proposal naturally fits in the class of techniques
using local knowledge about complex systems (see
for example the Hebbian learning rule (Hebb, 1949)
in the case of neural networks).
There are two important aspects about our novel
immunization strategy we would like to stress. First,
our scheme, so as many other standard immunization
strategies, is strongly information-demanding. Of
course, a full knowledge about the complex system
is rather unlikely in real situations, then sampling and
interpolation (Ferguson et al., 2014), so as data assim-
ilative strategies (Rhodes and Hollingsworth, 2009)
have been recently developed. The second aspect
concerns the role of the tunable parameters in our
strategy. In fact, we compared our LMTI with other
benchmark strategies for an optimal choice of β and γ.
Such a choice consists in the evaluation of the com-
Probing Complexity with Epidemics: A New Reactive Immunization Strategy
121

Figure 4: Results for various immunization strategies on real networks (a-e). The LMTI scheme is compared to TI, AI and
HR strategies. The horizontal solid line is the epidemic threshold f = 0.05, while the horizontal dotted lines are 25% and
50% of the mean final density of recovered without any vaccination. For Internet AS (a), the horizontal dotted line is the 50%
of the mean final density of recovered without any vaccination.
peting roles of global and local features in the epi-
demic spreading and, in general, it depends on the
network model and its size, as well as on the epidemic
threshold. The study of such a dependence is gener-
ally a non-trivial theoretical task and goes beyond the
goal of the present paper. Instead, in our purely phe-
nomenological approach, we tuned the local param-
eters choosing the best pair (β,γ) by looking at the
performances of LMTI in reducing the epidemics. We
therefore did not identify a method to a priori fix the
best values of these parameters. Hopefully, this issue
can be addressed and theoretically better understood
in future works. In doing so, a more detailed exper-
imental analysis of the dependence of LMTI perfor-
mances on the free parameters is necessary.
In conclusion, several extensions of our work are
possible. For example, it can be generalized to other
classes of ideal networks with good theoretical con-
trol, like weighted or directed graphs. It can also be
applied to actual specific diseases, e.g. TBC, Xylella
fastidiosa (Alfinito et al., 2016) or Ebola infections.
In doing this, more realistic propagation models, like
the delayed SIR considered in (Agliari et al., 2013)
and a detailed cost benefit analysis are needed.
REFERENCES
Agliari, E., Asti, L., Barra, A., Scrivo, R., Valesini, G.,
and Wallis, R. S. (2013). Application of a stochastic
modeling to assess the evolution of tuberculous and
non-tuberculous mycobacterial infection in patients
treated with tumor necrosis factor inhibitors. PloS
one, 8(1):e55017.
Albert, R. and Barab
´
asi, A.-L. (2002). Statistical mechan-
ics of complex networks. Reviews of modern physics,
74(1):47.
Alfinito, E., Beccaria, M., and Macorini, G. (2016). Criti-
cal behavior in a stochastic model of vector mediated
epidemics. Scientific reports, 6.
Altarelli, F., Braunstein, A., Dall’Asta, L., Wakeling, J. R.,
and Zecchina, R. (2014). Containing epidemic out-
breaks by message-passing techniques. Physical Re-
view X, 4(2):021024.
Bornholdt, S. and Schuster, H. G. (2006). Handbook of
graphs and networks: from the genome to the internet.
John Wiley & Sons.
Cohen, R., Havlin, S., and Ben-Avraham, D. (2003).
Efficient immunization strategies for computer net-
works and populations. Physical review letters,
91(24):247901.
Colizza, V., Flammini, A., Serrano, M. A., and Vespignani,
A. (2006). Detecting rich-club ordering in complex
networks. Nature physics, 2(2):110–115.
Ferguson, J. M., Langebrake, J. B., Cannataro, V. L., Gar-
cia, A. J., Hamman, E. A., Martcheva, M., and Osen-
berg, C. W. (2014). Optimal sampling strategies for
detecting zoonotic disease epidemics. PLOS Compu-
tational Biology, 10(6):1–13.
Hebb, D. O. (1949). The Organization of Behavior: A Neu-
ropsychological Theory. Wiley, New York.
Hu, K. and Tang, Y. (2012). Immunization for complex net-
work based on the effective degree of vertex. Interna-
tional Journal of Modern Physics B, 26(06):1250052.
Jeong, H., Mason, S. P., Barab
´
asi, A.-L., and Oltvai, Z. N.
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
122

(2001). Lethality and centrality in protein networks.
Nature, 411(6833):41–42.
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., and
Barab
´
asi, A.-L. (2000). The large-scale organization
of metabolic networks. Nature, 407(6804):651–654.
Joyce, K. E., Laurienti, P. J., Burdette, J. H., and Hayasaka,
S. (2010). A new measure of centrality for brain net-
works. PLoS One, 5(8):e12200.
Kermack, W. O. and McKendrick, A. G. (1927). A con-
tribution to the mathematical theory of epidemics. In
Proceedings of the Royal Society of London A: Math-
ematical, Physical and Engineering Sciences, volume
115-772, pages 700–721. The Royal Society.
Liu, S., Perra, N., Karsai, M., and Vespignani, A. (2014).
Controlling contagion processes in activity driven net-
works. Physical review letters, 112(11):118702.
May, R. M. and Anderson, R. M. (1979). Population
biology of infectious diseases: Part ii. Nature,
280(5722):455–461.
Nian, F. and Wang, X. (2010). Efficient immunization
strategies on complex networks. Journal of theoret-
ical biology, 264(1):77–83.
Pastor-Satorras, R., Castellano, C., Van Mieghem, P., and
Vespignani, A. (2015). Epidemic processes in com-
plex networks. Rev. Mod. Phys., 87:925.
Pastor-Satorras, R. and Vespignani, A. (2002). Immu-
nization of complex networks. Physical Review E,
65(3):036104.
Pereira, T. and Young, L.-S. (2015). Control of epidemics
on complex networks: Effectiveness of delayed isola-
tion. Physical Review E, 92(2):022822.
Perra, N., Gonc¸alves, B., Pastor-Satorras, R., and Vespig-
nani, A. (2012). Activity driven modeling of time
varying networks. Scientific reports, 2.
Rhodes, C. and Hollingsworth, T. (2009). Variational data
assimilation with epidemic models. Journal of Theo-
retical Biology, 258(4):591 – 602.
Ruan, Z., Tang, M., and Liu, Z. (2012). Epidemic spreading
with information-driven vaccination. Physical Review
E, 86(3):036117.
Seidman, S. (1983). Network structure and minimum de-
gree. Social Networks, 5(3):269–287.
Stauffer, A. O. and Barbosa, V. C. (2006). Dissemination
strategy for immunizing scale-free networks. Physical
Review E, 74(5):056105.
Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics
of ‘small-world’ networks. Nature, 393(6684):440–
442.
Yan, S., Tang, S., Pei, S., Jiang, S., and Zheng, Z. (2014).
Dynamical immunization strategy for seasonal epi-
demics. Physical Review E, 90(2):022808.
Probing Complexity with Epidemics: A New Reactive Immunization Strategy
123
