
Task Offloading for Scientific Workflow Application in Mobile Cloud
Feifei Zhang, Jidong Ge, Zhongjin Li, Chuanyi Li, Zifeng Huang, Li Kong and Bin Luo
State Key Laboratory for Novel Software Technology, Software Institute, Nanjing University, China
jxzhang_ch@163.com, gjd@nju.edu.cn, lzjnju@126.com, lcynju@126.com, {141250051, dz1632001}@smail.nju.edu.cn,
Keywords: Mobile Cloud Computing, Scientific Workflow, Genetic Algorithm, Task Offloading.
Abstract: Scientific applications are typically data-intensive, which feature complex DAG-structured workflows
comprised of tasks with intricate inter-task dependencies. Mobile cloud computing (MCC) provides
significant opportunities in enhancing computation capability and saving energy of smart mobile devices
(SMDs) by offloading computation-intensive and data-intensive tasks from resource limited SMDs onto the
resource-rich cloud. However, finding a proper way to assist SMDs in executing such applications remains a
crucial concern. In this paper, we offer three entry points for the problem solving: first, a cost model based on
the pay-as-you-go manner of IaaS Cloud is proposed; then, we investigate the problem of mapping strategy
of scientific workflows to minimize the monetary cost and energy consumption of SMDs simultaneously
under deadline constraints; furthermore, we consider dataset placement issue during the offloading and
mapping process of the workflows. A genetic algorithm (GA) based offloading method is proposed by
carefully modifying parts of GA to suit the needs for the stated problem. Numerical results corroborate that
the proposed algorithm can achieve near-optimal energy and monetary cost reduction with the application
completion time and dataset placement constraint satisfied.
1 INTRODUCTION
Nowadays, smart mobile devices (SMD), e.g.,
smartphones and tablet-PCs, have been widely
employed as a major computing platform due to their
portability and compactness. As might be expected,
SMDs are gaining enormous popularity for
supporting computation intensive applications, such
as interactive gaming, image/video processing, e-
commerce, and online social network services
(Cohen, 2008), (Soyata, 2012). Those kinds of mobile
applications are typically resource-hungry, while the
computing capacity on mobile devices is often
limited. Thus, the gap between the gravimetric energy
density of rechargeable batteries and the power
demand of mobile devices for executing complex
tasks will continue to widen (Kumar, 2013), (Liu,
2013).
The elastic resource provisioning of cloud
computing promises to close the gap between the
limited resources of mobile devices and the growing
resource demands of mobile services through
offloading resource-intensive tasks. In mobile cloud
environments, cloud-based resource provisioning
extends beyond the public cloud. Thus, a valid
approach is to offload computation intensive parts of
applications to the cloud for execution. The basis of
this method is that a mobile application in MCC needs
to be decoupled into a series of tasks which can be
executed on the mobile device or on the cloud.
Although offloading such tasks can augment the
computing capability of mobile devices, it does not
always guarantee performance enhancement. On the
one hand, computation-intensive and data-intensive
applications may entail large data transfer between
the cloud and the mobile device as well as among
different VM nodes in cloud, which counteracts the
potential computing performance benefits and incurs
higher latency. On the other hand, when a mobile
device’s battery is either full or not a concern,
offloading mobile applications to the cloud will boost
unnecessary spending. Furthermore, in extreme
cases, the mobile device may be unable to afford the
energy required for heavy data transfers. Therefore,
to achieve better support for complex mobile
applications, a trade-off between local execution and
cloud execution for each task must be judiciously
made.
Another challenge is that obtaining offloading
solutions in mobile cloud environment is the NP-
136
Zhang, F., Ge, J., Li, Z., Li, C., Huang, Z., Kong, L. and Luo, B.
Task Offloading for Scientific Workflow Application in Mobile Cloud.
DOI: 10.5220/0006364501360148
In Proceedings of the 2nd International Conference on Internet of Things, Big Data and Security (IoTBDS 2017), pages 136-148
ISBN: 978-989-758-245-5
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

complete problem, and hence it takes a long time to
derive optimal solution for large-scale applications.
This work goes deep into the infrastructure level
of public cloud, takes the pay-as-you-go basis and
concrete cost model of cloud platform into
considerations, and further investigate the problem of
mapping strategy of scientific workflows to minimize
the monetary cost and energy consumption of SMDs
under deadline and data placement constraints in
MCC.
The main results and contributions of this paper
are as follows:
workflow mapping among virtual machine nodes
and SMDs. The workflow mapping details on
infrastructure level of public Cloud are considered
when building models for MCC environment,
which include the number of VM nodes leased,
the differ bandwidths, different cost per use and
different amount of available resources for each
VM type. In addition, a combined scheme of task
offloading between SMDs and Cloud as well as
task mapping among VMs in the cloud is
proposed to achieve better performance.
Concrete cost model. This approach further
considers the monetary cost of leasing virtual
machine nodes, which includes factors such as the
number of VM nodes leased, different cost per use
and different amount of available resources for
each VM type. With specific designing method,
the time cost model can be represented as a
weighted linear combination of a set of non-linear
functions of variables indicating the time units
paid. Sound decisions are made on the number
and types of required VMs.
Fix data placement constraint. It is unexpected to
migrate some datasets involving user privacy to
the public cloud. We address this issue during task
offloading and mapping process by forcing such
dataset-related tasks (fixed tasks) to be executed
locally on the mobile device.
GA-based workflow mapping algorithm. By
designing the encoding policy and genetic
operators adaptively based on the MCC
environment, we could simultaneously reduce the
search space, accelerate the search speed, and
enhance the search capacity.
2 RELATED WORK
Workflow scheduling for performance improvement
of scientific applications running in cloud
environment has been addressed in several research
studies (Calheiros, 2014), (Liu, 2016), (Xu, 2016),
(Wu, 2015). Zhu et al. (Zhu, 2016) propose FASTER
algorithm for real time workflow scheduling in the
virtualized cloud. Sahni et al. (Sahni, 2016) design
WPA task clustering technique to achieve maximum
possible parallelism among the tasks of a workflow
while minimizing overheads and resource wastage of
the system. Li et al. (Li, 2016) further consider
security and cost aware problem for heterogeneous
tasks of scientific workflow in clouds.
However, those workflow scheduling
methodologies cannot be directly applied to mobile
cloud environment. Considering the needs of mobile
cloud environment, there have been various studies
investigating task offloading problem from mobile
devices to the Cloud. Liang et al. (Liang, 2016) point
out that the high price of data transmission between
mobile devices and the remote cloud through cellular
networks is the major challenge in MCC. Guo et al.
(Guo, 2016) demonstrate that the maximum
completion time of its immediate predecessors, the
clock frequency and transmission power of the
mobile device can also be crucial factors in making
computation offloading selection. They then propose
a dynamic offloading and resource scheduling policy
to reduce energy consumption and shorten
application completion time. However, this
scheduling policy cannot guarantee an optimal result.
Elgazzar et al. (Elgazzar, 2014) develop a cloud-
assisted mobile service provisioning framework in
delivering reliable service. their framework performs
well in maximizing the performance gain and the
energy consumption on mobile system. Deng et al.
(Deng, 2015) propose a fault-tolerance mechanism
and use a modified GA algorithm to obtain a near-
optimal offloading strategy.
The task offloading algorithms mentioned above
focus on offloading computation-intensive tasks
which considers the frequent interactions between
users and devices. In such applications, data is mainly
from the control information sent by users and the fed
back information provided by the system, which are
different from data-intensive scientific workflow
applications.
The field of data placement had been deeply
studied. Yuan et al. (Yuan, 2010) use BEA algorithm
(McCormick, 1972) to distribute the data
dependencies into several data centres, where the
partitions with fixed location datasets are placed in
the proper data centres. Zhao et al. (Zhao, 2012)
propose a GA based data placement strategy to reduce
data movements between storage nodes and
computing nodes to overcome the limitations of
bandwidths between data centres. Deng et al. (Deng,
2011) utilize data placement strategy to place datasets
Task Offloading for Scientific Workflow Application in Mobile Cloud
137

and tasks onto appropriate places to minimize the
total amount of data transfer between datacentres.
The methods mentioned above try to find a proper
data placement strategy in multi- data centres
environment to either support the efficient execution
of scientific workflows or improve the performance
of data centres. Furthermore, the idea of data
placement is also applicable for mobile cloud
environment. In this work, the problem of fixed
location data is solved by forcing such dataset-related
tasks to be executed locally on the mobile device
whilst considering the performance of mobile
applications.
In general, processing time, energy consumption,
data placement and monetary cost are four typical
concerns for workflow execution in mobile cloud
environment. Given this motivation, we focus on
developing an energy-aware and cost-aware scientific
workflow task offloading strategy under deadline and
data placement constraints in Mobile Cloud
environments.
3 MOBILE CLOUD COMPUTING
MODEL
3.1 Workflow
This paper focuses on the general workflow
representation which includes parallel and sequence
control flow structure. Thus, a workflow application
W
,
, where
|
|
and
|
|
is modelled as
a Direct Acyclic Graph (DAG).
,
,⋯,
is
the set of tasks and
,
,
∈⋀
is
the set of data and control dependencies. An edge
of the form
,
exists if there is a data or control
dependency between
and
, case in which
is
said to be the predecessor of
and
is said to be the
successor of
. This relation indicates that the
execution of task
can only start after the
completion of task
. The set of predecessors and
successors of a task
is represented by
and
, respectively.
Thus,
and
are respectively
formulated as
∈∖
⋀
,
∈ (1)
∈∖
⋀
,
∈ (2)
For a given
,
denotes an entry task
satisfying
∅ (3)
and
denotes an exit task satisfying
∅ (4)
The weights assigned to the tasks represent their
workload, and the weights attached to the edges
represent the size of the data transferred between
tasks. The workload of
is
and the
data transfer size from
to
is denoted as
,
. Furthermore, each workflow has a
and an execution associated to it.
A
is defined as a time limit for the execution
of a workflow. In other word,
must be satisfied.
Let
and
be start time and finish time
of task
, respectively. Thus, it can be obtained that
0 and
.
What’s more, an application with multiple entry
or exit tasks can be converted to this model by adding
a pseudo
and/or a pseudo
and their
associated edge with zero weight to the DAG.
3.2 IaaS Cloud Model
The Cloud model consists of an IaaS service provider,
which provides high-performance computational
resources via virtual machines (VMs) over the
Internet to execute large scale scientific workflows.
Usually, IaaS platform provides a broad range of
instance types comprising varying configurations of
CPU, memory size and network bandwidth. Each
configuration is associated with corresponding cost of
per time interval.
We thus define an IaaS Cloud service
,
, where the infinite set
,
,⋯
describes all available VM instances in an IaaS
platform. Each VM instance has a VM type
associated to it. The set
,
,…,
describes
all the instance type where
is the number of instance
type in IaaS platform. Each VM type
is defined by
,
,
, where
denotes the
capabilities (number of cores) of VM type
, c
represents the cost per time unit of VM type
, and
is the bandwidth of instance type
. Different
types of VM instances differ from each other in
bandwidths, CPU capabilities and cost per use.
Intuitively, bandwidths and CPU capabilities are
proportional to the cost per use.
3.3 Mobile Communication System
To unify the representations in workflow mapping
problem, we use
,
,
to represent the
mobile communication system, where
is the SMD
instance,
refers to the type of SMD, is a base
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
138

station. This work is based on the scenario that one
SMD interacts with IaaS platform through a base
station.
A SMD is modelled as a 4-tuple
,
,,
where
is the CPU
processing capability (in cores number) of a mobile
device,
is the power consumption of a mobile
device when running tasks locally, / is the
power consumption of a SMD when transmits/
receives data.
A base station is a radio receiver/transmitter that
serves as the attachment point of the local wireless
network; it is represented as a tuple
,
where rs / rr is its transmission rate (in Kbps) for data
being uploaded/ downloaded to/from IaaS platform.
Please note that the SMD cannot execute the task
and send/ receive data at the same time, and pre-
emption is not allowed.
3.4 MCC Task Offloading
3.4.1 Local Execution
Before a task
is run locally, all its immediate
predecessors must have already been executed. The
start time of task
, denoted as
is calculated as
, max
∈
,
. (5)
is the available time of the SMD,
which changes dynamically during workflow
execution.
,
is the finish time of data
transmission between
and
. Because we don’t
consider the parallels between data transmission and
task execution, after
is decided to be executed on
SMD,
will be updated with the finish
time of output data transmission of
. To determine
the value of
,
, The following two cases for
’s immediate predecessor task
(i.e.
∈
)
are considered
:
If task
has been executed locally,
,
. (6)
other words, the transmission time between two
consistent tasks in SMD is zero. This is because
the data transfer time between tasks sequentially
executed on the same machine is negligible
compared with the data transfer time between
tasks allocated on different machines.
If task
has been offloaded onto the Cloud,
,
,
, (7)
where
,
,
. (8)
,
is the time spent receiving output
data of
from Cloud to the SMD. Usually, the
bandwidths of VM instances is wider than
wireless receiving channel. So, in this case, we
use the data receiving rate of the wireless
receiving channel
to compute data
transmission time.
The execution time of a workflow task depends on
its workload and the CPU capability of SMD. Here
we compute execution time for locally executed tasks
as follow:
, (9)
where
is the workload for the non-
offloaded task
to be locally executed at a mobile
device and
is the CPU capacity (cores) for
SMD. If
is not executed locally, then
0.
Thus, the finish execution time of local task can
be calculated as
. (10)
The task execution on the SMD can bring about
certain amount of energy consumption, which is
proportional to the local execution time. Intuitively,
given the power consumption
of mobile
terminal, energy consumption of locally executed
task
is given by
. (11)
3.4.2 Cloud Execution
Suppose that task
is to be offloaded onto the cloud.
The start execution time of task
, denoted by
,
is calculated as:
, max
∈
,
. (12)
is the available time of instance
, which
is dynamically changed during workflow execution.
Likewise, after
is decided to run on the instance
,
will be updated with the finish time of
output data transmission of
. Consider the several
cases for
’s immediate predecessor task
(i.e.
∈
):
If
has been mapped to the same instance as
,
then
,
, (13)
Task Offloading for Scientific Workflow Application in Mobile Cloud
139

which means the transmission time can be
neglected.
If
has been executed locally, then
,
,
, (14)
where
,
,
. (15)
denotes the data sending rate of the wireless
sending channel.
If
has been mapped to another instance in
Cloud, then
,
,
, (16)
where
,
,
,
,
0,
. (17)
and
are types of the instances to which
and
are mapped, respectively. The
communication bandwidths are usually differed
for different VM instance types, and the fact that
types with higher
have higher bandwidths is
intuitive. The bandwidths used in actual data
transmission is limited by smaller one.
In this work, all the tasks are assumed to be
parallelizable so that the multi-core CPU can be well
utilized. Therefore, the actual running time of
offloaded to the cloud depends on its workloads
and the CPU capabilities
of VM
instance
. Thus, we have
. (18)
The finish execution time of this offloaded task
can be calculated as
. (19)
For all the existing IaaS platforms, the basic
pricing rule is the same—charging per-instance
usage. VMs are charged per integer amount of time
units, and partial utilization of a period incurs charge
for the whole period. A typical example is Amazon
EC2, customers need to pay for full instance-used
hour even for few minutes’ lease. The initial start-up
time for VMs is ignored in this work.
It is assumed that the cost for executing a
workflow is linearly correlated to the total of CPU
cycles consumed. The time unit
of VM in which the
pay-per-use model based is a fix-size interval
specified by the provider. Thus, the total spending of
a workflow is the sum of costs of all the leased VMs.
Based on the above analysis, we use
c
to represent
the cost per time unit of VM type
. The monetary
cost of instance
is given by:
c
, (20)
where
∑
∈
∈∧
∧
(21)
and
,
,
⋀
,
,
0,
. (22)
A VM needs to stay in motion when receiving the
input data of running tasks. Thus, the service time of
a running task includes two parts: the actual execution
time and the input data receipt time. When calculating
input data receiving time, as is shown in Eq. (21), we
should consider the instances where the predecessor
tasks allocated to and derive their data transmission
time accordingly.
4 ALGORITHM DESIGN
In this section, we illustrate the genetic algorithm
based task offloading algorithm for scientific
workflow applications in MCC environment. This
algorithm runs on SMDs to achieve intelligence
interactions between SMDs and Cloud. GA is proved
to be an effective approach widely applied in
optimizing problems. Due to the special nature of
Mobile Cloud Computing, GA’s existing generic
operators cannot be directly applied to the mobile
cloud workflow mapping problem. From this base, a
modified set of GA operators, including encoding
strategy, initialization of population, mutation, and
crossover, is presented.
4.1 Task Offloading Problem
A workflow
,
models a scientific mobile
application. Given a mobile communication system
,
,
and an IaaS platform
,
, a
workflow mapping problem is to develop a solution
,
where and are relationships
which have tasks map to instances and instances map
to instance types, as
:→,
, (23)
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
140

:→,
, (24)
where
∪
,
∪
. It is intuitively
that
.
01234567
0
1234567
0
1234
Tasks:
Instances:
Types:
Figure 1: a valid mapping scheme for the DAG example.
In this paper, we consider the problem that some
tasks of an application can only be executed locally.
For such task
, its mapping relation is pre-defined
from task to instance:
. (25)
The set of such task can be denoted as
|
.
(26)
should be determined before task
offloading.
We mainly focus on optimal mapping strategies to
concurrently optimize the monetary cost and energy
consumption for running mobile applications
(workflows). To this end, the mapping strategy
objective function is defined as a weighted sum of
running application’s billing in IaaS cloud plus
energy consumption of mobile device; The goals of
the offloading problem
,
for mobile
communication system
and IaaS Cloud platform
are formulated as follows:
1
,
,
(27)
where
∗
|
∃
∈:
.
(28)
∗
denotes the set of VMs that needs to be leased
during workflow execution. The weight coefficient
, the range of which is from 0 to 1, is set based on
the battery status of SMD and budgets of the user;
e.g., when a mobile device’s battery is either full or
not really matters, higher values of
will be afforded;
lower values must be set when its energy drops below
a threshold. This weight can however be adjusted
based on specific users’ requirements if desired.
4.2 Encoding
As discussed in Section 4.1, a solution is a two-tuple
containing two maps and . A chromosome is
splatted into two strings to represent them
respectively.
The string
2 is a vector representation for
the map , in which an index represents a task and
its value represents the instance where this task will
be executed. For example,
2 makes
be assigned to the instance with index (represented
as
). The string 2 is a map from instance
indexes to their types, representing the mapping type.
For example,
2 indicates that the type
of instance
is .
Supposed that
|
∗
|
where
is a positive
integer. Because a task can only run on one instance
in IaaS platform or on SMD however one VM
instance can run multiple tasks sequentially, we have
. A heterogeneous environment can be
constructed by
instances in Cloud, where is
the number of instance types. Therefore, for each task
in the workflow, there is
location choices for
task execution.
However, in the proposed algorithm, those tasks
forced be executed locally on the SMD should be
excluded before encoding, otherwise it will
negatively affect the performance of genetic
algorithm.
2 5 0 1 2 6 4 0
0 2 1 1 3 2 4 2
01234567
task2ins
ins2type
2 5 0 1 2 6 4
1 2 1 3 2 4
0123456
123456
01234567
Figure 2: encoding strategy of chromosomes.
Supposed that the number of tasks belonging to
is (0), the number of tasks encoded
should be
. What’s more, for 2 string, it
is pre-defined that
200, so 20 is
excluded from string
2 (Fig. 2). As the fix-
length decimal encoding scheme is adopted, the
length of strings
2 and 2 is set to be
1 and respectively. In this way, it is
possible to index all instances using integers from
0
to
1 and all instance types using integers from
0 to 1.
4.3 Fitness Function
A fitness function is used to evaluate a possible
individual in finding the optimal solution. We use the
objective function in Eq. (27) to calculate the fitness
value of each chromosome. This objective function
Task Offloading for Scientific Workflow Application in Mobile Cloud
141

consists of two parts: the total monetary cost and the
total energy consumption for executing the whole
mobile scientific workflow. Both parts are combined
into one parameter with a user defined weighting
factor. The user requirements for each workflow can
be controlled through weights of the monetary cost
and the energy consumption.
However, it is necessary to consider the constraint
. For each iteration, GA
generates new mapping schemes, and calculate the
corresponding
and application completion time
.
Taken together, the fitness value for individual
in a population is given by
1
,
(29)
where
is a penalty factor taking an appropriate
value to punish individuals who violate the deadline
constraint. To further guarantee the advantage of
valid individuals, we have
0 when
.
Given a fitness function, GA would iteratively
find a near optimal solution as follows. First, a set of
population is initialized. Then, for each iteration,
chromosomes are selected, recombined by mutation
and crossover operations, then copied to the new
population for the next iteration. This procedure is
repeated until one of the following two terminating
conditions is satisfied: i) the maximum number of
iterations is reached, and ii) fitness value of the best
chromosome in consecutive populations does not
improve anymore.
4.4 Genetic Operators
4.4.1 Crossover
In the crossover phase, Chromosomes are recombined
for generating the next population. The selection is
based on a roulette-wheel method. The probability of
selecting a chromosome for recombination is related
to its fitness value
and is calculated as
follows:
∑
, (30)
where
(31)
and
is the size of current population.
Parent1:
Task2ins:2,5,0,1,2,6,4
Ins2type:2,1,1,3,2,4
Parent2:
Task2ins:1,6,2,0,4,3,0
Ins2type:3,1,4,3,4,2
2 5 0 1 2 6 4
2 1 1 3 2 4
1 6 2 0 4 3 0
3 1 4 3 4 2
task2ins
ins2type
tasks
instances
0123456
0123456
mask10011010
ins2type
instances
task2ins
tasks
123456
123456
mask2101101
2 5 2 0 2 3 4task2ins
tasks
0123456
1 6 0 1 4 6 0task2ins
tasks
0123456
3 1 4 3 2 2ins2type
instances
123456
2 1 1 3 4 4ins2type
instances
123456
Child1:
Task2ins:2,5,2,0,2,3,4
Ins2type:3,1,4,3,2,2
Child2:
Task2ins:1,6,0,1,4,6,0
Ins2type:2,1,1,3,4,4
Figure 3: mask-based crossover operation.
As is shown in Fig. 3, the uniform crossover
operation is done separately for string
2 and
2. In this way the contradictions between
mapping → and mapping → can be eliminated.
Take the crossover operator for the
2
strings as an example. First, the operator randomly
generates a bit string of 0’s and 1’s of chromosome
length
as a mask vector, which decides the
corresponding locus on parent chromosomes to
overlap or not. Then, each parent order string is
scanned from the beginning. For each position
, if
1, two parent chromosomes will swap
genes in position
; otherwise, no swap.
The strings 2 are operated in an
analogously way as string 2, except that the
length of mask vector should be .
4.4.2 Mutation
The mutation operator is to slightly modify
chromosomes in the population to enlarge the search
fields of GA. In this step, some genes on
chromosomes are chosen to mutate based on a
probability calculated with the consideration of the
energy consumption, monetary cost and
.
The probability of mutating chromosome
is
calculated as:
∑
, (32)
where
is calculated according to Eq. (31).
Thus, mutation rate for task offloading schemes
with more monetary cost and energy consumption are
higher than the others.
For the chromosomes to be mutated, polygenic
mutation strategy is adopted. The number of genes to
be mutated in a chromosome depends on its fitness
value. The smaller the fitness value is (which means
the quality of solution is better), the less the genetic
mutations in a chromosome. The reason behind is that
although traditional way of mutation can lead to
superior population diversity, it can also cause
chaotic generation of offspring chromosomes which
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
142

do not inherit the benefit parts from their parents.
Therefore, we modify the mutation operator to lead
the population to evolve towards more benefits for
fitness value minimization. The number of genetic
mutations of a chromosome is computed as follows:
, (33)
where is a constant. In practice, we usually set
in range 1/4,1/3 for string
2 and 1/4,1/3 for string 2.
denotes the scope of
current generation’s fitness value.
denotes the distance between the fitness
value of individual and minimum fitness value in
the current generation.
indicates the relative quality of individual in the
current population. A higher value of
indicates a
worse quality of individual ; otherwise, a better
quality. Therefore, by Eq. (33), the mutation bit
number can be adaptively determined: for good
quality individual, the mutation bit number is small or
even equal to 0; for bad quality individual, the
mutation bit number is slightly larger.
1 6 0 1 4 6 0task2ins
tasks
0123456
1 6 2 1 4 6 0task2ins
tasks
1 6 0 1 4 6 0
0123456
0123456
task2ins
tasks
1 6 4 1 0 6 0
0123456
task2ins
tasks
a b
Figure 4: Mutation Operator.
For 2 and 2 of individual , we
randomly generate
integers in range 0,…,
and
1,…, to decide the mutation positions,
respectively. Strings are mutated by a random choice
of two methods, with equal probability. The first
method is called “internal mutation”, which is by
swapping instance; the second one is “external
mutation”, which introduces new genes from outside.
4.4.3 Population Initialization
To accelerate the converge speed of genetic algorithm
as well as to ensure the constraints being satisfied, we
use the following two method to generate initial
population:
Heuristic-Based Method: In this method, we
generate the minimal-delay workflow map
without considering the energy consumption of
the SMD and the monetary cost for renting VMs.
We modify HEFT algorithm (Topcuoglu, 2002) to
jointly schedule tasks on the SMD and each VM
instance in cloud. For each task
in the
workflow, please note that if task
belongs to set
, it should be assigned to the SMD for
execution.
Random Generated method: we generate random
schedules for population initialization to increase
the diversity of the population. That is, for each
task in the workflow, randomly choose a machine
for execution. In a similar way, we need to ensure
that Eq. (26) is satisfied.
5 COMPLEXITY ANALYSIS
The computational complexity of the proposed
algorithm is calculated based on its initialization,
selection, crossover, mutation and fitness evaluation
operators. It is supposed that the algorithm iterates for
generations with a population size . i) The
computation complexity of the fitness value
calculation is
. Because the fitness value
calculation is done for each chromosome, the
complexity of fitness evaluation is
. ii) As the selection operator is based on a
roulette wheel method, in the worst case, an
scan is needed to do a simple query. iii) The time
complexity of crossover and mutation operator is
. iv) The complexity of the initialization
operator is
.
Thus, the overall complexity of the proposed
algorithm is
. In practice, is
usually much less then .Therefore, the most
time-consuming parts would still be the evolution
procedures, with the complexity of
.
6 PERFORMANCE EVALUATION
6.1 Experiments Setup
Several experiments are performed to investigate the
properties of the proposed algorithm. Simulations are
run on a machine with two Intel Core i7-6500U CPU
with 2.5 GHz and 2.59 GHz respectively with 8 GB
of RAM. All algorithms are implemented in Java 8.
mobile scientific workflows with random
computation tasks and structures are generated for
simulations. For each computation task, the
input/output data size and the workload are based on
a uniform distribution.
We use the parameters of IaaS platform in table 1
which is also used by (Zhu, 2016). It is supposed that
the CPU capability of mobile device is 2 (cores), the
Task Offloading for Scientific Workflow Application in Mobile Cloud
143

upload transmission rate is 4M/s, the power
consumption of task execution on mobile device is 2,
the power consumption of RF component when
sending and receiving data is 0.5 and 0.15,
respectively.
Table 1: IaaS parameters used in experiments.
Instance
Type
Number of
cores
Bandwidths
(M/ s)
Price
($/ h)
m1.small 1.7 37.5 0.06
m1.medium 3.75 81.25 0.12
m3.medium 3.75 81.25 0.113
m1.large 7.5 81.25 0.24
m3.large 7.5 81.25 0.225
m1.xlarge 15 125 0.48
m3.xlarge 15 125 0.45
m3.2xlarge 30 125 0.9
6.2 Compared Algorithms
The effectiveness of the proposed algorithm is
verified on a set of generated task graphs with
different specifications. The proposed algorithm is
referred to as GA in the following evaluations. We
compare the mapping result of GA to six baseline
algorithms.
Baseline 1 algorithm comprises of only the
heuristic initialization step of GA, which is used
to demonstrate the effectiveness of the modified
genetic operations.
Baseline 2 algorithm is the random algorithm
which randomly chooses machines for task
executions. It serves as a reference in the deadline
satisfaction rate evaluation. For each task in the
task graph, if it belongs to
, then it is
assigned to the SMD; else it is randomly assigned
to any machine for execution.
Baseline 3 algorithm uses the same genetic
operators as GA except adopting random
algorithm to generate initial population and it is
used to measure the performance of the modified
population initialization method.
Baseline 4 algorithm is a basic genetic algorithm
which uses uniform crossover and uniform
mutation.
Baseline 5 algorithm gives an optimal solution
(without deadline constraint) to estimate the upper
bounds of energy and cost minimization.
Baseline 6 algorithm is a genetic algorithm which
minimizes the
of workflow.
In addition, the following setups are used:
For GA, baseline 3, 4, 5 and 6 algorithms, the size
of population is 50 and the maximum iteration
number is 300, the crossover rate and mutation rate is
0.3 and 0.2 respectively. In addition, during
population initialization procedure, the populations
generated by heuristic based method and random
method are in a proportion of 1:1.
For GA, baseline 3 and 4 algorithms, a penalty
coefficient which can dynamically change per
generation
is introduced
. It is defined as:
0.05,
8
4,
. (34)
For baseline 6 algorithm, the workflow mapping
is repeated for 100 times and the most optimal one
(the
is minimized) is picked up.
Furthermore, to remove disturbance, we use the
same way to compute
and fitness value in
all algorithms.
6.3 Results and Discussions
There are four variables can possibly affect the
performance of workflow mapping algorithms: user
defined deadline,
, size of
set and the
number of tasks included in workflow. One variable
is tuned and the others are fixed in each evaluation.
6.3.1 Deadline Constraint Evaluation
A deadline is defined as a time limit for the execution
of the workflow. To analyse the algorithms in terms
of meeting user defined deadline, we plotted the
percentage of deadlines met for each user-defined
deadline value. The basic runtime is defined as the
execution time obtained with an offloading policy
that assigns each workflow task to the most powerful
virtual machine, which is rather efficient, as only
conditioned by data transfers. Therefore, the running
time range of the random generated workflow for the
simulation is within [65.8, 372.6] minutes. The
smallest deadline value is then defined as about 10
percent of the proportional base value for workflow
runtime and with an increment of 10 in the evaluation.
As a control, we set
0.5
and
|
|
|
|
0.2
.
Figure 5: the deadline satisfaction rate versus deadline
value.
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
144
The results are shown in Fig. 5. For baseline 2
algorithm, as the deadline value increases, the
deadline satisfaction rate increases. It can be inferred
that baseline 2 algorithm reflects the
distribution of general workflow mapping schemes.
The deadline satisfaction rate of GA is significantly
higher than baseline 2 algorithm with the range from
75% to 100% and mean value 94%. When deadline
value is less than 145, the satisfaction rate of baseline
3 algorithm is much lower than GA. However, it still
outperforms baseline 2 algorithm by an average of
22.7%. When deadline value is larger than 165,
almost all the mapping solutions produced by
baseline 3 algorithm satisfy the deadline constraint.
Figure 6: the average fitness value versus deadline value.
Fig. 6 reveals the average objective function value
of each algorithm when deadline changes. The
smaller the fitness function is, the better. Baseline 2
algorithm performs remarkably worse than the other
three algorithms. GA clearly outperform baseline 1
and 3 algorithms. When deadline value is less than
125, baseline 1 algorithm performs better than
baseline 3 algorithm. However, baseline 3 can still
defeat baseline 1 algorithm in most cases, although it
is lost to GA.
This simulation reveals that GA makes better
trade-off between deadline constraint satisfaction rate
and the optimization goals than other algorithms.
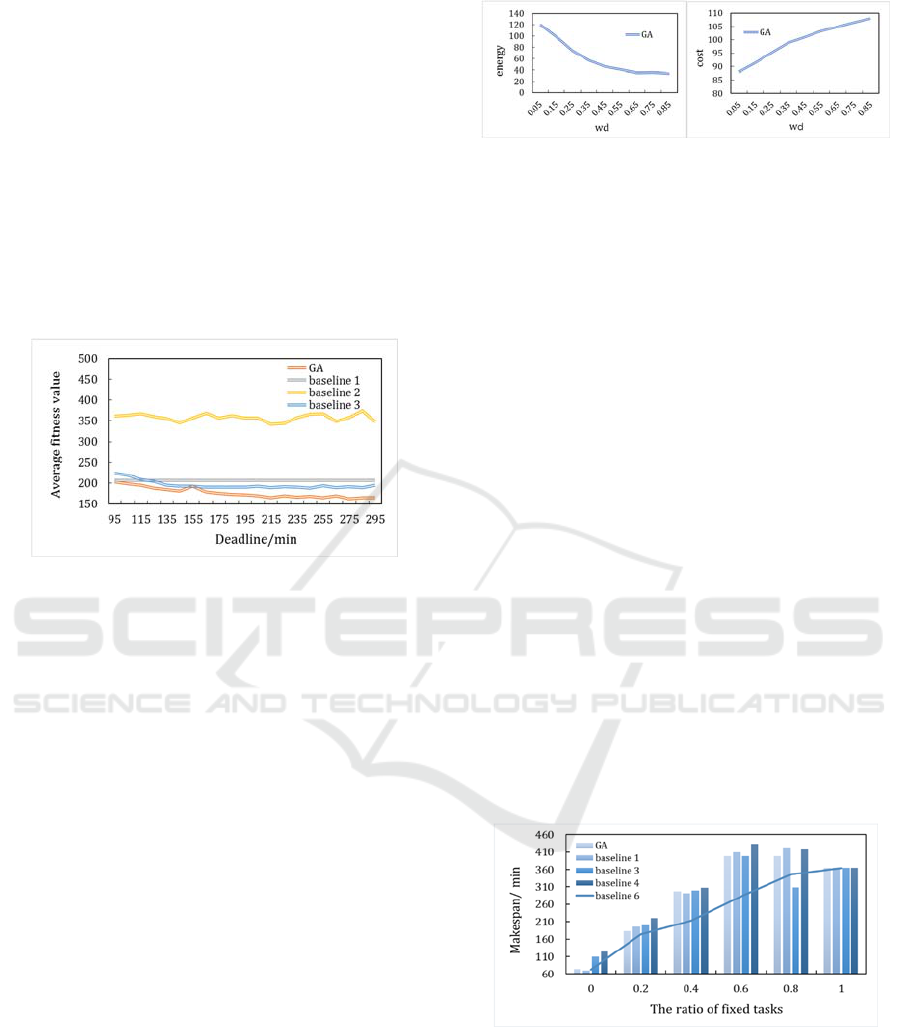
6.3.2
Value Evaluation
Based on Eq. (27), different values of
is used to
simulate different mobile device’s battery statuses
and budget situations. Fig. 7(a) and Fig. 7(b) shows
the effect that increased
value has on the energy
consumption and monetary cost respectively. When
value increases, the energy consumption of GA
decreases while monetary cost increases with
.
This is because
can manage the weight of energy
and cost, larger
value means more focusing on
energy minimization and properly allowing more
monetary cost.
(a) (b)
Figure 7: the average energy consumption versus
value
(a) and the average monetary cost versus
value (b).
6.3.3 Fixed Tasks Evaluation
Fig. 8 presents the effect that the increased size of
fixed tasks set has on the workflow execution time.
As expected, increased size of
tends to further
adds to execution time. The results show that with the
increase in size of
, the advantage of baseline 1
algorithm in minimizing
is diminishing.
When the weight value is 0.6 and 0.8, GA can
produce task offloading scheme whose
is
even smaller. When all tasks in the task graph are
executed locally, all the algorithms produce the same
result.
As is shown that baseline 1 algorithm is not robust
to the fixed tasks set size. That is, when the ratio of
fixed tasks grows, baseline 1 algorithm can no longer
generate the mapping scheme whose
is
minimized. The reason for this underperformance is
the recursion strategy of HEFT, which causes
processor selection of each step to be independent.
For example, if task
in task graph is assigned to
VM instance
according to HEFT, however it
belongs to
and should be executed locally on
SMD. This deviation will certainly interference with
the processor selection of its successor tasks.
Figure 8: the average versus the proportion of
fix tasks.
It can be observed that the larger the weight of
fixed tasks will cause poorer workflow execution
performance. Furthermore, baseline 1 algorithm is
used in GA to produce part of its initial population, so
it may cause performance deterioration of GA when
minimizing
. However, it is still able to
Task Offloading for Scientific Workflow Application in Mobile Cloud
145

produce a small enough
in a relatively
short time for population initialization which is better
than random initialize algorithm.
Figure 9: the normalized average objective value versus the
proportion of fix tasks.
To compare objective values among different
fixed tasks ratio conditions, we thus normalize the
average fitness values. Fig. 9 shows the normalized
average fitness value of GA, baseline 1, 3, 4 and 5
algorithms. GA always generates solution which is
the closest to the optimal one (baseline 5 algorithm)
on average.
6.3.4 Scalability Evaluation
We demonstrate the effectiveness of the proposed
algorithm on a set of generated task graphs with
different specifications. For load balancing concerns,
we set the ratio of fixed tasks to be 0.1. Five task
graphs with different task number for comparing GA
with baseline algorithms are generated. The fitness
value is plotted in Fig. 10 as a function of the number
of tasks in the scientific workflow. It can be observed
that the proposed algorithm always achieves the
lowest fitness values compared with baseline
algorithms.
Figure 10: the average fitness value versus number of tasks.
6.3.5 Running Time Analysis
As is mentioned in section 4.3, there are two terminal
conditions: i) the maximum number of iterations is
reached, and ii) the fitness value is converged to some
value. To objectively describe the time performance
Figure 11: the average running time versus the task
number.
of GA, the relationship of running time and the task
number of random workflow is presented in this
section. 10 test cases of varying sizes are involved in
the running time analysis. Over the ten separate runs
for each test case, the average running time of GA is
recorded. Fig.11 gives the experimental results.
There’s a significant trend with increased running
time going with larger task number, which matches
the complexity analysis of GA. However, the running
time could also be influenced by other parameters
such as mutation rate, crossover rate and the ratio
between the number of individuals generated by
heuristic based method and random method, etc. So,
the time performance can still be improved upon by
carefully tuning those parameters.
From all the above results, we conclude that the
proposed algorithm obtains task offloading with
significantly lower energy consumption and
monetary cost, besides requiring relatively short
execution time, making it a suitable candidate to
manage scientific workflow execution in mobile
cloud computing environment.
7 CONCLUSION AND FUTURE
WORK
This paper targets the task offloading problem for
mobile scientific workflows. Although there are
many existing workflow scheduling algorithms for
cloud computing environments, they have difficulties
in being directly applied to the Mobile Cloud
Computing. Therefore, we offer three entry points for
the problem solving: first, a cost model based on the
pay-as-you-go manner of IaaS Cloud is proposed;
then, we investigate the problem of task offloading
strategy of scientific workflows to minimize the
monetary cost and energy consumption of SMDs
under deadline constraints in MCC; furthermore, the
dataset placement problem is addressed during the
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
146

offloading and mapping process of workflows. A
genetic algorithm based task offloading method is
proposed by carefully modifying parts of a generic
GA to suit our needs for the stated problem. We test
the proposed algorithm on several random generated
workflows. Simulation results shows the proposed
algorithm can achieve a near-optimal energy and cost
minimization task offloading strategy with the
workflow deadline and data placement constraints
satisfied.
Fog computing is a new computing paradigm
which brings resource close to users to improve user
experience (Bonomi, 2012). However, its distributed
and heterogeneous nature can bring in uncertainty
during workflow execution which will harm the
reliability of scientific computation. The extended
work could be to efficiently organize the resource,
handle the intermediate data placement and storage
issue to support workflow execution in fog computing.
ACKNOWLEDGEMENTS
This work was supported by the Key Program of
Research and Development of
China (2016YFC0800803), the National Natural
Science Foundation, China (No.61572162,
61572251). Jidong Ge is the corresponding author.
REFERENCES
J. Cohen, 2008. Embedded Speech Recognition
Applications in Mobile Phones: Status, Trends, and
Challenges. IEEE International Conference on
Acoustics, Speech and Signal Processing IEEE, 5352-
5355.
T. Soyata, R. Muraleedharan, C. Funai, M. Kwon and W.
Heinzelman, 2012. Cloud-Vision: Real-time Face
Recognition Using a Mobile-Cloudlet Cloud
Acceleration Architecture. IEEE Symposium on
Computers and Communications IEEE, 59-66.
K. Kumar, J. Liu, Y.-H. Lu, and B. Bhargava, 2013. A
survey of computation offloading for mobile systems.
Mobile Networks and Applications, 18(1), 129-140.
Liu, F., Shu, P., Jin, H., & Ding, L., 2013. Gearing resource-
poor mobile devices with powerful clouds:
architectures, challenges, and applications. IEEE
Wireless Communications, 20(3), 14-22.
Calheiros, R. N., & Buyya, R., 2014. Meeting deadlines of
scientific workflows in public clouds with tasks
replication. IEEE Transactions on Parallel &
Distributed Systems, 25(7), 1787-1796.
Liu, J., Pacitti, E., Valduriez, P., De Oliveira, D., &
Mattoso, M, 2016. Multi-objective scheduling of
scientific workflows in multisite clouds. Future
Generation Computer Systems, 63(C), 76-95.
Xu, X., Dou, W., Zhang, X., & Chen, J., 2016. Enreal: an
energy-aware resource allocation method for scientific
workflow executions in cloud environment. IEEE
Transactions on Cloud Computing, 4(2), 1-1.
Wu, C. Q., Lin, X., Yu, D., Xu, W., & Li, L, 2015. End-to-
end delay minimization for scientific workflows in
clouds under budget constraint. IEEE Transactions on
Cloud Computing, 3(2), 169-181.
Zhu, Z., Zhang, G., Li, M., & Liu, X., 2016. Evolutionary
multi-objective workflow scheduling in cloud. IEEE
Transactions on Parallel & Distributed Systems, 27(5),
1344-1357.
Sahni, J., & Vidyarthi, D. P., 2016. Workflow-and-platform
aware task clustering for scientific workflow execution
in cloud environment. Future Generation Computer
Systems, 64, 61-74.
Li, Z., Ge, J., Yang, H., Huang, L., Hu, H., & Hu, H., et al.,
2016. A security and cost aware scheduling algorithm
for heterogeneous tasks of scientific workflow in
clouds. Future Generation Computer Systems, 65, 140-
152.
Liang Tong, Wei Gao, 2016. Application-aware traffic
scheduling for workload offloading in mobile clouds.
IEEE INFOCOM 2016 - IEEE Conference on
Computer Communications 2016.1-9.
Guo, S., Xiao, B., Yang, Y., & Yang, Y., 2016. Energy-
efficient dynamic offloading and resource scheduling in
mobile cloud computing. IEEE INFOCOM 2016 -
IEEE Conference on Computer Communications,1-9.
Elgazzar, K., Martin, P., & Hassanein, H., 2016. Cloud-
assisted computation offloading to support mobile
services. IEEE Transactions on Cloud Computing (1),
1-1.
Deng, S., Huang, L., Taheri, J., & Zomaya, A. Y., 2015.
Computation offloading for service workflow in mobile
cloud computing. IEEE Transactions on Parallel &
Distributed Systems, 26(12), 1-1.
Yuan, D., Yang, Y., Liu, X., & Chen, J., 2010. A data
placement strategy in scientific cloud workflows.
Future Generation Computer Systems, 26(8), 1200-
1214.
Mccormick, W. T., & White, T. W., 1972. Problem
decomposition and data reorganization by a clustering
technique. Operations Research, 20(5), 993-1009.
Zhao, E. D., Qi, Y. Q., Xiang, X. X., & Chen, Y., 2012. A
Data Placement Strategy Based on Genetic Algorithm
for Scientific Workflows. Eighth International
Conference on Computational Intelligence and
Security, 146-149.
Deng, K., Song, J., Ren, K., Yuan, D., & Chen, J., 2011.
Graph-Cut Based Coscheduling Strategy Towards
Efficient Execution of Scientific Workflows in
Collaborative Cloud Environments. Ieee/acm
International Conference on Grid Computing, 34-41.
Topcuoglu, H., Hariri, S., & Wu, M. Y., 2002.
Performance-effective and low-complexity task
scheduling for heterogeneous computing. IEEE
Task Offloading for Scientific Workflow Application in Mobile Cloud
147

Transactions on Parallel & Distributed Systems, 13(3),
260-274.
Zhu, Xiaomin, et al., 2016. Fault-Tolerant Scheduling for
Real-Time Scientific Workflows with Elastic Resource
Provisioning in Virtualized Clouds. IEEE Transactions
on Parallel & Distributed Systems, 27, 3501-3517.
Bonomi, F., Milito, R., Zhu, J., & Addepalli, S., 2012. Fog
computing and its role in the internet of things. Edition
of the Mcc Workshop on Mobile Cloud Computing, 13-
16.
IoTBDS 2017 - 2nd International Conference on Internet of Things, Big Data and Security
148
