
Design of Next Generation Smart Surface Transportation System
Francis Chang and Hari K. Garg
Department of Electrical and Computer Engineering, National University of Singapore, 4 Engineering Drive 3,
Singapore 117576, Singapore
Keywords: Multi-Objective Evolutionary Algorithm, Genetic Algorithm, Intelligent Transport System.
Abstract: Transportation systems of the future need to be adaptive, adoptive, and responsive in order to meet the
diverse challenges and ever-evolving demands. Conventional method of adding more resources on the road
does not enhance its utility, rather it creates traffic congestion. Optimization of the usage of existing
resources has been found to be one of the most effective solution to manage traffic congestion. The method
we propose consists in increasing the occupancy rate of each vehicle and utilize other untapped resources in
existing infrastructure. The resource optimization problem studied in this paper is NP hard, due to the
vehicle routing and resource matching problem. In this paper, we are focused on developing a Multi-
Objective Evolutionary Algorithm to optimize the use of taxi service not just as a carrier for people but also
as a transport system for parcel delivery. Preliminary experiment with real-world data shows that our
approach is able to quickly produce satisfactory solutions and the algorithm is able to provide an average of
17.7% improvement over conventional methods.
1 INTRODUCTION
Over the past decade or so, the transportation
systems in major cities round the world have rapidly
evolved to meet multiple challenges and demands
they have faced. In the public transportation domain,
taxies provide flexibility and comfort of door-to-
door rides, use existing road infrastructure, and
provide travel freedom that is comparable to travel
in a personal vehicle. However, this form of
vehicular transportation usually carries one or two
individuals, resulting in many empty seats and hence
a significant underutilization of the overall capacity.
Statistics reported by Nokia Research (Hartwig,
1997) show that vehicles in United Kindom have an
average occupancy of 1.5. The result of
underutilized transportation resources may lead to
detrimental effects such as traffic congestion, air
pollution, and increase in fuel consumption (Huang,
2015). Uber hired service allow passengers to
submit their trip request ahead of time. Uber
successfully demonstrated the concept of matching
demand to supply through technology. This is unlike
traditional taxi services that result in excessive and
unnecessary cruising and waiting in the hunt for
passengers (Takayama, 2011).
In recent years, we have seen an exponential
increase in e-commence (Jones, 2013). Consumers
are shifting away from physical high street brick-
and-mortar shopping to the comfort of purchasing
through online stores. Hence, products in
warehouses are no longer needed to be delivered to
retail stores, but directly to the customer's premises.
Conventional parcel delivery method may take days
to complete. However online giant Amazon noticed
that faster delivery time boost sales. Coupled with
perishable products (such as groceries) being sold
online, there has been a significant increase for on-
demand parcel delivery services.
In people transportation, carpooling (ride-sharing
of a vehicle) is known to resolve resource crunch
and increase occupancy rate. Overall, it has been
found to be one of the best solutions to manage
traffic congestions (Fagin, 1983) (Megalingam,
2011). However, passenger of the future may come
with diverse needs beyond the requirement for
physical transportation space. They may want to
charge their mobile device or stay connected
through alternative connectivity services such as
WiFi. When it comes to parcel delivery, fast and
efficient delivery requires the flexibility of on-
demand door-to-door rides like a taxi service. The
taxies today, in most instances, offer one or more
Chang, F. and Garg, H.
Design of Next Generation Smart Surface Transportation System.
DOI: 10.5220/0006376603590365
In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 359-365
ISBN: 978-989-758-242-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
359

empty seats. In future, other form of resources may
also be offered. This includes trunk space, power for
mobile devices, and even connectivity services (such
as WiFi). The future of transportation will need to be
adaptive to meet the diverse demands and needs.
In this study of transportation systems, we
analyze potential untapped resources and
opportunity that can be used in the future
transportation systems. It is critical to develop an
algorithmic approach for optimizing the matching of
driver, passenger, and delivery of parcels. In this
work, we carry out a theoretical study of Single
Driver to Multiple Passenger/Parcel (SDMP). The
SDMP arrangement means that each driver may pick
up and deliver one or more passengers and parcels
during their trip, in which the seat occupancy can be
increased while opening the available trunk space
for parcel delivery.
The organization of the paper is as follows.
Section 2 describes related intelligent transportation
system approaches. The problem formulation is
highlighted in Section 3. In Section 4, we present
our proposed MOEA approach. Section 5, presents
the experiental results. Final, our conclusions are
drawn in Section 6.
2 RELATED WORKS
As mentioned in the introduction, the diversity in the
demand and supply creates an unique multi-
objective optimization problem where a number of
objectives such as travel distance, trip duration and
services provided needs to be concurrently matched
and optimized for different stakeholders. In contrast
to single objective optimization, a solution to a
multi-objective optimization problem exists in the
form of alternate tradeoffs known as the Pareto
optimal set. In a Pareto optimal set, each objective
component of any non-dominated solution can only
be improved by degrading at least one of its other
objective component. Therefore, the multi-objective
optimization consists in discovery of a possible set
of Pareto optimal solutions for which decision maker
can select an optimal solution based on the current
situation.
The evolutionary algorithm inspired by Darwin’s
theory of evolution has been used often in search of
Pareto optimal set (Fonseca, 1995). It has been
successfully applied to a wide variety of problems
and shown to be capable of producing optimal or
near-optimal solution for multi-dimensional
problems (Ross, 1994). An evolutionary algorithm
function with a population of solutions is
represented in the form of chromosomes. Each
chromosome is encoded with a number of genes,
each gene representing a unit of information. The
algorithm searches for new solutions through the
process of combining (crossover) and altering
(mutation) of existing chromosomes in the
population. Upon creation of new chromosomes,
they are evaluated. Better quality solutions remain
while inferior solutions are eliminated from the
population. Through multiple generations, it
artificially simulates ‘natural selection’ in survival
of the fittest.
There are many research studies on matching
and optimizing transport related routing problem,
under some restrictive assumptions. (Huang, 2015)
designed an intelligent carpool system which
matches new passenger(s) to an existing trip. (Baker,
2003) describes the use of genetic algorithm in
vehicle routing problem (VRP) for goods delivery.
(Tan, 2007) has extended the use of mutli-objective
evolutionary computation to time constrained VRP
with stochastic demand. The actual demand is
revealed only when the vehicles arrive at the
customers premises.
In this paper, a Multi-Objective Evolutionary
Algorithm (MOEA) is applied to the pairing of
requests to the transportation resources. The
proposed approaches balance the benefits and trade-
off between stakeholders.
3 PROBLEM FORMULATION
The resource planning considered in this paper is
defined around the situation in which a number of
potential passenger and customer requests have
similar origin and destination. Such requests can
then be paired with a vehicle taking a route similar
to those requests. Passenger(s) or customer(s) submit
their trip request to a central server via smart
devices. Given this scenario, the problem at hand is
to decide which requests should be matched and
assigned to an available vehicle such that the
benefits attained by the primary stakeholders is
maximized. The four primary stakeholders that we
consider in our work are the transport company,
drivers, passengers and parcel’s customers.
This section presents the challenges and
constraints for the mutli-objective optimisation
problem. Each of the functional groups has a
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
360

different point of view to the optimization criteria.
When a (pick-up and drop-off location) request
information is sent to the transport company for
pairing, the computed optimized result will be
forwarded to the drivers for execution.
The definition of some of the frequently used
notations for the SDMP, leading to the formulation
of the mathematical model, is given as follows:
(1) Passenger Requests: The passenger request
set 1,2,3,…, represents the
passenger request. Each passenger request
contains pick-up and drop-off location, time
of request, number of seats, carry-on luggage
space and boolean service (such as WiFi or
mobile device charging service) required.
The pick-up and drop-off location will be use
determine and calculate the trip distances.
Time of request indicates the time in which
the request is put forward to the transport
company for pairing. Number of seats, carry-
on luggage space and boolean service are the
resources demand for the transportation to
fulfil.
(2) Customer Parcel Requests: Similar to the
passenger request set, 1,2,3,…,
represents the customer request for parcel
delivery. Parcel space designates the number
of storage units required while expiry time
sets the requirement for just-in-time delivery
of perishable product.
(3) Vehicles and Capacity constraints: Vehicles
capacity is normal random variable. Seating
capacity varies between 4 to 7 seats. Trunk
space used to hold parcels and carry-on
luggage up to 4 storage units. Boolean
service is provided on 50% the vehicle fleet.
(4) Node: A node is denoted by
,
,
and
, which represent the
pick-up and drop-off location of th
customers and passengers respectively.
(5) Travel Distance and Routing plan: The
travel distance between two points and
denoted by
,
is estimated
using city block calculation. The routing plan
consists a set of routes
,
,…,
. The
number of routes is equal the number of
paired resource and requests.
(6) Other Assumptions: It is assumed that each
passenger or customer request can only be
served by one driver with its available
resource. If the demand exceeds available
resources, the request will be dropped and
conclude as fail to pair.
In addition, there are two types of constraints in
the SDMP problem. Hard constraints are those
which must be satisfied for the pairing to be
considered legal, while soft constraints are
essentially preferences. An example of hard
constraint is the need to pair one vehicle with
sufficient resource to meet the seating capacity
requirement, on the other hand, soft constraint can
come as a form of additional service such as boolean
service (WiFi connectivity) for the passengers.
4 EVOLUTIONARY MULTI-
OBJECTIVE OPTIMIZATION
From the discussion in previous sections, it is clear
the SDMP is inherently a multi-objective problem.
This section presents our proposed approach using
MOEA specifically designed to solve the SDMP
problem by concurrently optimizing the four
objective functions. The proposed method comprises
of two phases: 1) producing sets of candidate blocks;
and 2) choosing of candidate for reproduction.
In the first phase, producing sets of candidate
blocks using chromosome representation and greedy
population initialisation to effectively generate
potential solutions. The resource and request pairs
are expressed in a chromosome representation which
also contains information on the vehicle, passenger
and customer requirements. The candidate solutions
generated by this module are determined to be a
feasible pairing before handing over to the Evolution
module.
Upon completing the generation of candidate
solutions, effectiveness of each candidate will be
evaluated through the use of fitness functions.
Candidate chromosome with better fitness score are
selected for genetic operations, crossover and
mutation. The mutation rate can be varied in
different MOEA generations to better optimize
existing candidate solutions.
4.1 Producing Sets of Candidate Blocks
Each route request by a passenger can be
represented by
,
,
,
,
,
,
,
, such that
is the identity
number,
is the pick-up,
is the drop-off
Design of Next Generation Smart Surface Transportation System
361

location,
is the required number of seats and
is the time in which the request is raised. A
similar chromosome structure is used for the
customer requests
,
,
,
,
,
. The available vehicle resources are
represented by
,
,
,
,
,
where
is the vehicle registration number,
is the seat capacity,
is the storage
capacity and
is the availablity of Boolean
service.
To efficiently construct an adaptive chromosome
such that the representation is flexible to be updated
and perform the genetic operations, the proposed
chromosome representation consists of an
Assignment Layer and Routing Layer. The
Assignment Layer is a combination of different
resource demand set, each set containing groups of
request that are assigned to the vehicles. The column
indices represent a vehicle while the index of the
requests are stored in different rows.
An example is illustrated in Fig 1,
,
and
are assigned to
,
and
are
assigned to
. Available storage space are
shown as dotted boxes.
has a capacity of 4
storage units and 3 are occupied,
has 2
assigned storage and 3 more available. The numbers
of segments can be dynamically modified to suit the
quantity of available resources.
Figure 1: Chromosome representation of Assignment
Layer.
The order in which the driver should pick-up and
drop-off which passenger or parcel is represented in
the Routing Layer. An example is illustrated in Fig.
2.
Figure 2: Expanded view of a chromosome, each vehicle
with the newly assigned request will have the waypoints
matrix update based on nearest distance order.
When a new generation is started, the Population
Initialisation module uses a 4 steps process to
generate the population. The population can be
described as
,⋯,
, where is the number of generations,
is the population size and is the a
candidate solution. First, the current assignments are
copied over from the previous result. They form a
basis for all candidate solutions to be built upon.
Request that have been assigned will not be re-
assigned to another vehicle. Hence, the transferring
of current result ensures continuity between
evaluations.
Second, a micro-function updates newly
available vehicles that have joined the evaluation,
these resource elements are inserted at the end of
each chromosome with no request assigned. All
vehicles which are logging off will also be removed
from the chromosome, assessment for fare charges
and next projected location will continue to update
but no new request will be assigned. Third, new
requests are extracted from the data set based on the
evaluation time interval. These new requests will be
randomly assigned into the base chromosome; each
generated chromosome will be checked for
feasibility so as to meet the hard and soft constraints.
Fig 3 shows new requests will be assigned to at least
one vehicle with vacant resource and no unique
request repeated within a candidate chromosome.
Finally, Fig 4 shows the individual assignment will
have their route waypoints re-organize based on
nearest distance order.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
362
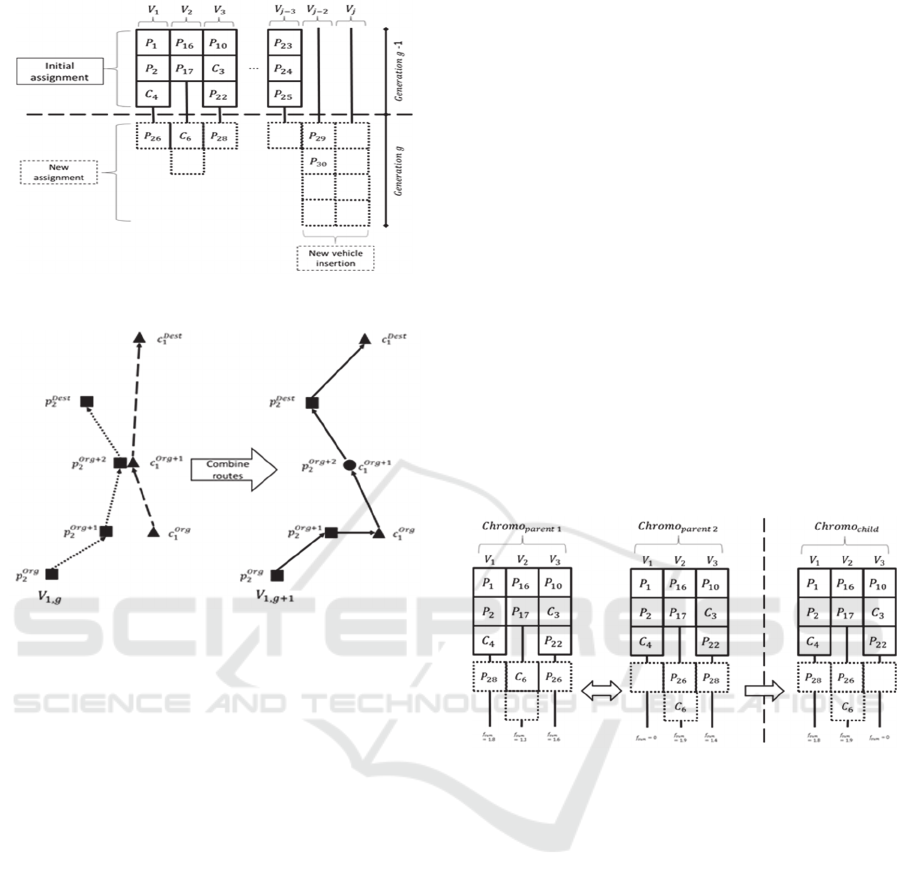
Figure 3: Assigning new of request to available vehicle.
Figure 4: Reorganisation of the route priority upon
assignment of new request.
4.2 Choosing of Candidate for
Reproduction
In order to evaluate the quality of individual
chromosomes, the fitness function is used to
determine the fitness score of each chromosome. To
facilitate the Evolutionary Algorithm, a fixed time
interval evaluation window is used to execute
requests as a batch.
4.2.1 Selection and Elitism
Upon evaluation of the population, the chromosomes
are sorted into highest fitness scores in ascending
order. The top chromosome will be directly
transferred to the next generation while the
remaining candidates will be filtered through a
selection process. Tournament selection is used to
select the candidate chromosomes for the genetic
operations. First, some number of chromosomes
are randomly copied from the population and the
two best individuals from this group are placed in
the intermediate pool as parents of the genetic
operations. With every generation, the bad
chromosomes will be lost and replaced by copies of
the better candidates. Some bad chromosomes may
contain quality trait, hence, to reduce the selection
pressure size of the tournament is set to ≪ .
4.2.2 Crossover
The first process used to produce new candidate
chromosome is crossover operator. In the
tournament selection, two parent chromosomes
(
) are selected and will be recombined
in hopes of producing better offspring. Fig 5
illustrates an example of the crossover process,
and
are selected
for mating and the subsequent recombination
produces
.
is the fitness value of
each chromosome to be maximised. The crossover
process does not change the initial chromosome, but
copies and transfers higher quality segments to the
offspring. Duplicate of the same passenger maybe be
generated through this process, therefore a post
process evaluation will verify if the chromosome is a
feasible solution. Invalid chromosome will be
handed over to the Chromosome Repair function.
Figure 5: Crossover operation of two parent chromosomes
to produce a single child chromosome.
4.2.3 Mutation
There are two mutation process customized to the
Genetic Evolution Module. The first type
interchanges new passenger requests between two
vehicles. As shown in Fig. 6 (Left), a single
is selected and the positions of the
individual requests are identified. The identified
individual will be swapped with the parent
chromosome to produce an offspring. This swap
mutation is not only restricted to passenger requests,
it can also be in the mixture of passenger request and
vacant seat, where probability
govern its
activation.
The second mutation process shown in Fig 6
(Right) is based on operation of multiple swaps.
First the tournament selection identifies a single
, this chromosome must contain
negative fitness score in some of the vehicle
Design of Next Generation Smart Surface Transportation System
363
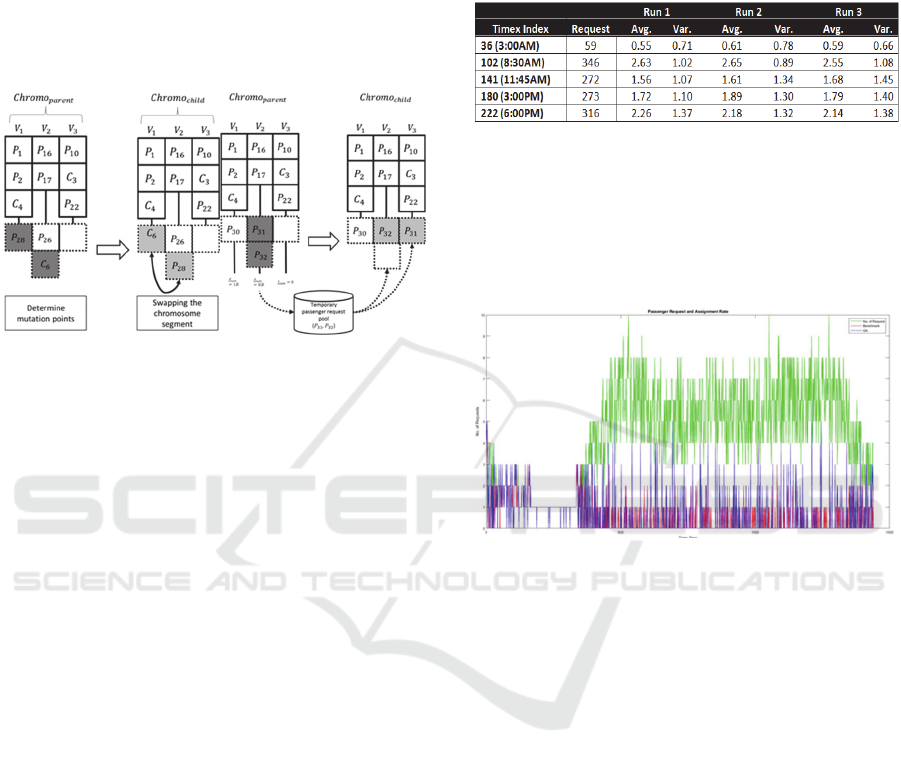
segment. All passenger requests with negative
fitness score are remove from the chromosome and
stored in a temporary passenger request pool. The
mutation operator will re-assign these requests to
vacant seats of the chromosome. The process is
intended to reduce the number of poor quality
assignment within a chromosome while increasing
the likelihood of higher occupancy rate of available
vehicles.
Figure 6: Mutation through swapping (Left) and Mutation
through replacement of negative fitness score segments
(Right).
5 PRELIMINARY RESULT AND
ANALYSIS
In this section, the method we propose is compared
with the method of random assignment. The
performance of both methods is evaluated via
benchmark simulation on SMRT Corporation
Singapore (https://www.smrt.com.sg) Taxi Dataset
(July 2014). In all our experiments, the parameters
of the evolutionary algorithm are as follows:
population size of 100, crossover probability of 0.8
and mutation probability of 0.05 to 1.0. The
termination criterion is 300 generations. Each time
window for computation is set at 5 minutes. The
algorithms are implemented using Matlab and all
scenarios were independently tested 5 times to
acquire an average performance.
The first and foremost objective of the
algorithms is to optimize the occupancy of the
vehicles. Table 1 shows that the proposed algorithm
is able to increase occupancy during peak hours
when demand exceeds supply. At the beginning of
the experiment (time index 36), there is a surplus in
supply of vehicles as compared to the demand,
hence a low rate of matches are possible. As the
simulation proceeds into the morning rush hour
(time index 102), there is a high rate of matching
with the average exceeding 2.55 passengers per taxi.
It is also observed that time index 180 shows higher
pairing as compared to time index 141 due to the
shift changeover.
Table 1: Result of successfully paired requests with
vehicles.
From the preliminary result shown in Fig 7, our
proposed method demonstrated that it can
successfully pair multiple requests into the given
resources much better than the benchmark method.
Experiment conducted using one day’s worth of
simulation dataset, shows on average 17.7%
improvement over the benchmark.
Figure 7: Successful pairing of resource with multiple
requests (Period : 1 day).
6 CONCLUSION
In this paper, we proposed a potential method using
Multi-Objective Evolutionary Algorithm which
pairs transport requests to a fleet of transport
vehicles. The proposed algorithm provides an
improved solution over the benchmark. However,
the analysis is not complete until all the fitness
functions of various stakeholders are formulated
based on real world scenarios. The SMRT
Corporation Singapore Taxi Dataset is relsatively
small as compared to the New York city open taxi
dataset. Therefore, the data points used may not be
sufficient to establish the true advantage of the
evolutionary algorithm.
The proposed future work includes comparing
our method with other state-of-the-art evolutionary
algorithms such as NSGA-II, or SPEA2, etc..
Further, we plan to improve the fitness functions for
the stakeholders that better represent real world
scenarios.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
364

ACKNOWLEDGMENTS
This research is supported by the National Research
Foundation, Prime Minister’s Office, Singapore
under its International Research Centre in Singapore
Funding Initiative.
REFERENCES
Baker, B.M. and Ayechew, M.A., 2003. A genetic
algorithm for the vehicle routing problem. Computers
& Operations Research, 30(5), pp.787-800.
Fagin, R. and Williams, J.H., 1983. A fair carpool
scheduling algorithm. IBM Journal of Research and
development, 27(2), pp.133-139.
Fonseca, C.M.M.D., 1995. Multiobjective genetic
algorithms with application to control engineering
problems (Doctoral dissertation, University of
Sheffield).
Hartwig, S. and Buchmann, M., 2007. Empty seats
traveling. Nokia Research Center Bochum, 11.
Huang, S.C., Jiau, M.K. and Lin, C.H., 2015. A genetic-
algorithm-based approach to solve carpool service
problems in cloud computing. IEEE Transactions on
Intelligent Transportation Systems, 16(1), pp.352-364.
Jones, C. Forbes Welcome. 2013. Forbes Welcome.
[ONLINE] Available at:
http://www.forbes.com/forbes/welcome/?toURL=http:
//www.forbes.com/sites/chuckjones/2013/10/02/ecom
merce-is-growing-nicely-while-mcommerce-is-on-a-
tear/&refURL=&referrer=#3eb219b55972. [Accessed
31 January 2017].
Megalingam, R.K., Nair, R.N. and Radhakrishnan, V.,
2011, April. Automated wireless carpooling system
for an eco-friendly travel. In Electronics Computer
Technology (ICECT), 2011 3rd International
Conference on (Vol. 4, pp. 325-329). IEEE.
Ross, P. and Corne, D., 1994. Applications of genetic
algorithms. AISB Quaterly on Evolutionary
Computation, 89, pp.23-30.
Takayama, T., Matsumoto, K., Kumagai, A., Sato, N. and
Murata, Y., 2011. Waiting/cruising location
recommendation for efficient taxi business.
International journal of System Applications,
Engineering & Development, 5, pp.224-236.
Tan, K.C., Cheong, C.Y. and Goh, C.K., 2007. Solving
multiobjective vehicle routing problem with stochastic
demand via evolutionary computation. European
Journal of operational research, 177(2), pp.813-839.
Design of Next Generation Smart Surface Transportation System
365
