An Efficient Replication Approach based on Trust for Distributed
Self-healing Systems
Nizar Msadek and Theo Ungerer
Institute of Computer Science, University of Augsburg, Universit
¨
atsstr. 6a, 86135 Augsburg, Germany
Keywords:
Autonomous Systems, Open Distributed System, Trust, Replication, High-performance Computing.
Abstract:
Replication typically occurs in a wide range of open distributed systems, especially in self-healing systems
(i.e., mainly for fault-tolerance purposes) and in high-performance computing (i.e., mainly for fast response
times). All these systems face a common issue: how can replicas automatically and efficiently be managed in
a system despite changing requirements of their environment? One way to overcome this issue is trust. The
contribution of this paper is a novel approach based on trust that provides a good management of replicas —
especially for those of important services — despite uncertainties in the behavior of nodes. Depending on the
importance level of a service possessing the replicas and the assessment of the trustworthiness of a node, we
can optimize the trust distribution of replicas at runtime. For evaluation purposes we applied our approach to
an evaluator based on the TEM middleware. In this testbed, the usage of trust reduced the replication overhead
by about 14% while providing a much better placement of important replicas than without trust.
1 INTRODUCTION
Implementing efficient and dependable replication
mechanisms for open distributed systems is a non-
trivial task (Halsall, 1996; Reif et al., 2016). This is
due to the fact that such systems are becoming in-
creasingly complex in their organizational structures,
especially when unknown heterogeneous entities
might arbitrarily enter and leave the network at any
time. Therefore, new ways have to be found to
develop and manage them. One way to overcome
this issue is trust (Msadek and Ungerer, 2016).
Using appropriate trust mechanisms, entities in
the system can have a clue about which entities to
cooperate with. This is very important to improve
the robustness of such systems, which depend on a
cooperation of autonomous entities (Msadek, 2016).
In this paper, we primarily focus on self-healing
and note that our goal is to develop an autonomous
replication mechanism based on trust that works
in a distributed manner and also ensures global
optimality. The mechanism should provide a good
replica management and placement — especially for
those of important services — despite non-benevolent
behavior of nodes in the network. Therefore, the
contribution of this paper leads to a methodology that
offers the following major points:
(i) an overview of the system model and the consid-
ered problem to indicate the specific purpose of
our research (see Sections 2 and 3),
(ii) a mechanism for specifying the importance level
of services based on the number of requests as
well as a mechanism to monitor the trust behav-
ior of nodes at runtime (see Section 4.1), and
(iii) a replication model considering the above intro-
duced points to manage the amount of replicas for
better trustworthiness of important services (see
Section 4.2).
All aspects are evaluated and discussed with respect
to a toolkit based on the TEM (Anders et al., 2013), a
trust-enabling middleware for building real-world dis-
tributed Organic Computing systems. Section 5 pro-
vides evaluation results of the proposed mechanism
and Section 6 aligns the trust-based approach in the
context of state-of-the-art systems. Finally the paper
is closed with a conclusion and future work in Sec-
tion 7.
2 SYSTEM MODEL AND
ASSUMPTIONS
We target a distributed system consisting of a finite set
of nodes N = {n
1
, n
2
.., n
n
}, representing machines
Msadek, N. and Ungerer, T.
An Efficient Replication Approach based on Trust for Distributed Self-healing Systems.
DOI: 10.5220/0006382601990206
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 199-206
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
199

which can interact with each other through a set of
messages. The i-th node is denoted by n
i
, or alter-
natively by i if it is not ambiguous. These nodes are
heterogeneous in terms of storage resources. Thus,
every node provides a storage space with a free ca-
pacity Capa
i
to offer services in the system a place
for storing their data. The set of services is de-
noted by S = {s
1
, s
2
.., s
k
} and the data of a service
s
j
is expressed by Data
j
. This data is replicated
among the nodes of the network. Thus, a Data
j
is partitioned into a set of owner and replicas with
Data
j
= {Owner
j
} ∪ {Repl
j,1
, Repl
j,2
, ..., Repl
j,r
j
}.
The Owner
j
is the central element that performs all
write requests. It has multiple replicas which repli-
cate its data. We assume that these replicas are com-
pletely identical to the owner in contrast to erasure
codes
1
. This means that the storage consumptions for
all replicas are the same, which is given by the value
Consum
j
. Whenever an Owner
j
performs a write re-
quest, it delivers an update with a new version of its
data to the replicas. These replicas are used to per-
form read requests and to overcome node failures.
Their amount is fixed so far as a system parameter
r
j
within the interval [R
min
, R
max
] to avoid that not too
many but also not too few replicas are created. Should
an owner of a data service fail, the system will elect
one of the replicas with the latest version to takeover
the role of owner. We also assume that the number of
requests may affect the importance level of services.
Services having a large amount of requests are consid-
ered to be important for the functionality of the entire
system. From this point of view, important services
are supposed to be rational in the sense that they want
to place their replicas as well as possible in the sys-
tem, by choosing only high trustworthy nodes.
3 PROBLEM STATEMENT AND
BASELINE
A crucial point in our system is the trustworthiness of
the service storage, especially for important services.
Their data should be hosted on trustworthy nodes hav-
ing a high degree of trustworthiness despite malicious
behavior of nodes in the network. Therefore, we for-
mulate the trustworthy replication management prob-
lem as follows. Given a set of services with different
importance levels and a network topology with a fi-
nite number of nodes representing possible replica lo-
1
An erasure code provides redundancy without saving the
identical complete copy of an object element. It divides
the element into m fragments and recodes them into n frag-
ments, where n > m. Details can be found in the paper
referenced here (Weatherspoon and Kubiatowicz, 2002).
cations, we are interested to determine a trustworthy
placement for replicas such that the trustworthiness of
important data is improved by hosting them on trust-
worthy nodes. On the other hand, the storage of nodes
should be optimized in terms of resource consump-
tions as well. To do so, four fundamental decisions
have to be considered: (1) which services are consid-
ered as more important than others in the system, (2)
when should the categorization of services be deter-
mined, (3) how to fix the right amount of replicas, and
(4) where to place these replicas on nodes. Depend-
ing on these decisions, different replication strategies
can be applied.
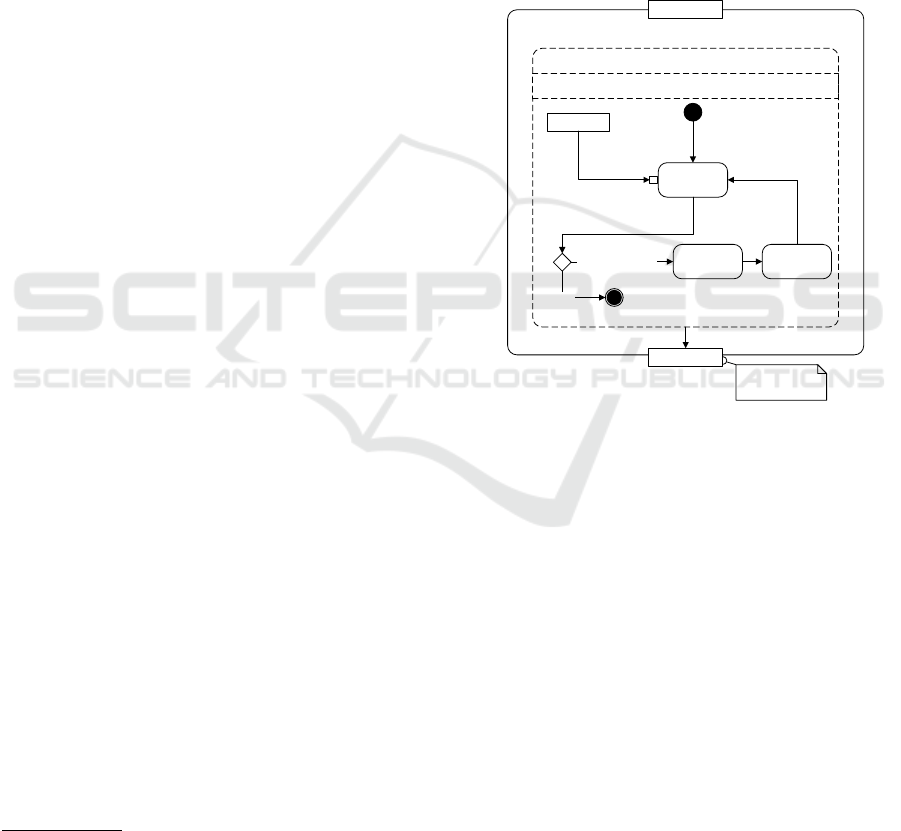
List
Baseline Replication
Managment
<<Loop>>
[replication] for all services from List
next service
Verify Replica
Amount
[Else]
[Amount<Threshold]
Select
Suitable Node
Put Node into
Replica Set
true/false
Whether valid
replication is found
Figure 1: Elementary representation of the baseline replica-
tion management.
Figure 1 shows the baseline replication strategy
considered in this work. It is based on thresholds for
determining the importance level of services. These
thresholds are fixed at design time and do not change
during run time. Then, a scheduler is used for creating
and assigning replicas. For every service, it selects a
node with a uniform probability without considering
its trust value or up probability and put it into a replica
set. If for example a node is already selected or its
storage space is full, it picks another new node, un-
til the given number of replicas reaches the threshold
R
max
for important services or the threshold R
min
for
unimportant services. This strategy has the ability to
improve the availability of service data in the system.
However, it is only suited for classical systems where
the benevolence of nodes is assumed (Schillo et al.,
1994), because all nodes are treated identically even
though some of them are less trustworthy than oth-
ers. In open distributed systems, it would not provide
good results due to the fact that unknown nodes might
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
200

arbitrarily enter and leave the network at any time.
Therefore, we propose to incorporate trust mecha-
nisms into the management of replicas.
4 THE TRUST-BASED
REPLICATION APPROACH
4.1 Models and Metrics
Our aim is to provide a continuous good trustworthi-
ness for data especially for important services and to
reduce the performance overhead produced by creat-
ing too many replicas in the system as well. As a con-
sequence, our approach should consider the following
factors: (1) We want a mechanism for specifying the
required trust of services based on their number of re-
quests. (2) We need a mechanism to regularly monitor
the trust behavior of nodes. (3) And we want a model
to manage the amount of replicas for better trustwor-
thiness of important services. It is worth mentioning
that all solutions provided should always be round-
based over the time to ensure that the system is con-
tinuously optimized at runtime.
4.1.1 Determine the Required Trust of Services
As mentioned, the number of requests plays a crucial
role in the categorization of services. Services with
a large number of requests are considered to be more
important than others in the system. They should have
a higher degree of required trust in order to be hosted
on trustworthy nodes. The baseline approach does not
take such a decision into account at runtime. It cate-
gorizes the importance level of services at the begin-
ning which is then not changed during execution. Our
aim is to give the system more responsibility by mov-
ing this decision from design-time to runtime. The al-
gorithm for this strategy consists of two phases which
are bounds calculation and required trust calculation
phase. In the first phase, we compute the cumulative
number of requests for each service s
j
∈ S at every
round k as follows:
Request
k
(s
j
)
= Request
k
(Owner
j
)
+
r
j
∑
i=1
Request
k
(Repl
j,i
)
(1)
Where Request
k
(Owner
j
)
stands for the number of read
and write requests performed by the owner until round
k is reached, and Request
k
(Repl
j,i
)
represents the total
number of read requests that were performed by every
replica i of s
j
until k is reached.
MinRequest
k
= {Request
k
(s
j
)
|∀s
i
, s
j
∈ S : Request
k
(s
i
)
≥ Request
k
(s
j
)
}
(2)
MaxRequest
k
= {Request
k
(s
j
)
|∀s
i
, s
j
∈ S : Request
k
(s
i
)
≤ Request
k
(s
j
)
}
(3)
Then, we determine the minimum and maximum
values over these requests by Equations 2 and 3.
By this means, the request number of every ser-
vice is always bounded between MinRequest
k
and
MaxRequest
k
. Values near to the MinRequest
k
re-
flect unimportant services, whereas values close to
MaxRequest
k
stand for important services. In the
second phase, we aim to compute the required trust of
each service. Assume that MinTrust and MaxTrust
are the desired thresholds for minimum and maxi-
mum trust set in the system, where 0 ≤ MinTrust ≤
MaxTrust ≤ 1. Then, a value of Request
k
(s
j
)
can
be mapped to a required trust value ReqTrust
k
(s
j
)
in
the new specified range [MinTrust, MaxTrust] using
min-max normalization as illustrated in Equation 4.
We give a high degree of trust for important ser-
vices by shifting the minimum and maximum num-
ber of requests to MinTrust and MaxTrust, respec-
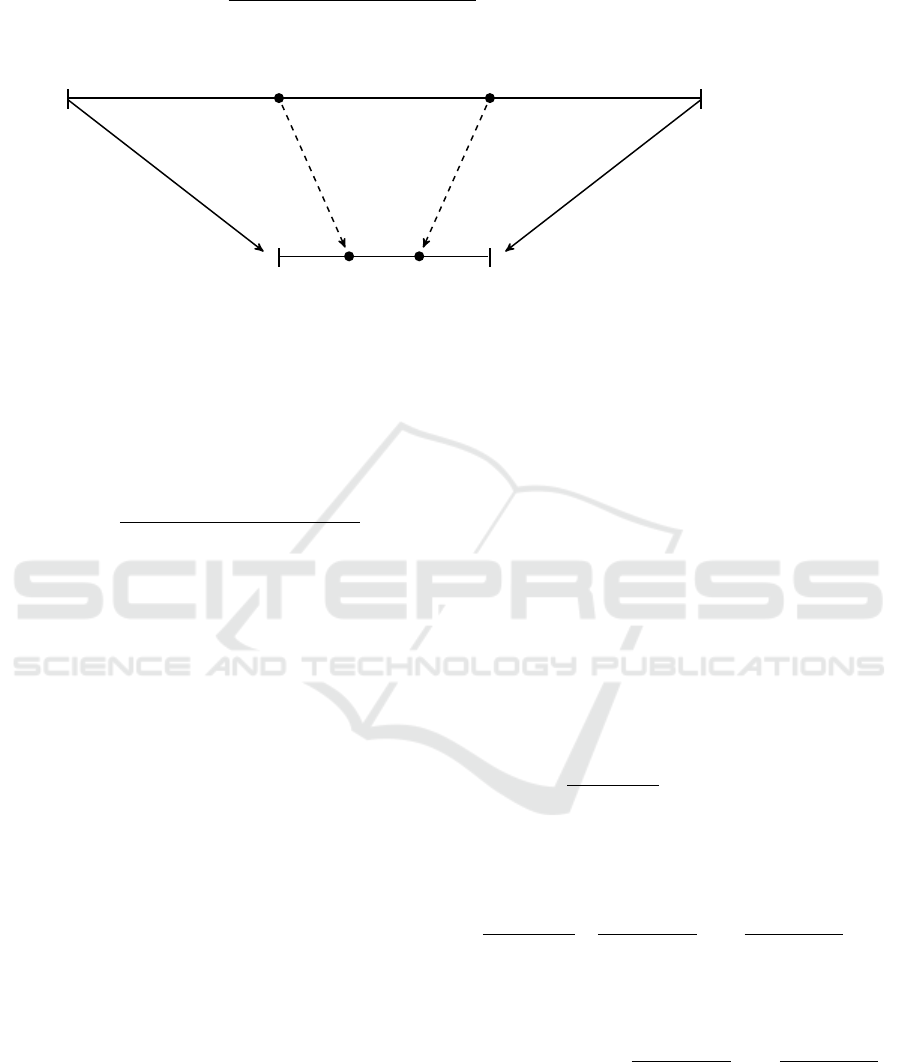
tively. Figure 2 shows – as example – the required
trust scores that can take services s
i
and s
j
after min-
max normalization. The original distribution of re-
quests is retained for both services and is then trans-
formed in required trust values in the new specified
range of [MinTrust, MaxTrust].
4.1.2 Assess the Trust Behavior of Nodes
A trust-based replication needs a component which
generates trust values based on direct experiences
to detect the presence of untrustworthy nodes in
the system. This trust generation can be measured
by regarding different facets of trust (Msadek and
Ungerer, 2016), such as reliability, availability,
functional correctness, and usability. The facet of
interest in this work is availability, since we are
interested to check the availability of nodes based on
their uptime in the last interaction steps. Also we
assume that the trust relation Trust between nodes is
always irreflexive on N , i.e., ∀n
i
∈ N :⇔ ¬(n
i
Trust
n
i
) meaning that we do not allow the possibility for
nodes to assess their own trust values. Otherwise,
nodes would trust themselves fully and the system
will be prone to exploitation from malevolent nodes.
Equation 5 shows the metric we set to calculate direct
trust using the facet availability.
An Efficient Replication Approach based on Trust for Distributed Self-healing Systems
201

ReqTrust
k
(s
j
)
=
Request
k
(s
j
)
− MinRequest
k
MaxRequest
k
− MinRequest
k
· (MaxTrust − MinTrust) + MinTrust (4)
(Original Range)
(New Specified Range)
MinRequest
k
MaxRequest
k
Request
k
(
s
i
) Request
k
(
s
j
)
MinTrust MaxTrust
ReqTrust
k
(s
i
)
ReqTrust
k
(s
j
)
Figure 2: Mapping of service requests from the range of [MinRequest
k
, MinRequest
k
] to required trust values in a new
specified range of [MinTrust, MaxTrust] using min-max normalization.
Trust
k
(n
i
,n
j
)
=
(
(1 − α) · Trust
k−1
(n
i
,n
j
)
+ α · Θ
k
n
j
if k ≥ 1
Trust
init
k = 0
(5)
Θ
k
n
j
=
Uptime of n
j
in period [k − 1, k]
Total time of period [k − 1, k]
(6)
Θ
k
n
j
∈ [0, 1] (7)
Trust
k
(n
i
,n
j
)
∈ [0, 1] (8)
k ∈ N (9)
In every round k, a node n
i
calculates a trust value
Trust
(k)
(n
i
,n
j
)
about its direct neighbor n
j
based on the
new observation Θ
(k)
n
j
and the previous trust value
Trust
(k−1)
(n
i
,n
j
)
. This trust value Trust
(k)
(n
i
,n
j
)
is always
within [0, 1] and reflects the subjective trust of node n
i
in node n
j
based on its experiences. A trust value of
Trust
(k)
(n
i
,c
i
)
= 0 means n
i
does not trust n
j
at all while a
value of 1 stands for full trust. The factor α ∈ [0, 1] de-
cides how strong the recent observations are weighted
compared to the previous ones. The larger the value
α, the more the result is computed by the recent obser-
vations. Initially, the trust value of n
j
is set to Trust
init
and in every round k an update occurs for Trust
(k)
(n
i
,n
j
)
.
With increasing number of mutual interactions over k,
we expect to correctly estimate the behavior of nodes
in the system. This is very important to prevent the
hazardous placements of replicas on nodes.
4.1.3 Perform the Placement of Replicas
A crucial point in the baseline algorithm is the trust-
worthy placement of service data. To guarantee a
specific level of trustworthiness the nodes hosting the
replicas have to be chosen correctly. An optimal se-
lection of these nodes is not considered in the baseline
version. Therefore, we are interested in our approach
to improve the replica placement by considering the
trust values of each replica. Let us assume the re-
quired trust of a service s
j
is known and that Owner
j
has multiple replicas {Repl
j,1
, Repl
j,2
, ..., Repl
j,r
j
}
which replicate its Data
j
. These replicas are dis-
tributed on different nodes and the trust behaviors of
nodes are independent of each other. The probability
of Data
j
to be in a trustworthy state at round k is rep-
resented by Trust
k
(Data
j
)
and its untrustworthiness is
denoted by Trust
k
(Data
j
)
= 1 − Trust
k
(Data
j
)
. It is obvi-
ous that Data
j
is in an untrustworthy state if and only
if all replicas as well as the owner are not trustworthy.
So the untrustworthiness of Data
j
can be determined
by Equation 10.
Trust
k
(Data
j
)
= Trust
k
(Owner
j
)
·
r
j
∏
i=1

Trust
k
(Repl
j,i
)

(10)
This means that the probability of at least one replica
to be in a trustworthy state can be written as follows:
Trust
k
(Data
j
)
= 1− Trust
k
(Owner
j
)
·
r
j
∏
i=1

Trust
k
(Repl
j,i
)

!
(11)
To ensure that this probability is always greater than
or equal to ReqTrust
k
(s
j
)
, we make use of Equation 12
as a condition.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
202

1 − Trust
k
(Owner
j
)
·
r
j
∏
i=1

Trust
k
(Repl
j,i
)

!
≥ ReqTrust
k
(s
j
)
(12)
By this means, solving the placement problem
consists of minimizing the amount of replicas r
j
needed such that the constraint of Equation 12 is met.
This is very important to prevent the hazardous place-
ments of replicas on nodes and to reduce the replica-
tion overhead during runtime.
4.2 The Replica Management Approach
The interaction between the activities of the trust-
based replication approach is illustrated in Figure 3.
In the first step, we make use of the trust metric
of Equation 5 — by regarding availability as a facet
of trust — to assess the behavior of nodes. Our met-
ric takes the advantage to converge to the true hid-
den trust values of nodes with increasing number of
mutual interactions over k. This is very important to
detect trust anomalies in node behavior and to allow
owners to decide where to place their replicas trust-
worthily in the system. Then an update is initiated at
every round k to refresh the trust values of nodes as
well as the recognition of important services at run-
time. Services with a large amount of requests are
considered to be important for the functionality of the
entire system. As a consequence, we give them a high
degree of required trust using Equation 4. Then, repli-
cas are managed for every service so that the condi-
tion of Equation 12 will hold. This replication man-
agement is accomplished by removing, replacing or
adding the minimum number of replicas for every ser-
vice. The smaller the amount of replicas is, the lower
the replication cost and the better the performance of
the system will be. Using trust, our replication man-
agement has the following benefits compared to con-
ventional replication systems: On the one hand it re-
duces the overall number of replicas produced in the
system. This optimization cost is continuously per-
formed over the system lifetime. On the other hand,
it improves the trustworthy placement of replicas on
nodes so that the more important replicas will be al-
ways placed only on highly trustworthy nodes.
5 EVALUATION
In this section, we investigate the effectiveness of
the trust-based replication approach. For the purpose
of evaluating and testing, an evaluator based on our
TEM (Anders et al., 2013) middleware has been im-
plemented which is able to simulate our approach
over a period of 2000 rounds. The evaluation net-
work consists of 1000 nodes where all nodes are able
to communicate with each other using message pass-
ing. Each node has a random storage capacity and is
judged by an individual trust value without any cen-
tral knowledge. The trust values of nodes are gener-
ated in two steps. Firstly, according to (Bernard and
Le Fessant, 2009; Rzadca et al., 2010), we created dif-
ferent behaviors of nodes with different proportions in
the system:
• Durable Trustworthy: with a mean value of 0.95
and proportion of 10%
• Stable Trustworthy: with a mean value of 0.87
and proportion of 25%
• Unstable Trustworthy: with a mean value of
0.75 and proportion of 30%
• Erratic: with a mean value of 0.33 and proportion
of 35%
Then, we added a Gaussian noise of σ = 0.1 to each
trust and capped the resulting value into [0, 1]. The
evaluation has been conducted using 100 services
(i.e., 50% of them are important and 50% unimpor-
tant). The service assignment has been performed
randomly to ensure that the proposed approach is
evaluated under a great variety of start conditions. Af-
ter the assignment, replicas are created in the system
using the following parameters:
• The minimum replication factor R
min
is set to 5.
• The maximum replication factor R
max
is set to 20.
Our goal is to recognize the importance level of ser-
vices solely based on the number of requests and to
improve the trustworthy placement of replicas at run-
time. Furthermore, replication cost should be reduced
in contrast to the baseline approach in order to get a
better performance in the overall system. Each eval-
uation scenario has been replayed 500 times and the
results have been averaged.
5.1 Trust Examination
In the following, it is demonstrated how the place-
ment of replicas can be improved — using the pro-
posed algorithm — in response to trust changes in the
environment. Therefore, the importance level of ser-
vices is changed during runtime. We varied the rate of
requests for every service and compared the deviation
of actual trust from the required trust. Figures 4(a)
and 4(b) show the results of this experiment without
and with trust, respectively.
The results attest a good performance for the trust-
based replication compared to the baseline approach.
An Efficient Replication Approach based on Trust for Distributed Self-healing Systems
203

List
Trust-Based Replication Management
<<Loop>>
next service
Assess the
trust of nodes
Determine the
required trust of
the service
<<Loop>>
[replication] for all services from List
[Rounds of iteration] for every round of k
Perform the
placement of replicas
Figure 3: Elementary representation of the trust-based replication management.
Most of services show either an equal or a better ac-
tual trust than the required trust. However, there exist
a small number of services which have a less trustwor-
thy state than the required value. This is explained by
the fact that nodes in our system have a limited capac-
ity available for storage. This makes the replica pro-
cess difficult for some services to find still unloaded
trustworthy nodes on which to place their replicas.
5.2 Overhead Examination
To establish replication, replicas need to be created in
the system. In the following, this overhead is investi-
gated for the baseline and the trust-based replication
approach. For this experiment, the same settings as
above have been used and Figure 5 shows its result.
The values on the x-axis stand for the replica-
tion approach used and the total number of replicas
is depicted on the y-axis. To perform detailed mea-
surements, we separated the important services from
unimportant ones and calculated also the replica over-
head created for each category. From the results, we
can observe that the overhead is reduced by about 20
% for important services. But for unimportant ser-
vices, the overhead is maintained nearly at a constant
level. This is because the condition set in the system
does not tolerate to produce less replicas than R
min
for unimportant services. Overall, we can say that the
cost of replication is decreased using our approach by
about 14% for all services. This means that the con-
sideration of trust does not prevent our algorithm to
save overhead by placing the replicas.
6 RELATED WORK
As far as we know, a previous study of replication
for self-healing systems based on trust in open and
distributed environments has never been done be-
fore. However, some works have already been done
on their design, for instance Spanner (Corbett et al.,
2013) which is a system designed by Google, Ori-
File (Mashtizadeh et al., 2013), MinCopysets (Cidon
et al., 2013), Scada (Kirsch et al., 2014), Calv-
inFS (Thomson and J. Abadi, 2015) etc. Our ap-
proach differs from the current state of the art in four
major points. First, the benevolence assumption of
nodes is not made in our work. In contrast, we use
the social concept of trust to mitigate hazards that can
occur from placing replicas randomly in the system.
Second, our approach can adapt to changing behavior
of nodes as well as to changing condition of services.
Third, it possesses a regulation mechanism to save
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
204

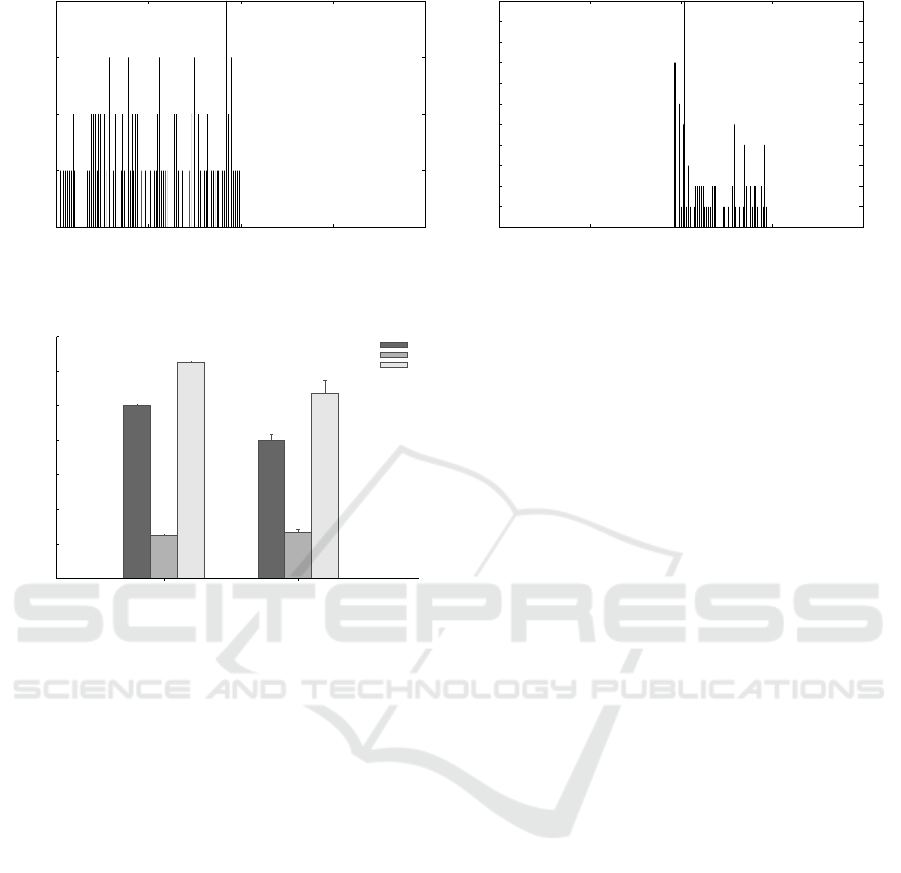
0
1
2
3
4
-1 -0.5 0 0.5 1
Number of services
Actual Trust - Required Trust
(a) Using the baseline replication approach.
0
1
2
3
4
5
6
7
8
9
10
11
-1 -0.5 0 0.5 1
Number of services
Actual Trust - Required Trust
(b) Using the trust-based approach.
Figure 4: The density of trust deviations.
0
200
400
600
800
1000
1200
1400
Without Trust With Trust
Total Number of Replicas
Important Services
Unimportant Services
All Services
Figure 5: Measuring the impact of overhead for different
categories of services using the trust-based vs. the baseline
replication approach.
replica overhead at runtime, and finally it is appli-
cable to any kind of trust-aware Recommender Sys-
tems (Kiefhaber et al., 2013). Thus, we want to com-
pare our mechanism to systems that employ the same
approach. The closest approach to us is to perform the
replica placement based on a forecast regarding the
availability of nodes. For example, the authors of (Li
et al., 2015) analyze how to maximize the number
of objects that remain available when node failures
occur. Existing systems based on such availability
placement include (Rzadca et al., 2010; Mills et al.,
2015; Bhagwan et al., 2003; Bernard and Le Fessant,
2009). The main disadvantage of those approaches
is that they do not take the priority of services into
account and need a high computation power to per-
form the placement. This would not be suitable for
ubiquitous or embedded systems. Very recently, the
authors of (H. Noor et al., 2016) proposed an inter-
esting replication technique based on trust to mini-
mize the impact of inoperable TMS instances in the
system. Based on an artificial exponential distribu-
tion to model trust, the authors estimate the trust of
each node and determine the amount of replica ac-
cordingly. However, as exponential distributions are
memoryless they cannot be used to predict trust as
we do in this work. The second disadvantage of this
approach is that it does not consider the number of re-
quests to determine the importance level of services
at runtime.
7 CONCLUSION
In this paper, a novel replication approach for self-
healing systems is proposed. It is based on the notion
of trust to improve the trust distribution of replicas
and to minimize replication overhead in the system.
The algorithm makes use of a trust metric to model the
trust relationship between nodes, which is missing in
most existing state of the art systems. Then, a mathe-
matical model is formulated to determine the required
trust of each service based on how many times it was
requested in the last rounds. This is important to en-
hance the management of replicas for better trustwor-
thiness of important services. An evaluation is pro-
vided with respect to a real-world Organic Computing
middleware. Overall, the results show a better trust
distribution for replicas with a significant reduction
in overhead when compared to the baseline. How-
ever, there are still some studies to be done for future
work. For instance, further improving the trust distri-
bution of replicas and further decreasing the replica-
tion overhead. We also plan to investigate more the
categorization of services by including other factors
such checkpoint size and service centrality (Cao et al.,
2016; Pantazopoulos et al., 2011).
REFERENCES
Anders, G., Siefert, F., Msadek, N., Kiefhaber, R., Kosak,
O., Reif, W., and Ungerer, T. (2013). Temas a trust-
enabling multi-agent system for open environments.
Technical report, Universit
¨
at Augsburg.
An Efficient Replication Approach based on Trust for Distributed Self-healing Systems
205

Bernard, S. and Le Fessant, F. (2009). Optimizing peer-to-
peer backup using lifetime estimations. 2nd Interna-
tional Workshop on Data Management in Peer-to-peer
systems, page 8.
Bhagwan, R., Moore, D., Savage, S., and Voelker, G. M.
(2003). Replication strategies for highly available
peer-to-peer storage. Future Directions in Distributed
Computing, Volume 2584 of the series Lecture Notes
in Computer Science:153 – 158.
Cao, J., Arya, K., Garg, R., Matott, L. S., Panda, D. K.,
Subramoni, H., Vienne, J., and Cooperman, G. (2016).
System-level scalable checkpoint-restart for petascale
computing. CoRR, abs/1607.07995:1–18.
Cidon, A., Stutsman, R., Rumble, S., Katti, S., Ousterhout,
J., and Rosenblum, M. (2013). Mincopysets: Deran-
domizing replication in cloud storage. Proceedings of
the 10th USENIX Symposium on Networked Systems
Design and Implementation.
Corbett, J. C., Dean, J., Epstein, M., Fikes, A., Frost, C.,
Furman, J. J., Ghemawat, S., Gubarev, A., Heiser,
C., Hochschild, P., Hsieh, W., Kanthak, S., Kogan,
E., Li, H., Lloyd, A., Melnik, S., Mwaura, D., Na-
gle, D., Quinlan, S., Rao, R., Rolig, L., Saito, Y.,
Szymaniak, M., Taylor, C., Wang, R., and Woodford,
D. (2013). Spanner: Google&rsquo;s globally dis-
tributed database. ACM Trans. Comput. Syst., 31:8:1–
8:22.
H. Noor, T., Z. Sheng, Q., Yao, L., Dustdar, S., and
H.H. Ngu, A. (2016). Cloudarmor: Supporting
reputation-based trust management for cloud services.
IEEE Transactions on Parallel & Distributed Systems,
27:367 – 380.
Halsall, F. (1996). Data Communications, Computer Net-
works, and Open Systems. Addison-Wesley; Elec-
tronic Systems Engineering Series.
Kiefhaber, R., Jahr, R., Msadek, N., and Ungerer, T. (2013).
Ranking of direct trust, confidence, and reputation in
an abstract system with unreliable components. In The
10th IEEE International Conference on Autonomic
and Trusted Computing (ATC-2013).
Kirsch, J., Goose, S., Amir, Y., Wei, D., and Skare, P.
(2014). Survivable scada via intrusion-tolerant repli-
cation. IEEE Transactions on Smart Grid, 5:60 – 70.
Li, P., Gao, D., and Reiter, M. K. (2015). Replica placement
for availability in the worst case. IEEE 35th Interna-
tional Conference on Distributed Computing Systems
(ICDCS), 67:599 – 608.
Mashtizadeh, A. J., Bittau, A., Huang, Y. F., and Mazi
`
eres,
D. (2013). Replication, history, and grafting in the
ori file system. Proceedings of the Twenty-Fourth
ACM Symposium on Operating Systems Principles,
ACM:151–166.
Mills, K. A., Chandrasekaran, R., and Mittal, N. (2015).
Algorithms for replica placement in high-availability
storage. The Computing Research Repository (CoRR),
abs/1503.02654.
Msadek, N. (2016). Increasing the Robustness of Self-
Organizing Systems By Means of Trust Practices. PhD
thesis, University of Augsburg.
Msadek, N. and Ungerer, T. (2016). Trust as important fac-
tor for building robust self-x systems. In Trustworthy
Open Self-Organising Systems.
Pantazopoulos, P., Karaliopoulos, M., and Stavrakakis,
I. (2011). Centrality-driven scalable service migra-
tion. Proceedings of the 23rd International Teletraffic
Congress, 978-0-9836283-0-9:127–134.
Reif, W., Anders, G., Seebach, H., Stegh
¨
ofer, J.-P., Elis-
abeth, A., H
¨
ahner, J., M
¨
uller-Schloer, Christian,
and Ungerer, T. (2016). Trustworthy Open Self-
Organising Systems. Birkh
¨
auser.
Rzadca, K., Datta, A., and Buchegge, S. (2010). Replica
placement in p2p storage: Complexity and game the-
oretic analyses. IEEE 30th International Conference
on Distributed Computing Systems (ICDCS), 67:599 –
609.
Schillo, M., Funk, P., Stadtwald, I., and Rovatsos, M.
(1994). Using trust for detecting deceitful agents
in artificial societies. Proceedings of the Ibero-
American Conference on Artificial Intelligence (IB-
ERAMIA ’94), 14:825 – 848.
Thomson, A. and J. Abadi, D. (2015). Calvinfs: Consis-
tent wan replication and scalable metadata manage-
ment for distributed file systems. 13th USENIX Con-
ference on File and Storage Technologies (FAST 15),
USENIX Association:1 –14.
Weatherspoon, H. and Kubiatowicz, J. D. (2002). Era-
sure coding vs. replication: A quantitative compari-
son. Peer-to-Peer Systems, 2429 of the series Lecture
Notes in Computer Science:328 – 337.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
206