
Learning Spatial Constraints using Gaussian Process for Shared Control
of Semi-autonomous Mobile Robots
Kun Qian
1,2
, Dan Niu
1,2
, Fang Fang
1,2
and Xudong Ma
1,2
1
Key Laboratory of Measurement and Control of CSE, Ministry of Education, No.2, Sipailou, Nanjing 210096, China
2
School of Automation, Southeast University, No.2, Sipailou, Nanjing 210096, China
Keywords:
Mobile Robot, Gaussian Process, Shared control, Semi-autonomous, Wi-Fi Signal Strength.
Abstract:
In this paper, a novel human-robot shared control approach is proposed to solve the problem of semi-
autonomous mobile robot navigation with the spatial constraints of maintaining reliable Wi-Fi connection.
In particular, the presented approach benefits from using Gaussian Process Regression method to learn the
distribution of indoor Wi-Fi signal strength (WSS) and to fuse it with the environmental occupancy probabil-
ity. The resulting WSS-Occupancy hybrid map is further utilized for generating paths that prevent the robot
from violating the spatial restriction. A shared control strategy is designed to implement the WSS-aware nav-
igation behaviour. The approach is evaluated by both simulation and real-world experiments, in which the
results validate the practicability and effectiveness of the approach.
1 INTRODUCTION
With the increasing prevalence of wireless LAN
in indoor environments, tele-operated mobile robots
have been applied to environment inspection and
monitoring applications(Sgouros and Gerogiannakis,
2003)(Pitzer et al., 2012). In situations that spatial
constraints other than obstacles are imposed to such
a networked mobile robot, full tele-operation may not
be reliable enough and semi-autonomous robots(Tang
et al., 2009) with human-robot collaboration have be-
come important in network robotic system.
In the context of this study, the focus is particu-
larly on an unknown spatial constraint of maintain-
ing reliable Wi-Fi connections during robot naviga-
tion. Our motivation originates from the fact that in
indoor environments, when a robot navigates through
an area with poor Wi-Fi signal strength (WSS), the
tele-operation system may temporarily lose control
over the robot, neither can continuous and high qual-
ity tele-presence (visual and audio) feedback be en-
sured.
By treating the Wi-Fi distributionas a static spatial
constraint here, the solution is to design a WSS-aware
navigation behavior for ensuring continuous and reli-
able Wi-Fi connection during the robots exploration.
We define the problem mentioned above as spatially
restricted navigation of a tele-operated mobile robot.
Intuitively, learning the distribution of spatial con-
straints in the environment can be benefit to prevent
a robot from violating the restriction. Learning the
spatial distribution of an indoor environment from a
mobile platform can be formulated as a well-known
regression problem, i.e., to predict sensor values at
locations where the robot doesn’t traverse. Gaussian
Process(Rasmussen and Williams, 2006)(Qian et al.,
2016) is a powerful formalism for predict the prob-
ability distributions over sensor values at uncovered
locations. In Jadaliha’s work(Jadaliha et al., 2012),
the authors employed Gaussian Processes (GPs) to
build non-parametric probabilistic models using data
from a pilot sensor work deployment, for monitoring
spatial phenomena of interest. In order to handle the
diffusion and patches effects of complex interaction
of gas, Stachniss(Stachniss et al., 2009) proposes to
learn two-dimensional spatial models of gas distribu-
tions using a sparse Gaussian process mixture model,
which accurately represents the smooth background
signal and the areas with patches of high concentra-
tions. These recent studies(Krause et al., 2008)(Fer-
ris and D. Hahnel, 2006)(Xu et al., 2011)(Xu and
Choi, 2011)(Engel et al., 2003)(Ko et al., 2007) have
shown that Gaussian processes are an attractive mod-
eling technique in this context since they do not only
provide an estimate of sensory data for each point in
the space but also the predictive uncertainty. To our
best knowledge, the GPs approach has not yet been
applied to model the indoor Wi-Fi signal strength dis-
Qian, K., Niu, D., Fang, F. and Ma, X.
Learning Spatial Constraints using Gaussian Process for Shared Control of Semi-autonomous Mobile Robots.
DOI: 10.5220/0006382902010208
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 201-208
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
201

tribution.
Another challenge is how to utilize the recovered
spatial constraints to implement spatially restricted
navigation behaviors of a robot. Semi-autonomous
navigation will outperform full tele-operation when
spatial constraints are considered. Two major prob-
lems are concerned in this paper:
• Firstly, if the spatial distribution of WSS is recov-
ered by the GPs, the distribution should be inte-
grating with the occupancy grid map in order to
achieve a WSS-aware navigation behaviour.
• Secondly, a semi-autonomous behaviour of robot
is desired to correct the path designated by the re-
mote user and prevent itself from entering the ar-
eas with low WSS.
To deal with semi-autonomous control of mobile
robots, human-robot shared control methods(Li et al.,
2015) have been applied when multiple inputs and
multiple constraints are considered. The concept of
shared control is to select between the two sources
of commands and combine them to ensure task ac-
complishment while satisfying dynamic constraints.
However, to our best knowledge, there is little re-
search towards the solution of the WSS-aware navi-
gation problem.
In this paper, we propose a practical problem
called WSS-aware navigation of a tele-operated mo-
bile robot, which is an example of a general con-
cept of spatially restricted navigation. To tackle
this problem, we present an approach that enables
semi-autonomous navigation of a tele-operated mo-
bile robot by learning WSS-Occupancy hybrid map,
in which Gaussian Process is used as an effective
model to learn the WSS distribution with limited
number of training samples and predict the WSS dis-
tribution in a coordinate frame that is consistence
with the robots occupancy grid map. The concept
of shared control is introduced to implement a semi-
autonomous navigation behaviour of mobile robot
that can avoid the risk of violating the constraints, i.e.,
continuous and reliable Wi-Fi connection during nav-
igation is ensured.
2 WEB-BASED ROBOTIC
SYSTEM FOR MONITORING
A web-based robotic system is developed for re-
mote environment monitoring. The mobile robot is
equipped with a HOKUYO laser range finder for self-
localization and obstacle avoidance and a video cam-
era for capturing local video streams. The onboard
computer integrates a network card to measures the
Wi-Fi signal strength (WSS). The web-based robotic
system is built with three-layer architecture, as shown
in Figure 1:
• Web Client Layer (WCL). The WCL provides a
user with a client GUI to monitor the remote envi-
ronments as well as to get access to the direction
control of a robot.
• Network Service Layer (NSL). The NSL is com-
prised of a Web server and an Audio/VideoServer.
Another key role of NSL is to conduct the shared
control strategy, and thus the shared control effect
is transparent to the user.
• Local Robot Control Layer (LRCL), The
LRCL runs various ROS (Robot Operating
System)(Quigley et al., 2009) based nodes to
access robot hardware and to perform perception,
localization, navigation, mapping and other mod-
ules. The proposed WSS distribution mapping
function is also deployed in LRCL for creating
and storing the robots knowledge about the
spatially constrained environment.
Mobile
client
Streaming
x Recognition
x Decision making
Perception
x Localization
x Navigation
Navigation
x Audio
x Video
Mapping
Web Client Layer Network Service Layer Local Robot Control Layer
Shared control
Web server(LAMP)
A/V server
Service management
Autonomous control
Sensor data acquisition
Motor control
Node management
Full supervision Full autonomousSemi-autonomous
Roles of human
intervene
Browser
client
Internet
LAN
x SLAM
x WSS mapping
Direct control
Monitoring
Server
Figure 1: Web-based robotic system architecture.
A browser-based GUI is also provided to receive
human input commands from keyboard, joystick and
other types of interface, as shown in Figure 2. Given
the direction human input commands and the robots
autonomous control commands, the concept of shared
control is to select between the two sources of com-
mands and combine them to ensure task accomplish-
ment while satisfying dynamic constraints.
In our remote monitoring application, a typical
constrain concerned in this paper is to maintain solid
Wi-Fi connection for ensuring smooth video stream-
ing. With regard to this, the key to shared control
is to model the distribution of indoor Wi-Fi signal
strength and fuse such spatial distribution with the en-
vironment occupancy probability distribution, which
we define as WSS-Occupancy hybrid map building.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
202

Based on this a decision making module is proposed
to select or combine the commands from human in-
puts and the robots autonomous control inputs gener-
ated from a navigation controller based on the WSS-
Occupancy hybrid map. The shared control frame-
work is shown in Figure 3.
Figure 2: Browser-based GUI.
Direct control
command
Autonomous control
command
Keyboard,
joystick
interface
Task
allocation
Localization & Navigation
WSS-Grid hybrid map
learning
Decision making
Audio/Video
feedback
GUI
Sever
Shared control
Figure 3: Shared control framework.
3 LEARNING WSS SPATIAL
DISTRIBUTION
3.1 WSS Samples Accquisition
A robot explores the environment and constructs the
grid map of the environment using its onboard laser
sensor readings. In the situation of both robot posi-
tion and environmental map are unknown, the popu-
lar GMapping algorithm(Grisetti et al., 2007) is em-
ployed to implement highly efficient SLAM (simulta-
neously localization and mapping).
As the exploration and mapping proceeds, the
robot simultaneously captures the Wi-Fi signal
strength (WSS) from the network card of the onboard
computer along the path it travels. At every fixed time
interval t the robot encapsulates the WSS data as each
data packet:
D = (x
i
,y
i
)|i = 1, 2,...,n (1)
in which x
i
is the positions of sample points, and y
i
is the WSS measured at the corresponding position
timestamp t
i
.
3.2 Learning WSS Distribution with
Gaussian Processes
A Gaussian process defines a distribution over a space
of functions. Let D = {{x
1
, ¯y
1
},{x
2
, ¯y
2
},...,{x
n
, ¯y
n
}}
be a set of training data generated from a noisy pro-
cess ¯y
i
= f(x
i
) + ε
i
, where x
i
∈ R
d
is an input sam-
ple data and y
i
∈ R is a target or an observation. ε
i
is additive Gaussian noise with zero mean and un-
known variance σ
2
ε
, i.e.,ε ∼ N(0,σ
2
ε
). A Gaussian
Process considers f(·) as a random function and esti-
mates the posterior distribution p( f|D) based on the
prior p( f) and the training data D. A GP prior p( f)
is completely specified by its mean function and co-
variance function,i.e., f ∼ GP(m
f
,k
f
),which can be
formulated as:
p( f (x)) ∼ N(m
f
(x),k
f
(x,x)) (2)
Assuming that we have two input points x
p
and x
q
,
and the corresponding function values at these points
are f(x
p
) and f(x
q
), respectively. We consider a prior
mean function m
f
≡ 0 and a typical squared exponen-
tial (SE) covariance function, or called kernel func-
tion:
cov(y
p
,y
q
) = k
SE
(x
p
,x
q
) + δ
pq
σ
2
ε
(3)
in which:
k
SE
(x
p
,x
q
) := α
2
exp
−
1
2
(x
p
− x
q
)
T
Λ
−1
(x
p
− x
q
)
(4)
with x
p
,x
p
∈ R
d
. In the above equation,
Λ = diag([l
2
1
,..., l
2
d
]) is a diagonal matrix of squared
characteristic length-scales l
2
i
, i = 1, ...,d. α
2
is the
signal variance and δ
pq
is the Kronecker symbol that
is unity when p = q and zero otherwise.
If we denote X as the entire set of input values,
Equation (3) can be rewritten as:
cov(y) = K + σ
2
ε
I (5)
where K is the n×n covariance matrix with K[p,q] =
k
SE
(x
p
,x
q
). The prior over function f depicted by
Equation (5) indicates that one can generate the ma-
trix K from a set of input values X and then sample a
set of corresponding target values y ∼ N(0,K + σ
2
ε
I).
Given a training dataset D of n input-
output pairs that contains samples positions
Learning Spatial Constraints using Gaussian Process for Shared Control of Semi-autonomous Mobile Robots
203

X = {x
i
|i = 1,2,..., n} and their corresponding
WSS values y = {y
i
|i = 1,2,..., n}, a GP model is
trained. Based on the trained GP model the posterior
distribution can be computed. For a new input x
∗
that represents a position where WSS at this position
is never measured, the joint conditional distribution
of the estimated target value y
∗
can be estimated by
the prediction distribution p(y
∗
|x
∗
,D). The posterior
over function values, conditioned on the training
data X and y is Gaussian with mean µ
x
∗
and variance
σ
2
x
∗
(Deisenroth et al., 2014):
p( f (x
∗
)|x
∗
,X,y) = N(µ
x
∗
,σ
2
x
∗
) (6)
where
µ
x
∗
= k
∗
T
(K + σ
2
ε
I)
−1
y (7)
σ
2
x
∗
= k(x
∗
,x
∗
) − k
T
∗
K + σ
2
ε
I
−1
k
∗
(8)
The chosen kernel function determines the perfor-
mance of the GP regression. The hyper-parameters
of a GP with Gaussian kernel for a particular dataset
can be learned from the training data, in which the
hyper-parameters are derived by maximizing the log
marginal likelihood using empirical Baysian infer-
ence(Rasmussen and Williams, 2006).
3.3 Fusion of Grid Map with Wi-Fi
Signal Strength Distribution
The learned WSS distribution map models the spa-
tial distribution of WSS within a given indoor context.
We use Equation (9) to transfer raw WSS data S into
G
W
that takes similar value as a grey image pixel:
G
W
= 255(S + S
min
)/(S
max
− S
min
) (9)
, in which S
min
and S
max
are the lower bound and the
upper bound of transformation, which are set as:
S
min
= −113dBm (10)
S
max
= 0dBm (11)
, according to our inspection of the range of sam-
ple WSS values in typical indoor environments. We
define the minimal value of WSS that ensures reli-
able network connection in the environment is S
accept
and thus the corresponding value after the transform
is G
accept
. Furthermore, since the Wi-Fi distribution
map is learned on actual sensor readings recorded at
locations in the world coordinate that is consistent
with the occupancy grid map of the environment, the
WSS distribution map can be fused with the occu-
pancy grid map, resulting in a WSS-Occupancy hy-
brid grid map. Denote G
I
as the grey value of a pixel
in the occupancy grid map and G
W
are defined in
Equation (9). The resulting grey value G
B
of the cor-
responding pixel in the WSS-Occupancy hybrid grid
map is given in Equation (12):
G
B
= {
G
W
G
W
< min(G
accept
,G
W
)
G
I
else
. (12)
4 SHARED CONTROL
STRATEGY
Using the WSS-Occupancy hybrid grid map de-
scribed in Section 3, a desired trajectory can be com-
puted by a regular navigation controller that is com-
prised of a global path planner and a reactive local
planner. The path will ensure goal-directed naviga-
tion while avoid the robot to pass through the areas
with low WSS, so that continuous network connec-
tion will be strictly ensured.
Using a local path planner such as VFH or ND
algorithm(Minguez and Montano, 2005), the au-
tonomous control set u
r
is obtained. Given the hu-
man direct control u
h
= [v
h
,w
h
]
T
and the output of the
reactive local planner u
r
= [v
r
,w
r
]
T
, in which v and
w represent the translational speed and the rotational
speed of the robot, respectively, the shared controller
adopted in this work can be formulated as a combi-
nation of both two sources of command as shown in
Equation (12). ρ is the allocation weight with domain
0 ≤ ρ ≤ 1.
u
s
= (1− ρ)u
h
+ ρu
r
(13)
Since a robot control command will not exactly
cause ideal movement but introducing certain uncer-
tainties, we roughly predict the distribution of the
robot’s possible future positions in a small time inter-
val ∆t ahead by adding Gaussian noises to the transla-
tional and rotational velocity. Firstly we assume that
the robot’s heading is constant but the translational
velocity is v, thus the robot’s possible movements are
placed along a vector
−→
OA after ∆t. Then we assume
that the robot’s rotational velocity changes randomly
within [−∆w, ∆w] in ∆t. The result is a fan-shaped
area as shown in Figure 4 that contains all possible
u
r
.
Let the feasible autonomouscontrol input set asU
r
and feasible human input set asU
h
. Four types of rela-
tionships between U
r
and U
h
as shown in Figure 5 are
considered. If U
h
is a subset of U
r
, i.e.,U
h
⊆ U
r
, the
tele-operation command is regarded safe for ensuring
both goal-reaching and obstacle avoidance. In this
case, any ρ that satisfies 0 ≤ ρ ≤ 0.5 can be taken to
generate a synthetic control command. In three other
situations such asU
r
⊆ U
h
, U
h
∩U
r
6= {O,U
h
,U
r
} and
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
204
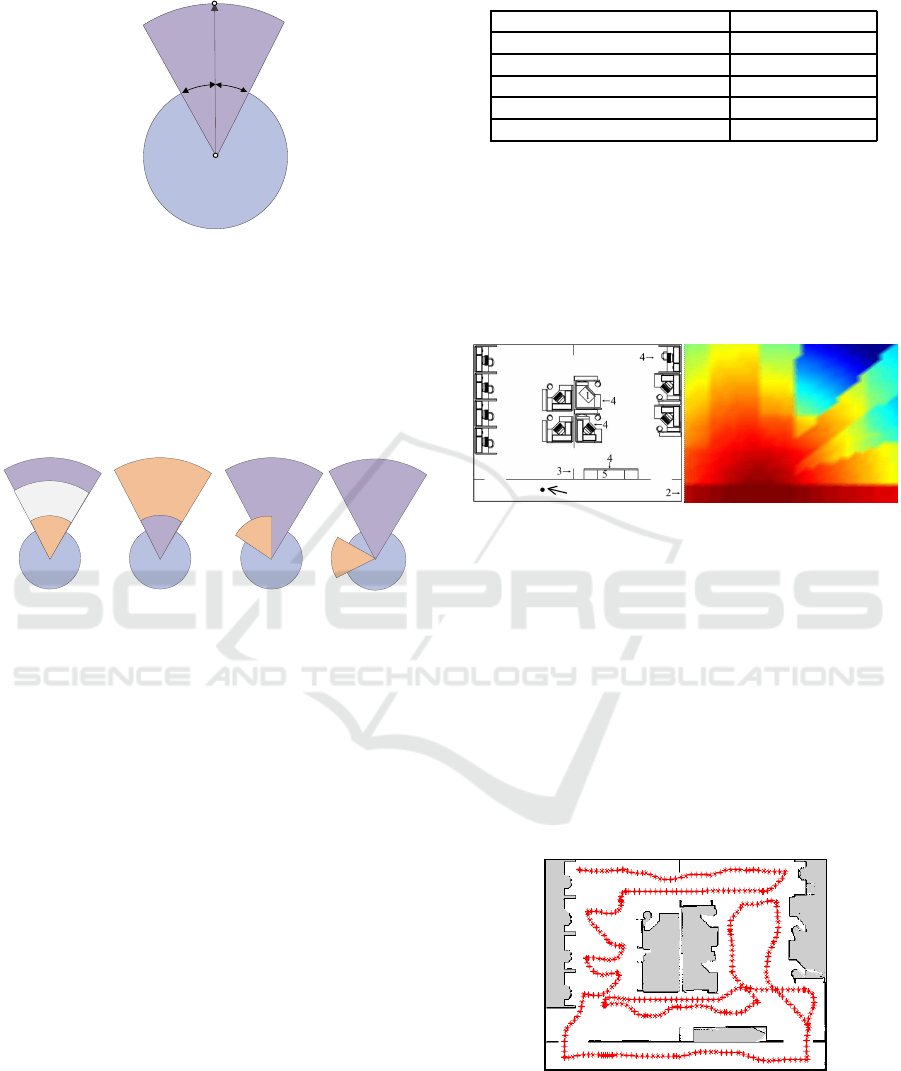
R
O
A
U
r
ƸwƸt
ƸwƸt
vƸt
Figure 4: Definition of U
r
.
U
h
∩U
r
= {O}, the tele-operation commands exceed
the safe range of the autonomous decision and it is
therefore difficult for the user to manually direct the
robot to achievethe goal while meeting the constrains.
In this case, we simply assign the allocation weight
ρ = 1 to ensure successful task accomplishment by
robot’s autonomy only.
R
U
r
U
h
R
U
r
U
h
R
U
r
U
h
R
U
r
U
h
U
s
(a) (b) (c) (d)
Figure 5: Four types of relations between U
h
and U
r
.
5 EXPERIMENTS
5.1 WSS-Occupancy Hybrid Mapping
We firstly verify the performance of WSS distribu-
tion mapping in a simulation experiment. A Wi-Fi
signal generator is utilized to simulate the Wi-Fi sig-
nal that travels in a simulated indoor environment as
shown in Figure 6(a). In the simulation, we use In-
door Propagation model, a.k.a, the MK model(Motley
and Keenan, 1988), to generate the ground truth Wi-Fi
distribution. This model takes into consideration the
signal decline when it travels through various kinds
of obstacles. Table 1 gives the signal attenuation rate
when the signal propagates through different types of
obstacles, such as walls, wood or glasses, et al.
The MK model based simulator uses Equation
(14) to compute the predicted path loss for a testing
receiver place:
S
pico
= S
0
+ 10× n
0
× log(x) + (N
1
S
1
+ L+ N
n
S
n
)
(14)
in which S
0
equals to the pass loss at 1m from the
transmitter, n
0
is the signal attenuation rate long the
Table 1: WI-FI Signal attenuation rate.
Types of obstacles Attenuation rate
electromagnetic interference 30 ∼ 50dBm
Concrete walls 12 ∼ 32dBm
Block walls 5 ∼ 15dBm
Wooden walls 3 ∼ 8dBm
Glasses 1 ∼ 5dBm
propagation path due to electromagnetic interference,
x is the distance between the transmitter place and
the testing receiver place, N
i
is the number of inte-
rior walls between the transmitter and testing receiver
place and S
i
is the loss factor of different interior wall
materials. The result of the simulated WSS distribu-
tion is shown in Figure 6(b), which is taken as the
ground truth.
Wireless AP
(a) (b)
Figure 6: Simulated environment and the ground truth.
Using a Stage(Vaughan, 2008) based robot sim-
ulator, a robot travels through the environment and
obtains the training dataset. Figure 7 shows the re-
sults of occupancy grid map and the robot trajectory
for collecting the WSS sample data. Subsequently, a
WSS distribution map is trained with Gaussian Pro-
cess Regression method and the predicted WSS spa-
tial distribution in shown in Figure 8. The result is
evident that by utilizing a limited number of training
samples, a smooth 2D spatial distribution of WSS can
be inferred and the WSS at positions that is not mea-
sured can be predicted.
Figure 7: Robot trajectories for collecting the training sam-
ples.
In addition, a WSS-Occupancy hybrid map is ob-
tain by fusing the WSS distribution map with the oc-
cupancy grid map, resulting in WSS-aware path plan-
ning results. A comparison of WSS-aware and non
Learning Spatial Constraints using Gaussian Process for Shared Control of Semi-autonomous Mobile Robots
205

r
y
/m
r
x
/m
-40
-60
-80
-100
-120
WSS/dBm
0
2
4
6
8
1
0
0
2
4
6
8
Figure 8: Learned WSS distribution.
WSS-aware path planning results are shown in Figure
9. The result implies that using a WSS-Occupancy
hybrid map instead of a traditional occupancy grid
map, the robot detours to avoid entering areas with
poor WSS. In the experiment the threshold is taken
as S
accept
= −75dBm, i.e., G
accept
= 68 to obtain the
shaded area in Figure 9(b). A comparison of the WSS
captured along two different paths is shown in Fig-
ure 10, which indicates that the WSS-aware naviga-
tion behavior guarantees continuous and reliable Wi-
Fi connection.
A
B
Path
(a) Without WSS-constrain
Area with low
WIFI signal
strength
Path
(b) With WSS-constrain
Figure 9: Path planning results.
5.2 Shared Control using
WSS-Occupancy Hybrid Map
The shared control performance was further validated
in two other real world environment scenarios. The
Area with low
WSS
Non WSS-
aware path
WSS-aware path
Figure 10: The WSS along two paths.
experiment made use of Turtlebot mobile robot plat-
form in an office environment of size about 100m
2
,
where Wi-Fi networks were deployed over multiple
Access Points (APs). Scenario 1 was designed as a
WSS-aware navigation trial experiment. The actual
position of the Access Point (AP) in the testing en-
vironment was outside the room as marked in Figure
11. By building the WSS-Occupancy hybrid map of
the environment the robot was aware of the area with
low WSS, depicted by the shaded area in Figure 11.
When the robot was steered by a remote user to travel
from point A toward the top-right corner of the map
as shown in Figure 11, the shared controller drove the
robot to avoid the area with low WSS, as shown by
the Part B of the trajectory in Figure 11. The results
of the translational and rotational velocity of the robot
during the corresponding trial test are given in Fig.12,
which reveal the decision making results of the shared
controller. The result implies that a robot is capable of
adapting its behavior to reduce the risk that confronts
with the spatial constrains we have exerted.
A
B
C
x
y
Full autonomous to
avoid the area with low
WIFI signal
Part A: Tele-operation only
Part B: Full autonomous
Part C: Tele-operation only
Area with low WIFI signal
Wireless
Access Point
Figure 11: Shared control result in scenario1.
Scenario 2 validates the effectiveness of human
supervision for assisting robot’s autonomy. The task
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
206

A B C
Translational velocity
*
-
Shared control result
Tele-operation input
Autonomous control input
(a) Translational Velocity
A B C
Rotational velocity
*
-
Shared control result
Tele-operation input
Autonomous control input
(b) Rotational Velocity
Figure 12: The robot’s velocity in scenario1.
assigned to the robot in this scenario was to travel
from P1 to P3 autonomously, but the robot had to
travel through a short part of corridor which is too
narrow for a robot to pass on its own. When the
robot’s path planner failed to report a path across the
corridor, the shared controller with ρ = 0 led to full
human supervision, which was achieved by receiving
human direction control through the GUI. The robot
therefore successfully reached the goal. This experi-
ment indicates that the proposed shared control strat-
egy is also beneficial to the general purposes of semi-
autonomous control in a web-based robotic system.
6 CONCLUSIONS
In this paper, a novel human-robot shared control
approach is proposed to solve the problem of semi-
autonomous navigation with a static spatial constraint
of maintaining reliable Wi-Fi connection. In the train-
ing mode, a robot explores the environment while
building the WSS-Occupancy hybrid map based on
Gaussian Process Regress method. In the runtime
A
B
C
x
y
P1
P2
P3
B
P2
Pass through the
narrow corridor by
human supervision
Part A: Full autonomous
Part B: Tele-operation only
Part C: Full autonomous
Wireless
Access Point
Figure 13: Shared control result in scenario2.
mode, the robot utilizes the WSS-Occupancy hybrid
map in a shared control framework to generate paths
that prevent itself from entering areas with low Wi-
Fi signal strength. A series of experimental stud-
ies have been performed, where promising results are
obtained. The presented approach can be extended
to solve other similar problem of spatially restricted
navigation of a tele-operated mobile robot to reduce
the risk of violating the constraints while reaching the
goal.
ACKNOWLEDGEMENTS
This work is supported by supported by the Na-
tional Natural Science Foundation of China (Grant
No. 61573101, 61573100 and 61504027) and the
NSF of Jiangsu Province(NO.BK20140647).
REFERENCES
Deisenroth, P. M., Fox, D., and Rasmussen, C. E.
(2014). Gaussian processes for data-efficient learning
in robotics and control. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 37:408–423.
Engel, Y., Mannor, S., and Meir, R. (2003). Bayes meets
bellman: The gaussian process approach to temporal
difference learning. In Proceedings of the 20th In-
ternational Conference on Machine Learning, pages
154–161.
Ferris, B. and D. Hahnel, D. (2006). Gaussian processes for
signal strength-based location estimation. In Robotics
Science and Systems.
Grisetti, G., Stachniss, C., and Burgard, W. (2007).
Improved techniques for grid mapping with rao-
blackwellized particle filters. IEEE Transactions on
Robotics, 23:34–46.
Jadaliha, M., Xu, Y., Choi, J., Johnson, N., and Li, W. M.
(2012). Gaussian process regression for sensor net-
Learning Spatial Constraints using Gaussian Process for Shared Control of Semi-autonomous Mobile Robots
207

works under localization uncertainty. IEEE Transac-
tions on Signal Processing, 61:223–237.
Ko, J., Klein, D. J., Fox, D., and H?hnel, D. (2007). Gaus-
sian processes and reinforcement learning for identifi-
cation and control of an autonomous blimp. In IEEE
International Conference on Robotics and Automa-
tion, pages 742–747.
Krause, A., Singh, A., and Guestrin, C. (2008). Near-
optimal sensor placements in gaussian processes.
Journal of Machine Learning Research, 9:235–284.
Li, Z., Yang, C., Zhao, S., and et al (2015). Shared control
of an intelligent wheelchair with dynamic constraints
using brain-machine interface. In 8th International
Conference on Intelligent Robotics and Applications,
pp.260-271. Springer.
Minguez, J. and Montano, L. (2005). Sensor-based robot
motion generation in unknown, dynamic and trouble-
some scenarios. Robotics and Autonomous Systems,
52:290–311.
Motley, A. and Keenan, J. (1988). Personal communication
radio coverage in buildings at 900 mhz and 1700 mhz.
Electronics Letters, 24:763–764.
Pitzer, B., Osentoski, S., and G. Jay, e. a. (2012). Pr2 remote
lab: An environment for remote development and ex-
perimentation. In IEEE International Conference on
Robotics and Automation, pp. 3200-3205. IEEE.
Qian, K., Ma, X., Dai, X., Fang, F., and Zhou, B. (2016).
Gaussian process based iaq distribution mapping us-
ing an interactive service robot. Journal of Ambient
Intelligence and Smart Environments, 8:359–373.
Quigley, M., Conley, K., Gerkey, B. P., Faust, J., Foote, T.,
Leibs, J., Wheeler, R., and Ng, A. Y. (2009). Ros: an
open-source robot operating system. In ICRA Work-
shop on Open Source Software.
Rasmussen, C. E. and Williams, C. K. I. (2006). Gaussian
processes for machine learning. The MIT Press, Cam-
bridge, Massachusetts, London.
Sgouros, N. M. and Gerogiannakis, S. (2003). Robot tele-
operation environments featuring wap-based wireless
devices. Journal of Network and Computer Applica-
tions, 26:259–271.
Stachniss, C., Plagemann, C., and Lilienthal, A. J. (2009).
Learning gas distribution models using sparse gaus-
sian process mixtures. Autonomous Robots, 26:187–
202.
Tang, H., Cao, X., Song, A., and et.al. (2009). Human-
robot collaborative teleoperation system for semi-
autonomous reconnaissance robot. In IEEE In-
ternational Conference on Mechatronics and
Automation,pp.1934-1939.
Vaughan, R. (2008). Massively multiple robot simulations
in stage. Swarm Intelligence, 2:189–208.
Xu, Y. and Choi, J. (2011). Adaptive sampling for learn-
ing gaussian processes using mobile sensor networks.
Sensors, 11:3051–3066.
Xu, Y., Choi, J., and Oh, S. (2011). Mobile sensor net-
work coordination using gaussian processes with trun-
cated observations. IEEE Transactions on Robotics,
27:1118–1131.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
208
