Cartographic Scale and Minimum Mapping Unit Influence on LULC

Modelling

David García Álvarez

Departamento de Análisis Geográfico Regional y Geografía Física, Universidad de Granada, Granada, Spain

Keywords: Scale, Minimum Mapping Unit, CORINE, SIOSE, LULC Modelling, Dinamica Ego.

Abstract: Two models at two different scales (1:25.000 and 1.100.000) were calibrated using two different Land Use

and Land Cover maps at such cartographic scales (SIOSE and CORINE) and with a different Minimum

Mapping Unit (0.2-0.5ha and 25ha). Differences between models were assessed through cross-tabulation

analysis (quantity and allocation disagreement) and spatial metrics (pattern disagreement). The models

results have been very different depending on the scale considered, although most of the disagreement

comes from the contrasting input maps. In any case, the scale at which the models were calibrated have

proved to influence the pattern modelled and the quantity and allocation of changes.

1 INTRODUCTION

Depending on the considered scale, spatial data can

offer different information about the studied features

and the relationship between them. In consequence,

scale influences any analysis of geographical data,

including Land Use and Land Cover (LULC)

modelling.

Usually scale is understood as cartographic scale

(ratio), extent (map size or study are size) or grain,

which is sometimes referred as spatial scale

(O’Sullivan and Perry, 2013). The temporal and

thematic resolution are also considered part of the

concept of scale, together with the Minimum

Mapping Unit (MMU) (Castilla et al., 2009), that is,

the smallest size area unit to be mapped. A smaller

MMU means a more detailed map, whereas a bigger

MMU reduces such detail. In the last case, smaller

features are not drawn and, consequently, the map

representation only focus on the dominant features.

Several papers have addressed the scale

influence on LULC modelling, focusing on the grain

or spatial resolution (Blanchard, Pontius Jr. and

Urban, 2015), extent (Verburg A. Veldkamp, 2004),

temporal resolution (Rosa et al., 2015) and, in the

case of CA models, neighbourhood size (Pan et al.,

2010). However, there is a lack of research about

how the cartographic scale and the Minimum

Mapping Unit (MMU) of the data vary the model

results.

Several studies proved the MMU influence on

pattern analysis and landscape metrics calculation

(Saura, 2004; Kelly, Tuxen and Stralberg, 2011).

This shows how MMU affects GIS analysis and,

therefore, the need to evaluate this component of

scale.

Figure 1: Asturias Central Area location. Sources:

National Topographic Map 1:200.00.

The objetive of this paper is to study the effects

of cartographic scale and MMU on LULC modelling

through the comparison of two models calibrated at

two different scales (1:100.000 and 1:25.000). We

study the quantity and allocation disagreements as

Álvarez, D.

Cartographic Scale and Minimum Mapping Unit Inﬂuence on LULC Modelling.

DOI: 10.5220/0006383003270334

In Proceedings of the 3rd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2017), pages 327-334

ISBN: 978-989-758-252-3

327

well as the pattern disagreement consequence of the

dissimilar data used in the scenarios generated by

the models. From this point forward, when referring

to scale we refer to the cartographic scale and

MMU.

2 STUDY AREA AND DATA SETS

2.1 Study Area

The test area was the Asturias Central Area, the

most dynamic space of Asturias (Spain) (Fig. 1).

The main changes are from rural covers to urban and

industrial spaces.

2.2 Data Sets

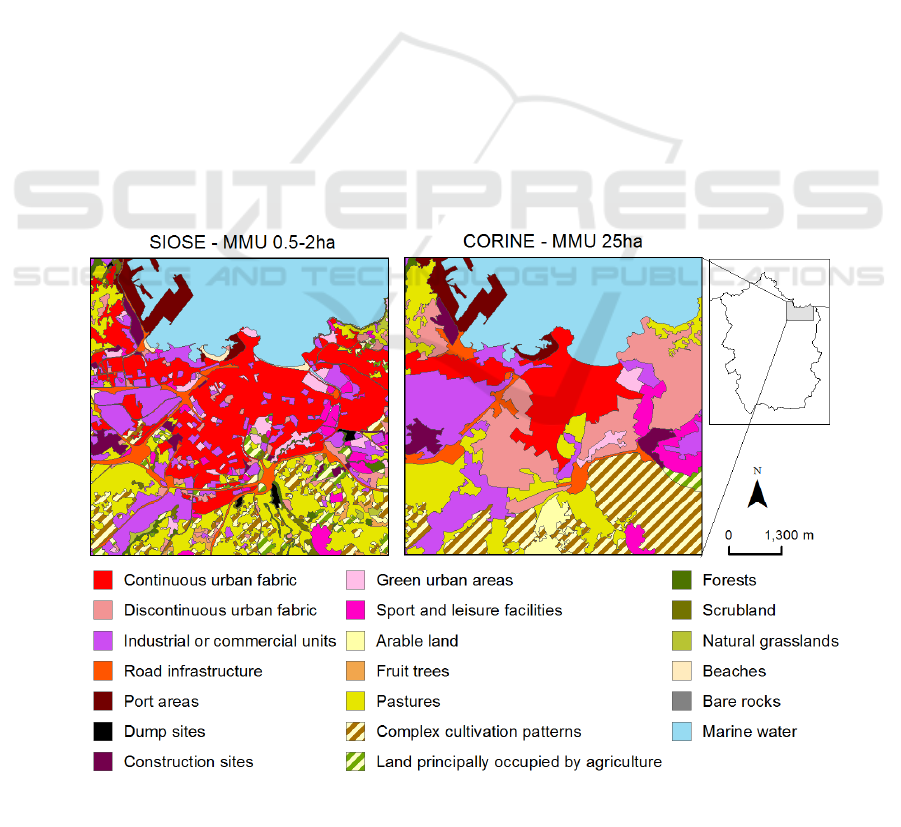
Two LULC maps at two cartographic scales and

with different MMU were employed: CORINE

(1:100.000; 25ha) and SIOSE (1:25.000; 0.5-2ha)

(Fig. 2).

Whereas SIOSE was obtained by photo-

interpretation of aerial imagery, CORINE was made

from a generalization of SIOSE. Therefore, both

maps refer to the same base dates (2005 and 2011)

and the differences between them are a result of the

generalization process, that is a result of the different

scale rules (MMU).

There is not a final land cover map for SIOSE.

Its data base gives information about the proportions

of every cover that compose every polygon, but

there is not a unique label that identifies all

polygons. Therefore, we carried out a generalization

of that statistical information in a way that the

geometry (polygons) is defined by a unique cover

(label). This was made through the implementation

of translation rules according to the proposal of

Delgado Hernández (2016).

To make comparable the two maps, they were

reclassified according to the same legend. Although

coarser scales usually tie in with simpler thematic

resolutions, since our objective is to analyse the

influence of cartographic scale and MMU on LULC

modelling, we have kept the thematic resolution

constant. Otherwise, the results would show the

general influence of all components of scale on

LULC models. Moreover, both map cartographic

scales (1:25.000 and 1:100.000) are regional.

Accordingly, both fit well with the proposed legend.

Finally, both data sets were rasterized at 12.5m

(SIOSE) and 50m (CORINE) following the criteria

proposed by Hengl (2006) in the search for the

Figure 2: Input maps comparison for an example area (Gijón). Sources: SIOSE (2011) and CORINE (2012)

GAMOLCS 2017 - International Workshop on Geomatic Approaches for Modelling Land Change Scenarios

328

minimum influence of the rasterization on our

analysis. That is why we have not used the reference

CORINE resolution (100m).

3 METHODS

3.1 Model Calibration and Simulation

Two models were implemented in Dinamica EGO,

one for SIOSE (1:25.000 model) and another one for

CORINE (1:100.000 model). Dinamica is a

recognized stochastic cellular automata model,

which is in addition very flexible (Mas et al., 2014).

This allowed to set up both models according to the

same criteria.

Two functions compose Dinamica EGO:

expander and patcher. The expander function models

new pixels as an expansion of previous patches,

whereas the patcher function models new pixels as a

new patch, isolated from previous patches of the

same class. More information about these functions

and the model architecture can be found in Soares,

Cerqueira and Pennachin (2002).

Dinamica Ego models transitions. Therefore,

different transitions were selected for each model

according to the changes measured by each pair of

input maps (Table 1). Only those transitions with a

minimum quantity of changes (>10ha) were

considered. Like the modelling objective is to study

how artificial surfaces expand, there were selected

only those transitions which transition to an artificial

cover.

Drivers were chosen according to expert criteria

(interviews) and literature review. When a

correlation greater than 0.5 between two drivers was

detected, one of them was removed from the model.

The driving forces included in the model are:

roads, train stations, residential and industrial

buildings, coastline, leisure facilities, population

density, slopes, planning, substratum and industrial

ports. When possible, drivers were obtained from

sources with similar scales to the implemented

models (1:25.000 and 1:100.000).

Driving forces relation with changes was

calibrated through the Weights of Evidence method,

which is part of Dinamica EGO. The two models

were run with the same weights of evidence,

according to expert criteria. This is possible because

Dinamica allows the user to modify manually the

obtained weights.

The model parameters (size and variance of new

patches) were established according to real changes

(2005-2011). Finally, when some strange or

incorrect behaviour was detected, it was corrected

manually. Thus, it was applied a manual and expert

calibration.

Once the model was calibrated, a simulation was

run to the year 2020, which fits well with the short

calibration period (six years). Transition rates for the

simulation year (2020) are a modification of the

rates of change for the calibration period according

to real trends of change for the modelled period, as

pointed out by experts.

Table 1: In grey, transitions modelled by the two models.

In white, transitions modelled by only one.

From To

Construction sites

Continuous urban

fabric

Pastures

Construction sites

Discontinuous urban

fabric

Pastures

Construction sites

Industrial and

commercial units

Arable lands

Pastures

Complex cultivation patterns

Land principally occupied by

agriculture

Forests

Natural grasslands

Scrubland

Construction sites Infrastructures

Forests

Mineral extraction

sites

Scrubland

Arable land

Pastures

Dump sites

Forests

Dump sites

Construction sites

Arable land

Pastures

Complex cultivation patterns

Land principally occupied by

agriculture

Forests

Natural grasslands

Scrubland

3.2 Data Analysis and Assessment

Disagreements were calculated for the input maps

and for the changes simulated, that is without

considering the permanent areas. Disagreements for

input maps give us information about how the

difference of the initial data can explain the results

generated by the models.

Quantity and allocation disagreements were

analysed through the matrix proposed by Pontius Jr.

and Millones (2011). For the pattern disagreement, a

series of spatial metrics were calculated through

FRAGSTATS 4.2. These are: Number of Patches

Cartographic Scale and Minimum Mapping Unit Inﬂuence on LULC Modelling

329

(NP), Area-Weighted Mean Patch Area (AWMPA)

and Patch Cohesion Index (PCI). Their selection was

based in how much information they provided, that

is how well they express the difference between the

compared maps.

4 RESULTS

4.1 Quantity and Allocation

Disagreement

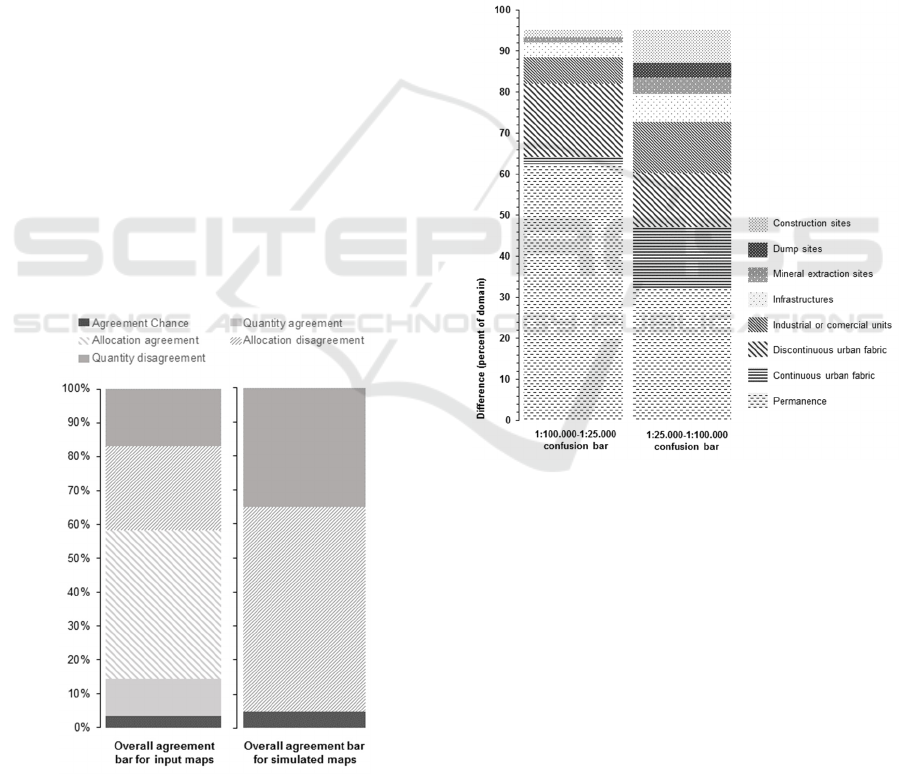
There is an important difference in the quantity and

allocation of classes between the two input maps

(SIOSE and CORINE) because of their different

scale. Only around the 44% of the area in one map

corresponds to the same category in the other map

(Fig. 3).

In consequence, each map measures different

types and quantity of changes. This has resulted in

the consideration of different transitions for the two

models (Table 1). Also, like the areas where every

class is located are different (25% allocation

disagreement), the simulated changes will locate in a

different position. Since there are two models which

simulate different transitions and the location of the

classes where the transition takes place are probably

different, there is a low probability that the changes

simulated by both models would be similar.

Figure 3: Overall agreement bars for input and simulated

maps.

This is what Figure 3 tell us: the only agreement

between simulated changes by the two models is due

to chance. Depending on the input maps used, the

model produces a very different result. The 95% of

the changes simulated by the two models are

different (Fig. 4)

Figure 4 allows to see the quantity disagreement

between the simulated changes depending on the

class considered. Each confusion bar is composed by

various sections, which represent the proportion of

pixels that are allocated to a different class on the

other simulation. When the section for any particular

class (e.g. continuous urban fabric) is larger in one

bar than on the other, there is a quantity

disagreement, which is proportional to the difference

between the two sections in both bars.

Figure 4: The first bar depicts the simulated areas in the

1:100.000 model that are not the same in the 1:25.000

model. The second bar depicts the simulated areas in the

1:25.000 model that are not the same in the 1:100.000

model.

The simulated changes are greater in the

1:25.000 model than in the 1:100.000 model: the

size of the confusion bar for permanence is greater

in the 1:100.000 model than in the 1:25.000 model

(Fig. 4). Hence, regarding the total area simulated as

change by both models, in the 1:100.000 model only

the 38% of the area is change, whereas in the

1:25.000 model that is true for the 68% of the area.

This is because, due to the smaller MMU, SIOSE

allows to detect small changes. Whereas only

changes over 5ha are drawn in CORINE, SIOSE

represents every change bigger than 0.4ha.

GAMOLCS 2017 - International Workshop on Geomatic Approaches for Modelling Land Change Scenarios

330

The quantity disagreements at the class level are

related to the quantity disagreements between input

maps. E.g. there is more quantity disagreement for

continuous urban fabric in the 1:25.000 model than

in the 1:100.000 model because the area of the

continuous urban fabric is bigger in the input maps

of the first model (SIOSE) than in the input maps of

the second model (CORINE).

Figure 5: Agreement bars per category for simulated

changes in the two models (1:100.000 and 1:25.000).

Like the only agreement between simulated

changes is due to chance, the allocation

disagreement bars at the class level don´t give us

extra information (Fig. 5). Most of the area in the

bars are disagreements and, therefore, their

information corresponds to the disagreements

showed by Figure 4.

No allocation agreement is achieved because,

whereas the drivers are the same in the two models,

the candidate areas to transition are located in

different places. The bigger the quantity and

allocation disagreement between input maps, the

bigger the probability that a same pixel is located in

a different place in the two maps and, therefore, the

bigger the probability that the candidate pixel to

transition would be different in the two models.

4.2 Pattern Disagreement

The pattern simulated by the two models is related to

the input maps pattern. However, when one

compares real changes (2005-2011) to simulated

changes, the results show how the model behaves

similarly independent of the considered scale.

Despite of the bigger MMU for CORINE (25ha)

than for SIOSE (0.5-2ha), there are not big

differences in the fragmentation of changes for the

1:100.000 and 1:25.000 models (Table 2). In fact,

some classes show a bigger area-weighted mean

patch area (polygon mean area corrected by the

polygon size) for the model at a finer scale than for

the model at a coarser scale. Likewise, the number

of changing patches increases with the simulation

for the coarser model, whereas it falls for the finer

model.

Whereas the effect of the MMU rule is evident

for the real changes (input maps cross tabulation),

we can´t perceive it in the simulated changes (Table

Table 2: Spatial metrics at the class level for real (2005-2011) and simulated (2011-2020) changes.

Simulated changes

2011-2020

Number of pathes Area-weighted mean patch area Patch cohesion index

1:25 1:100 1:25 1:100 1:25 1:100

Continuous urban fabric 44 13 10.7344 3.3967 95.0723 71.0631

Discontinuous urban fabric 79 88 11.9334 16.5856 93.7738 80.4932

Industrial or commercial units 81 42 14.9641 8.1407 95.7527 79.9843

Infrastructures 15 4 14.5344 32.3644 96.4041 92.4082

Mineral extraction sites 35 5 1.9123 3.537 90.3935 72.052

Dump sites 11 4 7.7488 5.1667 94.9689 77.3581

Construction sites 118 26 3.3104 2.9085 90.2173 63.8639

Input maps changes

2005-2011

Number of pathes Area-weighted mean patch area Patch cohesion index

SIOSE CORINE

Continuous urban fabric 72 4 19.5006 12.5078 96.4369 86.0809

Discontinuous urban fabric 130 19 11.6396 43.5088 93.5797 92.4059

Industrial or commercial units 130 23 26.328 34.0165 95.7127 89.8172

Infrastructures 8 1 13.3087 35.75 96.6727 93.0449

Mineral extraction sites 64 2 5.3172 18.8616 92.89 88.8021

Dump sites 34 8 5.578 7.3148 93.4537 80.6492

Construction sites 95 10 37.7259 83.333 97.3597 95.4769

Cartographic Scale and Minimum Mapping Unit Inﬂuence on LULC Modelling

331

2). That is because the models work at the pixel

level, regardless of the MMU. Since the pixel size is

much smaller than the MMU (156m

(1:25.000) vs

0.2-0.5ha (SIOSE) and 0.25ha (1.100.000) vs 25ha

(CORINE)), there is not much difference in the

model behaviour because of the MMU.

The bigger the contrast between the MMU and

the pixel size, the more evident the effects of the

model behaviour in the resultant pattern. That is the

reason why the 1:100.000 model show a more

contrasted behaviour regarding to real changes than

the 1:25.000 model.

Like there are not MMU rules, the connection or

aggregation of simulated changes (patch cohesion

index) is smaller than the aggregation of real

changes in both models, although the contrast is

again more pronounced for the coarse scale model

than for the fine scale one.

5 DISCUSSION

5.1 Input Maps

Input maps play an essential role on the model

results. Therefore, knowing the uncertainty of the

data sets which we are using it is critical in

modelling research (Verburg, Neumann and Nol,

2011), since most of the model conclusions will be a

consequence of how these maps reflect reality.

The results have showed important differences

between input maps (SIOSE and CORINE). This has

been a great limitation for the models agreement: the

dissimilar quantities and allocations of the same

categories turn out on different possibilities to

allocate the same transitions.

Working with maps at lower thematic resolutions

can help to achieve a higher agreement between

input maps. Thus, uncertainty is usually lower at

coarser scales since local changes are omitted

(Verstegen et al., 2012).

5.2 Model Calibration

The finer the scale considered, the bigger the

information that input maps provide. Accordingly,

maps at finer scales (SIOSE) show a bigger quantity

and types of changes than maps at coarser scales

(CORINE). In consequence, transition rates

(estimated quantities of changes) and potential

transitions (type of changes modelled) are different

depending on the scale of the model: the quantity of

changes and the number of transitions are bigger for

the 1:25.000 model than for the 1:100.000 model.

The provision of more information about reality

can be seen as an advantage because we can

understand better the dynamics of our study area.

However, it is also a limitation when we need to

manage tons of complex information to calibrate the

model. At finer scales, transitions rarely occur alone

and different transitions happen together. The

patterns of change are also more complex.

When using fine scale maps, we also need to pay

attention to the possible noise in the data. The finer

the scale considered, the greater the possibility to

find noise (small changes that are not real changes).

This noise will influence the results of our model.

Thus, the modeller has to find a balance between

data detail and model complexity. More detail but

much more complexity is worse than less detail and

a very simple model (Wainwright and Mulligan,

2013). The perfect balance would be a manageable

complexity level which is in accordance with the

detailed added to the model.

Also, depending on the dynamics that the

modeller can explain, a finer or coarser scale should

be chosen. The 1:100.000 and 1:25.000 models were

calibrated using the same driving forces, despite of

the fact that their input maps show different

dynamics.

The SIOSE maps show small changes, because

of the small MMU, that are not correctly modelled

since there are not additional drivers to explain

them. For certain classes, like dump sites, the

1:25.000 model identifies more changes. However,

most of these new changes come from processes that

are different to the processes which cause the

changes identified by the 1:100.000 model. Like we

model in both cases the changes with the same

drivers, the 1:25.000 model extrapolates changes

from one process to changes from other processes.

If there is only information for the main

dynamics of the study area, a coarse scale model,

like the 1:100.000 model, is advisable. However, if

we can explain also the small changes which are

visible in SIOSE, the 1:25.000 model is maybe the

best option.

Nevertheless, CORINE maps only reflects the

bigger changes in the Asturias Central Area.

Because of the scarce dynamics of this area when

compared with metropolitan areas or other big cities,

the changes showed by CORINE are few and with

very specific locations. Therefore, it is difficult to

extract an organic growing pattern from that data.

Consequently, depending on the area studied and

its characteristics, most of the dynamics can only

emerge at specific scales. If the urban sprawling

comes from small urban patches, a fine scale map is

GAMOLCS 2017 - International Workshop on Geomatic Approaches for Modelling Land Change Scenarios

332

needed. However, in the opposite case, a coarse map

can be sufficient.

Therefore, every scale has some advantages and

limitations. The modeller mission is, as pointed out

previously, to find a balance between all the

requirements.

5.3 Simulations

The two scenarios generated by the two calibrated

models are very different. The agreement between

them is only by chance. Most of this difference

comes from the contrasted information in the input

maps (quantity and allocation disagreement). The

stochastic component of the model must have

influenced the results also. Nevertheless, the scale

and resolution at which the model is set up also have

played a role in the resultant scenario.

Grain is considered as spatial scale and it is

related to the others concepts of scale: small MMU

imply finer spatial resolution than larger units. Then,

models at finer scales (1:25.000, 12.5m) simulate

more pixels than models at coarser scales

(1:100.000, 50m). As a result, the quantity of pixels

to allocate is not the same for models at different

scales and resolutions: the bigger the resolution, the

bigger the quantity of pixels to allocate and the more

likely the model to make a mistake. Therefore, the

probability to make a mistake is greater for finer

scale models than for coarser scales models.

Similar studies which have focused the analysis

on the influence of the spatial resolution on LULC

modelling have reached similar conclusions

(Marceau et al., 2005; Pan et al., 2010).

In addition, there is an incoherence between the

model resolution (12.5m and 50m) and the MMU

(0.2-0.5ha and 25ha). This makes the pattern of the

simulated scenarios more fragmented than the initial

pattern, especially when we are working with maps

that have big MMU, like CORINE. The model

allocates changes as pixels whereas input maps only

show changes that meet the MMU. In consequence,

the changes allocated by the model will be smaller

than the changes measured by the input maps.

Model validation through techniques that

compare the generated scenario with the real map

for the same date are not completely reliable.

Whereas the scenario doesn´t meet with the MMU

rules, the reference map does. Consequently, they

are never going to show the same information. A

real change that only affects a pair of pixels won´t

be reflected in the reference maps because it doesn´t

comply with the minimum required size. However,

the model does can simulate correctly that change.

Dinamica EGO allows the user to achieve the

wished simulation pattern through the functions

expander and patcher. One can decide how much

pixels will be allocated as expansion of previous

patches and how much pixels will conform new

patches for every simulated category. The user can

decide also, for every transition, the mean and

variance of the new patches generated.

Although that seems a solution for the proposed

problem (Soares-Filho et al., 2003), that did not

work for our study area. The mean and variance

parameters are only considered when there is an

enough variety of candidate areas of different sizes

for a specific transition. A candidate area is possible

when inside a polygon of the destination category of

the transition there is a suitable area, that is an area

that, according to the model driving forces, has a

value above 0.

Suitable areas for transitions are going to be

smaller in models at finer scales (1:25.000) than in

models at coarser scales (1:100.000) because of the

respective size of the polygons in each model

(MMU). Therefore, models at finer scales (smaller

MMU), as far as their input maps are composed by

small polygons, find more difficult to vary the

desired pattern than models at coarser scales (bigger

MMU).

Patch-based models can be a solution for all

these problems (Wang and Marceau, 2013).

4 CONCLUSIONS

There is an important source of uncertainty

consequence of the chosen scale in LULC

modelling, as it is in any GIS analysis.

Firstly, this uncertainty comes from the input

maps dissimilarity. LULC data for the same area

offer different information depending on the

cartographic scale and minimum mapping unit

(MMU). The input maps selected, as far as they

show a specific representation of a given area, will

provide different input parameters to the LULC

model.

Making these maps simpler (e.g. decreasing

thematic resolution) can reduce the dissimilarity

between them at the expense of model complexity.

Secondly, uncertainty comes from the scale at

which the model is set up. Modelled patterns are

dependent on the spatial resolution, which is linked

with the MMU: small MMU imply finer spatial

resolution than larger units. The quantity and detail

of changes also vary with the scale. Models at finer

scales manage more information than models at

Cartographic Scale and Minimum Mapping Unit Inﬂuence on LULC Modelling

333

coarser scales, although they are more complex to

calibrate since the greater the quantity of

information, the higher the model complexity. How

the modeller manages this complexity can introduce

additional uncertainty in the model. Therefore, the

user must strike a balance between model

complexity and explanatory power.

ACKNOWLEDGEMENTS

This work has been supported in part by project

SIGEOMOD_2020. BIA2013-43462-P (Spanish

Ministry of Economy and Competitiveness and the

Feder European Regional Development Fund). The

author is also grateful to the Spanish Ministry of

Economy and Competitiveness and the European

Social Fund for the funding of his research activity

(Ayudas para contratos pre-doctorales para la

formación de doctores 2014).

REFERENCES

Blanchard, S. D., Pontius Jr., R. G. and Urban, K. M.

(2015) ‘Implications of Using 2 m versus 30 m Spatial

Resolution Data for Suburban Residential Land

Change Modeling’, Journal of Environmental

Informatics, 25(1), pp. 1–13. doi:

10.3808/jei.201400284.

Castilla, G., Larkin, K., Linke, J. and Hay, G. J. (2009)

‘The impact of thematic resolution on the patch-

mosaic model of natural landscapes’, Landscape

Ecology, 24(1), pp. 15–23. doi: 10.1007/s10980-008-

9310-z.

Delgado Hernández, J. (2016) Methodology of

classification extraction from descriptive systems of

land cover and land use. doi:

10.13140/RG.2.1.2639.5921.

Hengl, T. (2006) ‘Finding the right pixel size’, Computers

and Geosciences, 32(9), pp. 1283–1298. doi:

10.1016/j.cageo.2005.11.008.

Kelly, M., Tuxen, K. A. and Stralberg, D. (2011)

‘Mapping changes to vegetation pattern in a restoring

wetland: Finding pattern metrics that are consistent

across spatial scale and time’, Ecological Indicators.

Elsevier Ltd, 11(2), pp. 263–273. doi:

10.1016/j.ecolind.2010.05.003.

Marceau, D. J., others, Ménard, A. and Marceau, D. J.

(2005) ‘Exploration of spatial scale sensitivity in

geographic cellular automata’, Environment and

Planning B: Planning and Design, 32(5), pp. 693–714.

doi: 10.1068/b31163.

Mas, J.-F., Kolb, M., Paegelow, M., Camacho Olmedo, M.

T. and Houet, T. (2014) ‘Inductive pattern-based land

use/cover change models: A comparison of four

software packages’, Environmental Modelling &

Software, 51, pp. 94–111. doi:

10.1016/j.envsoft.2013.09.010.

O’Sullivan, D. and Perry, G. L. W. (2013) Spatial

Simulation: Exploring Pattern and Process.

Chichester: John Wiley & Sons.

Pan, Y., Roth, A., Yu, Z. and Doluschitz Reiner, R. (2010)

‘The impact of variation in scale on the behavior of a

cellular automata used for land use change modeling’,

Computers, Environment and Urban Systems, 34(5),

pp. 400–408. doi:

10.1016/j.compenvurbsys.2010.03.003.

Pontius Jr., R. G. and Millones, M. (2011) ‘Death to

Kappa: birth of quantity disagreement and allocation

disagreement for accuracy assessment’, International

Journal of Remote Sensing, 32(15), pp. 4407–4429.

doi: 10.1080/01431161.2011.552923.

Rosa, I. M. D., Purves, D., Carreiras, J. M. B. and Ewers,

R. M. (2015) ‘Modelling land cover change in the

Brazilian Amazon: temporal changes in drivers and

calibration issues’, Regional Environmental Change,

15(1), pp. 123–137. doi: 10.1007/s10113-014-0614-z.

Saura, S. (2004) ‘Effects of remote sensor spatial

resolution and data aggregation on selected

fragmentation indices’, Landscape Ecology, 19(2), pp.

197–209. doi:

10.1023/B:LAND.0000021724.60785.65.

Soares, B. S., Cerqueira, G. C. and Pennachin, C. L.

(2002) ‘DINAMICA - a stochastic cellular automata

model designed to simulate the landscape dynamics in

an Amazonian colonization frontier’, Ecological

Modelling, 154(3), pp. 217–235. doi: 10.1016/S0304-

3800(02)00059-5.

Soares-Filho, B. S., Corradi Filho, L., Coutinho Cerqueira,

G. and Leite Araujo, W. (2003) ‘Simulating the spatial

patterns of change through the use of the dinamica

model’, in Anais XI SBSR

, pp. 721–728.

Verburg, P. H., Neumann, K. and Nol, L. (2011)

‘Challenges in using land use and land cover data for

global change studies’, Global Change Biology, 17(2),

pp. 974–989. doi: 10.1111/j.1365-2486.2010.02307.x.

Verburg A. Veldkamp, H. P. (2004) ‘Projecting landuse

transitions at forest in the Philippines at two spatial

scales’, Landscape Ecology, 19, pp. 77–98. doi:

10.1023/B:LAND.0000018370.57457.58.

Verstegen, J. A., Karssenberg, D., van der Hilst, F. and

Faaij, A. (2012) ‘Spatio-temporal uncertainty in

Spatial Decision Support Systems: A case study of

changing land availability for bioenergy crops in

Mozambique’, Computers, Environment and Urban

Systems, 36(1), pp. 30–42. doi:

10.1016/j.compenvurbsys.2011.08.003.

Wainwright, J. and Mulligan, M. (2013) Environmental

Modelling: Finding Simplicity in Complexity. Second

edi. Edited by J. Wainwright and M. Mulligan. John

Wiley & Sons.

Wang, F. and Marceau, D. J. (2013) ‘A patch-based

cellular automaton for simulating land-use changes at

fine spatial resolution’, Transactions in GIS, 17(6), pp.

828–846. doi: 10.1111/tgis.12009.

GAMOLCS 2017 - International Workshop on Geomatic Approaches for Modelling Land Change Scenarios

334