SAT-based Cryptanalysis of Authenticated Ciphers from the

CAESAR Competition

Ashutosh Dhar Dwivedi

, Miloš Klou

cek

, Paweł Morawiecki

, Ivica Nikoli

, Josef Pieprzyk

1,4

and Sebastian Wójtowicz

Institute of Computer Science, Polish Academy of Sciences, Warsaw, Poland

Faculty of Mathematics and Physics, Charles University in Prague, Prague, Czech Republic

Nanyang Technological University, Singapore

Electrical Engineering and Computer Science School, Science and Engineering Faculty,

Queensland University of Technology, Brisbane, Australia

Keywords:

SAT Solvers, SAT-based Cryptanalysis, Logic Cryptanalysis, Authenticated Encryption, CAESAR.

Abstract:

We investigate six authenticated encryption schemes (ACORN, ASCON-128a, ICEPOLE-128a, Ketje Jr,

MORUS, and NORX-32) from the CAESAR competition. We aim at state recovery attacks using a SAT

solver as a main tool. Our analysis reveals that these schemes, as submitted to CAESAR, provide strong resis-

tance against SAT-based state recoveries. To shed a light on their security margins, we also analyse modiﬁed

versions of these algorithms, including round-reduced variants and versions with higher security claims. Our

attacks on such variants require only a few known plaintext-ciphertext pairs and small memory requirements

(to run the SAT solver), whereas time complexity varies from very practical (few seconds on a desktop PC) to

‘theoretical’ attacks.

1 INTRODUCTION

A cryptographic algorithm which provides both con-

ﬁdentiality and authenticity, is called an authenticated

encryption (AE) or simply an authenticated cipher. It

encrypts and authenticates messages using both a se-

cret key (shared by the sender and the receiver) as well

as a public number (called a nonce). AE algorithms

are often built as various combinations of block ci-

phers, stream ciphers, message-authentication codes

and hash functions. Several solutions have been stan-

dardised by ISO/IEC and one of the most widely used

is AES-GCM (National Institute of Standards and

Technology, 2007), which is an authenticated cipher

based on the Advanced Encryption Standard (AES)

(AES, 2001).

In many modern applications, performance and

security requirements are set so high that the current

AE standards established a decade ago struggle to

meet them. A good such example is VMWare View,

which is a remote desktop protocol supported by

low-cost terminals from various manufacturers. The

VMWare 2010 documentation recommends switch-

ing from AES-GCM to a faster cipher for “the best

user experience”. Additionally, the most efﬁcient

hardware implementation of AES-GCM does not

reach the full potential due to the bottleneck caused

by slow multiplication in Galois ﬁelds. Apart from

efﬁciency issues, there are also security problems that

seem to plague legacy AE algorithms.

The great interest and importance of AE have

been manifested by the announcement of a new public

call for AE algorithms — the CAESAR competition

(CAESAR, ). The contest has started in 2014 and has

received worldwide attention. In the ﬁrst round, 57

algorithms were submitted and now (October 2016)

in the third round, 16 ciphers are still in the race. The

competition is planned to ﬁnish by the end of 2017

and “will identify a portfolio of authenticated ciphers

that (1) offer advantages over AES-GCM and (2) are

suitable for widespread adoption".

The primary concern for all AE schemes is a

sound security evaluation. As a rule, the initial evalu-

ation has been given by the designers of the schemes,

while possible improvements by third-party crypt-

analysis. Cryptanalysis of AE schemes is particu-

larly demanding as the attacker works with more con-

straints than in a typical cryptanalysis framework for

Dwivedi, A., Klou

cek, M., Morawiecki, P., Nikoli

c, I., Pieprzyk, J. and Wójtowicz, S.

SAT-based Cryptanalysis of Authenticated Ciphers from the CAESAR Competition.

DOI: 10.5220/0006387302370246

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 237-246

ISBN: 978-989-758-259-2

237

block ciphers or hash functions.

Our Contribution

We investigate the resistances of a chosen set of CAE-

SAR schemes against state recovery attacks. Our

analysis is based on SAT solvers and falls into the

so-called logic cryptanalysis. A state recovery attack

may pose a real threat to the scheme as the known

state often allows to forge tags or even to recover the

secret key. We follow a two-stage approach. First,

we construct a SAT problem that corresponds to the

state recovery of a scheme. Usually, we need only

a handful of ciphertext blocks and the analysis is in

the known plaintext framework. Then, we run a SAT

solver to ﬁnd a solution of the problem. We use

lingeling or its parallel variant plingeling — one

of the best SAT solvers according to the latest SAT

competitions. For each problem, we typically run the

solver on 8 cores for a few days.

We analyse six CAESAR schemes, namely

ACORN (Wu, ), ASCON-128a (Dobraunig et al.,

), ICEPOLE-128a (Morawiecki et al., 2014), Ketje

Jr (Bertoni et al., b), MORUS (Wu and Huang, ),

and NORX-32 (Aumasson et al., 2014b). All ex-

cept ICEPOLE-128a are the third-round candidates

from the CAESAR competition. We omit the CAE-

SAR candidates with large, 8-bit S-boxes

as the al-

gorithms with big and complex S-boxes are known to

be very difﬁcult for SAT solvers and give very little

hope for a successful attack.

Our analysis reveals that all the algorithms (their

full variants, as submitted to the CAESAR competi-

tion) are resistant against SAT-based state recovery.

That is, attacking these schemes with SAT solver is

infeasible even when one is given impractically large

time (but not more than the claimed security level).

Next we focus on approximating their security mar-

gin, and thus we consider weakened versions of the

schemes. We do this by either reducing the number

of rounds or by simplifying the round function. Al-

ternatively, we artiﬁcially increase the security level

expected from ciphers and use it to benchmark our

attacks. In Table 1, we summarize our main results.

For instance, we are able to launch a state recovery

against ICEPOLE-128a when it uses 4 rounds (in-

stead of the original 6). Similarly, we can recover the

state of Ketje Jr, if the claimed security level is higher

than 165 bits (in the original submission, the claimed

security level is 96 bits).

Note, we have started the analysis before the announce-

ment of the third-round candidates and then ICEPOLE-

128a was still in the race.

Recall that several CAESAR candidates are based on

Table 1: SAT-based state recovery.

Cipher Key size Rounds Complexity Reference

ICEPOLE-128a 128 (128) 4 (6) 2

108

Section 3.2

ASCON-128a 128 (128) 2 (8) 2

Section 3.3

NORX-32 128 (128) 1.5 (4) 2

Section 3.4

Ketje Jr >165 (96) full 2

165

Section 3.1

MORUS >370 (128) full 2

370

Section 4.1

Related Work

As a tool, SAT solvers have been used in the CAE-

SAR competition. Laﬁtte et al.(Laﬁtte et al., 2016)

perform SAT-based state recovery of ACORN, but

end up with a state recovery which requires higher

complexity than a simple brute force attack. Stoffelen

(Stoffelen, 2016) used SAT solvers to ﬁnd optimized

S-box implementations for several proposals includ-

ing ASCON, ICEPOLE, Ketje and many others. An

interesting work is a new automated tool for ﬁnding

linear characteristics, where some developed heuris-

tics are inspired by modern SAT solvers (Dobraunig

et al., 2015b). The tool was applied to some schemes

from the CAESAR competition. Note that references

regarding the analysed ciphers are given right after a

description of a given cipher (Section 3).

Outline

After this brief introduction to authenticated encryp-

tion, SAT-based cryptanalysis and a summary of our

results, the paper is organized as follows. In Section

2 we ﬁrst show how authenticated encryption is re-

alised with the sponge/duplex construction. Next, we

describe the CICO problem and its relevance to our

SAT-based state recovery attacks. Section 3 is our

main contribution, where we give details on the anal-

ysis and experiments we carried out. Concluding re-

marks are given in the last section.

2 PRELIMINARIES

2.1 Sponge-based Authenticated

Encryption Schemes

Bertoni et al. introduced the sponge function

in (Bertoni et al., a). The sponge function and its sister

construction called the duplex construction (Bertoni

et al., 2011) can be used to design a wide range of

cryptographic algorithms including authenticated en-

cryption schemes. The duplex construction is used

for a relatively large group of algorithms submitted

AES (which uses 8-bit S-boxes)

SECRYPT 2017 - 14th International Conference on Security and Cryptography

238

pad

K || nonce

ciphertext C

pad

plaintext P

ciphertext C

pad

plaintext P

ciphertext C

pad

plaintext P

tag T

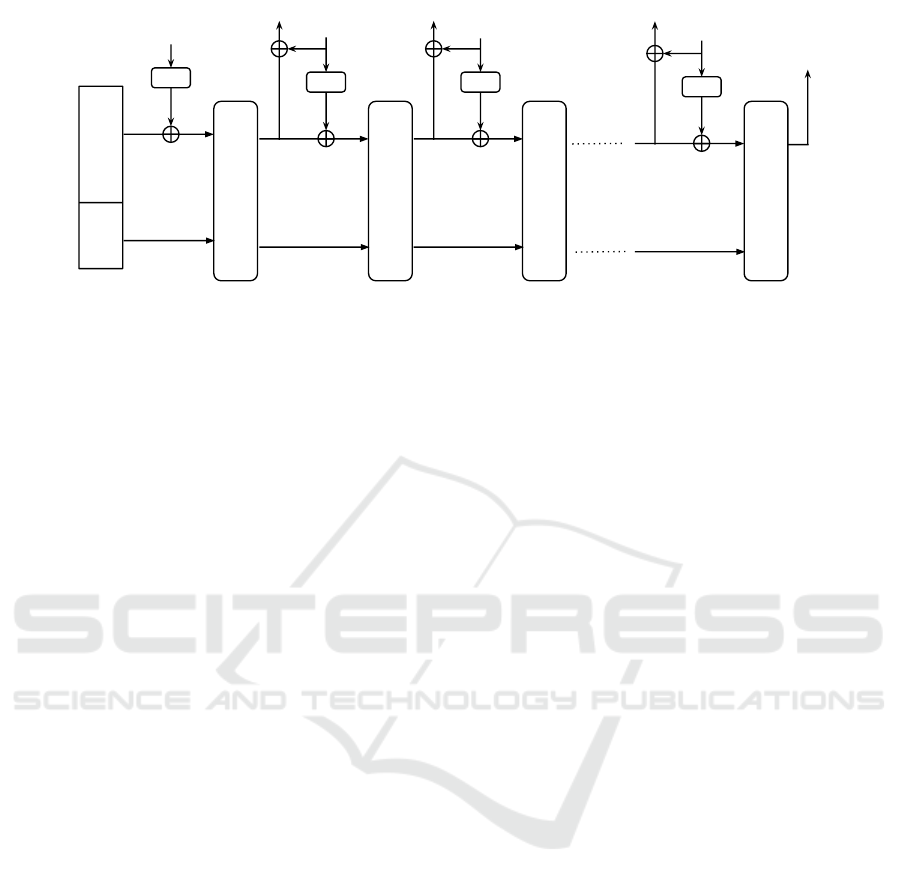
Figure 1: Authentication encryption scheme based on the duplex construction.

to the CAESAR competition. We analyse four such

algorithms: ASCON, ICEPOLE, NORX and Ketje.

The duplex construction is based on a ﬁxed per-

mutation (or transformation) determined by the fol-

lowing two parameters: bitrate r and capacity c. The

sum of the two parameters gives the input/output

length or the state size. For a ﬁxed state size, differ-

ent values for bitrate and capacity provide trade-offs

between speed and security. A higher bitrate gives a

faster algorithm with lower security and vice versa.

The duplex construction absorbs input blocks (plain-

text) into the bitrate part of the permutation f . If an

input block is smaller than r bits, it gets padded to the

full r bits. After processing by the permutation f , r-

bit output blocks (ciphertext) are squeezed out. Note

that the capacity part of the state is never directly ma-

nipulated, neither for absorbing nor for squeezing.

Authenticated encryption with associated data

(AEAD) can be realized using the duplex construc-

tion. Figure 1 shows a typical application. First, a

secret key K and a nonce is absorbed into the initial

state and the permutation f is called. The following

steps are iterations performed for pairs: plaintext P

and ciphertext C

, where i = 0, ..., n. For the plain-

text P

, the ciphertext C

is computed by XOR-ing the

plaintext with the bitrate part squeezed out from the

state. After P

is absorbed, the bitrate part becomes

. The permutation f is called again and the next

iteration proceeds. Besides plaintext blocks, public

associated data blocks can be processed by absorb-

ing them without encryption. The encryption is com-

pleted by squeezing a r-bit authentication tag T .

The analysed AE algorithms are different al-

though they preserve the general duplex construction.

Their security heavily depends on the internal permu-

tation f , typically implemented as a sequence of ele-

mentary operations called rounds. It is expected that

if the permutation f applies more rounds, then the

cryptanalysis becomes more complex and the relevant

AE becomes more secure (but also slower).

2.2 CICO Problem

In (Bertoni et al., a) it was shown that the constrained-

input constrained-output (CICO) problem is essential

for security of cryptographic sponges and primitives,

which are built upon them. The problem can be stated

as follows. We are given a function f (e.g. a permuta-

tion), which maps input bits to output bits. Some bits

are ﬁxed and a problem is to determine unknown parts

of input and output states, such as the input-output

mapping is valid. A generalization of the CICO prob-

lem is the multi-block CICO problem, where we deal

with a number of f calls and states between them.

(See Figure 3.) Again, our task is to determine un-

knowns.

Let us now see how the CICO problem refers to

the sponge-based authenticated cipher shown in Fig-

ure 1. If we know plaintext-ciphertext pairs (a known

plaintext framework), then XORing such a pair gives

the r-bit part of the state (bitrate part). Thus, we can

take two consecutive plaintext-ciphertext pairs and try

to determine the unknown part of the states (capacity

part). Clearly, such a state-recovery attack is captured

by a notion of the CICO problem. For some algo-

rithms, such as Ketje, the bitrate is very small (e.g.

one byte) and to uniquely recover the actual state we

need more plaintexts-cipher blocks. This scenario is

captured by the multi-block CICO problem.

A natural way to solve the CICO problem is to

express it as a set of algebraic equations in a set of

unknowns and apply algebraic techniques for solving

these equations. One of such generic techniques (or

tools) is a SAT solver.

2.3 SAT-based Cryptanalysis

SAT is the ﬁrst known NP-complete problem, proven

by Stephen Cook in 1971 (Cook, 1971). A SAT solver

is an algorithm that decides whether a given propo-

sitional (boolean) formula has a satisfying valuation.

SAT-based Cryptanalysis of Authenticated Ciphers from the CAESAR Competition

239

input output

Figure 2: CICO problem.

f f f

? ? ?

Figure 3: Multi-block CICO problem.

Finding a satisfying valuation is infeasible in general,

but many SAT instances can be solved surprisingly

efﬁciently. There are many competing algorithms

for solving SAT instances and many implementations,

most of them have been developed over the last two

decades as highly optimized versions of the Davis,

Putnam, Logemann and Loveland (DPLL) procedure

(Davis et al., 1962; Davis and Putnam, 1960). Mod-

ern SAT solvers use ﬁnely tuned algorithms and data

structures to ﬁnd a solution for a given instance coded

in a conjunctive normal form (CNF) form. To solve

an instance of a problem, (1) the instance is ﬁrst trans-

lated into a corresponding SAT instance (in such a

way that a satisfying valuation represents a solution

to the instance) and (2) a SAT solver is run to ﬁnd one

or more satisfying valuations.

The ﬁrst connection between the SAT problem

and cryptography dates back to (Cook and Mitchell,

1997), where a suggestion appeared to use crypto for-

mulae as hard benchmarks for propositional satisﬁa-

bility checkers. Courtois and Pieprzyk (Courtois and

Pieprzyk, 2002) translated cryptographic structures

into large systems of low degree equations showing

a potential of algebraic approach in analysis of block

ciphers. Interestingly, SAT solvers were successfully

applied against KeeLoq — the cipher deployed in car

industry (Courtois et al., 2008). Recently, a SAT

solver approach was used to prove a resistance of

the Salsa20 cipher against differential cryptanalysis

(Mouha and Preneel, 2013).

(1) CNF Generation

In practice, a formula given to a SAT solver has to

be expressed in a Conjunctive Normal Form (CNF).

Therefore, for each scheme we need to convert the

instance of CICO (or multi block CICO)into a CNF

(solution of which corresponds to the unknown bits of

the input and the output in the CICO problem). Most

operations in the analysed ciphers can be easily de-

scribed by short bitwise equations, with the AND and

XOR operators. For such operations a translation is

straightforward. For instance, the 1-bit XOR equation

z = x ⊕ y has the corresponding CNF form

(x ∨ y ∨ z) ∧ (x ∨ y ∨ z) ∧ (x ∨ y ∨ z) ∧ (x ∨ y ∨ z) (1)

For S-boxes, which are typically speciﬁed as a

truth table, we try two approaches. First approach

is to use the bitwise speciﬁcation for a given S-box

and convert simple bitwise equations to the CNF. A

drawback of this simple approach is that we need to

add extra temporary variables. The other approach

is to give the truth table of an S-box to the Espresso

minimisation tool (Rudell, 1986) and obtain the CNF.

In some cases Espresso produces much smaller CNFs

(fewer number of clauses). We conﬁrm the validity of

the generated CNF by checking if a solution (output

bits) found by a SAT-solver corresponds to the actual

solution from test vectors for a given authenticated ci-

pher.

(2) SAT Solvers

We have considered several SAT solvers as potential

candidates, including CryptoMiniSat, plingeling,

treengeling, glucose. Most of them performed

very well on the latest SAT competitions (particularly

in the parallel track category). After certain num-

ber of tests, we have decided to use the SAT solver

plingeling as in our experiments it outperforms the

other solvers.

3 ANALYSIS OF SPONGE-BASED

SCHEMES

In this section we present our state recovery attacks

on six AE schemes from the CAESAR competition.

We divide the schemes into two groups: sponge-based

(given in Sect. 3) and other (in Sect. 4). For each al-

gorithm we give a brief description and details of the

attack.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

240

3.1 Ketje

Ketje is an authenticated encryption algorithm which

targets memory-constrained devices (Bertoni et al.,

b). The scheme supports two families of ciphers,

namely Ketje Sr and Ketje Jr. Ketje Sr uses 400-

bit states and is based on the round-reduced Keccak-

f[400] permutation, whereas Ketje Jr operates on 200-

bit states with the Keccak-f[200] as the underlying

permutation. In our analysis, we focus on Ketje Jr.

The permutation of Ketje Jr has the bitrate of

r = 16, capacity of c = 184 and supports keys of

lengths up to 182 bits. The claimed security level is

(c − 1 − log

M) bits, where M is a number of blocks

observed online (data complexity). For example, if

data complexity is limited to 2

blocks, then the se-

curity level is 184 − 1 − 23 = 160 bits, provided that

a key is at least 160-bit long. The Ketje Jr family sub-

mitted to the CAESAR competition claims the 96-bit

security level with the data complexity limit of 2

block observations. In our SAT analysis, we aim at

verifying the claimed security level.

A small bitrate (16 bits) of Ketje Jr suggests that

we should focus on the multi-block CICO problem.

We investigate the following scenarios:

• Basic. In this scenario, we take the outputs of 13

consecutive rounds (as the ratio of state size to the

bitrate is 12.5) and try to recover the state from

these outputs. The available information from col-

lected data is translated into a corresponding SAT

instance with 6440 variables and 44944 clauses.

The SAT solver was unable to ﬁnd a solution

within a reasonable time (most of our solvers were

running on 8 cores for a few days).

• Guess in the middle. In the second scenario, we

guess t bits of the state in the middle round (i.e.

the round n

/2). This is to say that apart from the

2 output bytes of each of the n

rounds, we know

t bits in the middle. Consequently, the complex-

ity of the state recovery has increased by factor of

, i.e., the complexity is a product of 2

and time

taken by a SAT solver working on the instance.

After guessing 17 bytes in the middle (t = 8 · 17 =

136 bits) and observing outputs of 4 rounds, we

know 17 + 4 · 2 = 25 bytes. This is enough to de-

termine the entire 25-byte state uniquely

. The re-

sulting SAT instance is deﬁned by 1640 variables

and 10520 clauses. We were able to solve it in-

stantaneously. Increasing the output rounds to 5

(and reducing the guessed bytes in the middle to

15) did not lead to better results.

There is a high probability that ﬁxing 25 bytes of out-

puts from different rounds correspond to a unique 25-byte

state at certain round.

• Guess in every round. In the third scenario, we

guess additional b bits of the state for each of n

rounds. Therefore, the complexity of the state re-

covery has increased by a factor of 2

·b

. To ﬁnd

a unique solution, the parameters should satisfy

(16+b)

≥ 2

200

. When n

= 3, we guess 6 bytes

per round and an additional byte in middle round,

hence we guess 3 · (6 + 2) + 1 = 25 bytes in total.

This is translated into an appropriate SAT instance

with 1160 variables and 7080 clauses, which has

been solved instantaneously. We also tried a dif-

ferent strategy by guessing 3 · 6 + 1 = 19 bytes. It

turns out that we can still recover the state. How-

ever, increasing a number of rounds does not lead

to better results. We have tried n

= 4 and 4-byte

guesses per round plus an additional guess in the

middle. Unfortunately, the corresponding SAT

instances with 1640 variables and 10520 clauses

cannot be solved quickly. In fact, even if we know

25 output bytes but n

= 4, we still cannot ﬁnd a

solution.

We conclude that guessing in the middle turns out

to be the best strategy: it needs 136-bit guesses in

the middle round to recover the state. Correspond-

ing SAT instances are solved in ≈ 2.7 seconds on the

8-core PC (an average value out of 100 trials). If we

assume that a time taken by a solver is roughly equiva-

lent to 2

Ketje Jr calls

, then complexity of the state

recovery is 2

136+29

= 2

165

. Therefore, instances of

the Ketje Jr family, which offer security levels higher

than 165 bits, are susceptible to SAT-based analysis

and they will not meet the claimed security levels.

3.2 ICEPOLE

ICEPOLE is a family of hardware-oriented authenti-

cated ciphers (Morawiecki et al., 2014). There are

two main variants of the algorithm, one with 128-

bit key and 1024-bit block size (rate), the other one

with 256-bit key and 960-bit rate. The cipher was de-

signed for high-throughput network nodes, hence it’s

big 1280-bit state. The underlying permutation is an

iterative transformation with a linear MDS matrix fol-

lowed by a layer of 5-bit S-boxes. A 12-round permu-

tation is used in both the initialization and ﬁnalization

stages, while a 6-round permutation is applied for the

Output bits taken from 13 rounds (13 × 16 = 208 bits)

should correspond to a unique 200-bit state. In 1 second,

on the 8-core 2GHz PC, we evaluate around 2

13-round

Ketje Jr calls. We stress that it is very difﬁcult to precisely

convert a time taken by a solver to Ketje Jr evaluations. For

example, operations on cores may not scale as one would

expect, different platforms and implementations might af-

fect time as well.

SAT-based Cryptanalysis of Authenticated Ciphers from the CAESAR Competition

241

processing stage. ICEPOLE has an additional param-

eter called the secret message number, which has a

similar effect as the extra key addition in ASCON.

In 2014, Huang et al. presented differential-linear

cryptanalysis of ICEPOLE, where both a nonce and

secret message are reused (Huang et al., 2015). It

helped to reﬁne the nonce-misuse resistance in the al-

gorithm. In (Dobraunig et al., 2015a), the forgery at-

tack was performed on the round-reduced ICEPOLE-

128 (up to 4 rounds). Dobraunig et al. also found lin-

ear characteristics, up to 6 rounds, using an automated

tool they created (Dobraunig et al., 2015b). More

references to third-party cryptanalysis can be found

on the ICEPOLE ofﬁcial webpage (Morawiecki et al.,

2014).

In our analysis we focus on the ICEPOLE vari-

ants without a secret message number, speciﬁcally

ICEPOLE-128a. For this variant, once we know the

state, we can invert the permutation and get the secret

key. ICEPOLE-128a works with the 128-bit key and

the 1024-bit bitrate. So, we are dealing with a relevant

CICO problem that is deﬁned for 1024 known input

and output bits (the bitrate part), while the remaining

256 bits of the capacity part are unknown. Since the

1024-bit bitrate part is much bigger than the 256-bit

capacity part, we need only two consecutive plaintext-

ciphertext pairs to uniquely determine the state.

A single round of the ICEPOLE permutation is

described by a CNF with 12416 variables and 39424

clauses. Note that the two steps of the ICEPOLE algo-

rithm, namely ρ (rotation along lanes) and π (permu-

tation between lanes) do not increase complexity of

the CNF relations as they permute the state bits only.

We are able to recover the state for the 4-round

permutation (the original ICEPOLE uses 6 rounds).

To make our attack successful, we need to guess 64

bits in the middle (e.g., after 2 rounds). So, the

time complexity of our attack is 2

· t, where t is

a time taken by a solver to ﬁnd a solution. The at-

tack has been implemented on a desktop PC 3.7 GHz

with 8 threads and t is around 13 hours. This is

roughly equivalent to 2

ICEPOLE encryptions on a

given PC. Thus, time complexity of the 4-round key-

recovery attack is about 2

64+44

= 2

108

3.3 ASCON

ASCON is a family of authenticated encryption algo-

rithms (Dobraunig et al., ). The designers specify two

variants whose bitrates are 64 and 128. The size of the

key, nonce and tag are 128 each. The state consists of

ﬁve 64-bit words so it is 320-bit long. The algorithm

uses two permutations p

and p

that are constructed

from the same elementary permutation round. The

round is built from three basic operations: constant

addition, a 5-bit S-box layer and a linear transforma-

tion. It is worth noting that the sponge-based mode

in ASCON is made stronger by extra key addition

in initialization and ﬁnalization. This is to prevent a

straightforward key-recovery once the whole state is

known.

The designers analysed their algorithm through a

number of techniques and their ﬁndings were pub-

lished at CT-RSA’15 (Dobraunig et al., 2015c). Their

best result was a key-recovery attack on 6 rounds (out

of 12). In 2016, Tezcan presented truncated, impos-

sible and improbable differential attacks, achieving

5 rounds of the permutation. More references can

be found on the ASCON ofﬁcial website (Dobraunig

et al., ).

We analyse ASCON-128a, where both the bitrate

and key have 128 bits. First, we try the state recov-

ery that follows the one described for ICEPOLE. For

the CICO problem corresponding to the attack, 128

bits of both input and output are known and we hope

that our SAT solver ﬁnds the (unknown) capacity part

of the state. We have derived CNF relations for a

single round with 2304 variables and 7936 clauses.

Although the CNF is smaller than the corresponding

CNF for ICEPOLE, solving it turns to be more difﬁ-

cult and we can reach two rounds only. This counter-

intuitive phenomenon has been also observed in the

related work (Homsirikamol et al., 2012). Interest-

ingly, what makes a CNF instance difﬁcult is not the

‘width’ (or a total number of variables and clauses)

but the ‘depth’ of the formula (number of literals in

clauses). The ASCON S-box is more complex than

the ICEPOLE S-box. This seems to be the main rea-

son for increased complexity of solving ASCON CNF

instances, despite the fact that ASCON has a state that

is four times smaller than the one in ICEPOLE.

For ASCON, the key-recovery attack is not

straightforward due to an extra key addition in the

initialization and the ﬁnalization phases. We try to re-

cover the key assuming that the state is already recov-

ered and known to the attacker. This time the CICO

problem models the ﬁnalization phase, where an un-

known input is the secret key and a known output is

a 128-bit authenticated tag. Basically, the problem in

hand looks very similar to the state-recovery consid-

ered earlier. As expected, our SAT solver is able to

ﬁnd the secret key for 2 rounds only. A time taken by

a solver is roughly equivalent to 2

ASCON encryp-

tions.

We have considered 3- and 4-round variants with

some bits guessed in the middle (e.g. 64 bits after 1.5

rounds) but these instances turn to be too difﬁcult for

the solver.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

242

3.4 NORX

NORX is a family of authenticated ciphers with two

main variants based on 32 or 64-bit words. It was op-

timized to be efﬁcient in both software and hardware

with a SIMD-friendly core. The underlying permuta-

tion F is inspired by the ChaCha stream cipher (Bern-

stein, ). However, the integer addition is replaced by

a simple bitwise operation. Thus NORX relies only

on the bitwise XOR, AND, rotations, which leads to

better hardware efﬁciency and somewhat simpliﬁes

the cryptanalysis. The round function operates on a

state composed of 16 words in a similar fashion to the

hash function BLAKE (Aumasson et al., ). The rec-

ommended variant of NORX works with 256-bit key,

256-bit tag and 128-bit nonce, whereas a number of

rounds is 4.

In (Aumasson et al., 2014a), the designers of

NORX have investigated differential and rotational

properties of the algorithm. More recently, state and

key recovery on 2-round variants have been presented

(Bagheri et al., 2016). These results were obtained

with the ‘guess and determine’ technique and the in-

ternal differential attack. Interestingly, using higher-

order differential analysis, a 4-round distinguisher

was shown (Das et al., 2015). However, the distin-

guisher cannot be used to attack the whole scheme,

but only to show a weakness of the underlying per-

mutation in NORX.

Our analysis is focused on the version with 32-bit

words called NORX32. This version has a 512-bit

state. During the encryption phase, NORX32 uses 4

BLAKE-like rounds to process a plaintext block of

12 words (i.e. the rate of the sponge is 384 bits).

Note that the authors claim 128-bit security level for

this variant. The state recovery of NORX32 can be

looked as an instance of the CICO problem and be

converted into a relevant SAT instance. We start from

the state recovery for encryption reduced to a single

round. We assume that we are given two consecutive

pairs of known plaintext-ciphertext and try to recover

the state. The resulting SAT instance is deﬁned with

2560 variables and 16896 clauses. It is solved in a

matter of seconds, so the state recovery of NORX32

reduced to one round is feasible.

We try to extend our analysis to 1.5 rounds. For

this scenario, the SAT instance has 3584 variables and

24960 clauses. However, it is beyond the reach of the

SAT solver. To progress, we guess extra bits of the

state. More precisely, we guess bits from the capacity

part of the output state and also from the state of the

middle round. To introduce additional ﬂexibility, we

employ two guessing strategies: consecutive guessing

of bits of state words (i.e. if we guess 80 bits of the

state, then it means we know 2.5 words) and partial bit

guessing, where we ﬁx the values of a few bits of each

(unknown) word of the state. It turns out that regard-

less of the guessing strategy, we still need to guess

around 64 bits of the state to make SAT instances fea-

sible for the solver. For instance, if we guess one ad-

ditional word in both the input and output, then the re-

sulting SAT instance (3584 variables, 25024 clauses)

can be solved in a few seconds. A time taken by a

solver is roughly equivalent to 2

encryptions, then

the total time complexity of the attack is 2

64+32

= 2

If we guess one word at the end, and one in the mid-

dle, we end up with a similar complexity. However,

only the ﬁrst type of guessing (the consecutive bits)

leads to such results. The partial guessing does not

lead to a feasible SAT instance when the number of

guesses is around 64.

We try to recover the state for the variant of

NORX32 reduced to 2 rounds, but the total complex-

ity (bit guesses and workload of the SAT solver) is

over 2

128

. The most efﬁcient recovery that we have

found requires 56 bit guesses in the middle state and

56 bit guesses of state at the output (i.e. 2

112

fac-

tor only for bit guesses). The SAT solver still needs

around 10 seconds to produce a solution, thus the to-

tal complexity exceeds a simple state recovery based

on an exhaustive key search.

To summarize, given two consecutive pairs of

plaintext-ciphertext, it is possible to recover the state

of the 1-round NORX32 in a matter of seconds. If

NORX32 is reduced to 1.5 rounds, the recovery is still

possible, although its time complexity of 2

makes

the attack only theoretical. Since there is no any ex-

tra key addition in the initialization phase, the state

recovery is equivalent to the key recovery for NORX.

4 ANALYSIS OF OTHER

SCHEMES

4.1 MORUS

MORUS is a family of authenticated encryption al-

gorithms, suitable both for hardware and software

efﬁcient implementations. It has three variants:

MORUS-640-128, MORUS-1280-128 and MORUS-

1280-256, where the ﬁrst number denotes a state size,

and the second number is a key size, both given in

bits. The state consists of 5 words (either 128-bit or

256-bit, depending on the variant). The state update

function has 5 very similar rounds. There are four

operations, namely XOR, AND, rotation in words

(denoted by ≪) and rotation in subwords (denoted

SAT-based Cryptanalysis of Authenticated Ciphers from the CAESAR Competition

243

by Rotl). Every round modiﬁes only two registers,

one is modiﬁed by ≪, while the other one by a set

of ANDs, XORs, and Rotl. Security of the algo-

rithm heavily depends on a strong initialization phase,

where the state update function is called 16 times.

MORUS does not rely on any speciﬁc mode, partic-

ularly it is not a sponge construction. Its encryption

process can be seen as a stream cipher with large state

which is updated continuously. For a full descrip-

tion of the algorithm, we refer the reader to (Wu and

Huang, ).

In (Mileva et al., 2015), Mileva et al. pre-

sented MORUS analysis, including the forgery at-

tack. However, all the attacks reuse nonce, which vio-

lates MORUS security requirements. Some concerns

about MORUS security is highlighted in (Saarinen,

2015), where the author claims that MORUS repre-

sents signiﬁcantly elevated adaptive-chosen-plaintext

attack risk.

We investigate the SAT-based state recovery of

MORUS-640. At message processing phase, a single

call of state update functions takes one 128-bit mes-

sage word and outputs one 128-bit ciphertext word.

With 128-bit key, the claimed security level is 128

bits. As the ratio of the state size to the cipher-

text block size is 5, we need 5 consecutive pairs

of plaintext-ciphertext to recover the state (almost)

uniquely.

To keep our analysis simple, we assume that 5

plaintext blocks are all-zero blocks, that is we are op-

erating in the chosen-plaintext framework

. We pro-

ceed according to the following scenarios:

• Basic. We reduce the state recovery of MORUS-

640 to a SAT instance, which encodes 5 consecu-

tive calls to the state update function. As a result,

we get an instance with 3200 variables and 34560

clauses. Our SAT solver has failed to ﬁnd a solu-

tion.

• Simpliﬁed output function. For MORUS-640, a

ciphertext block C is calculated from a simple for-

mula C = P⊕ S

⊕(S

≪ 96)⊕(S

), where P

is a plaintext block and S

.. .S

are 4 state words

obtained from the state update function. Here we

simplify the formula by taking only the ﬁrst word

C = P ⊕ S

. As we work in a chosen plaintext sce-

nario and assume that plaintext blocks are all-zero

blocks, then C = S

. For this simpliﬁed version

of MORUS-640, a corresponding SAT instance

(that aims to recover a state) has 3200 variables

and 31360 clauses. Even though now we have a

smaller number of clauses, the instance is still in-

We can switch to the known-plaintext attack at the ex-

pense of increasing a number of clauses in SAT instances.

feasible for our SAT solver — a few days of pro-

cessing has failed to ﬁnd a solution.

• Toy variant with a reduced word size. We

would like to ﬁnd out whether a signiﬁcant re-

duction of a word size makes the problem eas-

ier for a solver. We try to estimate the com-

plexity of the SAT-based state recovery by solv-

ing a reduced version of MORUS-640 with 60 in-

stead of 640 state bits. We need to modify the

algorithm for the reduced state size. XOR and

AND operations are applied in a straightforward

way, while rotations are adjusted so they reﬂect

the original design as closely as possible. Conse-

quently, for the word-reduced version of MORUS,

the corresponding SAT instance consists of 300

variables and 3240 clauses. The SAT solver is

able to ﬁnd a solution in a few days of computa-

tion. However, the generic key-recovery requires

guesses only (as an appropriate key size of the

variant is 12 bits only). We conclude that the SAT-

based approach does not break the algorithm as

it would take much more time then the exhaus-

tive search of the key. Even though this is not a

formal proof that MORUS-640 is immune to the

SAT-based state recovery, it is a good indication

that the algorithm stands strong against this type

of analysis.

The above ﬁndings suggest that MORUS-640

does not show any weakness against analysis with

SAT solvers.

Let us examine an upper bound on the security

level of this scheme. Here, as in previous analysis, we

mount the state recovery attack to get the secret key.

Let us recall that a ratio of the state size to the cipher-

text block size is 5, thus we need to encode 5 consec-

utive calls to the state update function (getting 5 ci-

phertext blocks) to determine the state uniquely. We

start our experiment using a big number of guessed

state bits, making the instance easy to solve. Then,

we gradually reduce the number of guessed bits and

stop when the state recovery starts taking more than

a few seconds. This allows us to quantify the time

complexity of appropriate SAT instances.

We have many choices about which state variables

should be guessed. We experiment with guessing con-

secutive bits of the state and also with guessed bits

which are spread equally over 5 words of the state. It

turns out that we get the best results, when we guess

consecutive bits in the ‘middle’, that is after the sec-

ond call to the state update function. On average, we

need 340 guessed bits to have a formula solved. If we

approximate the time taken by a solver by a factor of

, we can conclude that MORUS-640 cannot offer

a security level higher than around 340 + 30 = 370

SECRYPT 2017 - 14th International Conference on Security and Cryptography

244

bits. Please note that it does not affect MORUS se-

curity claims as it is speciﬁed only to support either

128- or 256-bit keys. However, MORUS works on a

big internal state and one can be tempted to adjust the

algorithm for bigger keys and corresponding security

levels. Then our analysis shows there is a limit.

4.2 ACORN

ACORN is basically a stream cipher based on lin-

ear feedback shift registers (LFSR). It operates on

the 293-bit state, which is split into a short ‘buffer’

segment followed by 6 LFSRs. This design allows

for 32 bits to be processed in parallel, leading to ef-

ﬁcient hardware and software implementations. In-

terestingly, plaintext bits are not only XORed with

keystream (to produce ciphertext), but also XORed

into the main feedback function. Having the state di-

rectly affected by plaintext helps realize the authentic-

ity property. The main feedback function is the only

non-linear part of the state update. For a full descrip-

tion of the algorithm, see (Wu, ).

There are two ways we could mount the state re-

covery attack for ACORN. First, one can encode the

whole initialization phase into a SAT formula with

key bits as unknowns and some keystream bits as an

input. However, this approach is infeasible as there

are 1792 steps in the initialization phase, so the for-

mula is too big and complicated for a solver. The

other approach is to take an arbitrary state in the en-

cryption phase and generate keystream equations in

the state variables. Again, for 293 unknowns in the

state, the problem turns out to be too hard for a solver.

To make the problem easier, we ﬁx some state bits and

with 170 known bits we are able to recover the state

in about 8 hours. However, guessing that many bits

makes our analysis much above an exhaustive search

for a 128-bit key.

We conclude that ACORN is strong against SAT-

based cryptanalysis. Particularly, we notice that state

bits involved in an equation for one keystream bit are

not present in the following 40 keystream equations.

Consequently, it is hard to build a set of equations,

which have common variables and at the same time

are not too complex. We also notice that the state

update function creates long XOR equations, which

are known to be difﬁcult for SAT solvers. We believe

these two factors contribute the most to the resistance

against our SAT-based attack. Because ACORN has

no rounds or blocks that could be reduced, there is no

simple and natural way of creating a reduced or toy

version that we would be able to break.

5 CONCLUSION

Our ﬁndings have ﬁlled an important and common

gap in the cryptanalysis of CAESAR proposals — the

resistance of the schemes against SAT-based state re-

covery attacks. We have analysed six authenticated

encryption algorithms from the CAESAR competi-

tion and our extended analysis has shown that none of

these schemes, as submitted to CAESAR, allows even

a “theoretical" break using SAT-based state recovery

attacks. On the other hand, some round-reduced ver-

sions or variants with artiﬁcially increased security

levels are susceptible to state and key recovery at-

tacks. This helps to quantify the security margin and

we conclude the analysed ciphers have a sufﬁcient se-

curity margin against SAT-based cryptanalysis.

REFERENCES

AES (2001). Advanced Encryption Standard (AES). Na-

tional Institute of Standards and Technology (NIST),

FIPS PUB 197, U.S. Department of Commerce.

Aumasson, J., Jovanovic, P., and Neves, S. (2014a). Anal-

ysis of NORX: Investigating Differential and Rota-

tional Properties. In Progress in Cryptology - LAT-

INCRYPT 2014 - Third International Conference on

Cryptology and Information Security in Latin Amer-

ica, Florianópolis, Brazil, September 17-19, 2014,

Revised Selected Papers, pages 306–324.

Aumasson, J.-P., Henzen, L., Meier, W., and

Phan, R. C.-W. SHA-3 proposal BLAKE.

http://www.131002.net/blake/.

Aumasson, J.-P., Jovanovic, P., and Neves, S. (2014b).

Norx: parallel and scalable aead. In European Sympo-

sium on Research in Computer Security, pages 19–36.

Springer.

Bagheri, N., Huang, T., Jia, K., Mendel, F., and Sasaki, Y.

(2016). Cryptanalysis of Reduced NORX. In Fast

Software Encryption - 23rd International Conference,

FSE 2016, Bochum, Germany, March 20-23, 2016,

Revised Selected Papers, pages 554–574.

Bernstein, D. J. ChaCha, a variant of Salsa20.

https://cr.yp.to/chacha/chacha-20080120.pdf.

Bertoni, G., Daemen, J., Peeters, M., and

Van Assche, G. Cryptographic Sponges.

http://sponge.noekeon.org/CSF-0.1.pdf.

Bertoni, G., Daemen, J., Peeters, M., and Van Assche, G.

(2011). Duplexing the sponge: Single-pass authen-

ticated encryption and other applications. In Selected

Areas in Cryptography - 18th International Workshop,

SAC 2011, Toronto, ON, Canada, August 11-12, 2011,

Revised Selected Papers, pages 320–337.

Bertoni, G., Daemen, J., Peeters, M., Van Assche, G., and

Van Keer, R. CAESAR submission: KETJE v2 .

http://ketje.noekeon.org.

SAT-based Cryptanalysis of Authenticated Ciphers from the CAESAR Competition

245

CAESAR. CAESAR: Competition for Authenticated En-

cryption: Security, Applicability, and Robustness.

http://competitions.cr.yp.to/caesar.html.

Cook, S. A. (1971). The complexity of theorem-proving

procedures. In Proceedings of the third annual ACM

symposium on Theory of computing, STOC ’71, pages

151–158, New York, NY, USA. ACM.

Cook, S. A. and Mitchell, D. G. (1997). Finding Hard In-

stances of the Satisﬁability Problem: A Survey. pages

1–17. American Mathematical Society.

Courtois, N., Bard, G., and Wagner, D. (2008). Algebraic

and Slide Attacks on KeeLoq. In Nyberg, K., edi-

tor, Fast Software Encryption, volume 5086 of LNCS,

pages 97–115. Springer Berlin / Heidelberg.

Courtois, N. and Pieprzyk, J. (2002). Cryptanalysis of

Block Ciphers with Overdeﬁned Systems of Equa-

tions. In Zheng, Y., editor, Advances in Cryptology

— ASIACRYPT 2002, volume 2501 of Lecture Notes

in Computer Science, pages 267–287. Springer Berlin

/ Heidelberg.

Das, S., Maitra, S., and Meier, W. (2015). Higher Order Dif-

ferential Analysis of NORX. IACR Cryptology ePrint

Archive, 2015:186.

Davis, M., Logemann, G., and Loveland, D. (1962). A ma-

chine program for theorem-proving. Communications

of the ACM, 7(5):394–397.

Davis, M. and Putnam, H. (1960). A computing procedure

for quantiﬁcation theory. Journal of the ACM, 7:201–

215.

Dobraunig, C., Eichlseder, M., and Mendel, F. (2015a).

Forgery Attacks on Round-Reduced ICEPOLE-128.

In Selected Areas in Cryptography - SAC 2015 - 22nd

International Conference, Sackville, NB, Canada, Au-

gust 12-14, 2015, Revised Selected Papers, pages

479–492.

Dobraunig, C., Eichlseder, M., and Mendel, F. (2015b).

Heuristic tool for linear cryptanalysis with applica-

tions to CAESAR candidates. In Iwata, T. and Cheon,

J. H., editors, ASIACRYPT 2015, Part II, volume 9453

of LNCS, pages 490–509. Springer, Heidelberg.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schläffer,

M. (2015c). Cryptanalysis of Ascon. In Nyberg, K.,

editor, CT-RSA 2015, volume 9048 of LNCS, pages

371–387. Springer, Heidelberg.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schläffer,

M. Ascon A Family of Authenticated Encryption Al-

gorithms. http://ascon.iaik.tugraz.at.

Homsirikamol, E., Morawiecki, P., Rogawski, M., and Sre-

brny, M. (2012). Security Margin Evaluation of SHA-

3 Contest Finalists through SAT-based Attacks. In

11th Int. Conf. on Information Systems and Industrial

Management, volume 7564 of LNCS. Springer Berlin

Heidelberg.

Huang, T., Tjuawinata, I., and Wu, H. (2015). Differential-

linear cryptanalysis of ICEPOLE. In Leander, G., edi-

tor, FSE 2015, volume 9054 of LNCS, pages 243–263.

Springer, Heidelberg.

Laﬁtte, F., Lerman, L., Markowitch, O., and Heule, D. V.

(2016). SAT-based cryptanalysis of ACORN. IACR

Cryptology ePrint Archive, 2016:521.

Mileva, A., Dimitrova, V., and Velichkov, V. (2015).

Analysis of the Authenticated Cipher MORUS (v1).

In Cryptography and Information Security in the

Balkans - Second International Conference, Balkan-

CryptSec 2015, Koper, Slovenia, September 3-4, 2015,

Revised Selected Papers, pages 45–59.

Morawiecki, P., Gaj, K., Homsirikamol, E., Matusiewicz,

K., Pieprzyk, J., Rogawski, M., Srebrny, M., and Wój-

cik, M. (2014). ICEPOLE: High-Speed, Hardware-

Oriented Authenticated Encryption. In Cryptographic

Hardware and Embedded Systems - CHES 2014 -

16th International Workshop, Busan, South Korea,

September 23-26, 2014. Proceedings, pages 392–413.

http://www.icepole.org.

Mouha, N. and Preneel, B. (2013). A Proof that the

ARX Cipher Salsa20 is Secure against Differential

Cryptanalysis. Cryptology ePrint Archive, Report

2013/328. http://eprint.iacr.org/.

National Institute of Standards and Technology (2007).

Recommendations for Block Cipher Modes of Opera-

tion: Galois/Counter Mode (GCM) and GMAC. NIST

special publication 800-38D.

Rudell, R. L. (1986). Multiple-Valued Logic Minimiza-

tion for PLA Synthesis. Technical Report UCB/ERL

M86/65, EECS Department, University of California,

Berkeley.

Saarinen, M. O. (2015). The BRUTUS automatic cryptana-

lytic framework - Testing CAESAR authenticated en-

cryption candidates for weaknesses. Journal of Cryp-

tographic Engineering, 6(1):75–82.

Stoffelen, K. (2016). Optimizing S-Box Implementations

for Several Criteria Using SAT Solvers. In Fast

Software Encryption - 23rd International Conference,

FSE 2016, Bochum, Germany, March 20-23, 2016,

Revised Selected Papers, pages 140–160.

Wu, H. ACORN: A Lightweight Authenticated Cipher (v3).

https://competitions.cr.yp.to/round3/acornv3.pdf.

Wu, H. and Huang, T. The Authenticated Ci-

pher MORUS. https://competitions.cr.yp.to/caesar-

submissions.html.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

246