Using Constraint Cellular Automata to Simulate Urban Development

in a Cross-border Area

J.-P. Antoni

, V. Judge

1,2

, G. Vuidel

and O. Klein

LaboratoireTheMA, UMR 6049 CNRS and University of Burgundy Franche-Comté, 4 boulevard Gabriel, F-21000 Dijon,

32 rue Mégevand, F-25000 Besançon, France

LISER - Luxembourg Institute of Socio-Economic Research, 11 porte des Sciences, L-4366 Esch-sur-Alzette, Luxembourg

Keywords: Cellular Automata, Markov Chains, Cross-border Area, Land Use Scenarios, Prospective.

Abstract: Urban sprawl and space consumption have become key issues in sustainable territorial development.

Traditional planning approaches are often insufficient to anticipate their complex spatial consequences,

especially in cross-border areas. Such complexity requires the use of dynamic spatial simulations and the

development of adapted tools like LucSim, a CA-based tool offering solutions for sharing spatial data and

simulations among scientists, technicians and stakeholders. Methodologically, this tool allows us to simulate

future land use change by first quantifying and then locating the changes. Quantification is based on Markov

chains and location on transition rules. The proposed approach is implemented on the Strasbourg-Kehl

cross-border area and calibrated with three contrasting prospective scenarios to try to predict cross-border

territorial development.

1 CONTEXT AND RESEARCH

OBJECTIVES

In the current context of increasing urbanization and

daily mobility, urban sprawl and space consumption

have become crucial issues for achieving sustainable

territorial development (European Environment

Agency 2006). This problem is further complicated

in the case of cross-border areas where operational

procedures on each side of the frontier differ from an

administrative, legal and cultural point of view.

Moreover, open border areas are currently

undergoing particular growth dynamics which have

given rise to numerous cross-border spatial planning

issues. In this context, the Strasbourg-Ortenau

Eurodistrict Project (French-German cross-border

territory) is promoting the development of cross-

border initiatives in what is a pilot scheme for the

EU. Within this pilot region, we will be focusing

specifically on the Strasbourg-Kehl cross-border

Area (SKA).

Trans-national territorial analyses are constrained

by the problem of geographical information and data

harmonization (i.e. scale, temporality, accuracy of

data). Classical planning approaches and methods

are therefore often incapable of addressing the

complexity of these situations and predicting their

spatial implications. In this context, spatial

simulations are widely viewed as an appropriate tool

to help planner stake decisions. Such simulations

rely on several kinds of simulations models, among

which Cellular Automata (CA) are particularly well

designed for managing spatial planning issues.

CA are considered useful tools for modeling and

simulating urban development because they allow us

to implement simple spatial rules based on empirical

knowledge that take into account the role of

neighborhood in urban growth processes. They have

been widely used to simulate land use changes and

scenarios for future urban development in different

contexts. The seminal work of Couclelis (1985,

1987), White and Engelen (1993), Batty and Xie

(1994) and later Clarke et al. (1997) paved the way

for CA to be considered a powerful tool for

modeling and simulating spatial phenomena of

various types. The research on CA gathered new

momentum during the 2000s in a surge in research

that coincided with a second wave of faster and

cheaper computational capacities (Torrens 2000,

Benenson and Torrens 2004, Couclelis 2005,

Koomen et al. 2011). The aim of this paper is to

present prospective urban development scenarios for

the Strasbourg-Kehl area in the medium term.

366

Antoni, J-P., Judge, V., Vuidel, G. and Klein, O.

Using Constraint Cellular Automata to Simulate Urban Development in a Cross-border Area.

DOI: 10.5220/0006387703660369

In Proceedings of the 3rd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2017), pages 366-369

ISBN: 978-989-758-252-3

2 METHODOLOGY

From a methodological point of view, the LucSim

CA model can be defined as a constrained cellular

automata designed to aid decision-making in urban

and land planning. Its main original feature

(compared to similar geographical CA) is to simplify

the land-use evolution processes into two

“fundamental” steps, namely the quantification and

location of future land use changes. Land use is

assessed within a cellular grid space obtained from

the European Corine Land Cover classification.

2.1 Quantification of Land Use

Changes

Our first step was to quantify the land use change

process. Comparing two static land use images or

vectors (1990, 2006) is of little interest in the

context of a dynamic simulation, but finding out

what happens between each image can enable us to

formulate a transition process. By comparing the

land use categories date by date and cell by cell, it is

possible to determine cellular changes between t and

t+1, and identify the land use dynamics.

Theoretically, each cell can move from one land use

category to another, or remain in the same category.

The dynamics of the model can therefore be

presented as a series of possible transitions from one

land use category k at time t to another land use

category l at t+1.

The Markov chain process gives us the chance to

prospectively calculate future states from known

past states, based on observation of past trends and

probabilities. According to the method, this

calculation is based on the assumption that future

changes will follow the trend of past changes, but as

it is based on a matrix calculation, this trend is not

necessarily linear. In our case, LucSim uses the

original transition matrix to calculate the number of

cells in each land use category in 2022, 2038, 2054,

etc., from 1990 and 2006 land uses (same interval of

16 years between each date). This system gives us a

better picture of urban dynamics by calculating land

use vectors for each future date. It also indicates that

the total number of cells that should be urbanized

(including UR, IN and EQ categories) by 2038 is

8,811.

2.2 Location of Land Use Changes

The second step was to try to identify the location of

land use changes with a method based on Cellular

Automata. Cellular Automata have the double

advantage of being able to determine the land use

category of cells according to their neighbourhood,

and also to integrate the previous Markovian

process. By definition, CA are based on the

assumption that the class of each cell is determined

by its neighbourhood, or in our case, by the land use

categories of surrounding cells within a given radius.

CA can then be constrained with the results of

the Markov chain to produce a model for land use

change simulations. This means that the CA

transition process from one given category to

another is automatically halted when the number of

cells given by the MC for each date is reached. This

CA transition process is based on transition rules

that allow us to consider different configurations.

The main problem is then to define relevant rules to

simulate realistic scenarios of spatial development, a

generalized problem in all modelling and especially

in model calibration.

3 SPATIAL DEVELOPMENT

SCENARIOS

We decided to base all our scenarios on the general

assumption that new built-up areas can only be

developed on agricultural fields. These scenarios

present three contrasted configurations for land use

changes in 2038: urban sprawl, urban densification

and cross-border development based on the bridge

connections available on the SKA specific test-field.

Although results are calculated at the original 100

meters resolution of the land use cells, they are

aggregated and mapped within a larger grid with a

resolution of 4,000 meters to improve visualization

of the changes.

3.1 Landscape Sprawl

The main idea of the “Landscape Sprawl” (LS)

scenario is that future residential preferences will

favor natural landscapes and rural amenities, as well

as relative proximity to slightly dense urban areas

(villages).

Figure 1: “Landscape sprawl” scenario: land use changes

simulation in 2038.

Using Constraint Cellular Automata to Simulate Urban Development in a Cross-border Area

367

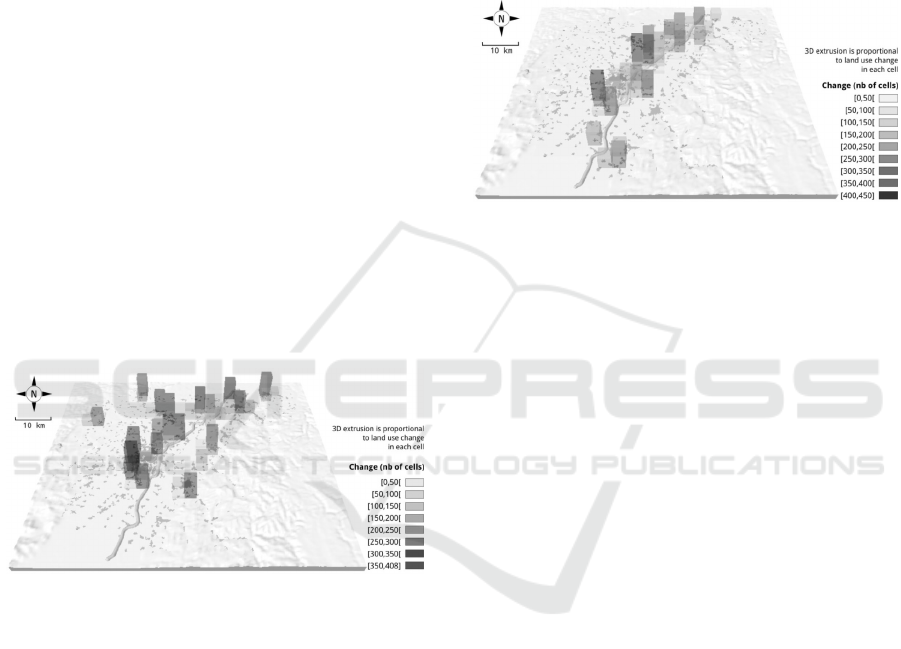
The LS scenario (Fig. 1) leads to a gain of 8,976

cells in only 2 CA iterations. This result can be

explained by considering spatial configurations that

are very generic and numerous in the case of the

rules created above. LucSim therefore quickly spots

the cells that meet the requirements to be

transformed into urban land. A typical example of

this process of urbanization can be seen between the

“Piémont” area and the high density urban area of

Strasbourg. We can also observe a generalized

expansion of areas with low urban density (max

200) and a high dispersion of the cells that become

urbanized. Nevertheless, this general dispersion is

quite homogeneous except for a slight concentration

around small cities. The urban expansion on the

German side appears to be more linear than in

France, which is probably due to the topographic

features in that area.

3.2 Urban Densification

The main idea of the “Urban Densification” (UD)

scenario is that future residential preferences will

favor dense urban areas, close to urban amenities

(e.g. parks, sport and leisure facilities), but relatively

far away from industry and related nuisances.

Figure 2: “Urban densification” scenario: land use changes

simulation in 2038.

The UD scenario (Fig. 2) produces a gain of 9,391

cells in 9 iterations. A much higher number of

iterations is needed because the rules for this

configuration make the transition less likely to

happen. Moreover the Markov constraint can only

be achieved when newly urbanized cells are taken

into account. This explains why the process is

slower and more iterations are required to converge

toward the solution provided by the set of rules for

the UD scenario. In this case new urbanization is

concentrated around the bigger cities and expands on

the existing urban structure rather than following the

area’s physical geography features. The fact that the

existing urban area is already much larger on the

French side favors further urbanization on this side.

The urban density is clearly higher than in the LS

scenario (max 408).

3.3 Bridge Transbordering

The main idea of the “Bridge Transbordering” (BT)

scenario is that future residential preferences will

favor mixed residential areas (with both LS and UD

scenarios), located in quite heavily urbanized areas

near the border crossing points.

Figure 3: ‘Bridge Transbordering’ scenarios: simulation of

land use changes in 2038.

The BT scenario (Fig. 3) leads to gains of 8,852

cells in 10 iterations, roughly the same number as

the UD scenario. As in the previous scenario, few

spatial configurations are adapted to the transition

towards urban land use categories. This situation

leads to urban development being highly

concentrated in certain places in the study area (max

450), most of which are close to the River Rhine and

its crossing points (bridges, ferry). New high density

urban development is also predicted around the big

cities. Urban development will be essentially linear

and more intensive on the French side (especially

around the southern part of Strasbourg city, and

close to the Gambsheim dam). The three places most

affected in the German part are: Lahr, Kehl and

around Baden-Baden.

4 DISCUSSION

The three residential development scenarios

presented above in succinct form were developed on

the basis of expert judgement. From a scientific

point of view, our results have not been validated.

Forecasting the future in a complex context is

difficult and in the absence of a crystal ball, there is

no known technique for validating future urban

development results at such a fine scale.

Nevertheless the various scenarios involve realistic

processes and rules based on accurate expert

knowledge to provide images of the future that can

be used in debate and decision-making about

GAMOLCS 2017 - International Workshop on Geomatic Approaches for Modelling Land Change Scenarios

368

desirable urban development and land-use changes.

In this context, the objective of the model is not to

separate France from Germany by offering

independent analyses or forecasts for each one, but

to reflect on scenarios for their common future

development.

5 CONCLUSION

By comparing these different scenarios, we can see

that this model can assess the impact of single

neighbourhood rules on urban development. This

global modelling enables us to study urban changes

easily and efficiently. Breaking down the process

into two steps (MC+CA) makes it sufficiently

straightforward to be simultaneously understood by

all the stakeholders involved in urban planning.

LucSim therefore allows a wide range of different

points of view to be considered and specific actions

to be imagined for territorial development and

innovation, within the perspective of more

sustainable land and urban planning.

ACKNOWLEDGMENTS

The research presented in this chapter is part of the

Smart.Boundary project supported by the Fonds

National de la Recherche in Luxembourg and CNRS

in France (ref. INTER/CNRS/12/02). The authors

would like also to thank the Grasp Program of

LISER for allowing cross-collaboration between the

two teams based in Luxembourg and France.

REFERENCES

Antoni J-P, 2006, Calibrer un modèled’évolution de

l’occupation du sol urbain. L’exemple de Belfort,

Cybergeo : European Journal of Geography

http://cybergeo.revues.org/2436.

Antoni J-P, 2009, Un territoire de projet à co-construire.

In: Grossouvre (de) H, Maulin E (eds) Euro-District

Strasbourg-Ortenau : la construction de l’Europe

réelle. Xénia, pp 25–31

Basse RM, Omrani H, Charif O, et al., 2014, Land use

changes modelling using advanced methods: Cellular

automata and artificial neural networks. The spatial

and explicit representation of land cover dynamics at

the cross-border region scale. Applied Geography

53:160–171.

Batty M, Xie Y, 1994, From Cells to Cities. Environment

and Planning B: Planning and Design 21:531–538

Benenson I, Torrens PM, 2004, Geosimulation: Automata-

based modeling of urban phenomena, 1st edition.

Wiley

Berchtold A, 1998, Chaînes de Markov etmodèles de

transition. Applications aux sciences sociales. Hermes

Science Publications, Paris

Clarke KC, Hoppen S, Gaydos L, 1997, A Self-Modifying

Cellular Automaton Model of Historical Urbanization

in the San Francisco Bay Area. Environment and

Planning B: Planning and Design 24:247–261.

Couclelis H, 1985, Cellular Worlds: a framework for

modeling micro-macro dynamics. Environment and

Planning A 20:99–109.

Couclelis H, 1987, Cellular dynamics: How individual

decisions lead to global urban change. European

Journal of Operational Research 30:344–346

Couclelis H, 2005, “Where has the Future Gone?”

Rethinking the Role of Integrated Land-Use Models in

Spatial Planning. Environment and Planning A

37:1353–1371.

Durr MJ, Kayali ML, 2014, Six millions d'habitants pour

l'Alsace, Chiffres pour l'Alsace, 50

European Environment Agency, 2006, Urban sprawl in

Europe: the ignored challenge. EEA Report.

Feller W, 1968, An Introduction to Probability Theory and

Its Applications, 3rd edition. Wiley

Koomen E, Hilferink M, Borsboom-Van Beurden J, 2011,

Introducing Land Use Scanner. In: Koomen E,

Borsboom-Van Beurden J (eds) Land-Use Modelling

in Planning Practice. Springer, pp 3–21

Timmermans HJP, 2003, The Saga of Integrated Land

Use-Transport Modeling: How Many More Dreams

Before We Wake Up? 10th International Conference

on Travel Behaviour Research. Lucerne, Switzerland,

p 35.

Torrens PM, 2000, How cellular models of urban systems

work (1. theory). CASA Working Paper Series

White R, Engelen G, 1993, Cellular automata and fractal

urban form: a cellular modelling approach to the

evolution of urban land-use patterns.

Environment and

Planning A 25:1175–1199

Using Constraint Cellular Automata to Simulate Urban Development in a Cross-border Area

369