
Aircraft Attitude Determination Algorithms Employing Gravity Vector
Estimations and Velocity Measurements
Ra
´
ul de Celis and Luis Cadarso
European Institute for Aviation Training and Accreditation (EIATA), Rey Juan Carlos University,
28943 Fuenlabrada, Madrid, Spain
Keywords:
IMU, GNSS, Attitude Determination, Sensor Model, Projectile, Terminal Guidance.
Abstract:
Precision on Navigation, Guidance and Control of aircraft is dependent on the precision of the measurement
system both for position and attitude. It is well known in aerospace engineering that the rotation of an aircraft
or space vehicle can be determined measuring two vectors in two different reference systems. Velocity vector
in an aerospace vehicle can be determined in an inertial reference frame directly from a GNSS-based sensor.
Also this velocity vector can be determined by integrating the acceleration measurements in an aircraft body
fixed reference frame. By estimating gravity vector in an inertial reference frame, which currently is perfectly
tabulated, and in a body reference frame, and combining these measurements with the velocity vector, rotation
of the body can be determined. Application of these concepts is especially interesting in order to substitute
high-precision attitude determination devices, which are usually expensive as they are forced to bear high
solicitations as for instance G forces.
1 INTRODUCTION
Obtaining precise attitude information is essential for
navigation and control. The effectiveness of naviga-
tion and control is determined by the degree of preci-
sion of the navigation and control systems, including
inertial measurement units (Ma et al., 2011). There is
an extensive body of literature regarding attitude es-
timation using various sensor inputs (Crassidis et al.,
2007).
Traditionally, in order to obtain accurate values
for determining attitude, expensive and/or weighty
units, such as as laser or fiber optic gyroscopes and
accelerometers, or their MEMS equivalents, must
be employed. High-performance electro-static gy-
roscopes require expensive vacuum-packaging, to
maintain the high-Q of the MEMS (Ismail et al.,
2015). Moreover, when high-demanding maneuvers
are performed this equipment may become extremely
expensive.
It is well-known that the attitude of an aero-
vehicle can be determined by integrating the angular
rates (pitch, roll, and yaw rates) of the vehicle. Never-
theless, accuracy requirements usually cannot be sat-
isfied by using the inexpensive sensors (Ma et al.,
2011). This problem becomes even more important
when the vehicle cannot be reused: low-cost attitude
determination systems are of key importance for these
applications. For example, (Gebre-Egziabher et al.,
2000) describe an attitude determination system that
is based on two vector measurements of non-zero,
non-co-linear vectors. Using the Earth’s magnetic
field and gravity as the two measured quantities, a
low-cost attitude determination system is proposed.
(Gebre-Egziabher et al., 1998) develop an inexpen-
sive Attitude Heading Reference System for general
aviation applications by fusing low cost automotive
grade inertial sensors with GPS. The inertial sen-
sor suit consists of three orthogonally mounted solid
state rate gyros. (Eure et al., 2013) describe an atti-
tude estimation algorithm derived by post-processing
data from a small low cost Inertial Navigation System
recorded during the flight of a sub-scale commercial
off the shelf UAV. Estimates of the UAV attitude are
based on MEMS gyro, magnetometer, accelerometer,
and pitot tube inputs. (Henkel and Iafrancesco, 2014)
state that low-cost GNSS receivers and antennas can
provide a precise attitude and drift-free position in-
formation, but accuracy is not continuous. Inertial
sensors are robust to GNSS signal interruption and
very precise over short time frames, which enables
a reliable cycle slip correction, but low-cost inertial
sensors suffer from a substantial drift. The authors
propose a tightly coupled position and attitude deter-
mination method for two low-cost GNSS receivers, a
gyroscope and an accelerometer and obtain a heading
Celis, R. and Cadarso, L.
Aircraft Attitude Determination Algorithms Employing Gravity Vector Estimations and Velocity Measurements.
DOI: 10.5220/0006393203770385
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 377-385
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
377

with an accuracy of 0.25
◦
/baseline length [m] and an
absolute position with an accuracy of 1 m. Similar de-
velopments may be found within space vehicles, for
example in (Springmann and Cutler, 2014).
However, as stated in (Yun et al., 2008), many of
the presented methods such as the ones employing lo-
cal magnetic field vectors, are only valid for estimat-
ing the orientation of a static or slow-moving rigid
body. In the research described in this paper, two
measured quantities are used to obtain attitude infor-
mation for high dynamic vehicles: speed and grav-
ity vectors. They are obtained in two different refer-
ence frames using a GNSS sensor and a strap-down
accelerometer.
1.1 Contributions
The main contribution of this paper is the develop-
ment of a novel algorithm which aims at avoiding
the use of gyroscopes, and its implicit high costs if
high precision is required (Ismail et al., 2015), in
a long term and to require lower performance gy-
roscopes for attitude determination in the immediate
term. This is pretended to decrease costs in attitude
sensors and even to improve attitude determination by
applying filtering techniques, especially for artillery
device purposes, where high solicitation force condi-
tions increase the price of precise attitude determina-
tion devices such as gyroscopes.
Nonlinear simulations based on ballistic rocket
launches are performed to determine real attitude and
compare it to the estimated attitude obtained from the
algorithms. The applicability of the proposed solu-
tion for aircraft flight navigation, guidance and con-
trol, and for ballistic rocket terminal guidance, where
attack and side-slip aerodynamic angles are relatively
small, is also demonstrated.
This paper is organized as follows. Section II de-
scribes the problem in detail. Section III is devoted to
flight dynamics and sensor models. Section IV shows
simulations results. Finally, in Section V some con-
clusions and further work are drawn.
2 PROBLEM DESCRIPTION
Attitude determination is a fundamental field in
aerospace engineering, as maneuvers in order to
change vehicle trajectories are governed by aerody-
namic forces, which depend directly on ship orienta-
tion angles. Furthermore, attitude in artillery rockets
terminal phase is vital as it determines factors such
as penetrability of payload or countermeasures avoid-
ability. Therefore, developing algorithms to improve
attitude determination is a cornerstone in guidance,
navigation and control research.
One of the techniques to determine attitude is to
calculate it from the director cosine matrix (DCM)
which completely determines the rotation of a body.
Two reference frames are defined, one fixed to the
body and another one as a reference. In order to ob-
tain the DCM, a geometrical plane defined in both
reference triads must be obtained. Every geometrical
plane is defined by two vectors. Therefore, knowing
the same two vectors expressed in the two reference
frames, the DCM can be calculated.
2.1 Triad Definition
Two axes systems are defined in order to express
forces and moments: North-East-Down (NED) axes
and Body (B) axes. NED axes are defined by sub in-
dex NED. x
NED
pointing north, z
NED
perpendicular to
x
NED
and pointing nadir, and y
NED
forming a clock-
wise trihedron. Body axes are defined by sub index
B. x
B
pointing forward and contained in the plane
of symmetry of the aircraft, z
B
perpendicular to x
B
pointing down and contained in the plane of symme-
try of the aircraft, and y
B
forming a clockwise trihe-
dron. The origin of body axes is located at the center
of mass of the aircraft.
2.2 Involved Vectors Determination
If a GNSS sensor device is equipped on the aircraft,
velocity vector can be directly expressed from sen-
sor measurements in the NED triad. Expression for
velocity in NED is defined on equation (1), where
v
x
NED
,v
y
NED
and v
z
NED
are the components of this ve-
locity vector in NED axes.
−−→
v
NED
= [v
x
NED
,v
y
NED
,v
z
NED
]
T
(1)
The same velocity vector expressed in body triad
can be obtained from a set of accelerometers equipped
on the ship, one on each of the axes. This devices
are able to measure acceleration. After integration
of each of the components along the time, velocity
vector is obtained as it is expressed on equation (2),
where a
x
B
,a
y
B
and a
z
B
are the components of the ac-
celeration vector in body axes.
−→
v
B
=
Z
[a
x
B
,a
y
B
,a
z
B
]
T
dt (2)
Another vector expressed in the two reference
frames is required in order to define the rotation.
Gravity vector is easily determined in NED triad as
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
378

it always points to z
NED
, as it is shown on equation
(3). g is the gravity acceleration modulus that in this
model is a fixed constant of value 9.81m/s
2
. For more
complicated models it may be modeled depending on
the latitude and longitude of the aircraft.
−−−→
g
NED
= g[0,0,1]
T
(3)
The keystone of the presented attitude determi-
nation method is determining gravity vector in body
axes. Rudimentary inertial measurement units are
able to determine this gravity vector in order to sub-
tract it from measured acceleration and provide better
results for position and velocity calculations in body
axes. The methods to calculate this gravity vector are
well developed in (Mizell, 2003). For example by de-
termining the continuous component of the measured
acceleration employing a low pass filter as it is in-
dicated on equations 4 and 5, on where Jerk on body
axes is calculated by the derivation of acceleration and
after that integrated in order to obtain non-continuous
component of acceleration, then, by subtracting this
non-continuous component to the measured accelera-
tion, gravity vector is estimated.
−−−→
Jerk
B
=
d
dt
[a
x
B
,a
y
B
,a
z
B
]
T
(4)
−→
g
B
= [a
x
B
,a
y
B
,a
z
B
]
T
−
Z
−−−→
Jerk
B
dt (5)
Another method to obtain gravity vector is by in-
tegrating the mechanization equations (Savage, 2000)
and manipulate consequently the resulting equations.
In this paper it is assumed that gravity vector in body
axes is provided directly by the inertial sensor, with its
associated error. It is defined in equation (6), where
g
x
B
,g
y
B
and g
z
B
are gravity vector components ex-
pressed in body axes.
−→
g
B
= [g
x
B
,g
y
B
,g
z
B
]
T
(6)
3 ATTITUDE DETERMINATION
ALGORITHM
In order to simplify the calculus, an orthonormal base
must be defined in both axes systems, B and NED.
This orthonormal base is defined by unitary vectors
~
i,
~
j and
~
k expressed in both bases and defined by ex-
pressions (7), (8), (9), (10), (11) and (12).
−−→
i
NED
=
−−→
v
NED
k
−−→
v
NED
k
(7)
−−→
j
NED
=
−−→
v
NED
×
−−−→
g
NED
k
−−→
v
NED
×
−−−→
g
NED
k
(8)
−−→
k
NED
=
−−→
i
NED
×
−−→
j
NED
−−→
i
NED
×
−−→
j
NED
(9)
−→
i
B
=
−→
v
B
k
−→
v
B
k
(10)
−→
j
B
=
−→
v
B
×
−→
g
B
k
−→
v
B
×
−→
g
B
k
(11)
−→
k
B
=
−→
i
B
×
−→
j
B
−→
i
B
×
−→
j
B
(12)
After defining an orthonormal base in the two sys-
tems of axes, the expression to determine the DCM is
indicated on (13), where
h
−→
i
B
,
−→
j
B
,
−→
k
B
i
is a 3x3 square
matrix composed of orthonormal vectors in body
triad,
h
−−→
i
NED
,
−−→
j
NED
,
−−→
k
NED
i
express the same concept in
NED triad, and DCM
B,NED
is the director cosine ma-
trix that transforms NED triad into body triad.
h
−→
i
B
,
−→
j
B
,
−→
k
B
i
= DCM
B,NED
h
−−→
i
NED
,
−−→
j
NED
,
−−→
k
NED
i
(13)
The DCM matrix can be solved from (13) as it is
shown in (14). Note that employing an orthonormal
base simplifies the calculation of the inverse matrix as
it is the transposed matrix.
After obtaining the director cosine matrix, the
rotation must be characterized. The most suitable
method to express this rotation is through quater-
nions, as they avoid any possible singularities on the
poles of rotation (Kuipers et al., 1999). The matrix
equation that relates DCM
B,NED
and quaternions is
showed in (15), where q
i
for i =
{
0,3
}
, are the quater-
nions, and M
j,k
for j =
{
1,3
}
and k =
{
1,3
}
are the
DCM matrix coefficients.
The expressions in (16), (17), (18) and (19) may
be used in order to solve quaternions.
DCM
B,NED
=
h
−→
i
B
,
−→
j
B
,
−→
k
B
ih
−−→
i
NED
,
−−→
j
NED
,
−−→
k
NED
i
−1
=
h
−→
i
B
,
−→
j
B
,
−→
k
B
ih
−−→
i
NED
,
−−→
j
NED
,
−−→
k
NED
i
T
(14)
DCM
B,NED
=
M
1,1
M
1,2
M
1,3
M
2,1
M
2,2
M
2,3
M
3,1
M
3,2
M
3,3
=
=
q
2
0
+ q
2
1
−q
2
2
−q
2
3
2(q
1
q
2
+ q
0
q
3
) 2(q
1
q
3
−q
0
q
2
)
2(q
1
q
2
−q
0
q
3
) q
2
0
−q
2
1
+ q
2
2
−q
2
3
2(q
2
q
3
+ q
0
q
1
)
2(q
1
q
3
+ q
0
q
2
) 2(q
2
q
3
−q
0
q
1
) q
2
0
−q
2
1
−q
2
2
+ q
2
3
(15)
Aircraft Attitude Determination Algorithms Employing Gravity Vector Estimations and Velocity Measurements
379

q
0
=
1
2
√
1 + Tr if Tr > 0
1
2
C
1
(M
2,3
−M
3,2
) if Tr ≤ 0 and M
1,1
≥ M
2,2
and M
1,1
≥ M
3,3
1
2
C
2
(M
3,1
−M
1,3
) if Tr ≤ 0 and M
2,2
> M
1,1
and M
2,2
> M
3,3
1
2
C
3
(M
1,2
−M
2,1
) if Tr ≤ 0 and M
3,3
> M
2,2
and M
3,3
> M
1,1
(16)
q
1
=
1
2
C
0
(M
2,3
−M
3,2
) if Tr > 0
1
2
p
1 +M
1,1
−M
2,2
−M
3,3
if Tr ≤ 0 and M
1,1
≥ M
2,2
and M
1,1
≥ M
3,3
1
2
C
2
(M
1,2
+ M
2,1
) if Tr ≤0 and M
2,2
> M
1,1
and M
2,2
> M
3,3
1
2
C
3
(M
3,1
+ M
1,3
) if Tr ≤0 and M
3,3
> M
2,2
and M
3,3
> M
1,1
(17)
q
2
=
1
2
C
0
(M
3,1
−M
1,3
) if Tr > 0
1
2
C
1
(M
1,2
+ M
2,1
) if Tr ≤0 and M
1,1
≥ M
2,2
and M
1,1
≥ M
3,3
1
2
p
1 +M
2,2
−M
1,1
−M
3,3
if Tr ≤ 0 and M
2,2
> M
1,1
and M
2,2
> M
3,3
1
2
C
3
(M
2,3
+ M
3,2
) if Tr ≤0 and M
3,3
> M
2,2
and M
3,3
> M
1,1
(18)
q
3
=
1
2
C
0
(M
1,2
−M
2,1
) if Tr > 0
1
2
C
1
(M
3,1
+ M
1,3
) if Tr ≤0 and M
1,1
≥ M
2,2
and M
1,1
≥ M
3,3
1
2
C
2
(M
2,3
+ M
3,2
) if Tr ≤0 and M
2,2
> M
1,1
and M
2,2
> M
3,3
1
2
p
1 +M
3,3
−M
1,1
−M
2,2
if Tr ≤ 0 and M
3,3
> M
2,2
and M
3,3
> M
1,1
(19)
where, Tr, C
0
, C
1
, C
2
and C
3
are defined by (20),
(21), (22), (23), and (24), respectively.
Tr = M
1,1
+ M
2,2
+ M
3,3
(20)
C
0
=
1
√
1+Tr
if
√
1 + Tr > 0
0 else
(21)
C
1
=
(
1
√
1+M
1,1
−M
2,2
−M
3,3
if
p
1 + M
1,1
−M
2,2
−M
3,3
> 0
0 else
(22)
C
2
=
(
1
√
1+M
2,2
−M
1,1
−M
3,3
if
p
1 + M
2,2
−M
1,1
−M
3,3
> 0
0 else
(23)
C
3
=
(
1
√
1+M
3,3
−M
1,1
−M
2,2
if
p
1 + M
3,3
−M
1,1
−M
2,2
> 0
0 else
(24)
It is known that quaternions themselves are
enough to express rotations without singularities, but
it is also known than conceptually they are difficult to
be visualized. An easier manner to define these ro-
tations is by means of Euler angles. Concretely, the
most common aeronautical rotation is defined by roll
(φ), pitch (θ), and yaw (ψ) angles. The expressions
that relate quaternions with Euler angles are defined
by (25), (26) and (27).
φ = atan2[2(q
2
q
3
+ q
0
q
1
),q
2
0
−q
2
1
−q
2
2
+ q
2
3
] (25)
θ = asin[−2(q
1
q
3
−q
0
q
2
)] (26)
ψ = atan2[2(q
1
q
2
+ q
0
q
3
),q
2
0
+ q
2
1
−q
2
2
−q
2
3
] (27)
These Euler angles obtained from measurements
may be used to characterize rotations and angular
speeds in navigation guidance and control algorithms.
4 FLIGHT DYNAMICS AND
SENSOR MODEL
The flight dynamics model in (de Celis et al., 2017)
is employed. The equations of motion are integrated
using a fixed time step RungeKutta scheme of fourth
order to obtain a single flight trajectory. A set of bal-
listic simulated shots, with no wind perturbations, is
performed varying shot angle from 15
◦
to 75
◦
taking
1
◦
steps, and also varying initial azimuth angle from
0
◦
to 360
◦
taking 45
◦
steps. An example of these tra-
jectories for a shot angle of 45
◦
and for the whole set
of azimuths is shown in Figure 1.
Figure 1: Trajectories for 45
◦
on initial pitch shot angle and
8 different azimuths.
GNSS sensors are modeled adding a white noise
of null average and maximum absolute values of m
p
=
3m and of m
v
= 0.01m/s for position and velocity,
respectively, to the simulated values obtained from
model.
Accelerometers are modeled as second order sys-
tems, with a natural frequency of 300 Hz and a damp-
ing factor of 0.7. A white noise of null average and
maximum absolute value of m
a
= 10
−6
m/s
2
and a
bias of 10
−6
m/s
2
is added. Note that accelerometers
will provide both acceleration in body axes, which
will be employed on the determination of velocity
vector in body axes, and gravity vector in body axes.
The modeling of the sensors has been based on
relatively low-cost equipment. This fact will induce
significant errors on measurements, which will deter-
mine the suitability of the attitude calculation method.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
380

Figure 2: Comparison between estimated and real magni-
tudes for aircraft roll angle (φ) for a shot angle of 45 deg.
and azimuths of 0
◦
(left), 45
◦
(right) and 90
◦
(bottom).
However, as it is shown in the following section,
the results are accurate enough for terminal guidance
tasks in artillery.
5 SIMULATION RESULTS
Simulation results are presented using the nonlinear
flight dynamics model (de Celis et al., 2017), where
data employed was validated from real flights and
model accuracy tested, in order to demonstrate suit-
ability of attitude determination algorithm. A set of
ballistic simulated shots was performed as defined in
the previous section, in order to compare estimated
and simulated attitudes. MATLAB/Simulink R2016a
on a desktop computer with a processor of 2.8 Ghz
and 8 GB RAM was used.
In order to compare the estimated attitude against
real or simulated attitude, the following expressions
are represented in Figures 2, 3 and 4: φ
real
−φ
estimated
,
θ
real
−θ
estimated
and ψ
real
−ψ
estimated
. All these fig-
ures represent results for a shot angle of 45
◦
and three
different azimuth angles: 0
◦
, 45
◦
and 90
◦
. Note that a
larger amount of simulations have been performed, as
Figure 3: Comparison between estimated and real magni-
tudes for aircraft pitch angle (θ) for a shot angle of 45 deg.
and azimuths of 0
◦
(left), 45
◦
(right) and 90
◦
(bottom).
Figure 4: Comparison between estimated and real magni-
tudes for aircraft yaw angle (ψ) for a shot angle of 45 deg.
and azimuths of 0
◦
(left), 45
◦
(right) and 90
◦
(bottom).
Aircraft Attitude Determination Algorithms Employing Gravity Vector Estimations and Velocity Measurements
381

Figure 5: Representation of x
B
gravity component Root
Mean Squared Error along the whole trajectory for each
shot angle and for the 8 azimuths tested.
Figure 6: Representation of y
B
gravity component Root
Mean Squared Error along the whole trajectory for each
shot angle and for the 8 azimuths tested.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
382

Figure 7: Representation of z
B
gravity component Root Mean Squared Error along the whole trajectory for each shot angle
and for the 8 azimuths tested.
it was defined previously, but the results are virtually
the same.
Note that in the worst of the situations the differ-
ence between real and estimated attitude is lower than
a magnitude order of 10
−2
, which assures the appli-
cability of the presented algorithms together with the
sensors employed and their associated noises.
In order to quantify the error made in each of
the shots along the whole simulated trajectories,
the Root Mean Squared Error (RMSE) for each of
the 3 Euler angles (RMSE
θ
0
,AZ
0
φ
), (RMSE
θ
0
,AZ
0
θ
) and
(RMSE
θ
0
,AZ
0
ψ
), and for each of the three compo-
nents of gravity vector in body axes (RMSE
θ
0
,AZ
0
g
x
B
),
(RMSE
θ
0
,AZ
0
g
y
B
) and (RMSE
θ
0
,AZ
0
g
z
B
), are calculated in
(28), (29), (30),(31), (32), and (33). These errors de-
pend on the shot launch angle (θ
0
) and azimuth (AZ
0
).
RMSE
θ
0
,AZ
0
φ
=
s
H
(φ
real
−φ
computed
)
2
dσ
H
dσ
(28)
RMSE
θ
0
,AZ
0
θ
=
s
H
(θ
real
−θ
computed
)
2
dσ
H
dσ
(29)
RMSE
θ
0
,AZ
0
ψ
=
s
H
(ψ
real
−ψ
computed
)
2
dσ
H
dσ
(30)
RMSE
θ
0
,AZ
0
g
x
B
=
s
H
(g
x
B
real
−g
x
B
computed
)
2
dσ
H
dσ
(31)
RMSE
θ
0
,AZ
0
g
y
B
=
s
H
(g
y
B
real
−g
y
B
computed
)
2
dσ
H
dσ
(32)
RMSE
θ
0
,AZ
0
g
z
B
=
s
H
(g
z
B
real
−g
z
B
computed
)
2
dσ
H
dσ
(33)
The computed components of gravity vector,
g
x
B
computed
, g
y
B
computed
and g
z
B
computed
are obtained in the
reality directly from inertial measurement unit sen-
sors, concretely by accelerometers with its associ-
ated error. On simulations performed these g
x
B
computed
,
g
y
B
computed
and g
z
B
computed
are estimated through the fol-
lowing algorithms that take in account previously cal-
culated director cosine matrix on (14) and the errors
of accelerometers. The model of gravity vector esti-
mator is described by (34) on where
−→
e
acc
is the error
Aircraft Attitude Determination Algorithms Employing Gravity Vector Estimations and Velocity Measurements
383
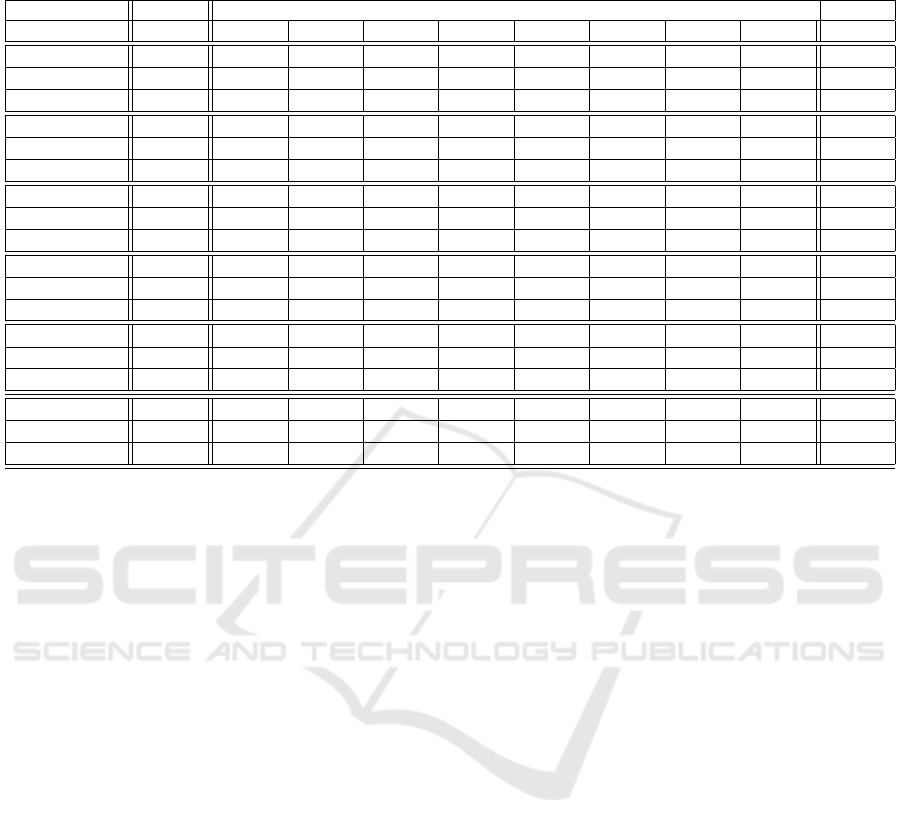
Table 1: Representation of quadratic errors along the whole trajectory for a set of shot angles and for the 8 azimuths tested
and calculation of a representative mean parameter.
Azimuth AZ
0
(deg)
Shot Angle (deg.) 0 45 90 135 180 225 270 315 Total
15 QE
θ
0
,AZ
0
φ
7.69E-07 1.01E-07 1.00E-06 1.93E-06 1.10E-06 3.92E-07 1.30E-06 9.77E-07 3.82E-07
15 QE
θ
0
,AZ
0
θ
2.32E-04 2.29E-04 2.24E-04 2.21E-04 2.19E-04 2.17E-04 2.12E-04 2.09E-04 7.80E-05
15 QE
θ
0
,AZ
0
ψ
7.69E-06 6.84E-07 6.49E-06 9.87E-06 8.16E-06 9.29E-07 4.58E-06 1.01E-05 2.46E-06
30 QE
θ
0
,AZ
0
φ
3.24E-06 2.38E-06 1.05E-06 2.33E-06 1.05E-06 3.52E-07 6.13E-07 1.62E-06 6.48E-07
30 QE
θ
0
,AZ
0
θ
1.46E-04 1.50E-04 2.31E-04 2.28E-04 2.27E-04 2.24E-04 2.21E-04 2.16E-04 7.36E-05
30 QE
θ
0
,AZ
0
ψ
1.44E-05 6.29E-06 7.72E-06 1.25E-05 7.41E-06 1.17E-06 6.60E-06 1.54E-05 3.53E-06
45 QE
θ
0
,AZ
0
φ
2.45E-06 1.78E-06 2.04E-06 3.91E-06 9.67E-07 3.04E-07 7.51E-07 1.44E-06 7.10E-07
45 QE
θ
0
,AZ
0
θ
1.40E-04 1.43E-04 1.46E-04 1.50E-04 2.32E-04 2.32E-04 2.28E-04 2.24E-04 6.77E-05
45 QE
θ
0
,AZ
0
ψ
1.10E-05 4.14E-06 1.41E-05 2.08E-05 1.12E-05 9.04E-07 6.63E-06 1.50E-05 4.26E-06
60 QE
θ
0
,AZ
0
φ
2.55E-06 1.43E-06 1.69E-06 2.05E-06 3.02E-06 2.03E-06 9.50E-07 1.66E-06 7.13E-07
60 QE
θ
0
,AZ
0
θ
1.36E-04 1.38E-04 1.41E-04 1.43E-04 1.46E-04 1.49E-04 2.34E-04 2.31E-04 5.98E-05
60 QE
θ
0
,AZ
0
ψ
1.14E-05 3.02E-06 1.29E-05 1.67E-05 1.52E-05 5.60E-06 7.26E-06 1.44E-05 4.16E-06
75 QE
θ
0
,AZ
0
φ
1.46E-06 1.20E-06 1.27E-06 2.56E-06 2.78E-06 1.56E-06 1.66E-06 3.72E-06 7.76E-07
75 QE
θ
0
,AZ
0
θ
1.33E-04 1.35E-04 1.36E-04 1.38E-04 1.40E-04 1.43E-04 1.46E-04 1.49E-04 4.95E-05
75 QE
θ
0
,AZ
0
ψ
1.10E-05 2.47E-06 9.40E-06 1.45E-05 1.40E-05 4.04E-06 1.46E-05 1.75E-05 4.25E-06
Total QE
θ
0
,AZ
0
φ
1.01E-06 7.02E-07 6.55E-07 1.19E-06 8.96E-07 5.27E-07 5.02E-07 9.42E-07 2.95E-07
Total QE
θ
0
,AZ
0
θ
7.24E-05 7.29E-05 8.09E-05 8.08E-05 8.81E-05 8.80E-05 9.42E-05 9.29E-05 2.97E-05
Total QE
θ
0
,AZ
0
ψ
5.05E-06 1.70E-06 4.72E-06 6.85E-06 5.19E-06 1.42E-06 3.87E-06 6.57E-06 1.70E-06
associated to the accelerometer:
g
x
B
computed
g
y
B
computed
g
z
B
computed
=
=
q
2
0
+ q
2
1
−q
2
2
−q
2
3
2(q
1
q
2
+ q
0
q
3
) 2(q
1
q
3
−q
0
q
2
)
2(q
1
q
2
−q
0
q
3
) q
2
0
−q
2
1
+ q
2
2
−q
2
3
2(q
2
q
3
+ q
0
q
1
)
2(q
1
q
3
+ q
0
q
2
) 2(q
2
q
3
−q
0
q
1
) q
2
0
−q
2
1
−q
2
2
+ q
2
3
·
·
0
0
9.81
+
−→
e
acc
(34)
Table 1 shows the Root Mean Squared Errors for
the 3 Euler angles for different shot angles and az-
imuths. The first column shows the shot angle and
the second one the displayed error (RMSE
θ
0
,AZ
0
φ
),
(RMSE
θ
0
,AZ
0
θ
and RMSE
θ
0
,AZ
0
ψ
). The rest of the
columns show the numerical values of the errors for
different azimuths. Finally right column named to-
tal, represents the Root Mean Squared Errors for the
set of azimuths represented on the same row. Equally
the last three rows represent the Root Mean Squared
Errors for the set of shot angles represented on the
same column. Finally the three values of the bottom-
right corner can be considered as an estimation of the
whole error of the attitude calculation algorithms.
Figures 5, 6 and 7 show the following Root
Mean Squared Errors: RMSE
θ
0
,AZ
0
g
x
B
, RMSE
θ
0
,AZ
0
g
y
B
and
RMSE
θ
0
,AZ
0
g
z
B
along the whole trajectory for each shot
angle and for the 8 azimuths.
Note that the obtained Root Mean Squared Errors
for all the measures of interest presented in this paper
are small enough to consider the proposed algorithm
for estimating attitude of high dynamic vehicles at a
low cost. Comparison between real aircraft attitude,
which can be assumed near to the attitude provided
by a precise gyroscope, and the attitude obtained by
exposed algorithms, never differ from 10
−3
degrees,
which is a very accurate value for most of the projec-
tile applications.
6 CONCLUSIONS
A novel low-cost approach for estimating attitude of
aerial platforms has been proposed. This approach is
based on the measurement of two different vectors:
speed and gravity vector. They are measured in two
different reference frames using a GNSS sensor and a
set of accelerometers. The presented algorithm is of
special interest for high dynamic vehicles where other
low-cost approaches, such as the ones using magne-
tometers, are not suitable.
Nonlinear simulations based on ballistic rocket
launches are performed to obtain ideal attitude and
compare it to the attitude obtained by the proposed
approach. Computational results show that errors
made are small enough to consider the presented al-
gorithm as a good candidate for using it within a con-
trol algorithm. Note that the low-cost needed compo-
nents make this approach highly interesting for non-
re-usable vehicles.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
384

REFERENCES
Crassidis, J. L., Markley, F. L., and Cheng, Y. (2007). Sur-
vey of nonlinear attitude estimation methods. Journal
of guidance, control, and dynamics, 30(1):12–28.
de Celis, R., Cadarso, L., and S
´
anchez, J. (2017). Guid-
ance and control for high dynamic rotating ar-
tillery rockets. Aerospace Science and Technology.
http://dx.doi.org/10.1016/j.ast.2017.01.026.
Eure, K. W., Quach, C. C., Vazquez, S. L., Hogge,
E. F., and Hill, B. L. (2013). An application
of uav attitude estimation using a low-cost iner-
tial navigation system. NASA/TM2013-218144.
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/
20140002398.pdf.
Gebre-Egziabher, D., Elkaim, G. H., Powell, J., and Parkin-
son, B. W. (2000). A gyro-free quaternion-based at-
titude determination system suitable for implementa-
tion using low cost sensors. In Position Location and
Navigation Symposium, IEEE 2000, pages 185–192.
IEEE.
Gebre-Egziabher, D., Hayward, R. C., and Powell, J. D.
(1998). A low-cost gps/inertial attitude heading ref-
erence system (ahrs) for general aviation applica-
tions. In Position Location and Navigation Sympo-
sium, IEEE 1998, pages 518–525. IEEE.
Henkel, P. and Iafrancesco, M. (2014). Tightly coupled po-
sition and attitude determination with two low-cost
gnss receivers. In Wireless Communications Sys-
tems (ISWCS), 2014 11th International Symposium
on, pages 895–900. IEEE.
Ismail, A., Ashraf, K., Metawea, A., Mostfa, I., Saeed,
A., Helal, E., Essawy, M., Abdelazim, M., Ibrahim,
M., Raafat, R., et al. (2015). A high-performance
self-clocked digital-output quartz gyroscope. In SEN-
SORS, 2015 IEEE, pages 1–4. IEEE.
Kuipers, J. B. et al. (1999). Quaternions and rotation
sequences, volume 66. Princeton university press
Princeton.
Ma, D.-M., Shiau, J.-K., Wang, I., Lin, Y.-H., et al. (2011).
Attitude determination using a mems-based flight in-
formation measurement unit. Sensors, 12(1):1–23.
Mizell, D. (2003). Using gravity to estimate accelerome-
ter orientation. In Proc. 7th IEEE Int. Symposium on
Wearable Computers (ISWC 2003), volume 252. Cite-
seer.
Savage, P. G. (2000). Strapdown analytics, volume 2. Strap-
down Associates Maple Plain, MN.
Springmann, J. C. and Cutler, J. W. (2014). Flight results of
a low-cost attitude determination system. Acta Astro-
nautica, 99:201–214.
Yun, X., Bachmann, E. R., and McGhee, R. B. (2008). A
simplified quaternion-based algorithm for orientation
estimation from earth gravity and magnetic field mea-
surements. IEEE Transactions on instrumentation and
measurement, 57(3):638–650.
Aircraft Attitude Determination Algorithms Employing Gravity Vector Estimations and Velocity Measurements
385
