Multi-agent Deep Reinforcement Learning for Task Allocation in

Dynamic Environment

Dhouha Ben Noureddine

1,2

, Atef Gharbi

and Samir Ben Ahmed

LISI, National Institute of Applied Science and Technology, INSAT, University of Carthage, Tunis, Tunisia

FST, University of El Manar, Tunis, Tunisia

Keywords:

Task Allocation, Multi-agent System, Deep Reinforcement Learning, Communication, Distributed Environ-

ment.

Abstract:

The task allocation problem in a distributed environment is one of the most challenging problems in a multi-

agent system. We propose a new task allocation process using deep reinforcement learning that allows cooper-

ating agents to act automatically and learn how to communicate with other neighboring agents to allocate tasks

and share resources. Through learning capabilities, agents will be able to reason conveniently, generate an ap-

propriate policy and make a good decision. Our experiments show that it is possible to allocate tasks using

deep Q-learning and more importantly show the performance of our distributed task allocation approach.

1 INTRODUCTION

In an autonomous multi-agent system (MAS), agents

can cooperate and complete hard tasks through task

allocation. So they need to manage tasks unpre-

dictably. To improve the execution performance, dis-

tributed task allocation can make the collaboration

and communication between agents perfect. However

an agent is locally visible only, it is unable to observe

behaviors or get all knowledge about other agents in

the system.

To overcome the task allocation problem en-

countered during system execution, we propose a

new approach, Task Allocation Process using Co-

operative Deep Reinforcement Learning strategy

(TAP CDQL), which combines the advantages of

centralized and distributed learning approaches in lit-

erature. By learning agents can teach each other how

to allocate tasks, so that the task allocation becomes

easier and less complicated. Especially, if agents

share their past task allocation experiences (exploita-

tion) to become a useful knowledge that can be used

for future task allocation process (exploration), it will

be possible to enhance the system efﬁciency. In our

study, communication is intensively used: when an

agent perceives a task, it follows a protocol of mes-

sages with his neighbors to fulﬁll this task that may

potentially perform it. In order to allow agents co-

ordinate their behavior together and discover auto-

matically this protocol, we use the Deep Q-Networks

(DQN) which we investigate it to improve the per-

formance and quality of the decentralised allocation

using insights from centralised approaches. So the

role of DQN is to enable groups of agents to learn ef-

fectively coordinated policies in task allocation prob-

lems. In this paper, we propose an algorithm that

shows how to learn to manage and allocate efﬁciently

resources and tasks. In other words: we ask if agents

can learn to manage resources on their own? And how

many agents interact with each others to allocate tasks

in a distributed environment using learning capabili-

ties?

The contributions of this paper are twofold.

First we propose a Cooperative Deep Reinforcement

Learning approach combining single-agent and multi-

agent learning. Then we propose the distributed task

allocation applying this strategy; which is allowing

agents to request help from cooperating neighbors.

This would be done by allocating tasks to different

learner agents who may be capable each of perform-

ing different subsets of those tasks and exploiting

multiple sources of learned knowledge. By this way,

agents can achieve more efﬁcient and robust tasks

allocation in loosely coupled distributed multi-agent

systems’ environments.

We compare our approach to other task alloca-

tion methods and we demonstrate that with this ap-

proach, agents can learn not only to allocate tasks ef-

ﬁciently, but also agents will be prepared properly for

new tasks. The remainder of this paper is organized

Noureddine, D., Gharbi, A. and Ahmed, S.

Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment.

DOI: 10.5220/0006393400170026

In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 17-26

ISBN: 978-989-758-262-2

as follows: we brieﬂy introduce a background on the

reinforcement learning and deep learning in Section

2. This is followed by Section 3 in which detail the

proposed Cooperative Deep Reinforcement Learning

Strategy. Then, a distributed task allocation approach

is illustrated in Section 4. Section 5 discusses our ex-

periments, and some concluding remarks are drawn

and future works mentioned in Section 6.

2 BACKGROUND

In this section we deﬁne some fundamental notions

that are essential to understand our work: we begin

with a brief review on Markov decision process MDP

then we introduce the reinforcement learning and ﬁ-

nally we tackle the deep Q-learning.

2.1 Markov Decision Process

A Markov Decision Process MDP is a discrete-time

model for the stochastic evolution of a system’s state,

under control of an external input (the agent’s action

or agents’ joint action). It also models a stochastic re-

ward that depends on the state and action. (Strens and

Windelinckx, 2005)

An MDP is given by 4-tuple < S, A, T, R > where: S

is a set of states; A is a set of actions; T is a stochas-

tic transition function deﬁning the likelihood the next

state will be s

′

∈ S given current state s ∈ S and ac-

tion a ∈ A : P

′

|s, a); and R is a stochastic reward

function deﬁning the likelihood the immediate reward

will be r ∈ R given current state s ∈ S and action

a ∈ A : P

(r|s, a).

2.2 Reinforcement Learning

The software agents in the Reinforcement Learning

RL (Sutton and Barto, 1998) learn to maximize their

expected future sum of rewards R by interacting with

an environment and learn from sequential experience.

The environment is typically formulated as an MDP.

An RL agent behaves according to a policy π that

speciﬁes a distribution over available actions at each

state.

An RL agent observes the current state s

at each dis-

crete time-step t, selects action a

according to a pol-

icy π, receives the reward r

t+ 1

thereafter, and transi-

tions according to some probability distribution to a

new state s

t+ 1

. The agent’s objective is to maximize

their expected discounted rewards, R

= r

+γ∗r

t+ 1

∗ r

t+ 2

+ ..., where γ ∈ [0, 1] is a discount factor. So

the action-value function is deﬁned as follows:

Q(s, a) = E

= s, a

= a] (1)

An agent is learning on-policy if it learns about the

policy that it is currently following. In the off-policy

setting an agent learns from experience of another

agent or another policy, e.g. a previous policy

(Heinrich and Silver, 2016).

Q-learning (Watkins and Dayan, 1992) is a popular

off-policy RL method. It learns about the greedy pol-

icy, which at each state takes the action of the highest

estimated value. Storing and replaying past experi-

ence with off-policy RL from the respective transi-

tions is known as experience replay (Lin, 1992). Fit-

ted Q-Iteration (FQI) (Ernst et al., 2005) is a batch

RL method that replays experience with Q-learning.

Neural Fitted Q-Iteration (NFQ) (Riedmiller, 2005)

and Deep Q-Network (DQN) (Mnih et al., 2015) are

extensions of FQI that use neural network function

approximation with batch and online updates respec-

tively.

However, the main shortcoming of RL in many

applications, is the intractable computation because

of the dimensionality which limit it heavily for real

physical systems. One solution for this dimension-

ality problem is to apply the concept of Deep Q-

Networks.

2.3 Deep Q-Learning

Recently Deep Learning (DL) has became the big

buzz words in artiﬁcial intelligence ﬁeld. The

progress in DL have played a key role in solving a

number of challenging RL dilemmas, including video

games ((Koutnik et al., 2013); (Mnih et al., 2013);

(Mnih et al., 2015)), computer vision ((Krizhevsky

et al., 2012), (Sermanet et al., 2013), (Mnih, 2013)),

high-dimensional robot control ((Levine et al., 2015),

(Assael et al., 2015), (Watter et al., 2015)), speech

recognition ((Dahl et al., 2012), (Graves et al.,

2013)), visual attention (Ba et al., 2015) and the Atari

learning environment (ALE) ((Guo et al., 2014),

(Mnih et al., 2015), (Stadie et al., 2015), (Wang et al.,

2015), (Schaul et al., 2016), (Hasselt et al., 2016),

(Oh et al., 2015), (Bellemare et al., 2016), (Nair et al.,

2015)).

Deep Q-Networks

The basic idea of DQN (Mnih et al., 2015) is to rep-

resent the Q-function by using a neural network pa-

rameterised by θ to represent Q(s, a, θ). DQNs are

optimised by minimising:

(θ

) = E

s,a,r,s′

[(γ

DQN

− Q(s, a, θ

))

] (2)

ICSOFT 2017 - 12th International Conference on Software Technologies

At each iteration i, with target y

DQN

r + γmax

′

Q(s

′

, a

′

, θ

−

). Here, θ

−

are the param-

eters of a target network that is frozen for a number

of iterations while updating the online network

Q(s, a, θ

). The action a is chosen from Q(s, a, θ

)

by an action selector, which typically implements

an ε-greedy policy that selects the action that max-

imizes the Q-value with a probability of 1 − ε and

chooses randomly with a probability of ε. DQN uses

experience replay (Lin, 1993): during learning, the

agent builds a dataset of episodic experiences and is

then trained by sampling mini-batches of experiences.

Independent Deep Q-Networks

(Tampuu et al., 2015) relies on the work of Deep-

Mind and explores how multiple agents controlled by

autonomous DQN interact when sharing a complex

environment. He deﬁnes an extended settings in

which each agent a observes the global s

, chooses

an individual action a

, and receives a team reward,

, shared among all agents. (Tampuu et al., 2015)

address this settings with a framework that combines

DQN with independent Q-learning, in which each

agent a independently and simultaneously learns its

own Q-function Q

(s, a

, θ

). While independent

Q-learning can in principle lead to convergence prob-

lems, it has a strong empirical track record ((Shoham

and Leyton-Brown, 2009), (Zawadzki et al., 2014)),

and was successfully applied to two-player pong.

Deep Recurrent Q-Networks

The last two approaches assume full observability.

Contrary to the environments partially observable, the

input s

is hidden and the agent receives only an ob-

servation o

that is correlated with s

, but in general

does not disambiguate it. (Hausknecht and Stone,

2015), propose the deep recurrent Q-networks to ad-

dress single-agent, partially observable settings. In-

stead of approximating Q(s, a) with a feed-forward

network, they approximate Q(o, a) with a recurrent

neural network that can maintain an internal state and

aggregate observations over time. This can be mod-

elled by adding an extra input h

t− 1

that represents the

hidden state of the network, yielding Q(o

, h

t− 1

, a).

For notational simplicity, we omit the dependence of

Q on θ.

3 COOPERATIVE DEEP

REINFORCEMENT LEARNING

STRATEGY

Generally in task allocation approaches, an agent de-

composes a problem into tasks and it has mostly a

task which cannot complete it by itself. It thus sends

a resource announce message to his neighbors which

answer for the announced message if they have the

ability to do such a task and they are idle at that time.

These approaches have no mechanism for reasoning

about future task sequence. It is clear that a precise

estimation for future tasks is impossible. But agents

may have some expectations on the future task se-

quence when they use past experiences. Having such

information about future task sequence is possible if

agents have learning ability which transforms past ex-

periences to a helpful advice. So in a prior knowl-

edge about these tasks, it would be possible to opti-

mize system performance by planning based-learning

the tasks execution which it completed by each agent.

However, such knowledge is not accessible for most

MAS applications.

Based on the hypotheses of partial observabil-

ity, asynchronism related to MAS and all agents are

fully cooperative, a learning-based task allocation

approach is proposed to overcome the problem ex-

plained above. Therefore we combine the central-

ized and distributed learning to solve task alloca-

tion problem. By the proposed method, cooperating

agents learn how to communicate with others agents

to achieve the overall goal of the system. The knowl-

edge obtained in learning process is used to make de-

cision about agent’s task solving ability. The major

difference between single-agent and multi-agent sys-

tems in terms of deep reinforcement learning is that

for a single-agent the environment can be deﬁned as

an MDP. However in multi-agent case, the environ-

ment is no longer stationary because of the unpre-

dictable changes resulting from independent decision

making and agents’ acting mechanisms.

In this section, we deﬁne two approaches used

for a Cooperative Deep Q-Learning CDQL strategy

for task allocation where cooperating agents learn to

communicate between themselves before taking ac-

tions. Each agent is controlled by a deep feed-forward

network (Sukhbaatar et al., 2016), which addition-

ally has access to a communication channel carrying a

continuous vector. Through this channel, they receive

the summed transmissions of other agents. However,

what each agent transmits on the channel is not spec-

iﬁed a-priori, learning instead is. Because the com-

munication is continuous, the model can be trained

via back-propagation, and thus can be combined with

Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment

standard single agent RL algorithms.

3.1 Single-agent Learning

In a Single-agent Learning, we use the approach

DRQN (Hausknecht and Stone, 2015) to select ac-

tion taken into account the partial observability. All

the agents aim to maximize the same discounted sum

of rewards R. The basic idea behind our approach

is all agents independently learn parameters and treat

other agents as a part of the environment. In fact ac-

tions can be divided into environment and communi-

cation actions and the Q-values are computed from

these two types of actions. Then agents cooperatively

learn common Q-values by considering joint actions.

So learning process is realized either by each agent by

observing all environmental changes or by communi-

cating with all agents.

We consider the Q-network of an agent a by

, c

′

t− 1

, h

t− 1

, a

), where h

t− 1

represent the indi-

vidual hidden of the agent a, o

the observation ,

′

t− 1

the messages from other agents during commu-

nication and a

the environment action of the agent

a. During decentralized execution (in the next para-

graph), each agent uses its own copy of the learned

network, evolves its own hidden state, chooses its own

actions, and communicates with other agents only

through the communication channel.

3.2 Multi-agent Learning

Multi-agent Learning is the direct application of

Single-agent Learning to multi-agent case. In other

word the distributed deep Q-Learning is the combi-

nation of the centralized one with Q-networks, not

only to share parameters but to push gradients from

one agent to other agents through the communica-

tion channel. By this purpose, each individual agent

learns its own Q-values as a result of its states and ac-

tions which is independent of other agents’ actions.

Otherwise, through this method agents can give each

other feedback about their communication actions to

improve the efﬁciency of the overall system. Actu-

ally, communication in this study is any kind of mes-

sage between agents, such as an announce messages,

a tasks allocation, a refuse or proposal message, a suc-

cess or failure response of the allocation, information

delivery, etc.

We use then the Communication Neural Net

model (CommNet) (Sukhbaatar et al., 2016) to com-

pute the distribution over tasks and actions at a given

time t. CommNet, is a simple controller for multi-

agent reinforcement learning that is able to learn

continuous communication between a dynamically

changing set of agents. Sukhbaatar deﬁnes s

the

agent’s view of the environment state. The in-

put to the controller is the concatenation of all state-

views s = {s

, ..., s

}, and the controller Φ is a map-

ping a = Φ(s), where the output a is a concatenation

of discrete environment actions a = {a

, ..., a

} for

each agent and communication actions c = {c

, ..., c

Note that this single controller Φ encompasses the in-

dividual controllers for each agents, as well as the

communication between agents. The architecture for

Φ that is built from modules f

which take the form

of multilayer neural networks. Here j ∈ {0, ..., K},

where K is the number of communication steps in the

network. Each f

takes two input vectors for each

agent a

: the hidden state h

and the communica-

tion c

, and outputs vector h

j+1

. The main body of

the model (Sukhbaatar et al., 2016) then takes as in-

put the concatenated vectors h

= [h

, h

, ..., h

], and

computes:

j+1

= f

, c

) (3)

j+1

I − 1

∑

′

6=i

j+1

′

(4)

CommNet (Sukhbaatar et al., 2016) allows communi-

cation between multiple agents and cooperated tasks,

the communication protocol is learned from scratch

simultaneously with agents policies. Before putting

up the reactions, agents have access to a broadcast

channel that can transmit continuous practice between

them. This continuous communication makes the

learning much easier because the communication pro-

tocol can be treated that procreation. Also the archi-

tecture is modularthat allowsthe number of regions to

dynamically change. Thus the (CommNet), (i) takes

the state-view of all agents s, passes it through the en-

coder, (ii) iterates h and c in equations (3) and (4) to

obtain h

, (iii) samples actions a for all agents, ac-

cording to a decoder function q(h

4 TASK ALLOCATION PROCESS

USING CDQL STRATEGY

In this study, we make the simplifying assumption of

full cooperation between agents as mentioned above.

We propose a new approach: Task Allocation Process

using Cooperative Deep Q-learning TAP

CDQL for

task allocation that combine the advantages of cen-

tralized and distributed deep Q-learning approaches.

It is distributed in nature but it aims to remove be-

haviour conﬂicts of traditional distributed learning ap-

proaches.

ICSOFT 2017 - 12th International Conference on Software Technologies

4.1 The Problem Description

Task allocation problem can be simply described as

that an agent has a task which it cannot complete by

itself. We thus formulate the social task allocation

problem in this subsection. We deﬁne A a set of

agents: A = {a

,..., a

}. Agents need resources

to complete tasks. We denote R = {r

,..., r

} the

collection of the resource types available to A. Each

agent a ∈ A controls a ﬁxed amount of resources

for each resource type in R, which is deﬁned by a

resource function: rsc : A × R → N. Moreover, we

assume agents are connected by a social network.

Deﬁnition 1 (Social Network). An agent social net-

work SN = (A, AE) is an undirected graph, where A

is a set of agents and AE is a set of edges connecting

two agents.

We suppose a set of tasks T = {t

, t

,..., t

} arrives at

such an agent social network. Each task t

∈ T is then

deﬁned by the tuple {u(t

), rsc(t

), loc(t

)}, where

u(t

) is the utility gained if task t

is accomplished

(we assume that the utility is identical to the reward

∑

i=1

t+ i

) that is used in Deep Q-Learning at

each discrete time-step t) and the resource function

rsc : T × R → N speciﬁes the amount of resources

required for the accomplishment of task t

. Further-

more, a location function loc : T → A deﬁnes the

locations (i.e., agents) at which the tasks arrive in the

social network. An agent a that is the location of a

task t

, i.e. loc(t

) = a, is called the manager of this

task. Each task t

∈ T needs some speciﬁc resources

from the agents in order to complete the task. The

exact assignment of tasks to agents is deﬁned by a

task allocation.

Deﬁnition 2. Each agent a ∈ A is composed of 5-

tuple {AgentID(a), Neig(a), Resource(a), State(a),

, c

′

t− 1

, h

t− 1

, a

)}, where AgentID(a) is the

identity of agent a, Neig(a) is a set which indicates

the neighbors of agent a, Resource(a) is the resource

which agent a contains, State(a) demonstrates the

state of agent which will be described later, and

, c

′

t− 1

, h

t− 1

, a

) the Q-network of the agent

a, (where h

t− 1

represent the individual hidden of

the agent a, o

the observation, c

′

t− 1

the messages

from other agents during communication and a

the

environment action of the agent a).

Deﬁnition 3 (Task allocation). We consider a set of

tasks T = {t

, t

,..., t

}, a set of agents A = {a

,..., a

}

in a social network SN, all agents are cooperating

to maximize reward R in the environment to achieve

an overall goal of MAS, and a task allocation is a

mapping φ : T × A × R → N.

4.2 The Principle of Distributed Task

Allocation using CDQL Algorithm

In an open MAS, we deﬁne three types of agents: the

agent which requests help for its task is called Man-

ager, the agent which accepts and performs the an-

nounced task is called Participant and the agent that

receives another agent’s commitments for assistance

to ﬁnd Participants is called Mediator. Initially, no

information is known about any of the agents in the

MAS. Nonetheless, as problems are solved, informa-

tion about agents can be learned using our Coopera-

tive Deep Reinforcement Learning Strategy for task

allocation problem. To guarantee a coherent behav-

ior of the whole distributed system, we deﬁne the fol-

lowing idea: we suppose that Neig(a

) stores only di-

rectly linked neighboring agents of agent a

We introduce three states in a complex adaptive

system, i.e. States = (Busy, Committed, Idle), and

an agent can be only in one of the three states at any

time step. When an agent is a Manager or Participant,

the state of that agent is Busy. When an agent is a

Mediator,the agent is in Committed state. An agent in

Idle state is available and not assigned or committed

to any task. For efﬁcient task allocation, it’s supposed

that only an Idle agent can be assigned to a new task

as a Manager or a partial fulﬁlled task as a Participant,

or Committed to a partial fulﬁlled task as a Mediator.

A partial fulﬁlled task is a task, for which a full group

is in formation procedure and has not yet formed.

After a problem is decomposed into tasks and the

Manager sends resource announce message to all its

neighbors, the Idle Participants submit bids on the

tasks each is able to allocate. These proposals al-

low the system to learn each agent’s task solving abil-

ity. At each discrete time-step a task is announced,

a record of each Participant agent’s bid is recorded

for the particular task type. In subsequent task an-

nouncements, the announcement is not broadcast to

all agents but to only a small group Participant learned

agents) that has responded to similar announcements

in earlier problems. When new Participant agents

become active, they receive every type of announce-

ment until their abilities are learned. Through CDQL

each agent’s task solving capability, the system might

eventually switch from task announcement and bid-

ding to task assignment based on agent learning abil-

ity and load. En brief, the task allocation policy is

learned through experience by using our CDQL Strat-

egy. The idea of the algorithm is illustrated as fol-

lows:

• When the Manager agent denoted as A

should

Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment

apply distributed task allocation (i.e. it doesn’t

have all the required resources), it sends re-

source announce messages, ResAnnounceMess =

<AgentID(A

), TaskID(t

), Resource(t

)>,

to all its neighbors.

• These neighboring agents receiving the ResAn-

nounceMess message sent by A

– If (state (neighboring agent) = Idle) Then the

neighboring agent A

proposes with informa-

tion about the types of resources it contains,

the execution time, the utility, the identities of

them and the Q-network namely ProposeMess

= <AgentID(A

), Resource(A

), Execute(A

Utility(A

), Q-network(A

)>.

– Else (state (neighboring agent) = Busy) the A

refuses and sends the following message Re-

fuseMess = <AgentID(A

)>.

• A

uses CommNet (Sukhbaatar et al., 2016), (i.e.

it takes the state-view s of all A

neighboring

agents, passes it through the encoder, iterates h

and c in equations (3) and (4) to obtain h

, and

samples actions a for all neighboring agents, ac-

cording to q(h

– If (A

identiﬁes the learning state-view s in

accordance with the required resources and if

it’s satisﬁed with many neighbor’s resource

proposals) Then A

will select communica-

tion action c using the roulette selection in

accordance with the Q

, c

′

t− 1

, h

t− 1

, a

) for

state s and choose the agent having the high-

est utility (reward), denoted as A

, and the state

of A

will be changed to Busy. In case the A

ﬁnds several agents having the highest utility

then it chooses the agent A

proposing the least

execution time.

– Else A

is satisﬁed with only one neighbor’s

resources, then A

will choose this agent with-

out any utility consideration.

The Manager sends a contract to the cho-

sen agent A

composed of 4-tuple, Contract

= <AgentID(A

), AgentID(A

), TaskID(t

Resource(A

)>.

• After obtaining the response from its different

neighbors, then A

compares the available re-

sources from its neighbors, i.e. Resoneig(A

with the resources required for its task t

namely Rsc(t

). (Here, Resoneig(A

) =

∈Neig(A

)

Resource(A

)). This comparison

would result in one of the following two cases.

– If (Rsc(t

) ⊆ Resoneig(A)) Then A

can

form a full group for task t

directly with its

neighboring agents.

– Else (Resoneig(A) ⊂ Rsc(t

)) In this condi-

tion, the A

can only form a partial group for

task t

. It then commits the task t

to one

of its neighbors. The commitment selection is

based on the number of neighbors each neigh-

bor of A

maintaining. The more neighbors

an agent has, the higher probability that agent

could be selected as a Mediator agent to com-

mit the task t

• After selection, A

commits its partial fulﬁlled

task t

to the Mediator agent, denoted as A

A commitment consists of 4-tuple, Commitment

= < AgentID(A

), AgentID(A

), TaskID(t

Rsc(t

)

>, where Rsc(t

)

is a subset of

Rsc(t

), which contains the unfulﬁlled required

resources. Afterwards, A

subtracts 1 from N

max

and attempts to discover the agents with available

resources from its neighbors. If any agents satisfy

resource requirement, A

will send a response

message, back to A

. The A

then directly

makes contract with the agents which satisfy the

resource requirement. If the neighboring agents

of A

cannot satisfy the resource requirement ei-

ther, A

will commit the partial fulﬁlled task t

to one of its neighbors again.

• This process will continue until all of the resource

requirements of task t

are satisﬁed, or the N

max

reaches 0, or there is no more Idle agent among

the neighbors. Both of the last two conditions, i.e.

max

= 0 and no more Idle agent, demonstrate the

failure of task allocation. In these two conditions,

disables the assigned contracts with the Par-

ticipants, and the states of these Participants are

reset to Idle.

• When ﬁnishing an allocation for one task, the

system is restored to its original status and each

agent’s state is reset to Idle.

5 EXPERIMENTS

In order to strengthen the validity and to demonstrate

the quality of our approach, we have simulated our

TAP

CDQL approach in different networks. To test

the efﬁciency of our algorithm, we compare it with

the Greedy Distributed Allocation Protocol (GDAP)

(Weerdt et al., 2007) and our previous distributed task

allocation algorithm (Gharbi et al., 2017) that it does

not use the CDQL strategy (we called TAP). In this

subsection, we ﬁrst deﬁne GDAP brieﬂy. Then, we

introduce the experiment environment’ settings. At

the end, we depict the results and the relevant analy-

sis.

ICSOFT 2017 - 12th International Conference on Software Technologies

5.1 Greedy Distributed Allocation

Protocol (GDAP)

GDAP (Weerdt et al., 2007) is selected to handle task

allocation problem in agent social networks. It’s de-

scribed brieﬂy as follows: All Manager agents a ∈ A

try to ﬁnd neighboring contractors (the same as Par-

ticipant in this paper) to help them with their tasks

= {t

∈ T|loc(t

) = a}. They begin with offering

the most efﬁcient task. Beyond all tasks offered, con-

tractors select the task having the highest efﬁciency,

and send a bid to the related manager. A bid con-

sists of all the resources the agent is able to supply

for this task. If sufﬁcient resources have been of-

fered, the manager selects the required resources and

informs all contractors of its choice. When a task is

allocated, or when a manager has received offers from

all neighbors but still cannot satisfy its task, the task

is removed from its task list. And this is the main

disadvantage of GDAP that it only relies on neigh-

bors which may cause several tasks unallocated due

to limited resources, while our approach tries to solve

this problem.

5.2 Experimental Settings

We have implemented TAP

CDQL, TAP and GDAP

in JAVA and we have tested them. We have repeated

the same experiment determinate in (Weerdt et al.,

2007) to deliver the performance of our approach.

There are two different settings used in our exper-

iment. The ﬁrst setup has done in the Small-world

networks in which most neighbors of an agent are

also connected to each other. The second setup has

done in the Scale free networks. And the results are

compared with the results when there is no learning.

Setting 1: we consider the number of agents is 40,

the number of tasks is 20, the number of different

resource’s types is 5, the average number of resources

required by each task is 30 and the average number

of resources needed by each tasks is 30. We assume

that tasks are distributed uniformly on each Idle agent

and resources are allocated uniformly to agents. The

only changeable variable in this setting is the average

number of neighbors. This setting is destined for

representing the inﬂuence of neighbors’ number on

the performance of TAP CDQL, TAP and GDAP.

Setting 2: we ﬁx the average number of neighbors

at 10. We consider the number of agents increases

and varies from 100 to 2000. We ﬁx the ratio be-

tween the number of agents and tasks at 5/3 and the

resource ratio at 1.2. The number of different resource

types is 20 and the average resource requirement of

a tasks is 100. The tasks are uniformly distributed.

This setting is deﬁned to demonstrate the scalability

of TAP

CDQL, TAP and GDAP in a large scale net-

works with a ﬁxed average number of neighbors.

The algorithms have been evaluated according to two

criteria in this experiment, which are the Utility Ra-

tio (the ratio between the summation of the success-

fully completed (allocated) tasks and the total number

of tasks as described in Subsection 4.1. If the Utility

Ratio is higher, that means more tasks can be allo-

cated, so the performance is better.) and the Execu-

tion Time (is the performing time of the algorithms in

each network under different situations respectively.).

The unit of execution time is millisecond. For sim-

plicity, we suppose that once a task has been allo-

cated to a Participant, the Participant would success-

fully ﬁnish this task and without failure.

5.3 Experiment Results and Analysis

Experiment results and analysis from setting 1: we

would like to test in this experiment the inﬂuence

of different average number of neighbors on algo-

rithms and the learning impact on allocating tasks per-

formance. We remark in Figure 1 the Utility Ratio

of TAP

CDQL in different networks is more reliable

than of TAP and GDAP algorithms. In the one hand,

for the reason that the distribution of tasks in GDAP

is only depending on the Manager neighbors, contrary

to ours and TAP in the case of need at other agents are

allocated (i.e. not only the neighbors). On the other

hand, cooperating agents in TAP

CDQL are likely to

select neighboring agents though our CDQL strategy.

Figure 1: The Utility ratio of TAP CDQL, TAP and GDAP

depend on the average number of neighbors in different type

of networks.

Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment

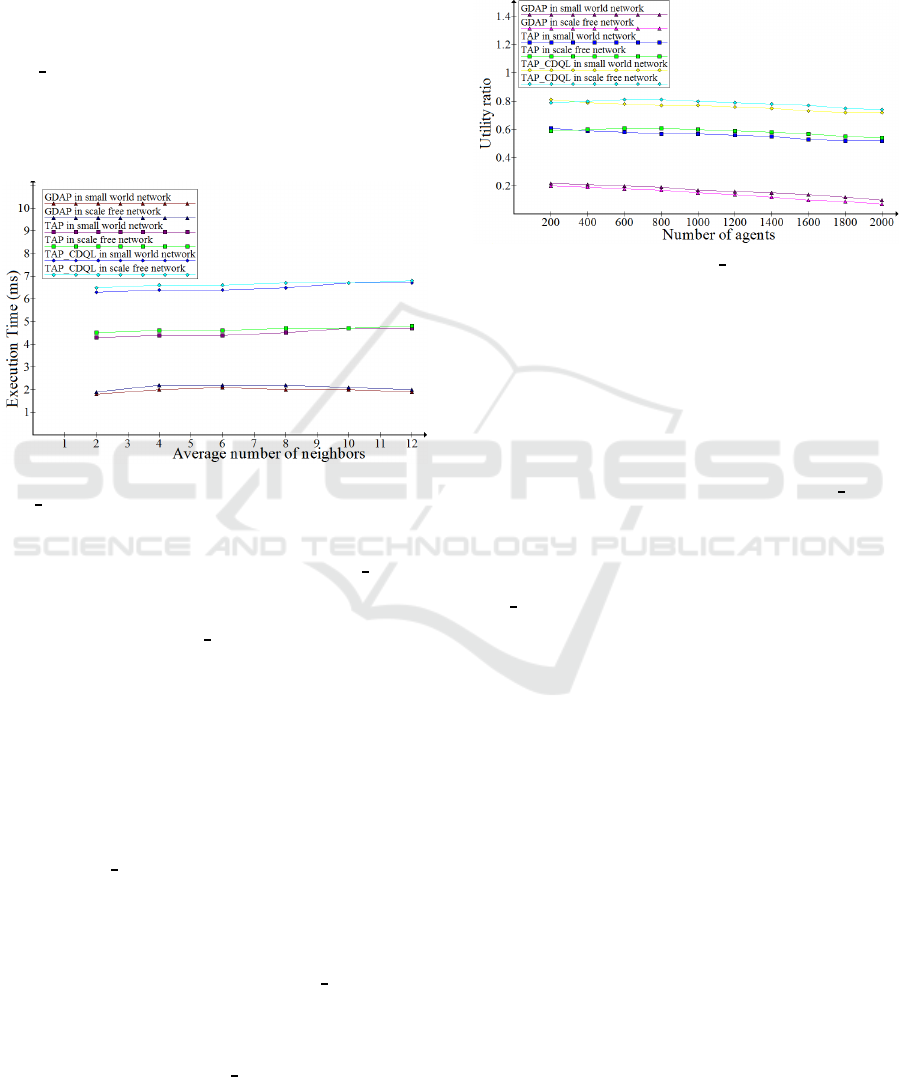
We can mention another factor to compare

approaches which is the network type. The results

of GDAP in a small world network is higher than

in a scale free network, and this is because the

most agents have a very few neighbors in the small

network. In opposite, in the scale free network when

the average number of neighbors increases the GDAP

performance decreases. Therefore, this factor does

not affect the performance of our both algorithm

TAP CDQL and TAP as we take into consideration

enough neighbors to obtain satisfactory resources

for processing its tasks without reallocating tasks

farther and during learning the agents improve the

information delivery process.

Figure 2: The Execution time in millisecond of the

TAP

CDQL, TAP and GDAP depend on the average num-

ber of neighbors in different type of networks.

Figure 2 presents the Execution Time of TAP

CDQL,

TAP and GDAP algorithms in different networks

depend on the average number of neighbors. The

Execution Time of TAP

CDQL and TAP is higher

than that of GDAP since during execution the agents

in our algorithms reallocate tasks when resources

from neighbors are unsatisfying. Furthermore, we

note that the results of GDAP in a small world

network is higher than in a scale free network, but

compared to our algorithms are still lower and this

is because it considers only neighbors which could

decrease the time and communication cost during

task allocation process. Moreover, the Execution

Time of TAP

CDQL is higher than that of TAP and

this is due to the announce message is not broadcast

to all agents but to only the learned agents.

Experiment results and analysis from setting 2: we

would like to test the scalability of TAP

CDQL, TAP

and GDAP in different large network scales like appli-

cations running on the internet. The Figure 3 presents

the Utility Ratio of GDAP which is constantly de-

scending while that our TAP

CDQL, TAP algorithms

can save the stability and it’s higher than GDAP with

the increasing of number of agents and learned agents,

the communication between them based on the learn-

ing and simultaneously the number of tasks in a large

network scale. In fact, we can argue this case by the

rising proportionally of the network scale, the tasks

and the resource types.

Figure 3: The Utility ratio of TAP CDQL, TAP and GDAP

depend on the number of agents in different type of net-

works.

Moreover the condition in small world network is bet-

ter than that in scale free network. And this is justi-

ﬁed by the same reason described above that in scale

free network, several agents only have a few neigh-

bors which is not good for GDAP. Compared with

GDAP, our algorithms is more competitive and it is

beneﬁted from task reallocation but the TAP

CDQL

is much better than TAP in term of the overall goal

achievement and this is by learning which tasks each

agent can allocate, task allocation becomes simpler.

Figure 4 presents the Execution Time of

TAP

CDQL, TAP and GDAP in different network

types. GDAP spends less time when there are more

agents in the network. This is because there are

more tasks despite the average number of neighbors

is ﬁxed. Accordingly, more reallocation steps cannot

be avoided towards allocating these tasks, that leads

to soaring in time and communication overhead. Fur-

thermore, the graphs show that the GDAP and our

approaches almost behave linearly and the time con-

sumption of GDAP keeps a lower level than ours.

This can be supposedly interpreted that GDAP only

relies on neighboring agents.

6 CONCLUSION

In this paper, we propose a task allocation approach

using cooperative Deep Q-Learning improving the

system performance by means of past task allocation

experiences. An important originality of our work is

the use of neural network learning and reinforcement

learning, to which a great attention is payed in this

ICSOFT 2017 - 12th International Conference on Software Technologies

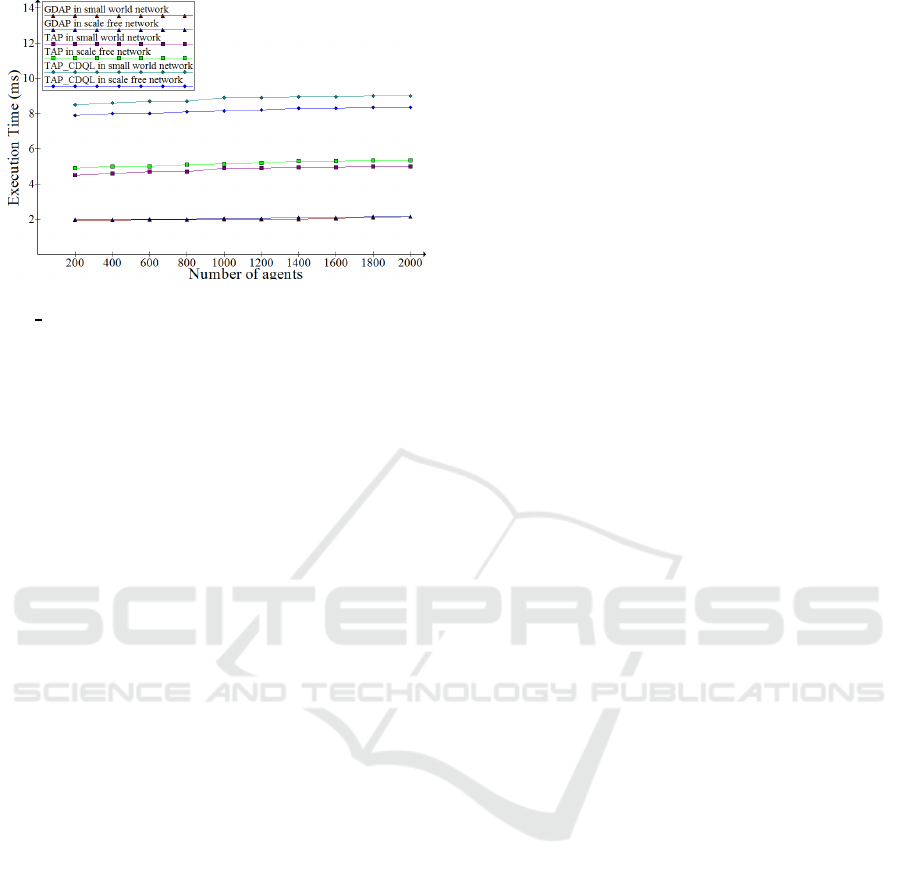
Figure 4: The Execution time in millisecond of the

TAP

CDQL, TAP and GDAP depend on the number of

agents in different type of networks.

paper. Our approach combines a single agent learn-

ing with CommNet which improves the communica-

tion and social cooperation between agents, and con-

sequently the agents’ group performance. It also in-

cludes the increasing of communication knowledge

between agents. This method performs the task allo-

cation policy which enhance the efﬁciency of the sys-

tem. We experimentally show that our approach can

handle the task allocation problem. Although our ap-

proach overcomes some dilemmas, one of the aspects

that we did not fully exploit is its ability to handle het-

erogeneous agent types. Furthermore, due to decen-

tralization and reallocation features, it still has several

deﬁciencies. All these problems will be faced in near

future work, that will focus on assessing the mecha-

nism’s ability to deal with larger state action spaces

than the one exempliﬁed in this paper and review the

performance beneﬁts compared to the heavier-weight

alternative solutions.

REFERENCES

Assael, J., Wahlstrom, N., Schon, T., and Deisenroth,

M. (2015). Data-efﬁcient learning of feedback poli-

cies from image pixels using deep dynamical models.

arXiv preprint arXiv:1510.02173.

Ba, J., Mnih, V., and Kavukcuoglu, K. (2015). Multiple

object recognition with visual attention. In Proc. of

3rd International Conference on Learning Represen-

tations (ICLR2015).

Bellemare, M., Ostrovski, G., A., A. G., Thomas, P. S., and

Munos, R. (2016). Increasing the action gap: New op-

erators for reinforcement learning. In Proc. of Thirti-

eth AAAI Conference on Artiﬁcial Intelligence (AAAI-

16).

Dahl, G. E., Yu, D., Deng, L., and Acero, A. (2012).

Context-dependent pre-trained deep neural networks

for large-vocabulary speech recognition. IEEE Trans-

actions on Audio, Speech, and Language Processing,

20(1):30–42.

Ernst, D., Geurts, P., and Wehenkel, L. (2005). Tree-based

batch mode reinforcement learning. Journal of Ma-

chine Learning Research, pages 503–556.

Gharbi, A., Noureddine, D. B., and Ahmed, S. B. (2017). A

social multi-agent cooperation system based on plan-

ning and distributed task allocation: Real case study.

In under review in Proc.of the 12th International Con-

ference on Evaluation of Novel Approaches to Soft-

ware Engineering (ENASE’17), Porto, Portugal.

Graves, A., Mohamed, A. R., and Hinton, G. E. (2013).

Speech recognition with deep recurrent neural net-

works. In Proc. of IEEE International Conference on

Acoustics, Speech and Signal Processing (ICASSP),

pages 6645–6649.

Guo, X., Singh, S., Lee, H., Lewis, R., and Wang, X.

(2014). Deep learning for real-time atari game play

using ofﬂine monte-carlo tree search planning. In

Proc. of 27th Advances in Neural Information Pro-

cessing Systems (NIPS 2014), pages 3338–3346.

Hasselt, H. V., Guez, A., and Silver, D. (2016). Deep re-

inforcement learning with double q-learning. In Proc.

of Thirtieth AAAI Conference on Artiﬁcial Intelligence

(AAAI-16).

Hausknecht, M. and Stone, P. (2015). Deep recurrent q-

learning for partially observable mdps. arXiv preprint

arXiv:1507.06527.

Heinrich, J. and Silver, D. (2016). Deep reinforce-

ment learning from self-play in imperfect-information

games. arXiv preprint arXiv:1603.01121.

Koutnik, J., Cuccu, G., Schmidhuber, J., and Gomez, F.

(2013). Evolving large-scale neural networks for

vision-based reinforcement learning. In Proc. of 15th

annual conference on Genetic and evolutionary com-

putation, ACM, pages 1061–1068.

Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. Advances in Neural Information Process-

ing Systems, 25:1106–1114.

Levine, S., Finn, C., Darrell, T., and Abbeel, P. (2015). End-

to-end training of deep visuomotor policies. arXiv

preprint arXiv:1504-00702.

Lin, L. (1992). Self-improving reactive agents based on re-

inforcement learning, planning and teaching. Machine

learning, 8(3-4):293–321.

Lin, L. (1993). Reinforcement Learning for Robots Using

Neural Networks. PhD thesis, Carnegie Mellon Uni-

versity, Pittsburgh.

Mnih, V. (2013). Machine Learning for Aerial Image La-

beling, PhD thesis. PhD thesis, University of Toronto.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., and Riedmiller, M.

(2013). Playing atari with deep reinforcement learn-

ing. arXiv preprint arXiv:1312-5602.

Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,

Antonoglou, I., Wierstra, D., Riedmiller, M., Ried-

miller, M., Fidjeland, A. K., Ostrovski, G., Petersen,

S., Beattie, C., Sadik, A., Antonoglou, I., King, H.,

Kumaran, D., Wierstra, D., Legg, S., , and Hassabis,

Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment

D. (2015). Human-level control through deep rein-

forcement learning. Nature, 518(7540):529–533.

Nair, A., Srinivasan, P., Blackwell, S., Alcicek, C., Fearon,

R., Maria, A., Panneershelvam, V. D., Suleyman,

M., Beattie, C., Petersen, S., Legg, S., Mnih, V.,

Kavukcuoglu, K., and Silver, D. (2015). Massively

parallel methods for deep reinforcement learning. In

Proc. of Deep Learning Workshop, ICML.

Oh, J., Guo, X., Lee, H., Lewis, R., and Singh, S. (2015).

Action-conditional video prediction using deep net-

works in atari games. In Proc. of 28th Advances in

Neural Information Processing Systems (NIPS 2015),

pages 2845–2853.

Riedmiller, M. (2005). Neural ﬁtted q iterationﬁrst ex-

periences with a data efﬁcient neural reinforcement

learning method. In Machine Learning: ECML 2005,

Springer, pages 317–328.

Schaul, T., Quan, J., Antonoglou, I., and Silver, D. (2016).

Prioritized experience replay. In Proc. of 5th In-

ternational Conference on Learning Representations

(ICLR).

Sermanet, P., Kavukcuoglu, K., Chintala, S., and LeCun, Y.

(2013). Pedestrian detection with unsupervised multi-

stage feature learning. In Proc. of 26th International

Conference on Computer Vision and Pattern Recogni-

tion (CVPR 2013), IEEE, pages 3626–3633.

Shoham, Y. and Leyton-Brown, K. (2009). Multiagent sys-

tems: Algorithmic, game-theoretic, and logical foun-

dations. Cambridge University Press, New York.

Stadie, B., Levine, S., and Abbeel, P. (2015). Incentivizing

exploration in reinforcement learning with deep pre-

dictive models. arXiv preprint arXiv:1507.00814.

Strens, M. and Windelinckx, N. (2005). Combining plan-

ning with reinforcement learning for multi-robot task

allocation. Adaptive Agents and Multi-Agent Systems

II, 3394:260–274.

Sukhbaatar, S., Szlam, A., and Fergus, R. (2016). Learn-

ing multiagent communication with backpropagation.

In 29th Conference on Neural Information Processing

Systems (NIPS 2016), Barcelona, Spain.

Sutton, R. and Barto, A. (1998). Introduction to reinforce-

ment learning. MIT Press Cambridge.

Tampuu, A., Matiisen, T., Kodelja, D., Kuzovkin, I., Korjus,

K., Aru, J., Aru, J., and Vicente, R.(2015). Multiagent

cooperation and competition with deep reinforcement

learning. arXiv preprint arXiv:1511.08779.

Wang, Z., de Freitas, N., and Lanctot, M. (2015). Dueling

network architectures for deep reinforcement learn-

ing. arXiv preprint arXiv:1511.06581.

Watkins, C. and Dayan, P. (1992). Q-learning. Machine

learning, 8(3-4):279–292.

Watter, M., Springenberg, J. T., Boedecker, J., and

M.A.Riedmiller (2015). Embed to control: A locally

linear latent dynamics model for control from raw im-

ages. In Proc. of 28th Advances in Neural Information

Processing Systems (NIPS 2015).

Weerdt, M., Zhang, Y., and Klos, T. (2007). Distributed

task allocation in social networks. In The Proceedings

of 6th Autonomous Agents and Multi-agent Systems

(AAMAS 2007), Honolulu, Hawaii, USA, pages 500–

507.

Zawadzki, E., Lipson, A., and Leyton-Brown, K. (2014).

Empirically evaluating multiagent learning algo-

rithms. arXiv preprint arXiv:1401.8074.

ICSOFT 2017 - 12th International Conference on Software Technologies