A Virtual Sensor for Integral Tire Force Estimation using Tire
Model-less Approaches and Adaptive Unscented Kalman Filter
Manuel Acosta, Stratis Kanarachos and Michael E. Fitzpatrick
School of Mechanical, Aerospace and Automotive Engineering, Coventry University, Coventry, U.K.
Keywords:
Virtual Sensors, Tire Force Estimation, Unscented Kalman Filter, Adaptive Kalman Filter, Neural Networks.
Abstract:
In this paper, a novel approach to estimate the longitudinal, lateral and vertical tire forces is presented. The
innovation lies a) in the proposition of a modular state estimation architecture that lessens the tuning effort and
ensures the filter’s stability and b) in the estimation of the longitudinal velocity relying only on the wheel speed
information.The longitudinal forces are estimated using an Adaptive Random-Walk Linear Kalman Filter. The
lateral forces per axle are estimated by combining an Adaptive Unscented Kalman filter and Neural Networks.
The individual tire lateral forces are inferred from the axle lateral forces using the vertical load proportionality
principle. The individual tire vertical forces are estimated using a steady-state weight transfer approach, in
which the roll stiffness distribution is considered. The state estimator is implemented in Simulink
R
 and
simulations are carried out in the vehicle dynamics simulation software IPG CarMaker
R
. The virtual sensor
is tested in aggressive and steady-state maneuvers, exhibiting in both cases a remarkable performance.
1 INTRODUCTION
Latest advances found in the literature indicate that
Modern Automotive Control Systems (e.g Drift Con-
trol) will be required to maximize the vehicle safety at
the limits of adhesion (Acosta et al., 2016; Gray et al.,
2012; Velenis et al., 2011; Chakraborty et al., 2011).
In order to guarantee an accurate and robust actua-
tion of these systems, it is necessary to have a precise
knowledge of a large number of vehicle states, such
as the vehicle body slip or the longitudinal wheel slip.
Nevertheless, direct measurement of these signals is
in most situations neither cost-effective nor reliable
and thus state estimation approaches are required.
Despite some attempts found in literature em-
ploying vehicle model-less approaches (Hrgetic et al.,
2011; Klier et al., 2008), the standard methodology to
estimate the vehicle states is to use model-based es-
timation techniques. Depending on the nature of the
analytical equations used to model the vehicle behav-
ior, linear or nonlinear observers are employed. The
Extended Kalman Filter (EKF) and the Unscented
Kalman Filter (UKF) are often used for nonlinear ve-
hicle state estimation (Doumiati et al., 2012), the lat-
ter being most suitable for problems exhibiting strong
nonlinearities (Doumiati et al., 2009). As the vehi-
cle behavior depends greatly on the friction forces
generated by the tires, a precise knowledge of these
forces is required in order to have a reliable estimation
of the vehicle states. Tire force estimation based on
tire models such as the Magic Formula or the Dugoff
model (Pacejka, 2012) has been covered extensively
in the literature (Doumiati et al., 2012; Antonov et al.,
2011; Gao, 2010; Wenzel et al., 2006).
While tire model-based estimation is straightfor-
ward once an accurate tire model is available, the
generation of a precise model is not trivial, and in-
volves extensive experimental testing. Moreover, the
outputs from the model are subjected to uncertainties
due to the influence of other vehicle subsystems (e.g.
elasto-kinematics from the suspension system). In or-
der to overcome these limitations and avoid the neces-
sity of employing a specific tire model, many authors
have focused on tire model-less approaches (Acosta
and Kanarachos, 2016; Hrgetic et al., 2014; Hamann
et al., 2014; Albinsson et al., 2014; Cho et al.,
2010). Tire model-less approaches can be grouped
into stochastic or random-walk (Hrgetic et al., 2014;
Hamann et al., 2014; Cho et al., 2010), open loop (Al-
binsson et al., 2014), and data-based (Acosta and Ka-
narachos, 2016).
When random-walk modeling is employed, the
tire forces are treated as steady-state variables, and
the time evolution of the variable is provided entirely
by the measurement update stage of the filter. In or-
der to achieve a fast response, it is necessary to assign
386
Acosta, M., Kanarachos, S. and Fitzpatrick, M.
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter.
DOI: 10.5220/0006394103860397
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 386-397
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

large weights to the corresponding terms of the pro-
cess covariance matrix (Doumiati et al., 2012), with
the subsequent increase in the noise level of the esti-
mated signal. In this paper, an adaptive process co-
variance matrix handled by a Fuzzy Logic controller
is employed to overcome this issue. In addition, while
other works assume that the vehicle velocity is mea-
surable (e.g. using a GPS system (Hamann et al.,
2014; Baffet et al., 2009)) this variable is inferred
from the wheel rotating speed in this work, and an
adaptive UKF is proposed to limit the effect of the
wheel speed fluctuations during hard braking. The
rest of the paper is structured in the following man-
ner.
In Section 2, relevant background about Kalman
Filtering is provided, and the Linear and Unscented
Kalman Filters are formulated. The structure of the
virtual sensor is described in Section 3, where the
models employed in the vertical, longitudinal and pla-
nar dynamics blocks are presented. Simulation results
are provided in Section 4. Finally, conclusions and
further research steps are discussed in Section 5.
2 BACKGROUND
2.1 Linear Kalman Filter
The state-space formulation is adopted to present the
Linear Kalman Filter (LKF). Thus, a generic linear
system can be expressed by the equations (1-2).
X
k+1
= A
k
X
k
+ B
k
U
k
+ w
k
(1)
Y
k+1
= C
k
X
k
+ v
k
(2)
The terms w
k
and v
k
are the plant and measure-
ment noises respectively, and it is assumed that these
noises can be approximated by a zero mean uncorre-
lated gaussian distribution (3-4).
w
k
≈ N(0,Q
k
) (3)
v
k
≈ N(0,R
k
) (4)
The estimation process is computed in two steps.
First, the time step prediction is performed using the
plant model, (5). At the same time, an initial covari-
ance matrix P
k+1|k
is computed based on the plant
covariance matrix Q, (6).
• Prediction:
ˆ
X
k+1|k
= A
k
ˆ
X
k|k
+ B
k
U
k
(5)
P
k+1|k
= A
k
P
k|k
A
k
T
+ Q
k
(6)
During the second step, the initial estimates
ˆ
X
k+1|k
are corrected using the measurement vector
Y
k
and the Kalman gain K
k+1
.
• Measurement Correction:
K
k+1
= P
k+1|k
H
k
T
[H
k
P
k+1|k
H
k
T
+ R
k
]
−1
(7)
ˆ
X
k+1|k+1
=
ˆ
X
k+1|k
+ K
k+1
[Y
k
− H
k
ˆ
X
k+1|k
] (8)
P
k+1|k+1
= [I− K
k+1
H
k
]P
k+1|k
(9)
Finally, the relative importance of the process
model (prediction step) or the measured variables
(measurement correction) on the estimation is ad-
justed by the selection of the process and measure-
ment covariance matrices Q and R.
2.2 Unscented Kalman Filter
The Unscented Kalman Filter (UKF) is employed in
problems that exhibit strong nonlinearities and has
been exploited in previous works to handle the vehicle
nonlinear behavior (Antonov et al., 2011; Doumiati
et al., 2009). As occurred in the linear case, the state-
space formulation is used, and a generic nonlinear
system is modeled by expressions (10-11).
X
k+1
= f(X
k
,U
k
) + w
k
(10)
Y
k+1
= h(X
k
,U
k
) + v
k
(11)
The filter is based on the Unscented Transforma-
tion (UT), which offers a statistical alternative to the
analytical linearization carried out in the Extended
Kalman Filter (EKF). A small set of deterministically
selected sigma points are propagated through the sys-
tem and the system nonlinearities are inferred from
the statistics of these points. The spread of the sigma
points is determined by the selection of the scaling
parameters α and κ, which are related by expression
(12), (Rhudy and Gu, 2013; Wan and Van Der Merwe,
2000).
λ = α
2
(L+ κ) − L (12)
Where the length of the state vector is denoted by
L. In this paper, the plant and measurement noises
are considered additive, and thus the formulation of
the UKF is reduced to the formulation of the standard
or unaugmented UKF (Rhudy and Gu, 2013). The
matrix of sigma points is formed using the equation
(13), where the number of rows is given by L and the
number of columns corresponds to 2L+ 1.
χ
k
=
h
ˆ
X
k|k
,
ˆ
X
k|k
+
q
ΘP
x,k|k
,
ˆ
X
k|k
−
q
ΘP
x,k|k
i
(13)
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
387

Where Θ is equal to (λ + L). The matrix square
root (
p
P
x,k|k
) is calculated using the Cholesky
method, which calculates a lower triangular matrix
representative of the square root, expression (14).
q
P
x,k|k
q
P
x,k|k
T
= P
x,k|k
(14)
The sigma points are then propagated through the
nonlinear system using equation (15).
X
k+1|k
i
= f(χ
k
i
,U
k
) (15)
After that, the post-transformation mean and co-
variance are calculated using weighted averages, (16-
17).
ˆ
X
k+1|k
=
2L
∑
i=0
η
m
i
X
k+1|k
i
(16)
P
k+1|k
= Q
k
+
+
2L
∑
i=0
η
c
i
(X
k+1|k
i
−
ˆ
X
k+1|k
)(X
k+1|k
i
−
ˆ
X
k+1|k
)
T
(17)
Where the weights η
c
i
and η
m
i
are calculated using
equations (18-20).
η
m
0
=
λ
λ+ L
(18)
η
c
0
= η
m
0
+ 1− α
2
+ β (19)
η
c
i
= η
m
i
=
1
2(L+ λ)
(20)
The parameter β is known as the secondary scal-
ing parameter (Rhudy and Gu, 2013). Similarly, the
matrix of sigma points is propagated through the ob-
servation function (h) using expression (21).
Y
k+1|k
i
= h(χ
k
i
) (21)
The predicted output (
ˆ
Y
k|k
), output covariance
matrix (P
yy
k+1
) and cross-covariance matrix (P
xy
k+1
) are
calculated using equations (22-24).
ˆ
Y
k+1|k
=
2L
∑
i=0
η
m
i
Y
k+1|k
i
(22)
P
yy
k+1
= R
k
+
+
2L
∑
i=0
η
c
i
(Y
k+1|k
i
−
ˆ
Y
k+1|k
)(Y
k+1|k
i
−
ˆ
Y
k+1|k
)
T
(23)
P
xy
k+1
=
2L
∑
i=0
(X
k+1|k
i
−
ˆ
X
k+1|k
)(Y
k+1|k
i
−
ˆ
Y
k+1|k
)
T
(24)
The covariance matrices calculated in the previ-
ous step are then used to compute the Kalman gain
(K
k+1
), equation (25).
K
k+1
= P
xy
k+1
(P
yy
k+1
)
−1
(25)
Finally, the states estimated in the first stage of the
filter are corrected using the expression (26), and the
covariance matrix is updated with equation (27).
ˆ
X
k+1|k+1
=
ˆ
X
k+1|k
+ K
k+1
(Y
k+1
−
ˆ
Y
k+1|k
) (26)
P
k+1|k+1
= P
k+1|k
− K
k+1
P
yy
k+1
K
k+1
T
(27)
3 OBSERVER STRUCTURE
The complete structure of the virtual sensor proposed
in this work is depicted in Fig. 1. A modular ap-
proach is selected in order to achieve a better control
over the individual blocks (longitudinal, vertical, and
lateral force estimation), and avoid the burden of tun-
ing an observer with a large number of states.


... .
Fx estimation (LKF)
Planar dynamics (UKF)
Fy estimation (NN)


Fz estimation (RLS)



y
























Proportionality








.
.
^
^ ^
^
^ ^
^
^
^
^
Figure 1: Modular structure of the virtual sensor for three-
axis tire force and planar dynamics estimation.
The virtual sensor consists of three principal
blocks: vertical force estimation block (Open loop,
steady-state model), longitudinal force estimation
block (Adaptive Linear Kalman Filter), and vehicle
planar dynamics block (Hybrid Neural Networks -
Adaptive Unscented Kalman Filter). The tire nor-
mal forces (F
zi
) are estimated from the longitudi-
nal (a
x
) and lateral (a
y
) accelerations using a quasi-
static weight transfer model, refer to Section 3.1.
A Recursive Least Squares (RLS) block is used to
filter the noise embedded in the signals (Albinsson
et al., 2014). The RLS formulation is omitted due
to space limitations and can be consulted in (Young,
2011). The vertical forces are employed to calculate
the wheel loaded radius (r
i
) using a linear tire stiff-
ness model, refer to Section 3.1.2. The wheel ra-
dius (r
i
), wheel speed (w
i
), master cylinder pressure
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
388

(MC
press
), engine drive torque (T
f
) and transmission
ratio (η
i
) are fed into an Adaptive Random-Walk Lin-
ear Kalman Filter to estimate the individual longitu-
dinal forces (F
xi
). A non-constant process covariance
matrix (Q
LKF
) is used to achieve a trade-off between
dynamic response and noise rejection. The transient
content of the longitudinal dynamics is captured by
monitoring the rate of change of the engine revolu-
tions (Revs) and the rate of change of the brake pedal
position (Pedal
brk
). A Fuzzy Logic controller adjusts
the process covariance matrix (Q
LKF
) based on these
inputs, refer to Section 3.2.1.
The individual longitudinal forces are then
lumped together at each axle and passed through the
planar dynamics block. An important contribution of
this work is that additional instrumentation to mea-
sure the vehicle ”true” velocity (e.g. GPS) is not re-
quired, and the wheel rotating speeds are used instead.
As these signals are not reliable during hard decelera-
tions (wheel-lock) or hard accelerations (wheel-spin),
an adaptive measurement covariance matrix (R
UKF
)
is used to adjust the relative contribution of the pro-
cess model and the measured speeds depending on the
driving situation, refer to Section 3.3.2.
The axle lateral forces (F
yf
,F
yr
) are estimated in
the (UKF) using a data-based approach. These are in-
ferred in a Neural Network structure (NN) from the
vehicle longitudinal acceleration (a
x
) and the axle lat-
eral slips (α
i
). A UKF propagates the modeling un-
certainties through the vehicle planar dynamics model
for estimating the yaw rate (
˙
ψ), longitudinal velocity
(v
x
), and lateral velocity (v
y
). Finally, the individual
lateral forces (F
yi
) are obtained using the vertical load
proportionality principle (Albinsson et al., 2014). In
the following subsections, the details regarding each
block are presented.
3.1 Vertical Force Estimation
A quasi-static weight transfer model is used to esti-
mate the tire vertical loads (28). In this model, the un-
sprung masses and the suspension dynamics are dis-
regarded, and the front and rear roll center heights are
assumed to lie on the ground. Additionally, the road is
considered a completely flat surface, and thus wheel
dynamic loads derived from the road irregularities are
not considered. The lateral weight transfer is assumed
to depend on the roll stiffness at each axle (K
φ
i
), and
the height (h) and the longitudinal position (l
i
) of the
center of gravity.
ˆ
F
z
i, j
= F
zo
i
± ma
x
h
2WB
±
± a
y
mh
K
φ
i
+ mh(WB− l
i
)/WB
tw
i
(K
φ
f
+ K
φ
r
− mh)
(28)
With i ∈ { front,rear} and j ∈ {left,right} . For
further details regarding vertical force modeling, (Py-
lypchuk and Chen, 2014; Doumiati et al., 2012;
Doumiati et al., 2008) can be consulted.
3.1.1 Proportionality Principle
The vertical proportionality principle states that the
forces generated by the tires follow a coulomb fric-
tion law, and thus can be obtained from the prod-
uct of the tire-road friction coefficient and the nor-
mal load. While this approximation does not consider
the load sensitivity (Pacejka, 2012) associated to the
weight transfer, it provides an estimate of the indi-
vidual tire forces with a reasonable accuracy and has
been employed in previous works to calculate the in-
dividual tire lateral forces from the axle forces (Al-
binsson et al., 2014).
ˆ
F
y
i, j
=
ˆ
F
y
i
ˆ
F
z
i, j
ˆ
F
z
i,left
+
ˆ
F
z
i,right
+ Ω (29)
The constant Ω has been added to take into ac-
count the tire asymmetric behavior derivedfrom ”ply-
steer” or tire conicity effects, (Pacejka, 2012).
3.1.2 Loaded Radius
The wheel loaded radius is computed using a linear
vertical stiffness model, expression (30).
ˆr
i, j
= r
o
i
−
F
zo
i, j
−
ˆ
F
z
i, j
K
tire
(30)
Where the tire radius at nominal load (F
zo
i, j
) is de-
noted by r
o
i
, the tire vertical stiffness is K
tire
, and the
tire vertical damping is neglected.
3.2 Longitudinal Force Estimation
The tire longitudinal forces are estimated from the
wheel rotating dynamics, equation (31).
I
tot
˙w = τ− F
x
r− F
z
f
res
r (31)
In this paper, a regular front-wheel-drive vehicle with
an open differential is studied, and a basic drive-
line architecture is considered (Kiencke and Nielsen,
2005). The torsional stiffness, damping, and rotat-
ing inertias of the drive shafts are disregarded. A
perfect coupling between the engine output shaft and
the gearbox input shaft is assumed when the clutch is
fully engaged, and the total driveline inertia (I
tot
) is
calculated using the system of equations (32).
I
tot
=
(
I
w
, clutch = 1
0.5I
eng
η
2
gear
η
2
dif f
+ I
w
, else
(32)
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
389

Where I
w
is the wheel inertia, I
eng
is the engine
inertia, and η
gear
, η
dif f
are the gear and differential
(final drive) ratios respectively. Thus, the total inertia
seen from the wheel is no longer considered constant
(Hamann et al., 2014; Hrgetic et al., 2014) but ad-
justed based on the clutch position.
τ
f
= T
eng
η
gear
η
dif f
− T
brk, f
(33)
τ
r
= −T
brk,r
(34)
The net torque (τ) is calculated as the difference
between the driving and the braking (T
brk
) torques,
expressions (33 - 34). Concerning the latter term, a
proportional model based on the brake force distribu-
tion is employed (Hamann et al., 2014; Hrgetic et al.,
2014), expressions (35-36).
T
brk, f
= K
f
P
f
(35)
T
brk,r
= K
r
P
r
(36)
The constants K
f
and K
r
are proportional gains
that transform the brake pressure into braking torque,
and account for the friction between the brake pad
and the disc, and net braking force application point
among other factors. The wheel rotating dynamics
equation is written in state-space form using expres-
sions (37-39),
˙x
1
=
u
1
− x
2
r− F
z
f
res
r
I
tot
(37)
˙x
2
= 0 (38)
y = x
1
(39)
with the vector of states formed by the wheel speed
and the longitudinal force (x = {w, F
x
}), the former
being the unique system output (y). The net torque
is the input to the system (u = {τ}), and the verti-
cal force necessary to compute the rolling resistance
is introduced as a disturbance input (d = {F
z
}). The
rolling resistance coefficient is denoted by f
res
, and
is considered constant for simplicity. The loaded ra-
dius and total driveline inertia are modeled as time-
varying parameters. Finally, the estimation of the sys-
tem states is carried out using the linear Kalman Filter
presented in Section 2.1.
3.2.1 Adaptive Process Covariance Matrix
The state-space formulation presented in the previous
subsection treats the longitudinal force as a random-
walk variable (˙x = 0). This approach assumes that
the variable remains constant during the time update
stage of the filter, and relies entirely on the mea-
surement update stage to determine how the vari-
able evolves in time. If the fast convergence of
the random-walk variable is required during transient
situations (e.g. hard braking) the process covari-
ance terms must be assigned large weights (i.e. the
assumption of quasi-static longitudinal forces is no
longer valid). On the other hand, during steady-state
situations in which the rate of change of the longitudi-
nal forces is reduced (e.g. coast down), lower values
of the process covariance matrix are preferred in order
to reduce the noise level.
6
8
4
2
Q (2,2)
x10
4
0
50
100
150
200
0
0.5
1
 
!"#
 $
 %evs
 $
0
1
0.5 1
0
1
1e3
1
 
!"#
 $
 Revs
 $
200500
0
1e51e4
0
(rad/s
2
)
(1/s)
L
H
Q (2,2)
L
H
Q
Low
Q
High
 %evs
 $
 
!"#
 $
Q
High
Q
High
Q
High
H
H
L
L Q
Low
Figure 2: Fuzzy Logic Controller to handle the adaptive
process covariance matrix based on the positive rate of
change of the engine revolutions (rad/s
2
) and the rate of
change of the normalized brake pedal position (1/s).
An adaptive process covariance matrix is pro-
posed to use the most appropriate values during each
situation using a Fuzzy Logic Controller, Fig. 2.
During constant speed situations in which the rate of
change of the brake pedal is null and the engine rev-
olutions remain constant, the second term of the pro-
cess covariance matrix is assigned low values. When
the engine revolutions increase abruptly (full throt-
tle) or the brake pedal position varies (braking force
build-up) the second term of the process covariance
matrix is increased to achieve fast convergence of the
random-walk force, Section 4.1.
3.2.2 Wheel Lock
In this paper, the braking torque is modeled as a static
torque, and thus the wheel rotating dynamics expres-
sion is not suitable to estimate the longitudinal forces
during severe wheel lock (the wheel rotating speed
remains zero, and does not accelerate in the opposite
direction). During these situations, the tire slides on
the road, and the tire longitudinal force can be ap-
proximated by the product of the vertical load and the
friction coefficient (40).
F
x,lock
= µ
dyn
F
z
(40)
Where the dynamic friction coefficient (µ
dyn
) can
be calculated from the longitudinal acceleration and
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
390

the vehicle mass. The expression (41) is used to han-
dle wheel locking situations,
ˆ
F
x
= (1−W)
ˆ
F
x,rot
+W
ˆ
F
x,lock
(41)
where the factor W is null while the wheel rotating
speed is above a certain threshold, and is unity when
this threshold is passed. A more sophisticated strategy
can be used to avoid excessive chattering if continu-
ous wheel locking is expected (e.g. drivingon gravel).
3.3 Lateral Force Estimation
The lateral forces are estimated using a vehicle planar
dynamics model, expressed in state-space form by the
equations (42 - 44).
˙
γ
1
=
1
m
(ζ
2
cos(ζ
1
) − F
yf
sin(ζ
1
) + ζ
3
) + γ
2
γ
3
(42)
˙
γ
2
=
1
m
(F
yf
cos(ζ
1
) + ζ
2
sin(ζ
1
) + F
yr
) − γ
1
γ
3
(43)
˙
γ
3
=
1
I
ψ
(F
yf
cos(ζ
1
)l
f
+ ζ
2
sin(ζ
1
)l
f
− F
yr
l
r
) (44)
The vehicle mass is denoted by (m), the yaw in-
ertia by (I
ψ
), and the distances from the front and
rear axles to the center of gravity by (l
f
,l
r
). The
angle steered by the front wheels and the estimated
axle longitudinal forces are the inputs to the system
(ζ
ζ
ζ = {δ,
ˆ
F
xf
,
ˆ
F
xr
}). The state vector is formed by the
yaw rate, longitudinal velocity, and lateral velocity
(γ
γ
γ = {
˙
ψ,v
x
,v
y
}). The axle lateral forces are calculated
using the nonlinear tire-road friction function (45).
F
y
= f(α,a
x
) (45)
This expression depends on the longitudinal ac-
celeration and the axle wheel slips, which are calcu-
lated using a small angle approximation (Kanarachos,
2012) with expressions (46-47).
α
f
= δ−
γ
1
l
f
+ γ
3
γ
2
(46)
α
r
=
−γ
3
+ γ
1
l
r
γ
2
(47)
Finally, equations (42-47) are integrated into an
UKF using the formulation presented in Section 2.2.
3.3.1 Neural Networks
The axle lateral forces F
y
are estimated by a Neural
Networks structure, Fig. 3. The longitudinal accel-
eration is used in the NN structure in order to predict
the reduction in the lateral force during combined lon-
gitudinal and lateral excitation (force coupling), thus
permitting an accurate vehicle state estimation in non-
constant speed events (e.g. braking in a turn). At each
time step, the UKF sigma-points are generated and
the sigma axle slips are formed. These sigma axle
slips are propagatedthrough the NN to handle the tire-
road friction nonlinearities and the sigma-axle lateral
forces are obtained and re-injected into the UKF.
NN (Fy Estimation)
... .
UKF Observer



{, !}
"{#, 
$
}
%
$&
'{!,(
$
, (

}
^

)

*
(1-10-1 Static NN)
%
$
%
$

)

*
^
^
^
.
.
Figure 3: Unscented Kalman Filter for lateral force estima-
tion.
The datasets necessary to train the NN structure
were generated in IPG-CarMaker
R
 using an experi-
mentally validated compact-class vehicle model and a
state-of-the-art Magic Formula 6.1 tire model (Pace-
jka, 2012). Open Loop aggressive maneuvers (Step
steer) covering different longitudinal acceleration lev-
els (Braking, Power On) were simulated for this pur-
pose. Finally, the NN were trained in Matlab
R
 us-
ing the Levenberg-Marquardt backpropagation algo-
rithm and a 70/15/15% dataset division was selected
after performing a sensitivity analysis. The stability
of the NN structure was studied following the method-
ology described in (Belic, 2012). For further details,
(Acosta and Kanarachos, 2016) can be consulted.
3.3.2 Adaptive Measurement Covariance Matrix
In the UKF described in this section, it is assumed that
the longitudinal velocity measured using a GPS sys-
tem is not available, and only the wheel speed signals
can be used as a reliable measurement. Nevertheless,
the wheel speed signals do not represent accurately
the real vehicle velocity during hard braking or ag-
gressive accelerations. In order to adjust the relative
importance given to the process model or the mea-
sured wheel speeds, the measurement covariance ma-
trix is varied according to the master cylinder pressure
signal (MC
press
). During driving or coast down situa-
tions, the reference velocity is calculated as the aver-
age of the non-driven(rear) wheels. Conversely, when
braking occurs and the speed calculated from the non-
driven wheels is prone to fluctuation (MC
press
above
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
391

a certain threshold), the second diagonal term of the
matrix R
UKF
is increased, and the relative importance
given to the measured wheel speeds is reduced. Dur-
ing the following stages of this research, it is intended
to evaluate the suitability of this approach in estimat-
ing the reference speed (v
x
) required to compute the
wheel longitudinal slips, which is particularly difficult
in all-wheel-drive systems during off-road driving.
4 RESULTS
The state estimator was constructed in Simulink
R
 and
integrated into the vehicle dynamics simulation soft-
ware IPG-CarMaker
R
. The discretization time was
set to 1ms, and the measurable quantities were ac-
quired at a frequency of 100Hz using a zero-order
hold block. An additive white gaussian noise model
was used to incorporate the uncertainties associated
with the measurement equipment in the simulation
signals, (RaceLogic, 2015; Bosch, 2006), Table 1.
An experimentally validated model representative of
a compact-class vehicle and a Magic Formula 6.1 tire
model were employed during the simulations.
Table 1: Standard deviation of the noises added to the sim-
ulation signals.
σ
˙
ψ
(rad/s)
σ
a
x
(m/s
2
) σ
a
y
(m/s
2
)
0.002 0.01 0.01
σ
w
(rad/s) σ
T
f
(Nm)
σ
MC
press
(bar)
0.1 1 1.82
The parameters of the virtual sensor are detailed in
Table 2. The suspension parameters were determined
in a series of steady-state Slow Increasing Steer tests.
Table 2: Virtual Sensor parameters.
l
f
(m) l
r
(m) m(kg)
0.95 1.54 1200
I
w
(kgm
2
) I
eng
(kgm
2
) t
wf
(m)
1.05 0.064 1.45
K
φ, f
(KNm/rad) K
φ,r
(KNm/rad) t
wr
(m)
31.74 29.30 1.45
I
ψ
(kgm
2
) f
res
(−) h(m)
1668 0.01 0.66
A preliminary tuning of the UKF and LKF was
carried out manually based on a systematic trial and
error method. An optimized version of this observer
will be presented in the future employing Swarm In-
telligence optimization routines (Kanarachos et al.,
2016). In the following, the results obtained with the
preliminary virtual sensor are presented.
4.1 Driving / Braking Tests
The tests performed in Table 3 were simulated to eval-
uate the performance of the virtual sensor under lon-
gitudinal excitation.
Table 3: Acceleration and Braking tests. FA
∗
: Full Accel-
eration, GB
∗
: Gentle Braking, PB
∗
: Partial Braking, HB
∗
:
Hard Braking.
Test Initial speed Drv/Brk
∗
#1 Acceleration 20kph FA
#2 Braking 150kph GB/PB/HB
The results concerning the acceleration test (#1)
are depicted in Fig. 4. The vehicle accelerates hard in
a straight line from first to sixth gear. The estimation
of the individual longitudinal forces carried out by the
LKF blocks is very precise and the estimated signals
track very well the longitudinalforce fluctuations dur-
ing gear shifting. As a front-wheel-drive vehicle is
employed during the simulations, the contribution of
the rear forces is null during the entire test. Finally,
a slight offset appears in the longitudinal velocity at
high speed due to the aerodynamic drag, which is
not considered in the vehicle longitudinal equilibrium
equation (42). Despite this, the overall performance
of the observer is remarkable, and the longitudinal
velocity is well approximated by the UKF. A com-
parison between the state estimator behavior using a
constant or a time-varying process covariance matrix
is shown in Fig. 5.
5
F
x
FL (KN)F
x
FR (KN)
0
-5
5
0
-5
F
x
RL (KN)
5
0
-5
F
x
RR (KN)
5
0
-5
0 20 3010
time (s)
IPG Signal Estimation
vx (m/s)
50
0
Figure 4: Longitudinal forces and longitudinal velocity
(Test #1).
The details regarding the adaptive process covari-
ance matrix were covered in Section 3.2.1. As can be
observed, the LKF tracks with high precision the sim-
ulation signal when the term Q
LKF
(2,2) is assigned
high values, with the side effect of a high noise level.
On the other hand, the noise level is reduced with a
low covariance value, but the dynamic response of the
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
392

Q
LKF
(2,2)
100
1
RPM (x1000)
4
2
0 20 3010
time (s)
6
x10
3
F
x
FL (KN)
5
-5
Q
LKF
(2,2) Large
Q
LKF
(2,2) Adaptive
Q
LKF
(2,2) Small
IPG signal
Figure 5: Comparison between constant and adaptive pro-
cess covariance matrix (Test #1).
random-walk signal is very poor, and the convergence
to the simulation signal is very slow. Thus, the adap-
tive matrix presents the best trade-off between noise
rejection and dynamic response.
5
F
x
FL (KN)F
x
FR (KN)
0
-5
5
0
-5
F
x
RL (KN)
5
0
-5
F
x
RR (KN)
5
0
-5
0 10 155
time (s)
IPG Signal Estimation
vx (m/s)
50
0
Figure 6: Longitudinal forces and longitudinal velocity
(Test #2).
The results of the braking test (#2) are presented
in Fig. 6. The vehicle circulates in a straight line at
high speed, and a sequence of braking events (gentle,
partial, hard) is performed. Although some offset is
seen in the last braking input (t ≈ 14 − 16s) the es-
timation of the longitudinal forces performed by the
LKF is remarkable, and the longitudinal velocity is
approximated with high accuracy by the UKF. This
offset is caused by the wheel locking phenomena, in
which the wheel rotating dynamics equations are no
longer valid, and the longitudinal force is the product
of the vertical force and the friction coefficient.
In order to evaluate the performance of the adap-
tive UKF, a comparison between the constant and
adaptive measurement covariance term (R
UKF
(2,2))
is depicted in Fig. 7. If a high value is selected, the
UKF uses predominantly the longitudinal dynamic
equilibrium equation to compute the longitudinal ve-
locity, and any mismatch in the longitudinal forces
estimated by the LKF is reflected in the longitudinal
R
UKF
(2,2)
100
1
MC
press
(bar)
50
0
0 10 155
time (s)
100
x10
2
vx (m/s)
50
0
R
UKF
(2,2) Large
R
UKF
(2,2) Adaptive
R
UKF
(2,2) Small
IPG signal
Figure 7: Comparison between constant and adaptive mea-
surement covariance matrix (Test #2).
speed estimate (constant offset in the green curve).
On the other hand, if a lower value is used (violet
trace), the UKF relies more on the rear wheel speed
and does not approximate well the real longitudinal
speed during hard braking events in which abrupt
wheel speed fluctuations occur. The adaptive strategy
approximates with high accuracy the real longitudi-
nal speed in spite of the wheel speed fluctuations or
the model uncertainties.
4.2 Vehicle Dynamics Tests
The tests presented in Table 4 were simulated to test
the performance of the virtual sensor under combined
longitudinal and lateral excitation.
Table 4: Braking-in-a-turn (BIT) and ADAC Lane Change
(LC) tests. CD
∗
: Coast down, PB
∗
: Partial Braking.
Test Init. speed A
y
Drv/Brk
∗
#3 ADAC LC 95kph Limit CD
#4 BIT 60kph Limit PB
For simplicity, active systems such as Anti-lock
Braking System (ABS), Electronic Stability Program
(ESP) or Electronic Brakeforce Distribution (EBD)
are not considered in this work. The interaction of the
state estimator with these systems will be addressed
in future stages of this research.
The tire forces estimated during the execution of
the Allgemeiner Deutscher Automobil-Club (ADAC)
Lane change (#3) are portrayed in Fig. 8. This test
is executed in coast down conditions, and thus the
tires do not generate significant longitudinal forces.
The lateral forces predicted by the virtual sensor fol-
low closely the simulation signals, what indicates the
suitability of the vertical proportionality principle to
infer the individual lateral forces from the axle lat-
eral forces. Concerning the normal forces, some dis-
crepancies are observed in the estimates of the front
axle (t ≈ 21s). The maximum offset occurs during
the second gate of the lane change, during which the
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
393

10
F
y
FL (KN)
0
-10
10
5
0
IPG Signal Estimation
10
F
y
FR (KN)
0
-10
10
F
y
RL (KN)
0
-10
10
F
y
RR (KN)
0
-10
F
z
FL (KN)
10
5
0
F
z
FR (KN)
10
5
0
F
z
RL (KN)
10
5
0
F
z
RR (KN)
5
0
F
x
FL (KN)
-5
5
0
F
x
FR (KN)
-5
5
0
F
x
RL (KN)
-5
5
0
F
x
RR (KN)
-5
time (s) time (s)
18 20 22 24 18 20 22 24
Figure 8: Lateral (F
y
), Vertical (F
z
), and Longitudinal (F
x
)
tire forces estimated during the simulation of the ADAC
Lane Change Test.
1
yawR (rad/s)vx (m/s)
0
-1
50
0
vy (m/s)
5
0
-5
18 22 2420
time (s)
IPG Signal Estimation
Figure 9: Yaw rate (
˙
ψ), longitudinal velocity (v
x
), and lat-
eral velocity (v
y
) estimated during the simulation of the
ADAC Lane Change test.
lateral weight transfer is maximum and the axle roll
stiffness may change due to the contribution of the
bump stops. In addition, wheel lift is observed in the
rear inner wheel (F
z,RR
) at this point. The vehicle mo-
tion states computed by the UKF are presented in Fig.
9. Overall, the estimation of the lateral velocity is re-
markable, and the large lateral slide that occurs during
the second gate (t ≈ 20− 22s) is approximated by the
observer with high accuracy.
The results obtained in the Braking-in-a-turn test
(#4) are presented in Figures (10-11). In this test, the
vehicle accelerates steadily following a left-handed
turn (R = 100m). The estimation of the vehicle states
is particularly difficult in these conditions due to the
low dynamic content of the maneuver, and thus an in-
significant error can contribute after some seconds to
generate a large drift in the estimated signals. In this
case, the latter issue is not observed, and the forces
generated by the tires are approximated very well by
10
F
y
FL (KN)
0
-10
10
5
0
IPG Signal Estimation
10
F
y
FR (KN)
0
-10
10
F
y
RL (KN)
0
-10
10
F
y
RR (KN)
0
-10
F
z
FL (KN)
10
5
0
F
z
FR (KN)
10
5
0
F
z
RL (KN)
10
5
0
F
z
RR (KN)
5
0
F
x
FL (KN)
-5
5
0
F
x
FR (KN)
-5
5
0
F
x
RL (KN)
-5
5
0
F
x
RR (KN)
-5
time (s) time (s)
0 5 10 15
0 5 10 15
Figure 10: Tire forces estimated in the Braking-in-a-turn
test.
0.5
yawR (rad/s)
vx (m/s)
0
50
0
vy (m/s)
2
0
-2
14 16 1715
time (s)
IPG Signal Estimation
BRK
MC
press
(bar)
50
0
BRK
18
Figure 11: Vehicle motion states estimated in the Braking-
in-a-turn test.
the virtual sensor. The tires of the outer side (front
right, rear right) generate the majority of the lateral
force due to the positive weight transfer. The lon-
gitudinal force estimates track well the gear shifting
(t ≈ 2.5, t ≈ 12.5) events during the vehicle accelera-
tion. At t = 15s, a partial braking input is introduced
with the aim to excite the lateral dynamics and gen-
erate some instability in the vehicle. Due to the com-
bination of high speed and high lateral force, the yaw
damping of the vehicle is reduced in these circum-
stances, and the yaw dynamics exhibit an oscillatory
response when the brakes are applied gently Fig. 11.
During the braking action, the lateral forces are
diminished due to the force coupling, and the vehicle
slides laterally to the outer side of the turn. In ad-
dition, the axle lateral forces do not decrease in the
same proportion, and a slight overshoot in the yaw
rate is observed. Overall, the precision of the UKF is
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
394

remarkable, and the lateral velocity is approximated
accurately during the initial part of the test (steady-
state) and after the application of the braking input
(transient).
4.3 Metrics
Finally, in order to quantify numerically the preci-
sion of the virtual sensor, the normalized root means
square (NRMS), expression (48), and the root means
square (RMS) of the estimation error were computed
for the tire forces and the vehicle states (Acosta et al.,
2016; Doumiati et al., 2012).
e = 100
∑
N
k=1
p
( ˆy
k
− y
k
)
2
max(|y|)
1
N
(48)
Where ˆy
k
is the estimated signal and y
k
is the real
signal obtained from the simulation model. The nu-
merical values corresponding to the vehicle states are
provided in Table 5. The spaces corresponding to the
NRMS have been left blank when the level of excita-
tion is null and expression (48) presents a singularity.
Table 5: NRMS and RMS error of the vehicle states.
Test e
˙
ψ
(%)
e
vx
(%) e
vy
(%)
#1 - 1.59 -
#2 - 0.99 -
#3 1.63 1.04 1.31
#4 3.39 1.22 1.92
Test σ
˙
ψ(rad/s)
σ
vx
(m/s) σ
vy
(m/s)
#1 0.01 0.63 0.02
#2 0.01 0.41 0.02
#3 0.01 0.28 0.04
#4 0.01 0.31 0.03
Table 6: NRMS and RMS error of the lateral forces.
Test e
FyFL
(%) e
FyFR
e
FyRL
e
FyRR
#1 - - - -
#2 - - - -
#3 2.42 2.88 2.52 3.34
#4 18.27 3.73 23.84 4.92
Test σ
FyFL
(N) σ
FyFR
σ
FyRL
σ
FyRR
#1 72.34 73.56 152.33 86.59
#2 69.54 65.34 99.64 91.22
#3 153.14 119.18 101.31 135.47
#4 172.08 162.14 95.52 140.99
The states are accurately estimated by the UKF,
and the NRMS values keep below the 5% threshold
for all the tests performed. The errors of the individ-
ual tire lateral forces are presented in Table 6. Max-
imum NRMS values are seen in the tires of the inner
side (FL, RL) during the execution of the Braking-
in-a-turn Test (#4). As these tires are unloaded and
develop low lateral forces the NRMS metric tends to
magnify the signal error. The accuracy of the virtual
forces is very precise and values below the 5% thresh-
old are observed in the forces generated by the outer
tires. The errors obtained for the individual longitu-
dinal tire forces are detailed in Table 7. Maximum
NRMS errors are noticed during moments of low lon-
gitudinal excitation (e.g. coast down or free-rolling
in the rear axle). When the longitudinal force is high
(front axle during test #1, four wheels during test #2)
the error level remains less than 10 percent.
Table 7: NRMS and RMS error of the longitudinal forces.
Test e
FxFL
(%) e
FxFR
e
FxRL
e
FxRR
#1 7.52 7.52 22.25 22.25
#2 5.34 5.35 3.66 3.81
#3 11.26 13.24 36.86 8.90
#4 6.68 6.63 7.69 2.30
Test σ
FxFL
(N) σ
FxFR
σ
FxRL
σ
FxRR
#1 211.03 211.17 19.96 19.98
#2 204.93 205.02 39.90 41.47
#3 39.26 36.81 22.59 23.52
#4 90.18 90.03 55.12 12.93
Finally, the errors corresponding to the vertical
tire forces are detailed in Table 8. Overall, the estima-
tion errors are acceptable, and the open loop weight-
transfer block performs well in both steady-state and
transient situations.
Table 8: NRMS and RMS error of the vertical forces.
Test e
FzFL
(%) e
FzFR
e
FzRL
e
FzRR
#1 3.57 3.54 2.76 2.79
#2 3.13 3.10 4.37 4.34
#3 3.38 3.79 3.37 3.49
#4 5.28 1.39 2.54 1.89
Test σ
FzFL
(N) σ
FzFR
σ
FzRL
σ
FzRR
#1 136.33 135.17 82.19 83.12
#2 171.59 169.95 113.19 112.39
#3 232.99 250.48 144.90 161.80
#4 192.67 84.07 61.70 79.13
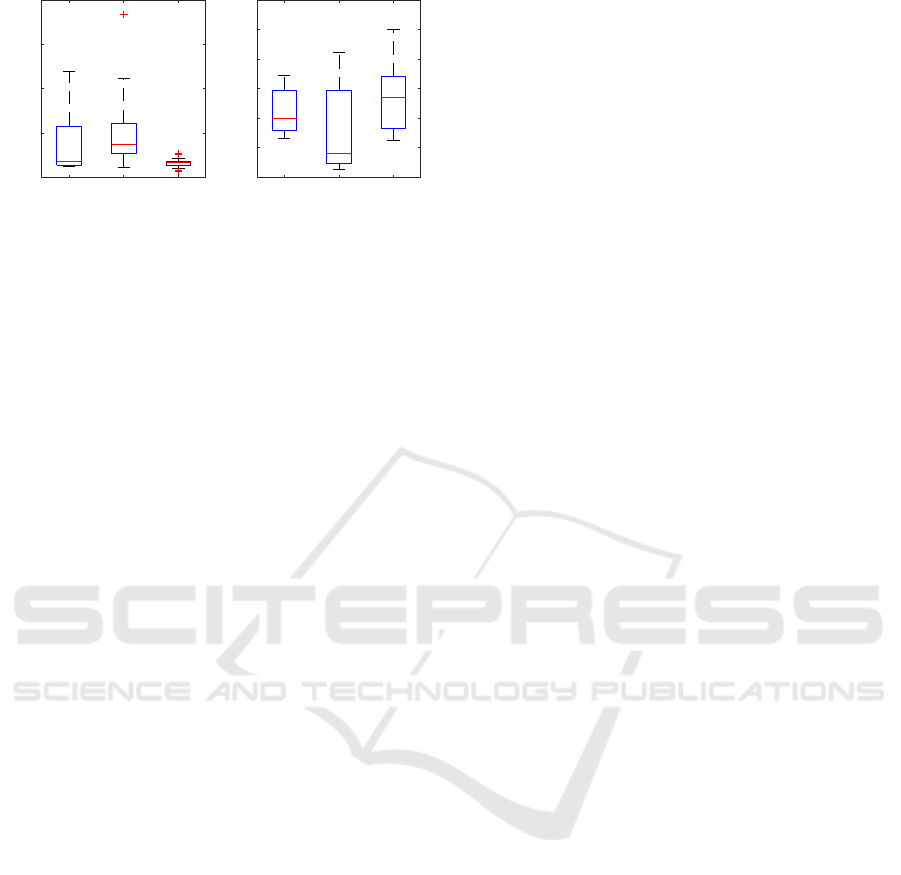
The boxplots of the NRMS and RMS tire force
errors are depicted in Fig. 12. The large whiskers
show some dispersion in the NRMS error of the lon-
gitudinal and lateral forces due to the influence of the
tests in which low excitation occur (e.g. longitudinal
forces during ADAC lane change). Values found in
the literature for the NRMS error range from 5% to
10% (Doumiati et al., 2012; Hamann et al., 2014),
for Slalom and Lane Change maneuvers. In these
works, additional assumptions such as the availabil-
ity of a valid tire model (Doumiati et al., 2012), or the
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
395

300
250
200
150
100
50
0






RMS (N)






0
10
20
30
NRMS (%)
40
Figure 12: Box plots of the estimated tyre forces.
calculation of the lumped axle forces and the mea-
surement of the longitudinal velocity (Hamann et al.,
2014) have been considered. Error metrics have not
been provided in other related works (Hrgetic et al.,
2014), limiting the possibility of establishing a more
detailed performance comparison.
5 CONCLUSIONS
In this paper, a virtual sensor to predict the friction
forces developed by each tire and the principal vehi-
cle planar states has been presented. Individualblocks
to estimate the three-axis tire forces are integrated fol-
lowing a modular approach to form the complete state
estimator structure. As tire model-less approaches are
used in the observer, precise a priori knowledge about
the tire friction characteristics is not necessary. A
stochastic approach is used to estimate the tire forces
in the longitudinal direction by means of a random-
walk adaptive Linear Kalman filter, whereas a data-
based approach is used to estimate the axle lateral
forces. The nonlinear tire-road interactions in the
lateral direction are captured by a Neural Networks
structure. Finally, the individual tire lateral forces are
obtained applying the vertical proportionality princi-
ple, and the tire normal forces necessary for this are
computed using a steady-state open-loop observer.
An important contribution of this work is the
use of adaptive covariance matrices to improve the
performance of the Kalman Filters. A good trade-
off between noise rejection and dynamic response is
achieved in the random-walk Linear Kalman Filter
using an adaptive process covariance matrix handled
by a simple Fuzzy logic controller. Concerning the
vehicle planar dynamics block, an adaptive measure-
ment covariance matrix is employed in the Unscented
Kalman filter to improve the accuracy of the longitu-
dinal velocity inferred from the wheel speed, thus lim-
iting the negative influence of the wheel speed fluctu-
ations and avoiding the use of additional instrumenta-
tion (e.g. GPS).
The graphs and numerical results presented in this
paper demonstrate the remarkable performance of the
virtual sensor under combined excitation in the longi-
tudinal and lateral directions. Moreover, the state es-
timator approximates very well the vehicle states not
only under high dynamic excitation but also during
steady-state situations. The refinement of the verti-
cal force estimation block in addition to an optimal
tuning of the observer parameters using Swarm In-
telligence algorithms will be pursued during the next
stages of this research.
ACKNOWLEDGEMENTS
This project is part of the Interdisciplinary Train-
ing Network in Multi-Actuated Ground Vehicles
(ITEAM) European program and has received fund-
ing from the European Unions Horizon 2020 research
and innovation program under the Marie Skodowska-
Curie grant agreement No 675999. M. E. Fitzpatrick
is grateful for funding from the Lloyds Register Foun-
dation, a charitable foundation helping to protect life
and property by supporting engineering-related edu-
cation, public engagement and the application of re-
search.
REFERENCES
Acosta, M. and Kanarachos, S. (2016). Tire lateral force
estimation and grip potential identification using neu-
ral networks, extended kalman filter, and recursive
least squares. Neural Computing and Applications,
Springer, pages 1–21.
Acosta, M., Kanarachos, S., and Blundell, M. (2016). Agile
maneuvering: From rally drivers to a finite state ma-
chine approach. In IEEE Symposium Series on Com-
putational Intelligence.
Albinsson, A., Bruzelius, F., Jonasson, M., and Jacobson,
B. (2014). Tire force estimation utilizing wheel torque
measurements and validation in simulations and ex-
periments. In Proceedings of the 12th International
Symposium on Advanced Vehicle Control.
Antonov, S., Fehn, A., and Kugi, A. (2011). Unscented
Kalman filter for vehicle state estimation. Vehicle Sys-
tem Dynamics, 49(9):1497–1520.
Baffet, G., Charara, A., and Lechner, D. (2009). Estima-
tion of vehicle sideslip, tire forces and wheel corner-
ing stiffness. Control Engineering Practice, 17:1255–
1264.
Belic, I. (2012). Neural networks and static modeling.
Recurrent Neural Networks and Soft Computing, Dr.
Mahmoud ElHefnawi.
Bosch (2006). Hochdrucksensor Produktinformation.
Chakraborty, I., P.Tsiotras, and Lu, J. (2011). Vehicle pos-
ture control through aggressive maneuvering for mit-
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
396

igation of t-bone collision. In IEEE Conference on
Decision and Control.
Cho, W., Yoon, J., Yim, S., Koo, B., and Yi, K. (2010). Esti-
mation of tire forces for application to vehicle stability
control. IEEE Transactions on Vehicular Technology,
59(2):638–649.
Doumiati, M., Charara, A., Victorino, A., and Lechner, D.
(2012). Vehicle Dynamics Estimation using Kalman
Filtering. Wiley-ISTE.
Doumiati, M., Victorino, A., Charara, A., Baffet, G., and
Lechner, D. (2008). An estimation process for vehi-
cle wheel-ground contact normal forces. In IFAC pro-
ceeding Volumes.
Doumiati, M., Victorino, A., Charara, A., and Lech-
ner, D. (2009). Estimation of vehicle lateral tire-
road forces: A comparison between extended and
unscented kalman filtering. In Control Conference
(ECC).
Gao, X. (2010). Nonlinear estimation of vehicle sideslip
angle based on adaptive extended kalman filter. SAE
Technical Papers.
Gray, A., Gao, Y., Lin, T., Hedrick, K., Tseng, H., and
Borrelli, F. (2012). Predictive control for agile semi-
autonomous ground vehicles using motion primitives.
In American Control Conference.
Hamann, H., Hedrick, J., Rhode, S., and Gauterin, F.
(2014). Tire force estimation for a passenger vehicle
with the unscented kalman filter. In IEEE Intelligent
Vehicles Symposium.
Hrgetic, M., Deur, J., Ivanovic, V., and Tseng, E. (2014).
Vehicle sideslip angle ekf estimator based on nonlin-
ear vehicle dynamics model and stochastic tire forces
modeling. SAE International Journal of Passenger
Cars - Mechanical Systems.
Hrgetic, M., Deur, J., Pavkovic, D., and Barber, P. (2011).
Adaptive ekf-based estimator of sideslip angle us-
ing fusion of inertial sensors and gps. SAE Interna-
tional Journal of Passenger Cars - Mechanical Sys-
tems, 4(1):700–712.
Kanarachos, S. (2012). A new min-max methodology for
computing optimised obstacle avoidance steering ma-
neuvers of ground vehicles. International Journal of
Systems Science, (45):1042–1057.
Kanarachos, S., Griffin, J., and Fitzpatrick, M. (2016). Effi-
cient truss optimization using the contrast-based fruit
fly optimization algorithm. Computers and Structures,
(182):137–148.
Kiencke, U. and Nielsen, L. (2005). Automotive Control
Systems: For engine, driveline, and Vehicle. Springer.
Klier, W., Reim, A., and Stapel, D. (2008). Robust estima-
tion of vehicle sideslip angle – an approach w/o vehi-
cle and tire models. In Proceedings of the SAE World
Congress.
Pacejka, H. (2012). Tire and Vehicle Dynamics.
Butterworth-Heinemann.
Pylypchuk, V. and Chen, S. (2014). Tire force estimation
with strain gauge measurement. In ASME 2014 Inter-
national Mechanical Engineering Congress and Ex-
position, IMECE.
RaceLogic (2015). RLVBIMU04 Inertial Motion Unit Tech-
nical datasheet. Racelogic.
Rhudy, M. and Gu, Y. (2013). Understanding Nonlinear
Kalman Filters, Part II: An implementation Guide. In-
teractive Robotics Letters, Tutorial.
Velenis, A., Katzourakis, D., Frazzoli, E., Tsiotras, P., and
Happee, R. (2011). Steady-state drifting stabiliza-
tion of rwd vehicles. Control Engineering Practice,
19(11):1363–1376.
Wan, E. A. and Van Der Merwe, R. (2000). The unscented
kalman filter for nonlinear estimation. In Adaptive
Systems for Signal Processing, Communications, and
Control Symposium.
Wenzel, T., Burnham, K., Blundell, M., and Williams, R.
(2006). Dual extended kalman filter for vehicle state
and parameter estimation. Vehicle System Dynamics:
International Journal of Vehicle Mechanics and Mo-
bility, 44:153–171.
Young, P. (2011). Recursive Estimation and Time-Series
Analysis. Springer.
A Virtual Sensor for Integral Tire Force Estimation using Tire Model-less Approaches and Adaptive Unscented Kalman Filter
397