A Lightweight Integrity Protection Scheme for Fast Communications in

Smart Grid

Alireza Jolfaei and Krishna Kant

Department of Computer Science, Temple University, Philadelphia, U.S.A.

Keywords:

GOOSE Message, Integrity Protection, Permutation, Phasor Measurement, Substation Automation System.

Abstract:

Due to the mission-critical nature of energy management, smart power grids are prime targets for cyber-attacks.

A key security objective in the smart grid is to protect the integrity of synchronized real-time measurements

taken by phasor measurement units (PMUs). The current communication protocol in substation automation

allows the transmission of PMU data in absence of integrity protection for applications that strictly require

low communication latency. This leaves the PMU data vulnerable to man-in-the-middle attacks. In this paper,

a lightweight and secure integrity protection algorithm has been proposed to maintain the integrity of PMU

data, which ﬁlls the missing integrity protection in the IEC 61850-90-5 standard, when the MAC identiﬁer

is declared 0. The rigorous security analysis proves the security of the proposed integrity protection method

against ciphertext-only attacks and known/chosen plaintext attacks. A comparison with existing integrity

protection methods shows that our method is much faster, and is also the only integrity protection scheme

that meets the strict timing requirement. Not only the proposed method can be used in power protection

applications, but it also can be used in emerging anomaly detection scenarios, where a fast integrity check

coupled with low latency communications is used for multiple rounds of message exchanges.

1 INTRODUCTION

The supervisory control and data acquisition

(SCADA) systems in emerging smart grids monitor,

control and protect power system components by

making use of a network of phasor measurement units

(PMUs) and phasor data concentrators (PDC). As

shown in Figure 1, synchronous PMUs and PDCs are

installed in various locations (key substations) of the

transmission and distribution lines. PMUs measure

voltage magnitude, phase, and line frequency 30 to

60 times a second; and send these measurements

along with the global position system (GPS) loca-

tion of the PMU to PDCs. This is done through

a publish-subscribe mechanism, where the PMUs

work as publishers to which the PDCs subscribe.

A PDC receives data from many (typically 3 to 32)

PMUs, and then sorts and aggregates the received

data based on the time-tag. The aggregated data is

then relayed using a two-way communication system

to a number of local control centers (LCCs), which

coordinate their actions interacting with a federated

control center (FCC). Subsequently, LCCs draw

the best overall snapshot solution using all PMU

measurements (Weng et al., 2016).

Transmission

Distribution

Generation

Costumers

Transmission Substation

Subtransmission

Distribution

Substations

Transmission

Distribution

Generation

Costumers

Transmission Substation

Subtransmission

Distribution Substations

PMU

PDC

PMU

PDC

PMU PDC

LCC

FCC

LCC

Figure 1: Typical model of a power grid architecture.

Control centers use the IEC 61850-90-5 standard

to communicate with smart measurement units (IEC

61850-90-5, 2012). This standard utilizes a generic

object oriented substation event (GOOSE) proto-

col for fast relay-to-relay communications. Since

GOOSE messages are time critical, they are only as-

Jolfaei, A. and Kant, K.

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid.

DOI: 10.5220/0006394200310042

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 31-42

ISBN: 978-989-758-259-2

Table 1: Size of payload data under various PMU/PDC con-

ﬁgurations

Number

of PMU

voltage

PMU

data

size

PDC data size Applicability

channels (bytes) 3 PMUs 6 PMUs 10 PMUs

1 40 104 200 328

Single phase

line in dis-

tribution sys-

tems

3 56 120 216 344

3-phase

power trans-

mission

lines

6 80 144 240 368

power trans-

mission lines

8 96 160 256 384

power trans-

mission lines

10 112 176 272 400

power trans-

mission lines

Table 2: Allowed values for MAC value calculation.

Identiﬁer MAC algorithm Key size (bits)

0 None None

1 SHA-256 80

2 SHA-256 128

3 SHA-256 256

4 AES-GMAC 64

5 AES-GMAC 128

sociated with three layers of the open systems inter-

connection (OSI) model, namely, physical, data-link,

and application layers. IEC 61850 utilizes a standard-

ized Ethernet frame with a maximum payload size of

1492 bytes (Fan et al., 2015). The number of required

measurements depends on the topology of the power

grid as well as the requirements of optimal estimation

of the system states (Martin, K., Zwergel, A., and Ka-

postasy, D., 2015). Generally, in each substation, the

principal bus voltages should be included in the mea-

surement set. To this end, several PMUs are normally

used to cover a large substation. The size of mea-

surement data depends on the number of voltages that

a PMU measures. Table 1 gives the size of payload

data in transmission and distribution substations un-

der various PMU/PDC conﬁgurations.

Although the utilization of PMUs has facilitated

the efﬁcient management and delivery of power in

current smart grids, it is vulnerable to integrity at-

tacks. The standard for formatting and delivery of

PMU data (IEEE Standard C37.118 (Martin et al.,

2008)) includes no end-to-end security mechanisms,

and transmits messages in plaintext without any

mechanism to protect their integrity. Although, a

cyclic redundancy check (CRC) (Sobolewski, 2003)

is used in the PMU data frame, the integrity protec-

tion of a CRC is null, as it cannot detect intentional

tampering. To this end, IEC 61850-90-5 mandates

the use of a number of message authentication code

(MAC) algorithms (Table 2), which are determined by

an identiﬁer in the message header based upon latency

requirements. However, the complete deployment

of this standard will take a long time (Seyed Reza

et al., 2016) because of the compatibility issues of the

standard as well as the hardware issues. For exam-

ple, there are still many PMUs and PDCs in opera-

tion that have no cryptographic acceleration (Pappu

et al., 2013). In addition, when the latency implied

by the MAC implementation cannot be tolerated, IEC

61850-90-5 allows the transmission of messages in

the absence of integrity protection, as shown in Ta-

ble 2. This mainly happens in protection applications

where time is critical and therefore a fast message

communication is required. Examples of time criti-

cal applications are load shed (Adamiak et al., 2014)

and synchrophasor-assisted transfer trip (Kundu and

Pradhan, 2014) where a trip signal is sent from a sub-

station to another that could be more than 100 miles

away. In such applications, the use of MAC algorithm

is largely disabled by setting the identiﬁer to zero.

This leaves the PMU data vulnerable to man-in-the-

middle attacks, which can alter the current phasor of

the bus, for instance, to a value greater than the maxi-

mum rated current of the line or even to zero amperes.

This would trigger protective relays to switch on and

off, which could be costly to electrical equipment and

perturb the grid, potentially leading to blackouts.

Delay requirements for power system networks

depend on a number of parameters, such as the spe-

ciﬁc protection equipment used. Most power line

equipment can endure faults or short circuits for up

to approximately ﬁve power cycles before experienc-

ing irreversible damage or affecting other segments

in the network. This translates to total fault clearance

time of less than 84 ms. However, as a safety pre-

caution, actual operation time of protection systems

is limited to approximately 70 percent of this period,

including fault recognition time, command transmis-

sion time and line breaker switching time (Wetterwald

P. and Raymond J., 2015). Some system components,

such as large electromechanical switches, require par-

ticularly long time to operate and take up the major-

ity of the total clearance time, leaving only a 10 ms

window for the communications part of the protection

scheme, independent of the distance to travel. Given

the sensitivity of the issue, communication networks

impose requirements that are even more stringent, for

instance IEC 61850 standard limits the transfer time

for protection messages to

cycle or 4 ms (for 60 Hz

lines) for the most critical messages.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

To meet the 4 ms latency requirement, we are thus

compelled to look for a more lightweight and a non-

hash-based solution. A potential solution is in the

use of a fast checksum, which has the advantage of

having less computational cost. Checksums are com-

mon methods for detecting accidental data corruption,

for instance, in TCP (Zander et al., 2007) and ZLIB

(Soﬁa et al., 2015); and compared to MACs, they im-

pose much less computational overheads. However,

since checksums can be easily spoofed, we propose a

novel integrity protection method, which hides check-

sum bits inside payload data using a fast bit permuta-

tion technique. Our rigorous security analysis shows

no weaknesses in the proposed method, and demon-

strates no simple method of recovering the secret key.

We also conﬁrm the security of the proposed integrity

protection method against ciphertext-only attacks and

known/chosen plaintext attacks. To the best of our

knowledge, the proposed method is the ﬁrst secure

technical solution that meets the strict communication

latency requirements in protective relaying in trans-

mission and distribution substations.

The remainder of this paper is organized as fol-

lows. Section 2 summarizes the related work. Sec-

tion 3 provides details of the proposed embedding

and integrity veriﬁcation algorithms. The security of

the proposed method is evaluated using an adversarial

model in Sections 4. Section 5 evaluates the perfor-

mance of the proposed method with respect to compu-

tational complexity and running time, and the results

are compared with previous works. Finally, Section

6 concludes that the proposed scheme is secure, efﬁ-

cient and feasible.

2 RELATED WORK

Recent research has mainly been focused on preserv-

ing the integrity of PMU data in applications where

latency is on the order of seconds (rather than mil-

liseconds), such as static state estimation, power ﬂow

analysis and model validation. The integrity prob-

lem in such applications can be addressed using con-

ventional hash based techniques, such as a cipher-

based MAC (CMAC) (Dworkin, 2007) and a hash-

based MAC (HMAC) (Khan et al., 2007). How-

ever, these solutions cannot be used in power sys-

tem protection because of the latency implied by

the overheads. Despite the importance of data in-

tegrity in the protection of power equipment, only a

few technological solutions have been given, (Guo

et al., 2007; Zhang et al., 2008; Abuadbba and Khalil,

2015; Abuadbba et al., 2016), which mainly utilized

steganographic methods. Compared to crypto primi-

tives, steganographic methods normally require less

memory, power and processing capabilities, which

can suit the constrained capabilities of smart grid in-

frastructure.

In (Guo et al., 2007), Guo et al. proposed a fragile

watermarking method for protecting the integrity of

payload data. In this scheme, payload is ﬁrstly split

into groups of variable size. The size of the group

is determined adaptively as a function of the data it-

self. A secure hash function, such as MD5, is then

applied to each data element in the payload. If the

hash value is zero, then the data element marks the

end of the group. A watermark is formed by both the

current group hash value and the group hash value of

the next group. The watermark is stored in the least

signiﬁcant bits of all data elements. However, Guo et

al.’s watermarking scheme needs to compute a secure

hash function several times. Therefore, it is compu-

tationally expensive for the microprocessors used in

PMUs.

In (Zhang et al., 2008), Zhang et al. proposed

an end-to-end, statistical approach for the integrity

protection of sensory measurement data using a di-

rect spread spectrum sequence (DSSS) based water-

marking technique. In this scheme, the measurement

data, which is sent from the sender nodes, is visual-

ized as an image at different time snapshots, in which

every sender node is viewed as a pixel and its value

corresponds to the gray level of the pixel. Follow-

ing this equivalency, a watermark is embedded in this

image in a distributed fashion at each node. Given

the watermark as a prior knowledge, the receiver is

then able to verify the integrity of the measurement

data. However, the proposed method is disclosed us-

ing known/chosen plaintext attacks, because the size

of embedding data is much smaller than the size of

payload data, and watermarks are generated under the

same key.

In (Abuadbba and Khalil, 2015), Abuadbba and

Khalil proposed a steganographic method, which pro-

tects the integrity of smart grid readings by hiding a

conﬁdential information (a ﬁngerprint) bit-by-bit in-

side the detailed sub-band coefﬁcients of the discrete

wavelet transform (DWT) of the payload data. Al-

though this method is much faster than MAC-based

solutions, it cannot protect the integrity of the com-

plete payload data, because the adversary can simply

spoof a fradualent message by modifying the approx-

imation coefﬁcients of DWT of the payload data. In

other words, only one pair of covertext and stegotext

is enough to break the integrity protection algorithm.

In addition, the embedding process makes irreversible

distortions at the location of hidden bits in the cover-

text. Therefore, a portion of measurement data will be

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid

lost, which may impact the decision making process

of control centers. The transmitted stegotext is highly

prone to intentional (interference) and unintentional

(noise) attacks rendering the steganography based in-

tegrity protection solutions impractical. Indeed, any

slight change in the transmitted stegotext will result

in the loss of embedded information, and more sig-

niﬁcantly, loss of faith in the received GOOSE mes-

sage. To this end, Abuadbba et al. (Abuadbba et al.,

2016) combined a 3D DWT based steganographic

method with an error detection and correction tech-

nique, namely, BCH syndrome codes, to detect and

recover any change in the payload data. However,

the size of hidden data is much less than the size

of payload data, and therefore, similar to (Abuadbba

and Khalil, 2015), the location of the embedded data

is easily disclosed by making use of known/chosen

covertext attacks.

It follows that steganography by itself cannot suf-

ﬁciently address the integrity problem, and it needs to

be combined with another method, such as hashing or

encryption, to make the stegotext secure from attacks.

To this end, we propose a novel lightweight solution

for the integrity problem, which is secure from well-

known attacks.

3 PROPOSED INTEGRITY

PROTECTION SCHEME

The building blocks of the proposed scheme are ex-

plained in following subsections. The notations used

in the explanation are listed in Table 3.

3.1 16-bit Fletcher Checksum

The 16-bit Fletcher checksum has two variants: a

one’s complement and a two’s complement version.

In this paper, we used the former, because it pro-

vides better error detection than the latter (Nakassis,

1988). The 16-bit Fletcher checksum is calculated

iteratively over a sequence of 8 bit blocks, namely,

, P

, .. . , P

N−1

, by maintaining two unsigned one’s-

complement 16-bit accumulators R and S, whose

contents are initially zero. The pseudo-code of the

16-bit Fletcher checksum is given in Algorithm 1. It

could be shown that at the end of the Fletcher’s loop,

R will contain the 8-bit one’s complement sum of all

8 bit blocks in the payload data, and S will contain

N ·P

+ (N −1) ·P

+ ···+ P

N−1

. One advantage of

the Fletcher algorithm is that it detects the transposi-

tion of octets/words of any size within the data stream.

The error detection properties of the Fletcher check-

sum is comparable to CRCs (Sobolewski, 2003) with

Table 3: Notations.

Notation Description

N The number of bytes in a plaintext

A plaintext represented by an 8N-bit ar-

ray

X A checksum represented by a 16-bit array

An expanded text represented by a (8N +

15)-bit array

A ciphertext represented by a (8N + 15)-

bit array

p(i)

A binary value at the position i (0 ≤ i ≤

8N −1) of the plaintext

x(d)

A binary value at the position d (0 ≤d ≤

15) of the checksum

e(w)

A binary value at the position w (0 ≤w ≤

8N + 15) of the expanded text

c( j)

A binary value at the position j (0 ≤ j ≤

8N + 15) of the ciphertext

K The set of secret key

The set of N bytes in a plaintext P , that

is, P = {P

, P

, . . . , P

N−1

}

The set of N +2 bytes in a ciphertext C,

that is, C = {C

, . . . ,C

N+1

}

The set of byte locations for a plain-

text P with N bytes, that is, L =

{l | l = 0, 1, . . . , N −1}

Pr (P

, C

)

The probability that the resulting se-

quence of the t-th query and response is

, C

)

Pr(C

t+1

|(P

))

The probability that a ciphertext C

t+1

transmitted by the sender as the next mes-

sage, given the sequence of current query

and response pairs (P

, C

)

signiﬁcantly reduced computational cost.

3.2 Permutation-only Encryption

Scheme

The permutation-only encryption scheme shufﬂes the

bit locations within an expanded text E, which is con-

structed by appending the checksum X to the pay-

load data P . The bit permutation process dissipates

the statistical structure of the expanded text into long

range statistics. To permute the bit locations, a se-

quence of pseudo-random numbers is constructed by

a concatenation of three pseudo-random sequences

generated from a linear congruential pseudo-random

number generator, deﬁned by the following recur-

rence relation:

j+1

= (h ·y

+ q) mod 2

, (1)

where 0 ≤ j ≤ d

8N+16

e, h mod 4 = 1, q

mod 2 = 1, and y

is arbitrary. If h and

q are selected appropriately, for example,

h ∈ {2891336453, 29943829, 32310901} and

q ∈ {3, 5, 7}, the generated sequences pass formal

SECRYPT 2017 - 14th International Conference on Security and Cryptography

Algorithm 1: 16-bit Fletcher checksum.

1: procedure FLETCHER(P )

{Fletcher computes the checksum value X,

given a payload P }

2: R ← 0, S ← 0

3: for i ← 0, N −1 do

4: R ← (R + P

) mod 255

5: S ← (S + R) mod 255

6: end for

7: X ← (S 8) + R

 S  8 denotes a logical left shift of S by 8 bits

8: end procedure

Algorithm 2: Permutation-only encryption.

1: procedure PERMUTATION(E, K)

{Permutation rearranges the bit locations, given

an expanded textE and a key K = (y

, y

000

)}

2: for j ←0, d

8N+16

e do

3: y

j+1

←



·y

+ q



mod 2

4: y

j+1

←



·y

+ q



mod 2

5: y

000

j+1

←



·y

000

+ q



mod 2

6: y

3 j

← y

j+1

, y

3 j+1

← y

j+1

, y

3 j+2

← y

000

j+1

7: end for

8: X ← sort {y

}

8N+15

w=0

9: for j ←0, 8N + 15 do

10: c( j) ← e(x

)

11: end for

12: end procedure

statistical tests (Bellare et al., 1997). To avoid repe-

tition, differing seeds are used to initiate linear con-

gruential generators. The pseudo-random sequence

is then sorted in an ascending order, and therefore,

a unique index order number is obtained. To com-

plete the permutation, each bit of the expanded text

E is relocated according to its corresponding index

order. The permuted array forms the ciphertext C.

More precisely, C = {c( j) |c( j) = e(x

), for 0 ≤ j ≤

8N + 15}. The permutation-only encryption scheme

is described in Algorithm 2.

3.2.1 Cryptographic Properties

The recurrence relations used in Algorithm 2 are fast,

and require minimal memory (32 bits) to preserve the

state. This allows the simulation of multiple inde-

pendent streams. Moreover, there is no repetition in

the permutation sequence, because the period of each

linear congruential generator 2

is by design much

larger than 8N + 16. To further study the statistical

properties, the NIST SP800-22 tests (L’Ecuyer and

Simard, 2007) were applied to a sequences of 10 mil-

lion bits generated using the linear congruential gen-

erators. The test results are reported in Table 4 using

Algorithm 3: Checksum embedding.

1: procedure EMBEDDING(P , K)

{Embedding embeds a Fletcher checksum and

generates a ciphertext C, given a plaintext P and a

key K}

2: X ← FLETCHER(P )

3: E ← [P , X]

 P and X are concatenated to form E

4: C ← PERMUTATION (E, K)

5: end procedure

Algorithm 4: Integrity veriﬁcation.

1: procedure VERIFICATION(C, K)

{Veriﬁcation checks the integrity of a transmitted

payload, given a ciphertext C and a key K}

2: E ← PERMUTATION (C, K)

3: P ← [e(0), e(1), . . . , e(8N −1)]

4: X ← [e(8N), e(8N + 1),. . . ,e(8N + 15)]

5: X

← FLETCHER(P )

6: if X 6= X

then

7: Integrity veriﬁcation is failed

8: end if

9: end procedure

P-value, which summarizes the strength of the evi-

dence against the randomness (null) hypothesis. For

these tests, each P-value is the probability that a per-

fect random number generator would have produced

a sequence less random than the sequence that was

tested, given the kind of non-randomness assessed by

the test. A P-value less than 0.01 is an indication that

the randomness hypothesis is false with a conﬁdence

level of 0.99. As shown in Table 4, the sequence

passed the test.

The pseudo-random numbers generated by linear

congruential generators are known to be predictable

in their simplest form (Plumstead, 1983). Even if

the parameters y

, h, q, and b are unknown (used as

the secret key), the sequence of numbers produced

by a linear congruential generator is still predictable

given some of the y

for j (0 ≤ j ≤ 8N + 15) (Plum-

stead, 1983). However, this predictability does not

imply that a cryptographic algorithm using a linear

congruential generator is breakable, because the ran-

dom numbers used by the permutation algorithm are

intermediate values, which are not made public.

3.2.2 Salting Procedure

To avoid using the same permutation mapping, the

key is randomized with a salt value. Since GOOSE

is a connectionless protocol, it would require out-of-

band synchronization for employing key randomiza-

tion. Such out-of-band synchronization is difﬁcult

to achieve in the constrained substation environment.

Therefore, to avoid out-of-band synchronization, the

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid

Table 4: NIST SP 800-22 test results.

Tests P-value

Frequency test 0.8263

Frequency test within a block 0.0959

Runs test 0.4726

Test for the longest run of ones in a block 0.5797

Binary matrix rank test 0.7882

Spectral test 0.2366

Non-overlapping template matching test 0.4256

Overlapping template matching test 0.5724

Maurer’s “Universal statistical” test 0.8801

Linear complexity test 0.8063

Serial test 0.0802

Approximate entropy test 0.7637

Cusums test 0.6700

Random excursion test 0.2172

Random excursion variant test 0.4014

key is salted with the status number (a 32-bit counter)

in the GOOSE message to generate differing permu-

tations in every dlog

(8N + 16)e−1 PMU transmis-

sions, where N is he number of plaintext bytes. This

helps to resist certain types of cryptanalysis, such as

plaintext attacks and precomputed rainbow table at-

tacks (Oechslin, 2003). If the limit of the status num-

ber (that is, 2

) is reached, the GOOSE protocol re-

establishes the number (namely roll-over), and the

secret key is re-synced. For example, for N = 128

bytes, the key is salted every 10 transmissions using

a counter, which is 32 bits in most microprocessors.

Assuming PMU sampling rate of 60 per seconds, re-

keying is needed only every

seconds or 22 years,

which is much longer than re-syncing periods chosen

for other reasons.

3.3 Embedding and Veriﬁcation

Procedures

The Embedding and Veriﬁcation algorithms are de-

ﬁned over three sets, namely the plaintext P, the ci-

phertext C, and the key K, respectively. P is not an

arbitrary set, and it follows IEEE C37.118 (Martin

et al., 2008). For instance, the data communicated

by PMU can never be all 0’s or 1’s, as the frequency

value would never become zero or the time-stamp

would never become a negative value. Each key de-

termines a mapping from a set of plaintext into a set

of ciphertext, and vice versa. The embedding proce-

dure computes the checksum X of the plaintext P ;

it appends the checksum to the payload data P , and

then, permutes the expanded data using a fast keyed

bit shufﬂer. More precisely, C = Π

[P , X], where

X = FLETCHER(P ), and [P , X] denotes the con-

catenation of P and X. The embedding process is

described in Algorithm 3.

The content veriﬁcation procedure is the inverse

procedure of checksum embedding. To verify the in-

tegrity of transmitted messages, the receiver ﬁrst de-

crypts the received message C using a shared key

K; recomputes the checksum value X

, and then,

compares it with the embedded checksum X. If the

computed and received checksum mismatch, then this

shows that there was a message modiﬁcation. This

procedure is detailed in Algorithm 4.

4 SECURITY ANALYSIS

Mathematically, the adversary could be considered as

an oracle machine which has access to the sender’s

embedding function without knowing the key. The

adversary asks n number of queries from the sender’s

embedding function to obtain a set of n plaintext

and ciphertext pairs, that is, ∆ = {(P

, C

) | t =

1, 2, . . . , n}. If the adversary successfully breaks the

integrity protection algorithm, the location of the

checksum is disclosed, and therefore, the adversary

can create a forgery that cannot be detected by the

veriﬁcation algorithm of the receiver. The spooﬁng

query is successful if the adversary receives a posi-

tive veriﬁcation response (C

t+1

, 1) from the receiver.

This type of spooﬁng represents a rather strong adver-

sary, but is realistic in smart grid settings, since the

messages could be intercepted and potentially forged.

The above discussion suggests that deﬁning security

against such a strong adversary is usually not a simple

task.

Before we analyze the security of our proposed

method, we point out why simpler variants of the

same idea are insecure. Suppose that we encrypt the

payload data using pseudo-random permutations, that

is, C = Π

(P ). Permutation dissipates the statisti-

cal structure of the payload into long range statistics.

Choosing a permutation of large length size can ex-

ponentially increase the number of possible permu-

tations of payload, that is, #(π) = (8N)!. This ex-

ponential search space can make the statistical at-

tacks cumbersome by increasing the size of a pay-

load data. However, the encryption of payload bits

can only maintain data conﬁdentiality, rather than in-

tegrity. As explained in (Krawczyk, 2001), an adver-

sary can simply spoof a new message by modifying

the bits in transit.

Another variant is to hide a checksum inside

the payload data. This could be achieved by us-

ing a steganographic method, for instance, an LSB

method (Cogranne and Retraint, 2013). However, this

method is not secure from chosen-covertext attacks

and chosen-stegotext attacks (Cohen and Lapidoth,

SECRYPT 2017 - 14th International Conference on Security and Cryptography

2002). Only one pair of chosen covertext and ste-

gotext is enough to disclose the location of hidden

checksum, which is sufﬁcient to bypass the integrity

protection algorithm. This problem could be solved

by encrypting or hashing the embedded payload (that

is, expanded text). However, this solution is not ap-

propriate because of the high latency induced by cryp-

tographic primitives.

Now we analyze the security of the proposed in-

tegrity protection method, that is, C = Π

[P , X].

4.1 Ciphertext-only Attack

Theorem 1. The proposed integrity protection

scheme is secure from ciphertext-only attacks.

Proof. In a ciphertext-only attack, the adversary is

able to observe the transmitted ciphertext (that is, the

embedded GOOSE message), and then, recalculate

the checksum value of the ﬁrst N bytes in every pos-

sible permutation, that is, (8N +16)! checksum recal-

culations (in worst case). If the value of the recalcu-

lated checksum corresponds to the last two bytes of

a permutation, then the checksum bytes and their lo-

cations will be disclosed. However, this is infeasible

for a large N. As discussed in Section 1, the mini-

mum size of a PMU data is 40 bytes, which means

the adversary needs to recalculate at least 2.11×10

664

checksums. This number of computations is ex-

tremely large, and thus makes the ciphertext-only at-

tack impractical. A less computationally intensive ap-

proach is to simply try to guess the key. However,

brute-force attacks are not feasible, because the pro-

posed algorithm employs three 32-bit secret seeds (re-

call Algorithm 2), which makes the key size more

than 80 bits, that is, the minimum key space rec-

ommended by NIST (Barker et al., 2016). This re-

quires checking 10

possibilities, which too is infea-

sible.

4.2 Known-Plaintext Attack

In the following, we derive an information theoretic

bound on the success probability of the query adver-

sary, who spoofs after making t oracle queries, under

the assumption that the key is not changed during the

queries. To this end, we use the following lemmas for

the proof of Theorem 2.

Lemma 1. Let (P

, C

) be a pair of query

and response with Pr (P

, C

) 6= 0, let C

t+1

de-

note a ciphertext with Pr (C

t+1

| (P

, C

)) 6= 0,

and let K = K((P

, C

), (C

t+1

, 1)). Then,

Pr (C

t+1

|(P

, C

)) · log

(Pr (C

t+1

|(P

, C

))) ≤

∑

k∈K

Pr (k,C

t+1

| (P

)) · log

(Pr((P

, C

t+1

, 1))) ·Pr (C

t+1

|k, (P

, C

)).

Proof. Let γ denote a function of k. If k ∈K , then,γ =

1; otherwise, γ = 0. From Pr (C

t+1

| (P

, C

)) 6= 0, it

follows that K 6= ∅ and Pr((P

, C

), (C

t+1

, 1)) 6= 0.

Accordingly, we can deﬁne a probability distribution

((P

),C

t+1

)

on k as

((P

),C

t+1

)

(k) =

Pr (C

t+1

| (P

, C

)) ·γ(k)

Pr((P

, C

), (C

t+1

, 1))

(2)

Since Pr((P

, C

), (C

t+1

, 1)) =

∑

k∈K

Pr(k |

, C

)) · γ(k), then,

∑

k∈K

((P

),C

t+1

)

(k) = 1.

Therefore, Ψ

((P

),C

t+1

)

is a probability dis-

tribution. If Pr(C

t+1

| k, (P

, C

)) 6= 0, then,

γ(k, C

t+1

, (P

, C

)) = 1; thus, we can rewrite the

conditional entropy as

Pr (C

t+1

| (P

, C

)) =

∑

k∈K

Pr(k|(P

, C

))·Pr (C

t+1

|k, (P

, C

))·γ(k).

(3)

By the deﬁnition of Ψ

((P

),C

t+1

)

, we get

Pr (C

t+1

|(P

, C

)) =

∑

k∈K

((P

),C

t+1

)

(k)·

Pr((P

, C

), (C

t+1

, 1)) ·Pr (C

t+1

| k, (P

, C

)). (4)

Using Jensen’s Inequality (Briat, 2011) and Equation

2, we obtain

Pr (C

t+1

| (P

, C

)) ·log

(Pr (C

t+1

| (P

, C

))) ≤

∑

k∈K

((P

),C

t+1

)

(k) ·Pr((P

, C

), (C

t+1

, 1))·

Pr (C

t+1

| k, (P

, C

))·log

(Pr((P

, C

), (C

t+1

, 1))·

Pr (C

t+1

| k, (P

, C

))) =

∑

k∈K

Pr (k, C

t+1

| (P

, C

))·

log

(((P

, C

), (C

t+1

, 1))·Pr (C

t+1

| k, (P

, C

))).

(5)

This proves the lemma.

Lemma 2. For (P

, C

) ∈ ∆ with Pr (P

, C

) 6= 0,

H(C

t+1

|(P

, C

)) ≥−log

(Pr (P

, C

))+H(C

t+1

K, (P

, C

)).

Proof. From the deﬁnition of H(C

t+1

|(P

, C

)) and

the use of Lemma 1,

H(C

t+1

|(P

, C

)) ≥

−

∑

t+1

∈∆

Pr(C

t+1

|(P

, C

))·log

(Pr((P

, C

), (C

t+1

, 1))

−

∑

t+1

∈∆

∑

k∈K((P

),(C

t+1

,1))

Pr(k | (P

, C

))·

Pr(C

t+1

|k, (P

, C

))·log

(Pr(C

t+1

|k, (P

, C

))).

(6)

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid

This relation is expanded by the deﬁnition of

H(C

t+1

|K,(P

)) as

H(C

t+1

|(P

, C

)) ≥

−

∑

t+1

∈∆

Pr(C

t+1

|(P

, C

))·log

(Pr((P

, C

), (C

t+1

, 1))

+ H(C

t+1

| K, (P

, C

)). (7)

Since Pr(P

, C

) ≥ Pr((P

, C

), (C

t+1

, 1)), we have

H(C

t+1

| (P

, C

)) ≥

−log

(Pr

, C

)) + H(C

t+1

| K, (P

, C

)). (8)

This completes the proof.

We are now in position to prove the following

lower bound on the success probability of the query

adversary.

Theorem 2. Given the proposed integrity protection

scheme, let Pr

denote the probability of success of an

adversary, who spoofs after making t oracle queries.

Then, Pr

≥ |K|

−1

t+1

Proof. This proof is a direct application of the proof

used in (Rosenbaum, 1993) to the situation in which

the adversary makes oracle queries rather than ob-

serving messages. From the deﬁnition of the con-

ditional mutual information, I(K;C

t+1

| (P

, C

)) =

H(K |(P

, C

)) −H(K | C

t+1

, (P

, C

)) = H(C

t+1

, C

)) −H(C

t+1

| K, (P

, C

)). Hence, it is sufﬁ-

cient to show that log

(Pr

) ≥H(C

t+1

|K, (P

, C

)−

H(C

t+1

| (P

, C

)). By the deﬁnition of Pr

and us-

ing Jensen’s Inequality (Briat, 2011), we obtain

log

(Pr

) = log



∑

)∈∆

Pr(P

, C

) ·Pr

, C

)



≥

∑

)∈∆

Pr(P

, C

) ·log

(Pr

, C

)). (9)

The lower bound of log

(Pr

, C

)) proved in

Lemma 2 yields

∑

t+1

∈∆

Pr(P

, C

) ·log

(Pr

, C

)) ≥

∑

t+1

∈∆

Pr(P

)·(H(C

t+1

|K, (P

, C

))−H(C

t+1

|(P

, C

)))=

H(C

t+1

| K, (P

, C

)) −H(C

t+1

| (P

, C

)). (10)

Using Inequalities 9 and 10, we obtain

≥ 2

H(K|C

t+1

,(P

))−H(K|(P

))

. (11)

Accordingly, −log

(Pr

t+1

) ≤ −log

(Pr

× Pr

··· × Pr

) ≤ (H(K) − H(K|(P

, C

))) +

(H(K | (P

, C

)) − H(K|(P

, C

))) + ··· +

(H(K|(P

, C

)) − H(K|(P

t+1

, C

t+1

))) = H(K)

−H(K|(P

t+1

, C

t+1

))≤H(K). Therefore, log

(Pr

) ≥

−

t+1

H(K). Since keys are equally likely to be used,

and also as the probability of success after the

observation of t pairs of plaintext and ciphertext

is equal, we have H(K) = log

(|K|). Therefore,

log

(Pr

) ≥ −

t+1

log

(|K|). This proves the theo-

rem.

In the following, we explain a strategy that a query

adversary may undertake for known plaintext attacks.

Lemma 3. Given a permutation-only encryption

primitive, which operates on plaintexts with 8N + 16

number of binary entries, the number of required

known plaintexts n to perform a successful known-

plaintext attack is O (dlog

(8N + 16)e).

Proof. In a known-plaintext attack, to disclose the

permutation mapping, which works on arrays of 8N +

16 bits, it is sufﬁcient to input a plaintext with distinct

entries. However, from the practical point of view,

constructing a plaintext with distinct entries may not

be feasible, because each entry of the plaintext array

is from a ﬁnite set {0, 1}, and the number of entry

locations, that is 8N +16, exceeds the number of en-

try values. Therefore, a collection of plaintexts, all

of which have repeated entry values, is required to

uniquely determine the underlying permutation. This

problem is equivalent to splitting an array with dis-

tinct entries into a number of arrays whose entry val-

ues are equal or less than the maximum number of

entry values. To split the array, the adversary needs

to expand the entries using n digit expansions in radix

2, where n digits clearly produce 2

different values.

This implies the following relationship for the number

8N + 16 of entry locations:

< 8N + 16 ≤ 2

n+1

. (12)

The inequalities above indicate that the source en-

tries can be expanded by O (dlog

(8N + 16)e) dig-

its, and therefore, the source array can split into

O(dlog

(8N + 16)e) plaintexts. In other words,

O(dlog

(8N + 16)e) plaintexts construct a source ar-

ray with distinct entries.

4.3 Chosen-plaintext Attack

In a chosen-plaintext attack, which is a stronger no-

tion of security compared to a known-plaintext attack,

the aim is to ﬁnd a procedure with a reduced number

of required plaintexts.

Lemma 4. Given a permutation-only encryption

primitive, which operates on plaintexts with 8N + 16

number of binary entries, the number of required

chosen plaintexts n to perform a successful chosen-

plaintext attack is n = dlog

(8N + 16)e.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

Proof. Theoretically, the permutation mapping can

be easily deduced using a source array of size 8N +

16, whose entries are sequentially labeled with dis-

tinct values 0, 1, . . . , 8N + 15. However, this is not

practical, because the encryption/decryption primi-

tives only operate on binary values, which are less

than the number of entries. Therefore, to make the

attack feasible, the entries are ﬁrstly expanded by

dlog

(8N + 16)e digits with radix 2. This matrix is

then separated into dlog

(8N +16)enumbers of plain-

texts based on the digit positions in radix 2. Once

permutation is applied to the plaintexts, it produces

dlog

(8N +16)e ciphertexts with entries in radix 2. A

combination of ciphertexts using the positional digits

reveals the mapped locations.

We are now in position to prove the following the-

orem.

Theorem 3. The proposed integrity veriﬁcation

scheme is secure from known/chosen plaintext at-

tacks.

Proof. To falsify the data, the adversary needs to dis-

close the permutation mapping. To this end, fol-

lowing Lemmas 3 and 4, the adversary asks at least

dlog

(8N + 16)e queries from the oracle machine to

determine the permutation mapping. These queries

are made under the assumption that the same key is

used for generating plaintext and ciphertext pairs in

each and every queries. However, the keys are salted

to a frequency less than the required number of pairs

for a successful attack, and are all equally likely to

be used. Nevertheless, the adversary tries to imper-

sonate the sender by using only one query. Follow-

ing Theorem 2, the minimum probability of success

for such attacks is

√

|K|

, which is negligible. In ad-

dition, the adversary may try to ﬁnd the permutation

period, or may try to exhaust all possible permuta-

tion keys by asking numerous queries. Such an anal-

ysis could provide the adversary with a number of

plaintext and ciphertext pairs, which had been gen-

erated using the same key. However, the permuta-

tion domain grows exponentially by increasing the

size of payload, and this makes the attack computa-

tionally infeasible. For instance, given a payload data

with 100 bytes, 9.33 ×10

157

queries need to be asked

to exhaust all keys. This is computationally infea-

sible, and makes the proposed scheme secure from

known/chosen plaintext attacks.

4.4 Salt Attack

In a salt attack scenario, the adversary attempts to par-

tially disclose the key by comparing different pairs

of plaintext and ciphertext, which were made under

small modiﬁcations of salt value. Since the status

number has linear properties, the proposed scheme

seems to be vulnerable to off-path attacks (Gilad, Y.

and Herzberg, A., 2014). The adversary can observe

the initial messages, and hence, determine the status

number. The adversary can then perform a man-in-

the-middle attack, and fabricate a new status number

for the GOOSE message. To this end, the adversary

may increase the status number, because a message

with a lower status number than that of the previously

received message will not be processed. However, the

receiver can easily recognize the fake GOOSE mes-

sages through the veriﬁcation process. Any change in

the status number would result in a different permuta-

tion mapping, which makes the message veriﬁcation

fail at the receiver side. In addition, knowing the salt

value does not help in ﬁnding the secret key, because

permutation indices are constructed by the numerical

order of expanded key stream; and thus, it is not easy

to obtain the exact expanded key from permutation in-

dices. Furthermore, the permutation domain is long,

and this makes the adversarial analysis difﬁcult to ﬁnd

pairs which were encrypted under the same key.

Another attack strategy is to take control over the

status number, before the embedding process, on the

receiver’s side. To this end, the adversary may give

the same status (order) to GOOSE messages. This

may provide the adversary with a number of plain-

text and ciphertext pairs that are generated under the

same encryption key. Under such attack scenarios,

the security margin of the proposed scheme would be

dlog

(8N + 16)e chosen queries (as demonstrated in

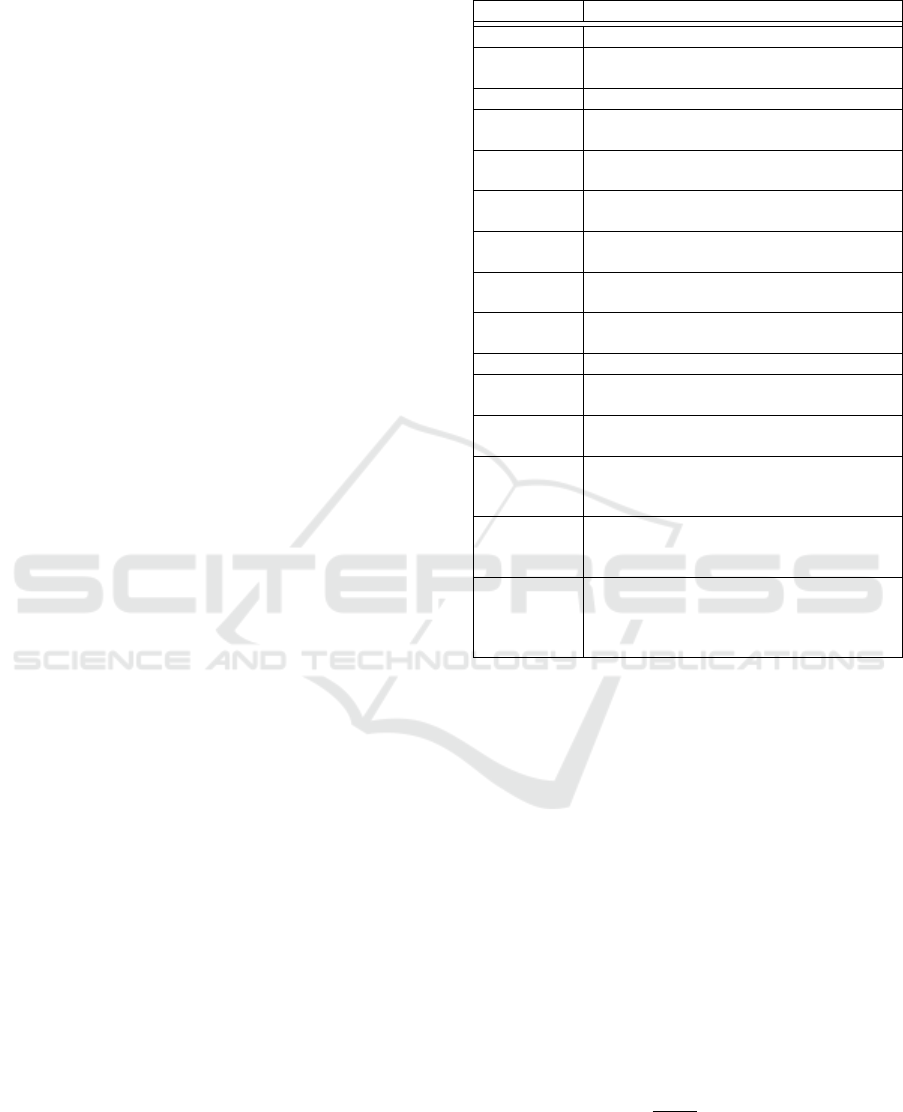
Figure 2). However, such physical attacks may be

impractical, because the access points of PMUs are

physically secured upon proper conﬁguration, which

prevents tampering and reprogramming. Nonetheless,

the adversary makes further effort to break the scheme

by making use of less number of chosen queries (even

one). Following Theorem 2, since the permutation

domain depends on the size of the plaintext, the min-

imum success probability of an adversary, who uses

only one query for an attack, is

√

(8N+16)!

, which is

negligible. Figure 3 depicts the log scale curve of the

minimum success probability of an adversary, who

uses at most dlog

(8N +16)e−1 queries. As shown

in Figure 3, this probability is negligible.

5 PERFORMANCE ANALYSIS

In addition to security analysis, the performance of

the integrity protection algorithm is also an important

factor to consider, especially for real-time GOOSE

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid

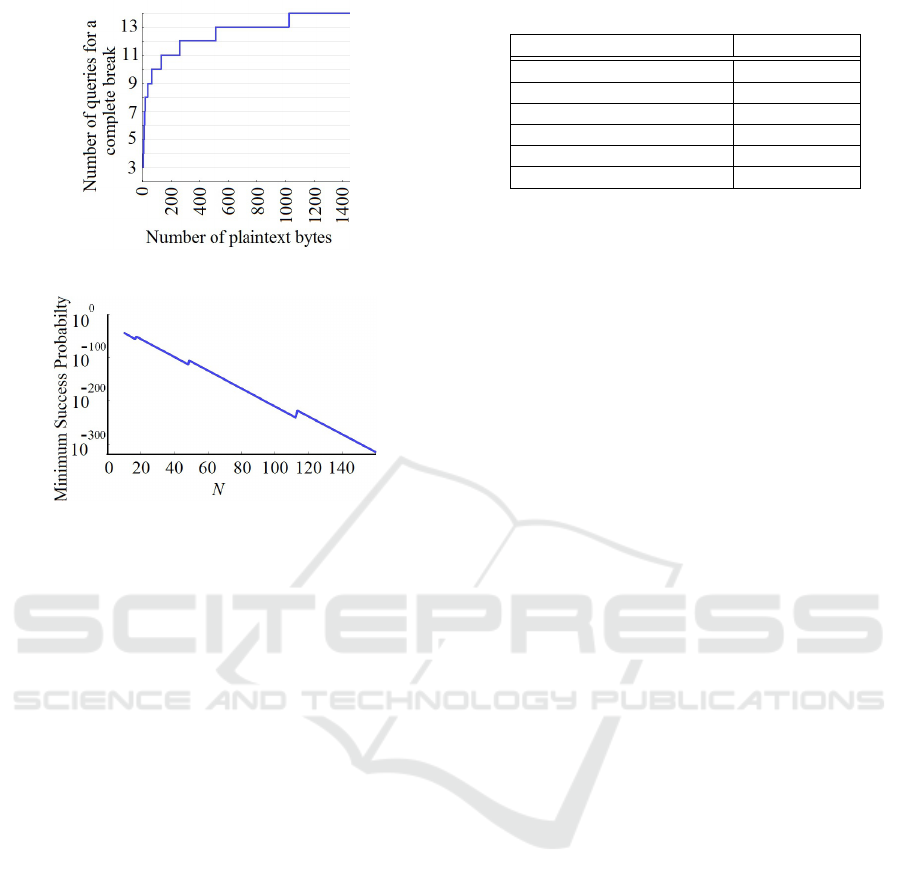
Figure 2: Number of required queries for a complete break.

Figure 3: Log scale curve of the minimum success proba-

bility of an adversary who uses at most dlog

(8N+16)e−1

queries.

communications, which require a high level of efﬁ-

ciency. The computational complexity of the integrity

protection algorithm is the summation of complexi-

ties of the 16-bit Fletcher checksum generation and

the bit permutation process. Given an array of length

n, the complexity of computing the 16-bit Fletcher

checksum is α ·n, where α is a constant. The compu-

tational complexity of the bit permutation process is

the sum of complexities of the pseudo-random num-

ber generation and the radix sorting procedure. The

computational complexity of generating n pseudo-

random numbers using a linear congruential genera-

tor is β ·n, where β is a constant. In addition, given an

array of length n, radix sorting rearranges the array in

linear time. Therefore, in the worst case, a permuta-

tion of an array with length n is achieved using µ ·n

computations, where µ is a constant. Accordingly, the

computational complexity of the integrity protection

algorithm is (α + β + µ) ·n.

Given that the maximum size of payload data is

1492 bytes, a feasible integrity protection method

should have a minimum throughput of higher than

373 kilobytes per second (KB/s). This allows par-

ties to communicate reliably within the maximum

acceptable latency (4 ms). Since the most re-

cent microprocessors in substation automation sys-

tems use ARM Cortex-M processor cores, we eval-

uated the throughput of the integrity protection al-

gorithm on an ARM Cortex-M0 platform with 48

Table 5: Algorithm performance comparison.

Algorithm Speed (KB/s)

Proposed method 424

MD5 147

ChaCha20-Poly1305 94

AES-128-CCM 70

AES-128-EAX 70

AES-128-GCM 41

MHz frequency. We used K = (1,2, 3) as a rep-

resentative key for the performance analysis. We

also compared our performance results with that of

MD5, ChaCha20-Poly1305, AES-128-CCM, AES-

128-EAX, and AES-128-GCM on the same platform

(Birr-Pixton, 2015; Mouha et al., 2014). The bench-

mark results on an ARM Cortex-M0 microprocessor

are shown in Table 5. Benchmarks show that all meth-

ods have the same computational complexity O(n),

where n is the number of message bytes. O(n) gives

an asymptotic bound c ·n, which describes a linear

growth for a signiﬁcantly large n. However, since n

is bounded, the constant factor c makes a difference

in running time. Compared to previous schemes, as

conﬁrmed by the run-time analysis shown in Table

5, the proposed integrity protection method is much

faster, and it is the only scheme that meets the mini-

mum speed requirement, that is, 373 KB/s. This fast

integrity checking opens the use of energy anomaly

detection methods when multiple message exchange

is required.

6 CONCLUSION

In this paper, we proposed a lightweight and se-

cure integrity protection algorithm for maintaining

the integrity of PMU data in protective relaying ap-

plications. To be more precise, our proposed algo-

rithm is used in the absence of integrity protection

in IEC 61850-90-5, when the HMAC identiﬁer is

set to zero. The proposed method computes a 16-

bit Fletcher checksum of the payload data, embeds

it into the payload data, and then, shufﬂes the pay-

load bits using a fast permutation-only encryption

scheme. We analyzed the security of our method with

respect to a query adversary. Our analysis showed

no weaknesses in the proposed method, and demon-

strated no simple method of recovering the secret key.

It also conﬁrmed the security of the proposed in-

tegrity protection method against ciphertext-only at-

tacks and known/chosen plaintext attacks. A com-

parison with a number of existing integrity protection

methods showed that despite having the same level of

computational complexity, the proposed method is

SECRYPT 2017 - 14th International Conference on Security and Cryptography

much faster, and it is the only integrity protection

scheme that meets the speed requirement.

Since the proposed integrity protection method

uses a symmetric encryption algorithm, its security

highly depends on the initial key agreement, rekey-

ing, and revocation. To this end, our future research

will be focused on secure and efﬁcient key manage-

ment between PMUs and PDCs in transmission and

distribution substations.

REFERENCES

Abuadbba, A. and Khalil, I. (2015). Wavelet based stegano-

graphic technique to protect household conﬁdential

information and seal the transmitted smart grid read-

ings. Information Systems, 53:224–236.

Abuadbba, A., Khalil, I., Ibaida, A., and Atiquzzaman, M.

(2016). Resilient to shared spectrum noise scheme for

protecting cognitive radio smart grid readings- BCH

based steganographic approach. Ad Hoc Networks,

41:30–46.

Adamiak, M., Schiefen, M. J., Schauerman, G., and Ca-

ble, B. (2014). Design of a priority-based load shed

scheme and operation tests. IEEE Transactions on In-

dustry Applications, 50(1):182–187.

Barker, E., Barker, W., Burr, W., Polk, W., and Smid, M.

(2016). Recommendation for key management part

1: General (revision 4). NIST special publication,

800(57).

Bellare, M., Goldwasser, S., and Micciancio, D. (1997).

“pseudo-random” number generation within crypto-

graphic algorithms: The DDS case. In Annual In-

ternational Cryptology Conference, pages 277–291.

Springer.

Birr-Pixton, J. (2015). Benchmarking mod-

ern authenticated encryption on e1 devices.

https://jbp.io/2015/06/01/modern-authenticated-

encryption-for-1-euro/.

Briat, C. (2011). Convergence and equivalence results for

the Jensen’s inequality–Application to time-delay and

sampled-data systems. IEEE Transactions on Auto-

matic Control, 56(7):1660–1665.

Cogranne, R. and Retraint, F. (2013). An asymptotically

uniformly most powerful test for LSB matching de-

tection. IEEE transactions on information forensics

and security, 8(3):464–476.

Cohen, A. S. and Lapidoth, A. (2002). The gaussian wa-

termarking game. IEEE Transactions on Information

Theory, 48(6):1639–1667.

Dworkin, M. J. (2007). Recommendation for block cipher

modes of operation: The CMAC mode for authenti-

cation. NIST special publication 800-38b, National

Institute of Standards and Technology (NIST).

Fan, Y., Zhang, Z., Trinkle, M., Dimitrovski, A. D., Song,

J. B., and Li, H. (2015). A cross-layer defense mecha-

nism against GPS spooﬁng attacks on PMUs in smart

grids. IEEE Transactions on Smart Grid, 6(6):2659–

2668.

Gilad, Y. and Herzberg, A. (2014). Off-path TCP injection

attacks. ACM Transactions on Information and Sys-

tem Security (TISSEC), 16(4):13.

Guo, H., Li, Y., and Jajodia, S. (2007). Chaining wa-

termarks for detecting malicious modiﬁcations to

streaming data. Information Sciences, 177(1):281–

298.

IEC 61850-90-5 (2012). Use of IEC 61850 to transmit syn-

chrophasor information according to IEEE C37. 118.

Khan, E., El-Kharashi, M. W., Gebali, F., and Abd-El-Barr,

M. (2007). Design and performance analysis of a uni-

ﬁed, reconﬁgurable HMAC-Hash unit. IEEE Trans-

actions on Circuits and Systems I: Regular Papers,

54(12):2683–2695.

Krawczyk, H. (2001). The order of encryption and authenti-

cation for protecting communications (or: How secure

is SSL?). In Annual International Cryptology Confer-

ence, pages 310–331. Springer.

Kundu, P. and Pradhan, A. K. (2014). Synchrophasor-

assisted zone 3 operation. IEEE Transactions on

Power Delivery, 29(2):660–667.

L’Ecuyer, P. and Simard, R. (2007). TestU01: A C li-

brary for empirical testing of random number gener-

ators. ACM Transactions on Mathematical Software

(TOMS), 33(4):22.

Martin, K., Hamai, D., Adamiak, M., Anderson, S., Be-

govic, M., Benmouyal, G., Brunello, G., Burger, J.,

Cai, J., Dickerson, B., et al. (2008). Exploring the

IEEE standard C37. 118–2005 synchrophasors for

power systems. IEEE transactions on power delivery,

23(4):1805–1811.

Martin, K., Zwergel, A., and Kapostasy, D. (2015).

PMU installation and conﬁguration requirements,

Public Manual, version no. 1.0, MISO energy.

https://www.misoenergy.org/Library/Repository/.

Mouha, N., Mennink, B., Van Herrewege, A., Watanabe, D.,

Preneel, B., and Verbauwhede, I. (2014). Chaskey: an

efﬁcient MAC algorithm for 32-bit microcontrollers.

In International Workshop on Selected Areas in Cryp-

tography, pages 306–323. Springer.

Nakassis, A. (1988). Fletcher’s error detection algorithm:

how to implement it efﬁciently and how to avoid the

most common pitfalls. ACM SIGCOMM Computer

Communication Review, 18(5):63–88.

Oechslin, P. (2003). Making a faster cryptanalytic time-

memory trade-off. In Annual International Cryptol-

ogy Conference, pages 617–630. Springer.

Pappu, V., Carvalho, M., and Pardalos, P. (2013). Opti-

mization and security challenges in smart power grids.

page 157. Springer.

Plumstead, J. B. (1983). Inferring a sequence generated

by a linear congruence. In Advances in Cryptology–

CRYPTO, pages 317–319.

Rosenbaum, U. (1993). A lower bound on authentication

after having observed a sequence of messages. Jour-

nal of Cryptology, 6(3):135–156.

Seyed Reza, F., Vanfretti, L., Ruiz-Alvarez, A., Mahmood,

F., Hooshyar, H., and Cairo, I. (2016). An IEC 61850-

90-5 gateway for IEEE C38. 118.2 synchrophasor data

transfer. In IEEE PES General Meeting, 17th to 21th

A Lightweight Integrity Protection Scheme for Fast Communications in Smart Grid

of July, 2016. Institute of Electrical and Electronics

Engineers (IEEE).

Sobolewski, J. S. (2003). Cyclic redundancy check. In En-

cyclopedia of Computer Science, pages 476–479. John

Wiley and Sons Ltd.

Soﬁa, A., Lewis, C., Jacobi, C., Jamsek, D. A., Riedy,

D. F., Vogt, J.-S., Sutton, P., and John, R. S. (2015).

Integrated high-performance data compression in the

IBM z13. IBM Journal of Research and Development,

59(4/5):7–1.

Weng, Y., Negi, R., Faloutsos, C., and Ili

c, M. D. (2016).

Robust data-driven state estimation for smart grid.

IEEE Transactions on Smart Grid, pages 1–12.

Wetterwald P. and Raymond J. (2015). Deterministic net-

working utilities requirements, IETF draft, detnet.

Zander, S., Armitage, G., and Branch, P. (2007). A survey

of covert channels and countermeasures in computer

network protocols. IEEE Communications Surveys &

Tutorials, 9(3):44–57.

Zhang, W., Liu, Y., Das, S. K., and De, P. (2008). Secure

data aggregation in wireless sensor networks: a water-

mark based authentication supportive approach. Per-

vasive and Mobile Computing, 4(5):658–680.

SECRYPT 2017 - 14th International Conference on Security and Cryptography