Reducing Variant Diversity by Clustering

Data Pre-processing for Discrete Event Simulation Models

Sonja Strasser and Andreas Peirleitner

Institute for Smart Production, University of Applied Sciences Upper Austria, Wehrgrabengasse 1-3, Steyr, Austria

Keywords: Clustering, Data Pre-processing, Variant Diversity, Discrete Event Simulation.

Abstract: Building discrete event simulation models for studying questions in production planning and control affords

reasonable calculation time. Two main causes for increased calculation time are the level of model details as

well as the experimental design. However, if the objective is to optimize parameters to investigate the

parameter settings for materials, they have to be modelled in detail. As a consequence model details such as

number of simulated materials or work stations in a production system have to be reduced. The challenge in

real world applications with a high variant diversity of products is to select representative materials from the

huge number of existing materials for building a simulation model on condition that the simulation results

remain valid. Data mining methods, especially clustering can be used to perform this selection automatically.

In this paper a procedure for data preparation and clustering of materials with different routings is shown and

applied in a case study from sheet metal processing.

1 INTRODUCTION

Manufacturing companies are faced with challenging

market situations. An increasing number of high

customized products have to be produced in shorter

periods of time in order to be competitive. The

fulfilment of customized orders results in a high

variant diversity and a high process variety (Jiao et

al., 2005). To manage this complexity successfully,

optimized decisions in production planning and

control are essential. As a result of optimized

planning decisions low costs, a high service level,

short lead times and a stable production can be

achieved.

Since analytical models for optimization often

lack the practical applicability, discrete event

simulation can be used to study the impact of certain

decisions in production planning and control. With

simulation the influence of different production

planning strategies (Huang et al., 1998, Jodlbauer and

Huber, 2008) or different dispatching rules for

production systems (Kutanoglu and Sabuncuoglu,

1999) can be compared and capacity estimations of

production systems can be made (Abdul-Kader and

Gharbi, 2002). For a discrete event simulation study

the most time consuming phase is the input data

collection and the model development (Perera and

Liyanage, 2000, Randell and Bolmsjo, 2001). So

efforts are made to develop flexible discrete event

simulation structures in an object oriented

environment (Borenstein, 2000, Anglani et al., 2002).

The developed simulation generator (SimGen) for

analysing production planning problems enables the

implementation of simulation models which are

parameterized by a database (Hübl et al., 2011).

Running simulation models can become a runtime

intensive task for instance in combination with

heuristic optimization methods for determining

optimized production planning parameters. So the

number of different materials which can be simulated

is limited, however real data from manufacturing

companies often include a high variant diversity. The

challenge for building a simulation model under such

conditions is to reduce the number of materials while

maintaining valid simulation results. Doing this

selection manually can become a very time

consuming task and so a framework using methods

from data mining, in particular clustering, is proposed

in this paper.

First related work for clustering products or

processes is discussed. Then the simulation generator

SimGen and its necessary input data are described in

more details. In the next section a framework for data

pre-processing including the reduction of material

numbers by clustering is presented. Towards the end

of the paper the proposed framework is applied in a

case study from sheet metal processing.

Strasser, S. and Peirleitner, A.

Reducing Variant Diversity by Clustering - Data Pre-processing for Discrete Event Simulation Models.

DOI: 10.5220/0006394401410148

In Proceedings of the 6th International Conference on Data Science, Technology and Applications (DATA 2017), pages 141-148

ISBN: 978-989-758-255-4

141

2 RELATED WORK

Clustering is an unsupervised method in data mining.

Unlike classification (supervised learning), clustering

doesn’t rely on predefined classes. Clustering

partitions data sets into groups according to their

similarity. Within one cluster, examples are similar to

one another and are dissimilar to objects in other

clusters (Han and Kamber, 2006). In manufacturing

the major areas where clustering is used are customer

service support, fault diagnostics, yield improvement

and engineering design (Choudhary et al., 2009).

In variant design it is advantageous to organize the

wide variety of products in clusters of similar

products (product families). Therefore it is necessary

to measure the distance between products based on

bill of materials (Romanowski and Nagi, 2005). A bill

of materials (BOM) is a hierarchical, structured

representation of products that contains information

about necessary parts, raw materials and quantities.

Forming generic bills of material (GBOMs) that

represent the different variants in a product family

can be used to facilitate the search for similar

previous designs and the configurations of new

variants (Romanowski and Nagi, 2004).

Another framework for identifying product

families based on data mining techniques is presented

in Chowdhury and Nayak, 2014. Here an Extended

Augmented Adjacency Matrix (EAAM) is proposed

as a representation of the BOM. Cosine similarity is

used to generate a similarity matrix of the EAAM

representations which is the input for a clustering

algorithm.

High product variant diversity results in a high

process variety and raises the importance of

addressing the correspondence between these

varieties in order to make good planning decisions

and maintain a stable production (Jiao et al., 2005). In

their approach the coordination between product and

process variety is based on the unification of BOM

data and routing data. Routing data describes the

sequence of operations which are executed to

manufacture a certain product and includes

specifications for production planning like set-up and

processing time. With a product-process variety grid,

for each customer order, the product design in terms

of BOM and production process can be configured.

Companies face a similar challenge when

generating assembly process plans in an environment

with high product and process complexity. Clustering

techniques can be used to identify similar products or

assembly processes and to group them according to

the similarity of their characteristics. Beyond that,

classification can be applied to classify new assembly

structures into the identified clusters (Wallis et al.,

2014).

Another application of clustering algorithms is the

solution of cell formation problems in the design of

cellular manufacturing systems. This requires the

identification of machine groups that can produce

parts with similar processing requirements.

Alhourani, 2013 developed a procedure for solving

the machine-part grouping problem using the

Similarity Coefficient Method. In this approach

important production data such as operations

sequence, production volume, lot size and routings

are considered.

In the framework presented in this paper, similar

production data is taken into account, but here the

objective is to group similar materials together in a

cluster, not the machines. In our approach it is not

proposed how to arrange machine into manufacturing

cells, this is assumed as given. In contrast the goal is

to identify similar materials. This is the prerequisite

for reducing a huge number of materials to a

manageable variant diversity for simulation

modelling.

3 SIMULATION OF

PRODUCTION SYSTEMS

A central issue of discrete event simulation in the

field of production planning and control is the

investigation of different parameter settings and

planning strategies in order to minimize overall costs

for inventory, setup and tardiness or maximize

service level. In the following the Simulation

Generator SimGen and the necessary input data for

the simulation models is presented.

3.1 Simulation Generator SimGen

The Simulation Generator SimGen, as presented in

Hübl et al., 2011, Felberbauer et al., 2012 or

Felberbauer et al., 2013 is a generic, scalable

simulation model and is parametrized by a database.

The advantage of the generic and scalable simulation

model is, that on model start up the necessary data is

loaded from the database and the production system

structure is generated automatically. Thereby,

different simulation scenarios can be defined without

any adaptation of the simulation model itself and

model functionalities can be reused. The logic is

implemented in the simulation model but the

parametrization is stored in the database and loaded

on model start up. In the simulation model a

DATA 2017 - 6th International Conference on Data Science, Technology and Applications

142

hierarchical production planning concept is

implemented, using Material Requirements Planning

(MRP). For all materials MRP production orders are

generated including start and end dates and quantities.

Then the four steps netting, lot sizing, backward

scheduling and BOM explosion are performed. The

input parameters for MRP are, among others,

planning parameters for the materials and the BOM.

3.2 Input for Simulation Models

The input data for the simulation model is exported

from the Enterprise Resource Planning Systems, pre-

processed and then stored in the database. Necessary

input data sets are:

 BOM

 Routing data including setup and processing times

 Production planning parameters like lot sizes,

planned lead times and safety stock for all

materials

 Shift calendars defining the available capacity,

including holidays

 Skill groups and number of employees

 Production program and forecast for end items

 Customer demand, order amount size and

corresponding customer required lead times

If product variant diversity is very high, this leads to

long computation times and an inappropriate level of

model details. Therefore for a simulation study on

optimal settings of planning parameters it is desirable

to reduce the number of materials to a reasonable

amount which does not harm the objective of the

simulation study.

4 FRAMEWORK FOR

REDUCING VARIANT

DIVERSITY

In this section a framework for selecting

representative raw materials from a huge number of

existing materials is presented. This framework can

be divided in two phases. In the first phase, the

necessary input-data has to be collected and different

data preparation steps are done. These steps are

necessary to make the data useable for the application

of the following clustering steps in the second phase.

4.1 Input-data

For the proposed approach two input data sets are

needed: a data set with the information of the bill of

material and another data set with the corresponding

routing of the materials in the production process.

4.1.1 Bill of Material Data (BOM Data)

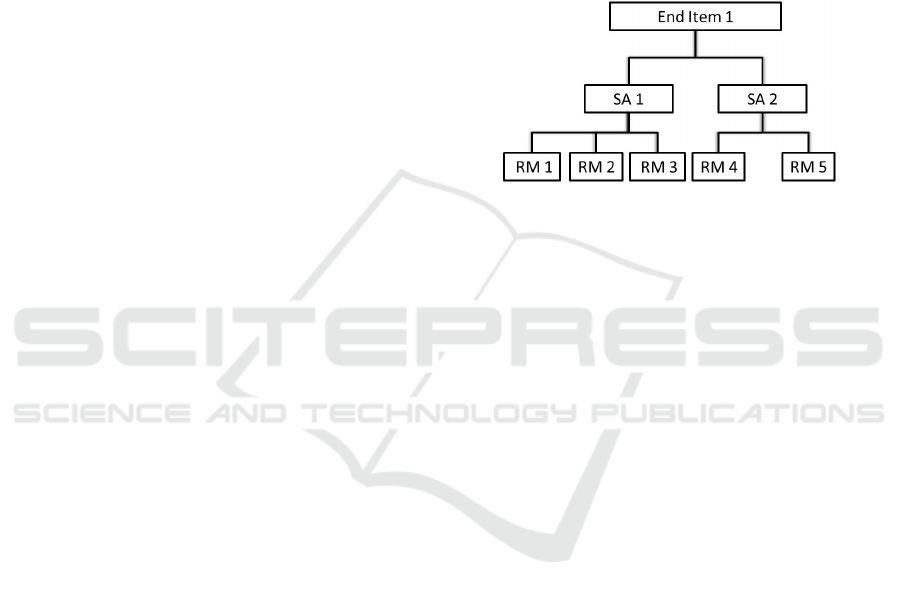
The relationships between end items, subassemblies

(SA) and raw materials (RM) is described by the bill

of material (see Figure 1). We assume that P different

end items are built from N subassemblies and each

subassembly can consist of different raw materials

which we denote shortly by materials. The number of

different materials is indicated with M.

Figure 1: Bill of Material.

BOM data is stored in a company’s database, but

there are no common guidelines concerning the

formatting and the attributes. For our purpose we

need a table of BOM data with the following

attributes (in columns):

 Material ID to identify each material uniquely.

 Subassembly ID related to the material in the first

column to identify the corresponding

subassembly uniquely.

 End item ID related to the subassembly and the

material in the first two columns to identify the

corresponding end item uniquely.

 Applied lot size policy for the material in the first

column, e. g. fixed order period (FOP), lot-for-lot

(LFL), fixed order quantity (FOQ), consumption-

based (CB).

If there are multiple end items with the same

combination of raw material and subassembly then

multiple rows in this input file are needed. The

material ID and end item ID are mandatory attributes.

All the other attributes are optional and can be

complemented by other attributes which are

important in a certain production environment.

4.1.2 Routing Data

A routing describes the sequence of workstations

passed through by a material in the production

process (Hopp and Spearman, 2008). The necessary

routing data has to be stored in a table with the

following attributes (in columns):

Reducing Variant Diversity by Clustering - Data Pre-processing for Discrete Event Simulation Models

143

 Material ID to identify each material uniquely.

 Work station (identified with a unique ID)

 Standard time at the corresponding work station.

 Operations sequence number to define at which

position this work station is used to process the

material

If the standard time isn’t available by default, it can

be calculated by the sum of processing time and the

quotient of set-up time and average lot-size. Since

commonly each material is processed by several work

stations, there are multiple rows in the routing data

table which correspond to the same material in order

to represent the whole operations sequence.

4.2 Data Preparation

In the first phase of the framework four steps of data

preparation are carried out (see Figure 2).

Figure 2: Data Preparation Steps.

4.2.1 Data Integration

As a first step the BOM-data and the routing data have

to be joined into a common master table, whereby the

material ID serves as primary key attribute. The

master table includes the attributes material,

subassembly, end item, lot size policy, work station,

standard time and operations sequence number.

4.2.2 Data Cleaning

In the data cleaning step examples with missing

values should be removed just like duplicate rows

which can occur for various reasons. Work stations

which are not relevant for building the simulation

model can be filtered. In some situations it can be

useful to combine similar work stations to a new

group of work stations if they perform the same

processing step. Finally for the sake of clarity the

master table should be sorted by end item,

subassembly, material and operations sequence

number. Now the operations sequence of each single

material of a certain subassembly and end item can be

read in subsequent rows.

4.2.3 Data Aggregation

The goal of this step is that the operations sequence

of each material appears in a single row and the

sequence of the workstations is displayed as a new

attribute. This can be achieved by data aggregation

for each end item and each subassembly in nested

loops. The data is grouped by material ID and the

other attributes in the aggregated data table are the

mode of the lot sizing policy, the sum of the standard

times, the operations sequence, subassembly ID and

end item ID.

4.2.4 Dummy Coding

There are two categories of attributes in the

aggregated data. On the one hand attributes like lot

size policy, sum of the standard times, operations

sequence and subassembly are attributes which will

be used for clustering in the second phase of the

proposed framework. On the other hand the attributes

material ID and end item provide information for a

unique identification and should not be included for

building clusters.

Further the operations sequence as a single

nominal attribute is not appropriate for clustering.

Measuring similarity of two materials would deliver

1 if there are identical sequences and 0 otherwise,

even if there is only a slight difference. For this reason

the operations sequence is split up into single work

stations and new attributes are generated by dummy

coding. Every work station defines a new attribute

which has value 1 if the material is processed at this

work station and 0 otherwise. In this way we get

various numerical attributes instead of one nominal

attribute. But measuring similarity of two materials

has more gradations now. The only thing which

cannot be detected by this kind of coding is the

chronological order of the operations. Operations

sequences A-B and B-A have identical attributes and

therefore a distance of 0. For practical application this

is negligible. Usually, due to technical dependencies,

the sequence of operations cannot be changed (e.g.

turning – milling – drilling).

In order to get only numeric attributes, dummy

coding is also applied to the lot size policy and the

DATA 2017 - 6th International Conference on Data Science, Technology and Applications

144

subassembly ID. This enables the use of k-means

clustering in the next step.

4.3 Clustering and Selection of

Materials

The goal of the second phase of the proposed

framework is the selection of representative materials

for each end item to reduce the high variant diversity.

This phase consists of two steps: The application of a

clustering method for each end item and the selection

of representative materials of each cluster (see Figure

3). For clustering the k-means algorithm is applied

because k-medoid results in considerable longer

calculation times and worse performance regarding

the average distance within each cluster.

4.3.1 k-Means Clustering

As all attributes in the prepared dataset are numeric,

k-means clustering can be applied. There are two

parameters which have to be defined for this data

mining method: the number of clusters k and a

measure to define the similarity of two examples. In

the proposed framework clustering is applied for

every end item. As end items consist of different

numbers of materials the number of clusters has to be

adjusted to the number of materials:

k (i 1,..., P)



(1)

where k

denotes the number of clusters and m

the

number of materials of end item i. The number k

rounded to the next integer. Constant c is determined

by selecting a number K of desired representative

materials (so that running the simulation model is

within an acceptable time-frame) and the assumption

that every cluster delivers one representative:

i1 i1

1MM

Kk m c

ccK



 



(2)

For measuring the similarity of two materials we use

cosine similarity:



i1 i1

cos A, B













(3)

where A and B are two row vectors in our dataset with

I attributes. RapidMiner provides different numerical

measures for clustering. But an analysis with the data

of the case study (see section 5) reveals that cosine

similarity outperforms other numerical measures

comparing them by averaging the distance between

the centroid and all examples of a cluster.

Figure 3: Clustering Steps.

The basic idea of k-means can be described by the

following steps:

Step 1: Initialize k different cluster centroids.

Step 2: Calculate the similarity between every

example and every cluster centroid

Step 3: Assign each example to the most similar

cluster centroid.

Step 4: Update the cluster centroid for each cluster by

calculating the arithmetic mean of all corresponding

examples.

Step 5: Repeat steps 2, 3 and 4 iteratively until no

change in the mapping of the examples occur.

This data mining method is applied to every end item

i and the result is the grouping of all relevant materials

into k

clusters.

4.3.2 Selection of Cluster Representatives

As a final step the selection of cluster representatives

is performed. Choosing the cluster centroid as cluster

representative results in unrealistic values of

attributes, because for instance decimal values can

occur for integer attributes. So the material with the

highest similarity to the cluster centroid is selected as

cluster representative. This step delivers k

representative materials for end item i and all in all K

materials are selected for the further use in the

simulation model.

Reducing Variant Diversity by Clustering - Data Pre-processing for Discrete Event Simulation Models

145

5 CASE STUDY

The described concept is applied to real-life

manufacturing data from sheet metal processing. The

high variant diversity in this production is represented

by 40,000 different material numbers, 400

subassemblies, 40 end items and up to 1,500

production orders every day. In a simulation model of

the complete sheet metal processing different

questions of production planning and control have to

be studied.

To guarantee a reasonable calculation time for the

simulation runs, the number of different materials has

to be reduced to a size of approximately 1000. Doing

this manually is a challenging and time consuming

task. So the framework shown above was applied

with RapidMiner 7.3, an open source software tool

for data mining and machine learning (Mierswa et al.,

2006).

5.1 Input Data

From the company’s databases the necessary input

data was extracted and saved in two different Excel-

files. The BOM-table includes 54,265 examples with

five different attributes:

 material ID

 subassembly ID

 end item ID

 corresponding business unit

 applied lot size policy

The routing-table consists of 369,535 examples with

six different attributes:

 material ID

 material name

 work station

 process ID

 operation description

 planned standard time (in hours)

The process ID includes information about the

sequence of the sheet metal processing steps. Sorting

the examples of the routing-table with a particular

material ID by ascending process ID results in a

correct sequence of the work stations which are run

by this material.

5.2 Data Preparation Steps

In the first phase of the framework the data

preparation steps according to section 4.2 are

performed. In the data cleaning step the business unit

which should be simulated is selected and only work

stations for in-house-manufacturing are extracted.

(External processing is not part of the simulation

model.) Another simplifying step was the aggregation

of all work stations with laser cutting.

To get the right sequence of work stations for

every material ID (for a certain end item and

subassembly) the examples are sorted by end item,

subassembly ID, material ID and process ID (see

Table 1). For instance for end item 1, subassembly

135 the material 30700 is passed from work station

W1 to W5 and W4 with lot size policy fixed-order

quantity 1. The standard times on these three work

stations are 0.011, 0.15 and 0.022 hours. After this

preparation step the dataset contains 183,103

examples.

Now all examples are aggregated by material ID

and the work stations are concatenated as a string to

represent the operations sequence for this material.

The attribute process ID is omitted in this

aggregation, it only served as an auxiliary attribute for

the sequence generation. Before proceeding with

clustering the sequence of work stations, the sub

assembly ID and the lot size policy are transformed

by dummy coding as described in section 4.2.4. The

result for the sample dataset after this aggregation is

shown in Table 2. For instance, material 21000,

which belongs to subassembly 135 and end item 1,

passes through the work stations W1 and W2 with

total standard time of 0.084 hours and lot size policy

Fixed-Order Period 28. After the aggregation step

34,192 examples with 119 attributes are available.

Apart from the end item, material ID and the total

standard time 75 different work stations, 37 different

subassemblies and 4 different lot size policies

generate the remaining attributes.

Table 1: Sample dataset after data preparation.

Table 2: Sample dataset after aggregation by material ID.

5.3 Clustering Steps

In the second phase of the framework the k-means

clustering algorithm is performed on the aggregated

dataset for 37 different end items separately. The

DATA 2017 - 6th International Conference on Data Science, Technology and Applications

146

number of desired representative materials is

specified with K = 2,000 considering that various

materials will appear in multiple clusters of different

end items and so the number of different

representative material will be much smaller than

2,000. The number of clusters k

for end item i is

calculated according to formula (1) and it varies from

5 to a maximum of 141.

Then immediately before the clustering

algorithm, the standard time is transformed to a range

of 0 to 1 to make it comparable to all other attributes

which are binary. Cosine similarity is used to measure

similarity between examples and k-means clustering

is applied to every end item. The results are 37 cluster

models with different number of clusters and

materials. For instance 562 materials which are part

of end item 35 are grouped in 28 clusters. Within one

cluster there are materials with similar properties

concerning the operations sequence, the type of

subassembly, total standard time and lot sizing policy.

To illustrate the result of this cluster model, the

number of materials and the number of different

operations sequences are displayed in Figure 4.

In the final step the cluster centroids are calculated

for every cluster of each end item. Then for every

cluster the similarity between the cluster centroid and

all examples belonging to this cluster is calculated.

Cosine similarity is used here again and the material

with the highest similarity is chosen as representative

material for this cluster.

This procedure results in a list of 1711

representative materials. This number is smaller than

K = 2000, because it can happen that some of the

clusters are empty. Furthermore some materials

appear multiple times in this list of representatives.

For instance the most frequent representative material

can be found in 18 different end items. But the

majority of 945 materials are unique. All together we

determined 1183 different materials by this approach.

This is a magnitude of material which can be used in

SimGen to generate a simulation model of the sheet

metal processing.

Figure 4: Number of materials and operations sequences for

end item 35.

Table 3: Frequencies of representative materials.

6 CONCLUSIONS

Real world manufacturing environments are

generally too complex to be modelled in discrete

event simulation accurately. The proposed

framework shows how to select a manageable and

representable number of materials for simulation

modelling. For this purpose the necessary input data

and preparation steps are shown in a first phase of the

framework. In the second phase a clustering

algorithm is applied to group similar materials and

finally one representative material is selected from

each cluster. This approach was applied in a case

study to real world manufacturing data from sheet

metal processing.

In further research the proposed framework

should be applied to other real world scenarios and a

comparison to other heuristic approaches for

selecting material is planned. The results of multiple

simulation runs have to be compared in order to

evaluate if the proposed framework delivers better

results than simple heuristic selection criteria. If the

results are promising this framework should be

integrated in the developed simulation generator

SimGen as an automatic data pre-processing step for

simulation modelling.

REFERENCES

Abdul-Kader, W. and Gharbi, A., 2002. Capacity

estimation of a multi-product unreliable production

line. International Journal of Production Research, 40

(18), 4815–4834.

Alhourani, F., 2013. Clustering algorithm for solving group

technology problem with multiple process routings.

Computers & Industrial Engineering, 66 (4), 781–790.

Anglani, A., et al., 2002. Object-oriented modeling and

simulation of flexible manufacturing systems: a rule-

based procedure. Simulation Modelling Practice and

Theory, 10 (3–4), 209–234.

Borenstein, D., 2000. Implementation of an object-oriented

tool for the simulation of manufacturing systems and its

application to study the effects of flexibility.

International Journal of Production Research, 38 (9),

2125–2142.

Choudhary, A.K., Harding, J.A., and Tiwari, M.K., 2009.

Data mining in manufacturing: A review based on the

Reducing Variant Diversity by Clustering - Data Pre-processing for Discrete Event Simulation Models

147

kind of knowledge. Journal of Intelligent

Manufacturing, 20 (5), 501–521.

Chowdhury, I.J. and Nayak, R., 2014. Identifying product

families using data mining techniques in manufacturing

paradigm. In: 12th Australasian Data Mining

Conference (AusDM 2014).

Felberbauer, T., et al., 2013. Application of a Generic

Simulation Model to Optimize Production and

Workforce Planning at an Automotive Supplier. In:

Proceedings of the Winter Simulation Conference 2013.

Washington DC, 2689–2697.

Felberbauer, T., Altendorfer, K., and Hübl, A., 2012. Using

a scalable simulation model to evaluate the

performance of production system segmentation in a

combined MRP and kanban system. In: Proceedings of

the Winter Simulation Conference 2012. Berlin, 1–12.

Han, J. and Kamber, M., 2006. Data mining: Concepts and

techniques. 3rd ed. San Francisco: Morgan Kaufmann.

Hopp, W.J. and Spearman, M.L., 2008. Factory Physics:.

3rd ed. Boston: Mc Graw Hill / Irwin.

Huang, M., Wang, D., and Ip, W.H., 1998. A simulation

and comparative study of the CONWIP, Kanban and

MRP production control systems in a cold rolling plant.

Production Planning & Control, 9 (8), 803–812.

Hübl, A., et al., 2011. Flexible model for analyzing

production systems with discrete event simulation. In:

Simulation Conference (WSC), Proceedings of the 2011

Winter Simulation Conference, 1554–1565.

Jiao, J., Zhang, L., and Pokharel, S., 2005. Coordinating

product and process variety for mass customized order

fulfilment. Production Planning & Control, 16 (6),

608–620.

Jodlbauer, H. and Huber, A., 2008. Service-level

performance of MRP, Kanban, CONWIP and DBR due

to parameter stability and environmental robustness.

International Journal of Production Research, 46 (8),

2179–2195.

Kutanoglu, E. and Sabuncuoglu, I., 1999. An analysis of

heuristics in a dynamic job shop with weighted

tardiness objectives. International Journal of

Production Research, 37 (1), 165–187.

Mierswa, I., et al., 2006. YALE: rapid prototyping for

complex data mining tasks: ACM.

Perera, T. and Liyanage, K., 2000. Methodology for rapid

identification and collection of input data in the

simulation of manufacturing systems. Simulation

Practice and Theory, 7 (7), 645–656.

Randell, L.G. and Bolmsjo, G.S., 2001. Database driven

factory simulation: a proof-of-concept demonstrator.

In: B.A. Peters, ed. Proceedings of the 2001 Winter

Simulation Conference: Crystal Gateway Marriott,

Arlington, VA, U.S.A., 9-12 December, 2001. New

York, N.Y., Piscataway, N.J., San Diego, Calif.:

Association for Computing Machinery; IEEE; Society

for Computer Simulation International, 977–983.

Romanowski, C.J. and Nagi, R., 2004. A Data Mining

Approach to Forming Generic Bills of Materials in

Support of Variant Design Activities. Journal of

Computing and Information Science in Engineering, 4

(4), 316.

Romanowski, C.J. and Nagi, R., 2005. On Comparing Bills

of Materials: A Similarity/ Distance Measure for

Unordered Trees. IEEE Transactions on Systems, Man,

and Cybernetics - Part A: Systems and Humans, 35 (2),

249–260.

Wallis, R., et al., 2014. Data Mining-supported Generation

of Assembly Process Plans. Procedia CIRP, 23, 178–

183.

DATA 2017 - 6th International Conference on Data Science, Technology and Applications

148