Non-singular Terminal Second Order Sliding Mode with Time Delay

Estimation for Uncertain Robot Manipulators

Yassine Kali

, Maarouf Saad

and Khalid Benjelloun

Department of Electrical Engineering, Ecole Mohammadia d’Ing

enieurs, Mohammed V University, Rabat, Morocco

Department of Electrical Engineering, Ecole de Technologie Sup

erieure, Montreal, QC H3C 1K3, Canada

Keywords:

Second Order Sliding Mode, Time Delay Estimation, Non-singular Terminal Sliding Surface, Lyapunov,

Uncertain Robot.

Abstract:

In this paper, a second order sliding mode with time delay estimation based on non-singular terminal sliding

surface is presented for high-accuracy tracking trajectory of uncertain robot manipulators. The design of the

proposed controller is based on a non-singular terminal sliding surface that overcomes the problem of singu-

larity and the restrictions of the exponent in classical terminal sliding surface. Then, a second order sliding

mode control scheme with time delay estimation is proposed to eliminate the chattering phenomenon and to

estimate the uncertainties and disturbances. Lyapunov theory is used to prove the ﬁnite-time convergence of

the sliding surface and its derivative. Finally, simulation results are presented to illustrate the effectiveness of

the proposed method.

1 INTRODUCTION

Nowadays, robot manipulators become increasingly

used in different industrial applications. For this rea-

son, many research has been proposed for control of

robot systems. The main control objective of robotic

system is to ensure high accuracy tracking trajec-

tory. However, robot manipulators suffer from vari-

ous model uncertainties (Craig, 1989), caused by fric-

tion, unmodeled dynamics, disturbances, and payload

parameters. In literature, many control algorithms

have been developed for uncertain robotic manipula-

tors, including adaptive control (Seraji, 1987), intelli-

gent controller such as fuzzy control (Yi and Chung,

1997; Guo and Woo, 2003) and neural network (Hsia

and Jung, 1995), backstepping (Slotine and Li, 1991;

Khalil, 1992), Sliding Mode Control (SMC) (Utkin,

1992; Utkin et al., 1999).

Sliding mode control, due to its robustness with

respect to uncertainties and to the simplicity of con-

trol law design, has received a wide attention from

the research community. The basic idea of SMC de-

sign is to select a user chosen sliding surface and to

then design a control law that forces the system’s tra-

jectory to reach and remain on the sliding surface.

However, SMC has many drawbacks, the major one

is the chattering phenomenon which comes from high

frequency switching of the control signal input (Frid-

man, 2001; Boiko and Fridman, 2005).

To solve this problem, numerous works have

been proposed. The ﬁrst proposition was to replace

the signum function by a smooth continuous func-

tion (Slotine and Li, 1991). However, this proposition

affects robustness and accuracy. Another approach

is to use the observer-based sliding mode (Liu and

Wang, 2012; Cao and Chen, 2014) where the goal

is to provide exact and robust estimation in order to

allow chattering reduction by a small choice of the

switching gain matrix. However, the control perfor-

mance can be reduced if the estimation is not accu-

rate.

In (Levant, 1993; Fridman and Levant, 2002; Sht-

essel et al., 2014), a Higher Order Sliding Mode

(HOSM) control has been proposed which provides

less chattering and better precision compared to clas-

sical SMC. HOSM operates on the higher order

derivative of the sliding surface unlike the conven-

tional SMC that acts on the ﬁrst derivative. Here, the

switching action appears in the higher derivatives of

the control and the control signal becomes continu-

ous. Therefore, the chattering phenomenon is atten-

uated. However, this technique doesn’t compensate

uncertainties growing in time or with the state vari-

ables.

Motivated to deal with all these problems, this

work will propose a robust controller for uncertain

226

Kali, Y., Saad, M. and Benjelloun, K.

Non-singular Terminal Second Order Sliding Mode with Time Delay Estimation for Uncertain Robot Manipulators.

DOI: 10.5220/0006394902260232

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 226-232

ISBN: Not Available

robotic manipulators. The proposed controller in this

paper is a combination of a new non-singular ter-

minal second order sliding mode and Time Delay

Estimation (TDE). Although, TDE has a very sim-

ple structure, its effectiveness to robotic manipula-

tors has been demonstrated through many applica-

tions (Youcef-Toumi and Ito, 1990; Hsia and Gao,

1990; Kali et al., 2015). TDE provides an estima-

tion of uncertainties by observing the inputs and the

states of the robot one step into the past while the new

non-singular terminal second order sliding mode will

be used to ensure fast transient response, ﬁnite-time

convergence of the sliding surface and its derivative

to zero and to reduce chattering.

The rest of the paper is arranged as follows. Sec-

tion 2 introduces the dynamic equation of n-link robot

manipulators and the control objective. In Section 3,

the proposed non-singular terminal second order slid-

ing mode and time delay estimation is designed and

the stability analysis using Lyapunov theory is estab-

lished. In Section 4, simulation results for 3-DOF

ANAT robot arm are provided to prove the effective-

ness of the proposed controller. Finally, the conclu-

sion is drawn in section 5.

2 PRELIMINARY

2.1 Robot Dynamics

Consider the dynamics of n-DOF robot manipulator

in the following matrix equation (Craig, 1989):

M(q) ¨q +C(q, ˙q) ˙q + G(q) = τ +τ

(1)

where q, ˙q, ¨q ∈ R

are the joint position, velocity and

acceleration vectors, respectively, M(q) ∈ R

n×n

is the

inertia matrix, C(q, ˙q) ∈ R

n×n

is the centrifugal and

Coriolis matrix, G(q) ∈ R

is the gravitational vector,

,τ ∈ R

denotes the disturbance and torque input

vectors, respectively.

Introducing a constant diagonal matrix M =

diag(m

,·· · , m

), the dynamic equation of the

robot manipulator given in partitioned form in equa-

tion (1) can be rewritten as follows:

M ¨q + H(q, ˙q, ¨q) = τ (2)

where:

H(q, ˙q, ¨q) = (M(q) − M) ¨q +C(q, ˙q) ˙q + G(q) − τ

(3)

For simplicity, let us denote H(t) := H(q, ˙q, ¨q) .

2.2 Problem Formulation

The control objective is to design a robust controller

to guarantee the ﬁnite-time convergence of the track-

ing error and its derivative to zero in presence of un-

certainties and external disturbances. To that end, the

controller will be designed and its stability analysis

carried out based on the following properties and as-

sumptions:

• Property 1: The inertia matrix M(q) in equa-

tion (1) is positive-deﬁnite symmetrical and

bounded such that:

0 < m

≤ kM(q)k ≤ m

< ∞

where m

and m

are two known positive con-

stants (Craig, 1989).

• Property 2: At time t = 0s, the joint acceleration

is 0 rad/s

which means τ(0) = H(0).

• Assumption 1: The joint position and velocity

states are measurable.

• Assumption 2: The joint velocity and accelera-

tion states are bounded.

• Assumption 3: the time derivative

(t) of the

functions H

(t) for i = 1,·· · ,n of the vector

H(t) = [H

(t),· ·· ,H

(t)]

are continuously dif-

ferentiable with respect to the time variable and

don’t vary largely during a small L period of

time (Youcef-Toumi and Ito, 1990).

3 CONTROLLER DESIGN

In this section, a new non-singular terminal second

order sliding mode with time delay estimation will be

designed to force the states to move along the slid-

ing manifold. Figure 1 shows the architecture of the

closed-loop system.

Figure 1: Block diagram of the closed-loop system.

3.1 Non-singular Terminal Sliding

Surface

Let q

∈ R

be the desired position trajectory and

ε = q − q

be the tracking error. Then, the proposed

Non-singular Terminal Second Order Sliding Mode with Time Delay Estimation for Uncertain Robot Manipulators

227

NTSM surface in (Tran and Kang, 2015) is given by:

σ =

ε + λ

−βt

(ε

ε)

−α

ε (4)

where λ

= diag(λ

) and λ

= diag(λ

) for i =

1,·· · , n are diagonal positive matrices, 0 < α < 1 and

β > 0. In (4), the term e

−βt

will decrease to zero when

t → ∞ and the proposed non-singular terminal sliding

surface will become linear. By choosing a suitable β,

the proposed surface will combine between the classi-

cal non-singular terminal sliding surface and the clas-

sical linear one.

Figure 2: Proposed non-singular terminal sliding surface in

phase plane.

Then, using equation (2), the time derivative of σ

is as follows:

3.2 Second Order Sliding Mode with

TDE

The sliding set of order r − th associated to manifold

is deﬁned in (Levant, 1993) by:

σ =

σ = · ·· = σ

(r−1)

= 0 (5)

Notice that the above equation represents an

r−dimensional condition on the system dynamics (r

denotes the relative degree of the system). For sec-

ond order dynamic system which is the case of our

system, r = 2. Then, the ﬁrst time derivative of σ is:

σ =

ε + λ

= ¨q − ¨q

+ λ

ε + λ

= M

−1

[τ − H(t)] − ¨q

+ λ

ε + λ

E (6)

where E is given by:

E = −βe

−βt

(ε

ε)

−α

ε + e

−βt

(ε

ε)

−α

−2αe

−βt

(ε

ε)

−α−1

(ε

ε)ε (7)

Now, lets deﬁne the new system formed by η

= σ

and η

σ, then:



= M

−1



τ −

H(t)



− q

(3)

+ λ

ε + λ

(8)

In Eq. (8), the time derivative

τ would be designed to

act on the second order derivative of the sliding sur-

face. Here, the time derivative,

τ would be designed

as a discontinuous signal, but its integral τ, would be

continuous by eliminating the high frequency chatter-

ing.

To determine a second order sliding mode, a new

surface is deﬁned for the system given in Eq. (8) as:

S = η

+ λ

(9)

where λ

= diag(λ

) is a diagonal positive matrix

and S satisﬁes:

S = −Ksign(S) (10)

where K = diag(K

,·· · , K

) denotes the posi-

tive diagonal switching gain matrix and sign(S) =

[sign(S

),sign(S

),·· · , sign(S

)]

with:

sign(S

) =







1, i f S

> 0

0, i f S

= 0

−1, i f S

< 0

(11)

Resolving Eq. (10) by using Eq. (8), the time deriva-

tive

τ(t) is obtained as:

τ(t) =

H(t) + Mu(t) (12)

where:

u(t) = q

(3)

− λ

ε − λ

E − λ

σ − Ksign(S) (13)

Then, by integrating both sides of the above equa-

tion between 0 and t and using Property 2 given in

Section 2, the new non-singular terminal second or-

der sliding mode is obtained as:

τ(t) = H(t) + M

u(t)dt (14)

Since H(t) has uncertain part, the control perfor-

mance will be affected. Then, based on Assump-

tion 3 given in Section 2, H(t) can be estimated using

a TDE (Youcef-Toumi and Ito, 1990) as:

H(t)

∼

H(t − L)

= τ(t − L) − M ¨q(t − L) (15)

where L is the estimation time delay. Clearly the accu-

racy of

H(t) improves as L decreases. In practice, the

smallest possible value of L is the sampling period.

The time delayed ¨q(t − L) signal can be obtained by

one of the following approximation:

¨q(t − L) =

q(t − L) − 2q(t − 2L) + q(t − 3L)

(16)

¨q(t − L) =

˙q(t − L) − ˙q(t − 2L)

(17)

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

228

Theorem 1. The proposed non-singular terminal sec-

ond order sliding mode with time delay estimation for

the uncertain robot system in Eq. (1) is given by:

τ(t) =

H(t) + M

u(t)dt

= τ(t − L) − M



¨q(t − L) −

u(t)dt



(18)

where u(t) is deﬁned in Eq. (13) and the switching

gains K

of Eq. (10) for i = 1, ··· ,n satisfy:

> δ

(19)

where δ

are positive constants that represents the

bounds of the derivative of the TDE error. In addi-

tion, the proposed controller ensures the convergence

of the sliding surfaces S

to zero in a ﬁnite-time:

r(i)

≤

(0)|

− δ

)

f or i = 1,·· · , n (20)

Proof. For the stability analysis of the overall sys-

tem, we have to ensure that S converges to zero. To

that end, the following Lyapunov function is selected:

V =

S (21)

Then, calculating its time derivative and substituting

the derivative of the control law

τ calculated from

Eq. (18) gives:

V = S

= S



−1



τ −

H(t)



− q

(3)

+ λ

ε + λ

E + λ



= S



−1

H(t) −

H(t)

− Ksign(S)



∑

i=1



(t) −

(t)

− K

sign(S

)



∑

i=1



∆

− K



≤

∑

i=1



|∆

| − K



(22)

Where ∆

(t) −

(t) denotes the derivative

of the TDE error. Otherwise, based on Assumption 3

∆

is bounded as follows:

|∆

| < δ

(23)

Then, Eq. (22) becomes:

V ≤

∑

i=1

|(δ

− K

) (24)

where δ

. Hence, to ensure

V negative-deﬁnite

for Lyapunov stability, the following condition must

be satisﬁed:

> δ

(25)

In addition, to prove the ﬁnite-time convergence

of the proposed controller, let us recall Eq. (24). Then,

eliminating the sum, dividing by |S

| and integrating

both sides between 0 and t gives:

|dt ≤

(δ

− K

)dt

(t)| − |S

(0)| ≤ (δ

− K

(26)

Assuming that t

is the time required to reach S

such as |S

)| = 0, one has:

≤

(0)|

− δ

)

(27)

This completes the proof.

Remark 1. In real-time, the measured signals are

contaminated by noise. The noise effect might be am-

pliﬁed when ¨q

t−L

is obtained using one of the approx-

imations in Eq. (16) and Eq. (17). To solve this prob-

lem, a LowPass Filter (LPF) may be used before im-

plementing the controller. However, the attenuation

of noise without using a LPF is possible by choosing

small values for M (Jin et al., 2011).

If a digital LPF with the cutoff frequency γ is

adopted, the control law can be modiﬁed as follows:

= γL(1 + γL)

−1

+ (1 + γL)

−1

t−L

(28)

where τ

denotes the calculated input before the ﬁlter

and τ

denotes the ﬁltered control input. Substituting

by its expression in (18), gives:

= τ

t−L

+ γL(1 + γL)

−1

dt] − ¨q

t−L

) (29)

Comparing Eq. (29) with the controller in Eq. (18),

then:

= γL(1 + γL)

−1

M (30)

Since γL(1 + γL)

−1

< 1, then, for very small value

of M, the same effect as using a digital LPF will be

obtained.

4 SIMULATION

In this section, the proposed controller is used for tra-

jectory tracking of an uncertain rigid manipulator sys-

tem. The ﬁnite-time convergence is illustrated in this

example. In addition, a comparison with another ro-

bust controller is presented to prove the effectiveness

of the proposed non-singular terminal sliding mode

control with time delay estimation.

Non-singular Terminal Second Order Sliding Mode with Time Delay Estimation for Uncertain Robot Manipulators

229

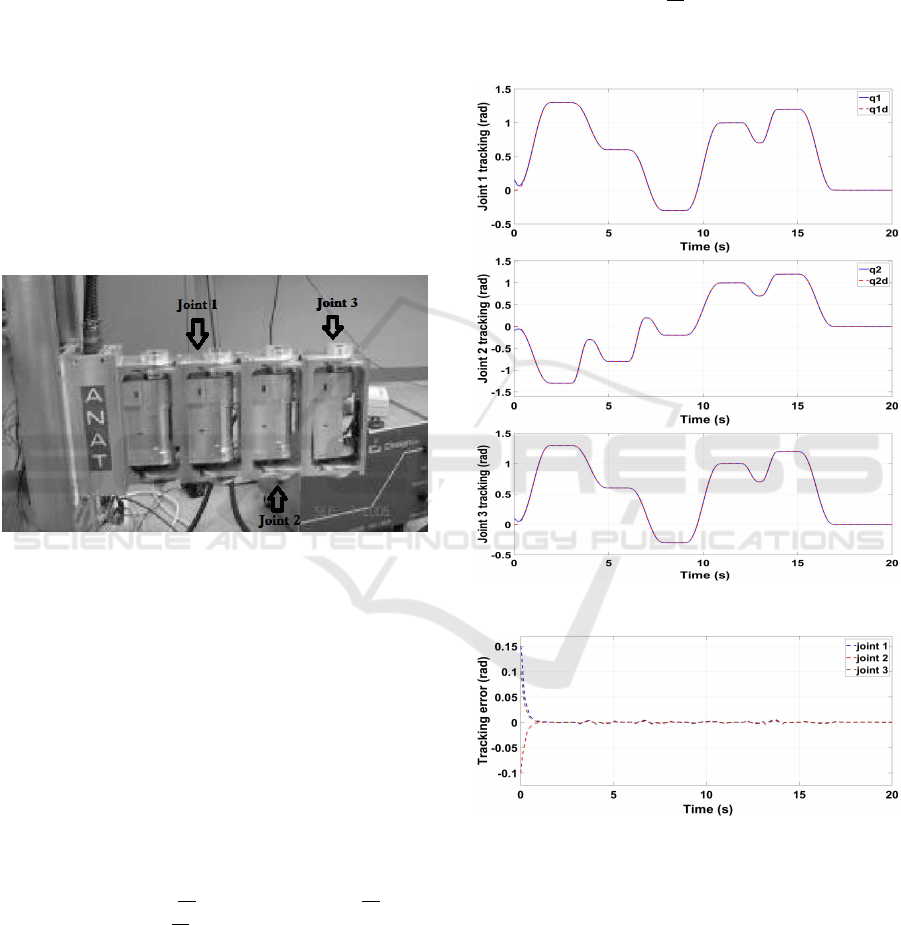
4.1 Robot System

The considered robot here is the 3-DOF ANAT robot

arm shown in Fig. 3. ANAT stands for Articulated

Nimble Adaptable Trunk. The dynamic model is fur-

ther speciﬁed in (Fallaha et al., 2011) by the well-

known equation for rigid manipulators in Eq. (1). The

system parameters are speciﬁed in (Kali et al., 2015).

The initial values of the joint position and velocity

are chosen as q

(0) = 0.15rad, q

(0) = −0.1rad,

(0) = 0.1rad and ˙q

(0) = ˙q

(0) = 0rad/s.

The robot model used for simulation veriﬁes the prop-

erties and assumptions given in Section 2. The distur-

bances τ

are considered in this paper as:





2sin(t) + 0.5sin(200πt)

cos(2t) + 0.5sin(200πt)

sin(t) + 0.5sin(200πt)





(31)

Figure 3: 3-DOF ANAT robot arm.

4.2 Controller Setting

The proposed controller has ﬁve diagonal matrices

with positive constant elements and two positive con-

stant elements that make the controller setting simple.

The steps are brieﬂy described as follows:

• Select the matrices λ

, λ

and the positive coefﬁ-

cients α and β of the non-singular terminal sliding

surface in Eq. (4).

• Select the matrix λ

of the second order sliding

surface in Eq. (9).

• Select L as small as possible (equal to the sam-

pling time interval T

• Tuning the matrix

M such as kI −M(q)

−1

Mk < 1.

The elements of M are chosen to be small posi-

tive values and increased gradually, while check-

ing the control performance by trial and error.

• The switching gain matrix K in Eq. (10) is cho-

sen such as the condition of stability in Eq. (25) is

veriﬁed, K should be further tuned to achieve the

optimal performance.

4.3 Results

The controller gains are chosen such the stability con-

dition is met:

= diag(5,5,5), λ

= diag(2,2,2),

= diag(30,30,30), M = diag(0.15,0.15,0.15),

K = diag(2,2,2), β = 0.4, L = 0.01s

Figure 4: Joint space tracking trajectory.

Figure 5: Joint space tracking error.

The results are shown in Fig. 4 through Fig. 6.

The proposed controller ensures the ﬁnite-time con-

vergence of the joint position to the desired position

with high accuracy, due to a good estimation of un-

certainties and disturbances as shown in Fig. 4 and

conﬁrmed by the small joint space tracking error in

Fig. 5. Furthermore, it can be seen from Fig. 6 that

the control torque inputs are chattering free.

To evaluate the performance of the proposed con-

troller, it is compared to the classical sliding mode

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

230

Figure 6: Control torque input.

with time delay in (Kali et al., 2015). The controller

gains are chosen as:

λ = diag(5,5,5),

M = diag(0.15,0.15, 0.15),

K = diag(2,2,2), L = 0.01s

The obtain results are given in the ﬁgures below.

Figure 7: Joint space tracking trajectory.

Comparing the results for both controllers, the

tracking performances are similar as depicted in Fig. 4

Figure 8: Joint space tracking error.

Figure 9: Control torque input.

and Fig. 7 and conﬁrmed in Fig. 5 and Fig. 8. How-

ever, it is clear that the chattering is still present in the

second method as shown in Fig. 9, while it is com-

pletely removed in the proposed method due to the

integration of the discontinous signal of the sign func-

tion as can be seen in Fig. 6

5 CONCLUSION

For an n-DOF uncertain robot manipulator, a new

non-singular terminal second order sliding mode with

time delay estimation is presented in order to achieve

the control objective. A sufﬁcient condition of sta-

bility is established using Lyapunov theory. The pro-

posed controller allows uncertainties estimation, chat-

tering reduction and ﬁnite-time convergence, while

the sliding surface ensures faster convergence in com-

parison with the classical linear sliding surface and

solves the problem of singularity of the classical ter-

minal sliding surface. Simulation results and com-

Non-singular Terminal Second Order Sliding Mode with Time Delay Estimation for Uncertain Robot Manipulators

231

parative study on a 3-DOF ANAT robot manipulator

show the effectiveness of the proposed controller.

ACKNOWLEDGEMENTS

This work was supported by Ecole de Technologie

Sup

erieure, Montreal, Canada and Ecole Mohamma-

dia d’Ing

enieurs, University of Mohammed V, Rabat,

Morocco.

REFERENCES

Boiko, I. and Fridman, L. (2005). Analysis of chattering in

continuous sliding-mode controllers. IEEE Transac-

tions on Automatic Control, 50:1442–1446.

Cao, Y. and Chen, X. B. (2014). Disturbance-observer-

based sliding-mode control for a 3-dof nanoposition-

ing stage. IEEE/ASME Transactions on Mechatronics,

19(3):924–931.

Craig, J. J. (1989). Introduction to Robotics: Mechanics

and Control. Addison-Wesley Longman Publishing

Co., Inc., Boston, MA, USA, 2nd edition.

Fallaha, C., Saad, M., Kanaan, H., and Al-Haddad, K.

(2011). Sliding-mode robot control with exponential

reaching law. IEEE Transactions on Industrial Elec-

tronics, 58.

Fridman, L. (2001). An averaging approach to chattering.

IEEE Transactions on Automatic Control, 46:1260–

1265.

Fridman, L. and Levant, A. (2002). Higher order sliding

mode. In Systems and Control Book Series.

Guo, Y. and Woo, P.-Y. (2003). An adaptive fuzzy slid-

ing mode controller for robotic manipulators. IEEE

Transactions on Systems, Man, and Cybernetics - Part

A: Systems and Humans, 33(2):149–159.

Hsia, T. and Gao, L. (1990). Robot manipulator control

using decentralized linear time-invariant time-delayed

joint controllers. IEEE International Conference on

Robotics and Automation,, 3:2070–2075.

Hsia, T. C. and Jung, S. (1995). A simple alternative to

neural network control scheme for robot manipula-

tors. IEEE Transactions on Industrial Electronics,

42(4):414–416.

Jin, M., Jin, Y., Chang, P., and Choi, C. (2011). High-

accuracy tracking control of robot manipulators us-

ing time delay estimation and terminal sliding mode.

International Journal of Advanced Robotic Systems,

8:65–78.

Kali, Y., Saad, M., Benjelloun, K., and Benbrahim, M.

(2015). Sliding mode with time delay control for

mimo nonlinear systems with unknown dynamics. In

International Workshop on Recent Advances in Slid-

ing Modes, April 9-11. Istanbul, Turkey.

Khalil, H. (1992). Nonlinear Systems. Macmillan Publish-

ing Company, New York.

Levant, A. (1993). Sliding order and sliding accuracy in

sliding mode control. International Journal of Con-

trol, 58:1247–1263.

Liu, J. and Wang, X. (2012). Advanced Sliding Mode Con-

trol for Mechanical Systems. Springer.

Seraji, H. (1987). Adaptive control of robotic manipulators.

In 26th IEEE Conference on Decision and Control,

volume 26, pages 599–602.

Shtessel, Y., Edwards, C., Fridman, L., and Levant, A.

(2014). Sliding Mode Control and Observation.

Springer, New York.

Slotine, J. and Li, W. (1991). Applied nonlinear control.

Printice-Hall international.

Tran, M.-D. and Kang, H.-J. (2015). Nonsingular terminal

sliding mode control of uncertain second-order non-

linear systems. Mathematical Problems in Engineer-

ing, 2015:1–8.

Utkin, V. (1992). Sliding mode in control and optimization.

Springer-Verlag, Berlin.

Utkin, V., Guldner, J., and Shi, J. (1999). Sliding mode

control in electromechanical systems. Taylor-Francis.

Yi, S. Y. and Chung, M. J. (1997). A robust fuzzy logic con-

troller for robot manipulators with uncertainties. IEEE

Transactions on Systems, Man, and Cybernetics, Part

B (Cybernetics), 27(4):706–713.

Youcef-Toumi, K. and Ito, O. (1990). A time delay con-

troller for systems with unknown dynamics. ASME

Journal of Dynamic System, Measurement and Con-

trol, 112:133–141.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

232