
Realistic Estimation of Model Parameters
Pavel Ettler
COMPUREG Plzeˇn, s.r.o., 306 34, Plze´n, Czech Republic
Keywords:
Parameter Estimation, Process Model, Probabilistic Distribution, Adaptive Control.
Abstract:
Most often, the normal distribution N plays the key role in the process modelling and parameter estimation.
The paper deals with realistic estimation of model parameters which takes into account limitations on pa-
rameters which arise in industrial applications of the model-based adaptive control. Here the limitation of
a normally distributed random variable is being modelled by specific distribution – the probabilistic mixture
D. It is shown that relationship between distributions N and D coincides with properties of the generalized
normal distribution G and that relations between their first and second statistical moments can be adequately
approximated by G’s cumulative distribution function and probability density function, respectively. The de-
rived method is then applied to estimation of bounded parameters. In combination with the idea of parallel
identification of the full and reduced models of the process, a working algorithm is derived. Performance of
the algorithm is illustrated by examples on both simulated and real data.
1 INTRODUCTION
The notion of adaptive control first appeared already
in the fifties of the last century – see, e.g. (
˚
Astr¨om
and Kumar, 2014) for further references. Its boom
started in the seventies with the expectation of broad
utilization of the adaptive control not only in the in-
dustrial practice. Presently, this type of control has
found its place in real applications but in the extent
far from earlier assumption. Among reasons of such
progress and today’s situation there is one that orig-
inates in the mismatch between the process model
and the real system or more likely, in disrespecting
such discrepancy which always exists in practice. It
is closely connected with the fact that measured data
which are available for the model and estimation of
its parameters are always burdened with uncertainty.
Searching for a model which preferably approx-
imates behaviour of the observed or even controlled
system in all situations and handling of every conceiv-
able exceptions turned out to be so demanding and
time-consuming that other types of control, PID con-
trol in particular, dominate the scene regarding num-
ber of applications. In effect, the model-based adap-
tive control is being employed just in cases where in-
creased demands on its implementation pay off and
when the search for a model based on the imperfect
data leads to an acceptable result.
It proves that the model-based control is facing the
problem which is inherent also for other theoretical
approaches to control: if we are “inside” the elabo-
rated theory everything fits together and all tasks seem
solvable. The problem occurs on the boundary of the
given theory and real world – the reality does not re-
spect prerequisites of the approach, the model is just
approximation of the real system, data are corrupted
by noise or burdened by uncertainty in general.
The aim of the paper is to contribute usefully to
solution of the problem in the borderland between
theory and reality.
1.1 Bounded Parameter Estimation
Bounded estimation issues are anything but new and
motivation for the solution exists in many application
fields which corresponds to the variedness of journals
and proceedings in which at least partial solutions are
being published. Nevertheless, it has been observed
(Murakami and Seborg, 2000; Kopylev, 2012) that
very few thorough monographs exist in this respect
(Van Eeden, 2006).
1.2 Existing Variety of Solutions
As the result, state of affairs is rather disorganized
but even so, the solutions can be divided by the type
of limitation being applied (with citation examples in
brackets):
• Limitation on the estimation error (Milaneseet al.,
1996),
• Limitation on the system noise (Norton, 1987),
• Confidence intervals (Mandelkern, 2002),
Ettler, P.
Realistic Estimation of Model Parameters.
DOI: 10.5220/0006395705270534
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 527-534
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
527

• Statistically bounded (soft-constrained) estima-
tion (Benavoli et al., 2006),
• Sharp restrictions on the parameter estimates
(K´arn´y, 1982; Benavoli et al., 2006; Ettler and
K´arn´y, 2010).
The presented solution belongs to the latter type.
2 PROCESS MODEL AND ITS
PARAMETERS
Consider a process model for which X
.
= [y(t),z(t)]
stand for vector of observations, where the output y
is in discrete time instants t = 1,2,. .. related to mea-
sured data
z(t) = [y(t − 1), ... , y(t − m
y
), (1)
= u
1
(t), ... , u
1
(t − m
u
),
= v(t), ..., v(t − m
v
),1]
Vector z is composed by m
y
samples of past
outputs y, m
u
+ 1 samples of controllable inputs u
and m
v
+ 1 samples of measurable disturbances v.
System output y is here considered as scalar for the
sake of simplicity, while inputs and disturbances
can be multidimensional. Number one as the last
vector element enables to consider an absolute term
alias offset. The considered stochastic relation is
parameterized by unknown parameters Θ with finite
dimension and can be described by the probability
density function (pdf) f(y| z,Θ).
Note: Most of the discussed variables are considered
to be time-variant. Nevertheless, the time index is
sometimes omitted in the following text for the sake
of simplicity.
2.1 Linear Gaussian Model
In practice, the linear regression model is mostly con-
sidered and the uncertainty is approximated by the
normal (Gaussian) probability distribution N defined
by two parameters
f(y|z,Θ) = N (ˆy,σ
2
y
) , (2)
where ˆy(t) = θ
′
(t)z(t) and
Θ = [θ, σ
2
y
] (3)
are unknown parameters of the system,
while θ = [ϑ
1
, ϑ
2
, ... , ϑ
m
]
′
, m = m
y
+ (m
u
+ 1) +
(m
v
+ 1)+ 1 and σ
2
y
stands for the variance of the sys-
tem noise. Equivalently, the model can be expressed
as
y(t) = θ
′
(t)z(t)+ e(t) (4)
with the system noise e(t) ∼ N (0,σ
2
y
).
2.2 Estimator of Unknown Parameters
Author’s regular choice regarding parameter estima-
tion is Bayesian probabilistic approach. Here un-
known parameters can be considered to be random
variables described by the pdf f(Θ| y,z). It can be
derived (Peterka, 1981; K´arn´y et al., 2005)) that for
the model (4) and fixed parameters the pdf is fully
specified by the positive definite information matrix
V which – after introduction of some type of forget-
ting (Kulhav´y and Zarrop, 1993) to allow tracking of
varying parameters – can be recursively updated as
V(t) = ϕV(t − 1) + [y(t),z(t)]
′
[y(t), z(t)], (5)
where ϕ ∈ (0,1i is forgetting factor. Partitioning of V
V =
V
y
V
′
zy
V
zy
V
z
(6)
enables to express the parameter estimates
ˆ
θ = V
−1
z
V
zy
. (7)
Variances of system noise and parameter estimates,
respectively, can be estimated as
ˆ
σ
2
y
=
V
y
−V
′
yz
V
−1
z
V
zy
κ
, (8)
ˆ
σ
2
ϑ
=
ˆ
σ
2
y
diag(V
−1
z
) , (9)
where
κ(t) = ϕκ(t − 1) + 1 . (10)
In real-time applications it is appropriate to work with
V in its factorized form V
−1
= LDL
′
(Peterka, 1981)
for the sake of numerical stability.
3 RESPECTING LIMITATIONS
OF REAL-LIFE QUANTITIES
Even if unlimited quantities exist in the real world,
our observations of them are always bounded. Find-
ings of consideration about an observed general
bounded variable will be used for the parameter es-
timates in the following sections.
3.1 Probabilistic Formulation of
Limitation
Consider a real-world variable ξ and its observation x
in discrete time instants t = 0,1,.... The observation
is bounded by x
= x
min
a x = x
max
which are given e.g.
by a sensor range. Then it holds
x(t) =
x
for ξ(t) ≤ x
ξ(t) for ξ(t) ∈ (x, x)
x for ξ(t) ≥ x .
(11)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
528

Let ξ be considered a normally distributed random
variable ξ ∼ N (µ
ξ
,σ
2
ξ
). Owing to the limitation (11),
distribution of x is not Gaussian but can be expressed
by a probabilistic mixture D the pdf of which is
composed by a central part of normal pdf and two
Dirac functions δ at boundary points of the interval
hx
,xi (Benavoli et al., 2006).
Then, the pdf of D is represented by
f
D
(x|µ
x
,σ
2
x
,x
,x) = Aδ(|ξ− x|) + (12)
f
N
(ξ ∈ hx
,xi|µ
ξ
,σ
2
ξ
) +
Bδ(|ξ−
x|) ,
where
A = F
N
(x
|µ
ξ
,σ
2
ξ
) (13)
B = 1− F
N
(
x|µ
ξ
,σ
2
ξ
) , (14)
where F
N
stands for cumulative distribution function
(cdf) of normal distribution and cdf of D reads
F
D
(x|µ
x
,σ
2
x
,x
,x) =
0 for ξ < x
F
N
(ξ|µ
ξ
,σ
2
ξ
) for ξ ∈ hx,xi
1 for ξ > x .
(15)
Example in Fig. 1 shows pdf and cdf of D with pa-
rameters µ
x
= 0.3, σ
2
x
= 0.7, x = −1 a x = 1.
-1 -0.5 0 0.5 1
0
0.1
0.2
0.3
0.4
0.5
-1 -0.5 0 0.5 1
0
0.2
0.4
0.6
0.8
1
Figure 1: Pdf and cdf of the probabilistic mixture D.
3.2 Distribution D and Parameter
Estimation
Obviously, properties of the normal distribution N
which make it exceptionally suitable for estimation
algorithm development cannot be expected in the het-
erogenous distribution D.
Exact solution can be found only in the case of one
bounded parameter (Benavoli et al., 2006). General
case leads to utilization of iterative numerical meth-
ods which are not very suitable for real-time applica-
tions. It is necessary to look for another solution.
3.3 Relations between Statistical
Moments of Distributions N and D
As a consequence of (11), mean values µ
x
, µ
ξ
and
variances σ
2
x
, σ
2
ξ
will differ while it holds
µ
x
∈ hx
, xi,
µ
x
> µ
ξ
for µ
ξ
< M
µ
x
= µ
ξ
for µ
ξ
= M
µ
x
< µ
ξ
for µ
ξ
> M
(16)
M = (x
+ x)/2 (17)
σ
2
x
∈ h0, σ
2
ξ
i . (18)
In the case of success to evaluate relation
{µ
ξ
,σ
2
ξ
,x
,x} → {µ
⋆
x
,σ
2⋆
x
} , (19)
while respecting conditions (17) and (18), it would be
possible to apply the rule for calculation of bounded
parameter estimates Θ.
3.4 Employment of the Generalized
Normal Distribution G
Extensive experiments led to the result that relations
between variances σ
2
N
and σ
2
D
of distributions N and
D can be successfully approximated by the pdf of the
generalized normal distribution G and relations be-
tween means µ
N
and µ
D
can be approximated by cdf
of the same distribution (see Appendix for properties
of distribution G).
Simple rules were found for computation of G’s
parameters µ
G
, α and β:
µ
G
: For the allowable range x ∈ h
x, xi, it is natural to
place the mean µ
G
in the middle M (17) of the
interval.
α: It is possible to define width of the distribution G
as a distance between inflection points of its pdf
while these points coincide with limits of the in-
terval h
x,xi. Then, parameter α can be expressed
as α = (x− x)/2.
β: Experiments have shown that the shape of f
G
re-
mains the same for constant ratio of the interval
span (i.e. of parameter α) to the standard devia-
tion σ
ξ
. Therefore the shape parameter β can be
defined as β = α/σ
ξ
.
To sum up, following relations hold for x
= 0, x = 1
and σ
ξ
= 1:
α =
x− x
2
(20a)
β =
α
σ
ξ
(20b)
µ
G
= x
+ α (20c)
Modification of equations (20) for general case is
described below.
Realistic Estimation of Model Parameters
529

3.5 Limiting Functions ℓ
µ
, ℓ
σ
2
As was already mentioned, group of equations (20)
allows to construct f
G
and F
G
which approximate re-
lationship between unboundedand bounded moments
for the special case (x
= 0, x = 1, σ
ξ
= 1).
Let call the limiting functions for both moments
ℓ
µ
, ℓ
σ
2
. Following restrictive conditions enabled to
find formulation of the functions for general values of
boundaries x
, x and variance σ
2
ξ
:
min
µ
ξ
∈R
ℓ
µ
(µ
ξ
|σ
2
ξ
,x
,x) = x (21a)
max
µ
ξ
∈R
ℓ
µ
(µ
ξ
|σ
2
ξ
,x
,x) = x (21b)
min
µ
ξ
∈R
ℓ
σ
2
(µ
ξ
|σ
2
ξ
,x
,x) = 0 (21c)
max
µ
ξ
∈R
ℓ
σ
2
(µ
ξ
|σ
2
ξ
,x
,x) = σ
ξ
(21d)
While f
G
is a non-negative symmetrical function,
its maximum lies in the middle µ
G
(20c) of the bound-
ing interval; therefore it holds for extreme values of
f
G
f
G,min
= 0 (22a)
f
G,max
= f
G
(µ
G
|µ
G
,α,β) . (22b)
As F
G
represents cdf it holds
F
G,min
= F
G
(ξ
−∞
|µ
G
,α,β) = 0 (23a)
F
G,max
= F
G
(ξ
∞
|µ
G
,α,β) = 1 (23b)
The first conversion coefficient can be specified from
(21d) and (22b)
K
σ
2
=
σ
2
ξ
f
G,max
(24)
and the second one follows from (21a), (21b) and (23)
K
µ
=
x− x. (25)
Now the sought limiting functions can be defined as
ℓ
µ
(µ
ξ
|σ
2
ξ
,x,x) = x+ K
µ
F
G
(µ
ξ
|µ
G
,α,β) (26a)
ℓ
σ
2
(µ
ξ
|σ
2
ξ
,x
,x) = K
σ
2
f
G
(µ
ξ
|µ
G
,α,β) . (26b)
The use of the limiting functions and quality of
approximation are illustrated in Fig. 2.
4 BOUNDED PARAMETER
ESTIMATION
Results obtained for general random variable x can
now be engaged for bounding of estimated parame-
ters. It can be formally described as
ˆ
θ
⋆
= ℓ
µ
(
ˆ
θ,
ˆ
σ
2
θ
,θ
,θ) (27a)
ˆ
σ
2⋆
θ
= ℓ
σ
2
(
ˆ
θ,
ˆ
σ
2
θ
,θ
,θ) , (27b)
-0.5 0 0.5 1 1.5
-0.5
0
0.5
1
1.5
-0.5 0 0.5 1 1.5
0
0.002
0.004
0.006
0.008
0.01
0.012
Figure 2: Limitations of the mean and variance of bounded
random variable x and their approximation by converted cdf
and converted pdf of distribution G. The conversions were
realized by the limiting functions ℓ
µ
, ℓ
σ
2
.
where symbol
⋆
denotes bounded values of original
estimates
ˆ
θ,
ˆ
σ
2
θ
and θ
, θ are lower and upper parame-
ter boundaries, respectively.
4.1 Special Case: Single Parameter
Consider a single parameter model
y(t) = ϑu(t) + e(t) . (28)
In this simple case, information matrix V can be
partitioned into scalars according to (6)
V =
V
y
V
′
zy
V
zy
V
z
=
v
y
v
zy
v
zy
v
z
. (29)
Given ϑ
, ϑ and limiting functions (27) for evalu-
ation of the limited estimate
ˆ
ϑ
⋆
, a modified matrix is
sought as
V
⋆
=
v
⋆
y
v
⋆
zy
v
⋆
zy
v
⋆
z
, (30)
which corresponds to bounded values
ˆ
ϑ
⋆
,
ˆ
σ
2⋆
ϑ
. Origi-
nal estimate can be described regarding to (7) as
ˆ
ϑ =
v
zy
v
z
. (31)
Using (8) the variance of output reads
ˆ
σ
2
y
=
v
y
− v
2
zy
/v
z
κ(t)
. (32)
Variance of the parameter estimate (9) is
ˆ
σ
2
ϑ
=
ˆ
σ
2
y
v
z
=
v
y
/v
z
− v
2
zy
/v
2
z
κ(t)
. (33)
The estimate of the bounded parameter is then given
by
ˆ
ϑ
⋆
=
v
⋆
zy
v
⋆
z
= ℓ
µ
(
ˆ
ϑ,
ˆ
σ
2
ϑ
,ϑ
,ϑ) . (34)
As the variance of measured output does not de-
pend on the estimated parameter it can be assumed
that
v
⋆
y
= v
y
(35)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
530

and therefore
ˆ
σ
2⋆
ϑ
=
v
y
/v
⋆
z
− v
⋆2
zy
/v
⋆2
z
κ(t)
. (36)
It holds (34)
ˆv
⋆
zy
=
ˆ
ϑ
⋆
ˆv
⋆
z
, (37)
which using (36) results in
ˆ
σ
2⋆
ϑ
=
v
y
/v
⋆
z
−
ˆ
ϑ
⋆2
κ(t)
= ℓ
σ
2
(
ˆ
ϑ,
ˆ
σ
2
ϑ
,ϑ
,ϑ) (38)
ˆv
⋆
z
=
v
y
κ
ˆ
σ
2⋆
ϑ
+
ˆ
ϑ
⋆2
. (39)
After introducing function ℓ
V
which modifies matrix
V while using relations (35), (37) and (39), the modi-
fied matrix can be written as
V
⋆
=
v
y
v
⋆
zy
v
⋆
zy
v
⋆
z
= ℓ
V
(V,
ˆ
ϑ
⋆
,
ˆ
σ
2⋆
ϑ
) . (40)
Resulting algorithm consists of two parts:
• Initialization
V
⋆
(0) = kI (41a)
κ(0) = 1 , (41b)
where I is an identity matrix and k > 0 is an ini-
tialization constant.
• One step of recursion
V(t) = ϕV
⋆
(t − 1) + [y(t),z(t)]
′
[y(t), z(t)]
(42a)
κ(t) = ϕκ(t − 1) + 1 (42b)
ˆ
ϑ(t) =
v
zy
(t)
v
z
(t)
(42c)
ˆ
σ
2
y
(t) =
v
y
(t) − v
2
zy
(t)/v
z
(t)
κ(t)
(42d)
ˆ
ϑ
⋆
(t) = ℓ
µ
(
ˆ
ϑ(t),
ˆ
σ
2
ϑ
(t),ϑ
,ϑ) (42e)
ˆ
σ
2⋆
ϑ
(t) = ℓ
σ
2
(
ˆ
ϑ(t),
ˆ
σ
2
ϑ
(t),ϑ
,ϑ) (42f)
V
⋆
(t) = ℓ
V
(V(t),
ˆ
ϑ
⋆
(t),
ˆ
σ
2⋆
ϑ
(t)) (42g)
4.1.1 Illustrative Example
Consider a model
y(t) = ϑu(t − 1) + e
y
(t) (43)
with one parameter
ϑ = 0.15 , (44)
where boundaries, noise and number of steps are
ϑ
= 0.0 ϑ = 0.25
e
y
(t) ∼ N (0,1)
n = 1000
(45)
The control signal was generated according to equa-
tion
u(t) = sin(t/20) . (46)
Behaviour of input u(t) and output y(t) are shown
in Fig. 3. Due to intentionally big variance of the sys-
tem noise, the harmonic component can be hardly rec-
ognized in the output signal.
0 100 200 300 400 500 600 700 800 900 1000
-4
-2
0
2
4
Figure 3: Special case: single parameter model – behaviour
of input and output.
The unbounded parameter was estimated by the
algorithm described in section 2.2. The bounded esti-
mate resulted from algorithm (42). Behaviour of both
unbounded (blue) and bounded (green) parameter es-
timates is depicted in Fig. 4. Value of the true param-
eter is represented by the yellow line and the black
lines show the given boundaries.
100 200 300 400 500 600 700 800 900 1000
-0.1
0
0.1
0.2
0.3
Figure 4: Special case: single parameter model – behaviour
of unbounded (blue) and bounded (green) parameter esti-
mates.
4.2 General Case
Exact solution for general case cannot be found be-
cause of the absence of a definite rule how to modify
an off-diagonal element in a general position within
the information matrix. An alternative solution had to
be found.
Let the parameters of the general model (4) be di-
vided into two parts
θ = [θ
a
, θ
b
] , (47)
where θ
a
is a m
a
-elements parameter vector for which
limitation should be applied and θ
b
is a m
b
-elements
Realistic Estimation of Model Parameters
531

vector of parameters without boundaries. It must hold
m = m
a
+ m
b
, m
a
< m, m
b
≥ 1 . (48)
Process model which uses all the defined parame-
ters can be called the full model
y = θ
′
a
z
a
+ θ
′
b
z
b
+ e , (49)
where z
a
, z
b
are parts of the data vector z (2) which
correspond to the parts of parameter vector (47).
Unbounded estimation can be based on the algo-
rithm from 2.2 while the vector Θ (3) was enlarged by
estimates of parameter variances σ
2
θ
Θ = [ θ,σ
2
θ
,σ
2
y
] . (50)
Note: Calculation of parameter variances accord-
ing to (9) is influenced by behaviour of the auxiliary
variable κ defined by (10). It might be better to calcu-
late the variances explicitly in a moving window the
length of which enables to tune sensitivity of the algo-
rithm to variance changes.
4.2.1 Basic Algorithm of Bounded Estimation
The basic algorithm can be divided into following
parts:
• Initialization of V and κ similarly to (41)
• One step of the recursion
– Estimation
ˆ
Θ = [
ˆ
θ,
ˆ
σ
2
θ
,
ˆ
σ
2
y
] of the full model.
– Application of the limiting function (27a) on
subset of the estimates
ˆ
θ
a
ˆ
θ
⋆
a
= ℓ
µ
(
ˆ
θ
a
,
ˆ
σ
2
θ, a
,θ
a
,
θ
a
) (51)
Vector of estimated parameters
ˆ
θ
◦
is now com-
posed by the bounded and unbounded estimates
ˆ
θ
◦
= [
ˆ
θ
⋆
a
,
ˆ
θ
b
] . (52)
4.2.2 Enlarged Algorithm
Bounded parameter estimates
ˆ
θ
⋆
a
from the basic al-
gorithm can be, for a particular recursion step, tem-
porarily considered known constants. Then, they can
be – together with corresponding data z
a
– moved to
the left side of model equation. It results in reduced
model
y−
ˆ
θ
⋆
′
a
z
a
= θ
′
b
z
b
+ e , (53)
the parameters θ
′
b
of which can be newly estimated
by the common algorithm from 2.2.
Thus, the basic algorithm is enlarged to consist of
parts
• Initialization of V and κ similarly to (41)
• One step of the recursion
– Estimation
ˆ
Θ = [
ˆ
θ,
ˆ
σ
2
θ
,
ˆ
σ
2
y
] of the full model.
– Employment of the limiting function (27a) on
subset of the estimates
ˆ
θ
a
ˆ
θ
⋆
a
= ℓ
µ
(
ˆ
θ
a
,
ˆ
σ
2
θ, a
,θ
a
,
θ
a
) (54)
– Moving
ˆ
θ
⋆
a
together with data z
a
to the left side
to create the reduced model (53)
– Estimation of parameters
ˆ
θ
⋆
b
of the reduced
model. Vector of estimated parameters
ˆ
θ
⋆
is
now composed by the bounded estimated pa-
rameters of the full model and by the modi-
fied estimate of unbounded parameters coming
from the reduced model
ˆ
θ
⋆
= [
ˆ
θ
⋆
a
,
ˆ
θ
⋆
b
] . (55)
The enlarged algorithm ensures lesser prediction
error than the basic algorithm. In many real cases is
the prediction error even comparable to the one of the
entirely unbounded estimate. Particular results can be
influenced by the choice of forgetting factors for esti-
mation of the full and reduced models.
4.2.3 Simulated Example
Consider a process model
y(t) = ϑ
1
y(t − 1) + ϑ
2
u(t − 1) + ϑ
3
+ e
y
(t) (56)
with parameters
ϑ
1
= 0.8 ϑ
2
= 0.3 ϑ
3
= 4.0
(57)
and given boundaries, noise and number of samples
ϑ
1
= 0.6
ϑ
1
= 0.9
ϑ
2
= 0.0
ϑ
2
= 0.35
e
y
(t) ∼ N (0,1)
n = 5000
(58)
The control signal was generated from
u(t) = u(t − 1) + e
u
(t) , (59)
where e
u
(t) is a random variable with the uniform dis-
tribution e
u
(t) ∼ U(−0.5,0.5).
Behaviour of input u(t) and output y(t) is shown
in Fig. 5.
Behaviour of parameter estimates is depicted in
Fig. 6. True parameters are represented by yellow
lines while black lines in the first two graphs repre-
sent their given boundaries. Unbounded estimates are
depicted in blue while the bounded ones are green.
The estimate of the single-parameter reduced model
is plotted in red in the lowermost graph.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
532
0 500 1000 1500 2000 2500 3000
-20
-10
0
10
20
30
40
Figure 5: Simulated example – input and output.
500 1000 1500 2000 2500 3000
0.5
0.6
0.7
0.8
0.9
1
500 1000 1500 2000 2500 3000
-0.1
0
0.1
0.2
0.3
0.4
0 500 1000 1500 2000 2500 3000
0
1
2
3
4
5
Figure 6: Simulated example – behaviour of unbounded
(blue) and bounded (green) parameter estimates. Estimated
parameter of the reduced model is plotted in red.
4.2.4 Real Data Example
The example is based on the real data set which was
used in (Ettler and K´arn´y, 2010). System output y is
represented by deviation of the output strip thickness
during the process of cold rolling. Its behaviour is
being approximated by the model
y(k) = ϑ
1
u(k− 1) + ϑ
2
v(k− 1) + ϑ
3
+ e
y
(k) , (60)
where index k means sample number while the sam-
pling is triggered by the movement of the rolled strip
and ∆k ∼ 0.08 m of the strip length. Control signal u
corresponds to so-called uncompensated rolling gap
of the rolling mill and the measured disturbance v is
represented by the nonlinear function of the rolling
force. The model is based on the gaugemeter princi-
ple, see, e.g. (Ettler and Andr´ysek, 2007) for details.
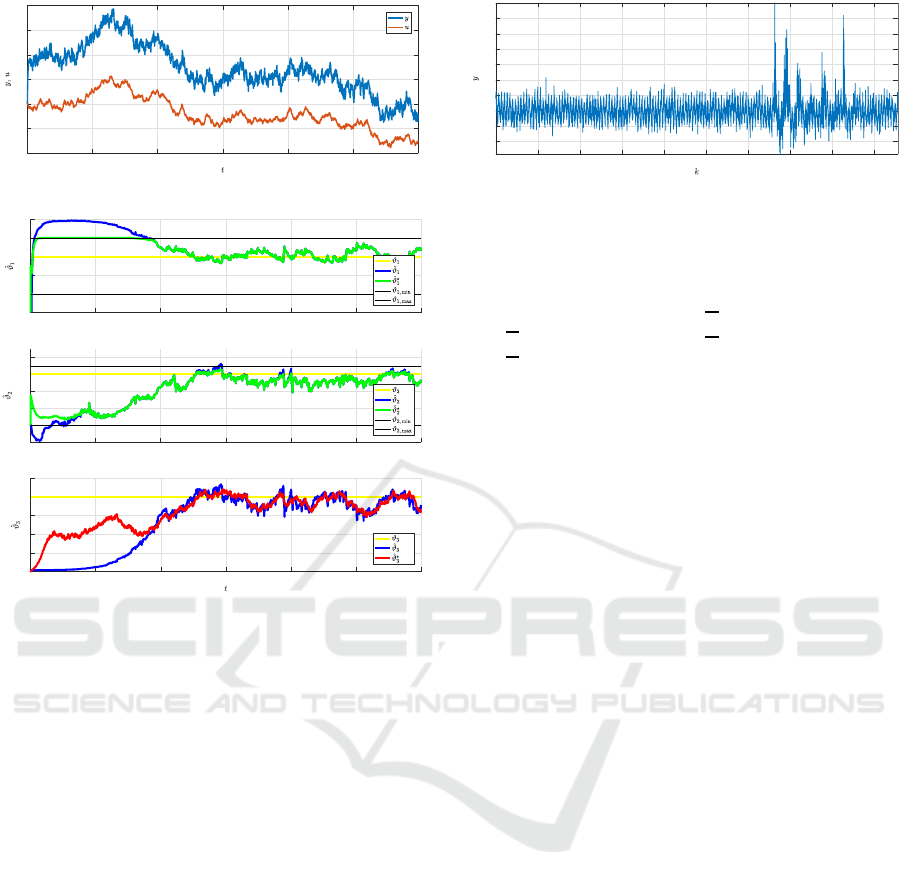
Fig. 7 shows undesirable variations of measured
output thickness in the interval k ∈ (3300, 4200)
which was caused by dirt influencing the contact
thickness measurement.
Situation depicted in Fig. 7 caused a temporary
discrepancy between both sides of the model (60)
which may drive unbounded parameter estimates out
of their reasonable ranges.
500 1000 1500 2000 2500 3000 3500 4000 4500
-20
-10
0
10
20
30
40
50
60
70
Figure 7: Real data example – the measured output.
Based on the knowledgeof the process, it was pos-
sible to determine boundaries for the first two model
parameters:
ϑ
1
= −1.0
ϑ
1
= −0.02
ϑ
2
= −100.0
ϑ
2
= 0.00
n = 4700
(61)
Behaviour of parameter estimates is shown in Fig.
8. The second unbounded parameter (in blue)
needs relatively long time k ∈ h1, 700i to reach the
allowed range, which can be explained by a moderate
excitation of the model because selected data come
from the middle of the rolled strip. Concerning the
bounded estimation, the situation is balanced by the
parameter of the reduced model (in red) in the third
graph.
Note: Real on-line identification starts with the
beginning of rolling when the system is excited
enough. Here the off-line identification starts in the
steady-state to illustrate behaviour of the estimator
under unfavorable conditions.
As a consequence of the measurement error dur-
ing k ∈ (3300, 4200), the blue unbounded estimates
ˆ
ϑ
1
,
ˆ
ϑ
2
exceeded their limits. The bounded estima-
tor coped with the problem reasonably which is il-
lustrated by the behaviour of the green bounded esti-
mates. Again, the red parameter of the reduced model
deviated from its unbounded version to minimize the
prediction error.
5 CONCLUSIONS
The paper deals with the realistic estimation of model
parameters which takes into account limitation on
model parameters existing in real applications.
In general, limitation of a random variable with
normal distribution N is described by the introduced
heterogenous probability distribution D. Relations
between mean and variance of both distributions can
be adequately approximated by cdf and pdf of the
generalized normal distribution G, respectively. After
Realistic Estimation of Model Parameters
533

500 1000 1500 2000 2500 3000 3500 4000 4500
-0.5
0
0.5
500 1000 1500 2000 2500 3000 3500 4000 4500
-100
-80
-60
-40
-20
0
500 1000 1500 2000 2500 3000 3500 4000 4500
0
50
100
150
200
Figure 8: Real data example – behaviour of unbounded
(blue) and bounded (green) parameter estimates. The es-
timated parameter of the reduced model is plotted in red.
determination of rules for construction of the fictive G
it was possible to introduce the limiting functions for
the mentioned statistical moments and integrate them
into recursive algorithm of bounded parameter esti-
mation. In addition, parallel estimation of the full and
reduced models enable to minimize the prediction er-
ror in each estimation step.
Behaviour of the estimator was illustrated on
simulated data and then on real data taken from a
cold rolling mill.
REFERENCES
˚
Astr¨om, K. J. and Kumar, P. (2014). Control: A perspective.
Automatica, (50):3–43.
Benavoli, A., Chisci, L., Farina, A., Ortenzi, L., and Zappa,
G. (2006). Hard-constrained vs. soft-constrained pa-
rameter estimation. IEEE Transactions on aerospace
and electronic systems, 42(4):1224 – 1239.
Ettler, P. and Andr´ysek, J. (2007). Mixing models to im-
prove gauge prediction for cold rolling mills. In Pro-
ceedings of the 12th IFAC Symposium on Automation
in Mining, Mineral and Metal Processing, Qu´ebec,
Canada.
Ettler, P. and K´arn´y, M. (2010). Parallel estimation respect-
ing constraints of parametric models of cold rolling. In
Proceedings of the 13th IFAC Symposium on Automa-
tion in Mineral, Mining and Metal Processing (IFAC
MMM 2010), pages 63–68, Cape Town, South Africa.
K´arn´y, M. (1982). Recursive parameter estimation of re-
gression model when the interval of possible values is
given. Kybernetika, 18(2):164–178.
K´arn´y, M., B¨ohm, J., Guy, T., Jirsa, L., Nagy, I., Nedoma,
P., and Tesaˇr, L. (2005). Optimized Bayesian Dynamic
Advising: Theory and Algorithms. Springer, London.
Kopylev, L. (2012). Constrained parameters in applications:
Review of issues and approaches. ISRN Biomathemat-
ics, 2012:Article ID 872956.
Kulhav´y, R. and Zarrop, M. B. (1993). On a general con-
cept of forgetting. International Journal of Control,
58(4):905–924.
Mandelkern, M. (2002). Setting confidence intervals for
bounded parameters. Statistical Science, 17(2):194–
172.
Milanese, M., Norton, J., Piet-Lahanier, H., and (Eds.),
E. W. (1996). Bounding Approaches to System Identi-
fication. Springer.
Murakami, K. and Seborg, D. E. (2000). Constrained pa-
rameter estimation with applications to blending op-
erations. Journal of Process Control, 10:195–202.
Norton, J. P. (1987). Identification and application of
bounded-parameter models. Automatica, 23(4):497–
507.
Peterka, V. (1981). Bayesian Approach to System Identifica-
tion In P. Eykhoff (Ed.) Trends and Progress in System
Identification. Pergamon Press, Eindhoven, Nether-
lands.
Toulias, T. L. and Kitsos, C. P. (2014). On the proper-
ties of the generalized normal distribution. Discus-
siones Mathematicae Probability and Statistics, 34(1-
2):3549.
APPENDIX
Generalized Normal Distribution
Symmetric version of the generalized normal distribution
G is defined by 3 parameters: µ
G
(location), α (scale) and
β (shape).
Pdf of G is given by
f
G
(x| µ
G
,α, β) =
β
2αΓ(1/β)
exp
(
−
x− µ
G
α
β
)
, (62)
where α > 0, β > 0 and Γ denotes the gamma function
Γ(x) =
Z
∞
0
t
x−1
exp(−t)dt . (63)
For β = 2, G coincides with the normal distribution
N (µ
G
,
α
2
2
). For β → ∞, G converges pointwise to uniform
density on (µ
G
− α,µ
G
+ α).
Cdf of G is given by
F
G
(x| µ
G
,α, β) = (64)
1
2
"
1+
sgn(x− µ
G
)
Γ(1/β)
γ
1/β,
x− µ
G
α
β
!#
,
where γ means the lower incomplete gamma function
γ(x,x
0
) =
Z
x
0
0
t
x−1
exp(−t)dt . (65)
Remaining properties of G can be found for example in
(Toulias and Kitsos, 2014).
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
534
