Novel Approach of Deriving Operational Procedures for a Complex

Research Facility

Nicolae Emanuel Marinic

a and Dragos¸ Dumitrescu

Horia Hulubei National Institute of Physics and Nuclear Engineering, Extreme Light Infrastructure - Nuclear Physics,

30 Reactorului, RO-077125, Bucharest-Magurele, Romania

Keywords:

Finite State Machines, Discrete Event Systems, Linear Temporal Logic, Controller Synthesis, Simulation,

Operational Procedures, MTSA.

Abstract:

Operational procedures represent a set of step-by-step actions on how to execute a complex task in which

safety plays the main role. Operational safety is employed for the protection of human operators and also of

the system components that may be very expensive and sensitive to malfunctions. Therefore, an automatic

method to generate and better understand the effects of the procedures over an entire plant is needed. For

this endeavour, each sub-system is modelled as a Finite State Process (FSP). The Modal Transition System

Analyser (MTSA) tool is used to generate and simulate a procedure for a given system behaviour and a set

of constraints. The presented plant model represents only a proof of concept and can be easily extended to

include further details of real systems.

1 INTRODUCTION

Extreme Light Infrastructure - Nuclear Physics (ELI-

NP) (Gales et al., 2016) (Ur et al., 2015), as a part

of ELI, the pan European distributed facility, aims

for producing laser-driven experiments related to nu-

clear physics. The facility, located in Magurele, Ro-

mania, will host several sub-systems used to pro-

duce the laser beam(s) (having six optical outputs),

beam transport (Ursescu et al., 2016) and experi-

ments (et.al., 2016). The facility complexity is given

by different aspects like:

• various experiments with variable ﬂexible set-ups

must be run in parallel (as user research facility),

• future upgrades must be taken into account,

• some operations are only performed by human op-

erators,

• and, last but not least, machine and human safety

are mandatory to be considered.

Thus, the sub-systems integration followed by the

safety operation of the facility as a whole is very im-

portant.

Given the model of a complex research facility

comprising multiple interacting sub-systems and con-

straints between them, it is necessary to ﬁnd the pro-

cedures to safely operate the facility such that all the

constraints are preserved. The models of each sub-

system are based on the list of requirements as de-

rived from the speciﬁcations. Each sub-system has a

local controller that takes care of the local operations

and that interacts through a limited number of signals

with the others. Sub-system interactions and regula-

tions imposed to operate such research facility gen-

erate different constraints that need to be translated

into logical conditions. The research facility has the

following components:

• HPLS - High Power Laser System;

• LBTS - Laser Beam Transport System;

• Experiment - Generic experiment using the laser

beam generated by the HPLS and transported by

LBTS systems.

The purpose of the research facility is to produce (us-

ing the HPLS) and provide (through the LBTS) to

a preselected area (represented by the Experiment)

laser beams with different characteristics for perform-

ing experiments. The entire optical path comprises

lasers, mirrors, lenses and other devices used to as-

sure the highest beam quality.

The primary aim of the paper is to show the means

to deﬁne a set of rules or procedures to safely operate

the research facility as a whole. Through modelling,

we also gain valuable insights about the caveats and

possible design extensions. Last but not least, the con-

196

Marinic

a, N. and Dumitrescu, D.

Novel Approach of Deriving Operational Procedures for a Complex Research Facility.

DOI: 10.5220/0006396401960203

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 196-203

ISBN: 978-989-758-265-3

troller obtained based on the given constraints can be

used to implement the real control algorithm used to

supervise the plant operations. All three subsystems

are highly complex and present very expensive com-

ponents that need to be protected against any types of

human errors.

The proposed work-ﬂow starts with the model def-

inition based on the system behaviour. Once the con-

trol objectives are established, the resulting controller,

if it exists, produces the desired system behaviour de-

ﬁned by these objectives. The simulation of the fa-

cility model and controller locates and corrects errors

early in design system. In the current paper, we pro-

pose to use the same approach to help with the deﬁni-

tion of procedures. The procedure deﬁnition activity

is usually done manually and is based on numerous

standards depending on the domain of activity (laser

safety, nuclear safety, etc.). The sole purpose of the

paper is to ease this process and not to replace it.

The paper is organized as follows. Section 2 pro-

vides background information on the composition of

all the sub-system models that form the plant and con-

straints. A short presentation of the theoretical frame-

work is made in Section 3. Section 4 describes an

example based on the models previously deﬁned in

Section 2. Lastly, Section 5 draws some conclusions

about the work and presents future directions.

2 THE FACILITY MODEL

The composition of all the sub-system models (HPLS,

LBTS, and Experiment) form the plant model (further

called the environment). The system states are writ-

ten with capital letters and the transitions (actions)

between states are in italics and always start with a

small letter. The ﬁlled states represent the moments

when laser is shooting, whereas the dotted ones rep-

resent a malfunction of the sub-system. Some tran-

sitions of the sub-systems have identical labels to be

concurrently enabled.

2.1 The High Power Laser System

The actual HPLS has 2 arms and 6 outputs (3 per arm)

through which laser beams are provided at different

powers (2 x 10PW, 2 x 1PW, and 2 x 100TW). The

high power laser shot can produce severe injuries or

destroy expensive components (mirrors, lenses, etc.).

Therefore, extra precautions must be taken. Nor-

mally, the HPLS needs an internal alignment phase

before shooting and presents different safeguards im-

plemented to safely switch off the laser beam. The

shut-down process is not instantaneous and while in

the ON state, the system has no restrictions related to

the number of laser shots per experiment. There is a

low power laser beam used for alignment operations

of the optics present in the downstream sub-systems

(LBTS and Experiment). For the sake of simplicity,

the following assumptions are considered:

• only one output of the laser is available and there-

fore only one experiment will be considered,

• the internal alignment phase is neglected; thus, the

HPLS is always aligned,

• the shut-down process is instantaneous since we

do not take time into consideration,

• the alignment beam feature is as an underlying

process and therefore we do not consider it.

To model the described system, we considered a

state diagram (see Figure 1) with 5 states as follows

{IDLE, ERR, READY, ON, OFF}. The initial state

is represented by the IDLE state. The laser shoots at

full power only when in the ON state. While in the

READY or OFF states, the laser is not shooting but

all the pre-conditions to run an experiment are met.

In case of an error, the system remains indeﬁnitely in

ERR state. An experiment starts with the expRdy and

ends by the expNxt transitions. The expFin transition

causes the HPLS to turn off the laser beam and go

to OFF state. From the OFF state, the model allows

to have multiple shoot, expFin transition sequences as

in reality (unlimited number of shots). Whereas from

ON state, a shoot transition blocks the HPLS and de-

termines transitioning to ERR state. The expNxt tran-

sition causes the HPLS to enter in IDLE state and al-

lows the user to prepare for a new experiment.

The following constraints are considered:

• a shoot transition can be only issued from the

READY and OFF states,

• at any moment a shoot, shoot, ... sequence is for-

bidden,

• if the above conditions are not fulﬁlled the HPLS

is blocked in an error state named ERR,

• an experiment is limited to only one shoot.

The constraints translation into logical statements and

further explanations related to the simulation lan-

guage are presented in Section 4.

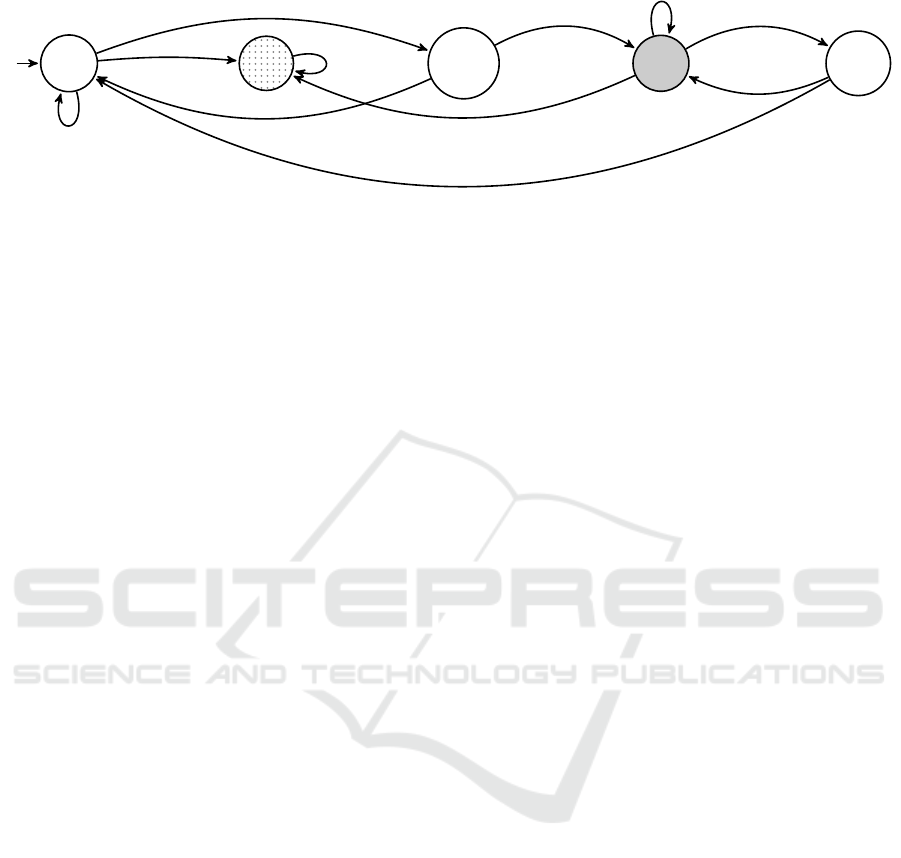
2.2 The Laser Beam Transport System

The LBTS represents the interface between the HPLS

and the experiments. The core of the laser transport

part are the beam transport lines for the six main out-

puts of HPLS that contain mirrors (ﬂat and parabolic)

of different sizes. Before each experiment set-up, the

Novel Approach of Deriving Operational Procedures for a Complex Research Facility

197

IDLE ERR

READY

ON OFF

idle

shoot

expRdy

lerror

shoot

expNxt

shooting

expFin

shoot

expNxt

Figure 1: The HPLS state diagram.

mirrors need to be aligned such that the laser beam

does not produce any damage to the LBTS compo-

nents and/or other unwanted effects. The high cost

of the mirrors and the sensitivity of beam alignment

makes this operation very important for the entire sys-

tem. The alignment is ﬁrst performed in plain air fol-

lowed by the one in vacuum. During an ongoing ex-

periment the LBTS remains in vacuum. The LBTS

can become unaligned (due to external conditions)

and the entire process must be restarted.

The LBTS model is described by a state dia-

gram (see Figure 2) with 5 states as follows {IDLE,

ALAIR, ALVAC, MISAL, ON}. The initial state of

the system is IDLE. Like in the case of HPLS, the

full power beam is only present while in the ON state.

The ALAIR and ALVAC represent the states where

the LBTS is aligned in air and vacuum respectively.

While in one of these two states, if the LBTS becomes

misaligned (the MISAL state) the alignment opera-

tion must be repeated. An experiment starts with the

expRdy and ends by the expNxt transitions. The tO f f

transition marks the fact that the LBTS is not under

vacuum anymore.

To summarize, the states during which the LBTS

is under vacuum are: ALVAC, MISAL and ON. In

the case of a new experiment, the following sequence

must take place (starting from the IDLE state) as:

alAir, alVac, expRdy.

The expRdy action marks the fact that pressure be-

tween the LBTS and the interaction chamber of the

Experiment are equalized (the valves of the LBTS are

opened) and the optics path is ready for the experi-

ment.

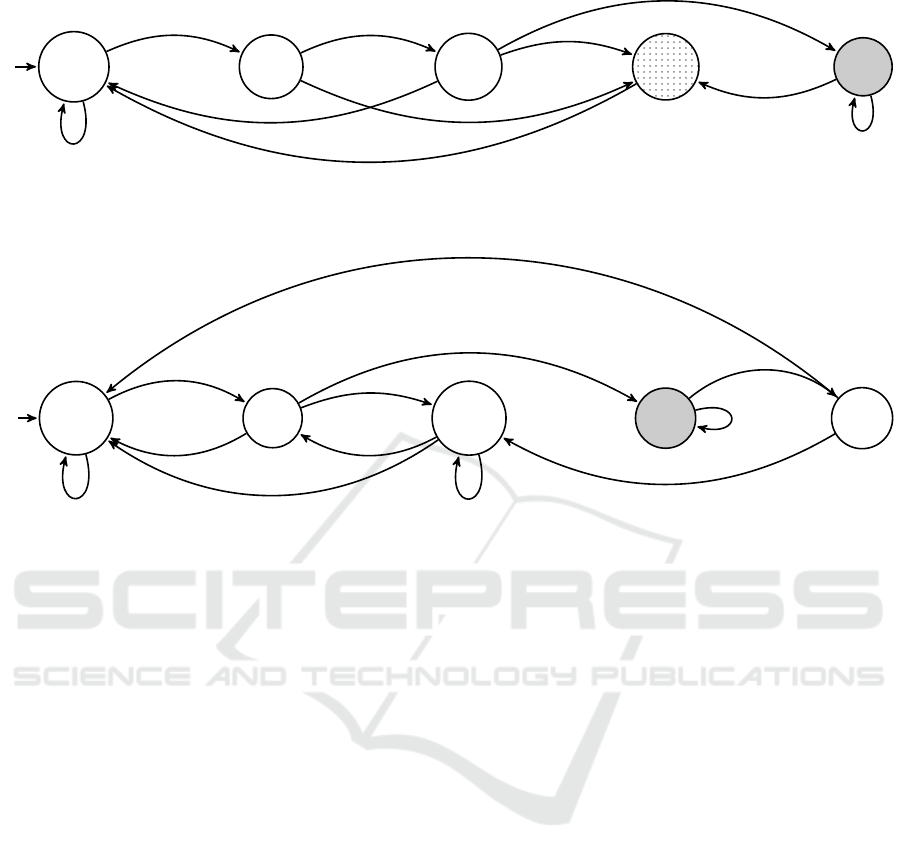
2.3 A Generic Experiment

The experiment room contains the Interaction Cham-

ber (IC) where the experiment set-up is installed and

the rest of equipment placed outside of the chamber

itself. Normally, after a number of experiments, the

pieces of equipment found in the experimental area

but outside of the IC must be replaced or upgraded

during a maintenance phase. After a new experiment

set-up is installed, it is necessary to be aligned with

the LBTS and HPLS.

A generic experiment has three alignment phases.

The ﬁrst phase is performed by using some mechan-

ical method (e.g. a theodolite) in plain air. The

next phase includes a low power laser beam from the

HPLS through LBTS (using the window gate valves).

During this phase, the LBTS must be already in the

ALVAC state. The last phase of the alignment with the

HPLS must be performed in vacuum when the gate-

valves of the LBTS are opened. Thus, during the ﬁrst

two phases, the IC door is unlocked and only during

the third phase it is closed .

The Experiment is modelled by a state di-

agram (see Figure 3) with 5 states as follows

{ESETUP, EALIG, EMAINT, ERUN, EEND}.

For the sake of simplicity, we consider only one state

during which the vacuum alignment is performed (the

EALIG state) instead of considering the full align-

ment process (for example alignment with a theodo-

lite or by using the the alignment beam of the HPLS).

The maintenance phase can only be accessed from the

EALIG state or when an experiment is ﬁnished (the

EEND state). The access inside of the IC is allowed

only after the tO f f , expIcEnter transition sequence

is performed. The expSet marks the moment when the

IC access is disabled. Like in the cases of LBTS and

HPLS, the expRdy marks the fact that the experiment

can start (gate valves of LBTS are opened, the entire

experiment set-up is aligned with the LBTS and the

HPLS beam). The high power laser beam is present

only while in the ERUN state.

After an experiment, radioactive contamination

may occur and therefore the access inside of the ex-

perimental area and the interaction chamber is re-

stricted. There are a set of detectors and ultimately

a person designated to measure the radioactivity level

that allow the access inside. This feature will be in-

cluded as a future extension of the model and pre-

sented in Section 4.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

198

IDLE

ALAIR

ALVAC MISAL ON

idle

alAir

alVac

alErr

expNxt

alErr

expRdy

tO f f

expNxt

shooting

Figure 2: The LBTS state diagram.

ESETU P EALIG EMAINT

ERUN EEND

idle

expSet

expIcEnt

expRdy

expMaint

idle

expIcEnt

expSet

shooting

expNxt

expMaint

expIcEnt

Figure 3: The Experiment state diagram.

3 THEORETICAL BACKGROUND

In this section, an overview of the main abstractions

used for deﬁning the model behavior as well as the

properties it must have in order to fulﬁl its safety con-

siderations is presented.

Note that the following theoretical aspects

are based on the work presented in (Joslin,

2013), (D’Ippolito et al., 2011), (Keller, 1976)

and (D’Ippolito et al., 2012). Also, when referring

to complex systems, it is often useful to segregate

between the known behaviour of the system and its

desired properties. To this end, the known machine

behaviour is described as a Labelled Transition Sys-

tem (LTS) (as deﬁned in (Keller, 1976)) under the as-

sumption of deterministic transitions between a ﬁnite

set of states, while the required system properties are

denoted as formulas in the Fluent Linear Temporal

Logic (FLTL) framework.

Deﬁnition 3.1. A LTS is a tuple S = (Σ

, Λ

, ∆

, σ

where Σ

is the set of all states known to the LTS, Λ

is the set of transition labels, ∆

⊂ Σ

×Λ

×Σ

is the

set of transitions and σ

∈ Σ

is the initial state.

Graphically, LTSs can be seen as graphs, where

nodes are depicted as circles, transitions are repre-

sented by arrows and transition labels are depicted by

the arrow superscripts (e.g. Figures 1, 2, 3). The ini-

tial state of the LTS is depicted by an arrow with no

start point and arriving at the given state (e.g. in ﬁgure

1, State IDLE).

Let σ

, σ

∈ Σ

be two states and λ ∈ Λ

a label.

(σ

, λ, σ

) ∈ ∆

can be expressed as: ”From state σ

given action λ, move to state σ

” and can be written

as σ

−→ σ

The parallel composition of two LTS S

, S

, de-

noted S

k S

can be seen as the parallel execution of

the two LTS. Formally, it can be seen as the cross-

product of the state-space of the two, with a cross-

product alphabet and composition rules that mimic

name-based synchronization in case of an action hav-

ing the same name.

The parallel composition between S

HPLS

, S

LBT S

and S

Experiment

(further called the environment and de-

picted in Figure 4) has 36 states and 129 transitions.

As can be observed, the resulting machine exhibits a

signiﬁcant amount of complexity and entails serious

strain upon human readability.

Deﬁnition 3.2. An LTS S = (Σ, Λ, ∆, σ

) is said to ac-

cept a sequence (trace) w = w

, w

, ... over the set Λ,

where w

∈ Λ if there is a trace: σ

..., with

∈ Σ, ∀n ∈ N, such that σ

i+1

−−→ σ

i+1

∀i ∈ N.

The set of all sequences accepted by a LTS S is

denoted Gen(S).

Novel Approach of Deriving Operational Procedures for a Complex Research Facility

199

Figure 4: S

HPLS

k S

LBT S

k S

Experiment

As LTS is the tool for describing system behav-

ior, a different tool is required for expressing the con-

straints that must be attained for such a system. To

this end, the Fluent Linear Temporal Logic is being

employed.

In the following, the Fluent Linear Temporal

Logic constructs are deﬁned and explained.

Deﬁnition 3.3. A ﬂuent over a LTS S = (Σ, Λ, ∆, σ

) is

tuple

I, O, Init

, where I ⊂ Λ, O ⊂ Λ and Init ∈ Bool.

Informally, a ﬂuent represents an abstract state -

or logical proposition - within the problem domain

which is enabled whenever an action λ ∈ I occurs and

is disabled whenever an action λ ∈ O occurs. Thus, a

ﬂuent describes a logical proposition in the context of

a LTS given an input word accepted by the LTS. An

intuitive wording for a ﬂuent f l is ”The system goes

into f l when encountering an input from the set I and

exits f l when encountering an input from the set O”.

In order to express constraints and desired out-

comes for a given composition of systems, the FLTL

formalism is employed, comprising a set of FLTL for-

mulas.

A FLTL - ﬂuent linear temporal logic - formula is

derived from a LTL (Linear Temporal Logic) formula

(Giannakopoulou and Magee, 2003) where basic for-

mulas are in fact ﬂuents. In LTL, formulas are either

basic formulas (predicates) or compositions of other

formulas (using logical operators or temporal opera-

tors).

Deﬁnition 3.4. A FLTL formula is given inductively:

φ , Fl | ¬φ | φ ∨ ψ | X φ| φ U ψ

Where φ, ψ are LTL formulas, Fl is a ﬂuent from

FLTL, ¬ is the logical not operator, ∨ is the logical

or operator, X is the next operator and U is the until

operator.

Additional operators are deﬁned based on the

aforementioned: []φ (always operator), <> φ (even-

tually operator), φ ∧ ψ (logical and operator) and

φ → ψ (φ implies ψ). Note that the always, eventually

and implies operators will be frequently employed in

solving the problem presented in the current paper.

An inﬁnite-length word is said to always satisfy

a FLTL formula if for any sufﬁx of the word, it still

satisﬁes the formula. An inﬁnite-length word is said

to eventually satisfy a FLTL formula if there is a sufﬁx

of the given word that satisﬁes the given formula. An

inﬁnite-length word is said to satisfy a FLTL φ → ψ

if φ is satisﬁed only given that ψ is also fulﬁlled.

An inﬁnite-length word is said to always even-

tually satisfy a FLTL formula if, for every sufﬁx of

the given word, the formula will eventually satisfy the

formula. More intuitively, the formula will be satis-

ﬁed inﬁnitely many times.

For the purposes of the current paper, the informal

deﬁnitions presented above are sufﬁcient to acquire

insights into the proposed solution. For further de-

tails, see (Joslin, 2013).

The problem of Safe Generalised Reactivity

(SGR(1)) has been thoroughly described in (Joslin,

2013). It is beyond the scope of this paper to present

the results of the aforementioned. Nevertheless, for

a better understanding, the formal deﬁnition of the

problem is provided, which will be explained brieﬂy.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

200

Deﬁnition 3.5. The SGR(1) LTS control problem is

as follows: Given a tuple ε = (E, H, A

) where E

is a deterministic environment described by an LTS,

is the set of controllable actions in LTS and

H =

{

(

0, I), (As, G)

}

, such that I = []ρ (always ρ),

As = ∧

i=1

([] <> φ

) and G = ∧

i=1

([] <> γ

), where

ρ, φ

, γ

are FLTL formulas, ﬁnd a controller (LTS

machine) M with the set of actions ⊆ A

such that

∀π ∈ Gen(EkM),then []π  I

and

∀π ∈ Gen(EkM),then π  (As → G)

where ρ is called safety property, φ

are the assump-

tions regarding the system evolution, and ψ

are the

liveness properties of the system under consideration.

Thus, the SGR(1) LTS control problem is that of

ﬁnding a controller, given a behaviour of the sys-

tem and some goals. The second goal imposed in

the above deﬁnition is called liveness goal. In free

speech, it can be expressed as: knowing that the sys-

tem will fulﬁl several properties inﬁnitely many times

- i.e. it will evolve -, then ensure that a set of prop-

erties are fulﬁlled inﬁnitely many times when com-

posed with the generated controller. In the current pa-

per, due to the nature of the application proposed, the

safety properties will mostly be taken into account.

They can be read as: for whatever sequence of actions

that may occur in EkM (the environment controlled

by the generated controller), then the safety property

will always hold.

The problem of controller synthesis has been

solved in (Joslin, 2013). The description of inter-

nals of the algorithm that performs this speciﬁc task

is out of the scope of the current paper. Nevertheless,

a tool that offers the capabilities expressed above ex-

ists (D’Ippolito et al., 2008) and has been success-

fully used for a number of applications: controller

synthesis for a robot arm (Braberman et al., 2013) or

in automatic synthesis of behavior protocols for com-

posable web-services (Bertolino et al., 2009); (Isley,

2017) presents more case studies.

The approach to solving the problem described

within this paper was to utilize the notions of LTS

and FLTL formulas and the MTSA tool to check and

enforce several safety constraints in the depicted en-

vironment. The following section describes the ap-

proach to this end and several assumptions that aided

in the understanding and modeling of the system at

hand.

4 PRACTICAL EXAMPLE

The current framework presents a proof-of-concept of

the operational procedures design for a complex re-

search facility. Figure 5 presents the work-ﬂow for

automatically generating a procedure. First step is

the modelling of each sub-system and its implemen-

tation as a FSP by exploiting the compositional prop-

erty used to describe the LTSs described in (Magee

and Kramer, 2006). Next step is to deﬁne the set of

constraints that can be either local or between sub-

systems.

With the help of MTSA tool, the existence of a

controller given set of constraints can be checked.

This step can have multiple iterations and may in-

clude further model modiﬁcations or reﬁnements of

the constraints.

Models

Constraints

Database

MTSA

Controller

∃

Yes

No No

Procedure

Figure 5: Automatic Procedure Generation.

The set of allowed transitions after the parallel

composition of the controller with the environment

represents the procedure. The result automatically

satisﬁes the imposed constraints and can be visually

checked with the MTSA tool. Further, we present

an example based on the models deﬁned in Sec-

tion 2. The environment can be already challeng-

ing for a human operator to ﬁnd a controller that

generates a feasible trace without violating the im-

posed constraints. The set of controllable transitions

is {expRdy, shoot, expNxt, alAir, alVac, expSet,

expIcEnt, expMaint} and represents the signals that

can be enabled or disabled such that the feasible trace

is accepted. The set of imposed constraints is:

• P1 - the LBTS must be ﬁrst aligned in air before

starting the experiment alignment:

fluent AF_alAir = <alAir,{alErr,expNxt}>

fluent AF_expSet =

<expSet,{expMaint,expNxt,alErr}>

Novel Approach of Deriving Operational Procedures for a Complex Research Facility

201

assert EXPALAIR = [](AF_expSet -> AF_alAir)

ltl_property P1 = EXPALAIR

• P2 - only after the experimental set-up is aligned the

alignment in vacuum is performed:

assert EXPALVAC = [](AF_alVac -> AF_expSet)

ltl_property P2 = EXPALVAC

• P3 - the entire system is declared ready for a new

experiment only after vacuum alignment was success-

ful:

fluent AF_expRdy = <expRdy,{expNxt}>

fluent AF_alVac = <alVac,{alErr, expNxt}>

assert EXPREADY = [](AF_expRdy ->AF_alVac)

ltl_property P3 = EXPREADY

• P4 - the access in the interaction chamber is allowed

only after the vacuum was removed post tO f f transi-

tion:

fluent AF_InVac = <alVac,tOff>

fluent AF_IcEnter =

<expIcEnt, expSet> initially 1

assert F_ENTERIC = [](AF_InVac -> !AF_IcEnter)

ltl_property P4 = F_ENTERIC

• NotInError - the ERR state is avoided:

fluent AF_AvoidError = <lerror,A\{lerror}>

ltl_property NotInError =

[](!(AF_AvoidError))+{A})

By running the MTSA tool, we ﬁnd a 16 states

controller that allows the following feasible trace:

alAir, expSet, alVac, expRdy,

(shoot, expFin, shoot, expFin, ...),

expNxt, tO f f , expIcEnt → ...(alAir)

representing the operational procedure for running an

experiment in Experiment by using the HPLS and the

LBTS. A literal translation of the procedure can be:

Procedure 1. Running a generic experiment:

Precondition: HPLS, LBTS and Experiment in IDLE

state;

1. Align the LBTS in air (alAir transition);

2. If 1 then set-up the experiment in the IC (expSet

transition);

3. If 2 then align the LBTS in vacuum (alVac transi-

tion);

4. If 3 then start the shooting (shoot transition);

5. If experiment stops then experiment is ﬁnished

(expFin transition);

1 If experiment resumes then re-start the shooting

(go to 4);

2 Else experiment is ﬁnished;

Postcondition: After an experiment, always prepare

for the next one (expNext transition) as follows:

6. If 3 was successful then remove the vacuum (tO f f

transition);

7. Enable the access into the IC (expIcEnt transi-

tion);

Besides the current trace we can investigate other

traces to check if further constraints can be imposed.

Since the alErr transition is not controllable, it can

happen at any time. It must be observed that there

is no restriction regarding the number of shots (per-

formed experiments) or the maintenance procedure

(expMaint transition). Therefore, we added the fol-

lowing constraint:

• MAINTENANCE - after a number of shots (de-

ﬁned by Max) it is mandatory to perform the mainte-

nance procedure:

const Max = 2 //maximum number of shoots

range Int = 0..Max

MAINTENANCE(N=0) = SHOOT[N],

SHOOT[v:Int] = (

when(v<Max) shoot->SHOOT[v+1]|

when(v==Max) {shoot,alVac}->ERROR |

when(v>0) expMaint->SHOOT[0] |

A\{expMaint,shoot}->SHOOT[v]).

• SHOOTSLIMIT - multiple shoots cycles are not

allowed:

SHOOT_ONCE = (shoot->expNxt->SHOOT_ONCE).

For the latter constraints together with the previ-

ous set, the MTSA tool produces a state machine with

67 states that represents the controller enforcing the

following behaviour:

1. an experiment cannot contain multiple shooting

sequences (shoot, shoot, ...) and,

2. there can be only Max experiments carried out in

total and,

3. the Max + 1 time, the maintenance oper-

ation must be performed by including the

expMaint transition in the execution sequence

(alVac, expSet, expMaint, expSet...)

The new procedures can be described as:

Procedure 2. Running a generic experiment:

Precondition: HPLS, LBTS and Experiment in IDLE

state;

1. Align the LBTS in air (alAir transition);

2. If 1 then set-up the experiment in the IC (expSet

transition);

3. If 2 then align the LBTS in vacuum (alVac transi-

tion);

4. If 3 then start the shooting (shoot transition);

5. If experiment stops then experiment is ﬁnished

(expFin transition);

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

202

Postcondition: After an experiment, always prepare

for the next one (expNext transition) as follows:

6. If 3 was successful then remove the vacuum (tO f f

transition);

7. Enable the access into the IC (expIcEnt transi-

tion);

Procedure 3. The maintenance operations

(expMaint transition) must pe performed after 2

consecutive experiments at most.

Procedure 2 is identical to 1 with the exception

that it can contain only one shoot, expFin sequence.

The latter enforces maintenance operations after a

predeﬁned number of experiments.

5 CONCLUSIONS

The current work proposes a novel approach for de-

riving operational procedures for a complex facil-

ity where multiple sub-systems interact between each

other. The constraints can be either local (at the

sub-system level) or global (between different sub-

systems). By using the MTSA software, we can au-

tomatically generate and simulate a procedure such

that the effects of the constraints can be understood.

A high workload represents the development of the

models based on the deﬁned requirements. Further-

more, the constraint deﬁnition may include multiple

iterations based on their effects over the entire system

(the parallel composition of all sub-systems).

Future extensions of the current work are mostly

aimed to developing the models by including more

details regarding their behaviour. However, by aug-

menting the models complexity, the constraints deﬁ-

nition will remain the same but their number will be

increased (based on the newly introduced states and

transitions). The ultimate goal for all further devel-

opments is the complete automation of different steps

(eg. automatic alignment procedure, automatic mis-

alignment detection and correction, etc.) and the im-

plementation of the synthesised controller for the au-

tomation of the entire operational process.

ACKNOWLEDGEMENTS

We would like to thank the members of the ELI-

NP team with special thanks to Ioan D

ancus¸ (for the

fruitful insights regarding the alignment process) and

Daniel Ursescu (for reviewing and his valuable re-

marks). This work is supported by the Project Ex-

treme Light Infrastructure Nuclear Physics (ELI-NP)

- Phase II, a project co-ﬁnanced by the Romanian

Government and European Union through the Euro-

pean Regional Development Fund.

REFERENCES

Bertolino, A., Inverardi, P., Pelliccione, P., Pelliccione, P.,

and Tivoli, M. (2009). Automatic synthesis of behav-

ior protocols for composable web-services. In Pro-

ceedings of the the 7th Joint Meeting of the European

Software Engineering Conference and the ACM SIG-

SOFT Symposium on The Foundations of Software En-

gineering, pages 141 – 150.

Braberman, V., D’Ippolito, N., Piterman, N., Sykes, D., and

Uchitel, S. (2013). Controller synthesis: From mod-

elling to enactment. In Proceedings of the 2013 Inter-

national Conference on Software Engineering, pages

1347 – 1350.

D’Ippolito, N., Braberman, V., Piterman, N., and Uchitel, S.

(2011). Synthesis of live behaviour models for fallible

domains. In 2011 33rd International Conference on

Software Engineering (ICSE), pages 211–220.

D’Ippolito, N., Braberman, V., Piterman, N., and Uchitel, S.

(2012). The Modal Transition System Control Prob-

lem, pages 155–170. Springer Berlin Heidelberg.

D’Ippolito, N., Fischbein, D., Chechik, M., and Uchitel, S.

(2008). Mtsa: The modal transition system analyser.

In 2008 23rd IEEE/ACM International Conference on

Automated Software Engineering, pages 475–476.

et.al., F. N. (2016). Laser driven nuclear physics at elinp.

Romanian Reports in Physics, 68:S37S144.

Gales, S., Balabanski, D. L., Negoita, F., Tesileanu, O., Ur,

C. A., Ursescu, D., and Zamﬁr, N. V. (2016). New

frontiers in nuclear physics with high-power lasers

and brilliant monochromatic gamma beams. Physica

Scripta, 91(9):093004.

Giannakopoulou, D. and Magee, J. (2003). Fluent model

checking for event-based systems. SIGSOFT Software

Engineering Notes, 28(5):257–266.

Isley, P. (2017). The modal transition system analyser.

http://mtsa.dc.uba.ar/.

Joslin, P. (2013). Synthesis of event-based controllers for

software engineering. PhD thesis, Imperial College

London.

Keller, R. M. (1976). Formal veriﬁcation of parallel pro-

grams. Commun. ACM, 19(7):371 – 384.

Magee, J. and Kramer, J. (2006). Concurrency: State Mod-

els and Java Programs. Wiley Publishing, 2nd edition.

Ur, C., Balabanski, D., Cata-Danil, G., Gales, S., Morjan,

I., Tesileanu, O., Ursescu, D., Ursu, I., and Zamﬁr, N.

(2015). The elinp facility for nuclear physics. Nuclear

Instruments and Methods in Physics Research Sec-

tion B: Beam Interactions with Materials and Atoms,

355(9):198 – 202.

Ursescu, D., Cheriaux, G., Audebert, P., Kalashnikov, M.,

Toncian, T., Cerchez, M., Kaluza, M., Paulus, G.,

Priebe, G., Dabu, R., Cernaianu, M., Dinescu, M.,

Asavei, T., Dancus, I., Neagu, L., Boianu, A., Hooker,

C., Barty, C., and Haefner, C. (2016). Laser beam de-

livery at eli-np. Romanian Reports in Physics, 68:S11

S36.

Novel Approach of Deriving Operational Procedures for a Complex Research Facility

203