New SLICOT Routines for Standard and Descriptor Systems
Vasile Sima
1
and Andreas Varga
2
1
National Institute for Research & Development in Informatics, 8–10 Bd. Mares¸al Averescu, Bucharest, Romania
2
DLR-Oberpfaffenhofen (Retired), Gilching, Germany
Keywords:
Descriptor Systems, Generalized Eigenvalues, Numerical Methods, Software, Stability.
Abstract:
New routines included into the SLICOT Library for standard and descriptor systems are presented. The un-
derlying numerical methods, the functionality and the main features of the added software are described. The
topics covered include stable/unstable and finite/infinite spectrum separation, additive spectral decomposition,
and removing the non-dynamic modes. The main implementation issues are also addressed. Numerical results
obtained using the software on a large set of examples of various complexity and difficulty are summarized.
The results reported highlight the performance and capabilities of this SLICOT Library extension.
1 INTRODUCTION
Consider a linear time-invariant system in a descriptor
state-space representation of the form
Eλx(t) = Ax(t)+Bu(t), y(t) = Cx(t)+ Du(t), (1)
with x(t) the n-dimensional state vector, u(t) and y(t)
the m-dimensional and p-dimensional input and out-
put vectors, respectively, and E, A, B,C, and D the de-
scriptor,state, input, output, and feedthrough matrices
of suitable sizes, with E and A square and E possibly
singular. According to the system type, λx(t) := ˙x(t)
or λx(t) := x(t + 1), for a continuous- or discrete-time
system, respectively. The system (1) is alternatively
denoted as (A − λE, B,C, D), where D can be omit-
ted if D = 0. The case E = I
n
, the identity matrix
of order n, corresponds to a standard state-space re-
alization and any descriptor realization with nonsin-
gular E can be reduced to an equivalent standard sys-
tem (E
−1
A − λI
n
,E
−1
B,C,D). However, this reduc-
tion must be generally avoided if E is ill-conditioned
with respect to inversion.
If the matrix pencil A− λE is regular (i.e., det(A−
λE) 6≡ 0), then (1) can also be considered as an order n
descriptor system realization of the rational p × m
transfer-function matrix,
G(λ) = C(λE − A)
−1
B+ D, (2)
where λ is here a complex variable corresponding to
the Laplace transform or Z-transform. Any p× m ra-
tional matrix G(λ) has a descriptor realization of the
form (1) which satisfies (2). Also, there exist min-
imal order realizations, with least possible order n.
This connection between descriptor systems and ra-
tional matrices is the basis for the development of
numerically reliable algorithms for manipulating ra-
tional matrices via their equivalent descriptor realiza-
tions.
Continuous-time descriptor systems are often
used for modelling certain mechanical systems, e.g.,
with contact phenomena, or interconnected systems
with algebraic loops, while discrete-time descriptor
systems are often encountered for modelling eco-
nomic processes. Descriptor representations are es-
sential for appropriate numerical operations with
rational (transfer-function) matrices, as highlighted
in (Varga, 2017) for solving fault diagnosis problems.
Two linear matrix pencils play an important role in
defining and characterizing the properties of transfer-
function matrices (2) via their equivalent descriptor
realizations (1). The regular pole pencil P(λ) = A−
λE is useful to characterize the pole structure of (2)
via its Weierstrass canonical form, while the system
matrix pencil
S(λ) =

A− λE B
C D

,
defines the zero and singularity structures of (1) via
its Kronecker canonical form. The knowledge of
the pole and zero structures allows to state sim-
ple conditions to characterize important properties
of the transfer-function matrix (2), such as proper-
ness, stability, minimum-phase, or of the descriptor
system (1), such as controllability, observability, fi-
nite or infinite stabilizability or detectability, or ir-
Sima, V. and Varga, A.
New SLICOT Routines for Standard and Descriptor Systems.
DOI: 10.5220/0006396605350542
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 535-542
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
535

reducibility. The numerical computation of Weier-
strass and Kronecker canonical forms involves pos-
sibly ill-conditioned (non-orthogonal) transformation
matrices. Numerically reliable algorithms and proce-
dures for descriptor systems, as discussed in the fol-
lowing sections, resort to alternative forms, like gen-
eralized Schur form and Kronecker-like forms, which
provide all the above structural information and are
obtainable using orthogonal transformations.
Descriptor systems are investigated in several
books, e.g., (Duan, 2010), and many technical papers,
e.g., (Demmel and K˚agstr¨om, 1993; K˚agstr¨om and
Van Dooren, 1990; Misra et al., 1994; Van Dooren,
1981; Varga, 1990; Varga, 1996). Related numeri-
cal issues are addressed, for instance, in (Anderson
et al., 1999; Demmel and K˚agstr¨om, 1993; Golub
and Van Loan, 2012; Van Dooren, 1981; Varga, 1996;
Varga, 2004; Varga, 2017).
This paper presents the main new routines in-
cluded by the authors into the SLICOT Library
1
for
standard and descriptor systems, the underlying nu-
merical techniques, as well as a summary of the re-
sults obtained using this software on a large set of ex-
amples of various complexity and difficulty from the
COMPl
e
ib collection (Leibfritz and Lipinski, 2003).
The organization of the paper is as follows. Section 2
summarises the main numerical techniques for sta-
ble/unstable and finite/infinite spectrum separation,
additive spectral decomposition, and non-dynamic
modes removal. Section 3 describes the functionality
of the main newly added SLICOT routines for stan-
dard and descriptor systems, as well as the essential
implementation issues. Section 4 summarizes part of
the numerical results obtained, highlighting the per-
formance and capabilities of this SLICOT Library ex-
tension. Section 5 contains some conclusions.
2 NUMERICAL TECHNIQUES
FOR DESCRIPTOR SYSTEMS
Many procedures for descriptor systems analysis
and control design involve the orthogonal reduction
of a matrix pencil A − λE, defined by a pair of
square matrices, (A,E), to the generalized real Schur
form (GRSF), using the standard QZ algorithm, see
e.g., (Golub and Van Loan, 2012). The transformed
pair is (
e
A,
e
E), with
e
A = Q
T
AZ,
e
E = Q
T
EZ, where
Q
T
Q = QQ
T
= I, Z
T
Z = ZZ
T
= I,
e
E is upper tri-
angular, and
e
A is block upper triangular, with diag-
onal blocks of order 1 and 2, corresponding to the
1
www.slicot.org
real and complex conjugate eigenvalues of the pen-
cil, respectively. (If the 2× 2 pairs of diagonal blocks
may have real eigenvalues, the pair is called upper
quasi-triangular.) The GRSF can be reordered, us-
ing also orthogonal transformation matrices, so that
the eigenvalues appear in any desired order along the
diagonal blocks of the transformed matrix pair. The
cost of reordering is small compared to the initial re-
duction cost. The real Schur form (RSF) of a ma-
trix,
e
A = Z
T
AZ, and an orthogonal transformation ma-
trix, Z, are similarly used for standard systems. These
computations can be performed using state-of-the-art
linear algebra software, such as LAPACK (Anderson
et al., 1999) or MATLAB
r
. The main advantage of
using orthogonal transformations is that the problem
conditioning is preserved, so that the errors in the data
are essentially not magnified during the calculations.
Several key problems for descriptor systems are
summarized below.
2.1 Stable/Unstable Separation
The reordering of GRSF can be used, for instance,
to separate the stable and unstable parts of a system.
Let (A − λE,B,C) be a descriptor system (1), and
let α define the desired boundary of the stability do-
main, with α ≤ 0 for the real parts of the eigenval-
ues, and α ≤ 1 for the moduli of the eigenvalues, for
continuous- and discrete-time systems, respectively.
(Choosing α = −τ or α = 1− τ in the continuous- or
discrete-time case, respectively, where τ > 0, imposes
a certain stability degree τ.) For convenience, assume
here that E is nonsingular. Denote Λ(A,E) the spec-
trum of the pencil A− λE, i.e., the set of its eigenval-
ues, {λ
i
, i = 1 : n} (multiplicities counted). Let Q and
Z be orthogonal matrices so that
Q
T
AZ =:
e
A =

e
A
11
e
A
12
0
e
A
22

,
Q
T
EZ =:
e
E =

e
E
11
e
E
12
0
e
E
22

, (3)
with
e
A− λ
e
E in GSRF,
e
A
j j
,
e
E
j j
of order n
j
, j = 1, 2,
and
Λ(
e
A
11
,
e
E
11
) = {λ
i
|ℜ(λ
i
) < α},
Λ(
e
A
22
,
e
E
22
) = {λ
i
|ℜ(λ
i
) ≥ α},
for a continuos-time system, and similarly, for a
discrete-time system, when ℜ(λ
i
), the real part of λ
i
above, is replaced by |λ
i
|, the modulus of λ
i
. There-
fore, the system (
e
A − λ
e
E,
e
B,
e
C), with
e
B := Q
T
B, and
e
C := CZ, is an equivalent system having all stable
eigenvalues in the leading positions. Then, the first
n
1
columns of the matrices Q and Z form orthogonal
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
536

bases for the left and right stable deflating subspaces
of (A,E). When E is singular, the infinite eigenval-
ues can be deflated, and the remaining system can be
handled in a similar way. The procedure is, however,
more involved.
2.2 Block Diagonalization
Some applications, as, for example, the computa-
tion of additive spectral decompositions of transfer-
function matrices, require that the separated parts
in (3) be decoupled (i.e.,
e
A
12
= 0 and
e
E
12
= 0).
This can be achieved by block-diagonalization with
two diagonal blocks. However, the procedure in-
volves non-orthogonal transformations. Here, it
is not necessary to make any stability related as-
sumption in (3), but only assuming that the spec-
tra of (
e
A
11
,
e
E
11
) and (
e
A
22
,
e
E
22
) are disjoint, i.e.,
Λ(
e
A
11
,
e
E
11
)
T
Λ(
e
A
22
,
e
E
22
) =
/
0. (A GRSF is needed
to proceed with efficient computations.) It is pos-
sible to simultaneously annihilate
e
A
12
and
e
E
12
by
solving for X and Y the generalized Sylvester equa-
tion (K˚agstr¨om and Van Dooren, 1990):
e
A
11
Y − X
e
A
22
= σ
e
A
12
,
e
E
11
Y − X
e
E
22
= σ
e
E
12
, (4)
where 0 ≤ σ ≤ 1 is a scaling factor, set to avoid over-
flow in X and Y. The condition on disjoint sets of
eigenvalues theoretically guarantees the existence of
a solution to (4) with σ = 1. The transformation ma-
trices for decoupling are
Q =

I
n
1
X
0 I
n
2

, Z =

I
n
1
−Y
0 I
n
2

,
so that the two diagonal pairs of submatrices of
(Q
e
AZ,Q
e
EZ) coincide to those of (
e
A,
e
E), while the
off-diagonal blocks,
e
A
12
and
e
E
12
, are annihilated. The
transformeddescriptorsystem with (
e
A,
e
E) in block di-
agonal form has
e
B = QB, and
e
C = CZ. The matrix D
is unchanged. With a partition of
e
B =

e
B
T
1
e
B
T
2

T
and
e
C =

e
C
1
e
C
2

, then (
e
A
1
− λ
e
E
1
,
e
B
1
,
e
C
1
,D) and (
e
A
2
−
λ
e
E
2
,
e
B
2
,
e
C
2
) represent an additive spectral decompo-
sition of the system transfer-function matrix.
When E = I
n
, the similarity transformation to a
system with state matrix in block-diagonal form is
e
A = U
−1
AU,
e
B= U
−1
B,
e
C =CU, U =

I
n
1
−X
0 I
n
2

,
where X is the solution of the standard Sylvester
equation,
e
A
11
X − X
e
A
22
= σ
e
A
12
. The inverse of U is
obtained by replacing −X by X.
2.3 Finite/Infinite Separation
When E is singular,some applications require decom-
positions of the form in (3) with the (1,2) blocks non-
zero or zero, but with a separation between finite and
infinite eigenvalues. Either finite or infinite eigenval-
ues can appear in the resulting leading diagonal block
pair. Let assume that the regular pole pencil A− λE
of the descriptorsystem (A−λE,B,C) has been trans-
formed to one of the forms (5) or (6)
Q
T
AZ =

A
f
⋆
0 A
i

, Q
T
EZ =

E
f
⋆
0 E
i

, (5)
Q
T
AZ =

A
i
⋆
0 A
f

, Q
T
EZ =

E
i
⋆
0 E
f

, (6)
where the subpencil A
f
− λE
f
contains the finite
eigenvalues, the subpencil A
i
− λE
i
contains the in-
finite eigenvalues, and ⋆ denotes sumatrices whose
values are not important in this context. Clearly, this
transformationrequiresthat E
f
and A
i
be nonsingular;
in implementations, both E
f
and A
i
are upper triangu-
lar. Other procedures than those in Subsections 2.1
and 2.2 are needed in this case. Specifically, the re-
duction algorithm in (Misra et al., 1994) can be used.
For (5), the first step of the algorithm reduces the sys-
tem to a SVD-like coordinate form,
Q
T
AZ =

A
11
A
12
A
21
A
22

, Q
T
EZ =

E
r
0
0 0

,
where E
r
is an upper triangular nonsingular matrix of
order r = rank(E) ≤ n. This can be obtained using
either singular value decomposition (SVD), or, more
efficiently, a (truncated) QR decomposition with col-
umn pivoting, followed by a special RQ decomposi-
tion (Golub and Van Loan, 2012). Then, the A
22
ma-
trix is reduced similarly to the QR-form
A
22
=

A
r
X
0 0

,
with A
r
an upper triangular nonsingular matrix of or-
der r
2
= rank(A
22
), and X a full matrix. The second
step performs the finite-infinite separation. The com-
putations are done on a block column permutation of
the matrices obtained in the first step, rewritten as
A :=

B
1
A
1
D
1
C
1

, E :=

0 E
1
0 0

, (7)
where, initially, E
1
= E
r
, A
1
= A
11
, C
1
= A
21
, B
1
=
A
12
, and D
1
= A
22
. The same block column per-
mutation acts on the transformed output matrix C.
A finite sequence of iterations is then applied to the
matrices in (7), exploiting the current structure. Ini-
tially, the order of the matrix D
1
is n − r, with the
New SLICOT Routines for Standard and Descriptor Systems
537

last ρ = n− r − r
2
rows zero, and the leading r
2
× r
2
submatrix, A
r
, upper triangular. At each subsequent
iteration, the current matrix D
1
is row compressed
using standard and rank-revealing QR factorizations
with column pivoting, and the transformations are ap-
plied to B and C
1
from the left. Then, the bottom part
of C
1
, corresponding to the zeroed part in D
1
, is col-
umn compressed via RQ factorization, while keeping
E
1
upper triangular. The transformations are also ap-
plied to A
1
, B
1
, B, from the left, and to A
1
and C, from
the right. The matrices D
1
and C
1
are redefined after
omitting the zeroed parts. The process ends when D
1
has maximal row rank. Another block column permu-
tation returns
A =


A
1
B
1
⋆
C
1
D
1
⋆
0 0 A
i


, E =


E
1
0 ⋆
0 0 ⋆
0 0 E
i


,
and C
1
is annihilated by rotations from the right (with
pivots in the diagonal elements of D
1
). Finally, the
matrices A
i
and E
i
have the staircase forms
A
i
=





A
0,0
A
0,k
·· · A
0,1
0 A
k,k
·· · A
k,1
.
.
.
.
.
.
.
.
.
.
.
.
0 0 · ·· A
1,1





, E
i
=





0 E
0,k
·· · E
0,1
0 0 ··· E
k,1
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· 0





,
(8)
where A
j, j
, j = 0,1,..., k, are nonsingular upper tri-
angular submatrices.
The same procedure is used for (6) by working on
the dual system (and interchanging m with p, and Q
with Z), and transforming the results by pertranspo-
sition,
A := PA
T
P, E := PE
T
P, B := PC
T
, C := B
T
P,
to preserve the shapes of A and E, where P is a matrix
with 1 on the secondary diagonal, and with 0 in the
other entries. (The transformation matrices are also
updated as Q := QP, Z := ZP.) Finally, the matrices
A
i
and E
i
have the staircase forms
A
i
=





A
1,1
·· · A
1,k
A
1,0
.
.
.
.
.
.
.
.
.
.
.
.
0 ··· A
k,k
A
k,0
0 ··· 0 A
0,0





, E
i
=





0 E
1,k
·· · E
1,0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· E
k,0
0 0 ··· 0





,
(9)
where A
j, j
, j = 0,1,..., k, are nonsingular upper tri-
angular submatrices. In both cases, the pair (A
0,0
,0)
contains the system non-dynamic infinite modes.
2.4 Removing the Non-dynamic Modes
The reduction to the SVD-like coordinate form can
be used to elliminate the non-dynamic modes of a de-
scriptor system, using the following procedure:
1. Reduce the system to the SVD-like coordinate
form (Q
T
AZ − λQ
T
EZ,Q
T
B,CZ), where
Q
T
AZ =


A
11
A
12
A
13
A
21
A
22
0
A
31
0 0


,
Q
T
EZ =


E
11
0 0
0 0 0
0 0 0


, Q
T
B =


B
1
B
2
B
3


,
CZ =

C
1
C
2
C
3

, (10)
where E
11
and A
22
are upper triangular invertible
matrices.
2. Compute the reduced descriptor system with-
out non-dynamic modes as (A
r
− λE
r
,B
r
,C
r
,D
r
),
where
A
r
=

A
11
− A
12
A
−1
22
A
21
A
13
A
31
0

,
E
r
=

E
11
0
0 0

, B
r
=

B
1
− A
12
A
−1
22
B
2
B
3

,
C
r
=

C
1
−C
2
A
−1
22
A
21
C
3

,
D
r
= D−C
2
A
−1
22
B
2
. (11)
3. Optionally, reduce the descriptor system to the
normalized form with A
r
:= diag(E
−1
11
,I)A
r
, B
r
:=
diag(E
−1
11
,I)B
r
, E
r
= diag(I,0).
The reduced system order is n− r
2
, r
2
:= rank(A
22
).
3 IMPLEMENTATION ISSUES
The functionality of several new main routines
for standard and descriptor systems, added to the
SLICOT Library, is briefly described.
MB03QG reorders the diagonal blocks of a selected
principal subpencil of an upper quasi-triangular ma-
trix pencil A − λE, together with their generalized
eigenvalues, using orthogonal equivalence transfor-
mations Q and Z as in (3). After reordering, the
leading block of the subpencil has generalized eigen-
values in a suitably defined domain of interest, usu-
ally related to stability/instability in a continuous- or
discrete-time sense. The system type, stability option,
and a bound α for the real parts or moduli of the gen-
eralized eigenvalues have to be specified on input.
TB01PX finds a reduced (controllable, observable,
or minimal) state-space representation (A
r
,B
r
,C
r
) for
an original state-space representation (A,B,C) using
the following procedure:
1. If a minimal or controllable realization is desired,
the pair (A,B) is reduced by orthogonal similar-
ity transformations to the controllability staircase
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
538

form (Van Dooren, 1981), and a controllable real-
ization (A
c
,B
c
,C
c
) is extracted, where A
c
results
in an upper block Hessenberg form.
2. If a minimal or observable realization is desired,
the same algorithm is applied to the dual of the
system (A
c
,B
c
,C
c
) or (A,B,C), respectively, to
extract an observable realization (A
r
,B
r
,C
r
). In
the first case, the resulting realization is also con-
trollable, and thus minimal. The state matrix A
r
is
in an upper block Hessenberg staircase form.
TB01UY finds a controllable realization for the lin-
ear time-invariant multi-input system
λx = Ax+ B
1
u
1
+ B
2
u
2
, y = Cx,
where A, B
1
, B
2
, and C are n × n, n × m
1
, n × m
2
,
and p× n matrices, respectively, and A and

B
1
B
2

are reduced to an orthogonal canonical form using
(and optionally accumulating) orthogonal similarity
transformations, which are also applied to C. Specif-
ically, the system (A,

B
1
B
2

,C) is reduced to the
triplet (
e
A,

e
B
1
e
B
2

,
e
C), where
e
A = U
T
AU,

e
B
1
e
B
2

=
U
T

B
1
B
2

,
e
C = CU, with
e
A =

A
c
⋆
0 A
nc

,

e
B
1
e
B
2

=

B
c
1
B
c
2
0 0

,
and A
c
and

B
c
1
B
c
2

given by
A
c
=








A
11
A
12
··· A
1,q−2
A
1,q−1
A
1q
A
21
A
22
··· A
2,q−2
A
2,q−1
A
2q
A
31
A
32
··· A
3,q−2
A
3,q−1
A
3q
0 A
42
··· A
4,q−2
A
4,q−1
A
4q
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 · ·· A
q,q−2
A
q,q−1
A
qq








,

B
c
1
B
c
2

=






A
1,−1
A
1,0
0 A
2,0
0 0
.
.
.
.
.
.
0 0






, (12)
where the block A
i,i−2
is a τ
i
× τ
i−2
full row rank ma-
trix (with τ
−1
= m
1
, τ
0
= m
2
), i = 1,...,q, and q/2
is the controllability index of the pair (A,

B
1
B
2

).
The size of the block A
nc
is equal to the dimension of
the uncontrollable subspace of the pair (A,

B
1
B
2

).
The implemented algorithm (Varga, 2003) represents
a specialization of the controllability staircase algo-
rithm of (Varga, 1981) to the special structure of B.
TG01HU is primarily intended for a descriptor sys-
tem (A − λE, B,C) with nonsingular E, where B =
[B
1
B
2
] is an n × (m
1
+ m
2
) matrix, with B
i
an
n × m
i
submatrix, i = 1,2, and it reduces the pair
(A− λE,[B
1
B
2
]) to the form
Q
T

B
1
B
2
A− λE

diag(I
m
1
+m
2
,Z) =

B
c
1
B
c
2
A
c
− λE
c
⋆
0 0 0 A
nc
− λE
nc

, (13)
where Q and Z are orthogonal, and
1) the pencil

B
c
1
B
c
2
A
c
− λE
c

has full row rank
n
r
for all finite λ ∈ C, and it is defined by (12) and
E
c
=




E
11
E
12
··· E
1q
0 E
22
··· E
2q
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· E
qq




,
where E
ii
is a τ
i
× τ
i
upper triangular matrix.
2) the pencil A
nc
− λE
nc
is regular, of order n−n
r
,
with E
nc
upper triangular, and it contains the uncon-
trollable finite eigenvalues of the pencil A − λE and
possibly some of the uncontrollable infinite eigenval-
ues.
The right transformations are also applied to the
matrix C. The implemented algorithm (Varga, 2004)
is a specialization of the controllability staircase al-
gorithm in (Varga, 1990) to the special structure of B.
The implementation is more general: A and E are up-
per block triangular, and E may have a given number
of nonzero subdiagonals.
TG01GD finds a reduced descriptor represen-
tation (11), (A
r
− λE
r
,B
r
,C
r
,D
r
), without non-
dynamic modes, for a descriptor representation (A −
λE,B,C,D). Optionally, the reduced descriptor sys-
tem can be put into a standard form with the leading
diagonal block of E
r
identity.
TG01LD computes orthogonal transformation ma-
trices Q and Z which reduce the regular pole pen-
cil A − λE of the descriptor system (A − λE,B,C) to
the form (5) or to the form (6), where the subpen-
cil A
f
− λE
f
, with E
f
nonsingular and upper triangu-
lar, contains the finite eigenvalues, and the subpen-
cil A
i
− λE
i
, with A
i
nonsingular and upper triangu-
lar, contains the infinite eigenvalues. The subpencil
A
i
− λE
i
is in a staircase form (8) or (9), respectively.
Optionally, the submatrix A
f
is further reduced to an
upper Hessenberg form.
TG01MD computes orthogonal transformation ma-
trices Q and Z which reduce the regular pole pencil
A− λE of the descriptor system (A− λE,B,C) to the
form (5) or (6), where the pair (A
f
,E
f
) is in a GRSF,
with E
f
nonsingular and upper triangular, and A
f
in RSF. The subpencil A
f
− λE
f
contains the finite
eigenvalues. The pair (A
i
,E
i
) is in a GRSF with both
A
i
and E
i
upper triangular. The subpencil A
i
− λE
i
,
with A
i
nonsingularand E
i
nilpotent, contains the infi-
nite eigenvalues, and it is in a block staircase form (8)
or (9), respectively.
New SLICOT Routines for Standard and Descriptor Systems
539

TG01ND computes equivalence transformation ma-
trices Q and Z which reduce the regular pole pencil
A− λE of the descriptor system (A− λE,B,C) to one
of the forms
QAZ =

A
f
0
0 A
i

, QEZ =

E
f
0
0 E
i

,
QAZ =

A
i
0
0 A
f

, QEZ =

E
i
0
0 E
f

,
where the pair (A
f
,E
f
) is in a GRSF, with E
f
nonsin-
gular and upper triangular, and A
f
in RSF. The sub-
pencil A
f
− λE
f
contains the finite eigenvalues. The
pair (A
i
,E
i
) is in a GRSF with both A
i
and E
i
upper
triangular. The subpencil A
i
− λE
i
, with A
i
nonsingu-
lar and E
i
nilpotent, contains the infinite eigenvalues,
and it is in a block staircase form (8) or (9), respec-
tively. This decomposition corresponds to an additive
decomposition of the transfer-function matrix of the
descriptor system as the sum of a proper term and a
polynomial term.
TG01PD computes orthogonal transformation ma-
trices Q and Z which reduce the regular pole pen-
cil A − λE of the descriptor system (A − λE,B,C) to
a GRSF with ordered generalized eigenvalues. The
pair (A,E) is reduced to the form
Q
T
AZ =



⋆ ⋆ ⋆ ⋆
0 A
1
⋆ ⋆
0 0 A
2
⋆
0 0 0 ⋆



, Q
T
EZ =



⋆ ⋆ ⋆ ⋆
0 E
1
⋆ ⋆
0 0 E
2
⋆
0 0 0 ⋆



,
where the subpencil A
1
− λE
1
contains the eigenval-
ues which belong to a suitably defined domain of in-
terest, and the subpencil A
2
− λE
2
contains the eigen-
values which are outside of the domain of interest.
Optionally, the pair (A, E) is assumed to be already in
a GRSF and the reduction is performed only on the
subpencil A
12
− λE
12
defined by rows and columns
from l to u of A− λE, with 1 ≤ l ≤ u ≤ n.
TG01QD computes orthogonal transformation ma-
trices Q and Z which reduce the regular pole pen-
cil A − λE of the descriptor system (A − λE,B,C) to
a GRSF with ordered generalized eigenvalues. The
pair (A,E) is reduced to the form
Q
T
AZ =


A
1
⋆ ⋆
0 A
2
⋆
0 0 A
3


, Q
T
EZ =


E
1
⋆ ⋆
0 E
2
⋆
0 0 E
3


,
where the subpencils A
k
− λE
k
, for k = 1,2,3, contain
the generalized eigenvalues which belong to certain
domains of interest.
Most of the algorithms are backward stable. The
number of floating point operations is of the order
of n
3
. State-of-the-art numerical linear algebra al-
gorithms are used, including QR and RQ factoriza-
tion with pivoting, incremental condition estimation,
Householder transformations and Givens rotations,
etc. BLAS 3 calls are used whenever possible, to in-
crease efficiency. Optimal workspace size can option-
ally be precomputed by several subroutines. Options
are available to deal individually with the one or two
transformation matrices. The options are
’N’ (do not
compute a transformation matrix), ’I’ (compute it
with identity initialization), or
’U’ (update the matrix
given on entry). TG01ND has an option to compute the
direct or inverse transformation matrices, and
TG01ND
and TG01QD have an option to exhibit either the finite
or the infinite eigenvalues in the leading positions.
4 NUMERICAL RESULTS
An extensive testing has been performed to evaluate
the new routines. Some examples from the litera-
ture have been used to verify the correctness of the
delivered results. For a performance investigation,
examples from the COMPl
e
ib collection (Leibfritz
and Lipinski, 2003) have been used. The collection
contains 124 standard continuous-time examples, but
with variations, a total of 168 systems can be de-
fined. All 151 systems with order less than 1000, and
one larger system, have been tried. Note that some
COMPl
e
ib examples were derived from systems with
general, but nonsingular matrix E, by multiplying the
matrices in the state equation in (1) by E
−1
from the
left. These examples have been modified for this pa-
per in order to be solved as descriptor (actually, gener-
alized) systems. Therefore, results for both standard
as well as generalized systems will be presented in the
following two subsections.
The computations have been performed in double
precision on an Intel Core i7-3820QM portable com-
puter (2.7 GHz, 16 GB RAM), under Windows 7 Pro-
fessional (Service Pack 1) operating system (64 bit),
with Intel Visual Fortran Composer XE 2015, and
MATLAB R2015b. Executable MEX-files have been
built using SLICOT routines and MATLAB-provided
optimized LAPACK and BLAS routines.
4.1 Results for Standard Systems
The set of examples tried have been obtained
calling the MATLAB script
examplevector from
COMPl
e
ib, with names selected with the string vector
Ex no sl . The default tolerance, set by the routinesto
n
2
ε
M
, where ε
M
is the relative machine precision, has
been used for rank computations.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
540

0 20 40 60 80 100 120 140 160
Example #
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
10
1
CPU time (sec)
CPU time (sec)
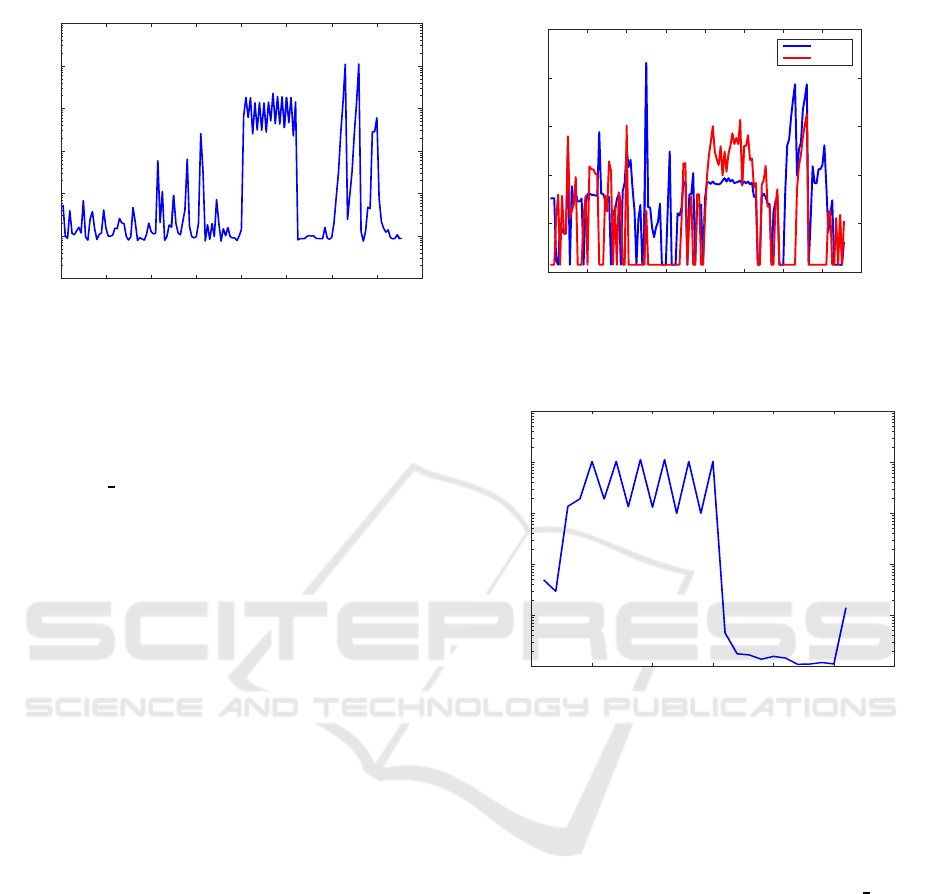
Figure 1: CPU times for computing minimal realizations
for 151 standard systems chosen from the COMPl
e
ib col-
lection.
Figure 1 shows the CPU execution times needed
to compute minimal realizations for the 151 standard
systems. The maximum CPU time is 1.11 seconds,
for the
CM6 IS example, with n = 960, m = 1, and
p = 2. Each of the other examples was solved in less
than 0.23 seconds. Moreover, there are 117 examples
each solved in less than 0.01 seconds, including 111
solved in less than one millisecond.
There are 32 systems found non-minimal. The re-
duction took place in step 1 (for 17 examples), and
in step 2 (for 21 examples) of the minimal realization
procedure in Section 3 (
TB01PX description). For six
examples, the order decreased in both steps.
The separation of the systems spectra into stable
and unstable parts has also been investigated. The sta-
bility degree τ has been set to −10
−8
. The CPU times
are comparable to those in Fig. 1.
Figure 2 shows the relative errors of the stable and
unstable poles after separation, compared to the orig-
inal ones. Their number is preserved for all problems.
There are 44 stable systems. The zero values of the
errors have been replaced by a value slightly smaller
than the smallest relative error, so that its logarithm
can be computed. The largest relative error is for ex-
ample
CSE2 , and it is due to a pair of real, very close
poles, with relative difference of 2.7877· 10
−9
.
4.2 Results for Generalized Systems
As mentioned before, a collection of 34 generalized
systems has been derived from the COMPl
e
ib exam-
ples for which the matrix E was available, usually in
binary
mat files (31 examples). Among these, 8 ex-
amples (
HF2Di , with i = 1, 2, ..., 8) have orders
greater than or equal to 2025, and only HF2D1 has
been separately tried. Only two examples,
TL and FS ,
have condition numbers for E larger than 4, namely,
0 20 40 60 80 100 120 140 160
Example #
10
-18
10
-16
10
-14
10
-12
10
-10
10
-8
Relative error
Relative errors of poles before and after separation
Stable
Unstable
Figure 2: Relative errors of the stable and unstable poles af-
ter separation, compared to the original ones, for 151 stan-
dard systems chosen from the COMPl
e
ib collection.
0 5 10 15 20 25 30
Example #
10
-4
10
-3
10
-2
10
-1
10
0
10
1
CPU time (sec)
CPU time (sec)
Figure 3: CPU times for computing minimal realizations
for 26 generalized systems, with order n ≤ 541, generated
from the COMPl
e
ib collection.
7.7579 · 10
6
and 3.77· 10
5
, respectively.
Figure 3 shows the CPU execution times needed
to compute minimal realizations for the 26 general-
ized systems with order n ≤ 541. The maximum CPU
time is 1.12 seconds, for the modified
HF2D1 M541
example, with n = 541, m = 2, and p = 3. Six exam-
ples (those with n ≥ 529) needed slighly more than
one second runtime. Each of the other examples was
solved in less than 0.25 seconds. Moreover, there are
13 examples each solved in less than 0.01 seconds,
including 10 solved in less than one millisecond.
Except for timing, the results reproduced those for
the corresponding standard systems. All, but two ex-
amples have been found as minimal. The original
non-minimal examples are
CSE1 and CSE2 ; for each
of them the order has been reduced by 1.
The modified example
HF2D1 , with n = 3796, m =
2, and p = 3, has also been tried, and found as min-
imal. The CPU time has been 795 seconds. On the
other hand, solving the corresponding standard sys-
tem needed 119 seconds.
New SLICOT Routines for Standard and Descriptor Systems
541

0 5 10 15 20 25 30
Example #
10
-18
10
-16
10
-14
10
-12
10
-10
10
-8
Relative error
Relative errors of poles before and after separation
Stable
Unstable
Figure 4: Relative errors of the stable and unstable poles
after separation, compared to the original ones, for 26 gen-
eralized systems, with order n ≤ 541.
The separation of the systems spectra into stable
and unstable parts has also been investigated. For de-
scriptor systems this includes a preliminary separa-
tion into finite and infinite parts. The infinite part is
void, since matrix E is nonsingular (but moderately
ill-conditioned for
TL and FS examples). The stability
degree τ has been set to −10
−8
, and the tolerance has
been set to 0, i.e., a default value was used. The CPU
times are comparable to those in Fig. 3.
Figure 4 shows the relative errors of the stable and
unstable poles after separation, compared to the orig-
inal ones. Their number is preserved for all prob-
lems. There are 3 stable systems:
TL , HF2D12 , and
HF2D13 . Example FS has 3 unstable poles, and each
of the other 22 examples have one unstable pole. The
largest relative error, recorded for the
CSE2 example,
is due to a pair of complex poles with imaginary parts
of about ± 6.5854 · 10
−9
, while the reordered poles
became real. Such a change is entirely motivated the-
oretically. Omitting these two poles, the relative error
for
CSE2 example becomes 2.7174· 10
−15
.
5 CONCLUSIONS
Numerical techniques and procedures for comput-
ing stable/unstable and finite/infinite spectrum sepa-
ration, additivespectral decomposition, and removing
the non-dynamic modes, have been discussed. These
techniques and procedures represent the theoretical
and practical foundation for the new routines included
by the authors into the SLICOT Library for standard
and descriptor systems. The functionality of several
main new routines has been briefly described, and
their essential features highlighted. Numerical results
obtained on a comprehensive set of examples from
the COMPl
e
ib collection have been summarized and
illustrate the performanceand capabilities of this SLI-
COT Library extension.
REFERENCES
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Dem-
mel, J., Dongarra, J., Du Croz, J., Greenbaum, A.,
Hammarling, S., McKenney, A., and Sorensen, D.
(1999). LAPACK Users’ Guide: Third Edition. SIAM,
Philadelphia.
Demmel, J. W. and K˚agstr¨om, B. (1993). The generalized
Schur decomposition of an arbitrary pencil A − λB:
Robust software with error bounds and applications.
Part I: Theory and algorithms. Part II: Software and
applications. ACM Trans. Math. Software, 19:160–
174, 175–201.
Duan, G.-R. (2010). Analysis and Design of Descriptor Lin-
ear Systems, vol. 23 of Advances in Mechanics and
Mathematics. Springer, New York.
Golub, G. H. and Van Loan, C. F. (2012). Matrix Computa-
tions. The Johns Hopkins University Press, Baltimore,
Maryland, fourth edition.
K˚agstr¨om, B. and Van Dooren, P. (1990). Additive decom-
position of a transfer function with respect to a speci-
fied region. In Proceedings of the International Sym-
posium on the Mathematical Theory of Networks and
Systems, MTNS-89, Amsterdam, The Netherlands,
Birkh¨auser, Boston.
Leibfritz, F. and Lipinski, W. (2003). Description of the
benchmark examples in COMPl
e
ib. Technical report,
University of Trier, Germany.
Misra, P., Van Dooren, P., and Varga, A. (1994). Computa-
tion of structural invariants of generalized state-space
systems. Automatica, 30(12):1921–1936.
Van Dooren, P. (1981). The generalized eigenstructure
problem in linear system theory. IEEE Trans. Au-
tomat. Contr., AC–26:111–129.
Varga, A. (1981). Numerically stable algorithm for stan-
dard controllability form determination. Electronics
Letters, 17:74–75.
Varga, A. (1990). Computation of irreducible generalized
state-space realizations. Kybernetika, 26(2):89–106.
Varga, A. (1996). Computation of Kronecker-like forms of
a system pencil: Applications, algorithms and soft-
ware. In Proceedings of the IEEE International Sym-
posium on Computer-Aided Control System Design,
Dearborn, MI, 77–82. IEEE.
Varga, A. (2003). Reliable algorithms for computing mini-
mal dynamic covers. In Proceedings of the 42nd IEEE
Conference on Decision and Control, Maui, Hawai’i
USA, 1873–1878. IEEE.
Varga, A. (2004). Reliable algorithms for computing min-
imal dynamic covers for descriptor systems. In Pro-
ceedings of the Mathematical Theory of Networks and
Systems, MTNS 2004, Leuven, Belgium.
Varga, A. (2017). Solving Fault Diagnosis Problems: Lin-
ear Synthesis Techniques. Springer, Berlin.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
542