
Asymmetric Heterogeneous Transfer Learning: A Survey
Magda Friedjungov´a and Marcel Jiˇrina
Faculty of Information Technology, Czech Technical University in Prague, Czech Republic
Keywords:
Asymmetric Heterogeneous Transfer Learning, Different Feature Space, Domain Adaptation, Survey, Data
Mining, Metric Learning.
Abstract:
One of the main prerequisites in most machine learning and data mining tasks is that all available data origi-
nates from the same domain. In practice, we often can’t meet this requirement due to poor quality, unavailable
data or missing data attributes (new task, e.g. cold-start problem). A possible solution can be the combi-
nation of data from different domains represented by different feature spaces, which relate to the same task.
We can also transfer the knowledge from a different but related task that has been learned already. Such a
solution is called transfer learning and it is very helpful in cases where collecting data is expensive, difficult
or impossible. This overview focuses on the current progress in the new and unique area of transfer learning
- asymmetric heterogeneous transfer learning. This type of transfer learning considers the same task solved
using data from different feature spaces. Through suitable mappings between these different feature spaces
we can get more data for solving data mining tasks. We discuss approaches and methods for solving this type
of transfer learning tasks. Furthermore, we mention the most used metrics and the possibility of using metric
or similarity learning.
1 INTRODUCTION
It can happen that while solving a data mining task
in some domain of interest we will have data avail-
able from different feature spaces. Different feature
spaces are two spaces, which are represented by dif-
ferent features. These spaces can originate from other
domains and we can divide them into source (usu-
ally contains data used for the training of the model)
and target feature space (contains data used for testing
of the model). We can also divide the domains into
source and target to distinguish where the data comes
from. Common machine learning methods assume
that the distributions of the individual attributes in the
used data are the same. However, in practice these as-
sumptions are often incorrect. Let us imagine that our
task is object classification, where our domain is rep-
resented by several pictures. Two images of the same
object may be of different dimensions of features be-
cause of different resolutions, illuminations or tilts. A
different task can be cross-lingual document classifi-
cation. For example labeled English documents are
widely available, but labeled Chinese documents are
much harder to obtain. These documents, English and
Chinese, do not share the same feature representation.
Transfer learning can use natural correspondence be-
tween feature spaces in order to create an automated
learner for Chinese documents. Transfer learning al-
lows the domains, tasks and distributions used in solv-
ing tasks to be different (Zheng, 2015).
In a broader context transfer learning can be re-
garded as a group of methods which fall into the cate-
gory of semantic-meaning based methods for cross-
domain data fusion. Data fusion consists of tech-
niques for integration of knowledge from various data
in a machine learning and data mining task (Zheng,
2015). Transfer learning concerns itself with knowl-
edge fusion rather than schema mapping and data
merging, which are more specific for traditional data
fusion and data integration being pursued by the
database community (Zheng, 2015; Bleiholder and
Naumann, 2009). Many terms exist for transfer learn-
ing, within this work you can also come across a re-
lated term - domain adaptation (Pan and Yang, 2009).
Domain adaptation is focused on the development of
learning algorithms, which can be easily transferred
from one domain to another (Daum´e III, 2009).
A general overview of transfer learning is given
in (Pan and Yang, 2009) and the newest survey was
introduced in (Weiss et al., 2016). The main moti-
vation, which is also the reason that transfer learning
methods are popular, is the automatization of map-
ping processes, saving of time and human resources,
the possibility of solving tasks without knowledge of
Friedjungová, M. and Ji
ˇ
rina, M.
Asymmetric Heterogeneous Transfer Learning: A Survey.
DOI: 10.5220/0006396700170027
In Proceedings of the 6th International Conference on Data Science, Technology and Applications (DATA 2017), pages 17-27
ISBN: 978-989-758-255-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

the domain, increasing usability of poor data, which
would be unusable on its own and often also the us-
ability of data from unused database structures.
In this survey we focus on the diversity of data
from different feature spaces in the same domain of
interest. We search for suitable mappings between
this data, which will maintain or decrease the error
of the predictive or classification model. In practice,
the mapping of data is often solved manually, but in
some cases this approach poses a combinatorial prob-
lem and almost always requires the presence of a do-
main expert. In the ideal case it would be beneficial to
find such an automatic mapping, which would enable
us to map the data between source and target feature
spaces in both directions. This research area is called
heterogeneous transfer learning and its position in the
field of transfer learning can be seen in Figure 1.
Heterogeneous transfer learning can be perceived
as a type of transductive learning. Transductive learn-
ing assumes that the source and target domains are
different. The domain consists of two components: a
feature space χ and a marginalprobability distribution
P(X), where X = x
1
, ..., x
2
∈ χ (Pan and Yang, 2009).
Heterogeneous transfer learning is proposed to handle
the cases where the task is the same, but the source
and target feature spaces are different (Pan and Yang,
2009). This difference can be that the marginal prob-
ability distributions of the data are different, but the
feature spaces between source and target domains are
the same. Transductive learning also assumes that we
havelabeled source data and unlabeled target data, but
heterogeneous transfer learning is able to work with
different combinations of labeled and unlabeled data
which will be demonstrated on examples in Section 2.
In this paper we focus on feature-based heterogeneous
transfer learning, which stems from the assumption
that the feature spaces between domains are different
and searches for ways of mapping this dissimilar data.
By difference we understand different distributions,
representations and dimensionality of data. Hetero-
geneous transfer learning is a relatively new field of
research and finds an application in such domains as
text classification, image recognition, activity recog-
nition, defect prediction etc.
There has been a large amount of work focus-
ing on transfer learning in machine learning literature
(See an overview by (Weiss et al., 2016)). However,
in this surveyarticle we givean overviewof asymmet-
ric heterogeneous transfer learning methods mainly
used in machine learning and data mining areas. This
survey does not provide an experimental comparison
of the individual methods. Most of the methods in the
surveyed papers are domain or task specific, thus they
reach the best performance on specific datasets. This
makes it impossible to provide a quality comparative
analysis on the same datasets. An open-source reposi-
tory of implemented solutions from each paper would
be helpful, but unfortunately this is not available. We
hope to provide a useful survey for the machine learn-
ing and data mining community.
The survey is organized as follows. In Section
2 you can find an explanation of this problem along
with the prerequisites for the problem of transfer
learning between different feature spaces. Section 2.1
briefly describes the solution based on common fea-
ture space. In section 2.2 we explain the available
methods in more detail. In Section 3 we introduce the
reader to the most used feature mappings in the field
of transfer learning. In the last Section 4 we bring a
brief summary of this survey and possible challenges,
which we would like to address in the future.
2 HETEROGENEOUS TRANSFER
LEARNING
In Figure 2 (altered figure from (Weiss et al., 2016))
we can see two approaches to the transformation of
data on a feature-based level, which are addressed by
different feature spaces. By transformation we un-
derstand operations (e.g. translation, scaling, etc.)
which have to be done for mapping of different fea-
ture spaces. One of these is symmetric transformation
(Figure 2.a). Symmetric transformation transforms
the source and target feature spaces into a common
latent feature space in order to unify the input spaces
of the domains. The second approach is asymmetric
transformation (Figure 2.b), which transforms source
feature space to the target feature space. Some meth-
ods presented in Section 2.2 perform the transforma-
tion in the opposite direction from the target domain
to the source domain. Some proposed methods are
usable in both directions. All presented approaches in
Section 2.2 are based on features (feature-based) (Pan
and Yang, 2009).
We consider two datasets as a running example
in this paper (shown on Figure 3). The data in these
datasets originate from different source and target do-
mains with different feature spaces. The datasets
consist of a different feature representation, distribu-
tion, scale, and density of data. Relations which con-
nect the datasets can exist between different feature
spaces, because the source and target domains must
be related in some way. These connections can be
called correspondences among features. The discov-
ery of as much common information as possible from
these different datasets is one of the problems in data
mining research. Thus, we are looking for suitable
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
18
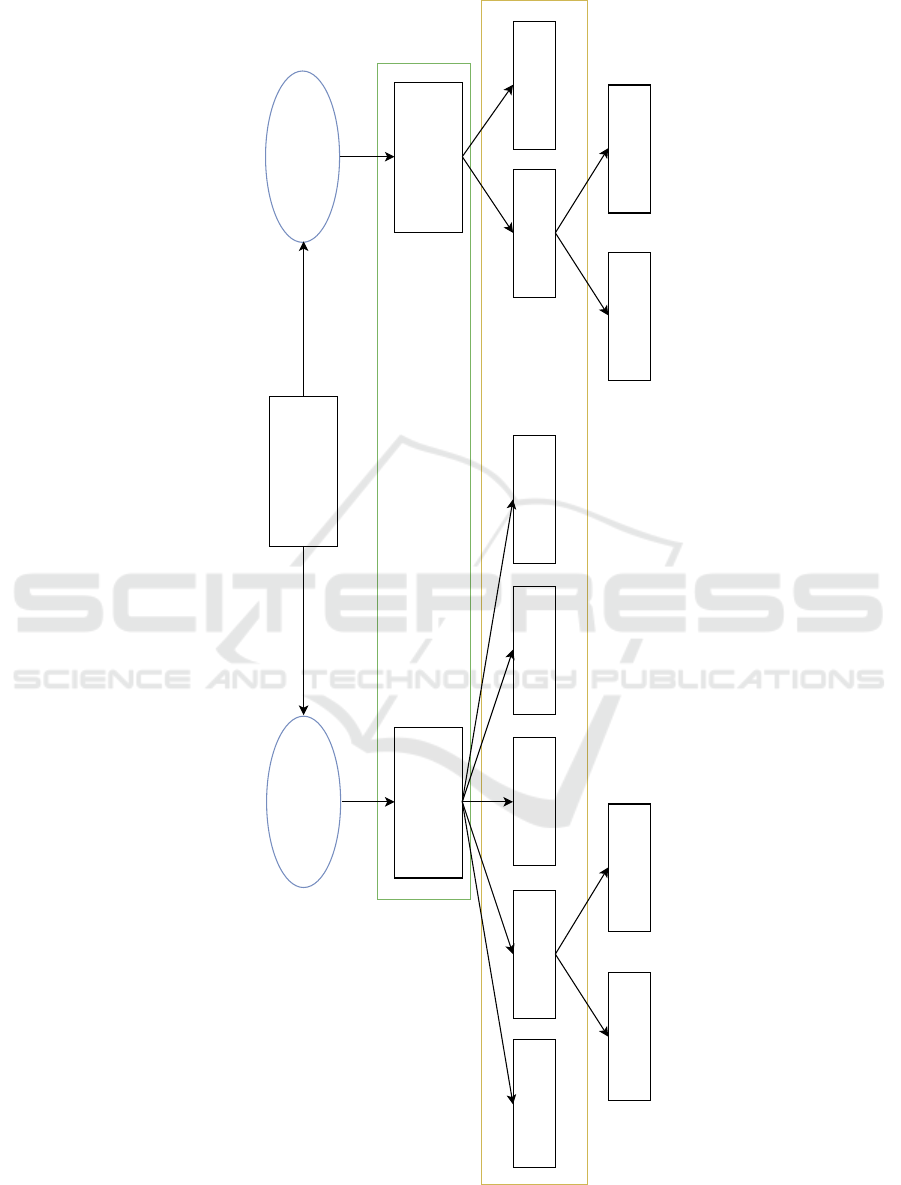
Transfer Learning
Heterogeneous
Transfer Learning
Homogeneous
Transfer Learning
Instance-based Relational-basedParameter-based
Inductive Learning Transductive Learning
Feature-based Hybrid-based
Symmetric Asymmetric
Feature-based
Symmetric Asymmetric
other domains
with same
feature space
same domain
with different
feature spaces
How is being transferred
What is being transferred
Label-based
Figure 1: A hierarchical overview of different transfer learning approaches.
Asymmetric Heterogeneous Transfer Learning: A Survey
19
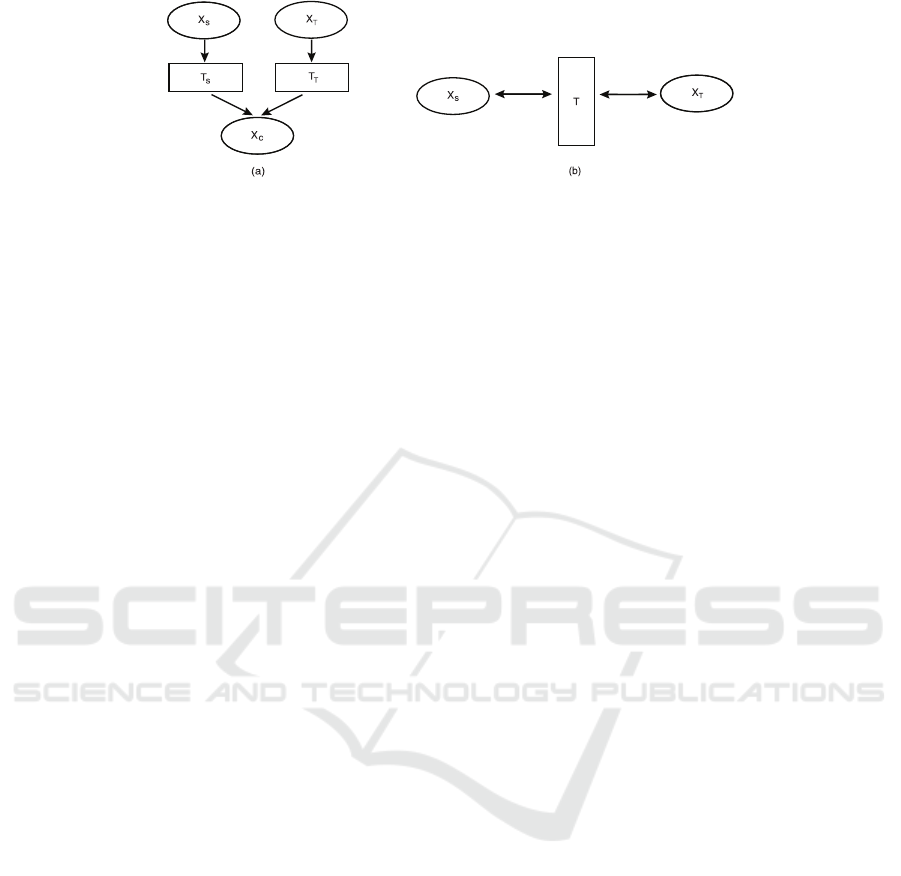
Figure 2: (a) Symmetric transformation mapping T
S
and T
T
of the source X
S
and target X
T
domains into a common latent
feature space. (b) Asymmetric transformation mapping T
S
of the source domain X
S
to target domain X
T
or vice versa from
target X
T
to source X
S
domain.
mapping functions for individual features from dif-
ferent feature spaces. In the ideal scenario, we are
looking for mapping in both directions, which would
be more general and would find a wide range of ap-
plication.
2.1 Symmetric Feature-based Approach
Most existing heterogeneous transfer learning meth-
ods assume that both source and target data can
be represented by a common homogeneous feature
space, called latent feature space. Thus, we are look-
ing for transformation mappings T
S
and T
T
to trans-
form source domain data X
S
and target domain data
X
T
to a new common latent feature space X
C
as is
shown in Figure 2 (Shi et al., 2010; Prettenhofer and
Stein, 2010; Wang and Mahadevan, 2011; Duan et al.,
2012). There exist a lot of tasks in the natural lan-
guage processing area. (Blitzer et al., 2006) introduce
structural correspondence learning (SCL) to automat-
ically induce correspondences among features from
different domains. SCL is based on the correlation
between certain pivot features. Pivot features are fea-
tures which behave in the same way for discrimina-
tive learning (e.g. classification) in both domains.
These features have the same semantic meaning in
both domains and are used to learn a mapping from
the different feature spaces to common latent feature
space. (Pan et al., 2008) learn a common latent fea-
ture space with low dimensionality. This common la-
tent space is learned using a new dimensionality re-
duction method called Maximum Mean Discrepancy
Embedding. Data from related but different domains
is projected onto this common latent feature space.
(Daum´e III, 2009) transform the source and target fea-
tures into a higher dimensional representation with
source, target and common components. They also
introduce an extension to this method which also
works for unlabeled data (Daum´e III et al., 2010).
(Shi et al., 2010) propose the Heterogeneous Spec-
tral Mapping (HeMap) method. The main idea of
HeMap is to find a common latent feature space for
two heterogeneous tasks. A spectral mapping of the
source and target feature spaces into a common latent
feature space is designed. A spectral mapping is de-
signed as an optimization task that maintains the orig-
inal structure of the data while minimizing the differ-
ence between the two domains. This mapping adopts
linear approaches such as rotation, scaling, permuta-
tion of row vectors and column vectors, etc. to find
a common latent feature space. (Pan et al., 2008) in-
troduce Transfer Component Analysis for dimension-
ality reduction of features in a common latent space.
A kernel-based feature mapping method has been in-
troduced by (Zhong et al., 2009). This method maps
the marginal distribution of data from different source
and target domains into common kernel space. A lot
of methods for the solution of the common latent fea-
ture space problem exist. We are not going to concern
ourselves with them any further in this work, because
we focus on asymmetric approaches.
2.2 Asymmetric Feature-based
Approach
Asymmetric transformation is perceived as a new and
unique approach alternative to symmetric transforma-
tion. It consists of finding transformations T
S
, which
would enable us to map source domain data X
S
to
target domain data X
T
with different feature spaces
(Kulis et al., 2011; Dai et al., 2008). In practice we
mostly encounter this version of the problem: we have
data from a source domain, which we map to data
from a target domain using various techniques. Af-
ter that we train a model (Figure 3 a). We can also
encounter a scenario where we have source and target
data from the same domain, on which we trained a
very good model. This model is successfully applied
in production. However, due to various reasons, the
target feature space changed and our model became
unable to react to the new data. In the case that we
are not able to modify the model, we have to find an
ideal mapping of target data to source while making
sure that the error of the model doesn’t change (Fig-
ure 3 b). This approach poses a big challenge in the
research area.
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
20
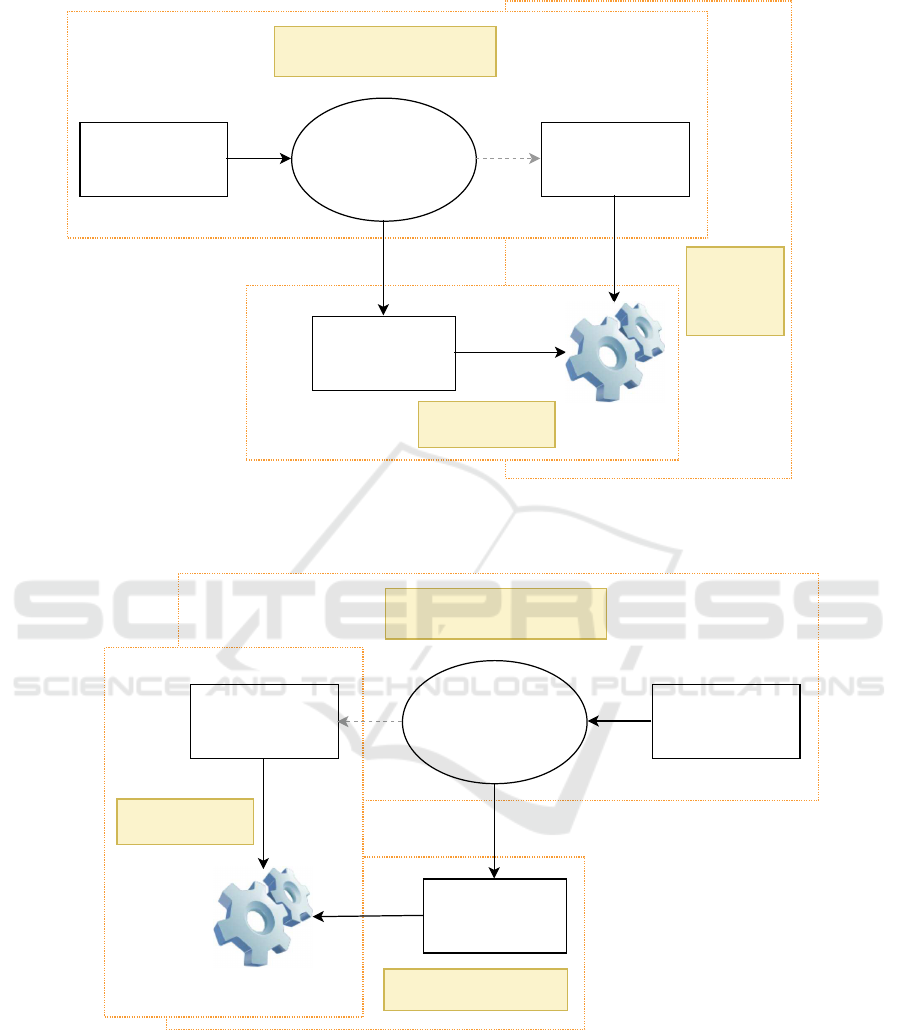
Dataset A
Source Feature Space Target Feature Space
Dataset B
Model
Transformation of source feature
space to target feature space
Step 1
Step 2
Step 3
(a)
Dataset A
Source Feature Space Target Feature Space
Dataset B
Model
Testing phase
(prediction, classification)
Testing phase
(prediction,
classification)
Transformation of target feature
space to source feature space
Step 1
Step 2
Step 3
(b)
Transformed
dataset A
Transformed
dataset B
Translators,
mapping methods,
metric and similarity
learning etc.
Translators,
mapping methods,
metric and similarity
learning etc.
Training phase
(building of model)
Training phase
(building of model)
Figure 3: There are two approaches in asymmetric transfer learning shown on (a) and (b). (a): Step 1 consists of mapping
dataset A to dataset B by using mapping methods. Step 2 consists of training the model based on data from the transformed
dataset A, step 3 contains the phase where we test the model on dataset B from target feature space. (b): Step 1 consists of the
training of the model based on data from dataset A from source feature space. In Step 2 we are looking for a mapping from
dataset B to dataset A. Step 3 shows the testing of the model based on transformed dataset B.
Asymmetric Heterogeneous Transfer Learning: A Survey
21

2.3 Overview of Presented Solutions
Asymmetric heterogeneous transfer learning finds ap-
plication in several practical domains, where mainly
methods of machine learning are employed. In this
section we will introduce several basic research ap-
proaches to solving tasks related to:
• computer vision – image classification;
• cross-language classification;
• cross-project defect prediction;
• activity recognition.
We start with the assumption that we have differ-
ent source and target feature spaces, but the same task,
as shown on Figure 3. However, if we also had a dif-
ferent task, we would first make use of the methods of
transfer between feature spaces followed by methods
of homogeneous transfer learning for the transfer of
knowledge between tasks (domains).
(Kulis et al., 2011) solved the problem of domain
adaptation for transferring object models from one
dataset to another by introducing a novel approach in
computer vision. The main idea is to learn an asym-
metric non-linear transformation that maps data from
one domain to another domain using supervised data
from both domains. The input consists of pairs of
inter-domain examples that are known to be semanti-
cally similar or dissimilar. This approach can also be
used in the case that some classes in the target domain
have missing labels. (Kulis et al., 2011) aims to gen-
eralize the model of (Saenko et al., 2010) in his pa-
per, which makes use of symmetric transformations.
The new approach of (Kulis et al., 2011) was called
Asymmetric Regularized Cross-domain transforma-
tion, shortly ARC-t. ARC-t shows how a general for-
mulation for the transfer learning problem can be ap-
plied in kernel space, resulting in non-linear transfor-
mations. The transformation matrix is learned in a
non-linear Gaussian RBF kernel space. The result-
ing algorithm is based on squared Frobenius regular-
ization (Kulis et al., 2013) and similarity constraints.
Similarity constraints are created for all pairs of data
in the same class by using a similarity function. It
helps us to decide which pairs of data are similar and
dissimilar. During testing the method showed certain
advantages compared to existing baseline approaches
such as k-nearest neighbors, SVM, domain and cross-
domain metric learnings and the feature augmentation
method proposed by (Daum´e III, 2009). The main
idea of feature augmentation is to duplicate features
in order to capture differences among domains. This
method is briefly discussed in Section 2.1.
(Zhou et al., 2014b) proposed a domain adaptation
method where data originates from heterogeneous
feature spaces of different dimensions. The method
includes a transformation matrix to map the weight
vector of classifiers learned from source domain to
target domain. This method works if the following re-
quirements are met: sparse feature representation and
class-invariant transformation. Sparse feature repre-
sentation means that a feature in one domain can be
represented by only several features in a different do-
main. The feature mapping across these domains is
linear. Class-invariant transformation means that the
feature mapping of some feature is invariant to dif-
ferent classes. To make the learning of a heteroge-
neous domain possible, the transformation matrix has
to learn the similarity between source and target do-
main data. This data can be transformed from source
feature space to target feature space and equivalently
vice versa. (Zhou et al., 2014b) used the scheme -
the Error Correcting Output Codes (ECOC) to gener-
ate binary classifiers for the multi-class classification
problem (Dietterich and Bakiri, 1995). With ECOC,
their solution, called Sparse Heterogeneous Feature
Representation (SHFR), can learn a transformation
matrix. Part of the learning process of the transfor-
mation matrix is the adoption of a multi-task learn-
ing method based on (Ando and Zhang, 2005). The
multi-task learning is based on learning more task si-
multaneously (Pan and Yang, 2009). SHFR method
(also in combination with ECOC) was tested against
DAMA (Dai et al., 2008), ARC-t (Kulis et al., 2011)
and HFA (Duan et al., 2012).
We are further going to state several examples
from practice. Heterogeneous transfer learning finds
numerous applications in the area of activity recogni-
tion. In this area the activities of daily living are mon-
itored through diverse sensors. This monitoring is a
crucial step in the future of elderly people care. There
is motivation to use existing data from other houses in
order to learn the parameters of the model for a new
house. The reason is that activity recognition mod-
els often rely on labeled examples of activities for
learning, which are missing in a new house. Activ-
ity recognition and discovery models usually include
information based on structural, temporal and also
spatial features of the activities (Cook et al., 2013;
Rashidi and Cook, 2010).
For the activity recognition task, (van Kasteren
et al., 2010; van Kasteren et al., 2008) introduce a
method in which sensors in the source domain are
mapped to similar sensors in the target domain. Semi-
supervised learning is used for learning parameters
of the Hidden Markov Model (HMM). They propose
a number of manual mapping strategies for mapping
sensors between different houses: intersect, duplicate,
union.
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
22

(Rashidi and Cook, 2010) also map sensors from
source to target domain based on location or function.
Their method is called Multi Home Transfer Learning
(MHTL). MHTL composes of 3 phases – activity ex-
traction (output heads to activity templates), mapping
and label assignment. The activity model consists
of various features from sensors, such as structural,
spatial and temporal. Their method is a good exam-
ple of the utilization of meta-features. Meta-features
are common for all data. It is a kind of mapping
allowing us to have a single common feature space
that can be used for all houses (van Kasteren et al.,
2010). In (Rashidi and Cook, 2010) meta-features are
first manually introduced into the feature space (for
every source-target pair). Then this feature space is
automatically mapped from the source to target do-
main. Other works using meta-features are (Blanke
and Schiele, 2010; van Kasteren et al., 2010).
(Harel and Mannor, 2011) designed a Multiple
Outlook Mapping algorithm (MOMAP). MOMAP
computes optimal affine mappings from different
source feature spaces (in their terminology outlooks)
to a target feature space by matching moments of
empirical distributions. These spaces are not related
through corresponding instances, but only through the
common task. The optimal affine mapping is a func-
tion of geometric projection which maps the points
lying on the same line onto one common point or
to the same number of other points. Affine map-
ping preserves the division ratio (Nomizu and Sasaki,
1995). In the MOMAP algorithm affine mapping is
represented by translation and rotation. The mapping
is done by matching moments of empirical distribu-
tions. The empirical distribution function is associ-
ated with an empirical measure of samples. Empirical
measure means random measure realization of a se-
quence of random variables. The moments are quan-
tiles from the empirical distribution function (van der
Vaart, 2000). Before mapping in the MOMAP al-
gorithm, the scaling of features of all spaces is re-
quired. The scaling aims to normalize the features
of all spaces to the same range. Then the mapping
is performed by translating the means of each class
to zero. Next, the rotation of the classes to fit each
other is done by a rotation matrix. Finally, we have to
translate the means of the mapped space to the final
space. The framework performance is demonstrated
on activity recognition data.
A lot of transfer learning methods solve situa-
tions where the difference between the source and
target domains is caused mainly by differences in
the marginal probability distributions of the domains
(Rashidi and Cook, 2010; Blitzer et al., 2007; Blitzer
et al., 2006). By marginal probability distribution
we mean probability distribution of the features con-
tained in the subset of a collection of random features.
(Feuz and Cook, 2015) propose a novel hetero-
geneous transfer learning technique called Feature-
Space Remapping (FSR). FSR can handle the differ-
ent feature spaces without the use of co-occurrence
data (correlated data), as is shown for example in
(Dai et al., 2008). FSR maps the data to a different
feature space using part of labeled data from the tar-
get domain to infer relations to the source domain.
FSR requires a one time manual specification of meta-
features and then can be applied to map multiple
source and target domains. (Feuz and Cook, 2015)
map the features from target feature space to differ-
ent source feature space. To achieve the feature map-
ping, they learn a mapping from each dimension in
the target feature space to a corresponding dimension
in the source feature space. FSR computes the av-
erage similarity between the source and target meta-
feature values for each pair between features from
source and target feature spaces. The similarity is
calculated between two meta-features as the absolute
value of the difference between meta-feature values
divided by the maximum possible difference between
the meta-features. As a product we get many-to-one
mapping.
One of the typical tasks of transfer learning is
language transformation between multilingual doc-
uments or web pages, specifically the transforma-
tion from one language to another. This task can
be solved by using automatic translators mentioned
in (Wei and Pal, 2010). Transfer learning is aim-
ing to solve the task without these tools, only us-
ing the transfer of knowledge between related feature
spaces. Most methods learn a feature mapping be-
tween source and target domain based on data cor-
respondences (Kulis et al., 2011; Dai et al., 2008).
Correspondence means that there exists some rela-
tionships between data from different feature spaces.
(Zhou et al., 2014a) present a hybrid heterogeneous
transfer learning (HHTL) framework. HHTL consists
of deep learning which learns a feature mapping from
the target domain to the source domain. HHTL simul-
taneously corrects the data bias on the mapped feature
space. This frameworkwas tested on multilingual text
mining tasks.
(Dai et al., 2008) propose to learn feature map-
ping based on the construction of feature correspon-
dences between different feature spaces. This con-
struction is called translator in (Dai et al., 2008). In
this work the language model is used. The language
model is a probability distribution over sequences of
words (Lafferty and Zhai, 2001). The language model
links the class labels to the features in the source
Asymmetric Heterogeneous Transfer Learning: A Survey
23

spaces and turns their translation to features in the
target spaces. This novel framework is called trans-
lated learning (TLRisk). The main idea of translated
learning is to translate all the data from source feature
space into a target feature space. We assume there
is no correspondence between instances in these dif-
ferent feature spaces. The language model proposed
by (Dai et al., 2008) consists of feature translation and
nearest neighbor learning. We can imagine this model
as a chain of links which is modeled using a Markov
chain and risk minimization. For the development of
a translator we need some co-occurrence data across
source and target spaces. Performance of the TLRisk
framework was shown on text-aided image classifica-
tion and on cross-language classification.
Software defect prediction is another important
application area in transfer learning and software en-
gineering. There is a possibility to build a predic-
tion model with defect data collected from a software
project and predict defects for new projects (cross-
project defect prediction CPDP) (Nam et al., 2013;
He et al., 2012; Ma et al., 2012; Rahman et al.,
2012). However, projects must have the same metric
set with identical meanings between projects. (Nam
and Kim, 2015) introduce heterogeneous defect pre-
diction (HDP) which allows heterogeneous metric
sets across projects. At first they apply feature se-
lection techniques to the source data. For feature se-
lection they used various feature selection approaches
widely used in defect prediction such as gain ratio,
chi-square, relief-F, and significance attribute evalu-
ation. Then the similarity between source and tar-
get data is computed and data is mapped. The sim-
ilarity of each source and target metric pair is mea-
sured by using several existing methods such as per-
centiles, Kolmogorov-Smirnov test and Spearman’s
correlation coefficient. A model for target labels pre-
diction is built using the mapped data.
3 FEATURE MAPPINGS
The main operation of transfer learning approaches
is the mapping of features. These features originate
from different feature spaces. We can map the fea-
tures into common feature space or we can look for
mapping from one feature space to another. Learning
optimal mapping is a significant problem in the ma-
chine learning community. By mapping we mean a
type of feature transformation which maps features
from one feature space to another. We face many
problems while mapping one feature space onto an-
other: different number of features, dimensionality,
distribution, used metrics etc. The number of possible
mappings between source and target spaces grows ex-
ponentially as the number of features increases. The
selection of a suitable mapping depends on the type
of data – numerical (each data instance is a numerical
feature vector) or structured (each instance is a struc-
tured object such as a string, a tree etc.), and on the
specific problem. If the number of feature combina-
tions doesn’t pose a combinatorial problem, it is pos-
sible to realize feature mapping in a manual way. (van
Kasteren et al., 2008) proposed a number of man-
ual mapping strategies: intersect, duplicate, union.
But manual mapping can be domain dependent as is
shown in (van Kasteren et al., 2008). (van Kasteren
et al., 2008) implemented their mapping solution for
different sensors in house activity recognition.
State-of-art of feature mapping consists of pre-
processing, dimensionality reduction and feature se-
lection methods. There exist works, which concern
themselves with dimensionality reduction (Si et al.,
2010; Dai et al., 2009; Pan et al., 2008; Blitzer et al.,
2006) and feature selection (Satpal and Sarawagi,
2007). We can also encounter feature weighting
methods. But a wide spectrum of the methods cov-
ers the preprocessing phase. In this work several
mapping approaches used within transfer learning are
presented. We can divide them into statistic and
metric methods. Statistic methods are represented
primarily in the Spearman’s correlation coefficient,
Kolmogorov-Smirnov test, Kullback-Leibler diver-
gence etc. We will focus more on pairwise metrics
which are based on measuring the distance or simi-
larity between data. As stated above, each problem
pertains to a specific domain which has its own se-
mantic notion of data similarity. This data similarity
can be difficult to express through standard metrics
such as Minkowski metrics (Bellet et al., 2013). The
solution seems to be learning the metric from data.
This approach is called metric learning or similarity
learning(Bellet et al., 2013; Kulis et al., 2013; Yang,
2006).
3.1 Metrics
There exist a lot of metrics, which can be used (tested)
during the mapping of features. The fundamental one
is the family of Minkowski distances including Eu-
clidean, Manhattan and Chebyshev distances. We can
also use cosine similarity for measuring the cosine of
the angle between two instances. It is widely used in
data mining (e.g. bag-of-words or for sparse vectors).
One of the popular methods for comparing structured
data is standard (Levenshtein) edit distance and its
mutations (e.g. Specific Cost Matrix, tree or stochas-
tic edit distance), where we search for the smallest
number of transformations (insertion, deletion or sub-
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
24

stitution of symbols), which is needed to transform
one string to another (Bellet et al., 2013). Many met-
rics exist as well as some good surveys (Bellet et al.,
2013; Kulis et al., 2013).
3.2 Metric and Similarity Learning
Similarity learning is a field of supervised learning
and its task is to discover a similarity function from
an example that measures similarity between two ob-
jects. It is closely related to metric distance learning,
which finds a distance function between data. These
two areas are closely connected to transfer learning or
domain adaptation, where during the mapping of indi-
vidual features between domains, we search for suit-
able methods of comparing the similarity of these fea-
tures. We can then perform mapping based on these
similarities which is represented by different transfor-
mations. We distinguish between linear (e.g. Maha-
lanobis distance learning and linear similarity learn-
ing) and nonlinear (e.g. kernelization of linear meth-
ods) metric learning (Wang et al., 2014; Saenko et al.,
2010). The following survey on metric learning by
(Bellet et al., 2013; Kulis et al., 2013; Yang, 2006)
can serve for more details. Even though metric learn-
ing is a hot topic and is successfully used for problems
in computer vision and other fields (e.g. (G. Chechik
and Bengio., 2010; Kulis et al., 2009; Chopra et al.,
2005)) as far as we know it is rarely used in the field of
transfer learning and domain adaptation. We can find
one of few applications in the symmetric approach
by (Saenko et al., 2010) who present a method that
adapts object models to new imaging conditions by
supervised learning of transformations which mini-
mizes the effect of domain-induced changes in the
feature distribution.
This trend is similar to symmetric heterogeneous
learning. However if a model is trained on one do-
main and then tested on another domain, it often re-
sults in poor performance (Saenko et al., 2010). One
approach to this problem can be the generalization of
the metric learning problem (Kulis et al., 2011). The
idea is to learn a transformation A that maps the data
from one domain to the other, thus leading to the in-
ner product. This approach can be applied even when
the dimensionalities of the two domains are different
(Kulis et al., 2013).
(Chopra et al., 2005) propose a convolutional net-
work for mapping data from source to target space.
This method produces a non-linear mapping that can
map any input vector of features to its corresponding
version in lower dimension. It is also important that
meta-features are learned from data and do not stem
from prior knowledge about the task.
(Wang et al., 2014) propose a novel metric al-
gorithm to transfer knowledge from source to target
domain in metric settings called Cross-Domain Met-
ric Learning (CDML). This method consists of three
steps: 1) minimizing the distance between different
distributions, 2) constructing two Gaussian distribu-
tions, one based on Mahalanobis distance to be learnt,
second based on the information geometry (Wang
and Jin, 2009) of target domain data, 3) constructing
two more Gaussian distributions, one based on Maha-
lanobis distance again, the second one based on the
labels and the geometry of source domain data. The
results of these steps are combined into the unified
loss function of CDML and by this combination the
discriminating power gained from the labeled source
domain data to the unlabeled target domain data is
transferred.
Another usage of metric learning can be in un-
supervised domain adaptation, where labeled source
data and unlabeled target data for learning are avail-
able. The aim is to unify source and target distribu-
tions. The solution can be the usage of a nonpara-
metric way of measuring the distribution difference
between the source and target samples called Maxi-
mum Mean Discrepancy (MMD)(Bellet et al., 2013).
This is used by (Geng et al., 2011) in a domain adap-
tation metric learning (DAML) algorithm. Further we
encounter a transfer metric learning (TML) approach
by (Zhang and Yeung, 2010), where the metric and
the task covariances between the source and target
tasks are learnt under a unified convex formulation.
Their work is based on multi-task metric learning with
transfer learning settings.
4 CONCLUSION AND
CHALLENGES
The majority of heterogeneous transfer learning ap-
proaches transfer source and target features to com-
mon feature space (see Section 2.1). The minority
of works concern themselves with the direct mapping
of source features to target features (see Section 2.3),
which is significantly more demanding because of the
necessity to search for a suitable mapping between
disparate but related spaces. The solutions are lim-
ited if we are dealing with labeled or unlabeled data.
Also a lot of work is done in computer vision and in
text classification, but there are a lot of other domains,
e.g. medical data or student performance data, where
transfer learning could be applied. There are a lot of
manual mapping strategies, but the problem remains
in their automatization together with finding the opti-
mal mapping. Optimal mapping means that the map-
Asymmetric Heterogeneous Transfer Learning: A Survey
25

ping is feasible in both directions between source and
target feature spaces. A lot of data is task or domain
specific and so the generalization of mapping trans-
formations poses a challenge. There are two ways of
automatic feature mapping: trying multiple mappings
or mapping by analogy. This is often computation-
ally very demanding. There are also some complica-
tions with the lack of overlap between feature spaces
and different dimensionality. We also have to con-
sider, whether there is any correspondence between
features. One of the remaining questions is the nega-
tive transfer within asymmetric heterogeneous trans-
fer learning and varying data. Also the adaptation of
metrics to varying data (e.g. lifelong learning, detec-
tion of concept drifts).
The main contribution of this paper is to provide
a summary of available up-to-date approaches and
methods in the area of heterogeneous transfer learn-
ing. We also aim to emphasize some of the open chal-
lenges within this area. Our future work will consist
of finding suitable feature mappings between differ-
ent source and target spaces. We would like to use
these mapped features, more precisely the data, in
machine learning models which were learnt on data
not mapped and evaluate their relative performance.
This paper forms a base for future work in the field
of asymmetric heterogeneous transfer learning using
methods of metric learning – this combination is not
very common as far as we know and thus it is one
of the main challenges which could bring an automa-
tized and generalized solution for asymmetric hetero-
geneous transfer learning problems.
ACKNOWLEDGEMENTS
This research has been supported by SGS grant No.
SGS17/210/OHK3/3T/18.
REFERENCES
Ando, R. K. and Zhang, T. (2005). A framework for learn-
ing predictive structures from multiple tasks and unla-
beled data.
Bellet, A., Habrard, A., and Sebban, M. (2013). A survey
on metric learning for feature vectors and structured
data.
Blanke, U. and Schiele, B. (2010). Remember and transfer
what you have learned - recognizing composite activ-
ities based on activity spotting. In 2010 International
Symposium on Wearable Computers. IEEE.
Bleiholder, J. and Naumann, F. (2009). Data fusion. In
ACM Computing Surveys (CSUR). ACM.
Blitzer, J., Crammer, K., Kulesza, A., Pereira, F., and Wort-
man, J. (2007). Learning bounds for domain adapta-
tion. In Advances in Neural Information Processing
Systems 21. MIT Press.
Blitzer, S. J., McDonald, R., and Pereira, F. (2006). Do-
main adaptation with structural correspondence learn-
ing. In Proceedings of the 2006 conference on empir-
ical methods in natural language processing. Associ-
ation for Computational Linguistics.
Chopra, S., Hadsell, R., and LeCun, Y. (2005). Learning
a similarity metric discriminatively, with application
to face verification. In IEEE Computer Society Con-
ference on Computer Vision and Pattern Recognition.
IEEE.
Cook, D. J., Feuz, K. D., and Krishnan, N. C. (2013). Trans-
fer learning for activity recognition: A survey. In
Knowledge and information systems. Springer Berlin
Heidelberg.
Dai, W., Chen, Y., Xue, G. R., Yang, Q., and Yu, Y. (2008).
Translated learning: Transfer learning across different
feature spaces. In Proceedings of the Twenty-Second
Annual Conference on Neural Information Processing
Systems.
Dai, W., Jin, O., Xue, G. R., Yang, Q., and Yu, Y. (2009).
Eigentransfer: a unified framework for transfer learn-
ing. In In Proceedings of the 26th Annual Interna-
tional Conference on Machine Learning. ACM.
Daum´e III, H. (2009). Frustratingly easy domain adapta-
tion.
Daum´e III, H., Kumar, A., and Saha, A. (2010). Frus-
tratingly easy semi-supervised domain adaptation. In
Proceedings of the 2010 Workshop on Domain Adap-
tation for Natural Language Processing. Association
for Computational Linguistics.
Dietterich, T. G. and Bakiri, G. (1995). Solving multiclass
learning problems via error-correcting output codes.
In Journal on artificial intelligence research.
Duan, L., Xu, D., and Tsang, I. W. (2012). Learning with
augmented features for heterogeneous domain adapta-
tion.
Feuz, K. D. and Cook, D. J. (2015). Transfer learning across
feature-rich heterogeneous feature spaces via feature-
space remapping (fsr). In ACM Transactions on Intel-
ligent Systems and Technology. ACM.
G. Chechik, V. Sharma, U. S. and Bengio., S. (2010). Large
scale online learning of image similarity through rank-
ing. In Journal of Machine Learning Research.
Geng, B., Tao, D., and Xu, C. (2011). Daml: Domain adap-
tation metric learning. In IEEE Transactions on Image
Processing. IEEE.
Harel, M. and Mannor, S. (2011). Learning from multi-
ple outlooks. In Proceedings of the 28th international
conference on machine learning.
He, Z., Shu, F., Yang, Y., Li, M., and Wang, Q. (2012).
An investigation on the feasibility of cross-project de-
fect prediction. In Automated Software Engineering.
Springer Berlin Heidelberg.
Kulis, B. et al. (2013). Metric learning: a survey. In Foun-
dations and Trends
R
in Machine Learning. Now Pub-
lishers, Inc.
DATA 2017 - 6th International Conference on Data Science, Technology and Applications
26

Kulis, B., Jain, P., and Grauman, K. (2009). Fast similarity
search for learned metrics. In IEEE Transactions on
Pattern Analysis and Machine Intelligence. IEEE.
Kulis, B., Saenko, K., and Darrell, T. (2011). What you saw
is not what you get: Domain adaptation using asym-
metric kernel transforms. In Computer Vision and Pat-
tern Recognition (CVPR), 2011 IEEE Conference on.
IEEE.
Lafferty, J. and Zhai, C. (2001). Document language mod-
els, query models, and risk minimization for informa-
tion retrieval. In Proceedings of the 24th annual in-
ternational ACM SIGIR conference on Research and
development in information retrieval. ACM.
Ma, Y., Luo, G., Zeng, X., and Chen, A. (2012). Trans-
fer learning for cross-company software defect predic-
tion. Elsevier.
Nam, J. and Kim, S. (2015). Heterogeneous defect predic-
tion. In Proceedings of the 2015 10th Joint Meeting
on Foundations of Software Engineering. ACM.
Nam, J., Pan, S. J., and Kim, S. (2013). Transfer defect
learning. In In Proceedings of the 2013 International
Conference on Software Engineering. IEEE.
Nomizu, K. and Sasaki, T. (1995). Affine differential ge-
ometry. Cambridge University Press, Cambridge, 1st
edition.
Pan, S. J., Kwok, J. T., and Yang, Q. (2008). Transfer learn-
ing via dimensionality reduction. In Proceedings of
the 23rd national conference on artificial intelligence.
Pan, S. J. and Yang, Q. (2009). A survey on transfer learn-
ing. In IEEE Transactions on knowledge and data en-
gineering. IEEE.
Prettenhofer, P. and Stein, B. (2010). Cross-language text
classification using structural correspondence learn-
ing. In Proceedings of the 48th annual meeting of the
association for computational linguistics.
Rahman, F., Posnett, D., and Devanbu, P. (2012). Recalling
the “imprecision” of cross-project defect prediction.
In In Proceedings of the ACM SIGSOFT 20th Inter-
national Symposium on the Foundations of Software
Engineering. ACM.
Rashidi, P. and Cook, D. J. (2010). Multi home transfer
learning for resident activity discovery and recogni-
tion.
Saenko, K., Kulis, B., Fritz, M., and Darrell, T. (2010).
Adapting visual category models to new domain. In
European conference on computer vision. Springer
Berlin Heidelberg.
Satpal, S. and Sarawagi, S. (2007). Domain adaptation of
conditional probability models via feature subsetting.
In In Proceedings of the 11th European conference
on Principles and Practice of Knowledge Discovery
in Databases. Springer Berlin Heidelberg.
Shi, X., Liu, Q., Fan, W., Wu, P. S., and Zhu, R. (2010).
Transfer learning on heterogeneous feature spaces via
spectral transformation. In Data Mining (ICDM),
2010 IEEE 10th International Conference on. IEEE.
Si, S., Tao, D., and Geng, B. (2010). Bregman divergence-
based regularization for transfer subspace learning. In
IEEE Transactions on Knowledge and Data Engineer-
ing. IEEE.
van der Vaart, A. W. (2000). Asymptotic statistics. Cam-
bridge University Press, Cambridge, 1st edition.
van Kasteren, T. L. M., Englebienne, G., and Krose, B. J. A.
(2008). Recognizing activities in multiple contexts us-
ing transfer learning. In AAAI Fall Symposium: AI in
Eldercare: New Solutions to Old Problems.
van Kasteren, T. L. M., Englebienne, G., and Kr¨ose, B. J. A.
(2010). Transferring knowledge of activity recogni-
tion across sensor networks. In International Confer-
ence on Pervasive Computing. Springer Berlin Heidel-
berg.
Wang, C. and Mahadevan, S. (2011). Heterogeneous do-
main adaptation using magnifold alignment. In IJCAI
Proceedings-International Joint Conference on Artifi-
cial Intelligence.
Wang, H., Wang, W., Zhang, C., and Xu, F. (2014). Cross-
domain metric learning based on information theory.
In 28th AAAI Conference on Artificial Intelligence.
Wang, S. and Jin, R. (2009). An information geometry ap-
proach for distance metric learning. In In Proceedings
of the 12nd International Conference on Artificial In-
telligence and Statistics.
Wei, B. and Pal, C. (2010). Cross lingual adaptation: an ex-
periment on sentiment classifications. In Proceedings
of the ACL 2010 conference short papers.
Weiss, K., Khoshgoftaar, T. M., and Wang, D. D. (2016).
A survey of transfer learning. In Journal of Big Data.
Springer Berlin Heidelberg.
Yang, L. (2006). Distance metric learning: a comprehensive
survey.
Zhang, Y. and Yeung, D.-Y. (2010). Transfer metric learn-
ing by learning task relationships. In Proceedings of
the 16th ACM SIGKDD international conference on
Knowledge discovery and data mining. ACM.
Zheng, Y. (2015). Methodologies for cross-domain data fu-
sion: An overview. In IEEE transactions on big data.
IEEE.
Zhong, E., Fan, W., Peng, J., Zhang, K., Ren, J., Turaga,
D., and Verscheure, O. (2009). Cross domain distri-
bution adaptation via kernel mapping. In Proceedings
of the 15th ACMSIGKDD international conference on
Knowledge discovery and data mining. ACM.
Zhou, J. T., Pan, S. J., Tsang, I. W., and Yan, Y. (2014a).
Hybrid heterogeneous transfer learning through deep
learning. In 28th AAAI Conference on Artificial Intel-
ligence.
Zhou, J. T., Tsang, I. W., Sinno, P. J., and Tan, M.
(2014b). Heterogeneous domain adaptation for multi-
ple classes. In International Conference on Artificial
Intelligence and Statistics.
Asymmetric Heterogeneous Transfer Learning: A Survey
27
