Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for

Mass Customisation Production Systems

Model Formulation, Presentation and Validation

Enrico Naidoo, Jared Padayachee and Glen Bright

Mechatronics and Robotics Research Group, Discipline of Mechanical Engineering, University of KwaZulu-Natal,

King George V Ave, Durban, South Africa

Keywords: Mass Customisation, Reconfigurable Fixtures, Group Technology, Optimisation Model, Mixed Integer

Linear Programming.

Abstract: A focal point of mass customisation production systems (a significant aspect of the fourth industrial

revolution) is the implementation of reconfigurable jigs and fixtures. Traditional methods for the treatment

of conventional fixtures are inadequate for those of the reconfigurable type. This paper describes the

implementation of an on-demand fixture manufacturing cell that would reside in a mass customisation

production system. The focus, in particular, is on the behaviour and optimisation of this cell in relation to

the production system. To achieve this, a multi-stage optimisation procedure was developed that involves

cluster analysis and a mixed inter linear programming (MILP) model to minimise total idle time (and thus

makespan) in the system.

1 INTRODUCTION

The onset of Industry 4.0 has led to an increased

research interest in mass customisation production

systems (Yao and Lin, 2016). A primary focus for

the successful implementation of such production

systems is the topic of reconfigurable jigs and

fixtures (Smith et al., 2013). Customised products

are unique and this has to be accounted for by

employing jigs and fixtures that can accommodate

constantly varying geometries. Reconfigurable jigs

and fixtures are workholding devices that can be

adapted to suit the specifications of each customised

product (Bi and Zhang, 2001). As such, the

scheduling of such a production system has to

consider the reconfigurable fixture as an active

influence on the workflow, and not as a constant

resource.

An on-demand fixture manufacturing cell that

serves a mass customisation production system was

developed as part of this research. This paper

presents an optimisation procedure that schedules

activities within the fixture manufacturing cell in

tandem with a part processing cell. This was

developed as a three-stage process, the last of which

is the primary focus of this paper. The first two

stages involve cluster analysis to optimally assign

parts to fixtures. The third stage utilises a mixed

integer linear programming (MILP) model that

minimises the total idle time in the system caused by

a lack of synchronisation between the two cells.

2 LITERATURE REVIEW

2.1 Fixtures

Fixtures are used to physically locate, hold and

support parts during a manufacturing process. Mass

customisation manufacturing requires fixtures that

can hold parts of varying geometry, and be able to

rapidly and cost effectively change configurations

according to these variations. Reconfigurable

fixtures are a low cost solution to this problem.

Recent advancements include pin-array fixtures and

phase-change materials. The most widely used

reconfigurable fixtures, however, are modular

fixtures. These consist of a constant fixture base

upon which different modules can be attached to

hold various parts (Bi and Zhang, 2001). An

example of such a fixture is the Blüco-Technik®

dowel fixture shown in Figure 1.

Naidoo, E., Padayachee, J. and Bright, G.

Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for Mass Customisation Production Systems - Model Formulation, Presentation and Validation.

DOI: 10.5220/0006396900170024

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 17-24

ISBN: 978-989-758-263-9

Figure 1: Blüco-Technik® dowel fixture (Bi and Zhang,

2001).

2.2 Group Technology

Mass customisation production systems aim to blend

the advantages of both job shops (high variability

but low volume) and dedicated manufacturing lines

(high volume but low variability) while minimising

their disadvantages (Fogliatto et al., 2012). Group

Technology can play a major role in achieving this.

Group Technology involves clustering similar parts

into part families, which increases the efficiency of

processing since the part family is then

manufactured in a specialised cell. Group

Technology has given rise to the cellular

manufacturing paradigm. Modular fixtures can be

effectively employed in cellular manufacturing

systems, since the fixtures can be specialised for the

part family associated with that cell. The fixtures are

customised according to variations within the part

family by adding and removing various modules

(Groover, 2001).

The modular concept is applied in this research

for implementing an on-demand fixture

manufacturing cell. The fixtures and unfinished parts

are handled separately until the two are assembled at

the point where the part requires the fixture for it to

be machined. The cellular manufacturing method is

used so that modifications can be made to the same

fixture base via fixture reconfigurations to serve

numerous variations of the part type it is associated

with.

2.3 Scheduling and Optimisation

A literary study of scheduling and optimisation

models that considered fixtures as part of the system

was conducted. This involved the typical job shop

scheduling problem and numerous modifications

thereof.

Thörnblad et al., (2013) conducted a study on a

multi-task cell at GKN® Aerospace Engine Systems

in Sweden. The problem was described as a flexible

job shop scheduling problem. A time-indexed

formulation was used. The objective was to

minimise the weighted tardiness, where the

weighting increased as tardiness increased. The task

was to assign a particular fixture to a job, and to

limit the number of fixtures of each type.

A genetic algorithm was used by Wong et al.,

(2009) to solve a resource-constrained assembly job

shop scheduling problem with lot streaming. The

objective was to minimise total lateness cost.

Resource constraints were used to place limits on the

tools and fixtures used in the system, which were

recyclable.

Yu et al., (2012) conducted a study on a

reconfigurable manufacturing system with multiple

process plans and limited pallets/fixtures. The

problem was solved using a priority rule based

scheduling approach, which compromised on

optimality but improved ease of implementation.

This simpler approach allowed the authors to

consider multiple objectives: minimising makespan,

minimising mean flow time, and minimising mean

tardiness. The problem was constrained to only

release jobs once the relevant pallet/fixture was

available.

Literature has revealed that fixture utilisation in a

production system was mostly limited to placing a

constraint on the availability of fixtures as a

resource. There was no research found that dealt

with a system that could manufacture and

reconfigure fixtures on-demand according to the

manufacturing process demands.

3 PROBLEM STATEMENT

3.1 Problem Description

The model presented in this paper describes a

production system where two manufacturing cells

exist to serve fixture reconfigurations and processing

of parts, respectively. This represents a microcosm

of a mass customisation production system that

utilises cellular manufacturing principles to address

the synchronicity required between reconfigurable

fixtures and the customised parts that they serve.

Pre-processed parts are to be processed in the part

processing cell; the fixture configuration required to

hold each of these parts is reconfigured on a fixture

base in the fixture manufacturing cell and delivered

to the part processing cell; each pre-processed part is

then mounted to the fixture base configured for it (its

fixture) so that it can be processed – this is a

fixture-part mapping; the post-processed part is then

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

Figure 2: Workflow through the production system being considered.

removed from the fixture and released, while the

fixture returns to the fixture storage system for it to

be reconfigured for another part thereafter. The

workflow through the production system is

described in Figure 2.

The fixtures considered for this problem are of

the reconfigurable modular type. The fixture base

consists of an array of drilled holes. It is

configurable with dowel pins as modules. The

specifications are as follows:

 Array pattern: 8x8 holes (64 holes total) per

fixture base;

 Pin range: 4-16 pins per fixture configuration.

The problem requires that parts be optimally

assigned to fixture bases such that the interchange

time between fixture configurations per fixture base,

i.e. fixture reconfiguration times, are minimised. The

problem also requires that fixtures be reconfigured

and parts with fixtures be processed synchronously.

These operations must be optimally scheduled such

that the total idle time in the production system is

minimised (thus minimising makespan). The MILP

model presented in this paper focuses on this

problem.

Total idle time was chosen to be the objective

function of the model. This is because delays in the

system would result from the idle time caused by

one cell (either Cell 1 or Cell 2) being occupied after

the other cell has completed its operation, thus

halting workflow in the system. As such, emphasis

has to be placed on ensuring that the operation times

for Cell 1 and Cell 2, for every fixture and part

combination, are as close to each other as possible

for every operation.

3.2 Problem Formulation

The optimisation model presented in this paper is the

final stage of a three-stage model. The three-stage

model aims to solve the problems presented in

Section 3.1 by separating the problem into three

different stages. These are as follows:

1. Clustering Stage - clusters similar parts to be

assigned to the same fixture base by minimising

the dissimilarity measure between the fixture

configurations for those parts.

2. Intracluster Sequencing Stage - sequences the

clustered parts for each fixture base to be ordered

such that the dissimilarities (and the

reconfiguration times, by implication) between

the fixture configurations on that fixture base are

minimised.

3. Final Sequencing Stage - minimises the idle time

in the system by scheduling pairs of fixture-part

mappings that yield a minimised time difference

between their fixture reconfiguration operation

(in Cell 1) and part processing operation (in Cell

2) for every time period.

The model presented in this paper isolates the third

stage only. The first two stages will be briefly

discussed.

The Clustering Stage computes a dissimilarity

measure (an adaptation of the Sokal and Michener

similarity measure (Choi et al., 2010)) for fixture

configurations required for n number parts to be

processed (set P). A comparative matrix is formed

from these values. The measure is non-Euclidean, so

multi-dimensional scaling is used to scale the

comparative distances to a two-dimensional plane,

where k-means clustering is used to cluster the parts

to m number of fixtures (set Q). A fail-safe heuristic

Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for Mass Customisation Production Systems - Model Formulation,

Presentation and Validation

is included to ensure that cluster sizes do not force

infeasible solutions. These clusters form the ordered

set I.

The Intracluster Sequencing Stage uses

hierarchical clustering with single linkage to

determine the optimal order of the elements within

each of these clusters. Treating the dissimilarity

measure as a distance, this order ensures that the

shortest distance is traversed for each cluster. This

should ensure that total reconfiguration time for each

fixture base is minimised. The output of this stage is

∈

i for each unordered set i

∈

The Final Sequencing Stage can be isolated by

artificially creating the outputs of the first two

stages. This has no influence on demonstrating the

effectiveness of the third stage. This stage only

requires the input of the elements that comprise of

the sets i

∈

I, i.e. n number of parts in m number of

fixtures, distributed feasibly (with 0 representing

empty slots when n is not a multiple of m).

3.3 The Model

The problem is modelled as a mixed integer linear

programming (MILP) problem and solved with a

branch and bound algorithm. The notation for the

entire problem is presented below.

3.3.1 Notation

p; pϵP, P= {1,…,n}

P is the set of parts to be processed;

p is an index of the ordered set P.

q; qϵQ, Q = {1,…,m}

Q is the set of fixtures available; q

is an index of the ordered set Q.

i; iϵI, I={1,…,m}

I is the set of i, i.e. a set of sets that

holds all p-q mappings between sets

P and Q ; i is an index of the

ordered set I.

î; îϵI, I={1,…,m}

î is an alternate index of the ordered

set I.

j; jϵi, i={1,…,|i|}

i is the unordered set of p-q

mappings corresponding

specifically to fixture q, j is an

index of the set i; j denotes a part p

that is mapped to the fixture q.

ĵ; ĵ ϵi, i={1,…,|i|}

ĵ is an alternate index of the

unordered set i.

k; kϵK, K={1,…,n+1}

K is the set of time periods in which

parts or fixtures are processed or

reconfigured, respectively; k is an

index of the ordered set K.

ǩ; ǩϵK, K={1,…,n+1}

ǩ is an alternate index of the ordered

set K.

Part processing time; time for part p

corresponding to fixture-part

mapping j

∈

i to be processed; T

is a

parameter.

îĵ

Fixture reconfiguration time; time

for fixture î to be reconfigured to

fixture configuration corresponding

to ĵ

∈

î from fixture configuration

corresponding to (ĵ-1)

∈

(implicitly), i.e. subsequent

reconfiguration for fixture î; R

îĵ

is a

parameter.

ijk

A binary decision variable; X

ijk

= 1

if fixture i is reconfigured for the

fixture-part mapping j

∈

i in time

period k, X

ijk

= 0 otherwise.

iîjĵkǩ

A decision variable; ω

iîjĵkǩ

= 1 if

fixture-part mapping j

∈

i that was

reconfigured in time period k is

processed in time period ǩ=k+1

whilst fixture-part mapping ĵ

∈

î is

synchronously being reconfigured

in time period ǩ, ω

iîjĵkǩ

= 0

otherwise.

iîjĵkǩ

A decision variable; φ

iîjĵkǩ

is the

absolute time difference between

part processing time T

for fixture-

part mapping j

∈

i reconfigured in

time period k, and fixture

reconfiguration time R

îĵ

for fixture-

part mapping ĵ

∈

î reconfigured in

time period ǩ=k+1, i.e. the idle time

for every time period where two

operations are synchronous.

3.3.2 Assumptions

The assumptions used to describe and simplify the

production system for this model are as follows:

 Fixture reconfiguration times are known.

 There are fewer fixture bases than parts; |Q|<|P|.

 The required number of fixtures are already

manufactured and stored, so that only

reconfigurations are now necessary.

 Transportation time between fixture

manufacturing cell and part processing cell is

negligible.

 Once a part or fixture is assigned to a period k, it

is processed or reconfigured, respectively,

without interruption.

 Flow is synchronised between Cell 1 and Cell 2;

a job does not exit Cell 1 until Cell 2 is available,

Cell 1 does not start a new job until the previous

job has exited the cell.

 Cell 1 and Cell 2 have a just-in-time workflow

policy (i.e. unit workflow).

 The fixture reconfigured in Cell 1 in time period

k is used to process the part assigned to it in

Cell 2 in the next time period ǩ=k+1.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

Figure 3: Example of how the final φ

iîjĵkǩ

decision variables are generated, based on the flow and synchronisation of fixture

reconfiguration operation and part processing operation in either cell.

3.3.3 Mathematical Model

Min

îĵǩ



















∀

1







ĵǩ







∗



ĵǩ





∀,∀

,∀



∈,∀

∈

,∀,

∀







(1)







ǩ







∗





ǩ

0

(1a)







ǩ







∗





ǩ

0

(1b)





ĵǩ





∗

ĵǩ



∀,∀

,∀



∈,∀

∈

,∀,

∀







(2)





ĵǩ







ĵǩ

1

(2a)





ĵǩ





0

(2b)





ĵǩ



ĵǩ

0

(2c)



îĵǩ

















1

∀

1

(3)







ĵǩ

1

∀;∀



∈;∀

∈



∈;∀;∀



(4)





1









∀

(5)





1







∀,



∈



(6)





∈



0,1





∀,∀



∈,∀



(7)





ĵǩ

0



∀,∀

,∀



∈,∀

∈

,∀,

∀







(8)





ĵǩ

0



∀,∀

,∀



∈,∀

∈

,∀,

∀







(9)

3.3.4 Model Description

The objective function aims to optimally match the

part processing time for fixture-part mapping j

∈

i and

fixture reconfiguration time for another fixture-part

mapping ĵ

∈

î such that the difference between them

is minimised for time period ǩ=k+1 (which

determines the fixture-part mapping j

∈

i to be

scheduled for fixture reconfiguration in time period

k). This minimises the idle time for either cell for

every time period k.

Constraint (1) calculates the absolute difference

between the part processing time related to

fixture-part mapping j

∈

i in Cell 2 and the fixture

reconfiguration time related to fixture-part mapping

∈

î in Cell 1 for time period ǩ=k+1 for every ω

iîjĵkǩ

As this constraint is non-linear, Constraints (1a) and

(1b) are used instead of (1) to linearise the absolute

value.

Constraint (2) ensures that the idle times

calculated in Constraints (1a) and (1b) are valid.

This is determined by ensuring that the binary

decision variables related to fixture-part mappings

∈

i and ĵ

∈

î for time periods k and ǩ=k+1,

Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for Mass Customisation Production Systems - Model Formulation,

Presentation and Validation

respectively (i.e. X

ijk

and X

îĵǩ

), must both be active

(equal to 1) for ω

iîjĵkǩ

>0. As this constraint is

quadratic, Constraints (2a) to (2c) are used instead of

(2) to linearise the non-linearity of (2).

Constraint (3) ensures that the number of ω

iîjĵkǩ

corresponds to the number of time periods in which

Cell 1 and Cell 2 perform operations synchronously,

i.e. one less than the total number of jobs (n-1) since

the first time period hosts an operation in Cell 1 only

(the first fixture reconfiguration).

Constraint (4) imposes the intracluster order on

the final sequence by ensuring that two fixture-part

mappings for the same fixture (j

∈

i and ĵ

∈

i) must

appear in time periods relative to each other that

correspond to the intracluster order (ǩ>k).

Constraint (5) ensures that there is only one

fixture-part mapping j

∈

i assigned to each time

period k. Constraint (6) ensures that each fixture-part

mapping j

∈

i is assigned to a time period k only once

in the schedule.

Constraint (7) is a bound stating that X

ijk

is a

binary variable. Constraints (8) and (9) are bounds

restricting φ

iîjĵkǩ

and ω

iîjĵkǩ

, respectively, to be

non-negative. This ensures that the linearising

constraints for these decisions variables perform

their desired function.

These constraints and bounds limit the problem

search space to remain within the behavioural

boundaries associated with the production system

described in Section 3.1 and the assumptions

presented in Section 3.3.2.

Figure 3 shows an example to demonstrate how

the binary decision variable associated with a given

fixture-part mapping takes on the form of both X

ijk

when in Cell 2 and X

îĵǩ

when in Cell 1. Please note

that the time period index in this figure only

describes the time period value assigned to the

binary decision variable for that absolute time period

- based on the indices of the binary decision variable

(ijk or îĵǩ) for either cell. This is because for

fixture-part mapping 1

∈

1 to be assigned to time

period 1, the operation time in Cell 2 (T

) has to be

considered alongside that for 1

∈

2 (R

îĵ

) when both are

synchronously operated on in time period 2. This

process produces the final decision variable φ

iîjĵkǩ

from which the workflow can be easily interpreted

from the indices, as shown in Figure 3.

3.4 Results

The model was solved using the MILP solver

integrated into MATLAB® 2016a. The solver used a

branch and bound algorithm to solve the problems

presented to it.

Problems with a fixture range of 2-4 fixtures and

a part range of 4-16 parts were formulated. The

operation time values were randomised integers

within a range of 15-45 seconds for fixture

reconfiguration operations (R

) and 30-90 seconds

for part processing operations (T

These problems and their solution results are

presented in Table 1. The problems were solved to

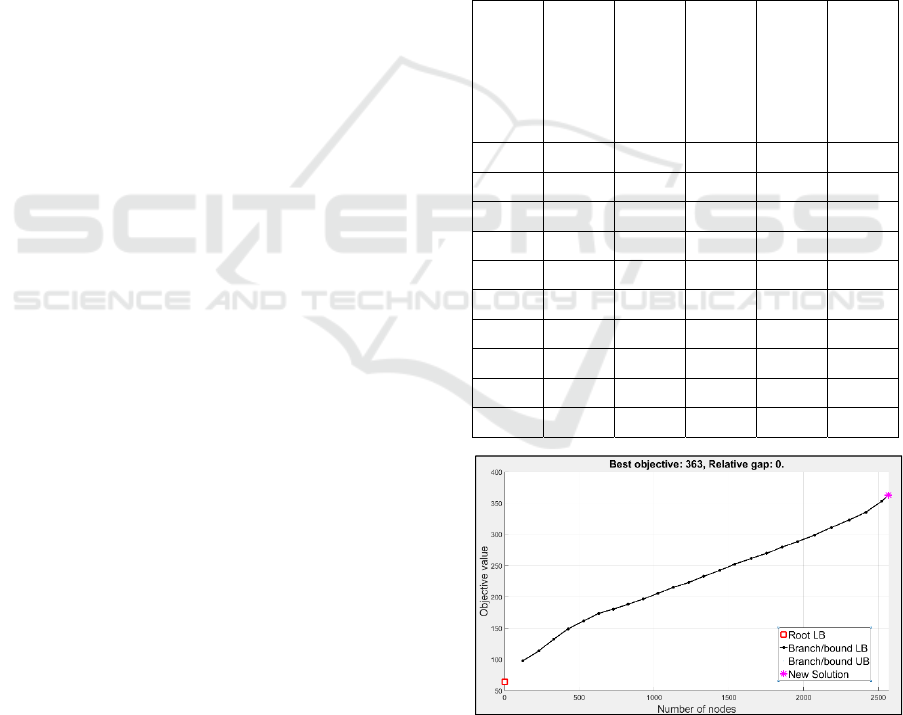
optimality. This is shown by the graphs of

convergence for the branch and bound algorithm

(Figure 4 to Figure 6 for a selection of the problems

presented in Table 1).

The test was executed on an Intel® Xeon® CPU

E3-1270 v3 at 3.50 GHz with 16 GB RAM on a

64-bit operating system.

Table 1: Sample problems and results.

Number of

Fixtures

Number of Parts

Number of

Variables

Variable Creation

Time (s)

Solution Time (s)

Convergence

2 4 64 0.044 0.719 Yes

2 6 216 0.111 0.611 Yes

2 8 512 0.424 1.027 Yes

2 10 1000 1.474 5.551 Yes

2 12 1728 4.305 49.12 Yes

3 6 276 0.142 0.752 Yes

3 9 945 1.156 8.583 Yes

3 12 2256 6.510 842.6 Yes

4 8 736 0.762 4.243 Yes

4 12 2520 7.407 6394 Yes

Figure 4: Convergence of 2 fixture/12 part problem.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

Figure 5: Convergence of 3 fixture/12 part problem.

Figure 6: Convergence of 4 fixture/12 part problem.

The sample problem size was not large. This was

due to limitations that resulted from both the

variable size increase and the solution time increase

for larger problems.

The results show that the variable size increases

by a decreasing factor for the linearly increasing

number of parts on a constant number of fixtures

(logistical growth). This growth in variable size

resulted in an exponential growth in solution times.

A similar observation of logistical growth was made

for the variable sizes that increased due to a linearly

increasing number of fixtures for a constant number

of parts. However, the solution times for this case

appear to increase logistically as well; as opposed to

the previous case, where solution times increased

exponentially.

The sharp growth in solution times from the

solver meant that limited fixture/part combinations

could be tested within a reasonable timeframe. As

the problem is NP-hard, it is expected that finding

exact solutions via the branch and bound algorithm

would be computationally expensive. The problem is

exasperated by the MATLAB® 2016a branch and

bound solver’s inability to utilise parallel processing

for this application, despite the multicore processor

of the machine used.

Optional parameters on the solver were adjusted

to yield solutions in minimum time. These included

the branch rule used (most fractional), node

selection criterion (minimum objective) and

algorithm used (primal-simplex), amongst others.

The tolerance parameters were also adjusted to cater

for the integer values used in the dataset.

The results from this sample problem set confirm

that the MILP model does create a schedule that

minimises the total idle time in the system. The

solver reached convergence for the sample set and it

was confirmed (by inspection) that the resultant

schedules from this algorithm were those of

minimum idle time.

4 CONCLUSIONS

This paper presented a three-stage procedure for the

optimal and combined scheduling of a synchronised

fixture and part manufacturing cell. The paper

focused on the third stage of the procedure where a

mixed integer linear programming (MILP) model

was used to optimally schedule the production

system The results demonstrated that the model

minimises the total idle time in the system, thus

saving on operating costs and tardiness penalties in

practice.

This is useful for mass customisation production

systems, where the use of reconfigurable fixtures in

the manufacturing process cannot be optimised with

conventional approaches.

Despite the logistical and exponential increases

in solution time (depending on which variable is

held constant – fixtures or parts), the MILP model is

valid for the production system described for a

problem of any reasonable size.

The MILP model is limited by the assumptions

listed in Section 3.3.2. Most of these are somewhat

redundant, as production systems would exhibit such

behaviour in most practical cases anyway. The unit

workflow requirement is a limiting factor, but this

could be edited to represent batch workflow quite

easily. The requirement that fixtures are already

made and waiting, is another limiting factor that is

not as readily solved.

Further work on this research topic involves

creating a heuristic to cope with larger-sized

problems more efficiently – producing sub-optimal

but good solutions with smaller variable sets and

reduced solution times. Other factors, such as the

influence of manufacturing new fixtures and

maintaining an optimal fixture inventory, can be

addressed in future research endeavours.

Optimal Scheduling of an on-Demand Fixture Manufacturing Cell for Mass Customisation Production Systems - Model Formulation,

Presentation and Validation

ACKNOWLEDGEMENTS

The financial assistance of the National Research

Foundation (NRF) towards this research is hereby

acknowledged (via the Blue Sky Research Grant:

91339). Opinions expressed and conclusions arrived

at are those of the authors, and are not necessarily to

be attributed to the NRF.

REFERENCES

Bi, Z.M. & Zhang, W.J., 2001. Flexible fixture design and

automation: Review, issues and future directions.

International Journal of Production Research, 39(13),

pp.2867–2894.

Choi, S.S., Cha, S.H. & Tappert, C.C., 2010. A Survey of

Binary Similarity and Distance Measures. Journal of

Systemics, Cybernetics & Informatics, 8(1), pp.43–48.

Fogliatto, F.S., da Silveira, G.J.C. & Borenstein, D., 2012.

The mass customization decade : An updated review

of the literature. International Journal of Production

Economics, 138(1), pp.14–25.

Groover, M.P., 2001. Chapter 15: Group Technology and

Cellular Manufacturing. In Automation, Production

Systems, and Computer-Integrated Manufacturing.

West Conshohocken, PA: Prentice-Hall, pp. 420–459.

Smith, S., Jiao, R. & Chu, C.H., 2013. Editorial: Advances

in mass customization. Journal of Intelligent

Manufacturing, 24(5), pp.873–876.

Thörnblad, K., Strömberg, A., Patriksson, M. & Almgren,

T., 2013. Scheduling optimization of a real flexible job

shop including side constraints regarding

maintenance, fixtures, and night shifts, Department of

Mathematical Sciences, Division of Mathematics,

Chalmers University and University of Gothenburg.

Wong, T.C., Chan, F.T.S. & Chan, L.Y., 2009. A

resource-constrained assembly job shop scheduling

problem with Lot Streaming technique. Computers

and Industrial Engineering, 57(3), pp.983–995.

Yao, X. & Lin, Y., 2016. Emerging manufacturing

paradigm shifts for the incoming industrial revolution.

The International Journal of Advanced Manufacturing

Technology, 85(5), pp.1665–1676.

Yu, J.M., Doh, H.H., Kim, J.S., Lee, D.H. & Nam, S.H.,

2012. Scheduling for a Reconfigurable Manufacturing

System with Multiple Process Plans and Limited

Pallets/Fixtures. International Journal of Mechanical,

Aerospace, Industrial, Mechatronic and

Manufacturing Engineering, 6(2), pp.232–237.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics