Robustness to Inertial Parameter Errors for Legged Robots Balancing on

Level Ground

Nirmal Giftsun, Andrea Del Prete and Florent Lamiraux

Laboratory for Analysis and Architecture of Systems, 7 Avenue du Colonel Roche, 31400 Toulouse, France

Keywords:

Humanoid Robots, Robust Control, Inverse-Dynamics Control, Optimization and Optimal Control.

Abstract:

Model-based control has become more and more popular in the legged robots community in the last ten

years. The key idea is to exploit a model of the system to compute precise motor commands that result

in the desired motion. This allows to improve the quality of the motion tracking, while using lower gains,

leading so to higher compliance. However, the main ﬂaw of this approach is typically its lack of robustness to

modeling errors. In this paper we focus on the robustness of inverse-dynamics control to errors in the inertial

parameters of the robot. We assume these parameters to be known, but only with a certain accuracy. We

then propose a computationally-efﬁcient optimization-based controller that ensures the balance of the robot

despite these uncertainties. We used the proposed controller in simulation to perform different reaching tasks

with the HRP-2 humanoid robot, in the presence of various modeling errors. Comparisons against a standard

inverse-dynamics controller through hundreds of simulations show the superiority of the proposed controller

in ensuring the robot balance.

1 INTRODUCTION

The problem of balancing for real legged robots is

still a challenge for the robotics community. Although

our understanding of this problem has remarkably im-

proved during the last 15 years, the robustness of the

state-of-the-art control algorithms is far from satisfac-

tory. For instance, during the recent DARPA Robotics

Challenge Finals (Pratt, 2015), all legged robots have

moved extremely cautiously, and, despite that, some-

times they could not avoid falling. Another striking

fact is the difference between what robots can do in

simulation where they easily perform extremely dy-

namics tasks and what they can do in the real world

where they struggle to execute slow movements in

structured environments. The gap between simula-

tion and real world can be explained through count-

less unmodeled uncertainties affecting these systems,

such as poor torque control, model uncertainties, sen-

sor noises and delays.

In our recent work (Del Prete and Mansard, 2016) we

have proposed an optimization-based controller that

tries to ensure the satisfaction of the physical con-

straints of the robot (force friction cones, joint accel-

eration limits and torque limits) despite errors in the

joint torque tracking. In this paper we move along

the same line, designing a robust controller that can

balance a legged robot despite bounded errors in its

inertial parameters.

1.1 State of the Art

Even though the problem of robustness is long-

standing and well-identiﬁed, it remains largely unan-

swered for legged robots. Some approaches focus ex-

clusively on the stability of the system rather than on

the feasibility of the trajectories. For instance, adap-

tive control (Kelly and Carelli, 1989) and time-delay

estimation (Jin et al., 2008) try to estimate and com-

pensate online for the major errors between nominal

and real dynamic model. Virtual model control (Pratt

et al., 2001) does not rely on the dynamic model of

the robot, which ensures robustness to errors in the

inertial parameters (Dietrich et al., 2013). The main

issue of these schemes is that they do not consider

inequality constraints, which makes it hard to imple-

ment them on real systems, given the large number of

bounds to which they are subject.

Other approaches are based on hand-tunable

heuristics. For instance, a common heuristic in Task-

Space Inverse Dynamics (TSID) (Del Prete et al.,

2015) which we adopt as well is to use a secondary

task to keep the robot posture close to a reference one,

in order to keep the movements far from the joint lim-

its. Similarly, to avoid slipping/tipping, it was pro-

posed to minimize the contact moments and the tan-

gential contact forces in the null space of the main

motion task (Righetti et al., 2010). Yet another com-

mon trick during locomotion is to maintain the cen-

Giftsun, N., Prete, A. and Lamiraux, F.

Robustness to Inertial Parameter Errors for Legged Robots Balancing on Level Ground.

DOI: 10.5220/0006397800370044

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 37-44

ISBN: 978-989-758-263-9

ter of pressure close to the center of the foot (Ka-

jita and Kanehiro, 2003). The robotics literature is

ﬁlled with these kinds of heuristics, which often are

the main reason behind the successful implementa-

tions on real platforms. However, these heuristics can

not ensure feasibility in the presence of any signiﬁ-

cant uncertainty and needs ad-hoc tuning depending

on the situation.

Finally, another class of works which includes this

paper makes use of robust optimization techniques to

formulate control and planning problems. Mordatch

et al. (Mordatch et al., 2015) considered several per-

turbed models of a humanoid robot to plan ofﬂine

a trajectory that is robust to uncertainties, reporting

success rate between 80% and 95% on a real plat-

form. Another recent work (Luo and Hauser, 2015)

has combined robust and time-scaling optimization

to plan trajectories that are robust to bounded er-

rors in friction coefﬁcients and joint accelerations,

whose magnitude can be estimated online through it-

erative learning. Nguyen and Sreenath (Nguyen and

Sreenath, 2015) have recently exploited control Lya-

punov functions and Quadratic Programs (QPs) to en-

sure stability despite bounded uncertainties in the lin-

earized system dynamics.

Contrary to (Mordatch et al., 2015; Nguyen and

Sreenath, 2015), the uncertainties modeled in this

paper affect the parameters of the system, so they

could be identiﬁed using set-membership identiﬁca-

tion techniques (Ramdani and Poignet, 2005). The

main contribution of this paper is a novel formula-

tion of the capture-point balance constraints, which

can be included in the Task-Space Inverse Dynam-

ics optimization problem to balance the robot despite

bounded uncertainties in its inertial parameters. Con-

trary to previous approaches that dealt with uncertain-

ties to inertial parameters, our approach allows us to

include inequality constraints in the problem formu-

lation. Thanks to this we can thus account for all the

constraints to which legged robots are subject, ensur-

ing the feasibility of the resulting trajectories.

1.2 Paper Overview

In Section 2 we model the uncertainty in the inertial

parameters of the robot through polytopes. Then we

present the TSID controller with capture-point con-

straints (Ramos et al., 2014) to ensure the balance of

the robot in case of no modeling errors. Section 3

presents an extension of the standard capture-point

inequalities that is robust to errors in the inertial pa-

rameters. We ﬁrst formulate the associated robust

optimization problem, and then use standard robust-

optimization techniques to reformulate it in a tractable

form.

Section 4 presents statistical results that compares

in simulation the standard and the robust controller in

a reaching task with the humanoid robot HRP-2 at dif-

ferent conditions. Regardless of the simulation condi-

tions, our results empirically demonstrate the superi-

ority of the proposed robust controller with respect to

standard TSID. Finally, Section 5 draws the conclu-

sions and discusses the future work.

2 INVERSE DYNAMICS IN TASK

SPACE WITH CAPTURE POINT

BALANCE CONSTRAINTS

To design a controller that is robust to errors in the

inertial parameters of the robot we have ﬁrst to un-

derstand how these errors affect the control action. In

this section we deﬁne the inertial parameters and we

present a standard Task-Space Inverse Dynamics con-

troller, which includes balance constraints. Through-

out the presentation we explicitly show the depen-

dency of the terms on the inertial parameters, while

we omit the dependency on the robot conﬁguration q

and velocities v because they are constant values at

each time step.

2.1 Inertial Parameters

We deﬁne the vector containing the 10 inertial param-

eters of link i as:

= (m

where m

∈ R is the mass, c

∈ R

is the center of

mass, I

∈ R

3×3

is the 3D rotational inertia matrix.

Both c

and I

are expressed in the local reference

frame of the link. Note that φ

does not contain di-

rectly c

, but it contains only its product with m

. This

is because the robot dynamics can be written in a lin-

ear form with respect to this parameterization of the

inertial parameters (Traversaro et al., 2015).

Now we can collect the inertial parameters of all

the N links of the robot in a single vector:

φ = (φ

,... ,φ

)

We assume that each link parameters φ

are not known

exactly, but we know that they lie inside a polytope

, i.e. φ

∈ U

. Hence also the vector φ lies inside a

polytope:

φ ∈ U = U

× ··· ×U

Note that since a polytope can be represented by a

set of linear inequalities, the constraint φ

∈ U

can be

expressed under the form A

≤ a

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

2.2 Task-space Inverse Dynamics

Now that we deﬁned the inertial parameters and the

associated uncertainty polytopes, we can see how

these uncertainties affect the controller.

The controller that we consider in this paper is

an optimization-based inverse dynamics controller,

which has become a standard for the control of legged

robots in recent years (Del Prete et al., 2015; Her-

zog et al., 2016; Sentis and Khatib, 2004; Saab et al.,

2011). Various formulations of the TSID optimiza-

tion problem exist and are often equivalent or simi-

lar (Del Prete et al., 2015). We write it here as an

optimization problem of the base and joint acceler-

ations ˙v ∈ R

n+6

, the contact forces f ∈ R

, and the

joint torques τ ∈ R

(Saab et al., 2013):

minimize

y=( ˙v, f ,τ)

||Ay − a||

subjectto



M(φ) −J

−S

0 0







˙v







−h(φ)

−



|τ| ≤ τ

max

(1a)

˙v

min

≤ ˙v ≤ ˙v

max

(1b)

f ∈ K (1c)

where J

∈ R

k×(n+6)

is the constraint Jacobian, M ∈

(n+6)×(n+6)

is the mass matrix, h ∈ R

n+6

contains

the bias forces, S ∈ R

n×(n+6)

is the selection matrix,

max

∈ R

are the maximum joint torques, ˙v

min/max

∈

n+6

are the acceleration bounds

, and K is the force

friction cone (which is typically linearized). The cost

function represents the error of the task, which is typ-

ically an afﬁne function of ˙v (i.e. a task-space accel-

eration):



task

0 0



| {z }

y − ( ¨x

des

task

−

task

| {z }

= ¨x

task

− ¨x

des

task

The task may be to track a predeﬁned trajectory of a

link, of the center of mass of the robot, or to regulate

the robot angular momentum.

2.3 Capture Point

Regardless of the task they are performing, legged

robots must take care of balancing (i.e. avoiding

to fall) at the same time. Balancing is fundamental

for legged robots and it has been extensively stud-

ied (Collette et al., 2008; Morisawa et al., 2012;

Goswami and Kallem, 2004; Hyon and Cheng, 2006;

The bounds of the joint positions and velocities are typ-

ically converted into joint-acceleration bounds (Rubrecht

et al., 2010)

Sherikov et al., 2014). This problem is particularly

well understood for robots in contact with a ﬂat ter-

rain only. In this case, the dynamics of the robot CoM

c is well approximated by a linear inverted pendulum.

In this model the robot is approximated as a point

mass (maintained at a constant height) supported by

a variable-length leg link (Pratt et al., 2006). The re-

sulting dynamics is:

¨c

(φ) = ω(φ)

(φ) − u),

where u ∈ R

is the Zero Moment Point (ZMP), which

is equivalent to the center of pressure (Wieber, 2002),

and ω(φ) =

(φ)

. The same dynamics can also be

obtained from the real dynamics of the robot CoM,

by assuming that ˙c

= 0 and the rate of change of the

robot angular momentum is null (Wieber et al., 2015).

Using this linear dynamics we can compute the point

on the ground where the robot can put its ZMP to in

order to stop its CoM:

ξ(φ) = c

(φ) +

˙c

(φ)

ω(φ)

This point is known as the capture point (Pratt et al.,

2006), the divergent component of motion or the ex-

trapolated center of mass (Wieber et al., 2015).

2.4 Capture-point Balance Constraints

Originally, the capture point was used to decide where

to make the robot step in order to recover from a

push (Pratt et al., 2006). More recently, Ramos et

al. (Ramos et al., 2014) proposed use it to ensure the

balance of the robot. The key idea is that, as long as

the capture point remains inside the convex hull of the

contact points (i.e. the so-called support polygon S),

the robot can balance without taking a step. To ensure

the balance of the robot we can then add to (1) an-

other set of inequalities to constrain the capture point

to remain inside the support polygon:

B(ξ(φ) + ∆t

ξ(φ)) ≤ b,

where

ξ(φ) ∈ R

is the time derivative of the capture

point, and the matrix B and the vector b deﬁne the sup-

port polygon (i.e. Bx ≤ b ⇐⇒ x ∈ S ). By expressing ξ

and its derivative as functions of c

and its derivatives

we get:



(φ) +

˙c

(φ)

ω(φ)

+ ∆t



˙c

(φ) +

¨c

(φ)

ω(φ)



≤ b



(φ) + α(φ) ˙c

(φ) +

∆t

ω(φ)

¨c

(φ)



≤ b,

where α(φ) = ∆t + ω(φ)

−1

. Finally we can express

the CoM acceleration ¨c

as a function of the joint

accelerations ˙v:

D(φ) ˙v + B (c

(φ) + α(φ) ˙c

(φ) + β(φ)) ≤ b, (2)

Robustness to Inertial Parameter Errors for Legged Robots Balancing on Level Ground

where:

D(φ) =

∆t

ω(φ)

com

(φ)

β(φ) =

∆t

ω(φ)

com

(φ)v

These inequalities are linear with respect to the joint

accelerations ˙v, so they can be added to the QP prob-

lem (1) to ensure the robot balance in case of no mod-

eling uncertainties.

3 ROBUSTNESS TO INERTIAL

PARAMETER ERRORS

In the previous section we saw that the inertial pa-

rameters appear in three different locations in the con-

troller optimization problem (1): i) in the mass matrix

M, ii) in the bias forces h, and iii) in the capture-point

inequalities (2). Unfortunately M and h depend on φ

in a highly-nonlinear way, so it is hard to deal with

it. In this paper we deal instead with the dependency

of the capture-point inequalities (2) on the inertial pa-

rameters. More in details, many terms in (2) depend

on φ, but we will focus on the dependency of the CoM

xy coordinates on φ. In other words, we want to solve

this optimization problem:

minimize

y=( ˙v, f ,τ)

||Ay − a||

subjectto



φ) −J

−S

0 0







˙v







−h(

φ)

−



(3a)

(1a),(1b), (1c)

φ) ˙v + Bc

(φ) ≤

φ) ∀φ ∈ U, (3b)

where

φ are the nominal inertial parameters (i.e. those

used by the standard controller) and:

φ) = b − B(α(

φ) ˙c

(

φ) + β(

φ))

Problem (3) is not tractable because it has an inﬁnite

number of inequality constraints—due to the capture-

point inequalities that need to be satisﬁed for all the

possible values of φ. In order to solve (3) we need

to reformulate it in a tractable form. To do that, we

will start by analyzing the relationship between c

and φ (which is linear). Then we will show how to

reformulate the robust capture-point inequalities (3b)

in a tractable form.

3.1 Dependency of CoM on Inertial

Parameters

The CoM of the robot is the average of the CoM of all

its links, weighted by their respective masses:

= P

∑

i=1

)

tot

∑

i=1

−1

tot



3×6



| {z }



.. . F



φ = Fφ,

(4)

where P =

1 0 0

0 1 0

, p

∈ R

is the position of the

reference frame of link i expressed in the world frame,

∈ R

3×3

is a rotation matrix from link i reference

frame to the world frame, and m

tot

is the total mass

of the robot. From (4) we can see that the robot

CoM is the ratio of two linear functions of the iner-

tial parameters—because m

tot

is clearly a linear func-

tion of φ. However, given that we can easily know the

robot total mass, we can assume that the uncertainty

in m

tot

be negligible. In the context of robustness we

can thus consider c

as a linear function of φ.

3.2 Robust Capture-point Inequalities

Now we want to reformulate the robust capture-point

inequalities into a tractable form. We can start by

rewriting the i-th line of (3b) using (4):

˙v + B

Fφ ≤

∀φ ∈ U,

where D

and

are the i-th lines of the associated

matrix/vector, and we dropped the dependency on the

nominal inertial parameters

φ for the sake of readabil-

ity. We can get rid of the quantiﬁer operator ∀ by

replacing the uncertain term with its maximum:

˙v + max

φ∈U

Fφ) ≤

(5)

We could compute the maximum of B

Gφ under the

constraint of φ belonging to the polytope U by solv-

ing a Linear Program (LP) for each capture-point in-

equality. However, that would be too computationally

expensive for a controller that typically has to run at

1 kHz because of the size of the LP (i.e. 10N vari-

ables and even more constraints). Luckily we show

now that we can solve this LP by solving N LPs of

much smaller size.

max

φ∈U

Fφ = max

φ∈U

∑

j=1

∑

j=1

max

∈U

(6)

Thanks to this reformulation, rather than maximizing

a linear function of the robot CoM, we can maxi-

mize a linear function of each link CoM. This boils

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

down to ﬁnding, for each link, the CoM position that

maximizes the dot product with the vector B

. If the

polytope of possible CoM positions has not many ver-

tices, this optimization can be performed by enumera-

tion. This means that we can compute the dot product

of B

with all the vertices of the CoM polytope and

then take the one that resulted in the largest value.

Since the vertices of the CoM polytope of each link

can be computed ofﬂine before starting the controller,

this operation is extremely computationally efﬁcient.

If we assume that each CoM polytope has n

ver-

tices and that the support polygon has n

sides, the

computation of max

φ∈U

Fφ for all i requires n

dot products of 3D vectors. For a typical scenario of

= 6, n

= 10 and N = 30, this gives 1800 dot prod-

ucts. On a standard computer this would take only a

few microseconds, so it is suitable for real-time con-

trol on a real robot.

Once this quantity has been computed, the robust

capture-point inequalities (3b) can be written as stan-

dard linear inequalities and problem (3) can be solved

by a standard QP solver.

4 TESTS

In this section, we present a series of simulation re-

sults that try to answer to the following question: what

improvement can we get in terms of fall prevention by

using the robust controller? We tested the proposed

controller on a typical humanoid tasks (i.e. whole-

body reaching) with the 30-degree-of-freedom hu-

manoid robot HRP-2. We carried out several batches

of tests, each batch differing for the simulated un-

certainties. Each batch was composed by 100 tests,

which is not enough for being a statistically signif-

icant sampling, but was dictated by the computation

time of our simulation environment (about 6 hours for

100 tests). Each test consisted in trying to perform the

reaching motion with the two controllers (classic and

robust) until the robot either fell or reached the end

of the motion. The inertial parameter errors changed

at each test, but they were the same for the two con-

trollers. We then measured the number of times each

controller drove the robot to a fall and the average dis-

tance between the ﬁnal end-effector position and the

desired target.

4.1 Simulation Environment

To assess the proposed controller we developed a ded-

icated simulation environment based on a state-of-

the-art algorithm for frictional contacts in multibody

systems (Kaufman et al., 2008). We integrated the

Table 1: Simulation parameters.

Symbol Meaning Value

∆t Simulation time step 0.002 s

˙v

max

Max joint acceleration 10rad s

−2

max

Max joint velocity 9.14rad s

−1

µ Force friction coefﬁcient 0.3

reach

Reaching weight 1

post

Posture weight 10

−2

f orce

Force minimization weight 10

−5

equations of motion of the system with a ﬁrst-order

Euler scheme with ﬁxed time step ∆t. Our choice

of not using an off-the-shelf simulator is motivated

by our desire to completely understand and control

the simulation environment. The inertial parameters

(masses and centers of mass) of the model used by

the controller did not match those of the model used

by the simulator. The random inertial-parameter er-

rors were generated using uniform distribution. For

masses, the maximum error was expressed in terms

of percentage of the real values. For centers of mass,

the maximum error was instead expressed in meters.

In each test we specify which uncertainties were sim-

ulated. Table 1 lists all the simulation and controller

parameters.

4.2 Task Description

The control objective was deﬁned by three tasks that

the robot had to perform at the same time. Since the

tasks are in conﬂict, we weighted them with hand-

tuned parameters, according to their importance. The

three tasks, in order of decreasing priority, are:

• reach the desired target with the right end-effector

(weight w

reach

)

• maintain initial joint posture (weight w

post

)

• minimize contact moments and tangential

forces (Righetti et al., 2013) (weight w

f orce

)

We carried out two sets of simulations. In both

cases HRP-2 executed a reaching motion that made

its capture point reach the boundaries of its support

polygon.

4.3 Test 1

In this test we set the right end-effector target far in

front of the robot. Fig. 1 shows some screen shots of

the simulations. To reach the target the robot must

move its CoM (and hence also its capture point) close

to the boundaries of its support polygon. Table 2

presents the results. Regardless of the magnitude

of the inertial parameter errors, the robust controller

Robustness to Inertial Parameter Errors for Legged Robots Balancing on Level Ground

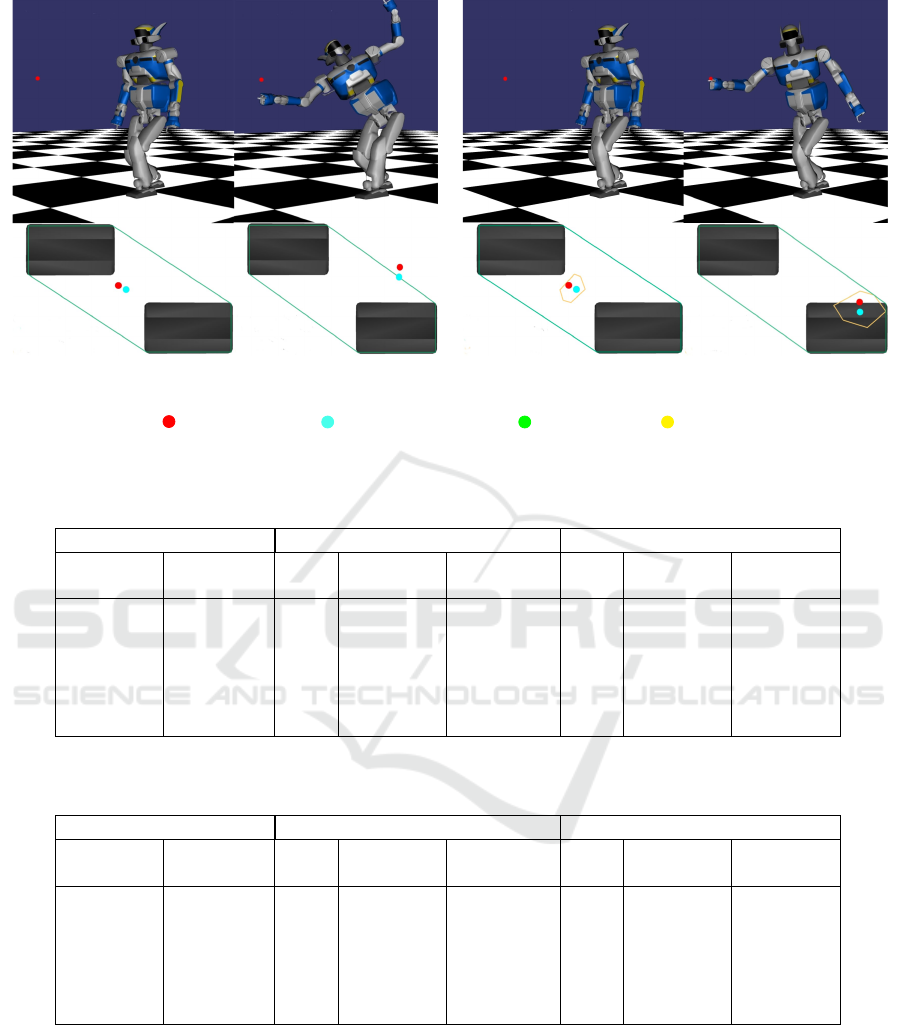
(a) Classic control illustrating the robot’s loss of balance

when the real capture point gets out of the support polygon.

(b) Robust control illustrating the robot right end effector

reaching close to the goal without losing balance.

Real Capture Point Estimated Capture Point Support Polygon Capture Point Polytope

Figure 1: Screenshots of HRP-2 executing Test 1 to reach the ball target with the robust controller.

Table 2: Results of Test 1. For each controller we show the number of falls (Falls), the average time to complete the motion

(Task Time) and the average distance of the end-effector to the target at the end of the motion (Task Error).

Uncertainties Classic Controller Robust Controller

Max Mass Max CoM Falls Task Time Task Error Falls Task Time Task Error

Error [%] Error[mm] [%] [s] [mm] [%] [s] [mm]

10 10 31 4.4 49 3 4.5 60

10 20 33 4.3 52 1 4.5 69

10 40 45 4.3 55 3 4.7 102

20 10 38 4.2 49 11 4.5 77

20 20 49 4.5 51 9 4.55 103

20 40 45 4.5 59 14 4.72 122

Table 3: Results of Test 2. For each controller we show the number of falls (Falls), the average time to complete the motion

(Task Time) and the average distance of the end-effector to the target at the end of the motion (Task Error).

Uncertainties Classic Controller Robust Controller

Max Mass Max CoM Falls Task Time Task Error Falls Task Time Task Error

Error [%] Error[mm] [%] [s] [mm] [%] [s] [mm]

10 10 29 3.94 2 0 3.4 2

10 20 35 3.4 2 2 3.0 2

10 40 42 3.86 4 0 2.6 4

20 10 43 3.6 3 0 2.8 4

20 20 45 3.5 3 0 2.5 4

20 40 45 3.0 5 0 2.1 5

managed to prevent the robot from falling almost al-

ways, while with the standard controller the robot fell

more than 30% of the times. However, since the tar-

get was far away from the robot, the robust controller

did not manage to reach it because that would have

required violating the robust balance constraints.

4.4 Test 2

In this test we moved the right end-effector target

closer to the robot, so that HRP-2 can reach it with-

out moving its CoM close to the support polygon

boundaries. However, we increased the desired speed

of reaching (by increasing the gains of the reaching

task). This affected the velocity of the CoM, which

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

in turns affected the capture point, making it reach

the boundaries of the support polygon. The differ-

ence with respect to Test 1 is that in this case also the

robust controller can reach the target. Table 3 sum-

marizes the results.

Similarly to Test 1, the classic controller leads the

robot to a fall in more than 30% of the cases. How-

ever, contrary to Test 1, this time the robust controller

also manages to reach the target, because it is located

closer to the robot. This test shows that being robust

does not necessarily implies that we have to sacriﬁce

performance.

5 CONCLUSION

This paper presented a novel optimization-based

inverse-dynamics controller that can balance a legged

robot despite bounded uncertainties in its inertial pa-

rameters. The controller is based on the state-or-the-

art control framework Task-Space Inverse Dynam-

ics. In particular, this work is based on the capture-

point inequalities (Ramos et al., 2014), which can

be included in the controller formulation to ensure

the balance of the robot on a level ground. We ex-

tended these capture-point inequalities to be robust to

bounded uncertainties in the inertial parameters of the

robot. The resulting optimization problem is still a

Quadratic Program with the same number of variables

and inequalities. Moreover, the time required for the

additional computation of the robust controller is neg-

ligible in this context (i.e. a few microseconds).

We tested the robust controller in simulations with

the HRP-2 robot, trying to reach a target position with

its right end-effector while balancing. We performed

several batches of 100 simulations each, introducing

different errors in the inertial parameters and vary-

ing the position of the target position and the required

speed of motion. Comparisons against a classic TSID

controller have shown impressive improvements in

terms of fall prevention.

5.1 Future Work

In the derivation of the robust controller we saw that

the inertial parameters appear in different terms of the

optimization problem. In this preliminary work we

focused only on how the uncertainties affect the CoM

position. We believe it should be possible to extend

this analysis to the other terms in the capture-point

inequalities: CoM velocity, CoM altitude, CoM Jaco-

bian and its time derivative. Extending it also to the

mass matrix and the bias forces is an interesting fu-

ture direction, but it seems more challenging because

of nonlinearities.

Another issue of the presented approach is that it

is rather conservative. As we saw in Test 1, this can

lead to poor performance, which can be unacceptable

on a real system. Modeling uncertainties with prob-

ability distributions (rather than with polytopes) may

lead to a less conservative behavior of the system, and

it is thus an interesting future direction. In our previ-

ous work (Del Prete and Mansard, 2016) we presented

another robust controller, which was robust to joint-

torque tracking errors. Integrating the two controllers

together seems to be feasible and it would provide ro-

bustness to both kinds of uncertainties.

In this preliminary work we focused on simula-

tions to validate the controller formulation and to test

it with different parameter errors. Of course, we plan

also to test the generated movements on the real HRP-

2 robot, to quantify how much it can beneﬁt from this

robustness.

ACKNOWLEDGEMENTS

The work leading to these results has received funding

from the European Communitys Seventh Framework

Programme (FP7/2007-2013) under grant agreement

No. 609206.

REFERENCES

Collette, C., Micaelli, A., Andriot, C., and Lemerle, P.

(2008). Robust balance optimization control of hu-

manoid robots with multiple non coplanar grasps and

frictional contacts. Proceedings - IEEE International

Conference on Robotics and Automation, pages 3187–

3193.

Del Prete, A. and Mansard, N. (2016). Robustness to Joint-

Torque Tracking Errors in Task-Space Inverse Dy-

namics. IEEE Transaction on Robotics (accepted for

publication).

Del Prete, A., Nori, F., Metta, G., and Natale, L. (2015). Pri-

oritized Motion-Force Control of Constrained Fully-

Actuated Robots: ”Task Space Inverse Dynamics”.

Robotics and Autonomous Systems, 63:150–157.

Dietrich, A., Ott, C., and Albu-Sch

affer, A. (2013).

Multi-objective compliance control of redundant ma-

nipulators: Hierarchy, control, and stability. In

2013 IEEE/RSJ international conference on intelli-

gent robots and systems, pages 3043–3050. IEEE.

Goswami, a. and Kallem, V. (2004). Rate of change of an-

gular momentum and balance maintenance of biped

robots. IEEE International Conference on Robotics

and Automation, 2004. Proceedings. ICRA ’04. 2004,

Robustness to Inertial Parameter Errors for Legged Robots Balancing on Level Ground

Herzog, A., Rotella, N., Mason, S., Grimminger, F., Schaal,

S., and Righetti, L. (2016). Momentum control with

hierarchical inverse dynamics on a torque-controlled

humanoid. Autonomous Robots, 40(3):473–491.

Hyon, S. and Cheng, G. (2006). Gravity compensation

and full-body balancing for humanoid robots. In

Humanoid Robots, 2006 6th IEEE-RAS International

Conference on, volume 00, pages 214–221.

Jin, M., Kang, S. H., and Chang, P. H. (2008). Robust com-

pliant motion control of robot with nonlinear friction

using time-delay estimation. Industrial Electronics,

IEEE Transactions on, 55(1).

Kajita, S. and Kanehiro, F. (2003). Biped walking pattern

generation by using preview control of zero-moment

point. In Robotics and Automation (ICRA), 2003 IEEE

International Conference on.

Kaufman, D. M., Sueda, S., James, D. L., and Pai, D. K.

(2008). Staggered projections for frictional contact in

multibody systems. ACM Transactions on Graphics,

27(5):1.

Kelly, R. and Carelli, R. (1989). On adaptive impedance

control of robot manipulators. Robotics and Automa-

tion, 1989. Proceedings., 1989 IEEE International

Conference on.

Luo, J. and Hauser, K. (2015). Robust Trajectory Optimiza-

tion Under Frictional Contact with Iterative Learning.

In Robotics, Science and Systems (RSS).

Mordatch, I., Lowrey, K., and Todorov, E. (2015).

Ensemble-CIO : Full-Body Dynamic Motion Plan-

ning that Transfers to Physical Humanoids. In

Robotics and Automation (ICRA), IEEE International

Conference on.

Morisawa, M., Kajita, S., Kanehiro, F., Kaneko, K., Miura,

K., and Yokoi, K. (2012). Balance control based on

Capture Point error compensation for biped walking

on uneven terrain. IEEE-RAS International Confer-

ence on Humanoid Robots, pages 734–740.

Nguyen, Q. and Sreenath, K. (2015). Optimal Robust Con-

trol for Bipedal Robots through Control Lyapunov

Function based Quadratic Programs. In Robotics, Sci-

ence and Systems (RSS).

Pratt, G. (2015). http://www.theroboticschallenge.org/.

Pratt, J., Carff, J., Drakunov, S., and Goswami, A. (2006).

Capture Point: A Step toward Humanoid Push Recov-

ery. 2006 6th IEEE-RAS International Conference on

Humanoid Robots.

Pratt, J., Chew, C.-m., Torres, A., Dilworth, P., and Pratt, G.

(2001). Virtual model control: An intuitive approach

for bipedal locomotion. The International Journal of

Robotics Research, 20(2):129–143.

Ramdani, N. and Poignet, P. (2005). Robust Dynamic Ex-

perimental Identiﬁcation of Robots With Set Mem-

bership Uncertainty. IEEE/ASME Transactions on

Mechatronics, 10(2):253–256.

Ramos, O. E., Mansard, N., and Soueres, P. (2014). Whole-

body Motion Integrating the Capture Point in the Op-

erational Space Inverse Dynamics Control. In Hu-

manoid Robots (Humanoids), 2014 14th IEEE-RAS

International Conference on.

Righetti, L., Buchli, J., Mistry, M., Kalakrishnan, M., and

Schaal, S. (2013). Optimal distribution of contact

forces with inverse dynamics control. The Interna-

tional Journal of Robotics Research, (January).

Righetti, L., Buchli, J., Mistry, M., and Schaal, S.

(2010). Inverse Dynamics With Optimal Distribu-

tion of Ground Reaction Forces for Legged Robots.

In Emerging Trends in Mobile Robotics - Proceedings

of the 13th International Conference on Climbing and

Walking Robots and the Support Technologies for Mo-

bile Machines, pages 580–587, Singapore. World Sci-

entiﬁc Publishing Co. Pte. Ltd.

Rubrecht, S., Padois, V., Bidaud, P., and De Broissia,

M. (2010). Constraints Compliant Control : con-

straints compatibility and the displaced conﬁguration

approach. In IEEE/RSJ Intenational Conference on

Intelligent Robots and Systems (IROS).

Saab, L., Mansard, N., Keith, F., Fourquet, J.-Y., and

Soueres, P. (2011). Generation of dynamic motion

for anthropomorphic systems under prioritized equal-

ity and inequality constraints. Robotics and Automa-

tion, IEEE International Conference on, pages 1091–

1096.

Saab, L., Ramos, O. E., Mansard, N., Soueres, P., and

Fourquet, J.-y. (2013). Dynamic Whole-Body Mo-

tion Generation under Rigid Contacts and other Uni-

lateral Constraints. IEEE Transactions on Robotics,

29(2):346–362.

Sentis, L. and Khatib, O. (2004). Task-oriented control of

humanoid robots through prioritization. International

Journal of Humanoid Robotics, pages 1–16.

Sherikov, A., Dimitrov, D., and Wieber, P.-b. (2014). Whole

body motion controller with long-term balance con-

straints. In Humanoid Robots (Humanoids), 2014 14th

IEEE-RAS International Conference on.

Traversaro, S., Del Prete, A., Ivaldi, S., and Nori, F. (2015).

Inertial parameters identiﬁcation and joint torques es-

timation with proximal force / torque sensing. In

Robotics and Automation (ICRA), 2015 IEEE Inter-

national Conference on.

Wieber, P.-B. (2002). On the stability of walking systems.

In Proceedings of the International Workshop on Hu-

manoid and Human Friendly Robotics, pages 1–7.

Wieber, P.-B., Tedrake, R., and Kuindersma, S. (2015).

Modeling and Control of Legged Robots. In Bruno Si-

ciliano and Oussama Khatib, editors, Springer Hand-

book of Robotics, 2nd Ed, chapter 48.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics