Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor

Networks

Evangelos D. Spyrou and Dimitrios K. Mitrakos

School of Electrical and Computer Engineering, Aristotle University of Thessaloniki, Egnatia Street, Thessaloniki, Greece

Keywords:

Transmission Power, Expected Transmission Count (ETX), Throughput, Fictitious Play, Lyapunov, Potential

Game.

Abstract:

One of the most important problems in the Wireless Sensor Network community is the enhancement of the

end-to-end throughput that strengthens the reliability of the network. Transmission power adjustment may

play a key role in accomplishing better throughput. Increasing transmission power to make the signal strength

better is the intuitive solution; however, this may introduce certain problems such as interference and more

energy consumption. However, decreasing the transmission power may result in a weak signal strength that

may result in unreliable links, which also affect throughput signiﬁcantly. One of the most important metrics

for link reliability is the Expected Transmission Count (ETX). We take the additive ETX from the basestation

to every node and we aim to optimise the route throughput by setting the transmission power accordingly.

We address these trade-offs and we propose a game-theoretic solution that aims to maximize the end-to-end

throughput between network nodes, while using the optimal transmission power. In this paper, we provide

the conditions for the convergence of our algorithm to a pure Nash equilibrium. We show that our algorithm

converges to the global optimum and that it is Lyapunov stable. We provide evidence that our algorithm

converges to the best response dynamics under the ﬁctitious play learning algorithm.

1 INTRODUCTION

End-to-end throughput (Li et al., 2001) is a major is-

sue in Wireless Sensor Networks (WSN)s. A WSN

comprises a set of links formed by nodes that trans-

mit their packets, in order to reach a basestation.

However, nodes experience interference during their

transmission, thereby making the transmission difﬁ-

cult. Furthermore, the delay of the transmission of

the packet increases, since the interfered node has to

do an exponential backoff (Committee et al., 1997)

and retransmit the packet. At the same time, this node

may be receiving packets making its link quality with

the sender to increase. Thereafter, the messages enter

a queue and need to be serviced with the minimum

delay, thus impacting the capacity of the link (Jun and

Sichitiu, 2003).

One approach to enhance the link quality between

nodes forming links, which expand to the network’s

reliability of communication is to increase the radio

transmission power level, in order to strengthen the

signal strength. Link quality is directly related to

throughput, as we can see in the novel paper present-

ing the Expected Transmission Count (ETX) metric

(De Couto et al., 2005). However, raising the trans-

mission power may result in packets being lost due

to the complexities of the wireless channel. An in-

crease in transmission power might cause an increase

in interference and collisions, decreasing the number

of packets received; hence, the end-to-end through-

put of the network. On the other hand, as we see

in (Spyrou and Mitrakos, 2015b), if the distance be-

tween the transmitter-receiver and interferer-receiver

is difference by approximately a factor of 2, interfer-

ence does not cause packet loss. This indicates that a

node may select a high transmission power level, in

order to strengthen its signal, without suffering from

packet loss. Moreover, packets using different trans-

mission powers may result in their packets simulta-

neously transmitted successfully, depending on their

distance and transmission power level (Moscibroda

et al., 2006).

There is a sweet spot in ETX related to transmis-

sion power levels that can keep throughput to a high

level, while not using a larger transmission power

level than necessary. The transmission power also

affects the energy consumption of the node, directly

inﬂuencing the lifetime of the WSN (Antonopou-

los et al., 2009). In order to handle this trade-

off, we present a ﬁnite strategy distributed game-

Spyrou, E. and Mitrakos, D.

Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor Networks.

DOI: 10.5220/0006399400170026

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 6: WINSYS, pages 17-26

ISBN: 978-989-758-261-5

theoretic approach that maximizes each node’s end-

to-end throughput, while using the optimal trans-

mission power from an optimisation point of view.

Speciﬁcally, we focus on the trade-offs between en-

ergy consumption, and ETX. We use game theory,

since it can appropriately describe the behavior of

selﬁsh nodes and ﬁnd an optimal solution in a dis-

tributed manner. Modeling systems with selﬁsh algo-

rithms have been shown to provide efﬁcient solutions

that improve network performance (Yeung and Kwok,

2006). We consider nodes to be individual players

that play selﬁshly in order to ﬁnd a best response for

their objectives. We propose a game-theoretic model

of the end-to-end throughput optimisation algorithm.

We call this algorithm Game-theoretic End-to-End

Throughput Optimisation Algorithm (GETOA).

The contributions in this paper are the following:

• We aim to solve the end-to-end throughput by util-

ising the additive ETX value.

• We show the relationship between ETX with ca-

pacity and delay.

• We formulate a game theoretic model with ﬁnite

strategies and show that it is a potential game.

This means that it converges to a Nash Equilib-

rium

• We show that it reaches the global optimum.

• We prove that the Nash Equilibrium is Lyapunov

stable.

This paper is structured as follows: Section 2 pro-

vides the related work, section 3 gives a brief descrip-

tion of game theory and potential games, section 4

gives the system model, section 5 provides our game-

theoretic algorithm, section 6 gives the results of our

approach and section 7 presents the conclusions and

the future work.

2 RELATED WORK

To the end of solving the end-to-end throughput is-

sue, there has been a plethora of approaches that dealt

with the Medium Access Control (MAC) layer (Sun

et al., 2015), (Ai et al., 2004),(Rajendran et al., 2006),

(wal, ). However, in this work we are addressing the

problem in the network layer and we are providing the

reader with necessary information regarding the rela-

tionship of capacity and delay with ETX. There are

practical works in the literature that implicitly show

enhancement of throughput by adjusting transmission

power and relate it to link quality (Son et al., 2004),

(Lin et al., 2016), (Hackmann et al., 2008). Hence,

in this work we are focusing on an approach that at-

tempts to enhance end-to-end throughput further up

the stack from the MAC layer.

Zeng et al. (Zeng et al., 2008) studied opportunis-

tic routing, which may cope with poor link reliabil-

ity by taking advantage of the broadcast nature and

spatial diversity of the wireless medium. The authors

target scenarios with multiple rates, interference, can-

didate selection and prioritisation on the maximum

end-to-end throughput or capacity of opportunistic

routing. By carefully considering wireless interfer-

ence, transmitter conﬂict graphs are composed, in or-

der to introduce concurrent transmitter sets as con-

straints related to the transmission conﬂicts or oppor-

tunistic routing. Thereafter, the maximisation of the

end-to-end throughput is formulated as a maximum-

ﬂow linear programming problem subject to the trans-

mission conﬂict constraints. Moreover, a rate selec-

tion method is proposed to perform a comparison of

multiple rate scenarios against single rate ones. The

results given in the paper provide evidence that end-

to-end throughput can be enhanced as well as that the

multiple rate scenario improves throughput as well.

Choi et al. (Choi and Lee, 2014) address the

multi-hop link property of link selection, where the

increase in the rate of link may be the reason for

the decrease of another link’s rate. The end-to-end

throughput in a multi-hop network is restricted by the

lowest rate of a link. This suggests that the max-min

fair allocation of the link rates constitutes an optimal

strategy that maximises end-to-end-throughput. The

authors suggest an approach that makes all link rates

equal, thus having the max-min fair allocation prop-

erty, using a transmission power control algorithm.

In particular this distributed algorithm operates by a

node averaging the link rates close to it and adjusts

its transmission power to accomplish the average rate.

Thereafter, it repeats this operation until all rates are

equalised. The results shown in the paper maximizes

end-to-end throughput while enhancing energy efﬁ-

ciency of multi-hop nodes.

Yu et al. (Yu et al., 2015) addressed the problem

of network capacity performance in the presence of

interference in a multi-hop wireless network, when

nodes are competing for the channel medium. In this

work, the minimisation of interference power, in or-

der to maximise network capacity is discussed. To

this end, the authors propose a consensus power con-

trol algorithm that maximises end-to-end throughput.

This algorithm adjusts the transmission powers of the

nodes to maximize the average end-to-end through-

put with a consensus coefﬁcient. Results in this work

show that maximum average end-to-end throughput

is achieved for all trafﬁc ﬂows and energy efﬁciency

WINSYS 2017 - 14th International Conference on Wireless Networks and Mobile Systems

is accomplished. The drawback of this approach lies

in the use of the algorithm in dense wireless network

deployments.

Durmaz Incel et al. (Incel et al., 2012) studied

the information collection in tree based sensor net-

work deployments. Hence, they evaluate methodolo-

gies that belong to the family of many-to-one com-

munication scheme, known as convergecast. The au-

thors consider time scheduling on a channel with and

without transmission power control settings. The for-

mer targets the minimisation of the required time slots

to achieve convergecast. The latter employs power

control to reduce schedule length using multiple fre-

quencies. The authors provide lower bounds on the

schedule length when interference complete dimin-

ishes, and suggest approaches that ensure the achieve-

ment of such bounds. Furthermore, performance of a

number of channel assignment methods suggest that

multi-frequency scheduling is enough to eliminate

most of the interference. The ﬁnding is that data rate

is not only dependent on interference; thus, spanning

trees are constructed that result in the improvement

of scheduling performance using a number of deploy-

ment densities.

Chantzis et al. (Chantzis et al., 2014), suggests

a scheme that aims to provide information regarding

the local network throughput impact on topological

properties, such as maintenance of neighbourhoods

and load balancing. To this end, the authors propose

a protocol that adaptively tunes transmission power

with low throughput settings where nodes accomplish

a degree of symmetric and coherent links. Further-

more, the network throughput is maximised provided

that degree is satisﬁed. Results show that link quality

and symmetry as well as links degree satisfaction can

be regulated appropriately by transmission power and

adaptive throughput control.

3 GAME THEORY AND

POTENTIAL GAMES

Game theory studies mathematical models of conﬂict

and cooperation (Von Neumann et al., 2007), between

players. Therefore, our meaning of the term game

corresponds to any form of social interaction between

two or more nodes. The rationality of a node is sat-

isﬁed if it pursuits the satisfaction of its preferences

through the selection of appropriate strategies. The

preferences of a node need to satisfy general ratio-

nality axioms, then its behavior can be described by

a utility function. Utility functions provide a quanti-

tative description of the node’s preferences and the

main objective is therefore the maximization of its

utility function.

In this work, we focus on strategic non-

cooperative games, since we consider nodes to act

as selﬁsh players that want to preserve their inter-

ests. The intuition behind this is that the nodes will

reach an optimal state, without having to pay a price

to maximize their payoffs. The Nash equilibrium

(Nash Jr, 1950) is the most important equilibrium in

non-cooperative strategic form games. It is deﬁned

as the point where no node will increase its utility by

unilaterally changing its strategy.

In 2008, Daskalakis proved that ﬁnding a Nash

equilibrium is PPAD-complete (Daskalakis et al.,

2009). Polynomial Parity Arguments on Directed

graphs (PPAD) is a class of total search problems

(Papadimitriou, 1994) for which solutions have been

proven to exist, however, ﬁnding a speciﬁc solution is

difﬁcult if not intractable. This development drove the

community to ’Potential Games’, since they guaran-

tee the convergence to pure Nash equilibria and best

response dynamics.

This class of games consists of the exact and or-

dinal potential games. This work employs exact po-

tential games and refer the reader to (Monderer and

Shapley, 1996) for details on the methodology. In or-

der to use exact potential games, it is essential to have

a potential function that has the same behavior as the

individual utility function, when a player unilaterally

deviates.

More formally:

A game G

N,A,u

, with N players, A strategy

proﬁles and u the payoff function, is an exact potential

game if there exists a potential function

V : A → R (1)

subject to

∀i ∈ N,∀σ

−i

∈ A

−i

,∀σ

,σ

∈ A

(2)

where σ

is the strategy of player i, σ

is the devi-

ation of player i, σ

−i

is the set of strategies followed

by all the players except player i and A

−i

is the set of

strategy proﬁles of all players except i such as

V (σ

,σ

−i

) −V (σ

,σ

−i

) = u

(σ

,σ

−i

) − u

(σ

,σ

−i

)

(3)

4 SYSTEM MODEL

We consider a wireless network that consists of a

number of nodes that transmit their data in a wire-

less fashion. The network is essentially an undirected

Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor Networks

graph G which has V number of vertices and E num-

ber of edges G = (V, E). Link asymmetry is consid-

ered, thereby the network nodes send data and ac-

knowledgment packets to each other.

One of the key issues of the wireless links, is the

number of link layer transmissions of a packet. This

is a good metric that aims to increase throughput of a

link as well as the network, by minimising transmis-

sions and, of course, retransmissions of packets. Thus

the metric ETX emerged, which is the average num-

ber of transmissions of data and ACK packets. A node

calculates ETX by obtaining the frame loss ratio of a

wireless link l with each of its neighbouring nodes in

the data direction, denoted as PRR

f rwd

. Thereafter it

continues by repeating the aforementioned procedure

in the opposite direction, denoted as PRR

bkwd

. ETX

is widely known as the inverse of the probability of

Packet Success Delivery given as

ET X

PRR

f rwd

∗ PRR

bkwd

(4)

As it is clear from equation (4) a link is perfect if

its ETX value is 1. Moreover, the route ETX is the

sum of the ETX of every link in the route. Hence, a

two-hop route of perfect links has an ETX of 2. As

we can see, the larger the ETX value the less reli-

able the links. ETX has several signiﬁcant features,

such as that it affects throughput, since it it depends

on delivery ratios. Also, it detects link asymmetry

by employing bidirectional ratios, uses precise link

loss ratio measurements, and penalizes routes with

more hops, which have lower throughput due to inter-

ference between different hops of the same path (Li

et al., 2001). In addition, ETX may implicitly lower

the energy consumption per packet, as each transmis-

sion or retransmission may increase a node’s energy

consumption.

At this point we will provide the relationship of

ETX with transmission power of each node. Note

that we consider a Rayleigh channel (Rappaport et al.,

1996). For a wireless link (i, j), the Packet Reception

Ratio PRR

i, j

is deﬁned as the ratio of the number of

packets received by node j over the number of pack-

ets sent by node i. This is the PRR

f rwd

and similarly,

PRR

j,i

is the PRR

bkwd

. It can be expressed by approx-

imation as

PRR

i, j

= (1 − ξ)

(5)

where l is the packet length in bits. The Bit Error

Rate (BER), which we denote as ξ

i, j

, is given by the

following formula (Fu et al., 2012)

i, j

1 −

i, j

1 + γ

i, j

(6)

Figure 1: ETX valued network.

where γ

i, j

is the Signal-to-Interference-plus-Noise

Ratio (SINR) of the transmission from node i to node

j. γ

i, j

is given by

i, j

∑

t6=i,t6= j

t, j

+ N

(7)

We model the wireless channel as a log-distance shad-

owing path loss channel, deﬁned as

PL(d) = PL(d

) + 10ηlog(

) + X

(8)

where PL(d) is the path loss at distance d, PL(d

) is

the path loss, which is known, at reference distance

, η is the path loss exponent and X

is the zero-

mean Gaussian random variable with standard devi-

ation σ. Our setting is based on a dynamic environ-

ment, possibly indoor, where the nodes transmit or

receive in a multipath manner. This setting is equiv-

alent to node mobility. Shadow fading and distance

based attenuation vary; hence, the instant value of the

magnitude of the received signal is a random variable

with Rayleigh probability density function. Here, we

assume that the channel coefﬁcients are constant for

a codeword, but there are independent and identically

distributed (i.i.d) for different blocks. For a set of dif-

ferent links, the channel fading coefﬁcients are statis-

tically i.i.d., which is a reasonable assumption, since

nodes are spatially deployed (Sadek et al., 2006).

State-of-the-art wireless routing protocols, such as

CTP (Gnawali et al., 2009), encapsulate ETX to en-

capsulate the routes packet reception quality by mak-

ing it additive. An example can be seen in ﬁgure 1. As

we can see, the ETX values of the links originating at

the basestation are being added as the network goes

downwards away from the basestation. Each node

selects its parent node that it transmits to depending

on the link quality of the available parents. For in-

stance, node G has an ETX value of 5.5 to reach node

WINSYS 2017 - 14th International Conference on Wireless Networks and Mobile Systems

A, which is the basestation. This implicitly provides

us substantial information regarding the hop-count of

the nodes in the network. Throughput of the network

may be optimised, since we can attempt to optimise

the link quality in entire routes.

Hence, we consider the additive route ETX that

we call AETX, which is given in equation (9). We

denote R is the set of nodes that create the links of a

route to the basestation for every node i ∈ R.

AET X =

∑

i=1

ET X

(9)

4.1 Relationship between AETX and

Capacity

We know that the capacity of the link is given by the

Shannon’s formula, which is a function of the SINR

between nodes i, j in equation (7) as

f (γ

i, j

) = W log

(1 + γ

i, j

) (10)

We can derive from equation (10) that the capacity of

the link is maximised when the SINR of the link is

maximum. From equation (5), it is straightforward to

see that when SINR increases PRR increases as well,

except when interference is too large, whereby the

node has its maximum PRR by using a transmission

power level lower than the maximum value (Hack-

mann et al., 2008). From equation (4) we can derive

that the smaller the value of AETX, the larger the ca-

pacity of the wireless link. Furthermore, it is intuitive

that we have a sweet spot of ETX that maximises the

capacity between the two nodes by using one of the

ﬁnite set of available transmission power levels. Fur-

thermore, we see that in a status of competition for

the wireless medium there is a value of the transmis-

sion power that is able to maximise the end-to-end

throughput of the nodes route to the basestation given

in equation (9) and maximise capacity at the same

time.

Additionally, we are required to show the relation-

ship between the AETX with the delay of the packet

transmission due to interference, which will present

in the following part of this paper. Our aim is to show

that the selection of the most appropriate transmission

power level will increase throughput and minimise the

delay of packet transmission as well.

4.2 Relationship between AETX and

Delay

In our network scenario we wish to satisfy certain

QoS requirements, such as keeping the transmission

and queuing delay smaller than an upper bound. We

denote the upper bound of the delay as d. We assume

that the incoming trafﬁc in our network is Poisson dis-

tributed with average packet arrival rate λ

and packet

length of N bits. Thus, we have the rate of the source,

which is given by r

= Mλ

. We assume that the pack-

ets are queued in a FIFO queue. The time required for

each packet transmission is given by

(11)

where R

is the transmission rate of the queued pack-

ets.

We encapsulate a similar approach with Meshkati

et al. (Meshkati et al., 2006) in our model, to indicate

the relationship of the transmission delay with AETX

and provide a QoS constraint. We consider an M/G/1

queue with Poisson trafﬁc with the aforementioned

parameter λ

and service time s

. We transform AETX

to be normalised to [0,1], in order to make it resemble

with AETX probability. To this end, the formula of

AETX, which we denote as AET X

norm

is given by

AET X

norm

1 − AET X

max

∗ AET X −

AET X

max

1 − AET X

max

(12)

where AET X

max

is the maximum value that AET X

can take give the hops that node i exists away from

the basestation. Hence, we have the Probability Mass

Function (PMF)

Pr{s

= mt

} = AET X

norm

(1 − AET X

norm

)

m−1

for m = 1,2...

Thereafter, the service rate µ

can be given by

AET X

norm

(13)

and the load is given by ρ

AET X

norm

The average packet delay as given by Meshkati is

given by

d = t

1 −

AET X

norm

− λ

AET X

norm

> λ

(14)

From equation (14), we can see that a larger

AET X

norm

leads to smaller delay. Hence, a smaller

AET X offers as quicker transmission of our packets.

Thus, we ﬁnd that we can deﬁne a utility function to

create a game-theoretic algorithm that will aim to op-

timise the end-to-end throughput in a hierarchically

routed network.

Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor Networks

5 GETOA

We consider a game-theoretic formulation of the net-

work Γ = (N,A,u), where N is the number of play-

ers/nodes, A is the set of available strategies to a

player and u represent the utility functions of the play-

ers.

We deﬁne the strategies of the players A =

,...p

as a set of ﬁnite values that correspond to

the transmission power settings of a wireless module.

Furthermore, we deﬁne the utility function of a player

i as

= −AET X + c

(15)

This a common deﬁnition of a utility function

that utilises pricing, in order to make the game more

efﬁcient (Spyrou and Mitrakos, 2015a; Tsiropoulou

et al., 2012). We transform the utility function of

(15) in the following manner. We use the negative

AETX to the power of two, in order to make the ﬁrst

term concave. The second term includes the variable

> 0, which is the cost of using the transmission

power p

and is assumed to be set to 1.

= −(AET X)

+ c

(16)

We formulate our game as an exact potential

game as shown below

Lemma 1. The game Γ described above with utility

functions as in (16) is an exact potential game and

its potential function is given by V = −

∑

(AET X)

∑

Proof.

V (p

, p

−i

)−V (p

, p

−i

) = u

, p

−i

)−u

, p

−i

∑

m∈N,m6=i

, p

−m

) − u

, p

−m

))

Since only one node can deviate

∑

m∈N,m6=i

, p

−m

) − u

, p

−m

)) = 0. Hence,

we conclude that Γ is an exact potential game. We

can derive the above from the proof of Monderer and

Shapley where

∂V (p)

∂p

∂u

(p)

∂p

,m ∈ N.

5.1 Equilibrium Analysis and Best

Response Dynamics

Remark 3.1: The potential function is signiﬁcant since

its maximisation, when a speciﬁc policy is played,

results in this policy being an equilibrium of the de-

signed game.

Since we have a ﬁnite strategy set, the potential

function needs to satisfy the Larger Midpoint Prop-

erty (LMP) (Ui, 2008). The converse is true as well;

As such, if a policy is an equilibrium, it maximises

the potential function. Our function in equation (16)

is concave. Thus, Schur concavity is ensured and spe-

ciﬁc majorisation properties are satisﬁed (Olkin and

Marshall, 2016). We will show that in the next part of

this section.

We consider two n-dimensional vectors δ(1),δ(2).

Deﬁnition 1: (Marshall et al., 2010) A vector δ(2)

majorises δ(1), which we denote as δ(1) ≺ δ(2), if

δ(2) is more ”unregular” in the following fashion:











∑

i=1

[i]

(1) ≤

∑

i=1

[i]

(2),k = 1,2,...,n − 1

∑

i=1

[i]

(1) =

∑

i=1

[i]

(2)

(17)

where δ

[i]

(m) is a permutation of δ

(m) satisfying

the condition δ

[1]

(m) ≥ δ

[2]

(m) ≥ ... ≥ δ

[n]

(m),m =

1,2.

From equation 16 we can derive that the largest

element of δ(2) is larger than the largest element

of δ(1). Similarly, the smallest element of δ(2) is

smaller than the smallest element of δ(1). Thereafter,

we proceed in showing that we can accomplish the

global optimum by investigating the Schur convexity

properties of majorisation.

Deﬁnition 2:: A function f : R

→ R is Schur con-

cave if δ(1) ≺ δ(2) suggests f (δ(1)) ≥ f (δ(2)).

Deﬁnition 1 dictates that there is strong majorisa-

tion; Proposition C.2 of (Marshall et al., 2010) sug-

gests that a function f : R

→ R is Schur-concave if

it is symmetric and concave, . In the next part we will

show that the potential function V is Schur-concave.

Lemma 2. Function V is concave in N

Proof. It is obvious that the function is concave. This

can be concluded since if the second derivative of the

potential function includes two terms, of which the

ﬁrst a concave term and the second will be set to 0.

Proposition 1. If the function u(p) is concave then

the function V (p) is Schur concave.

WINSYS 2017 - 14th International Conference on Wireless Networks and Mobile Systems

Proof. The proof is given by using the following

corollary from (Marshall et al., 2010).

Corollary 1. Let φ(x) =

∑

i=1

g(x) where g is concave.

Then φ is Schur-concave

Theorem 1. The GETOA algorithm reaches the glo-

cal optimum

Proof. These majorisation properties can be utilised

to show that our function follows LMP. Since our

function is Schur concave the global optimum p

∗

ma-

jorises another potential p

0∗

. Since V (p) is Schur

concave it follows by deﬁnition that V(p

0∗

) ≥ V (p

∗

Since, p∗ maximises the potential, this is only pos-

sible when V (p

0∗

) = V (p

∗

). Hence, p

∗

is the global

optimum. Moreover, when the maximiser is reached

we set the variable c

of the potential function (16)

equal to the derivative of its ﬁrst term −

∑

(AET X)

as in (Candogan et al., 2010). Thus, we have

∂u

∂p

= 0.

Using this result and the majorisation of the func-

tion, which is concave, we conclude that our approach

reaches the global maximum.

In our non-cooperative game formulation we in-

troduce the class of best-response dynamics, in which

every node updates its strategy, in order to maximise

its utility, given the strategies of the other nodes. We

denote the best-response dynamics with β

for the i

node, which satisﬁes

) = argmax

∈P

−i

) (18)

We are investigating ﬁnite actions for the nodes’

strategies; hence, the best response dynamics may

be addressed using the discrete-time ﬁctitious play

(DTFP) (Brown, 1951; Robinson, 1951). Fictitious

play has been proven to converge in ﬁnite potential

games (Monderer and Shapley, 1996).

In this paper, we are concentrating in the study of

the dynamical properties of our potential game. To

this end, we wish to show that the Nash Equilibrium

that our approach is converging to is Lyapunov stable

(Khalil and Grizzle, 1996).

Theorem 2. Let Φ = V

max

− V

min

> 0 a Lyapunov

function. The Nash Equilibrium that our algorithm

converges to is Lyapunov stable.

Proof. We know that the maximiser of our poten-

tial function is the globally optimal Nash equilibrium

∗

= V

max

= 0. We have that Φ(0) = 0. Hence, we

only need to show that −V

min

≤ 0. If we take the

derivative of −V

min

we have

−V

min

= −

∑

(−(p

1/2

l(H

i, j

(

∑

i∈N,k6=i

k, j

i, j

∑

i∈N,k6=i

k, j

) + 1)) − H

i, j

(

∑

i∈N,k6=i

k, j

i, j

(

∑

i∈N,k6=i

k, j

) + 1)

)))/(2((p

1/2

i, j

(

∑

i∈N,k6=i

k, j

i, j

∑

i∈N,k6=i

k, j

) + 1)))

1/2

)/2 + 1/2)

2l+1

((H

m,i

(

∑

s∈N,s6=i6=m

s,i

m,i

(

∑

s∈N,s6=i6=m

s,i

) + 1)))

1/2

/2 + 1/2)

i, j

(

∑

i∈N,k6=i

k, j

i, j

∑

i∈N,k6=i

k, j

)+1)))

1/2

)−c

)

(19)

Our transmission power strategies are p

> 0, the

channel gain is negative H

i, j

< 0 and l is an even num-

ber. In order to simplify equation (20) we denote

• f

= p

i, j

< 0

• f

∑

i∈N,k6=i

k, j

< 0

• f

∑

i∈N,k6=i

k, j

> 0

• f

∑

i∈N,k6=i

k, j

< 0

• f

= H

i, j

> 0

• f

∑

s∈N,s6=i6=m

s,i

< 0

• f

= H

m,i

< 0

• f

= p

1/2

> 0

Thus, we have

−V

min

= −

∑

(−(l f

i, j

( f

/( f

) + 1)) − f

/( f

( f

/( f

) + 1)

)))/

(2(( f

i, j

/( f

( f

/ f

+ 1)))

1/2

)/2 + 1/2)

2l+1

(( f

/( f

( f

/( f

) + 1)))

1/2

/2 + 1/2)

i, j

/( f

) + 1)))

1/2

) − c

) (20)

Even though the derivative is complex, we can see

that −V

min

≤ 0 in our strategy set. We also veriﬁed the

sign of the derivative through extensive simulations

Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor Networks

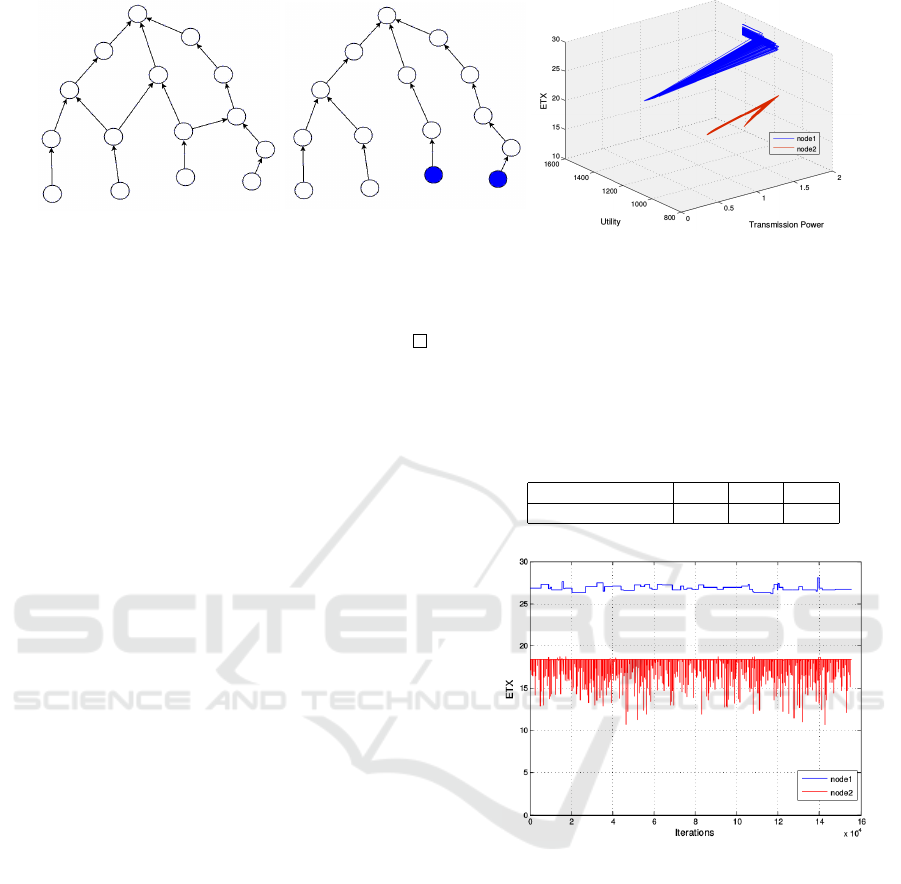
(a) Initial Topology of all the

nodes

(b) Final Topology of all the

nodes

Figure 2: Initial, Final Topologies and Utilities, Transmission Powers, ETX values of the Coloured Nodes.

on MATLAB. This means that the Nash Equilibrium

that our algorithm is reaching is stable.

6 RESULTS

We consider the network of 15 nodes, which is shown

in ﬁgure 2 (a). The arrows represent that the wireless

nodes operate in a hierarchical routing mode, where

each node unicasts its data to its selected parent. The

parent selection process is undertaken by evaluation

the ETX values of each node’s neighbours and choos-

ing the one with the least ETX value.

After the formation of the network and the opera-

tion of GETOA, the ﬁnal topology is shown in ﬁgure

2 (b). We can see that a route towards the basestation

has been formed for every mode based on the ETX

values of the upstream nodes.

The transmission power values that are selected

as strategies of the nodes come from the CC2020

datasheet (Datasheet, 2006) and are given in table 1.

The reason behind the selection is the fact that want

to see the operation of our algorithm in the gray areas

as identiﬁed in (Son et al., 2004). The operation of

GETOA initiates by selecting a random transmission

power level and then starts to perform the ﬁctitious

play part. We can see the utility function over time

of the blue nodes in ﬁgure 2 (c). Speciﬁcally, we can

see the convergence of the blue nodes to the transmis-

sion power 15.2 after they ﬂuctuate to transmission

power 13.9. Node 2 accomplishes a utility of approx-

imately 1180, an ETX value of 18.43. On the other

hand, node 1 achieves a utility of 1419 approximately

and its ETX value is approximately 26.

The utility of node 1 is decreasing from the ini-

tial one, since node 1 switched to transmission power

2; thus, increasing interference on node 1. Hence,we

can see in ﬁgure 3 that the ETX of node 1 is ﬂuctu-

ating, since its utility is decreasing for the aforemen-

tioned reason. On the other hand, the ETX value of

node 2 is slightly increasing by taking advantage of

the medium transmission power of node 1. Note that

both the nodes do not utilise transmission power 17.4,

since it creates more interference to other nodes; thus

making their utilities smaller, which can be veriﬁed in

(Hackmann et al., 2008).

Table 1: Tx power strategies.

Tx Power Levels p

Values 16.5 15.2 13.9

Figure 3: ETX Values of Blue Nodes.

7 CONCLUSIONS

In this paper we addressed the end-to-end through-

put optimisation using game theory. We established

a utility function based on the additive ETX from the

sink to each node and we priced it with a concave

price utilising the transmission power used for data

transmission. We showed that there is a relationship

between ETX with capacity and packet transmission

delay. Furthermore, we formulated our game theo-

retic model with ﬁnite strategies and showed that it is

a potential game. Moreover, we proved that the Nash

equilibrium we located is the global optimum as well,

using Schur concavity. Finally, we proved that the

WINSYS 2017 - 14th International Conference on Wireless Networks and Mobile Systems

Nash equilibrium our GETOA algorithm approached

to is Lyapunov stable.

The demonstration of our approach consisted of a

network of 15 nodes. We analysed the two blue nodes

that exist further down the network to check their be-

havior under our GETOA algorithm. We found that

one of the nodes increases its utility, while slightly

decreases its ETX value; thus exhibiting better end-

to-end reception. The other node, has to decrease its

utility function, since it was suffering from interfer-

ence. Both nodes converged to transmission power

15.2mA, out of the three available transmission power

levels.

Our future work includes the packet transmission

delay as a constraint to our utility function. This will

give us interesting results on the utility function. Fur-

thermore, we aim to compare our approach with a

log-linear learning algorithm (Monderer and Shapley,

1996) to investigate the differences in performance

and convergence.

REFERENCES

Approaching throughput-optimality in distributed csma

scheduling algorithms with collisions.

Ai, J., Kong, J., and Turgut, D. (2004). An adaptive co-

ordinated medium access control for wireless sensor

networks. In Computers and Communications, 2004.

Proceedings. ISCC 2004. Ninth International Sympo-

sium on, volume 1, pages 214–219. IEEE.

Antonopoulos, C., Prayati, A., Stoyanova, T., Koulamas, C.,

and Papadopoulos, G. (2009). Experimental evalua-

tion of a WSN platform power consumption. In IEEE

IPDPS, pages 1–8. IEEE.

Brown, G. W. (1951). Iterative solution of games by ﬁcti-

tious play. Activity analysis of production and alloca-

tion, 13(1):374–376.

Candogan, U. O., Menache, I., Ozdaglar, A., and Parrilo,

P. A. (2010). Near-optimal power control in wireless

networks: A potential game approach. In INFOCOM,

2010 Proceedings IEEE, pages 1–9. IEEE.

Chantzis, K., Amaxilatis, D., Chatzigiannakis, I., and

Rolim, J. (2014). Symmetric coherent link degree,

adaptive throughput-transmission power for wireless

sensor networks. In 2014 IEEE International Con-

ference on Distributed Computing in Sensor Systems,

pages 26–34. IEEE.

Choi, H.-H. and Lee, J.-R. (2014). Distributed transmit

power control for maximizing end-to-end throughput

in wireless multi-hop networks. Wireless personal

communications, 74(3):1033–1044.

Committee, I. C. S. L. M. S. et al. (1997). Wireless lan

medium access control (mac) and physical layer (phy)

speciﬁcations.

Daskalakis, C., Goldberg, P. W., and Papadimitriou, C. H.

(2009). The complexity of computing a nash equilib-

rium. SIAM Journal on Computing, 39(1):195–259.

Datasheet, C. (2006). 2.4 ghz ieee 802.15. 4 zigbee-ready rf

transceiver. Chipcon products from Texas Instruments.

De Couto, D. S., Aguayo, D., Bicket, J., and Morris, R.

(2005). A high-throughput path metric for multi-hop

wireless routing. Wireless Networks, 11(4):419–434.

Fu, Y., Sha, M., Hackmann, G., and Lu, C. (2012). Practical

control of transmission power for wireless sensor net-

works. In Network Protocols (ICNP), 2012 20th IEEE

International Conference on, pages 1–10. IEEE.

Gnawali, O., Fonseca, R., Jamieson, K., Moss, D., and

Levis, P. (2009). Collection tree protocol. In ACM

SenSys, pages 1–14.

Hackmann, G., Chipara, O., and Lu, C. (2008). Robust

topology control for indoor wireless sensor networks.

In Proceedings of the 6th ACM conference on Embed-

ded network sensor systems, pages 57–70. ACM.

Incel, O. D., Ghosh, A., Krishnamachari, B., and Chinta-

lapudi, K. (2012). Fast data collection in tree-based

wireless sensor networks. IEEE Transactions on Mo-

bile computing, 11(1):86–99.

Jun, J. and Sichitiu, M. L. (2003). The nominal capacity of

wireless mesh networks. IEEE wireless communica-

tions, 10(5):8–14.

Khalil, H. K. and Grizzle, J. (1996). Nonlinear systems,

volume 3. Prentice hall New Jersey.

Li, J., Blake, C., De Couto, D. S., Lee, H. I., and Morris, R.

(2001). Capacity of ad hoc wireless networks. In Pro-

ceedings of the 7th annual international conference

on Mobile computing and networking, pages 61–69.

ACM.

Lin, S., Miao, F., Zhang, J., Zhou, G., Gu, L., He, T.,

Stankovic, J. A., Son, S., and Pappas, G. J. (2016).

Atpc: Adaptive transmission power control for wire-

less sensor networks. ACM Transactions on Sensor

Networks (TOSN), 12(1):6.

Marshall, A. W., Olkin, I., and Arnold, B. (2010). In-

equalities: theory of majorization and its applica-

tions. Springer Science & Business Media.

Meshkati, F., Poor, H. V., Schwartz, S. C., and Balan,

R. V. (2006). Energy-efﬁcient power and rate con-

trol with qos constraints: a game-theoretic approach.

In Proceedings of the 2006 international conference

on Wireless communications and mobile computing,

pages 1435–1440. ACM.

Monderer, D. and Shapley, L. S. (1996). Potential games.

Games and economic behavior, 14(1):124–143.

Moscibroda, T., Wattenhofer, R., and Weber, Y. (2006). Pro-

tocol design beyond graph-based models. In Proc.

of the ACM Workshop on Hot Topics in Networks

(HotNets-V), pages 25–30.

Nash Jr, J. (1950). The bargaining problem. Econometrica:

Journal of the Econometric Society, pages 155–162.

Olkin, I. and Marshall, A. W. (2016). Inequalities: the-

ory of majorization and its applications, volume 143.

Academic press.

Papadimitriou, C. H. (1994). On the complexity of the par-

ity argument and other inefﬁcient proofs of existence.

Game-theoretic End-to-end Throughput Optimisation in Wireless Sensor Networks

Journal of Computer and system Sciences, 48(3):498–

532.

Rajendran, V., Obraczka, K., and Garcia-Luna-Aceves, J. J.

(2006). Energy-efﬁcient, collision-free medium ac-

cess control for wireless sensor networks. Wireless

Networks, 12(1):63–78.

Rappaport, T. S. et al. (1996). Wireless communications:

principles and practice, volume 2. Prentice Hall PTR

New Jersey.

Robinson, J. (1951). An iterative method of solving a game.

Annals of mathematics, pages 296–301.

Sadek, A. K., Yu, W., and Liu, K. (2006). When does coop-

eration have better performance in sensor networks?

In Sensor and Ad Hoc Communications and Networks,

2006. SECON’06. 2006 3rd Annual IEEE Communi-

cations Society on, volume 1, pages 188–197. IEEE.

Son, D., Krishnamachari, B., and Heidemann, J. (2004).

Experimental study of the effects of transmission

power control and blacklisting in wireless sensor net-

works. In Sensor and Ad Hoc Communications and

Networks, 2004. IEEE SECON 2004. 2004 First An-

nual IEEE Communications Society Conference on,

pages 289–298. IEEE.

Spyrou, E. D. and Mitrakos, D. K. (2015a). Approximat-

ing nash equilibrium uniqueness of power control in

practical wsns. arXiv preprint arXiv:1512.05141.

Spyrou, E. D. and Mitrakos, D. K. (2015b). On the homo-

geneous transmission power under the sinr model. In

4th International Conference on Telecommunications

and Remote Sensing, ICTRS 2015.

Sun, F., Li, L., and Jiang, Y. (2015). Impact of duty cycle

on end-to-end performance in a wireless sensor net-

work. In 2015 IEEE Wireless Communications and

Networking Conference (WCNC), pages 1906–1911.

IEEE.

Tsiropoulou, E. E., Katsinis, G. K., and Papavassiliou, S.

(2012). Distributed uplink power control in multiser-

vice wireless networks via a game theoretic approach

with convex pricing. IEEE Transactions on Parallel

and Distributed Systems, 23(1):61–68.

Ui, T. (2008). Discrete concavity for potential games. In-

ternational Game Theory Review, 10(01):137–143.

Von Neumann, J., Morgenstern, O., Rubinstein, A., and

Kuhn, H. (2007). Theory of games and economic be-

havior. Princeton Univ Pr.

Yeung, M. and Kwok, Y. (2006). A game theoretic approach

to power aware wireless data access. IEEE transac-

tions on mobile computing, pages 1057–1073.

Yu, Y., Shah, S., Tan, Y., and Lim, Y. (2015). End-

to-end throughput evaluation of consensus tpc algo-

rithm in multihop wireless networks. In 2015 Interna-

tional Wireless Communications and Mobile Comput-

ing Conference (IWCMC), pages 941–946. IEEE.

Zeng, K., Lou, W., and Zhai, H. (2008). On end-to-end

throughput of opportunistic routing in multirate and

multihop wireless networks. In INFOCOM 2008.

The 27th Conference on Computer Communications.

IEEE. IEEE.

WINSYS 2017 - 14th International Conference on Wireless Networks and Mobile Systems