An Improved Approach for Class Test Ordering Optimization using

Genetic Algorithms

Istvan Gergely Czibula, Gabriela Czibula and Zsuzsanna Marian

Department of Computer Science, Babes¸-Bolyai University, M. Kogalniceanu Street, Cluj-Napoca, Romania

Keywords:

Integration Testing, Class Integration Test Order, Genetic Algorithm.

Abstract:

Identifying the order in which the application classes have to be tested during the integration testing of object-

oriented software systems is essential for reducing the testing effort. The Class Integration Test Order (CITO)

problem refers to determining the test class order that minimizes stub creation cost, and subsequently testing

effort. The goal of this paper is to propose an efﬁcient approach for class integration test order optimization

using a genetic algorithm with stochastic acceptance. The main goal of the class integration test order problem

is to minimize the stubbing effort needed during the class-based integration testing. In our proposal, the com-

plexity of creating a stub is estimated by assigning weights to different types of dependencies in the software

system’s Object Relation Diagram. The experimental evaluation is performed on two synthetic examples and

ﬁve software systems often used in the literature for the class integration test ordering. The results obtained

using our approach are better than the results of the existing related work which provide experimental results

on the case studies considered in this paper.

1 INTRODUCTION

Class-based integration testing is a systematic test-

ing technique applied when the application classes

of a software are integrated in the ﬁnal software sys-

tem. The classes are integrated sequentially and after

adding each class the obtained system is tested. If no

errors have been found during testing at some point in

the integration, then the next application class will be

integrated. An important problem during integration

testing of object-oriented software systems is the one

of deciding the order in which the application classes

should be integrated in the ﬁnal software, called the

class integration test order (CITO) problem (Briand

et al., 2002b).

In most situations, there is a dependency relation

between the application classes, namely a class may

require another class to be available before it can be

tested. In cases when dependency cycles exist among

the application classes from a software system, the

dependency has to be broken and a stub for emulating

the behavior of the required class has to be created

(Assunc¸

ao et al., 2011). If, at a particular step during

class-based integration testing, one adds a class which

depends on another application class that has not been

integrated yet, a simulation of that class is necessary.

This is done by creating a stub for the required class,

more precisely a dummy class that replaces the re-

quired one and simulates its behavior. Stubs are those

parts of a software system that are built for simulating

components of the software which are not developed

or unit tested yet, but are needed to test classes that

depend on them (Briand et al., 2002b). There is a

difference between speciﬁc and generic stubs. A spe-

ciﬁc stub replicates only the class functionalities for a

speciﬁc client class, while the generic (realistic) stubs

reproduce all functionalities that the original class can

provide. Therefore when a class is used by many

client classes we will need only one generic stub, but

as many speciﬁc stubs as the number of client classes.

Since stub creation increases the cost of the integra-

tion testing process, it is essential to reduce stubbing

cost by determining a class order for integration test-

ing that minimizes the overall stubbing effort.

The CITO problem does not cover aspects related

to the actual creation of stubs nor does it approach

the problem of test case effectiveness. The main ob-

jective of the CITO problem is to reduce the number

of stubs needed, not to increase early bug detection.

Software developers are still responsible for creating

stub classes that closely model the effective class to

be stubbed.

There are numerous strategies proposed in the lit-

erature for solving the CITO problem with the aim of

minimizing the stubbing effort required during the in-

tegration process. The stubbing effort estimates the

Czibula, I., Czibula, G. and Marian, Z.

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms.

DOI: 10.5220/0006399500270037

In Proceedings of the 12th International Conference on Software Technologies (ICSOFT 2017), pages 27-37

ISBN: 978-989-758-262-2

cost for creating the stubs needed during the integra-

tion testing. It can be computed either as the num-

ber of needed stubs or considering measures related

to coupling, number of attributes and methods or the

complexity of the methods that need to be replicated.

Most of the solutions existing in the literature for

the CITO problem can be divided in two categories:

graph based approaches and genetic algorithm based

approaches (Bansal et al., 2009). The graph-based ap-

proaches consider the Object Relation Diagram which

represents the classes and the relationship between

them in object-oriented software systems.

In this paper we are approaching the CITO prob-

lem as a combinatorial optimization problem, with the

goal of determining the order in which the applica-

tion classes should be tested for minimizing the total

cost of stubbing. We consider the stubbing cost as

the effort for creating the speciﬁc stubs needed during

the class-based integration testing. The complexity of

creating a stub is estimated by assigning weights to

different types of dependencies (i.e., aggregation, as-

sociation, inheritance) in the software system’s Object

Relation Diagram (ORD).

The main contributions of this paper can be sum-

marized as follows.

• We propose an efﬁcient approach for class inte-

gration test order optimization using a genetic

algorithm with stochastic acceptance based on

a static analysis of object-oriented software sys-

tems. Our proposal improves the existing strate-

gies based on genetic algorithms for ﬁnding a

solution for the CITO problem and provides a

more general theoretical model that can be applied

for generic stubs and speciﬁc stubs with different

weighting strategies.

• We experimentally evaluate our approach on 7

case studies often used in the literature for the

class integration test ordering. The obtained re-

sults outperform existing related work which pro-

vide experimental results on the case studies con-

sidered in this paper.

The paper is organized as follows. We start by

reviewing in Section 2 existing approaches which

provide solutions for the CITO problem considering

weighted stubs and give experimental results on the

case studies that are considered in this paper. Our

approach based on a genetic algorithm with stochas-

tic acceptance for solving the CITO problem is intro-

duced in the Section 3. Section 4 describes the case

studies used for evaluation and also provides the ex-

perimental settings and results. In Section 5 we com-

pare the results obtained by our proposal with some

state-of-the-art techniques. Our conclusions as well

as several future research directions are presented in

Section 6.

2 RELATED WORK

In this section we will present a short overview of

existing approaches for the CITO problem, focusing

mainly on the ones that, like our approach, consider

that not every stub has the same complexity. Most of

these approaches build a graph, called Object Rela-

tion Diagram (ORD), where nodes represent the ap-

plication classes and directed edges represent the re-

lationships between these classes. Edges often have

labels that represent the type of the relationship be-

tween the two classes. The number of relationships

can be different from one approach to another, but the

most frequently used relations are inheritance, aggre-

gation and association.

If the ORD contains no cycles then a simple topo-

logical sorting can give the integration order. For

such systems, a bottom-up integration strategy can

be used, and no stubs are needed. But in most soft-

ware systems there are cyclic dependencies between

the classes in the ORD as shown by Melton and Tem-

pero in (Melton and Tempero, 2007) where a study

was conducted on 78 Java software systems with dif-

ferent sizes (from 17 to 11644 classes). The authors

concluded that almost all systems contained cycles,

moreover, about 85% of them contained strongly con-

nected components of at least 10 classes.

The ﬁrst paper that considered the CITO problem

was written by Kung et al. (Kung et al., 1995). They

consider an ORD with inheritance, aggregation and

association relations. The ﬁrst step of their approach

is to transform it into an acyclic one, by ﬁrst replacing

clusters of mutually reachable nodes with one single

node. A topological sorting of this acyclic graph will

give the major level of nodes. For ﬁnding the minor

level of nodes, the order inside the clusters, associa-

tion relations are removed, since every cycle has to

contain at least one association edge.

Major and minor level numbers are used by Tai

and Daniels as well (Tai and Daniels, 1997), but they

are computed differently. For assigning major level

numbers, only the inheritance and aggregation rela-

tions of the ORD are considered and a Depth First

Search (DFS) is performed. Minor levels are assigned

to nodes that have the same major level. Strongly

Connected Components (SCC) are identiﬁed for the

nodes belonging to the same major level, and to each

association edge e a weight is assigned as the sum

of the number of incoming edges to the source node

of e and the number of outgoing edges from the tar-

ICSOFT 2017 - 12th International Conference on Software Technologies

get node of e. The edge with the highest weight is

removed, because it has a higher chance of breaking

many cycles. This process is repeated until no cycles

are left.

Hanh et al. use Test Dependency Graph (TDG),

which is more detailed than an ORD, because it can

contain method-to-class and method-to-method rela-

tions as well. They present in (Hanh et al., 2001) two

integration strategies, a graph-based one and a genetic

algorithm (GA) based one. For the graph-based ap-

proach, called Triskell, they ﬁnd the node that partic-

ipates in the maximum number of cycles and remove

it (consider that it will be stubbed). This produces

one generic stub, and a speciﬁc stub for each incom-

ing edge into the node. Relation types are considered

only if two nodes participate in the same number of

cycles, in this case the node with more association re-

lations participating in cycles is removed. They repeat

the process until no cycles are left. The GA approach

considers only the number of stubs, no relations are

considered.

In (Briand et al., 2002b) Briand et al. propose a

graph-based approach, which identiﬁes SCC in the

graph, and for each association edge in each SCC

computes a weight which is similar to the weight

computed by Tai and Daniels, but instead of taking the

sum, for an edge they take the product of the number

of incoming edges to the source node and the number

of outgoing edges from the target node. They remove

the edge with the highest weight and continue until

no cycles are left. In (Briand et al., 2002a) Briand

et al. proposed a Genetic Algorithm based approach

as well. They use constraints to make sure that in-

heritance and aggregation relations will not be broken

(they specify partial ordering of nodes based on these

relations) and compute weights for association edges.

The weight of an association relation depends on the

complexity of the class represented by the target node,

and this complexity depends on the number of meth-

ods and/or number of attributes of the class.

While previous approaches considered weights

mainly just for association edges (since inheritance

and aggregation edges are never removed), the ap-

proach presented by Malloy et al. in (Malloy et al.,

2003) considers weights for 6 different relations:

association, composition, dependency, inheritance,

ownedElement, polymorphic. They use the ORD and

ﬁnd SCC in it. For each SCC they compute the weight

of the edges and remove the edge with the minimum

weight. For the experimental evaluation they use 7

case studies of different sizes and two different sets of

weights. The only difference between the two sets of

weights was the weight assigned to inheritance edges.

In the ﬁrst set of weights, inheritance has weight 2,

which is a low value, making it probable that inher-

itance edges will be removed. In the second set, in-

heritance has a weight of 100 which makes removal of

inheritance edges very unlikely. They conclude that in

the situations when no inheritance edges are removed,

approximately twice as much stubs are needed.

Another graph-based approach is the one pre-

sented by Abdurazik and Offutt (Abdurazik and Of-

futt, 2009). The novelty in their approach is that they

consider weights for both edges and nodes in the ORD

(though the weights for the nodes are computed con-

sidering the weights for the edges). They consider 9

different relations between classes and compute the

weight of an edge based on several measures of cou-

pling. Their algorithm computes for each edge a Cy-

cle to Weight Ratio, which considers both the number

of cycles that include that edge and the weight of the

edge. The edge with the maximum CWR is removed,

and the process is repeated until no cycles are left.

Bansal et al. present an approach which is based

on the approach presented by Malloy, but they in-

troduce two new relation types speciﬁc for C++ ap-

plications: friend coupling and exception coupling

and deﬁne weights to them: 25 and 5 (Bansal et al.,

2009). They also present an overview of existing

graph-based and genetic algorithm-based approaches.

3 METHODOLOGY

In this section we introduce our proposal for optimiz-

ing class integration test order using a genetic algo-

rithm (GA) with stochastic acceptance. GAs are used

due to their ﬂexibility and applicability in successful

solving of a large variety of optimization problems.

Our approach is based on a static analysis of

object-oriented software systems and on computing

the stubbing effort as the cost of creating the speciﬁc

stubs needed during the integration testing. Depend-

ing on the type of dependency between classes, cre-

ating a stub requires different cost (effort). We are

considering weighted stubs, thus the complexity of

creating a stub is computed by assigning weights to

different types of dependencies between the applica-

tion classes.

We start by describing in Section 3.1 how the class

relationships are considered in the literature for stub-

bing, followed by the dependencies and weighting

scheme considered in our approach. We present in

Section 3.2 the main characteristics of genetic algo-

rithms. Section 3.3 introduces the genetic algorithm

model proposed for the CITO problem.

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms

3.1 Stubbing Relationships

Kung et al. (Kung et al., 1995) show that if there are

no dependency cycles among classes in the ORD of a

software system, the integration order can be simply

obtained by performing a reverse topological ordering

of classes based on their dependencies (Briand et al.,

2002b). But if cyclic dependencies among classes can

be found, most existing strategies propose to broke

some dependencies for obtaining an acyclic graph and

then to apply a topological sorting on it. Breaking a

dependency requires that the target class needs to be

stubbed when integrating and testing the source class

(Briand et al., 2002b).

Three types of dependencies between application

classes in the ORD are considered by Kung et al.

(Kung et al., 1995): Association/Usage (As), Aggre-

gation (Ag) and Inheritance (I). In order to obtain an

acyclic graph, the authors propose the removal of as-

sociation relationships. They consider that an associ-

ation relationship exists in each directed cycle of an

ORD and this type of relation is the weakest one be-

tween related classes.

A literature review (Kung et al., 1995), (Tai and

Daniels, 1997), (Abdurazik and Offutt, 2006) re-

veals that by removing association relationships sim-

pler stubs are created compared to those obtained

by selecting aggregation or inheritance relationships.

Traon et al. (Traon et al., 2000) proposes a strategy al-

lowing to break aggregation or inheritance relations,

which may conduct to complex stubs. The results ob-

tained by Malloy et al. (Malloy et al., 2003) revealed

that the removal of inheritance relationships is more

effective for cycles breaking.

In our proposal we are considering a Weighted

ORD, in which each relationship (As, Ag and I) has

an associated weight. We consider the inheritance (I)

relationship as the strongest relationship between the

application classes, followed by the aggregation (Ag)

and then by the association (As) relationship which is

viewed as the weakest relation between the classes. A

stub class is a controllable replacement for an existing

dependency in the system, the main factor that inﬂu-

ences the effort needed for creating a stub is the type

of the dependency.

Based on the existing results in the literature we

assign the largest weight to the inheritance relation,

the smallest weight to the association relation and an

intermediate weight to the aggregation relation. This

weighting scheme reﬂects the relative effort needed to

implement a stub class for a particular client class that

has a dependency on the stubbed class.

3.2 Genetic Algorithms

Genetic Algorithms (GAs) represent a machine learn-

ing model which is inspired from the processes of

evolution in nature. They are speciﬁc type of meta-

heuristic optimization techniques from the computa-

tional intelligence domain used for solving search and

optimization problems. Even if there is no guarantee

that the GAs will converge to the global minimum,

since they are based on heuristics, they are able to pre-

vent the search from falling into local minima (Whit-

ley, 2001).

GAs are population based approaches and artiﬁ-

cial models for the biological processes of natural se-

lection and evolution. The main idea behind GAs is

that a population of individuals adapts to environmen-

tal changes over multiple generations, and the ﬁttest

individuals of the population are those who survive

longer (Melanie, 1999).

GAs start with a population of noInd candidate

solutions, also called individuals or chromosomes,

usually randomly generated. Each individual from

the population is characterized by a numerical value

called its ﬁtness, which indicates how “good” is that

individual for solving the considered problem. Over a

number of iterations (generations) or until acceptable

solutions are found, the population is evolved using

genetic operators as follows. A pair of chromosomes

is selected (using a selection strategy), then we cross-

over (with probability p

) the selected pair and form

two offspring and lastly we mutate the two offsprings

(with probability p

) and add the obtained individuals

in the new population. At the end of the iterative pro-

cess, the individual with the maximum ﬁtness from

the current population is reported as a solution.

Figure 1 describes the skeleton of a simple GA.

3.3 The Proposed GA Model

Let us consider that the analyzed software system S

is composed by a set of classes C

,...,C

. Start-

ing from the ORD graph built for the software sys-

tem and based on a static analysis of it, we aim to

identify an appropriate order in which the applica-

tion classes should be integrated (and tested) in the

ﬁnal software. The solution is viewed as a permu-

tation of the classes representing the integration or-

der that needs the minimum stubbing effort. Conse-

quently, the optimal solution for the CITO problem

is viewed as a permutation τ of {1, 2, . . . , n} which

minimizes the total cost for creating the stubs needed

when the classes are integrated and tested in the order

τ: C

= (C

,...,C

) (n > 1). The stubbing effort

required for the integration testing of a sequence of

ICSOFT 2017 - 12th International Conference on Software Technologies

Algorithm GA is:

Input: noInd - the number of individuals from the population

- the probability for mutation

- the probability for crossover

Output: best - the best individual (solution)

Begin

//a population of noInd individuals is initialized (usually randomly)

P ← initializePopulation();

//repeat until a termination criterion is met (number of generations, fitness, etc)

While not TERMINATION do

//the fitness of the individuals from the current population is computed

computeFitness(P);

//the new population is initialized

←

//repeat until noInd individuals are created

While |P

| < noInd do

//the survivors from the current population are preserved

← survive(P);

@ Select from P a pair (c

, c

) of chromosomes for crossover

@ With probability p

cross-over the pair (c

, c

) and form two offsprings

@ With probability p

mutate the offsprings and add the new individuals in P

EndW hile;

//the current population is replaced with the new population

P ← P

;

EndWhile

//the individual with the maximum fitness from the current population is reported

best ← maxFitness(P);

End GA

Figure 1: The skeleton of a GA.

classes C

= (C

,...,C

) is denoted by C ost

and is deﬁned as in Formula (1):

C ost(C

) =

∑

i=1

stub(C

i−1

,...,C

) (1)

where stub(C

i−1

,...,C

) represents the cost

for creating the weighted stubs for integrating the

class C

to the system formed by the classes

i−1

i−2

,...,C

}. This cost is computed by sum-

ming the weights associated with the relationships be-

tween class C

and all its neighboring classes from

the Weighted ORD which were not already integrated.

An individual from the GA population is an

integer-valued vector whose length is equal to the

number of application classes from the analyzed

software system and represents a possible order

for integrating the classes during the integration

testing. Thus, a candidate solution to the CITO

problem is encoded in an individual (chromosome)

ind = (ind

,ind

...ind

) representing a permutation

of {1,2,...,n} (1 ≤ ind

≤ n ∀i ∈ {1, 2 . . .n} and

ind

6= ind

∀1 ≤ i, j ≤ n,i 6= j).

We deﬁne the value of the ﬁtness function for a

given individual ind as in Formula (2).

f itness(ind) = Max − C ost(C

ind

) (2)

where Max represents a large positive constant. Con-

sidering the deﬁnition of the ﬁtness given in Formula

(2), maximizing the ﬁtness of a chromosome ind will

be equivalent with minimizing the stubbing cost re-

quired when the classes are integrated and tested in

the order C

ind

. Accordingly, the components of the

ﬁttest individual reported by the GA will give us the

class integration test order.

The improvements we propose to the classical

GA model are described in the following. In order

to assure a proper exploration of the search space

the initial population is generated using the follow-

ing heuristic. Given the fact that every chromosome

represents a permutation, the dimension of the search

space is n! where n is the number of classes in the

system. In order to evenly divide the search space

we will generate the k-combinations for the set of

classes, where k is chosen based on the size of the

initial population. For example if we have the set

of classes {A, B,C, D, E,F, G, H} we can generate 2-

combinations: {A, B}, {A,C},. . . in total 28 different

sets with 2 elements. We use the k-sets when gener-

ating the initial population by creating chromosomes

that start with genes according to the generated k-

combinations followed by randomly generated genes.

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms

The GA model we propose for solving the CITO

problem also considers a selection operator based

on the stochastic acceptance technique (Lipowski

and Lipowska, 2012). In this algorithm, the widely

used roulette-wheel selection operator used in the

population for reproduction is replaced with the

following one: an individual ind is randomly se-

lected and this selection is accepted with probability

f itness(ind)/ f itness(M), where M is the ﬁttest indi-

vidual (has the highest ﬁtness value). Through the

stochastic acceptance based selection operator, the

ﬁttest individual will always be accepted if selected.

Several studies in the literature indicate that the selec-

tion based on stochastic acceptance performs consid-

erably better than versions based on linear or binary

search (Lipowski and Lipowska, 2012).

In our proposed GA we used a variant of the Order

Crossover 1 operator, known as C1, which is speciﬁc

for using GAs for permutation problems (Whitley and

wook Yoo, 1995). Basically, a sequence of consecu-

tive genes is removed from the ﬁrst parent and is di-

rectly copied to the child. The remaining genes are

placed in the offspring in the order in which they ap-

pear in the second parent. From the time performance

viewpoint, C1 is the fastest crossover operator that

generates valid chromosomes (preserves the ordering

constrains).

The mutation operator is a variant of the swap mu-

tation, but we swap a randomly generated gene with

its adjacent gene.

We have also used elitism in our GA, which means

that the next generation will always contain a small

proportion (P

elitism

) of the ﬁttest individuals from the

current population.

4 COMPUTATIONAL

EXPERIMENTS

We provide in this section an experimental evalua-

tion of our GA approach presented in Section 3.3 for

solving the CITO problem on seven case studies often

used in the literature: two synthetic examples and ﬁve

real-life case studies.

For the GA model proposed in Section 3.3 we

used our own implementation, without any third party

libraries. The following parameter setting will be

used for all experiments: the constant Max used in

the ﬁtness computation was set to 10000; the num-

ber of individuals from the GA population noInd is

2 · C

; the mutation and crossover probabilities are

= 0.3 and p

= 0.3; the proportion P

elitism

used for

the elitism parameter was considered 0.1 (10% of the

population survives from one generation to another).

As a termination condition for our GA we used a pre-

deﬁned number of trials depending on the number of

application classes, 50 · n. Regarding the parameters,

we tried different values, but no signiﬁcant difference

was observed in the obtained results.

The experiments are conducted in two directions,

considering different weighting schemes for the stubs

in computing the stubbing effort.

1. Differential Weighting. We used the following

weights for the relationships between the applica-

tion classes: 30 for an Inheritance relation, 5 for

an Association relation and 20 for an Aggregation

relation. These values for the weights were se-

lected after analyzing the similar literature which

assigns weights for the stubs (Malloy et al., 2003),

as well as our software development experience.

The proposed weighting scheme reﬂects the effort

needed to implement a stub class for a particular

client class that has a dependency on the stubbed

class (see Section 3.1).

2. Equal Weighting. In this scheme, equal weights

(e.g. 1) are assigned for all stubs, independent of

the type of relationship between a client class and

the application class to be stubbed. Such a weight-

ing method allows us to determine non-weighted

speciﬁc stubs.

4.1 Case Studies

For our experiments, we have selected two synthetic

case studies and ﬁve software systems often used in

the CITO literature.

A description of the case studies is given in Ta-

ble 1, where the second column depicts the number

of classes and the third column presents the number

of dependencies between the application classes. For

each case study, the existing number of cycles be-

tween the application classes is given in the fourth

column. The number of cycles indicates the complex-

ity of the stubbing process, since a larger number of

cycles leads to a larger number of stubs needed in the

integration process.

In order to mitigate some threats to external va-

lidity issues, in our experiments we chose software

systems of various size, complexity and domain (as

shown in Table 1). Even if an industrial software

system would probably have more classes, for those

systems integration testing would be performed on

component-level, instead of class-level. Integration

of classes from one component should be done on the

class-level (Briand et al., 2002b).

The ﬁrst synthetic example consists of 8 classes,

and is presented in Figure 2. This case study was

ICSOFT 2017 - 12th International Conference on Software Technologies

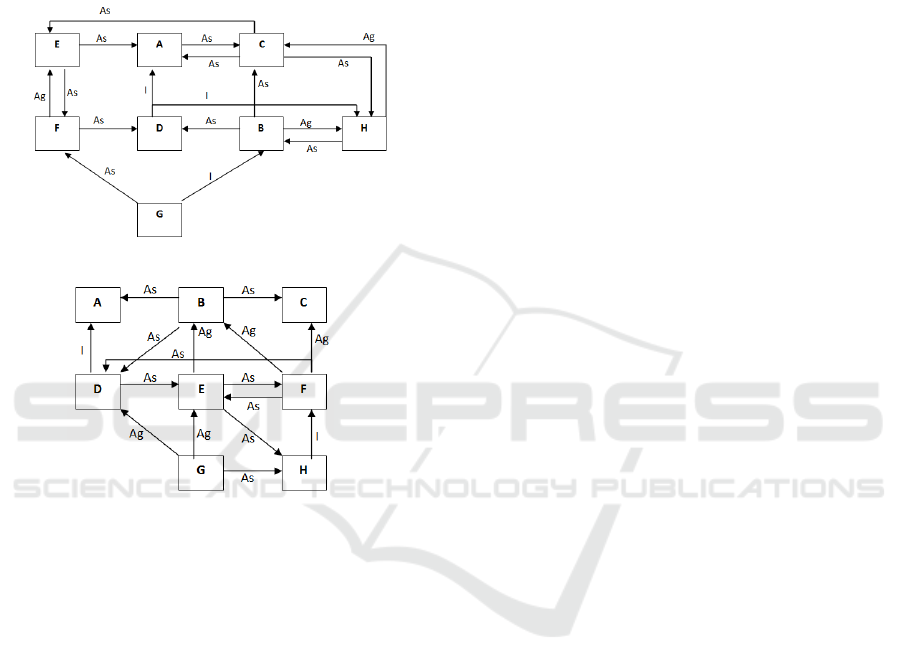
considered for evaluation in several papers approach-

ing the CITO problem (Hewett and Kijsanayothin,

2009), (Briand et al., 2002b), (Abdurazik and Of-

futt, 2009), (Borner and Paech, 2009), (Bansal et al.,

2009). Our second synthetic example consists of 8-

classes as well, and its Object Relation Diagram is

depicted in Figure 3. This example was previously

used in the CITO literature for weighted stubs (Hanh

et al., 2001).

Figure 2: ORD for the ﬁrst simple 8-class example.

Figure 3: ORD for the second simple 8-class example.

The other ﬁve case studies used in our experiments

are taken from the Briand benchmark (Briand et al.,

2002a) and used in different papers from the CITO

literature (Briand et al., 2002b), (Cabral et al., 2012).

The systems from this benchmark are the following:

ATM (automated teller machine simulation), Ant (a

Java-based build tool for maintaining, updating and

regenerating related programs and ﬁles according to

their dependencies), SPM (Security Patrol Monitor-

ing, a project developed by a graduate student at Car-

leton University), BCEL (Byte Code Engineering Li-

brary, a tool for analyzing, creating and manipulating

binary Java ﬁles) and DNS (a Java implementation of

the Domain Naming System). For all these systems,

we have used the Object Relation Diagram from the

Appendix provided by Briand et al. (Briand et al.,

2002a).

We have applied our GA-based approach for the

case studies presented in Table 1. Due to some ran-

domness in the execution, the GA was ran 20 times.

We found that, in every case, the solution reported is

the same, except for the Ant case study with equal

weighting. For this case study we have run our GA

100 times out of which in 85 cases it reported 9 stubs,

while in the other 15 cases it reported 10 stubs. In

Table 2 we give the most frequent number of stubs,

which is 9. Thus, under the considered parameter

setting, our GA with stochastic acceptance has a de-

terministic behavior for differential weighting for all

case studies. The number of speciﬁc weighted stubs

obtained by the proposed GA is shown in Table 2.

5 DISCUSSION AND

COMPARISON TO RELATED

WORK

Considering the results from Table 2 we can observe

that for the Ant and BCEL case studies there is a dif-

ference between the number of stubs needed in case

of differential and equal weighting. For both systems

we need less stubs if we do not take into consideration

the relation between the classes (i.e., we use equal

weighting). If we differentiate between the types of

relationships we need slightly more stubs but, for our

case studies, only association relations will be broken

(this can be seen by the ﬁtness of the best individual,

which is not reported in Table 2). This shows that dif-

ferential weighting can improve the total complexity

of the stubs needed to be created. Unfortunately, for

the other case studies this difference is not visible, but

this might be related to their size or to the distribution

of relations between classes (generally more than half

of the relations are associations). In the future we in-

tend to test our approach on larger systems as well to

further analyze the difference between the number of

stubs for the two weighting schemes.

For Table 2 we can observe that for each case

study, for the differential weighting scheme, the GA

provided the same number of stubs for all the 20 runs

of the algorithm. For the equal weighting scheme for

the Ant case study we had two different solutions (but

the solution with the less number of stubs is the most

frequently reported one). This suggests that using dif-

ferent weights might contribute to making the GA de-

terministic. In order to test this assumption we will

extend the experimental evaluation.

Regarding the selection of the weights for differ-

ent relations between classes, in the literature there

are different perspectives: it is commonly accepted

that association relations are the easiest to stub, but

there is no clear agreement regarding the difﬁculty for

stubbing aggregations and inheritance. There are ap-

proaches which consider that only associations can be

broken (for ex. (Briand et al., 2002a)). Malloy et al.

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms

Table 1: Description of the case studies.

Case study # of classes # of dependencies # of cycles

8-class ﬁrst example 8 17 11

(Hewett and Kijsanayothin, 2009)

8-class second example 8 15 7

(Hanh et al., 2001)

ATM (Briand et al., 2002b) 21 67 30

Ant (Briand et al., 2002b) 25 83 654

SPM (Briand et al., 2002b) 19 72 1178

BCEL (Briand et al., 2002b) 45 294 416091

DNS (Briand et al., 2002b) 61 276 16

in (Malloy et al., 2003) show through an example why

inheritance relations are complicated to be stubbed.

However, there might be situations, when stubbing a

base class is easier than breaking other relations (e.g.

if the base class is not abstract). Moreover, it is possi-

ble that by breaking inheritance relationships a lower

number of total stubs is required (Malloy et al., 2003).

This is why, a different approach for the CITO prob-

lem assigns weights for the classes from the ORD

instead of the relationships. Weights assigned for

classes can be determined based on the complexity

of the class: number of attributes, number of meth-

ods, etc. In the future we intend to investigate this

direction as well.

In the following we provide a comparison of the

results obtained by the proposed GA approach to the

results reported in the literature for the case studies

considered for evaluation. The comparison is de-

picted in Table 3. For the simple case studies we

have also computed the optimal number of stubs us-

ing a brute force approach. For the larger software

systems, the brute force method is not feasible, due

to its exponential time complexity. The best result

obtained using a non-brute force approach (i.e., the

one which reports the minimum number of weighted

stubs) is highlighted. For each result we indicate the

paper where the result was taken from.

For the brute force approach we implemented a

parallel algorithm based on Heap’s algorithm for gen-

erating permutations and we run the experiment on a

server machine with 16 cores. The running times for

the larger systems are over 48h while the proposed

GA approach ﬁnds the optimal ordering in less than

3 minutes/run for every system (the genetic algorithm

is not parallel, it uses only a single core). For the two

smaller systems the required time is less than 30 sec-

onds.

For the 8-class examples, we found in the lit-

erature results reported considering the differential

weighting scheme and the same weights as consid-

ered in our experiments (Bansal et al., 2009). Unlike

Table 2: Number of stubs obtained by our GA approach for

the case studies and the considered weighting schemes.

Case study Weighting # of stubs

scheme

8-class ﬁrst

Differential 4

example Equal 4

8-class second

Differential 2

example Equal 2

ATM

Differential 7

Equal 7

Ant

Differential 10

Equal 9

SPM

Differential 16

Equal 16

BCEL

Differential 60

Equal 58

DNS

Differential 6

Equal 6

for the simple 8-class case studies, for the case stud-

ies from the Briand benchmark there are no results

reported in the literature considering weighted stubs

as in our approach (i.e. assigning different weights for

speciﬁc types of relationships between the application

classes). For these systems, only the results obtained

for generic and speciﬁc stubs are available. That is

why, for the case studies from the Briand benchmark

we applied our GA with stochastic acceptance under

the equal weighting scheme which is equivalent to ob-

taining the speciﬁc stubs.

The ﬁrst line from Table 3 shows the results for

the ﬁrst 8-class example from Figure 2. Bansal et

al. (Bansal et al., 2009) report the results obtained

by several approaches from the literature on this case

study. The approach from Le Traon et al. provides

multiple solutions with different number of stubs and

we included all of them in the table. The second line

of Table 3 contains the comparison of the results for

the second 8-class example from Figure 3. This case

study was previously used by Hanh et al. (Hanh et al.,

ICSOFT 2017 - 12th International Conference on Software Technologies

Table 3: Comparison to related work considering weighted and speciﬁc stubs.

# Case study Weighting Approach # of

scheme stubs

8-class ﬁrst example Differential

Our GA solution 4

1 Brute force 4

weighting Tai et al. (Bansal et al., 2009) 5

Le Traon et al. (Bansal et al., 2009) 5

Le Traon et al. (Bansal et al., 2009) 6

Le Traon et al. (Bansal et al., 2009) 4

Briand et al. (Bansal et al., 2009) 4

Malloy et al. (Bansal et al., 2009) 6

Abdurazik et al. (Bansal et al., 2009) 4

8-class second example Differential

Our GA solution 2

2 Brute force 2

weighting Kung et al. (Hanh et al., 2001) 4

Tai and Daniels (Hanh et al., 2001) 2

Hanh et al. - Triskell strategy(Hanh et al., 2001) 2

Hanh et al. - Genetic algorithm (Hanh et al., 2001) 3

Ant

Equal

Our GA solution 9 or 10

Briand et al. (Briand et al., 2002b) 11

weighting Tai and Daniels (Briand et al., 2002b) 28

Le Traon et al. (Briand et al., 2002b) 19

ATM

Equal

Our GA solution 7

Briand et al. (Briand et al., 2002b) 7

weighting Tai and Daniels (Briand et al., 2002b) 8

Le Traon et al. (Briand et al., 2002b) 7

SPM

Equal

Our GA solution 16

Briand et al. (Briand et al., 2002b) 17

weighting Tai and Daniels (Briand et al., 2002b) 20

Le Traon et al. (Briand et al., 2002b) 27

BCEL

Equal

Our GA solution 58

Briand et al. (Briand et al., 2002b) 70

weighting Tai and Daniels (Briand et al., 2002b) 128

Le Traon et al. (Briand et al., 2002b) 67

DNS

Equal

Our GA solution 6

Briand et al. (Briand et al., 2002b) 6

weighting Tai and Daniels (Briand et al., 2002b) 27

Le Traon et al. (Briand et al., 2002b) 10

2001), where the result of several approaches are re-

ported for it. The next lines from Table 3 depicts the

comparison of the results obtained using our GA with

those provided by Briand et al. (Briand et al., 2002b)

on Ant, ATM, SPM, BCEL and DNS systems.

Table 3 show that the results provided by our GA

approach are better than or at least equal to the ap-

proaches existing in the literature considering the case

studies we used in our experiments. In 8 cases, the

number of weighted stubs obtained is the same as the

one from the related work, while in 18 situations a

smaller number of weighted stubs was obtained by

our approach. The comparison to the related work

is graphically illustrated in Figure 4. For each case

study we represent the average number of weighted

stubs reported in the literature and through the dashed

bars the number of weighted stubs reported by our GA

solution.

6 CONCLUSIONS AND FUTURE

WORK

We have approached in this paper the problem of class

integration test ordering and we proposed a genetic

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms

Figure 4: GA performance compared to the average perfor-

mance of the related work on the considered data sets.

algorithm with stochastic acceptance for deﬁning an

integration test order strategy for object-oriented sys-

tems. The goal is to identify, based on a static analysis

of object-oriented software systems, the test order re-

quiring a minimum stubbing effort. We considered a

weighted cost for creating the speciﬁc stubs needed

for testing. Seven case studies were considered in

our experimental evaluation, both synthetic examples

and systems used in the literature for the CITO prob-

lem. The results obtained using our approach outper-

formed those of existing similar work.

We plan to extend the experimental evaluation of

the proposed GA technique for real software sys-

tems and to consider a parallel implementation of

the GA, in order to test its scalability to larger sys-

tems. We will also investigate new dependencies be-

tween application classes for computing the stubbing

effort. Another possible direction to improve our pro-

posal would be to identify (possibly through machine

learning) appropriate values for the weights associ-

ated with the dependencies between the classes from

the software systems.

ACKNOWLEDGEMENTS

This work was supported by a grant of the Romanian

National Authority for Scientiﬁc Research and Inno-

vation, CNCS-UEFISCDI, project number PN-II-RU-

TE-2014-4-0082.

REFERENCES

Abdurazik, A. and Offutt, J. (2006). Coupling-based class

integration and test order. In Proc. of the 2006 In-

ternational Workshop on Automation of Software Test,

pages 50–56.

Abdurazik, A. and Offutt, J. (2009). Using coupling-based

weights for the class integration and test order prob-

lem. The Computer Journal, (5):557–570.

Assunc¸

ao, W. K. G., Colanzi, T. E., Pozo, A. T. R., and

Vergilio, S. R. (2011). Establishing integration test

orders of classes with several coupling measures. In

Proceedings of the 13th Annual Conference on Ge-

netic and Evolutionary Computation, GECCO ’11,

pages 1867–1874, New York, NY, USA. ACM.

Bansal, P., Sabharwal, S., and Sidhu, P. (2009). An inves-

tigation of strategies for ﬁnding test order during in-

tegration testing of object oriented applications. In

Proceedings of International Conference on Methods

and Models in Computer Science, pages 1–8.

Borner, L. and Paech, B. (2009). Integration test order

strategies to consider test focus and simulation effort.

In Proceedings of the First International Conference

on Advances in System Testing and Validation Lifecy-

cle, pages 80–85.

Briand, L. C., Feng, J., and Labiche, Y. (2002a). Exper-

imenting with genetic algorithms and coupling mea-

sures to devise optimal integration test orders. Tech-

nical Report TR SCE-02-03, Carleton University.

Briand, L. C., Labiche, Y., and Wang, Y. (2002b). Revisit-

ing strategies for ordering class integration testing in

the presence of dependency cycles. Technical Report

TR SCE-01-02, Carleton University.

Cabral, R. V., Pozo, A., and Vergilio, S. R. (2012). A pareto

ant colony algorithm applied to class integration and

test order problem. Lecture Notes in Computer Sci-

ence, pages 16–29. Springer.

Hanh, V. L., Akif, K., Traon, Y. L., and Jezequel, J.-M.

(2001). Selecting an efﬁcient oo integration testing

strategy: An experimental comparison of actual strate-

gies. In Proceedings of the 15th European Conference

on Object-Oriented Programming, ECOOP ’01, pages

381–401. Springer-Verlag.

Hewett, R. and Kijsanayothin, P. (2009). Automated test

order generation for software component integration

testing. In Proceedings of the 2009 IEEE/ACM In-

ternational Conference on Automated Software Engi-

neering, ASE ’09, pages 211–220, Washington, DC,

USA. IEEE Computer Society.

Kung, D., Gao, J., Hsia, P., Toyoshima, Y., and Chen, C.

(1995). A test strategy for object-oriented programs.

In Computer Software and Applications Conference,

1995. COMPSAC 95. Proceedings., Nineteenth An-

nual International, pages 239–244.

Lipowski, A. and Lipowska, D. (2012). Roulette-wheel se-

lection via stochastic acceptance. Physica A: Statis-

tical Mechanics and its Applications, 391(6):2193 –

2196.

Malloy, B. A., Clarke, P. J., and Lloyd, E. L. (2003). A

parameterized cost model to order classes for class-

based testing of c++ applications. In 14th Interna-

tional Symposium on Software Reliability Engineer-

ing, 2003. ISSRE 2003, pages 353–364.

Melanie, M. (1999). An Introduction to Genetic Algorithms.

The MIT Press.

Melton, H. and Tempero, E. (2007). An empirical study

of cycles among classes in java. Empirical Software

Engineering, 12(4):389–415.

ICSOFT 2017 - 12th International Conference on Software Technologies

Tai, K.-C. and Daniels, F. J. (1997). Test order for inter-

class integration testing of object-oriented software.

In Proceedings of the 21st International Computer

Software and Applications Conference, COMPSAC

’97, pages 602–607, Washington, DC, USA. IEEE

Computer Society.

Traon, Y. L., J

eron, T., J

equel, J.-M., and Morel, P.

(2000). Efﬁcient oo integration and regression testing.

IEEE Transactions on Reliability, 49(1):12–25.

Whitley, D. (2001). An overview of evolutionary algo-

rithms: practical issues and common pitfalls. Infor-

mation and Software Technology, 43(14):817 – 831.

Whitley, D. and wook Yoo, N. (1995). Modeling simple

genetic algorithms for permutation problems. In in

Foundations of Genetic Algorithms, pages 163–184.

Morgan Kaufmann.

An Improved Approach for Class Test Ordering Optimization using Genetic Algorithms