Maximising Patient Throughput using Discrete-event Simulation

Fraser L. Greenroyd

1,2

, Rebecca Hayward

, Andrew Price

, Peter Demian

and Shrikant Sharma

Centre for Innovative and Collaborative Construction Engineering, School of Civil and Building Engineering,

Loughborough University, Loughborouogh, U.K.

BuroHappold Engineering, Bath, U.K.

Keywords: Hospital Operations, Patient Scheduling, Discrete-event Simulation, Healthcare Delivery, Outpatient

Operations.

Abstract: As the National Health Service (NHS) of England continues to face tighter cost saving and utilisation

government set targets, finding the optimum between costs, patient waiting times, utilisation of resources,

and user satisfaction is increasingly challenging. Patient scheduling is a subject which has been extensively

covered in the literature, with many previous studies offering solutions to optimise the patient schedule for a

given metric. However, few analyse a large range of metrics pertinent to the NHS. The tool presented in this

paper provides a discrete-event simulation tool for analysing a range of patient schedules across nine

metrics, including: patient waiting, clinic room utilisation, waiting room utilisation, staff hub utilisation,

clinician utilisation, patient facing time, clinic over-run, post-clinic waiting, and post-clinic patients still

being examined. This allows clinic managers to analyse a number of scheduling solutions to find the

optimum schedule for their department by comparing the metrics and selecting their preferred schedule.

Also provided is an analysis of the impact of variations in appointment durations and their impact on how a

simulation tool provides results. This analysis highlights the need for multiple simulation runs to reduce the

impact of non-representative results from the final schedule analysis.

1 INTRODUCTION

The National Health Service (NHS) of England,

despite being viewed as one of the best health

systems in the Western world (Davis et al., 2014), is

facing some of the toughest challenges since its

inception in 1948 (NHS England, 2013). Since 2009

these challenges have been focussed heavily on cost

efficiencies and reducing overall operating costs

(Nicholson, 2009; Carter, 2016). The Department of

Health in England has taken steps towards making

cost savings in NHS facilities by removing

unwarranted variations, with a view that this will

save the NHS £5bn per annum by 2020 (Carter,

2016). The report by Lord Carter of Coles (2016)

estimates that £3bn of efficiency savings can come

from a combined optimised use of clinical staff

along with better estates and facilities’ management.

A review of the healthcare estates of the NHS in

England revealed that as much as 16% of occupied

floor area (m

) is either unsuitable for use, under-

utilised or not used at all (Health and Social Care

Information Centre, 2015). Of the floor area

available, 4.4% is reported as being under-utilised or

unused completely. It was recommended to the NHS

that the amount of unoccupied or underused space

should not exceed 2.5% (Carter, 2016) by April

2017.

However, the optimisation of space usage is not

the only concern the NHS has to consider. The

utilisation of clinical staff is highlighted as the

biggest area (£2bn per annum) of potential cost

savings through an optimised use of the clinical

workforce (Carter, 2016). This is further combined

with continued work towards improving patient

satisfaction (Nicholson, 2009; NHS England, 2014)

through a reduction in waiting times and crowding

(Bernstein et al., 2009). Similarly, changing

demographics gives rise to a changing NHS as the

needs of the population put a varying amount of

pressure upon the health service (Department of

Health, 2013).

There is a fine balance between the metrics by

which health providers are measured. Finding the

optimum between waiting times, clinician

utilisation, space utilisation and patient satisfaction

is increasingly challenging. There has been much

204

Greenroyd, F., Hayward, R., Price, A., Demian, P. and Sharma, S.

Maximising Patient Throughput using Discrete-event Simulation.

DOI: 10.5220/0006400002040214

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 204-214

ISBN: 978-989-758-265-3

work in both academia and industry to analyse

existing situations and provide solutions to improve

the efficiency and effectiveness of care in healthcare

facilities (Gunal and Pidd, 2006; Marcario, 2006;

Maviglia et al., 2007; Hendrich et al., 2008;

Bernstein et al., 2009; Dexter and Epstein, 2009;

Reynolds et al., 2011; Greenroyd et al., 2016).

It can be argued that at the core of these concerns

is the scheduling of patient appointments, with much

research available on systems to aid appointment

scheduling (Fetter and Thompson, 1965; Kuljis, Paul

and Chen, 2001; Harper and Gamlin, 2003; Gunal

and Pidd, 2010). It can be difficult to successfully

balance utilisation and satisfaction if the patient

scheduling is not optimised for the current clinic

setup. There are many factors which can impact the

effectiveness of the patient schedule including no-

shows, arrival patterns (i.e. a patient arriving either

early, on-time, or late for an appointment) and

appointment duration variations. A study into

operating theatre tardiness found that for every

minute a surgery started late, the department’s

staffing was increased by 1.1 minutes for an 8-hour

surgery day (Dexter and Epstein, 2009), thus

negatively affecting the department’s performance

and efficiency.

The primary challenge with scheduling is the

uncertainty in appointment durations, with high

variations in appointment durations viewed as a key

cause for clinical delays (Huang and Kammerdiner,

2013), increasing waiting times and clinic over-run.

There have been attempts in the literature to tackle

these concerns by accommodating variations into

scheduling, with the implementation of decision

trees (Huang and Kammerdiner, 2013), or by using

discrete-event simulation to compare scheduling

techniques (Lee et al., 2013).

2 RELATED WORK

The use of discrete-event simulation to model

hospital departments is well documented in the

literature (Jun, Jacobson and Swisher, 1999;

Anderson and Merode, 2007; Gunal and Pidd,

2010). Studies include making strategic decisions for

various departments (Ballard and Kuhl, 2006;

Denton et al., 2006; Vanberkel and Blake, 2007;

Leskovar et al., 2011); estimating capacity levels

and measuring waiting times (Werker et al., 2009);

analysing patient flows (Brenner et al., 2010; Zeng

et al., 2012); measuring policy impact (Fletcher et

al., 2007); and simulating patient scheduling and

utilisations (Harper and Gamlin, 2003; Werker et al.,

2009; Lee et al., 2013; Quevedo and Chapilliquén,

2014). It has been argued that the extensive use of

process modelling is limited in healthcare compared

with other industries (Harper and Pitt, 2004) due to

the complexity of the processes and the vast

amounts of data required to provide accurate models

(Antonacci et al., 2016).

Those that have used discrete-event simulation to

analyse patient scheduling do so in an attempt to

resolve issues such as reducing waiting times

(Harper and Gamlin, 2003), reduce planning time for

schedules (Werker et al., 2009) or compare

scheduling models (Lee et al., 2013). With the

exception of Lee et al. (2013) there are few studies

which measure the performance of scheduling

models against a range of metrics. Typically, studies

have focused on one key metric, while Lee et al.

(2013) evaluated four metrics including clinic

overtime, waiting times, unmet demand, and use of

appointment slots, but did not measure such metrics

as clinic room utilisation or clinician utilisation.

These tools are typically built to analyse and

solve specific scenarios at specific facilities.

However, there are some generic models produced

using techniques such as Business Process

Modelling and Notation (BPMN) to build accessible

simulation models for optimising healthcare

processes (Rolón et al., 2008; Antonacci et al.,

2016). BPMN requires users to understand the

notation used, which may make the approach

prohibitive to healthcare estates managers or

department managers.

This paper introduces a new tool with modifiable

inputs offering a reusable simulation model for

optimising patient scheduling. This tool gives the

ability to balance performance for a range of metrics

applicable to the NHS, including waiting times,

clinic utilisation, waiting room utilisation, clinician

utilisation, and clinic over-run.

Figure 1: Flowchart of using the tool.

Maximising Patient Throughput using Discrete-event Simulation

205

3 METHODOLOGY

The tool presented in this paper was built in

response to increased demand for outpatient services

at a NHS hospital in the UK. The NHS Trust

designed a new cancer treatment centre with specific

space allocated for outpatient services. However,

since the design and construction of this facility

began, demand for the outpatient services at the

existing facility has risen to a level higher than

anticipated. The Trust wished to produce optimal

patient schedules based on a variety of clinic

scenarios, such as number of rooms or clinicians

available while operating within a set of

performance targets for key metrics, including:

patient waiting times, clinician utilisation, clinic

utilisation, waiting room utilisation, and clinic over-

run. The purpose of the tool presented here was,

therefore, to identify appropriate levels of activity

(e.g. number of daily attendances) that the outpatient

department could accommodate to maximise the

utilisation of the clinic rooms and clinicians whilst

maintaining a positive patient and clinician

experience.

The Trust were operating two clinic models in

the outpatient department; a dedicated clinic model

where clinicians stay in one room for the clinical

day; and a hub and spoke model where clinicians use

a central hub to complete admin work (e.g. patient

notes). These have a smaller number of clinic rooms

to consult with patients (i.e. clinicians use any free

clinic room). These clinic models can operate in

parallel during a day with variable numbers of

clinicians and rooms across two floors of the

outpatient department. This paper details the

development, inputs, simulation and outputs of the

tool developed to aid clinic planning for the Trust.

Figure 1 shows the process users take using the tool

presented here.

3.1 Inputs

Two factors which negatively impact patient

scheduling, and hospital performance, are variations

in the appointment durations (i.e. the time a patient

spends with a physician) and arrival times (i.e.

whether a patient arrives early or late for their

appointment). For appointment duration variation,

an analysis of anonymised historical appointment

data was performed to identify the variation.

Historical data were provided for a five month

period between July and November 2015 for a range

of outpatient appointment types and included the

arrival time of the patient, totalling 4,945 data

points. Of this, some appointments were excluded

from analysis where the duration was less than five

minutes or greater than 90 minutes (278), or where

the appointment data were incomplete (919), for

example, if it did not specify the activity undertaken.

This was done to remove appointments which were

logged after they occurred (i.e. typically resulting in

very short appointment durations) and ones which

could not be specifically linked to the outpatient

services of this department. This gave a remaining

total of 3,748 data points for analysis. An average

(mean) appointment duration for low throughput

(24mins) and high throughput (22mins) clinic

models were extracted, along with the value

representing one standard deviation from this mean

appointment duration. Figure 2 shows the

distribution of appointment durations for the low

throughput model and Figure 3 shows the

distribution for the high throughput model from the

historical data.

The tool uses a number of inputs that define the

clinic day to be analysed, ranging from the number

of rooms and clinicians available, to the arrival

profile of patients. The inputs are modifiable by the

user at runtime, allowing them to simulate a variety

of scenarios. For example, users can simulate and

compare between 24 clinic rooms and 36 clinic

rooms with ease. Previous academic discussion has

noted that tools for this type of modelling are better

understood by users if the inputs have sensible

default values from the outset (Fletcher et al., 2007;

Gunal and Pidd, 2010). In acknowledgement of this,

the tool was developed with default values for each

input derived from discussions with the Trust and

analysis of the historical data. The inputs and their

default values are given in Tables 1 through 4.

The inputs provide a comprehensive analysis

model which evaluates the range of metrics defined

by the Trust. Of these inputs, some are related to the

clinician working practices and protocols. An

example of this is the clinician write-up period after

each appointment has been completed. This is the

time in which clinicians enter details of the patient’s

visit into their electronic records system, order

follow-up tests, and organise referrals as necessary.

For the dedicated clinic model, this occurs in the

same room as the appointment undertaken by the

clinician who does not leave, and so this time is

taken into account in the room turnaround (the time

taken for the room to be prepared for the next

patient). However, for the Hub/Spoke model, this

write-up time is conducted at the staff hub, allowing

the room to be freed up quicker for the next patient

to be seen by another clinician.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

206

3.2 Queues

Queueing is relatively simple in the dedicated

model, with patients arriving at the waiting area and

then waiting for a room to be free following the

room turnaround and the clinician write-up period.

However, for the Hub/Spoke model queuing is

slightly different, with there being a need for both a

room to be empty, and a clinician to be free. The

logic flow for this queue is presented in Figure 4.

Figure 2: Distribution of low throughput appointment

durations.

3.3 Patient Numbers

The objective of the tool is to produce an optimal

patient schedule that allows the department to

examine as many patients as possible in a given day

while keeping within the agreed target for a range of

metrics. As such, the tool does not take in a single

figure for the number of patients, but rather a range

and step size. This range is analysed, increasing by

the step size for each simulation run. This provides

the users output for each metric for the range of

patients, allowing them to compare schedules and

choose the optimal with ease.

Figure 3: Distribution of high throughput appointment

duration.

Table 1: Scenario inputs and default values.

Input

Default value

Description

Clinic hours

10 hours

How many hours does the clinic wish to run for?

Appointments per

day (min)

150

What is the smallest number of patients to simulate?

Appointments per

day (max)

500

What is the largest number of patients to simulate? Setting the maximum to

the same value as the minimum will result in a simulation run of just that

number of patients, regardless of step size.

Appointment step

size

What are the steps of patients to simulate? For the default values the patient

numbers simulated are: 150, 200, 250, 300, 350, 400, 450, 500.

Booking interval

15 minutes

What is the minimum amount of time between appointment slots. For

example, if a clinic starts at 9am, patients are given appointments at 9am,

9:15, 9:30, 9:45, etc.

Arrival profile –

percentage of early

arrivals

70%

How many patients will turn up early for their appointment.

Arrival profile –

percentage of late

arrivals

30%

How many patients will turn up late for their appointment.

Arrival profile –

minutes early

10 minutes

How early will patients turn up for their appointment. E.G. for a 9:15

appointment a patient will arrive at 9:05.

Arrival profile –

minutes late

9 minutes

How late will patients turn up for their appointment. E.G. for a 9:15

appointment a patient will arrive at 9:24.

Arrival profile – for

each clinic hour

Defaults as

above for

arrival profile

The user is given the option to define the arrival profile for each individual

hour of clinic operation for greater control of the profile.

Maximising Patient Throughput using Discrete-event Simulation

207

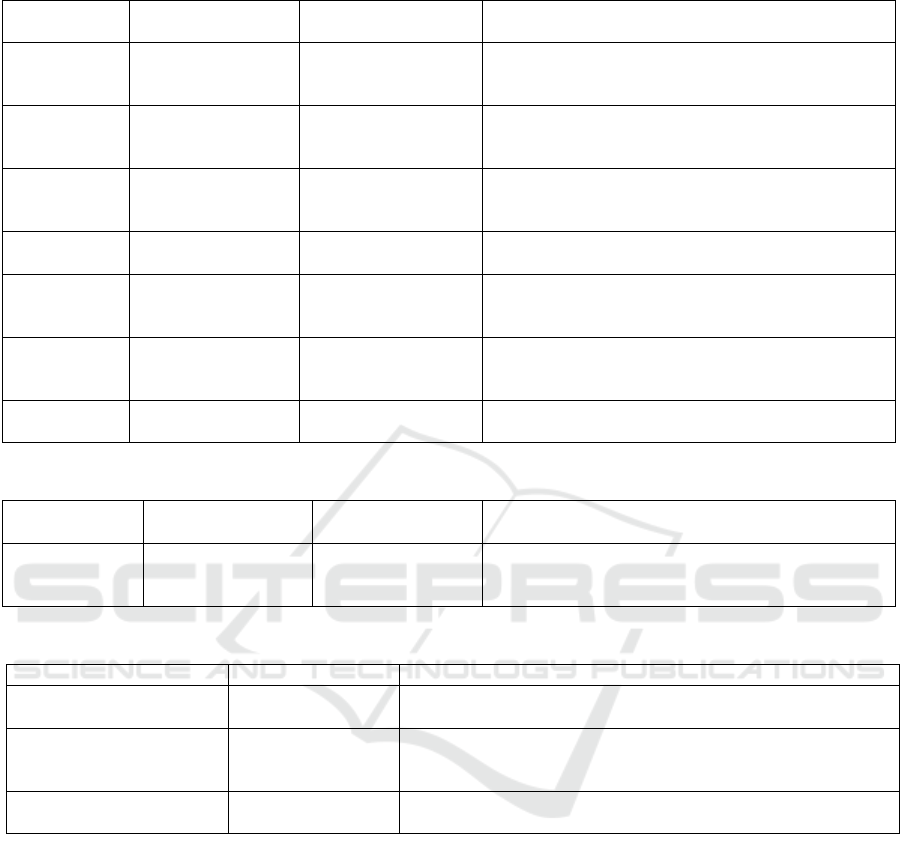
Table 2: Clinic inputs and default values.

Input

Default value

(low throughput)

Default value

(high throughput)

Description

Appointment

duration

24 minutes

22 minutes

The average appointment duration for each patient

type. The default value represents the average from

the analysis of historical data.

Standard

deviation

14 minutes

12 minutes

The time that represents one standard deviation from

the average, calculated from the analysis of historical

data.

Percentage of

patients

attending

50%

Of the patients being simulated, what is the

percentage split between the types the department

caters for?

Clinic model

Hub/Spoke

Dedicated

What clinic model are those types using? Boolean

between Hub/Spoke and Dedicated.

Number of

clinic rooms

12 rooms

How many clinic rooms are available to each clinic. If

both clinics are running a Hub/Spoke model then

these values are combined.

Number of

clinicians

13 people

12 people

How many clinicians are working each type. For

Dedicated clinics, the number of clinicians matches

the number of rooms.

Clinician

write up time

20 minutes

10 minutes

How long do clinicians spend after the appointment

writing up notes or conducting follow-up actions?

Table 3: Clinic model inputs and default values.

Input

Default value

(Hub/Spoke)

Default value

(Dedicated)

Description

Turnaround

time

5 minutes

2 minutes

How long does it take to get the room prepared for the

next patient. This is time the room cannot be used for

appointment activity.

Table 4: Acceptance criteria inputs and default values.

3.4 Arrival Profiles

Another variance which can impact on a clinic’s

operational efficiency is the arrival times of patients

with appointments. Patients rarely turn up for an

appointment at the time of that appointment. Rather

they turn up early, to ensure they make it, or are late

for a variety of reasons. For this, the arrival profile

can be defined by the user as a uniform profile, or

define an arrival profile for each hour of the clinic’s

operations. This means that if users spot a trend in

patients arriving late in, for example, the afternoon,

this can be built into the simulation model to analyse

the impact of this.

Patients that arrive early will be registered in the

model from their arrival time, and will be placed in

the queue to be seen based on their arrival. Patients

that arrive ahead of their appointment timeslot

earlier in the model may have the opportunity to

begin their appointment prior to the scheduled

appointment timeslot if a room and a clinician are

free when they arrive and no other patients are in the

queue ahead of them. If a room or clinician is not

free however then they join the queue to be seen

when the resources are available.

Patients that arrive late are processed depending

on how late they arrive. For the Trust, the policy is

for patients that arrive within 15 minutes of their

appointment timeslot to be seen before patients with

later appointments already in the queue. Effectively

this allows late patients up to 15 minutes grace to

jump the queue before enduring an unknown wait to

Input

Default value

Description

Maximum waiting time

30 minutes

How long is an acceptable wait time for patients from their arrival

time to the time they are seen.

Waiting room capacity

68 people

What is the capacity of the waiting area for patients to sit in?

Patients that arrive early for their appointment take up a seat in

the waiting area from their arrival time.

Staff hub capacity

32 people

What is the capacity of the staff hub for Hub/Spoke clinicians to

work in.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

208

Figure 4: Logic diagram of patients using Hub/Spoke

clinics.

be seen. For example, if patient A has an

appointment at 9:30 and arrives at 9:20, while

patient B has an appointment at 9:15 but arrives at

9:24, patient B will be seen before patient A.

However, if patient B arrives at 9:31, then patient A

will be seen before patient B.

3.5 Simulation

The simulation is provided by the discrete-event

simulation (DES) tool SmartProcessAnalyser,

developed by BuroHappold, which builds a set of

clinic rooms based on the inputs provided by the

user and produces a simulation model for the first

grouping of patients. This model is then executed

and analysis results exported to a spreadsheet file

before a new simulation model is generated for the

next simulation run.

3.6 Multiple Analysis

The results of a single simulation can be misleading

with the variance in appointment durations and

arrival times providing a different result each

simulation run. Though the tool uses a random

function to generate the patient appointment

duration and arrival time, it is feasible to have a

‘near-perfect’ day simulated where appointments are

relatively quick and so it might appear that the clinic

could handle more patients than simulated with a

quick finish. Equally it is possible to have a ‘near

disastrous’ day with long appointments which may

give the impression that the clinic could only handle

a small number of patients.

To account for this, an analysis was performed to

determine how many simulation runs would be

optimal to obtain a valid prediction of the average,

rather than allowing a ‘near-perfect’ or ‘near-

disastrous’ day to provide misleading results. The

output of this recommended 40 simulation runs be

performed for each set of inputs to account for the

variation between each simulation run and prevent

outliers from providing misleading outputs. Table 5

outlines the results of this analysis. The simulation

model executes the analysis for a single grouping for

a given number of runs before moving onto the next

grouping. For example, a simulation of 50-100

patients with a step size of 10 for 20 runs will

analyse 20 scenarios of 50 patients before moving

on to analyse 20 scenarios of 60 patients, and so on.

A similar technique was seen in the work of Harper

& Gamlin (2003) which ran a DES model for an Ear

Nose and Throat (END) department 40 times to

prevent outliers skewing the results.

The multiple run analysis was performed using

default values for the inputs, with the exception of

patient numbers which were set at 500 patients. For

each set of runs, the average results from that

simulation were taken and measured for their

variance and confidence level around the mean

(measured at 95% confidence of the mean). For the

single run analysis, the average values are also the

only values that are exported, as opposed to multiple

runs where the average value is the average of all

values in that simulation. For example, a five run

simulation shows the average of each of the five

results on the graph outputs. Each simulation was

run 20 times, giving 20 samples for each ‘run’ being

analysed, ranging from 20 simulation results (20

times 1 run) to 1000 simulation results (20 times 50

runs) in the analysis. The results shown in Table 5

show that the variance is reduced for each metric as

the more simulation runs are performed, until 50

runs is reached. At this point, some metrics variance

increases while others stay the same, suggesting that

40-50 runs per simulation is likely to provide a more

reliable result than 1 run per simulation.

Maximising Patient Throughput using Discrete-event Simulation

209

3.7 Analysis Results

The simulation exports the result of the analysis to a

spreadsheet file that can be examined in full by the

user and includes graphs that highlight the core

results of the simulations. This includes the

individual result for each simulation run for the user

to inspect if they so wish. The metrics included in

this tool are shown in Table 6. Each graph shows the

number of simulated patients along the X-Axis, and

for each patient grouping the average result after all

of the simulation runs. Also given are error bars

denoting the minimum result and maximum result of

all runs. Figures 5 through 8 provide examples of the

graph outputs following simulations using default

values.

The spreadsheet of results allows users to

explore the simulation results in detail. For each

metric an overall value (average of both clinic

models) is provided, as well as the result for each

clinic model. This is given for each simulation run.

For the room utilisation metrics, a detailed output of

the utilisation for each clinic type (and average of

overall) for each simulated minute is provided. This

is broken into the three states the room may be in,

idle (empty room ready for a patient), occupied

(with a patient), and being turned around (prepared

for the next patient). This allows users to analyse

periods of a simulated day when utilisations may be

lower than anticipated.

3.8 Result Interpretation

The tool provides the graph outputs on the user

interface (UI) for the user to work with as soon as all

of the simulations runs are completed, with the

detailed spreadsheet of data available to export.

However, the tool does not interpret the results to

make any recommendations of the best schedule to

adopt for the clinic. Rather, this interpretation is left

to the user, who can apply their experience and

knowledge to weight between each metric and select

the optimal patient schedule. For example, as

government focus shifts towards maximising

utilisation of space, it may become acceptable to

have a percentage of patients waiting more than a

given amount of time if the utilisation is increased.

Such trade-off decisions are left to the users, with

the tool providing no bias.

The error bars in the graphs shown in Figures

5 through 8 show the minimum and maximum

value of the results, with the columns denoting

the average result.

Figure 5: Percentage of patients waiting more than the

acceptance criteria.

Figure 6: Clinic room utilisation.

Figure 7: Waiting room utilisation.

Figure 8: Clinician utilisation.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

210

Table 5: Analysis results for multiple runs comparison (confidence of the mean measured at 95%).

Metric 1

Metric 2

Metric 6

Metric 7

Runs

Avg.

Var.

+/-

Avg.

Var.

+/-

Avg.

Var.

+/-

Avg.

Var.

+/-

76.5

16.3

2.5

63.8

0.8

0.6

2358.7

24824.7

97.7

266.8

566.6

14.8

75.2

1.8

1.3

63.6

0.1

0.3

2276.4

13711.6

56.4

261.3

63.0

5.5

76.3

2.2

0.9

63.8

0.2

0.3

2303.9

6737.0

50.9

261.4

91.8

5.9

75.9

1.0

0.6

63.8

0.2

0.3

2314

1044.2

20.0

262.9

26.1

3.7

75.5

2.1

0.9

64.0

0.0

2308.1

724.5

16.7

262.4

8.3

1.8

75.9

1.0

0.6

64.0

0.0

2313.4

461.8

13.3

264.4

4.9

1.4

76.0

0.9

0.6

64.0

0.0

2316.1

1545.0

24.4

263.9

16.1

2.5

Table 6 - List of outputs. * denotes a metric presented as a graph on the UI.

Metric 1*

Patients waiting >

x minutes

The percentage of patients whose waiting time exceeded the maximum

waiting time.

Metric 2*

Clinic room

utilisation

Clinic room demand as a percentage of capacity where demand is equal to

the total time spent by patients in rooms (for the given clinic hours) plus

the turnaround time (for the given clinic hours) plus the write-up time

(dedicated clinics only during clinic hours). Capacity is equal to the

number of rooms multiplied by the clinic hours.

Metric 3*

Waiting room

utilisation

Waiting area demand as a percentage of its capacity where demand is

equal to the total time spent by patient waiting for clinics (for the given

clinic hours) and capacity is the room capacity multiplied by the clinic

hours.

Metric 4*

Staff hub

utilisation

Staff hub demand as a percentage of its capacity where demand is the total

write-up time spent by Hub/Spoke clinicians in the hub (during clinic

hours only) and capacity is the hub capacity multiplied by the clinic hours.

Metric 5*

Clinician

utilisation

Clinician demand as a percentage of clinician capacity where demand is

equal to the total time spent with a patient or writing-up and capacity is

the number of clinicians multiplied by the clinic hours.

Metric 6*

Total patient

facing time (post

clinic)

The total amount of time spent by patients in appointments after the end of

the clinic hours. For patients whose appointment began prior to the end of

clinic hours, only the portion that occurred after the end of clinic hours is

included. For example, if patient A begins their appointment at 16:50 and

finishes at 17:15, with clinic hours finishing at 17:00, this would give a

patient facing time of 15 minutes. This is summed for all patients, so if

patient B has an appointment from 16:55 to 17:10, the total patient facing

time for A & B would be 25 minutes.

Metric 7

Clinic over-run

(mins)

The total amount of time after clinic hours until all patients have

completed the model. In the above example for metric 6, the clinic over-

run would be 15 minutes.

Metric 8

Patients waiting

(post clinic)

This is the number of patients who are still waiting to be seen at the end of

clinic hours.

Metric 9

Patients being

seen (post clinic)

This is the number of patients that are in appointments at the end of clinic

hours.

4 LIMITATIONS

Although the tool takes into account the variance in

appointment durations and arrival patterns, it does

not take into account other variances related to the

clinicians and facility which may impact on an

appointment schedule. For example, there is only a

fixed input for the length of time clinicians will

spend ‘writing up’ following an appointment.

However, this could be subject to variance

depending on the appointment, as follow-up tests

may need to be ordered, or subsequent appointments

Maximising Patient Throughput using Discrete-event Simulation

211

scheduled. This variance was unable to be captured

from the appointment history data used to calculate

the variance in appointment durations, and so the

default values for these inputs came from

discussions with experienced clinicians. However,

because the input is accessible to the user of the tool

the write-up time can be modified if the write-up

process or time changes.

Similarly, there is no variance accounted for in

the room turnaround times for each clinic type. The

clinic turnaround is the time it takes to prepare the

room for the next patient, which may include

changing bedsheets, replenishing equipment such as

gloves and needles, and removing expended

equipment. This variance was also unable to be

captured from historical data, though it is also less

likely to have as much variance as appointments and

clinician work. Turning a room round for the next

patient typically follows a given process for hygiene

and sanitary reasons and has a fixed protocol to be

followed. Thus, the impact of a variance in

turnaround times is likely to be negligible. However,

as with the clinician write-up input, this input is

exposed to the user to be modified as they see fit.

As the tool has been built for the outpatient

operations defined by the Trust, it follows a linear

unchanging clinic pathway for patients from arrival

to appointment to leaving the model. It does not take

into account other potential activities such as blood

work prior to or after the examination. However, the

underlying simulation engine allows for easy

adaptation at a later stage to include further

activities, both clinical and non-clinical, should

future scenarios warrant it. Full implementation

could allow users to build their own clinic pathway

for a patient, however, at present this is not a

function of the tool presented here.

5 DISCUSSION

This paper has presented a clinic planning tool that

is generalisable to any outpatient clinic wishing to

run dedicated, Hub/Spoke, or a mixture of both

clinic types, as well as incorporating variance in

patient appointment durations and arrival times for a

more accurate simulation. The variance for

appointment durations and arrival times was

calculated from 3,748 historical appointments.

However, the generic inputs are open to users of the

tool and thus allow for any Trust to adopt the tool to

produce their own simulation results with ease. This

allows the tool to be reused and prevents it being a

solution for one specific problem. Rather, this tool

can be used to tackle a range of appointment

scheduling problems provided sensible inputs are

given, saving a Trust the time and development cost

of developing their own tool.

With increasing budget restraints on the NHS, a

reusable tool that can be utilised by any hospital or

department is of benefit to the healthcare industry.

Its generic modelling inputs, not constrained by

spatial requirements, allow for reuse and easy

adoption by other healthcare providers. However, its

adaptability through the use of the extendable DES

engine also ensures the tool can evolve with policy

changes and continue to provide optimal patient

schedules.

6 CONCLUSIONS

The variance in appointment durations plays a large

part in the efficiency and operation of a clinic.

Though there may be attempts to standardise

appointment durations, variations will undoubtedly

occur as individual health concerns cannot always be

feasibly addressed in a strict appointment window.

As such, it is better to accept the variance and plan

with it, rather than to plan for no variance and

wonder why clinics are over-running every day and

clinicians are suffering from being overworked. This

tool assists with this, taking the variance and

randomness in appointment durations and building

this into the simulation model from the start. The use

of a generic input set-up to define the clinic model

allows the tool to be applicable to any department

utilising the given clinic models to find an optimal

appointment schedule.

The variance in outputs generated by each

individual simulation run has been highlighted as a

danger of incorporating variance in appointment

durations. This shows the need for multiple

simulation runs to be performed on a DES model to

reduce overall impact of outliers from producing

non-representative results and improve the

confidence in the outputs. The inclusion of clinician

resources for the clinic also allows for future

planning to be undertaken, by seeing the impact of

clinician changes (holiday, sickness, etc.) on the

system.

Finally, a range of metrics has been included in

the tool, providing a comprehensive analysis to the

user. The metrics offer output based on current

targets and guidelines for the NHS. These can be

easily adapted or added to as targets and guidelines

change. The end result of using the tool is the user’s

ability to produce an appointment schedule which

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

212

will allow for seeing the maximum number of

patients possible in a day without negatively

impacting clinic utilisation, clinician utilisation,

clinic over-run, or patient waiting times.

ACKNOWLEDGEMENTS

We would like to thank the Engineering and

Physical Sciences Research Council, and Centre for

Innovative and Collaborative Construction

Engineering at Loughborough University for

provision of a grant (number EPG037272) to

undertake this research project in collaboration with

BuroHappold Engineering Ltd.

REFERENCES

Anderson, J. G. and Merode, G. G. (2007) ‘Special issue

on health care simulation’, Health Care Management

Science, 10(4), pp. 309–310. doi: 10.1007/s10729-

007-9031-x.

Antonacci, G., Calabrese, A., D’Ambrogio, A., Giglio, A.,

Intrigila, B. and Ghiron, N. L. (2016) ‘A BPMN-based

automated approach for the analysis of healthcare

processes’, in Proceedings - 25th IEEE International

Conference on Enabling Technologies: Infrastructure

for Collaborative Enterprises, WETICE 2016, pp.

124–129. doi: 10.1109/WETICE.2016.35.

Ballard, S. M. and Kuhl, M. E. (2006) ‘The use of

simulation to determine maximum capacity in the

surgical suite operating room’, in Proceedings -

Winter Simulation Conference, pp. 433–438. doi:

10.1109/WSC.2006.323112.

Bernstein, S., Aronsky, D., Duseja, R., Epstien, S.,

Handel, D., Hwang, U., McCarthy, M., McConnell, J.,

Pines, J., Rathlev, N., Schafermeyer, R., Zwemer, F.,

Schull, M. and Asplin, B. (2009) ‘The effect of

emergency department crowding on clinically oriented

outcomes’, Academic Emergency Medicine, 16(1), pp.

1–10. doi: 10.1111/j.1553-2712.2008.00295.x.

Brenner, S., Zeng, Z., Liu, Y., Wang, J., Li, J. and

Howard, P. K. (2010) ‘Modeling and analysis of the

emergency department at university of Kentucky

Chandler Hospital using simulations’, Journal of

Emergency Nursing, 36(4), pp. 303–310. doi:

10.1016/j.jen.2009.07.018.

Carter, P. (2016) Operational productivity and

performance in English NHS acute hospitals:

Unwarranted variations. London.

Davis, K., Stremikis, K., Squires, D. and Schoen, C.

(2014) ‘Mirror, mirror on the wall, 2014 update: how

the US health care system compares internationally’,

New York (NY): Commonwealth Fund, 16.

Denton, B., Rahman, A., Nelson, H. and Bailey, A. (2006)

‘Simulation of a multiple operating room surgical

suite’, in Proceedings of the 38th conference on

Winter simulation, pp. 414–424.

Department of Health (2013) The NHS Constitution.

London.

Dexter, F. and Epstein, R. (2009) ‘Typical savings from

each minute reduction in tardy first case of the day

starts’, Anesthesia & Analgesia, 108(4), pp. 1262–7.

doi: 10.1213/ane.0b013e31819775cd.

Fetter, R. B. and Thompson, J. D. (1965) ‘The Simulation

of Hospital Systems’, Operations Research, 13(5), pp.

689–711. doi: 10.1287/opre.13.5.689.

Fletcher, A., Halsall, D., Huxham, S. and Worthington, D.

(2007) ‘The DH Accident and Emergency Department

model: a national generic model used locally’, Journal

of the Operational Research Society, 58(12), pp.

1554–1562. doi: 10.1057/palgrave.jors.2602344.

Greenroyd, F. L., Hayward, R., Price, A., Demian, P. and

Sharma, S. (2016) ‘Using Evidence-Based Design to

Improve Pharmacy Department Efficiency’, HERD:

Health Environments Research & Design Journal,

10(1), pp. 130–143. doi: 10.1177/1937586716628276.

Gunal, M. and Pidd, M. (2006) ‘Understanding accident

and emergency department performance using

simulation’, Simulation Conference, 2006. WSC 06.

Proceedings of the Winter, pp. 446–452.

Gunal, M. and Pidd, M. (2010) ‘Discrete Event Simulation

for Performance Modelling in Healthcare: A Review

of the Literature.’, Journal of Simulation, 4(1), pp. 42–

51.

Harper, P. R. and Gamlin, H. M. (2003) ‘Reduced

outpatient waiting times with improved appointment

scheduling: A simulation modelling approach’, OR

Spectrum, 25(2), pp. 207–222. doi: 10.1007/s00291-

003-0122-x.

Harper, P. R. and Pitt, M. A. (2004) ‘On the challenges of

healthcare modelling and a proposed project life cycle

for successful implementation’, Journal of the

Operational Research Society, 55(6), pp. 657–661.

doi: 10.1057/palgrave.jors.2601719.

Health and Social Care Information Centre (2015) Estates

Returns Information Collection: England 2014 to

2015. London.

Hendrich, A., Chow, M., Skierczynski, B. and Lu, Z.

(2008) ‘A 36-hospital time and motion study: How do

medical-surgical nurses spend their time?’, The

Permanente Journal, 12(3), pp. 25–34.

Huang, Y.-L. and Kammerdiner, A. (2013) ‘Reduction of

service time variation in patient visit groups using

decision tree method for an effective scheduling’,

International Journal of Healthcare Technology and

Management, 14(1–2), pp. 3–21. doi:

10.1504/IJHTM.2013.055081.

Jun, J., Jacobson, S. and Swisher, J. (1999) ‘Application of

discrete - event simulation in health care clinics: A

survey’, Journal of the Operational Research Society,

50(2), pp. 109–123. doi:

10.1057/palgrave.jors.2600669.

Kuljis, J., Paul, R. J. and Chen, C. (2001) ‘Visualization

and Simulation: Two Sides of the Same Coin?’,

Maximising Patient Throughput using Discrete-event Simulation

213

Simulation, 77(3/4), pp. 141–152. doi:

10.1177/003754970107700306.

Lee, S., Min, D., Ryu, J. -h. and Yih, Y. (2013) ‘A

simulation study of appointment scheduling in

outpatient clinics: Open access and overbooking’,

Simulation, 89(12), pp. 1459–1473. doi:

10.1177/0037549713505332.

Leskovar, R., Accetto, R., Baggia, A., Lazarevič, Z.,

Vukovič, G. and Požun, P. (2011) ‘Discrete event

simulation of administrative and medical processes’,

Zdravniski Vestnik, 80(5).

Marcario, A. (2006) ‘Are your hospital operating rooms

“efficient”’, Anesthesiology, (2), pp. 233–243.

Maviglia, S. M., Yoo, J. Y., Franz, C., Featherstone, E.,

Churchill, W., Bates, D. W., Gandhi, T. K. and Poon,

E. G. (2007) ‘Cost-benefit analysis of a hospital

pharmacy bar code solution.’, Archives of internal

medicine, 167, pp. 788–794. doi:

10.1001/archinte.167.8.788.

NHS England (2013) ‘The NHS belongs to the people: a

call to action’, NHS England, London.

NHS England (2014) Five year forward view. London.

Nicholson, D. (2009) ‘The Year: NHS chief executive’s

annual report 2008/09’, London: Department of

Health, p. 47.

Quevedo, V. and Chapilliquén, J. (2014) ‘Modeling a

Public Hospital Outpatient Clinic in Peru Using

Discrete Simulation’.

Reynolds, M., Vasilakis, C., McLeod, M., Barber, N.,

Mounsey, A., Newton, S., Jacklin, A. and Franklin, B.

D. (2011) ‘Using discrete event simulation to design a

more efficient hospital pharmacy for outpatients’,

Health Care Management Science, 14, pp. 223–236.

doi: 10.1007/s10729-011-9151-1.

Rolón, E., García, F., Ruiz, F., Piattini, M., Calahorra, L.,

García, M. and Martin, R. (2008) ‘Process Modeling

of the Health Sector Using BPMN: A Case Study’, in

Proceedings of the first international conference on

health informatics (HEALTHINF), pp. 173–178.

Vanberkel, P. T. and Blake, J. T. (2007) ‘A

comprehensive simulation for wait time reduction and

capacity planning applied in general surgery’, Health

Care Management Science, 10(4), pp. 373–385. doi:

10.1007/s10729-007-9035-6.

Werker, G., Sauré, A., French, J. and Shechter, S. (2009)

‘The use of discrete-event simulation modelling to

improve radiation therapy planning processes’,

Radiotherapy and Oncology. Elsevier Ireland Ltd,

92(1), pp. 76–82. doi: 10.1016/j.radonc.2009.03.012.

Zeng, Z., Ma, X., Hu, Y., Li, J. and Bryant, D. (2012) ‘A

Simulation Study to Improve Quality of Care in the

Emergency Department of a Community Hospital’,

Journal of Emergency Nursing. Emergency Nurses

Association, 38(4), pp. 322–328. doi:

10.1016/j.jen.2011.03.005.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

214