Preprocessing Graphs for Network Inference Applications
H. R. Sachin Prabhu and Hua-Liang Wei
Department of Automatic Control & Systems Engineering, The University of Sheffield,
Mappin Street, S1 3JD, Sheffield, U.K.
Keywords:
Bipartite Graphs, Reduced Graphs, Ordered Matching, Rank, Subnetworks.
Abstract:
The problem of network inference can be solved as a constrained matrix factorization problem where some
sparsity constraints are imposed on one of the matrix factors. The solution is unique up to a scaling factor
when certain rank conditions are imposed on both the matrix factors. Two key issues in factorising a matrix of
data from some netwrok are that of establishing simple identifiability conditions and decomposing a network
into identifiable subnetworks. This paper solves both the problems by introducing the notion of an ordered
matching in a bipartite graphs. Novel and simple graph theoretical conditions are developed which can replace
the aforementioned computationally intensive rank conditions. A simple algorithm to reduce a bipartite graph
and a graph preprocessing algorithm to decompose a network into a set of identifiable subsystems is proposed.
1 INTRODUCTION
The problem of network inference arises when regu-
latory pattern of a network is known and its outputs
are measured whereas the inputs that drive the net-
work and regulatory strengths are unknown. A reg-
ulatory pattern indicates causal relationships between
inputs and outputs of a network. In terms of steady-
state analysis of systems, input-output relationships
can be represented as a system of linear equations
where the coefficients of which represent steady-state
gains. The challenge is to simultaneously estimate
the regulatory strengths and input activities. In other
words, a data matrix is to be factorised into a prod-
uct of two matrices – a regulatory matrix and an in-
put matrix - such that the error in data reconstruction
is minimised. Such problems are common in studies
on social networks and biological regulatory networks
(Newman, 2003; Brugere et al., 2016).
It is hard to simultaneously estimate the matrix
factors using conventional techniques such as Princi-
pal Component Analysis or Singular Value Decom-
position as the structure of the regulatory matrix is
constrained (Liao et al., 2003). Network Compo-
nent Analysis (NCA) (Liao et al., 2003) solves the
network inference problem as a bilevel optimisation
problem while taking these constraints into consider-
ation. NCA imposes several rank conditions on the
regulatory matrix and input matrix in order to ensure
uniqueness to a certain degree of the estimates ob-
tained via optimisation. A regulatory network must
satisfy all relevant NCA rank conditions imposed on
it whereas the input matrix can only be assumed to
satisfy the conditions imposed on it.
The patterns found in complex real world net-
works are not random (Newman, 2003). Therefore,
there is a need to characterise such networks when-
ever possible. Regulatory networks can be formally
described using graphs and the benefits of doing so
are multifold. Parameter estimation is relatively eas-
ier as the solution space is well defined. Graph the-
oretical descriptions are more comprehensible to a
layman than matrix rank conditions. In addition to
that, subnetworks can be identified in cases where
parameter estimation for the original network is un-
solvable. These advantages motivated development
of graph theoretical interpretations of regulatory net-
works in (Boscolo et al., 2005) and (Fritzilas et al.,
2013). Identifying subnetworks refers to searching
for a part of regulatory pattern that allows application
of NCA in the context of this paper. It should not be
mistaken for parameter estimation.
Graph theoretical conditions that are based on
analysing the structure of regulatory matrix is de-
veloped in (Boscolo et al., 2005). These conditions
are comprehensible and offer a simple way to test
NCA compatibility of relatively smaller networks by
inspection. However, a more formal description is
possible. More importantly, proposed limit on num-
ber of outputs that an input can regulate is inaccu-
rate. Maximal matching property of a graph is used in
(Fritzilas et al., 2013) to obtain a formal and compu-
tationally simpler conditions to test a network for its
NCA compatibility. Though the matching condition
406
Prabhu, H. and Wei, H-L.
Preprocessing Graphs for Network Inference Applications.
DOI: 10.5220/0006401104060413
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 406-413
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

can greatly reduce the computational burden, there
are cases where some networks can be erroneously
classified as NCA compatible. Furthermore, both ap-
proaches present algorithms to identify largest NCA
compatible subnetwork, but they ignore rest of the
original network.
Two key problems addressed in this paper are
that of deriving an accurate comprehensible formal
description of NCA compatible regulatory networks
and decomposing NCA incompatible networks into a
set of NCA compatible subnetworks without ignor-
ing any part of the original network. In this paper, a
new graph property called ordered matching is intro-
duced. A formal description of NCA compatibile net-
works based on finding a maximal ordered matching
in a reduced graph is developed. A new algorithm to
reduce a graph is proposed and a method to decom-
pose a given network into a set of NCA compatible
subnetworks is proposed.
The paper is organised as follows - section 2
presents a formal description of the regulatory net-
work inference problem followed by graph theoretical
interpretations of NCA found in literature. Shortcom-
ings of those interpretations of NCA are demonstrated
in section 3 with the help of counter examples. Novel
NCA conditions are developed thereafter. Algorithms
to reduce a graph, test a network for NCA compatibil-
ity, and identify all NCA compatible subnetworks in
a given network are presented in the latter part of sec-
tion 3. The results of application of these algorithms
to an example network is presented in section 4.
2 PRELIMINARIES
2.1 Regulatory Network Inference
Consider a regulatory network with M outputs and L
inputs, L ≤ M. Let D ∈ R
M×N
be the output or data
matrix and S ∈ R
L×N
be the input or source matrix.
D
ik
and S
jk
, 1 ≤ k ≤ N respectively denote kth sample
of ith output and jth input. At steady-state, the system
is represented by a set of linear equations given by
D = W S (1)
Let Y = {v
i
, 1 ≤ i ≤ M} be the set of vertices cor-
responding to the outputs, X = {u
j
, 1 ≤ j ≤ L} be the
set of vertices corresponding to the inputs, and E =

(u
j
, v
i
), u
j
∈ X regulates v
i
∈ Y

be a set of edges.
Let W ∈ R
M×L
encode all the edge strengths. The
system in (1) is a bipartite graph G = {X ∪ Y, E,W }
with X and Y as its bipartitions. The regulatory pat-
tern of the system is given by the adjacency matrix of
G B(G) ∈ [0, 1]
M×L
defined as
B(G)
i j
=
(
1, if (u
j
, v
i
) ∈ E
0, otherwise
(2)
A mapping φ : R
M×L
7→ [0, 1]
M×L
can be defined such
that
φ(W ) = B(G)
The problem of regulatory network inference is such
that B(G) and D are known, whereas W and S are to
be estimated simultaneously. Regulatory network in-
ference problem is posed as an optimisation problem
below:
min
W,S
J (W, S) = kD −WSk
2
F
subject to φ(W ) = B(G)
(3)
where, k . k
F
denotes the Frobenius norm of a matrix.
Note that the objective is to be minimised si-
multaneously over W and S. Thus, this cannot be
solved as a standard quadratic program in one op-
timisation variable. Matrix factorization approaches
such as Principal Component Analysis and Singular
Value Decomposition are not applicable here because
of the constraint in (3). Network Component Analy-
sis (NCA) (Liao et al., 2003) proposes a bi-level opti-
mization based approach to factorize matrix D into a
product of two matrices
ˆ
W and
ˆ
S.
The following set of conditions is established in
(Liao et al., 2003) that W and S must satisfy for NCA
to be applicable:
1. W has full column rank, i.e., rank(W ) = L
2. Reduced submatrices W
u
j
, ∀u
j
∈ X have full col-
umn rank, i.e., rank(W
u
j
) = L − 1
3. S has full row rank, i.e., rank(S) = L
where, the reduced submatrix W
u
j
of W is ob-
tained by deleting from W the jth column and
every ith row such that φ(W )
i j
= 1. As W is
unknown apriori, it is to be replaced by B(G)
and W
u
j
by B(G)
u
j
= B(W
u
j
). Consider a sys-
tem with M = 10, L = 5, and W such that
Preprocessing Graphs for Network Inference Applications
407

φ(W ) = B(G), where B(G) is given by
B(G) =
u
1
u
2
u
3
u
4
u
5
v
1
1 1 0 1 0
v
2
0 0 1 1 0
v
3
0 0 1 1 0
v
4
1 1 0 1 0
v
5
0 0 1 1 1
v
6
0 1 0 1 1
v
7
1 0 1 0 1
v
8
1 1 1 0 1
v
9
1 0 0 0 1
v
10
0 1 1 0 1
(4)
B(G)
u
1
is obtained by deleting rows and columns as
shown in Fig. 1.
u
1
u
2
u
3
u
4
u
5
v
1
1 1 0 1 0
v
2
0 0 1 1 0
v
3
0 0 1 1 0
v
4
1 1 0 1 0
v
5
0 0 1 1 1
v
6
0 1 0 1 1
v
7
1 0 1 0 1
v
8
1 1 1 0 1
v
9
1 0 0 0 1
v
10
0 1 1 0 1
Figure 1: Deleting rows and columns to obtain B(H
u
1
(G)).
It can be easily verified that rank(B(G)) = L.
However, any regulatory network with φ(W ) = B(G)
as described in (4) will not be NCA compatible as the
submatrices B(G)
u
j
s are such that
rank(B(G)
u
j
)
(
= L − 1, j = 1, 2, 4
< L − 1, j = 3, 5
Testing for NCA compatibility is computationally
intensive as it involves checking ranks of L + 1 ma-
trices for a system with L inputs. Graph theoretical
interpretation of these conditions can reduce the in-
volved complexity to a great extent as explained in
the next section.
2.2 Graph Theoretical Interpretations
of NCA
Let N (u
j
) = {v
i
∈ Y |(u
j
, v
i
) ∈ E} be the set of neigh-
bours of some vertex u
j
∈ X . Trivially, N (u
j
) =
{v
i
|W
i j
= 1}. Given a graph G, G −V denotes an in-
duced subgraph obtained by deleting the set of ver-
tices V and all associated edges from G. A graph the-
oretical interpretation of submatrix W
u
j
of W , referred
to as reduced matrix in NCA literature, is defines as
Definition 1. An induced subgraph in the sense
of NCA H
u
j
(G) of G is defined as H
u
j
(G) = G −

u
j
, N (u
j
)

.
Definition 2. Let W ∈ R
M×L
be such that φ(W ) =
B(G). An induced submatrix W
u
j
is obtained by
deleting rows and columns of W such that φ(W
u
j
) =
B(H
u
j
(G))
B(H
u
j
(G)) is nothing but the submatrix B(G)
u
j
described in section 2.1.
Various constraints are imposed on NCA compat-
ible networks in (Boscolo et al., 2005) that are more
comprehensible compared to the original NCA rank
conditions. However, no computationally simple al-
gorithm is given to implement those. Moreover, the
condition imposed on the degree of input vertices
d(u
j
) = | N (u
j
)| ≤ L − 1 is inaccurate as demon-
strated in the next section. The interpretation in def-
inition 2 is implicitly introduced in (Fritzilas et al.,
2013) where it is argued that NCA conditions are
equivalent to finding a maximal matching of size L−1
in H
u
j
(G).
Definition 3. A matching in a bipartite graph G =
{X ∪Y, E,W } is a pair (X
1
,Y
1
), X
1
⊆ X,Y
1
⊆ Y such
that (u
j
, v
i
) ∈ E, |N (u
j
)∩Y
1
| = 1, and |N (v
i
)∩X
1
| =
1, ∀u
j
∈ X
1
, v
i
∈ Y
1
.
In other words, every vertex in a matching has a
unique neighbour and |X
1
| = |Y
1
| is the size of the
matching (X
1
,Y
1
). A maximal matching (X
∗
1
,Y
∗
1
) is
such that |X
∗
1
| ≥ |X
1
|, where (X
1
,Y
1
) is any other
matching in G. Let G
∗
1
denote a subgraph defined by
a maximal matching (X
∗
1
,Y
∗
1
). Its adjacency matrix
B(G
∗
1
) will have standard basis vectors e
i
, i.e., vectors
with 1 in ith position and rest of the entries being zero.
Thus
rank(B(G
∗
1
)) = |X
∗
1
|
This fact is forms the basis for the argument that
matching conditions are equivalent to the original
NCA conditions.
This interpretation of NCA reduces the problem of
computing rank of an induced submatrix to a compu-
tationally less intensive problem of finding a maximal
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
408

matching in bipartite graph. However, the case of du-
plicate vertices is not considered which may lead to
inaccurate descriptions of NCA compatible networks.
Merely finding a matching in G will not suffice as
demonstrated in the next section.
3 GRAPH PREPROCESSING FOR
NCA
The problem of identifying NCA compatible subnet-
works arises when a given regulatory network does
not satisfy the original NCA conditions. This prob-
lem is addressed in (Boscolo et al., 2005) and (Fritzi-
las et al., 2013) where they first develop graph theo-
retical description of compatible regulatory networks
and then propose methods to identify the largest NCA
compatible subnetwork. However, the set of condi-
tions claimed to be equivalent to the original NCA
conditions are rather inaccurate as shown with the
help of counter-examples in this section
Consider testing B(H
u
1
(G)) given by
B(H
u
1
(G)) =
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
3
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
v
10
1 1 0 1
(5)
against the conditions in (Fritzilas et al., 2013).
(X
∗
1
,Y
∗
1
), X
∗
1
⊂ X = {u
2
, u
3
, u
4
, u
5
},Y
∗
1
⊂ Y =
{v
2
, v
3
, v
5
, v
6
} defines a maximal matching of size
L − 1. B(H
∗
u
1
,1
) defined by this matching as shown
below
B(H
∗
u
1
,1
) =
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
3
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
(6)
Note that rankB(H
∗
u
1
,1
) = 3 < L − 1 as rows corre-
sponding to v
2
and v
3
are identical. Therefore, it is
possible to find a case where an induced submatrix
B(H
u
j
(G)) for some u
j
has rank smaller than L − 1,
but contains a maximal matching of size L − 1. This
observation is summarised as follows
Remark 1. Duplicate vertices can lead to wrong
classification of a network as NCA compatible
Consider the following submatrix of B(H
u
1
(G))
B
1
=
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
({v
2
, v
5
, v
6
}, {u
2
, u
3
, u
4
}) define a matching of size
3. Though rank(B
1
) = 3, this matching does not rep-
resent a set of linearly independent columns - col-
umn u
4
is linearly dependent on column u
2
and u
3
,
u
4
= u
2
+ u
3
.
Remark 2. A maximal matching may contain linearly
dependent vertices
Both remarks 1 and 2 show that a maximal match-
ing does not necessarily correlate to the rank of a
graph as argued in (Fritzilas et al., 2013).
It is evident that for B(G) in (4), d(u
j
) > L −
1, ∀u
j
∈ X. It can be verified that a subnetwork
formed by all rows of B(G) and columns u
1
, u
2
, and
u
4
is NCA compatible. This contradicts condition 2 of
Lemma 1 in (Boscolo et al., 2005) (page 292) which
limits d
u
to L − 1 for every u
j
∈ X.
Remark 3. d(u
j
), u
j
∈ X can be greater than L − 1
Novel conditions that resolve the issues pointed
out in remarks 1, 2 and 3 are presented in the next
section.
3.1 Novel NCA Compatibility
Conditions
Identifying a maximal matching (X
∗
1
,Y
∗
1
) is not nec-
essarily equivalent to calculating rank of the original
graph G
rank(B(G)) 6= |X
∗
1
|
as demonstrated in the previous section. The issue in
remark 1 arises as the vertex v
3
is a duplicate of v
2
in the sense that N (v
2
) = N (v
3
). Another maximal
matching (X
∗
2
,Y
∗
2
) of B(H
u
1
(G)) can be found where
X
∗
2
= {u
2
, u
3
, u
4
, u
5
} and Y
∗
2
= {v
2
, v
5
, v
6
, v
10
}.
B(H
∗
u
1
,2
(G)) defined by X
∗
2
and Y
∗
2
will contain all
rows in (5) except the second row. It can be veri-
fied that the rank of this matrix is L − 1 = 4, which is
equal to |X
∗
2
|. This demonstrates the need to reduce a
graph before finding a maximal matching. A reduced
bipartite graph is defined as follows
Definition 4. A reduced bipartite graph
¯
G = {
¯
X ∪
¯
Y ,
¯
E,
¯
W } is a subgraph of G such that
1.
¯
X ⊆ X and
¯
Y ⊆ Y
2. there are no isolated vertices, d(v) > 0, ∀v ∈
¯
X ∪
¯
Y
Preprocessing Graphs for Network Inference Applications
409

3. there are no duplicate vertices, N (v
1
) 6=
N (v
2
), ∀v
1
, v
2
∈
¯
X ∪
¯
Y
and,
¯
E ⊆ E and
¯
W ⊆ W are submatrices whose rows
and columns are indexed by
¯
X and
¯
Y .
A matching ({u
2
, u
5
, u
3
}, {v
2
, v
5
, v
6
}) in (6)
represents linearly independent columns of B(H
∗
u
1
,1
).
This demonstrates the need to rearrange the rows and
columns of the adjacency matrix of a bipartite graph
before looking for a maximal matching. It will be
shown in this section that imposing a partial order
based on degrees of vertices is helpful in simplifying
NCA compatibility conditions.
Definition 5. An ordered matching is a matching
(X , Y ) obtained from partially ordered sets D(X)
and D(Y ) where D(.) sorts a set of vertices in in-
creasing order of degrees of its elements.
The act of imposing such an order is referred to
as ordering a graph in the context of this paper. Let
D(G) denote an ordered graph. Ordering and re-
duction operations are independent of each other and
hence, can be executed in any order. The relationship
between graph reduction and ordering, and rank of a
graph can be derived as shown below.
Lemma 1. The rank of a bipartite graph G = {X ∪
Y, E,W } such that |X| ≤ |Y | can be determined as
rank(G) = |
¯
X
∗
(G)|
where, (
¯
X
∗
(G),
¯
Y
∗
(G)) define a maximal matching in
ordered reduced bipartite graph D(
¯
G).
Proof Rank of a graph is equal to the rank of re-
duced graph
¯
G (Li et al., 2012). Defining a partial
order D(.) on
¯
G does not affect its rank. It is suffi-
cient to show that (
¯
X
∗
,
¯
Y
∗
) a maximal matching in
ordered reduced graph D(
¯
G) corresponds to a set of
linearly independent columns in D(
¯
G), and hence, in
¯
G and G.
The ordered reduced graph D(
¯
G) has no duplicate
or isolated vertices. Assume that there exists a vertex
u
i
∈ D(
¯
X) the column corresponding to which can be
expressed as a linear combination of other columns in
the adjacency matrix B(D) = B(D(
¯
G)) as
B(D)
:i
= Σ
j6=i
α
j
B(D)
: j
Thus, for every v ∈ N (u
i
), there exists some u
j
∈
D(
¯
X), j 6= i such that v ∈ N (u
j
). Since every ver-
tex in a matching has exactly one neighbour, u
i
will
not be a part of any maximal ordered matching as the
columns corresponding to u
j
s will precede the col-
umn corresponding to u
i
in B(D). Thus, all columns
of B(
¯
G) corresponding to (
¯
X
∗
,
¯
Y
∗
) are linearly inde-
pendent. A similar argument with respect to the rows
of B(
¯
G) by replacing u with v and X by Y completes
the proof. 
A novel and simple set of conditions that is equiv-
alent to the original NCA conditions can now be de-
veloped.
Theorem 1. A regulatory network as described in (1)
is NCA-compatible if and only if every input vertex
u
j
∈ X is such that
|
¯
X
∗
(H
u
j
(G))| = L − 1
where G = (X ∪ Y, E,W ) is a bipartite graph repre-
senting the network, H
u
j
(G)s are induced subgraphs
of G, and
¯
X
∗
(.) represents a maximal ordered match-
ing in
¯
G.
Proof If every vertex u
j
∈ X satisfies the condition
in theorem 1, rank(W
u
j
) = L − 1 from Lemma 1. The
graph H
u
j
(G) + v for any u
j
∈ X and v ∈ N (u
j
) is
reduced and it will have a maximal ordered matching
of size L and hence rank(W ) = L.
Conversely, by definition, maximal ordered
matchings of size L − 1 can be found for all H
u
j
s of
NCA compatible networks.
We use the argument on rank of S provided in
(Liao et al., 2003). Thus, all original NCA conditions
are satisfied. 
3.2 Identifying NCA Compatible
Subnetworks
As pointed out towards the end of section 2.2 and
demonstrated in section 3, the conditions developed
in (Boscolo et al., 2005) and (Fritzilas et al., 2013) are
inaccurate graph theoretical interpretations of original
NCA conditions. Both present their own approaches
to identify NCA compatible subnetworks of NCA in-
compatible networks. Algorithm proposed in the for-
mer one starts with an initial guess on the largest NCA
compatible subnetwork and continues to add more in-
put vertices such that no NCA conditions are violated.
This requires an initial guess on largest NCA compat-
ible subnetwork. The simplest starting point could
be one where only one input vertex and its neigh-
bours are considered, but it is trivial to see that ran-
domly adding more vertices thereafter is a tedious
task. The latter proposes a more structured approach
where nicely separable subsets of X and Y are to be
identified. Nicely separable NCA compliant subnet-
works are those that have no vertices in common and
are NCA compatible (Fritzilas et al., 2013). The moti-
vation for our work comes from the fact that both for-
mer approaches look for the single largest NCA com-
patible subnetwork and ignore the rest of the vertices.
In addition to that, neither of the two are computation-
ally simple.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
410

Several matching algorithms are available in liter-
ature. In depth discussions on such algorithms can be
found in (Burkard et al., 2009). It is necessary to de-
fine a clear objective in order to find a suitable match-
ing - for example, an algorithm designed to find on-
line a maximum cardinality matching with minimum
cost is proposed in (Azad et al., 2015). Our objective
is to find matchings such that conditions of theorem
1 are satisfied. All the graphs that we consider for
preprocessing phase are unlabelled and undirected bi-
partite graphs. Thus, a set of relatively simple algo-
rithms proposed in this section are sufficient to meet
our objectives.
In this section, we propose simple approaches
to reduce a bipartite graph, identify a maximal or-
dered matching and decompose the whole network
into NCA compatible subnetworks. If a system at
steady state can be clearly represented as a regulatory
network as described in (1), the algorithms presented
in this section will not only avoid unnecessary compu-
tational overhead, but also provide a decomposition of
the network without ignoring any of the subnetworks.
A method to remove duplicate and zero rows and
columns is presentedbelow. This algorithm identi-
Algorithm 1: Conjugate reduction.
input: B ∈ R
M×L
STEP 1:
Set B
r
= B(¬B)
T
+ (¬B)B
T
and M = number of
rows in B
STEP 2:
for i = 1 to M do
for j = i + 1 to M do
if B
r
(i, j) == 0 then
remove row j from B
end if
end for
end for
STEP 3:
remove any zero rows from B
Repeat all steps with B = B
T
output: B
T
fies duplicates by looking for zero entries in the inner
product over binary field (Gudder and Latr
´
emoli
´
ere,
2009) of B(G) and its conjugate ¬B(G).
Reduced submatrix B(
¯
G) can be obtained by ap-
plying Algorithm 1 on B(G). In order to test a net-
work against the conditions in theorem 1, a maxi-
mal ordered matching should be found in B(
¯
G). In
order to do that, the rows and columns of B(
¯
G) are
rearranged in increasing order of number of ones in
them. Several matching algorithms available in liter-
ature can be used to find a maximal matching. How-
ever, a simple linear-search-and-eliminate based ap-
proach is sufficient as there is no need to minimise
any associated cost. It can be shown that such an al-
gorithm runs in O(L) time for B(
¯
G) with |
¯
X| = L. The
algorithm has not been described here for brevity.
We can now establish a simple approach to test
NCA-compatibility of a given network as described
in Algorithm 2.
Algorithm 2: NCA compatibility test.
input: B(G) ∈ R
M×L
if Σ
i
B
i j
(G) > M − L + 1 for any u
j
∈ X then
NCA-incompatible
else
Obtain B(
¯
G) using algorithm 1
if for any u
j
∈
¯
X, |
¯
X
∗
(H
u
j
(G))| < L − 1 then
NCA-incompatible
else
NCA-compatible
end if
end if
NCA compatible subnetworks can be identified if
a network is found to be incompatible after applying
Algorithm 2. This can be done by grouping together
vertices u
p
, u
q
∈ X such that u
p
∪
¯
X
∗
(H
u
p
(G)) is iden-
tical to u
q
∪
¯
X
∗
(H
u
q
(G)) as outlined below. All ver-
Algorithm 3: Graph preprocessing for NCA.
input: B(G) ∈ R
M×L
STEP 1: for every u
j
∈ X set
X
∗
j
=
¯
X
∗
(H
u
j
(G)) ∪ u
j
and n
j
= |X
∗
j
|
STEP 2: identify sets C
n
such that
u
p
, u
q
∈ C
n
⇒ X
∗
p
≡ X
∗
q
, ∀u
p
, u
q
∈ X
outputs: set
G
n
= ∪
u
p
∈C
n
(u
p
∪Y ), E
:,C
n
,W
:,C
n
)
tices in a set C
n
form maximal ordered matching of
size n with other vertices in the same set. In Algo-
rithm 3, E
:,C
n
and W
:,C
n
respectively represent subma-
trices of E and W with all rows and columns corre-
sponding to the vertices in set C
n
.
Algorithm 3 is not only capable of identifying
NCA compatible subnetworks, but also of implicitly
testing a network for NCA compatibility. If a network
is NCA compatible, Algorithm 3 returns one subnet-
work G
L−1
which is the original network G. Thus,
Algorithm 3 alone can be used to preprocess a graph
to identify NCA compatible subnetworks. The sub-
networks can then be inferred individually and recom-
bined to infer the whole network. Such a divide and
conquer approach is beyond the scope of this paper.
Preprocessing Graphs for Network Inference Applications
411

Part of the results of applying the algorithms in this
section to the regulatory network in (4) is presented
in the next section.
4 RESULTS
In this section, we apply the algorithms presented in
section 3.2 to the example network in (4). We demon-
strate each step involved in obtaining ordered match-
ings
¯
X
∗
(H
u
1
(G)) and
¯
X
∗
(H
u
2
(G)). Similar steps are
to be applied for vertices u
3
, u
4
and u
5
(not shown
here). The objective of the algorithms in (Boscolo
et al., 2005) and (Fritzilas et al., 2013) is to identify
largest possible NCA subnetwork while ignoring re-
mainder of the network whereas our goal is to divide
a given network into several NCA compatible subnet-
works. Thus, a comparison between results of apply-
ing those algorithms with the ones presented in this
section is unwarranted.
The first step in identifying NCA compatible sub-
networks is identifying maximal ordered matchings
for every vertex u
j
∈ X. Consider u
1
and u
2
. The
induced submatrix corresponding to u
1
B(H
u
1
(G)) is
given in (5) and that corresponding to u
2
B(H
u
2
(G))
is given below.
B(H
u
2
(G)) =
u
1
u
3
u
4
u
5
v
2
0 1 1 0
v
3
0 1 1 0
v
5
0 1 1 1
v
7
1 1 0 1
v
9
1 0 0 1
(7)
We reduce B(H
u
1
(G)) and B(H
u
2
(G)), impose the
order D(.) on the reduced versions B(
¯
H
u
.
(G)) and
then look for maximal matchings as demonstrated
next. The steps in reducing matrices are illustrated by
striking out duplicate rows and columns.
Reduced induced submatrices:
B(
¯
H
u
1
(G)) =
H
u
1
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
3
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
v
10
1 1 0 1
B(
¯
H
u
2
(G)) =
H
u
2
u
1
u
3
u
4
u
5
v
2
0 1 1 0
v
3
0 1 1 0
v
5
0 1 1 1
v
7
1 1 0 1
v
9
1 0 0 1
It can be seen that B(D(
¯
H
u
1
(G))) = B(
¯
H
u
1
(G))
as the columns and rows in B(
¯
H
u
1
(G)) are already
in increasing order of degrees of vertices. However,
the rows and columns of B(
¯
H
u
2
(G)) illustrated by
encircled vertices must be reordered as indicated by
the arrows here
Partial ordering:
B(D(
¯
H
u
2
(G))) =
u
1
←
u
4
→
u
3
u
5
v
2
0 1 1 0
↑ v
9
1 0 0 1
↓ v
5
0 1 1 1
↓ v
7
1 0 1 1
A linear search is conducted to look for the first 1 en-
try in every row, the row and column corresponding
to the found entry are eliminated. These steps are re-
peated for all columns until no more 1 entry is found
or all columns are exhausted. A set of vertices that
correspond to all the columns in which a 1 entry is
found defines a maximal matching. Finding first 1 en-
try in the first row of B(D(
¯
H
u
1
(G))) is illustrated by
encircling the entry and eliminating the correspond-
ing row and column by striking them out.
¯
H
u
1
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
v
10
1 1 0 1
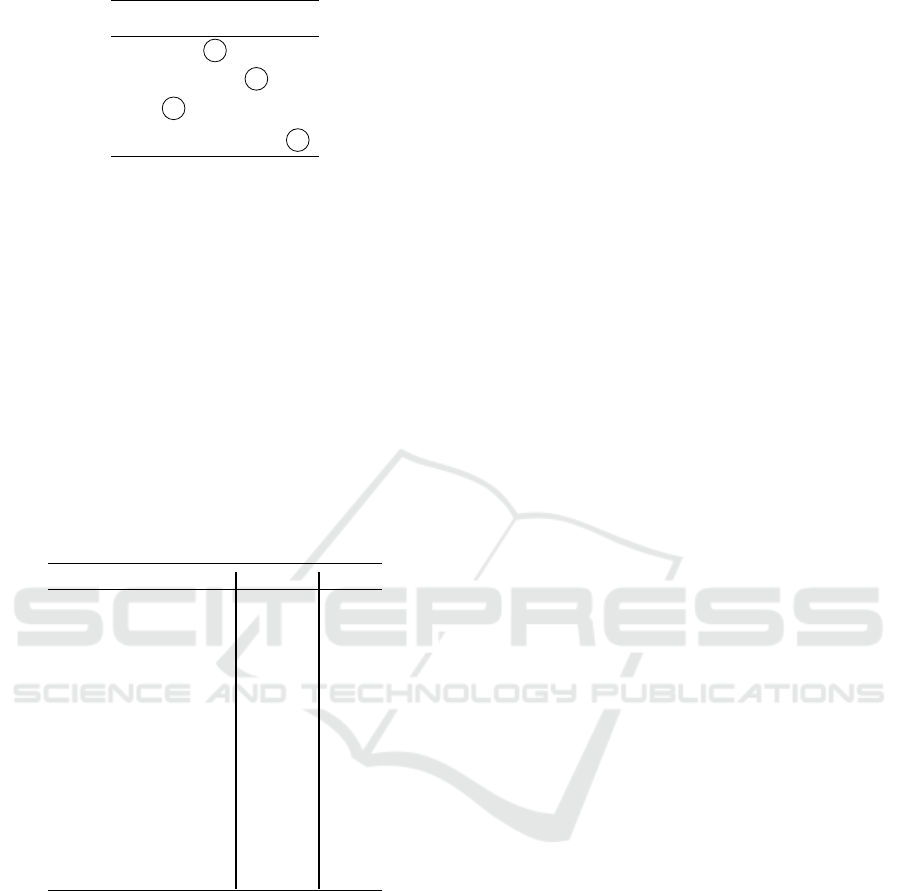
A maximal ordered matching in D(B(
¯
H
u
1
(G))) is
obtained as
(
¯
X
∗
(H
u
1
(G)),
¯
Y
∗
(H
u
1
(G)))
= ({u
3
, u
4
, u
2
, u
5
}, {v
2
, v
5
, v
6
, v
10
})
The encircled entries represent this maximal ordered
matching.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
412

¯
H
u
1
u
2
u
3
u
4
u
5
v
2
0 1 1 0
v
5
0 1 1 1
v
6
1 0 1 1
v
10
1 1 0 1
Executing all the illustrated steps on all induced sub-
matrices results in the following sets as indicated in
Step 1 of Algorithm 3:
X
∗
1
= {u
3
, u
4
, u
2
, u
5
} ∪ {u
1
} n
1
= 5
X
∗
2
= {u
3
, u
4
, u
1
, u
5
} ∪ {u
2
} n
2
= 5
X
∗
3
= {u
1
, u
2
, u
5
} ∪ {u
3
} n
3
= 4
X
∗
4
= {u
1
, u
3
, u
2
, u
5
} ∪ {u
4
} n
4
= 5
X
∗
5
= {u
1
, u
3
} ∪ {u
5
} n
5
= 3
The NCA compatible sets obtained as described
in Step 2 of Algorithm 3 are C
5
= {u
1
, u
2
, u
4
},
C
4
= {u
3
}, and C
3
= {u
5
}. Thus, the given NCA in-
compatible network can be decomposed into a collec-
tion of 3 NCA compatible subnetworks as illustrated
in Fig. 2
u
1
u
2
u
4
. u
3
. u
5
v
1
1 1 1 . 0 . 0
v
2
0 0 1 . 1 . 0
v
3
0 0 1 . 1 . 0
v
4
1 1 1 . 0 . 0
v
5
0 0 1 . 1 . 1
v
6
0 1 1 . 0 . 1
v
7
1 0 0 . 1 . 1
v
8
1 1 0 . 1 . 1
v
9
1 0 0 . 0 . 1
v
10
0 1 0 . 1 . 1
Figure 2: Decomposition of original network into subnet-
works.
5 CONCLUSIONS
In this paper, the need to consider graph theoreti-
cal interpretations of NCA was emphasized. It was
demonstrated that merely finding a maximal match-
ing in bipartite graphs may lead to wrong classifica-
tion of NCA incompatible networks as NCA compat-
ible. In order to overcome this issue, a new property
called ordered matching in a bipartite graph was in-
troduced. The rank of a bipartite graph was proven to
be equal to the size of an ordered matching in its re-
duced form. This result was used to develop new con-
ditions for NCA compatibility. A simple algorithm
to reduce a bipartite graph was proposed. An algo-
rithm was proposed to identify NCA compatible sub-
networks in a given network. The results presented
in this paper solve two important preprocessing prob-
lems - simplifying NCA compatibility conditions and
decomposing a network into identifiable parts.
REFERENCES
Azad, A., Buluc¸, A., and Pothen, A. (2015). A parallel tree
grafting algorithm for maximum cardinality match-
ing in bipartite graphs. In Proceedings of the 2015
IEEE International Parallel and Distributed Process-
ing Symposium, pages 1075–1084. IEEE Computer
Society.
Boscolo, R., Sabatti, C., Liao, J. C., and Roychowd-
hury, V. P. (2005). A generalized framework for
network component analysis. IEEE/ACM Transac-
tions on Computational Biology and Bioinformatics,
2(4):289–301.
Brugere, I., Gallagher, B., and Berger-Wolf, T. Y. (2016).
Network structure inference, A survey: Motivations,
methods, and applications. CoRR, abs/1610.00782.
Burkard, R., Dell’Amico, M., and Martello, S. (2009). As-
signment Problems, Revised Reprint. Other titles in
applied mathematics. Society for Industrial and Ap-
plied Mathematics (SIAM, 3600 Market Street, Floor
6, Philadelphia, PA 19104).
Fritzilas, E., Milani
¨
A, M., me Monnot, J., and Rios-Solis,
Y. A. (2013). Resilience and optimization of identifi-
able bipartite graphs. Discrete Applied Mathematics,
161(4-5):593–603.
Gudder, S. and Latr
´
emoli
´
ere, F. (2009). Boolean inner-
product spaces and boolean matrices. Linear Algebra
and its Applications, 431:274–296.
Li, H., Su, L., and Sun, H. (2012). On bipartite graphs
which attain minimum rank among bipartite graphs
with given diameter. Electronic Journal of Linear Al-
gebra, 23:1–14.
Liao, J. C., Boscolo, R., Yang, Y., Tran, L. M., Sabatti, C.,
and Roychowdhury, V. P. (2003). Network component
analysis: Reconstruction of regulatory signals in bio-
logical systems. Proceedings of the National Academy
of Sciences, 100(26):15522–15527.
Newman, M. E. J. (2003). The structure and function of
complex networks. SIAM Review, 45(2):167–256.
Preprocessing Graphs for Network Inference Applications
413