Applying Peg-in-Hole Actions with a Service Robot

Stefan-Daniel Suvei

, Leon Bodenhagen

, Thomas Nicky Thulesen

, Milad Jami

and Norbert Kr

uger

University of Southern Denmark, 5230 Odense M, Denmark

Novo Nordisk A/S, Novo Alle, 2880 Bagsvaerd, Denmark

Keywords:

Service Robot, Peg-in-Hole, Simulation.

Abstract:

A general requirement for any service robot is to be ﬂexible and capable of processing uncertainties, thus

making it adaptable for multiple tasks. As a result, learning the appropriate action parameters for a speciﬁc

action is a crucial task. The method presented in this paper is an incremental statistical learning method

that takes into consideration the uncertainties and the contact forces to ﬁnd the optimal parameter sets. The

method is inspired by solutions available in industrial robotics and it uses a dynamic simulator and Kernel

Density Estimation in order to ﬁnd the parameter sets that lead to a successful Peg-in-Hole action. The

solution obtained in the simulation is successfully tested on a real service robot.

1 INTRODUCTION

In industry, robotic solutions are well established.

One reason that facilitates the application of these

solutions is that the environment can be controlled,

such that uncertainties and thereby error sources are

minimized. Current approaches focus on enabling

robots to solve tasks despite of uncertainties. So-

lutions for handling uncertainties in e.g. assembly

processes include online pose estimation of relevant

items (Schwarz et al., 2015), use compliant manipula-

tors (Kashiri et al., 2014) or utilize re-planning (Main-

price et al., 2015).

Within the domain of service robotics, the prob-

lem of correctly handling uncertainties is crucial,

in particular when considering the fact that service

robots have to work in unstructured and dynamic en-

vironments where they need to assist or work along-

side humans. The challenge is to apply some of the

well-tested industrial solutions in the service robotics

ﬁeld. This is due to the fact that safety, the ease of use

and the ﬂexibility are important aspects that need to

be considered when talking about a service robot.

A good example of a process that can be trans-

ferred into service robotics from the industry and in

which uncertainties can create big challenges is the

classical tight ﬁtting Peg-in-Hole (PiH) process (Di-

etrich et al., 2010),(Lin et al., 2014). Viewed mostly

as an industrial, assembly type of task, many tasks

in the ﬁeld of service robotics such as collecting bot-

Figure 1: Care-O-Bot architecture. Left: Real platform.

Right: Simulated platform.

tles, disposing of trash or inserting cutlery into the

dishwasher compartiments can be consider to be PiH

actions.

Manually tuning the parameters that normally de-

ﬁne the PiH action is challenging, since there is no

guarantee that the selected solution will be successful

for each trial. Sensor-controlled actions can be used

to handle this type of situations, however, this gener-

ally leads to an increase in the overall process-time

and cost.

Another approach is to use action parameter opti-

mization techniques to reduce the number of samples

in the search space, like in (Sørensen et al., 2016),

where Kernel Density Estimation is used during the

learning phase to eliminate the sub-optimal areas of

the search space. This is done by considering the re-

sult of the experiments in the surrounding neighbor-

hood.

Our proposed method makes use of a dynamic

simulator and Kernel Density Estimation to do a post-

224

Suvei, S-D., Bodenhagen, L., Thulesen, T., Jami, M. and Krüger, N.

Applying Peg-in-Hole Actions with a Service Robot.

DOI: 10.5220/0006401702240231

In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 224-231

ISBN: 978-989-758-265-3

learning search through the parameter space and ﬁnd

those sets that lead to a successful Peg-in-Hole ac-

tion. In order to eliminate unpromising parameter

sets, process uncertainties and the appearance of con-

tact forces are taken into consideration. The result is

tested and veriﬁed on both a simulated and a real plat-

form.

2 RELATED WORK

With the rise of interest for service robotics, classical

robotic topics such as safe planning, visual servoing

and manipulation have recently regained focus, with

the goal of adapting some of the well-known indus-

trial methods to the more challenging home environ-

ment. Action-parameter learning, in particular, has

been of great concern, speciﬁcally because it is ap-

plicable to a large array of tasks, thus increasing the

ﬂexibility of the system. The learning process can be

done using the execution feedback data received from

the sensors and adapting the action process accord-

ing to the found environment constraints (Gams et al.,

2014), (Berio et al., 2016), by human demonstration

(Gams and Petri

c, 2016) or by using dynamic simu-

lation, thus facilitating an extended exploration of the

parameter space (Jørgensen and Petersen, 2008), (De-

try et al., 2011), (Sørensen et al., 2016).

As opposed to industrial robots, service robots

have to be ﬂexible in order to function in unstructured

and dynamic environments. As such, a rigid calibra-

tion of the tested setup is not a viable solution. For

systems that are required to manipulate the environ-

ment and are equipped with a camera, a way of over-

coming this issue is through position based visual ser-

voing (PBVS) (Cherubini et al., 2008). This method

uses the difference between the pose of the desired

target object and that of the manipulator to determine

the control error. For the target object, the pose es-

timation can be determined by using a 3D model of

the object and the homography, like in (Kyrki et al.,

2004). (Gratal et al., 2011) proposes an alternative

solution, by using a real-time model-based tracking

method to estimate the pose of the gripper.

Compared to other approaches, we address the

PiH task of inserting bottles into a crate using a ser-

vice robot, for which no special calibration, speciﬁc

environment manipulation (i.e. light adjustment, po-

sition control, etc.) or additional sensors (such as

force-torque sensors or compliant grippers) are used.

PBVS and dynamic simulation are utilized in order to

achieve the task with minimum contact force. The pa-

rameter set that describes the tested PiH action, along-

side the actual action path are determined in simula-

(a) Original RGB data (b) Modiﬁed RGB data

Figure 2: Visualization of the Aruco traker output - the two

markers are detected and the transformations between them

and the camera are computed.

tion. We demonstrate that the solution found in sim-

ulation can be directly used on a real platform, where

the PiH action is not only successful, but also gener-

ates low contact forces.

3 EXPERIMENTAL SETUP AND

METHODOLOGY

The Care-O-Bot (Graf et al., 2009) is a robotics plat-

form that was developed to be a mobile robot assis-

tant that actively supports humans in domestic envi-

ronments. A big advantage of the Care-O-Bot plat-

form (see Figure 1) is that it is equipped with multi-

ple sensors and has a modular hardware setup, which

makes it ﬁt for a large array of tasks, such as: pick-

and-place, object detection, human tracking, etc. The

main components of the Care-O-Bot are: the omnidi-

rectional mobile base, an actuated torso with 3 DoF,

the UR5 robotic arm, the UR connector (to which the

arm is attached), the tray, the head (which contains a

Carmine 3D Sensor and a high resolution stereo cam-

era) and three laser scanners. Using this platform, we

investigate the possibility of solving a PiH task that

consists of inserting bottles into a crate and learn the

best parameter sets that deﬁne this action.

3.1 Tracking and Visual Servoing

The PBVS method determines the error between the

pose estimation of the end effector and that of the de-

sired object (in this case, the bottle crate) and uses it

as a control error, in order to move the arm towards

the desired position. As follows, the control loop is

an endpoint closed loop, where both the end effector

and the crate are in the ﬁeld of view.

To ease the process of pose estimation and track-

ing, two AR (Augumented Reality) markers, de-

noted M1 and M2 in the following, are attached to

the gripper and the bottle crate. With the help of

the ”aruco ros” ROS tracker (Garrido-Jurado et al.,

Applying Peg-in-Hole Actions with a Service Robot

225

2014), the markers are detected and the transforma-

tion between them is determined. The obvious down-

side of this approach is that the markers must con-

stantly be detectable by the camera, which makes it

sensitive to the illumination level in the environment,

speciﬁcally since the robot was placed in a laboratory

with a lot of natural light. To overcome this issue,

we apply the Contrast Limited Adaptive Histogram

Equalization algorithm (Zuiderveld, 1994) on the in-

put RGB image data of ”aruco ros” tracker, thus im-

proving the overall contrast of the image, as can be

seen in Figure 2, and aiding the corner detection.

The two transformations are used in a classic lin-

ear interpolation algorithm that generates the incre-

mental displacements that will move the robotic arm

with the end effector towards the crate and decrease

the pose estimation error between the two AR mark-

ers.

The algorithm is repeated until the Euclidean dis-

tance between the two markers is smaller than a pre-

deﬁned threshold which will ensure that the gripper is

placed above the crate. To avoid overshooting this po-

sition, the incremental displacements decrease as the

Euclidean distance between the markers decreases.

Once the desired position is reached, the algorithm

updates the position of the crate based on a ﬁnal read-

ing of the M2 marker and then starts the Peg-in-Hole

action sequence.

Figure 3: The PiH action parameters.

3.2 Action Parametrization

The Peg-in-Hole action in our context is deﬁned by

two parameters (Figure 3) and is performed in four

steps (Figure 4). The parameters span the search

space and are deﬁned as follows:

x: The perpendicular distance between the hole and

the middle of the bottle bottom.

φ: The angle of the bottle in the initial position

relative to the hole vertical axis.

If we assume an ideal PiH action (i.e. no uncer-

tainties), the four steps that compose the action as a

whole are described as follows:

Initial Position: In the ﬁrst step the robot moves the

(a) (b) (c) (d)

Figure 4: The PiH action movements: (a) First linear mo-

tion. (b) Circular motion. (c) Second linear motion.

(d) Final position.

bottle from the position where it was left by the vi-

sual servoing algorithm towards the hole. At the end

of this motion, the bottle is at a perpendicular distance

of 5cm from the hole and tilted with an angle φ.

First Linear Motion: In the second step, the bottle

is moved linearly towards the hole (Figure 4(a)). The

movement stops when the end of the bottle is at a per-

pendicular distance X above from the hole. At this

point, the bottle is touching the edge of the hole.

Circular Motion: After the ﬁrst linear movement and

the contact with the hole’s edge, the bottle is rotated

until φ = 0, as depicted in Figure 4(b).

Second linear Motion: In the ﬁnal step, the bottle is

moved linearly down the hole and the bottle’s axis is

kept aligned with the hole (Figure 4(c)). In our pro-

posed solution, when the bottom of the bottle is inside

the hole after the second linear motion, the robot just

drops the bottle into the hole.

The PiH action is evaluated after the second linear

motion. For a successful action, the bottle has to be

partially inside the speciﬁed crate hole, such that a

simple release of the gripper would drop it in the hole

(see Figure 4(d)). This is conﬁrmed by checking the

pose of the bottle with respect to the hole. In the case

in which the bottle gets stuck by hitting the edge of

the hole, the action is labeled as a failure.

Using the described steps, the relative path be-

tween the bottle and the hole is computed for each

parameter set. This path is then executed in both the

simulated environment and on the real world setup.

The evaluation and labeling of the action (i.e. suc-

cess of failure) is done automatically in simulation

and manually for the real world platform.

3.3 Action Simulation

The action simulation is performed using different

values for the action parameters. The ranges of the

parameters are set beforehand and deﬁne the search

space. As such, the action is simulated within the pa-

rameter ranges of x ∈ [−3; 3]cm and φ ∈ [−45; 45]

◦

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

226

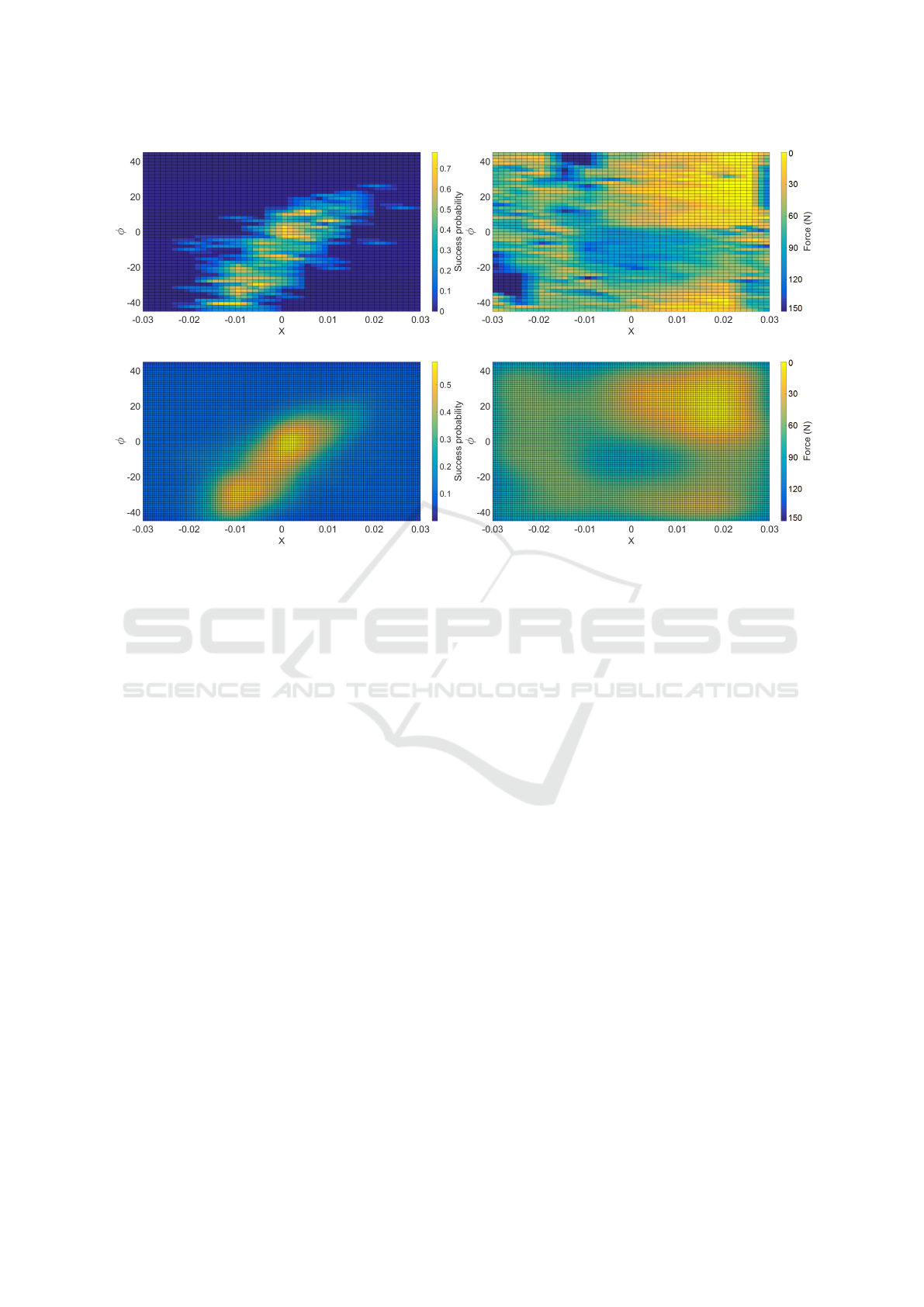
(a) Success probability map (b) Force proﬁle map

Figure 5: The success probability map and the force proﬁle map before and after KDE.

with step sizes of 5 mm and 2

◦

respectively.

To allow the learning sequence to deal with uncer-

tainties, positional and rotational noise is added to the

bottle frame and the hole frame in the action simula-

tion. This is done by randomly choosing a direction

from the XYZ-axes and multiplying it with a random

value from a normal distribution to the chosen direc-

tion. For the crate, the normal distribution has a mean

value of zero and a standard deviation of 3.5mm for

the position and 3

◦

for the rotation. For the bottle, the

standard deviation is 1mm and 0.5

◦

for the positional

and the rotational noise respectively. The ranges of

the uncertainties are based on the geometric models of

the bottle and crate used in the simulator and on pre-

liminary simulation tests. Due to the ﬁt of the bottle

and the hole, any positional error larger than 2.5 mm

on one of the XY-axes or a rotational error larger than

0.8

◦

on one of the PY-Euler angles will result in the

bottle getting stuck on the edge of the crate or apply-

ing forces on the crate, as observed in initial simula-

tion tests.

3.4 Action Learning

To learn the parameter values that will lead to a suc-

cessful task, the action is simulated 5 times for each

pair of parameters, where the perturbation for each

pair of samples is randomly selected as explained in

the previous paragraph. This leads to a total number

of 2925 individual tests of the PiH action. The results

are visualized using a success probability map as in

Figure 5(a).

To further narrow down the solution parameter

space, we also investigate the force proﬁle of the ac-

tions. For each parameter set, the average of the high-

est contact forces that characterized each repetition is

computed. A threshold is used to limit the maximum

allowed force to 150 N. The forces distribution can be

seen in Figure 5(b). We note that the measured con-

tact force is between the bottle and the hole for which

the insertion is tested. For this reason, in the upper-

right corner of the map, where the bottle is colliding

with the crate (but not with the actual hole edges) it

seems that there are little to no contact forces.

The next step is to multiply the Kernel Density

Estimations of the success probability map and of the

forces distribution, in order to choose a set of parame-

ters for which the action would be successful, while at

the same time the contact force between the bottle and

crate would be minimal. The result (seen in Figure 7)

is further discussed in section 4.1.

4 RESULTS

In this section, we show how by applying KDE on

the results of the Action Learning sequence, we can

Applying Peg-in-Hole Actions with a Service Robot

227

(a) Real world experiment

(b) Real world experiment with added noise

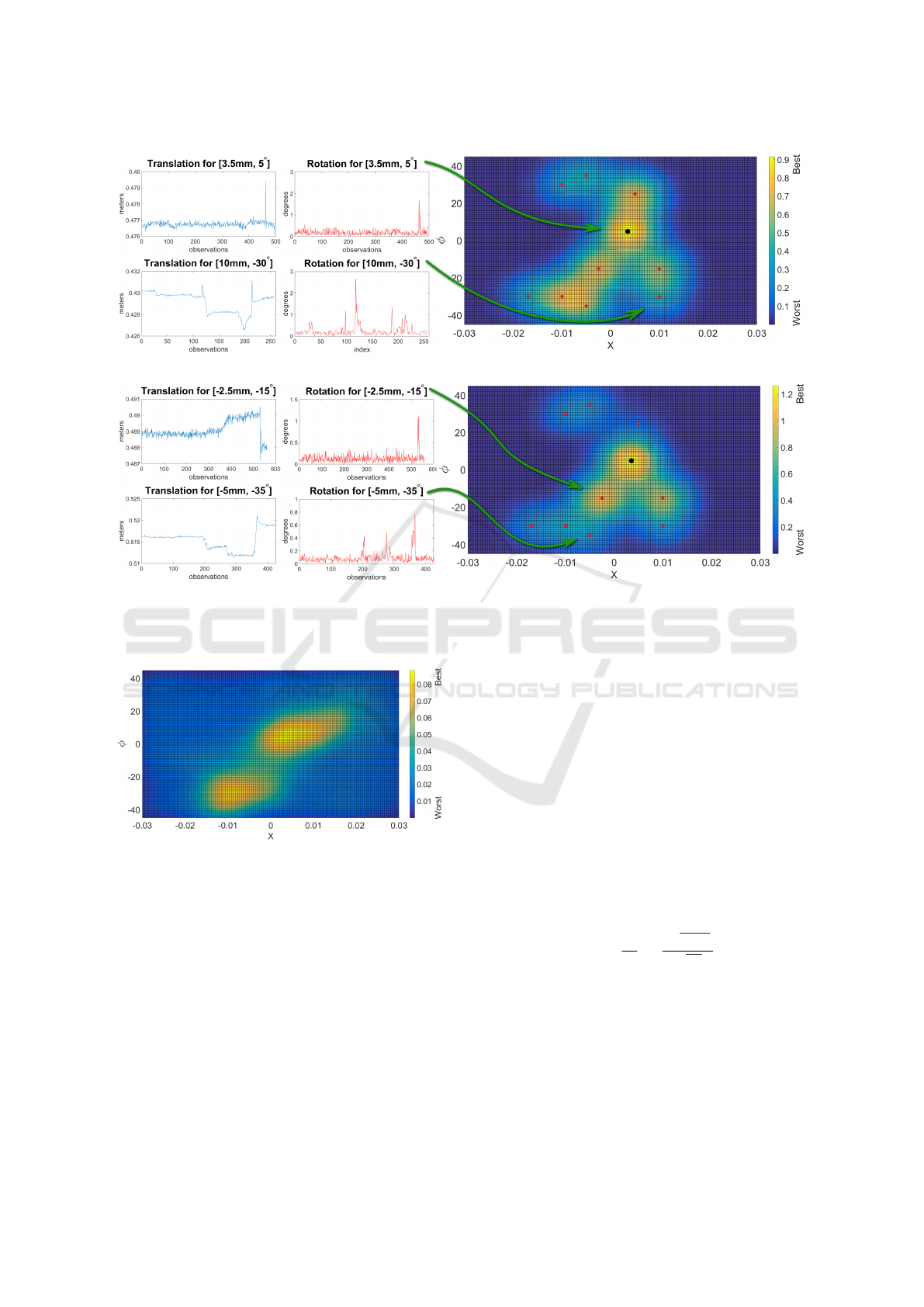
Figure 6: The KDE representation of the success and force proﬁle of the 10 tested parameter sets. The parameter sets are

marked with the red dots. The best set is marked with the black dot.

Figure 7: The multiplied KDE representation of the success

and force proﬁle.

reduce the parameter space and ﬁnd good parameter

sets that would yield a successful PiH action. We fur-

ther test a subset of the parameters on the real plat-

form and compare the result with the simulated ones.

4.1 Optimal Actions in Simulation

As mentioned in section 3.4, Kernel Density Esti-

mation is used for both the success probability (Fig-

ure 5(a)) and the force proﬁle map (Figure 5(b)) to

get a good overview of the structure of the data and a

good approximation of the best parameter sets.

The Matlab implementation of the KDE via dif-

fusion method (Botev et al., 2010) is used, in which

we use a multivariate Gaussian kernel and we de-

ﬁne each independent data sample as a vector of type

s = [x; φ; d], where x and φ are the two PiH action

parameters and d is either the success probability or

the force value for that speciﬁc parameter set. The

value of d is the one that decides the smoothing con-

tribution of each speciﬁc [x, φ] parameter set. In this

speciﬁc Matlab implementation, the kernel density is

estimated based on the smoothing properties of lin-

ear diffusion processes. If we consider (s

, s

, . . . , s

)

independent samples from an unknown continuous

probability function f , then the kernel density esti-

mator is deﬁned as:

f (s) =

∑

i=1

−

(s−s

)

√

2π

(1)

where h is the bandwidth and s is the point for which

the density is estimated.

As shown in (Botev et al., 2010), the construction

of a kernel density estimator can be (from a mathe-

matical perspective) compared to the process of com-

puting the amount of heat generated when heat ker-

nels are placed at each s

sample point. Knowing

that a heat kernel is the fundamental solution of the

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

228

Fourier heat equation,

f (s) can be computed. The ad-

vantage of this approach is that it also introduces a

plug-in bandwidth selection method which uses the

asymptotic properties of the resulting

f (s) estima-

tor to compute the asymptotically optimal plug-in

bandwidth h, without requiring any numerical opti-

mization, thus speeding up the process of ﬁnding the

promising parameter sets.

Because we are interested in ﬁnding the parameter

sets that yield both a success and a low contact force

between the bottle and the crate, a summation of the

two KDE’s (see Figure 7) is used for a better repre-

sentation of the data and the search space. Finding

the best parameter set means ﬁnding the maximum

of the density surface. This can be done by apply-

ing optimization algorithms, such as gradient ascent.

However, due to the nature of the data and because

the density is represented by a matrix where its size

is deﬁned by the x and φ parameters and the individ-

ual density values depend on d, the best parameter set

can be found by computing the maximum value of the

matrix. The best parameter set is found to be [3.5mm,

◦

]. Visualizing the KDE data representation, we can

observe that the density curve also has a second peak,

around [−10 mm, −30

◦

]. These two peaks correspond

to the main successful areas of the search space, rep-

resented in Figure 5(a) and Figure 5(c) and to the

lower force areas, as shown in Figure 5(b) and Fig-

ure 5(d). The success of the PiH action drops in-

between these two peaks due to the fact that the bottle

gets stuck on the edge of the hole and also applies

force on the crate.

4.2 Veriﬁcation on Real System

Compared to the real world case, the simulator is

more conservative because the slippage between the

bottle and the plastic gripper or the compliance of the

bottle, which can endure a big amount of deformation

before actually breaking, are not considered in sim-

ulation. Both of these phenomenons can potentially

lead to accidental successful trials, thus leading to a

wrong prediction of the outcome.

Based on the results obtained in the previous sub-

section, a set of real world experiments were per-

formed. The experiment starts with the visual servo-

ing part, as described in 3.1, where the robot arm is

moving the bottle towards the crate. Once the bottle

is at the desired position, the PiH action is performed,

using speciﬁed parameters as input (see Figure 8).

Aside from executing the selected ”best” parameter

set, we also investigate 9 other sets, chosen manually

from both promising and non-promising areas found

by the simulation phase in an attempt to show that the

real world results align with the ones found by simula-

tion. Each of the sets is tested 10 times and evaluated

manually. This means that the d value for each of the

individual samples s

∈(s

, s

, . . . , s

100

) has one of the

following values:

d =











0, if bottle fell from the gripper

1, if failure, with contact force

2, if success, with big contact force

3, if success, with medium contact force

4, if success, with small contact force

5, if success, with no contact force

Following the method described in the previous

subsection, we also apply KDE on the outcome of the

real world experiments (see Figure 6(a)). Analyzing

the KDE result, we can observe that the pattern of the

density curve is similar to the one suggested by the

simulation results in Figure 7. Additionally, the best

parameter set - found to be [3.5 mm, 5

◦

] by the simu-

lator - had a success rate of 100% on the real platform.

The parameter set [−10 mm, −30

◦

] corresponding to

the second peak had a success rate of 70%, thus con-

ﬁrming the validity of the data. The [−2.5 mm, −15

◦

]

and [5mm, 25

◦

] parameter sets also gave good results

due to the compliance and curved shape of the bottle,

which makes the insertion possible even if the edge of

the hole is touched.

As mentioned, the robot is not equipped with

a force-torque sensor. On order to verify that the

assumption about the forces is correct, a third AR

marker, was placed on the side of the crate. The

idea is that, when force is applied, the crate is moved

and thus the movement of the marker can be detected.

Moreover, we verify if the scale of the movement is

proportional to the strength of the contact force.

The translational movement of the AR marker is

investigated by tracking how the length of the position

vector (deﬁned for the marker frame) changes over

the course of the PiH action. Similarly, the rotation

is checked by tracking the changes in quaternion an-

gles during the action performance (see Figure 6(a)).

The spikes in the translation and rotation appear at the

moment any kind of contact force is applied. For the

[3.5mm, 5

◦

] parameter set, we can see that there is

only sub-millimeter and sub-degree movement, thus

suggesting that no major force is applied to the crate.

The registered movement is due to the fact that the

marker can be correctly tracked only within millime-

ter precision, so anything bellow that will be affected

by noise. The spikes that appear around the 460 mark

are generated by the bottle falling into the crate hole

when it is released from the gripper. On the other

hand, for the [10mm, −30

◦

] parameter set we can ob-

serve that when the bottle hits the edge of the crate,

Applying Peg-in-Hole Actions with a Service Robot

229

the tracker registers a movement of more than 3 mm in

translation and 2.5

◦

degrees in rotation. This suggests

that a bigger contact force is applied, which aligns

with the force estimation results in Figure 5(d) and

Figure 7.

4.3 Addition of Positional Noise

To further test the validity of the simulation results,

we opt to make a series of real world experiments

where we add extra positional uncertainty by not al-

lowing the system to update the position of the crate

before performing the PiH sequence. This means that

the robot blindly performs the PiH action, assuming

that the crate is placed in the correct position.

We investigate the same 10 parameter sets that

were tested in 4.2, again with 10 trials for each (a to-

tal of 100 experiments). The results are shown in Fig-

ure 6(b). It can be observed that, while some peeks

decrease compared to the case shown in Figure 6(a)

due to the appearance of higher forces, the data is

following a similar pattern to the one shown in the

previous subsection and as estimated by the simula-

tor. The best parameter set had again a success rate

of 100%. However, the success rate of the [−10mm,

−30

◦

] peak dropped to only 10%, thus proving that

not being able to update the position of the crate has

a huge impact on the success probability, even if the

positional difference is less than a few millimeters.

The movement of the side marker is also tracked

and the results are shown in Figure 6(b). For the good

parameter set [−2.5 mm, −15

◦

], little movement is

registered by the tracker, thus suggesting that no ma-

jor contact forces are applied on the crate during the

PiH action execution. The peak at the 520 mark is due

to the bottle dropping into the crate. For the [−5 mm,

−35

◦

] parameter set, a large movement of 1cm in

translation is registered, which suggests that the crate

was pushed hard with the bottle, once again conﬁrm-

ing the force estimation results in Figure 5(d) and Fig-

ure 7. These results show that the robot will fail even

when using some of the good parameter sets, if the

positional error is larger than a few centimeters and if

the system is not allowed to update and compensate

for it, thus underlining the importance of considering

the uncertainties when performing such a task.

5 FUTURE WORK

The presented method has shown that industrial so-

lutions can be used and applied successfully with a

service robot, in a home-like environment. Future re-

search will have to consider other industrial tasks that

could be adapted and used in similar service robotics

scenarios. In addition, because some of these tasks

are collaborative in nature, an investigation of the so-

cial implications of the human-robot interaction could

be carried out.

6 CONCLUSIONS

In this paper an industrial-robotics inspired approach

to solve the Peg-in-Hole task of inserting bottles into

a crate is proposed. The work is performed using the

Care-O-Bot service robot, without making use of ad-

ditional, specialized sensors, calibration or compliant

grippers. If we consider the parameterization of the

PiH action, as described in 3.2, than the goal of the

proposed method is to ﬁnd the best parameter sets -

i.e. parameters for which the PiH action yields both

a successful insertion of the bottle and a low or non-

existing contact force. The method starts by explor-

ing the parameter search space. This is done by it-

eratively simulating the PiH action together with us-

ing a learning algorithm that takes into consideration

the process uncertainties and the contact forces. Us-

ing Kernel Density Estimation, the parameter space is

then reduced to a subset of promising parameters.

Making use of this knowledge, real world experi-

ments are performed with the Care-O-Bot platform.

10 different parameter sets are selected from both

promising and non-promising areas of the parame-

ter space, as proposed by the learning algorithm, for

which the PiH action is repeated for 10 times. We

perform 200 experiments in two series - ﬁrst by just

running the action path and secondly by adding an

additional position error, by not allowing the robot

to update the position of the crate before perform-

ing the PiH action. Both experiment series showed

that the real world results align with the ones found

by the learning algorithm. More speciﬁcally, the best

parameter set proposed by the learning component

proved to have a success rate of 100%. This proves

that adapting and applying solutions developed for the

industrial robotics ﬁeld is a viable option for service

robotics, as long as the task uncertainties arising from

the unstructured environment in which a service robot

normally has to operate are taken into account.

ACKNOWLEDGEMENTS

This work was supported by Patient@home, funded

by the Danish Innovation Fond, and Health-CAT,

funded by European Regional Development Fund.

SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

230

Figure 8: The full action sequence: visual servoing (1-4) and Peg-in-Hole (5-6).

REFERENCES

Berio, D., Calinon, S., and Leymarie, F. F. (2016). Learn-

ing dynamic grafﬁti strokes with a compliant robot.

In IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems, pages 3981–3986.

Botev, Z. I., Grotowski, J. F., Kroese, D. P., et al. (2010).

Kernel density estimation via diffusion. The Annals of

Statistics, 38(5):2916–2957.

Cherubini, A., Chaumette, F., and Oriolo, G. (2008). A

position-based visual servoing scheme for following

paths with nonholonomic mobile robots. In IEEE/RSJ

Int. Conf. on Intelligent Robots and Systems, pages

1648–1654.

Detry, R., Kraft, D., Kroemer, O., Bodenhagen, L., Peters,

J., Kr

uger, N., and Piater, J. (2011). Learning grasp

affordance densities. Paladyn Journal of Behavioral

Robotics, 2(1).

Dietrich, F., Buchholz, D., Wobbe, F., Sowinski, F., Raatz,

A., Schumacher, W., and Wahl, F. M. (2010). On con-

tact models for assembly tasks: Experimental investi-

gation beyond the peg-in-hole problem on the exam-

ple of force-torque maps. In IEEE/RSJ Int. Conf. on

Intelligent Robots and Systems, pages 2313–2318.

Gams, A. and Petri

c, T. (2016). On-line modiﬁcations of

robotic trajectories: Learning, coaching and force vs.

position feedback. In Int. Conf. on Robotics in Alpe-

Adria Danube Region, pages 20–28. Springer.

Gams, A., Petric, T., Nemec, B., and Ude, A. (2014). Learn-

ing and adaptation of periodic motion primitives based

on force feedback and human coaching interaction.

In IEEE-RAS Int. Conf. on Humanoid Robots, pages

166–171.

Garrido-Jurado, S., noz Salinas, R. M., Madrid-Cuevas, F.,

and Mar

ın-Jim

enez, M. (2014). Automatic generation

and detection of highly reliable ﬁducial markers under

occlusion. Pattern Recognition, 47(6):2280 – 2292.

Graf, B., Reiser, U., H

agele, M., Mauz, K., and Klein, P.

(2009). Robotic home assistant care-o-bot 3 - product

vision and innovation platform. In IEEE Workshop on

Advanced Robotics and its Social Impacts.

Gratal, X., Romero, J., and Kragic, D. (2011). Virtual visual

servoing for real-time robot pose estimation. IFAC

Proceedings Volumes, 44(1):9017–9022.

Jørgensen, J. A. and Petersen, H. G. (2008). Usage of sim-

ulations to plan stable grasping of unknown objects

with a 3-ﬁngered Schunk hand. In IEEE Int. Conf.

on Intelligent Robots and Systems, Workshop - Robot

simulators: available software, scientiﬁc applications

and future trends.

Kashiri, N., Laffranchi, M., Tsagarakis, N. G., Margan,

A., and Caldwell, D. G. (2014). Physical interac-

tion detection and control of compliant manipulators

equipped with friction clutches. In IEEE Int. Conf. on

Robotics and Automation, pages 1066–1071.

Kyrki, V., Kragic, D., and Christensen, H. I. (2004).

New shortest-path approaches to visual servoing. In

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems, pages 349–354.

Lin, L. L., Yang, Y., Song, Y. T., Nemec, B., Ude, A., Rytz,

J. A., Buch, A. G., Kr

uger, N., and Savarimuthu, T. R.

(2014). Peg-in-hole assembly under uncertain pose

estimation. In Proc. of the 11th World Congress on In-

telligent Control and Automation, pages 2842–2847.

Mainprice, J., Hayne, R., and Berenson, D. (2015). Predict-

ing human reaching motion in collaborative tasks us-

ing inverse optimal control and iterative re-planning.

In IEEE Int. Conf. on Robotics and Automation, pages

885–892.

Schwarz, M., Schulz, H., and Behnke, S. (2015). RGB-

D object recognition and pose estimation based on

pre-trained convolutional neural network features. In

IEEE Int. Conf. on Robotics and Automation, pages

1329–1335.

Sørensen, L. C., Buch, J. P., Petersen, H. G., and Kraft, D.

(2016). Online action learning using kernel density

estimation for quick discovery of good parameters for

peg-in-hole insertion. In 13th Int. Conf. on Informatics

in Control, Automation and Robotics.

Zuiderveld, K. (1994). Contrast limited adaptive histogram

equalization. In Graphics gems IV, pages 474–485.

Academic Press Professional, Inc.

Applying Peg-in-Hole Actions with a Service Robot

231