
Improved Planning and Filtering Algorithm for Task-priority
Redundancy Resolution in Mobile Manipulation
Nagamanikandan Govindan and Asokan Thondiyath
Department of Engineering Design, Indian Institute of Technology Madras, Chennai, India
Keywords: Mobile Manipulator, Redundancy Resolution, Path Planning, Behavioural Control, Inverse Kinematics,
CLIK.
Abstract: Discrete time implementation of task-priority redundancy resolution using closed loop inverse kinematics
with fixed sampling time may lead to discretization chatter. The chattering effect is due to switching between
different closed loop behaviours whenever the corresponding external event has occurred. This effect causes
high frequency oscillation with finite frequency and amplitude in both joint space motion and operational
space motion which is highly undesired. In this paper, we propose a planning and filtering algorithm to
improve the robustness of task-priority redundancy resolution without having the effect of chattering, while
combining multiple closed loop behaviours. We also show how the null space projection in task- priority
control affects the operational space motion while switching between the behaviours. To demonstrate the
effectiveness of the proposed algorithm, three different case studies are presented for a planar mobile
manipulator with holonomic constraint. The results confirm that the proposed algorithm eliminates the chatter
and moves the end effector on a smooth trajectory.
1 INTRODUCTION
Mobile manipulator with holonomic constraints can
be modelled as a redundant system, which offers high
flexibility and versatility, even though the system is
non-commensurate. A robot is said to be
kinematically redundant, if the dimension of joint
space
is greater than the dimension of operational
space
,... The redundant degrees of
freedom (DoF) can be used to perform additional
tasks in joint space (Sciavicco et al., 2012). It can also
be viewed as an underdetermined system, where the
number of solutions in joint space is a finite set of
infinite number of solutions for a given admissible
range of operational space motion (Burdick, 1989).
In service domain, there is an increasing demand
for mobile manipulators to perform various high-
level behaviours which consists of reactive and
repeated tasks. Synthesizing controller for such high-
level behaviours is highly complicated and often such
high-level tasks are decomposed into primitive level
subtasks with individual low-level controllers, as
described in (Kress-Gazit, 2008). Various constraints
and conflicts among the tasks can be handled by
assigning the order of priority for each task, and the
resulting end-effector motion can be realized by
projecting the task having lower priority onto the null
space of the higher priority task, as proposed in
(Nakamura et al., 1987).
One of the main challenges in autonomous robot
control is the smooth change of its control scheme
while switching between different tasks. For
example, consider the end-effector of a manipulator
is commanded to move along a trajectory while
avoiding obstacles without violating the joint limits.
Here, trajectory tracking, obstacle avoidance, and
joint limit avoidance are the three behavioural tasks
and will be activated only on absolute necessity. Each
subtask describes the dynamics of the behaviour with
current state and sensor information, and the robot is
expected to execute many of such behaviours
simultaneously. Each task will generate its own
motion command which has to be combined through
suitable behavioural control scheme to achieve a
single motion command. The work presented by
(Antonelli et al., 2008) has investigated and compared
the null-space behavioural (NSB) control with the
existing methods in behavioural coordination. But, in
general, it is impossible to accomplish all the tasks
concurrently, because of the task conflict. To avoid
numerical drifting and task space error while solving
inverse kinematics using redundancy resolution,
Govindan, N. and Thondiyath, A.
Improved Planning and Filtering Algorithm for Task-priority Redundancy Resolution in Mobile Manipulation.
DOI: 10.5220/0006402002470253
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 247-253
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
247
some of the task can be modelled as closed loop
behaviour. The convergence analysis of Closed Loop
Inverse Kinematics (CLIK) in discrete domain and a
method to find the gain bounds can be found in (Falco
and Natale, 2011). The discrete time implementation
of CLIK with fixed sampling time may lead to
discretization chatter. The chattering problem arises
due to undesired system oscillation with finite
frequency and finite amplitude, when switching
between different control inputs as described in
(Guldner and Utkin, 2000). In (Falco and Natale,
2014), authors have proposed a technique to smoothly
switch between the tasks by handling the priorities.
However, they have not shown the significance of the
switching happening within the null space projection
itself, which may result in chattering in joint space.
This chattering problem in Null Space Based
(NSB) behavioural control has received less attention
in the existing literature. In this work, we propose a
planning and filtering algorithm which significantly
reduces the chattering effect while solving inverse
kinematics for mobile manipulators, using NSB
behavioural control at velocity level. To demonstrate
the effectiveness of the proposed algorithm, three
case studies are considered. Case 1 being NSB control
only, Case 2 being NSB control with filtering
algorithm and finally Case 3 for NSB control with
planning and filtering algorithm.
2 KINEMATICS
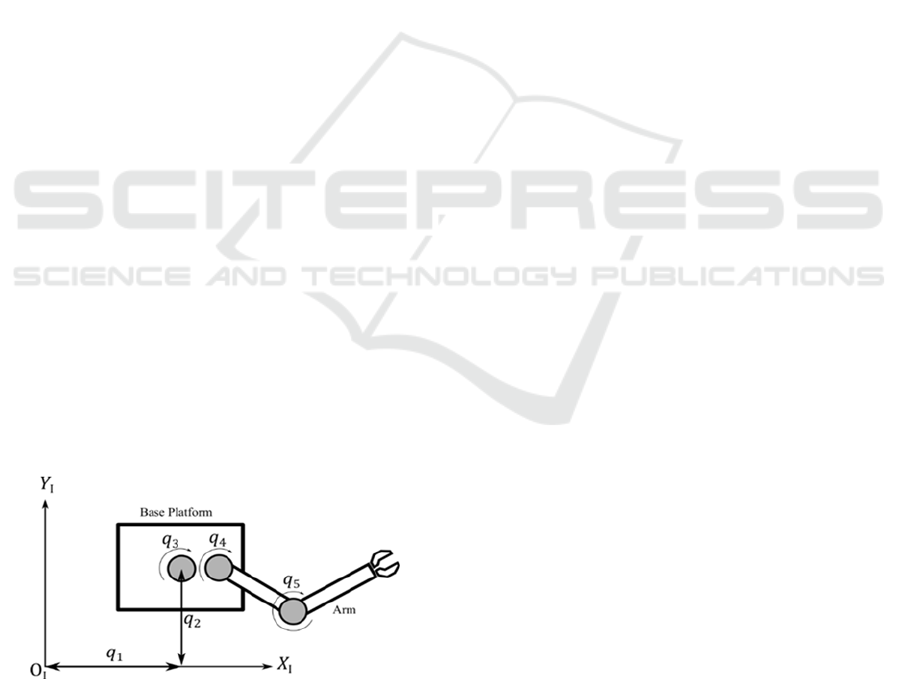
In this paper, we considered a 5-DoF planar mobile
manipulator as shown in figure 1 as a test platform for
simulation. The 3-DoF holonomic base platform is
kinematically modelled as two sliding joints and one
revolute joint, followed by the 2-DoF planar
manipulator.
Figure 1: Mobile Manipulator.
Let be the – dimensional operational space
vector variable and be the dimensional joint
space vector variable of the mobile manipulator. The
position kinematics can be generally expressed as
,
(1)
⋯
∈
⋯
∈
, 6
where, is a vector valued function which maps a
vector from joint space
to an operational
space
. Since is highly non-linear, finding a
closed form solution for inverse problem is not an
easy task. Hence, the first order linear algebraic
equation obtained by differentiating Eqn. 1 with
respect to time can be used to find the joint space
solution as:
(2)
∈
,
∈
,
∈
is the Jacobian matrix which is configuration
dependent and act as a linear operator. The inverse
kinematics problem of the redundant manipulator can
be solved by using redundancy resolution scheme.
3 TASK DESCRIPTION
As explained earlier, task execution by a redundant
manipulator brings in additional challenges like path
discontinuity and chatter. To illustrate this, we
considered a scenario where the end-effector of the
manipulator is commanded to move along a reference
trajectory while avoiding the obstacles in the
operational space by utilizing the redundancy. So the
tasks involved here are trajectory tracking and
obstacle avoidance. Each task can be interpreted as a
reactive one, where the motion of the robot depends
up on the information accumulated while performing
the task. Prioritizing and activating the task based on
the external event is carried out by a planning
algorithm. The planner would not have any prior
knowledge about the intended task, and the
appropriate controller will be activated only when the
corresponding event has occurred. The control law of
each behaviour in velocity domain is modelled as a
PD control to avoid the numerical drift while
integrating the joint velocity as discussed in the
following sections. Each controller will command the
motion or action based on its own objective and
sensor information.
3.1 Trajectory Tracking
The objective of this behaviour is to solve for joint
space solution for a given smooth operational space
trajectory with the bounded trajectory error. The end-
effector of the mobile manipulator is commanded to
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
248

track the trajectory as shown in figure 2 and the
corresponding position and velocity of the end-
effector are shown in figure 3 and figure 4
respectively. For trajectory tracking task Eqn. 2 can
be modified as
∈
,
∈
,
∈
(3)
The instantaneous velocity in joint space is computed
from the given position
and velocity
of end-
effector along with the tracking error term.
CLIK algorithm at velocity level will have the form
of
(4)
where,
∈
is the operational space vector, ∈
the joint space vector,
∈
the symmetric
positive definite matrix,
⁄
the Jacobian
matrix of the robot and
the pseudo inverse of
.
The dynamics of the error is governed by
(5)
The choice of Eigen values of
guarantees
convergence of error to zero and makes the system
asymptotically stable. The position feedback drives
the end-effector towards the trajectory to nullify the
tracking error, if it is drifted away from the reference
trajectory.
Figure 2: Commanded end-effector trajectory in operational
space.
Figure 3: Commanded end-effector position.
Figure 4: Commanded end-effector velocity.
3.2 Obstacle Avoidance
For obstacle avoidance task, the first order
differential equation as shown in Eqn.2 can be
modified as
∈
,
∈
,
∈
(6)
The highest priority is given to the obstacle avoidance
task, and the aim of this task is to ensure that no part
of the base-arm system should collide with obstacle
in the operational space. This can be done by
changing the configuration of the manipulator in joint
space by exploiting the redundancy. Each link of the
base-arm system is assumed to be equipped with
proximity sensors along the structure at every point
of interest (POI) where the robot has to maintain a
safe distance, as can be seen in figure 5. The extent of
sensing and range, at every POI, forms an influence
region.
Let be the set of all disjoint influence region,
be the set of all disjoint obstacle region and ϕ be an
empty set.
…
(7)
Figure 5: Location of obstacle and POI with respect to the
manipulator link.
Let the robot consists of joints,
be the
joint
variable and succeeding link will be the
link. Each
Improved Planning and Filtering Algorithm for Task-priority Redundancy Resolution in Mobile Manipulation
249

link have number of sensors, where
is the
position of
sensor of
link at POI.
be the
influence radius of
sensor of
link and
is the distance between POI
and the closest obstacle. Minimizing the potential
, would increase the clearance.
=
,
0,
otherwise
(8)
Depending upon the heading direction and distance
between the POI and obstacle, a suitable velocity
command is generated which ensures POI to be at a
safe distance from the obstacle.
The Jacobian
at every POI is calculated as
,
0
,
otherwise
(9)
where
,
The closed loop behaviour for obstacle avoidance can
be obtained as:
(10)
4 NULL SPACE BASED
BEHAVIORAL CONTROL
Every individual behaviour generates the motion
command, as it was acting alone. Then, the overall
motion command in joint space is computed by task
space redundancy resolution where the lower priority
task is projected onto the null space of higher priority
task as in Eqn. 11. By doing so, the conflicting motion
generated by lower priority can be removed. The first
term of Eqn. 11 represents the least norm solution as
mentioned in Eqn. 10 and the second term represents
the homogeneous solution.
(11)
Substituting Eqn. 4 and 10 in Eqn. 11 yields
(12)
For the given sampling time ∆
and joint position and
velocity at
, the joint position at
can be
computed as
∆
(13)
Most of the time, Jacobian matrix for every task has
to be computed continuously, whether or not the task
is active. To reduce the computational complexity,
the task Jacobian is computed only when the
corresponding task is active. As mentioned in the
obstacle avoidance behaviour,
would be computed
only if the task is active, and will remain as zero
matrix otherwise. This would cause the rapid
switching between first and second term of Eqn. 12
which leads to chattering effect. This chattering effect
is mainly due to the discrete time implementation of
task behaviours and is highly undesirable as it leads
to high wear and tear of mechanical components and
reduces the accuracy of the system. Though it is
possible to reduce the amplitude of chattering by
reducing the gain matrix, the transients will always
remain. The design of a filtering and planning
algorithm to reduce the effects of chattering and
associated trajectory changes are presented in the next
section.
5 PLANNING AND FILTERING
ALGORITHM
The chattering effect due to switching between two
closed loop behaviours can be eliminated by
replacing the joint variable
with an affine
combination of previous state
and present state
of joint variable as
(14)
where
=1 and 0
,
1, then
lies on
the line passing through
and
.
The value of has to be parameterized such that
the high frequency components can be suppressed.
Equation 14 can also be realized as a first order
discrete form of low pass filter. Therefore, for a given
sampling time ∆
, and a cut-off frequency
, present
state
, and previous state
, the filtered output
can be computed as
1
(15)
where
∆
∆
, ∈
0,1
Equation 15 can be modified and extended to joint
variable vector as
,
⇒
(16)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
250

where
Diag
…
is a positive
definite diagonal matrix, ∈
identity matrix.
Without loss of generality, by choosing least cut-
off frequency
among all the joints,
can be
simplified to
=. Joint variable
obtained from
Eqn. 16 can be used to update the joint position. The
above filter can reduce the chattering significantly.
However, there is a potential problem of trajectory
shift due to this filtering. The operational space
trajectory shift is due to the continuous filtering of
joint positions. This could be avoided by a low level
planning algorithm, where the filtering is activated in
case of external event, otherwise it will be
deactivated. This can be achieved by another affine
combination of
,
and
as
,
(17)
where
,∈
, ∈0,1
1,onl
y
when,⋂ϕ
0, ⋂
ϕ
(18)
Substituting Eqn. 16 in Eqn. 17 yields
1
(19)
Equation 19 represents the online planning and
filtering algorithm to eliminate the chattering and
associated trajectory errors.
6
SIMULATION STUDIES
Simulation studies were carried out to analyse the
performance of the filtering and planning algorithm.
Three case studies are performed: (a) NSB control
without enabling the algorithm, (b) NSB control with
filtering and (c) NSB control with planning and
filtering.
6.1 NSB Control without Enabling the
Proposed Algorithm
The mobile manipulator is commanded to track the
trajectory while avoiding obstacle using NSB
behavioral control presented in section IV.
From Eqn. 12, it is observed that if
⋂ϕ, the motion is only due to
⋂ϕ, the motion based on NSB
When ⋂ is empty, meaning
for all
and, there are no obstacles near the POI.
will
become zero matrix and the null space operator
will become identity matrix ∈
.
Then the resultant motion is only due to the motion
command
which is computed from trajectory
tracking behaviour. When ⋂ is not empty, at least
one of the obstacles is in the vicinity of POI. Hence,
the corresponding
will be computed and the
secondary task vector
will be realized by
projecting onto the null space of
. The closed loop
behaviour of obstacle avoidance pushes the end-
effector away from the trajectory, and ⋂ become
empty, as long as POI is not in the vicinity of obstacle.
Figure 6: Chattering effect in joint space.
Figure 7: Chattering effect in end-effector position (x, y are
the trajectory traced and x_c, y_c are commanded trajectory
of the endeffector).
Figure 8: Deviation of actual trajectory from the
commanded due to chattering effect.
Improved Planning and Filtering Algorithm for Task-priority Redundancy Resolution in Mobile Manipulation
251

When
, the closed loop behaviour of
secondary task pushes the end-effector to follow the
trajectory. This will lead to switching back-and-forth
between
and
which results in
high frequency oscillation in joint space as shown in
figure 6, which also propagates to end-effector
position as in figure 7. The resultant motion traced by
the end-effector in operational space is shown in
figure 8. These results clearly shows that when NSB
control is implemented with CLIK, it leads to heavy
chattering in the joint space as well as in the
operational space.
6.2 NSB Control with Filtering
Algorithm
As a preliminary study, the effect of filtering
algorithm alone on task execution was studied for the
mobile manipulator presented in Section 5. The filter,
as in Eqn. 16, was implemented and it was found that
the chattering was reduced significantly as shown in
figures 9 to 11 and the joint trajectory was smooth.
Figure 9: Joint space motion after filtering.
Figure 10: End-effector motion after filtering (x, y are the
trajectory traced and x_c, y_c are commanded trajectory of
the endeffector).
Figure 11: Trajectory traced by the end-effector while
avoiding obstacle with filtering.
Though the end effector position in the
operational space was smooth without any
oscillations, it was not following the commanded
path, as shown in figure 10. The commanded
trajectory and the path traced by a mobile manipulator
after filtering is shown in figure 11. Though the
manipulator is able to avoid the obstacle and reach the
target, there is a large deviation in the path traced by
the end effector.
Figure 12: Joint space motion after filtering and planning.
Figure 13: End-effector motion after filtering and planning.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
252

Figure 14: Trajectory traced by the end-effector while
avoiding obstacle with filtering and planning algorithm.
6.3 NSB Control with Planning and
Filtering Algorithm
The planning algorithm was implemented along with
the filtering algorithm to study the effect on NSB
control. Simulation results are shown in figures 12 to
14. The joint space motion and the operational space
motion are shown in figures 12 and 13. The planning
algorithm implemented using Eqn. 19 drastically
reduces the tracking error in operational space. With
the planning and filtering algorithm the path traced by
the end-effector, in the presence of obstacle, without
any chattering effect, can be seen in figure 14. The
end effector follows the commanded trajectory very
well, except for the region where obstacle is present
as shown in figure 13. These results confirm the
utility of the filtering and planning algorithm in
reducing the chatter and trajectory tracking error
while implementing NSB control for redundant
systems.
7 CONCLUSION
In this paper, an improved planning and filtering
algorithm has been presented for mobile manipulators
to avoid the chattering problem while solving inverse
kinematics using task priority with closed loop
behaviours. The filtering algorithm reduces the
chatter, however brings in trajectory errors. The
planning algorithm overcomes the trajectory error
and helps the manipulator to follow the desired
trajectory closely while avoiding obstacles.
Simulation results have been presented to show the
effectiveness of the proposed algorithm. It was shown
that the redundant mobile manipulator tracks the
reference trajectory without any high frequency
oscillations while avoiding obstacles.
REFERENCES
Sciavicco, L. and Siciliano, B., 2012. Modelling and
control of robot manipulators. Springer Science &
Business Media.
Burdick, J.W., 1989. On the inverse kinematics of
redundant manipulators: Characterization of the self-
motion manifolds. In Advanced Robotics: 1989 (pp. 25-
34). Springer Berlin Heidelberg.
Kress-Gazit, H. 2008, Transforming high level tasks to low
level controllers, Doctoral dissertation, University of
Pennsylvania.
Nakamura, Y., Hanafusa, H. and Yoshikawa, T., 1987.
Task-priority based redundancy control of robot
manipulators. The International Journal of Robotics
Research, 6(2), pp.3-15.
Antonelli, G., Arrichiello, F. and Chiaverini, S., 2008. The
null-space-based behavioral control for autonomous
robotic systems. Intelligent Service Robotics, 1(1),
pp.27-39.
Falco, P. and Natale, C., 2011. On the stability of closed-
loop inverse kinematics algorithms for redundant
robots. IEEE Transactions on Robotics, 27(4), pp.780-
784.
Guldner, J. and Utkin, V.I., 2000, June. The chattering
problem in sliding mode systems. In 14th Int. Symp.
Math. Theory Netw. Syst.(MTNS), Perpignan, France
(Vol. 11).
Falco, P. and Natale, C., 2014. Low-level flexible planning
for mobile manipulators: a distributed perception
approach. Advanced Robotics, 28(21), pp.1431-1444.
Improved Planning and Filtering Algorithm for Task-priority Redundancy Resolution in Mobile Manipulation
253
