
Mixed Fluid and Rigid Body Simulations
An Object Oriented Component Library based on the Physolator Framework
Waldemar Rose and Dirk Eisenbiegler
University of Furtwangen, Furtwangen, Germany
Keywords: Particle Modelling, Fluid Simulation, Rigid Body Simulation, Physolator, Java Framework, Object Oriented
Modelling.
Abstract: This paper presents an approach towards implementing physical simulations, where the physical system
consists of both fluids and movable rigid bodies. The approach is based on Physolator. Physolator is an
object oriented Java based framework for physical simulation. This paper introduces a library of Java
classes that are designed for building such simulations. The classes are designed to be used inside the
Physolator framework.
1 INTRODUCTION
Physical simulation is used in different domains and
there are various software tools tailored to the
specific needs of such domains. Fluid simulations
and rigid body simulations are such domains.
Fluid simulations describe the flow of gases and
liquids. A fluid simulation describes the actual
location of the fluids for each point in time, the
forces applied to the fluids and physical fields for
the flow velocity and pressure. Particle models are
frequently used for computer based physical
simulations (Greenspan, 1997, 1985, 2004,
Nijmeijer, 1992, Korlie, 1997, 1999, Pozrikidis,
2017). Particle simulations are challenging. It takes a
big number of particles to achieve a reasonable
accuracy. Therefore, such simulations usually
require big amounts of computing time.
Programmers have to spend a lot of time for
optimizations in order to achieve a reasonable
simulation accuracy within a limited computation
time.
Rigid body mechanics is about physical bodies,
that are not deformable. During the simulations, the
rigid bodies move, the shape however remains
unchanged. Different kinds of forces can apply to a
rigid body during simulation: gravity, magnetic
forces, sliding friction, static friction, rolling
friction, etc.. These forces accelerate rigid bodies
and change their translational and rotational
velocity. Furthermore, there are collisions between
rigid bodies. Collisions abruptly change the
translational and rotational velocity of the bodies
involved. Rigid body simulations are frequently used
in computer games and animated films. Game
engines usually contain a component named
“physics engine”. This kind of physics engine is
usually limited to rigid body physics. From a
computational point of view, rigid body simulations
are far less challenging than fluid simulations.
Physics engines inside computer games are designed
for real time execution. For a limited amount of
components, they succeed computing frames within
milliseconds. In a computer game, the accuracy of
the physical computation has to be reasonable in a
sense that the user of the computer game should get
the impression, that the virtual world of the
computer game behaves just like the real world.
Simulations inside computer games need not
necessarily produce results, that are precise in a
scientific sense.
This paper is about physical systems consisting
of both fluids and rigid bodies. Concepts from both
worlds, fluid simulation and rigid body simulation,
are to be applied. The next section describes how
such physical systems look like and gives an
example. The following section explains the concept
used to create models for such physical systems and
it explains, how to run such simulations. Finally,
there will be a section with algorithmic
considerations. Whenever you deal with particle
simulations, computing time matters. The final
section describes the algorithms and the concurrency
36
Rose, W. and Eisenbiegler, D.
Mixed Fluid and Rigid Body Simulations - An Object Oriented Component Library based on the Physolator Framework.
DOI: 10.5220/0006402600360044
In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 36-44
ISBN: 978-989-758-265-3
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

concepts used inside the library in order to achieve a
good performance.
2 MIXED FLUID AND RIGID
BODY SYSTEMS
This section describes, how physical systems with
fluids and rigid bodies look like. Using an example,
it is explained, what kind of components are used to
build up such systems and which physical effects
have to be considered.
Figure 1 shows a sequence of snapshots from a
physical simulation with water and rigid bodies. In
picture (I) you can see a basin filled with water. A
water drop is about to fall into the basin. The floor
of the basin and the wall on the left hand side are
fixed. On the right hand side of the basin, there is a
rectangular solid block. The block lies on the basin
floor. In the beginning, the block does not move.
Figure 1: Simulation with water and rigid bodies.
The water inside the basin applies a force
towards the block pushing the block rightwards.
Static friction, however, hinders the block from
moving. The static friction force is a counterforce to
the force from the water with the same absolute
value, but opposite direction. Static friction applies
as long as the block is not in motion and as long as
the force applied to the block does not exceed a
certain maximum. The maximal static friction force
is a constant. It depends on the force the block
applies to the floor of the basin and a static friction
coefficient. In the beginning, the absolute value of
the force from the water is smaller than the maximal
friction force.
As soon as the water drop falls inside the basin,
the force applied to the block increases. At a certain
point in time (II), this force exceeds the maximal
static friction force and the block starts moving
rightwards. At this point in time, static friction is
replaced by sliding friction. The sliding friction is
smaller than the static friction. Sliding friction
applies as long as the block is in motion. As soon as
the block moves to the right, also the water starts
moving rightwards (III). Since the water moves
rightwards, the water level inside the basin is
decreased. As a consequence, the force from the
water applied to the block lessens. As soon as this
force is smaller than the sliding friction, the total
force applied to the block is directed to the left. The
block is slowing down and finally stops (IV). As
soon as the block stops, sliding friction is replaced
by static friction and the block remains in this final
position.
Different kinds of physical effects have to be
considered when performing this simulation: forces
between the water particles, internal friction, forces
between the liquid and the rigid bodies, static
friction, sliding friction. Some of these effects are
related to fluid physics and some to solid body
physics.
Basically, the relationship between the physical
variables involved can be described via differential
equations. However, also points of discontinuity
have to be considered. At the point in time, when the
block starts moving, the static friction abruptly
vanishes and is replaced by sliding friction. At the
point in time, when the block stops moving, it is the
other way round: sliding friction is replaced by static
friction. Physical simulations are an appropriate
means for answering question like these: When will
the block start moving? How far will it move? When
will it stop moving?
Figure 2 shows a function plot with some of the
physical variables involved in this simulation. This
diagram shows the forces applied to the block. The
upper horizontal line represents a constant: the
maximal static friction. In the beginning, there are
two forces with the same absolute value: the force,
that the water applies to the block and the static
friction force. The value of this force is continuously
changing due to the movement of the water. As soon
as the force from the water reaches the maximal
static friction force, the block starts moving. As long
as the block is moving, there is still the force from
the water, but the counterforce does not have the
Mixed Fluid and Rigid Body Simulations - An Object Oriented Component Library based on the Physolator Framework
37
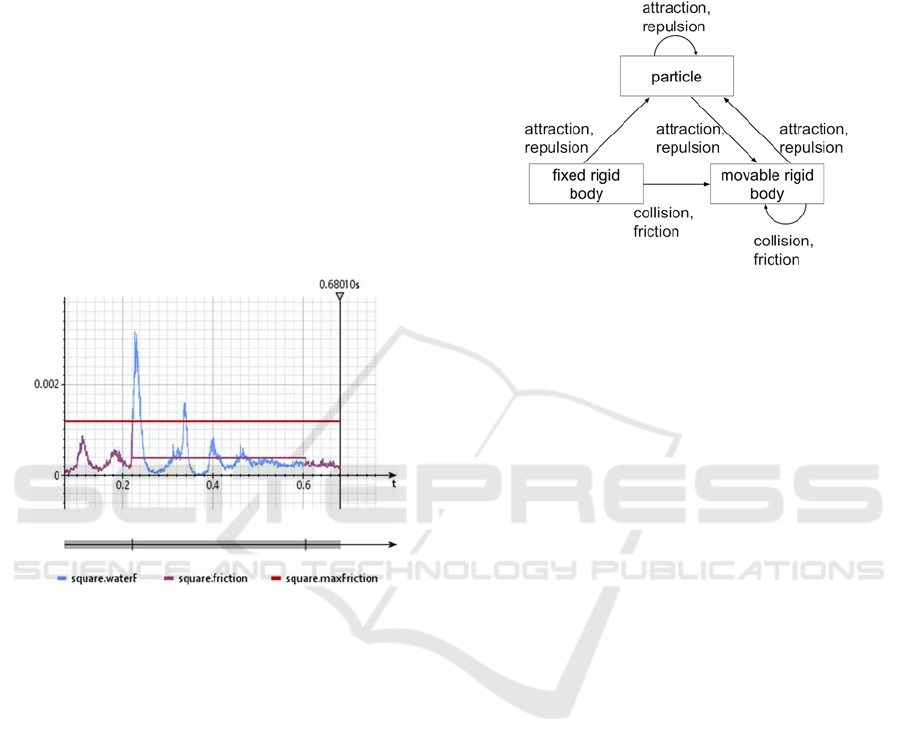
same absolute value any more. The counterforce is
the sliding friction force and this force is constant.
The total force applied to the block is the difference
between the force from the water and the dynamic
friction force. This force accelerates the block. As
the block moves rightwards, the water level is
reduced and therefore also the force, that the water
applies to the block, is reduced. As soon as the force
from the water is less than the sliding friction, the
total force is negative and the block is slowing
down. At a certain point in time the block stops.
Then sliding friction is replaced by static friction.
Since the force from the water is less than the
maximal static friction, the absolute value of the
counterforce produced by static friction equals the
force from water. The block stops and remains in its
final position.
Figure 2: Function plot.
Such physical systems consist of three different
kinds of physical components: fluid particles, fixed
rigid bodies and movable rigid bodies (see figure 3).
The basin with its floor and its wall on the left hand
side are fixed rigid bodies. The block is a movable
rigid body. There are attraction and repulsion forces
between the fluid particles and between the fluid
particles and the rigid bodies. The formulas from
Greenspan (Eisenbiegler, 1997) are used to describe
these forces. Various different forces could be
applied to rigid bodies, such as gravitation forces,
forces due to magnetic or electrical fields, static
friction, dynamic friction, forces due to springs
connected with the rigid body, Coriolis forces and
centrifugal forces. Besides, rigid bodies may also
collide in an elastic or inelastic manner. Appropriate
physical formulas have to be used to describe such
physical events.
In this example, there are no collisions. The only
movable component is a block. Earth gravitation
presses the block to the basin floor and the force
from the water particles pushes the block rightwards.
There is always friction between the block and the
basin floor. As long as the block stands still, there is
static friction and as long as the block is in motion,
there is sliding friction.
Figure 3: Physical effects.
3 CONCEPT
The physical systems from this paper have all been
created using a certain library of Java classes. This
library for mixed fluid and rigid body simulations is
to be referred as FRB library. The FRB library has
been created by Waldemar Rose and is based on the
pure fluid simulation library from Dirk Eisenbiegler
(Eisenbiegler, 2016b). The classes of the FRB
library provide building blocks for physical models
consisting of fluids and rigid bodies. It provides
physical components and it provides a generic
graphics component. Physical simulations with
fluids and rigid bodies are constructed by composing
these building blocks.
The physical systems presented in this paper are
all run inside the Physolator (Eisenbiegler, 2016a).
Physolator is a physical simulation framework. The
Physolator framework is implemented in Java and
also all the program code run inside this framework
is pure Java code. In order to simulate a physical
system, one first has to implement the physical
model using the Java programming language. Then
one loads the physical system to the Physolator
framework. Finally the physical simulation is started
from inside the Physolator (see figure 4). The FRB
library has been designed to be used inside the
Physolator.
The Physolator framework supports an object
oriented programming style. Physical systems,
graphical components and numerical procedures can
be developed independently and are linked by the
Physolator framework during run time. Physical
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
38

Figure 4: Physolator.
systems are implemented in a modular style, where a
physical system is built from components such as
point masses, springs, liquids etc.. Such components
are called physical components. They are defined as
Java classes. Each physical component represents a
part of a physical system with some physical
variables and formulas. Once you have defined such
components, you can reuse them in different
physical systems. In many cases, building a physical
system means just composing physical components:
build instances of the classes representing the
physical components, assign the variables of the
physical components appropriate values and link the
physical components together. Example: First create
some point masses, springs and pivot points. Then
assign appropriate constants to the physical
components: initial positions, masses, spring rates.
Finally, connect each end of a spring either with a
point mass or a pivot point.
Every physical system may have one or more
graphics components. Graphics components linked
to a physical system are automatically loaded
whenever the physical system is loaded. Graphics
components are used to visually represent the
current state of a physical system. During the
physical simulation, the variables of the physical
system change their values. A graphical
representation is easier to receive than a big number
of physical variable values. Therefore, graphics
components can be used to visually represent the
state of the physical system.
Graphics components are Java classes. For every
physical system one can implement a specific
graphics component tailored to this specific physical
system. The Physolator provides a means for
constructing generic graphical components. Generic
graphics components are tailored not to a single
physical system, but to a variety of physical systems
from a certain domain. They are reusable. Whenever
you implement a physical system for the specific
domain, you can simply use the generic graphics
component and you do not have to implement your
own graphics component.
4 THE FRB CLASS LIBRARY
The FRB library provides a set of physical
components plus some graphics components. Figure
5 shows the program code for the physical system
from section 2. Loading this piece of program to the
Physolator and starting the simulation results in the
Mixed Fluid and Rigid Body Simulations - An Object Oriented Component Library based on the Physolator Framework
39

1 public class SquareFriction extends MRBParticleSystem {
2
3 private final double sigma0 = 50e-5;
4 private final double rMax = 5 * sigma0;
5 private final Vector2D g = new Vector2D(0, -9.81);
6 private Line line =
7 new Line(new Vector2D(0.06, 0), new Vector2D(-0.03, 0));
8 public FrictionSquare square =
9 new FrictionSquare(0.00025, 0, 0.03, 0.02,line,0.6, 0.2);
10
11 public SquareFriction() {
12 beginStructure(rMax);
13
14 setParticleSchema(water, sigma0, g);
15 setMRBSchema(movableRigid, sigma0, g, square);
16 setRBSchema(rigid, sigma0);
17
18 line.schema = actualRBSchema;
19 addLine(-0.03, -0.001325, -0.03, 0.03);
20 addLine(line);
21 addMovableRigidBody(square);
22
23 fillRectangle(-0.02975,0.00025, 0, 0.015);
24 fillCircle(-0.015, 0.035, 0.01);
25
26 endStrukture();
27 }
28
29 public void initPlotterDescriptors(PlotterParameters r) {
30 r.add("square.acceleration.x, square.velocity.x",0.4, -1, 2);
31 r.add("square.F, square.friction",0.4, -1e-4, 10e-4);
32 }
33 }
Figure 5: Java program code.
simulation as shown in figure 1, figure 2 and figure
4.
The program code from figure 5 defines a new
physical system named SquareFriction.
SquareFriction inherits from class
MRBParticleSystem. MRBParticleSystem is part of
the FRB library. It provides some features and
presets that make developing physical systems with
fluids and rigid bodies easier. Due to this inheritance
relationship, the physical system SquareFriction is
automatically equipped with appropriate default
values simulation parameters and it is automatically
equipped with a generic visualization component
tailored to the needs of fluid and rigid body
simulations. Figure 1 shows snapshots of this
component during the simulation.
The program code from figure 5 defines a
physical system by combining physical components
and by providing them with the right parameters and
settings. Lines 3 and 4 define the core parameters for
the particle model: sigma0 is used to specify the
particles equilibrium distance and rMax is a
constant, that defines a maximal distance. Forces
between two particles are neglected, if the distance
between the particles is greater than rMax (see
section 5 for details). Line 5 defines the earth
gravitation acceleration. Lines 6 through 9 define a
squared rigid body resting on a horizontal line. First,
the horizontal line is defined and then the squared
rigid body. Line 9 creates the squared rigid body.
The first four parameters define its location, width
and height. The fifth parameter is the previously
defined horizontal line. The squared rigid body has
an internal link to the horizontal line. Parameters six
and seven define the friction coefficients for static
friction and dry sliding friction, respectively.
The constructor of the class (lines 11 through 27)
defines the physical system. The commands that
build up the physical system are located between the
commands beginStructure and endStructure. Lines
14 through 16 initialize some data structures that are
used as containers for fluid bodies and rigid bodies,
respectively. See (Eisenbiegler, 2016b) for details.
Line 18 defines the standard behaviour of fluids, that
are in touch with rigid bodies. Lines 19 through 21
define three rigid bodies: two lines representing the
floor and the wall at the left hand side and a squared
block. The lines representing the floor and the wall
on the left hand side are rigid bodies, that are not
movable. The block is a movable rigid body. Lines
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
40

23 and 24 define amounts of water. Initially, the
basin is filled with a rectangular amount of water
and there is a circular amount of water located above
the basin.
Lines 30 and 31 define, that there shall be two
plots: one plot with the acceleration and the velocity
of the block and one plot with the force applied to
the block and the actual total friction. For every plot,
one has to define the names of the variables that are
to be displayed, the range of time and the minimal
and maximal values (y range).
To summarize, the program code of figure 5
defines a physical system by creating components
from given classes from the FRB library. The
program code creates some of these components,
provides them with the right parameters and
interconnects them. There are no physical formulas
in this program code. As a user of the FRB library,
you can just combine the components and you do
not have to think about the underlying physics. The
formulas representing the underlying physics are
located inside the physical components of the FRB
library.
5 EXAMPLES
The approach presented in the previous section can
be used to define different kinds of physical systems.
Figures 6 through 9 give some examples. All these
simulations have been implemented with the help of
the FRB library in the same style as program code in
figure 5.
I II
III IV
V VI
VII VIII
Figure 6: Example A.
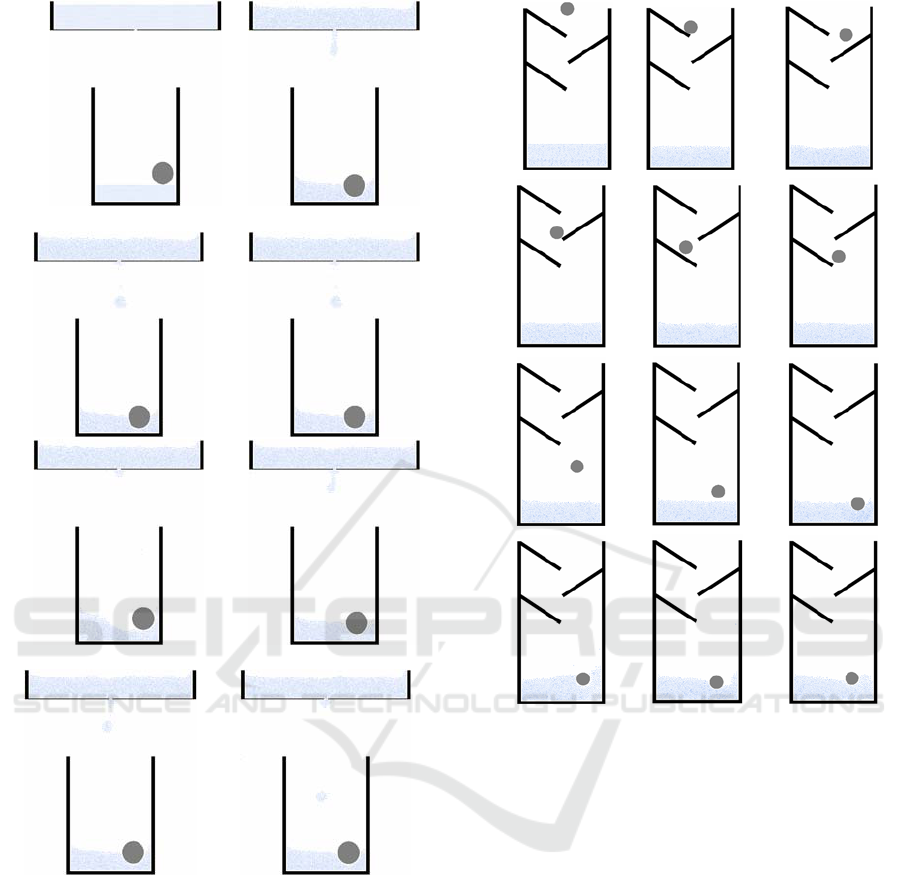
Figure 6 shows a physical system, that is similar
to the initial example from the previous section: a
basin with a block on one side and a fixed wall on
the opposite side. For a certain time, the block is
moved from left to right with a constant speed. Then
the block is stopped. As a result, the water inside the
basin starts moving. A wave moves from left to
right. When reaching the fixed wall on the right, the
wave is reflected and finally moves leftwards.
Figure 7 shows a ball, that is dropped into a
basin of water. As soon as the ball touches the water,
the water is pushed sideways and starts moving.
I II
III IV
V VI
Figure 7: Example B.
The physical system from figure 8 consists of
two basins of water. Due to a small hole in floor of
the upper basin, water drops from the upper basin to
the lower basin. The water drops falling into the
lower basin produce waves. In the lower basin, there
is a ball floating on the water. The waves move this
ball.
The physical system in figure 9 is similar to the
one from figure 7: a ball drops into a basin filled
with water. In figure 9, however, there are some
barriers. On its way down to the water, the ball hits
these barriers several time and rolls on them until it
finally plops into the water.
Mixed Fluid and Rigid Body Simulations - An Object Oriented Component Library based on the Physolator Framework
41
I II
III IV
V VI
VII VIII
Figure 8: Example C.
6 ALGORITHMIC
CONSIDERATIONS
The fluid simulation library from (Eisenbiegler,
2016b) provides a core infrastructure for modelling
pieces of fluid using particles. In a particle based
fluid simulation, the number of particles is crucial.
Theoretically, every particle interacts with every
other particle. For sake of simulation speed, a
maximum distance
is defined. Forces between
particles are neglected if their distance is greater
than
. A grid of boxes is used in order to effi-
I II III
IV V VI
VII VIII IX
X XI XII
Figure 9: Example D.
ciently find particles, that are in the neighbourhood
of some particle. The grid spacing is
. Every
box inside this grid is quadratic with the width and
height being
. All particles are assigned to
boxes in this grid. A hash map data structure is used
to efficiently find the neighbouring boxes. After
every movement of the particles, this data structure
is computed anew and all particles are assigned to
the boxes.
The FRB has been build on top of the fluid
simulation library (Eisenbiegler, 2016b). It provides
extra data structures for internally representing rigid
bodies. To achieve good results as to performance,
the algorithm for determining the particle-particle
forces has been enhanced using multi-threading.
Besides, an algorithm has been implemented for
efficiently determining the forces between particles
and rigid bodies.
In the fluid simulation library (Eisenbiegler,
2016b), a single threaded approach has been used to
determine the forces between the particles. When
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
42

working with several threads, one has to make sure,
that not more than one thread works with a particle
at the same time. To compute the forces for one
particle, one has to consider all particles from the
same box plus all the particles from the
neighbouring boxes. If two work with one particle at
the same time (reentrancy), this could lead to false
results. Synchronized methods would solve this
problem. However, they use locking and locking
could produce deadlocks. To synchronize the threads
and to avoid deadlocks, a specifically developed
synchronization strategy is to be used.
At a certain point in time every thread shall
determine the actual forces for all particles of some
box. To compute the forces of the particles in one
box, the thread also has to work with the particles
from the boxes in the direct neighbourhood. When
working with one box, no other thread shall work
with this box or its neighbours. If two threads are
determining the forces for two boxes, there must be
at least two boxes between these boxes.
Figure 10: Boxes used to avoid reentrancy.
Figure 10 explains the multi threading and
synchronization concept. In this figure, there are
several amounts of water. Each amount of water is
represented by a set of particles. During simulation,
an orthogonal grid of quadratic boxes is used and
each particle is assigned to one of the boxes. In
Figure 10, one can see vertical columns. Each
column represents a vertical sequence of boxes. The
width of the columns is
. At a point in time, one
thread shall compute the forces for all particles of
one column plus the forces applied from these
particles to the particles that are in the columns next
to the actual column. One has to make sure, that at
no time there are two threads working with columns
with less than two columns in between. Figure 10
shows a snapshot during computation. The grey
columns represent columns, where a thread is
currently computing the forces.
Threads are synchronized using the wait/notify
mechanism from Java to make sure, that at any time
there are at least two columns in between two active
threads. Figure 11 shows the pattern, that is used for
this synchronization. Each number represents one
column and each arrow represents a wait-notify-
relationship. The thread actually executing the
column at the starting point of the arrow has to
finish its work, unless the computation of the
column, that the arrow points to, cannot be started.
A thread at the end point of an arrow has to invoke
wait(). It is blocked unless the thread from the
starting point of the arrow sends him a notify()
signal.
Figure 11: Synchronization.
Rigid bodies are either represented by lines or by
circle segments. The algorithm shall compute all
forces, that particles apply to rigid bodies, and all
forces, that rigid bodies apply to particles.
Theoretically, one would have to consider all
combinations of rigid bodies and particles. To save
computing time, forces shall be neglected if the
distance is greater than
.
The algorithms used for computing the forces
between rigid bodies and particles use the grid of
boxes. One has to find all combinations of boxes and
rigid bodies, where the box is not more than
apart from the rigid body. More precisely: There is
at least one point inside the box, that is not more
than
apart from the rigid body. For every such
pair of rigid body and box, one has to iterate through
all particles and compute the actual distance to the
rigid body. If the distance between the particle and
the rigid body is not greater than
, then the force
between this particle and the rigid body is computed
and this force is added to the rigid body and to the
particle – with opposite signs.
But how to efficiently determine all
combinations of boxes and rigid bodies, that are not
more than
apart? There are two different
approaches, that are to be called algorithm A and
algorithm B. Algorithm A iterates through all boxes.
For every box, the algorithm determines the distance
to all rigid bodies. Algorithm B works the other way
round: It iterates through all rigid bodies. For every
rigid body, the algorithm walks along the rigid body
from the beginning point to the end point of the line
and computes the position of the boxes in the
neighbourhood of the line. For every such position,
it checks, if there is such a box with particles.
Determining the position of all box positions is easy
for lines. Beginning at the starting point of the line,
one simply has to add a small piece of the direction
Mixed Fluid and Rigid Body Simulations - An Object Oriented Component Library based on the Physolator Framework
43

vector to iterate through all the boxes, that are in the
neighbourhood of the line. Things are a little trickier
with circle segments. To solve this problem, the
algorithm uses the Bresenham algorithm
(Bresenham, 1965). This algorithm has initially been
invented to draw circular lines using a plotter.
The user of the FRB library can choose between
algorithm A and algorithm B. The result is always
the same, but the computing efficiency is different.
It depends on the physical system, which of them is
faster. Algorithm A performs well for a smaller
number of particles and boxes and for a reasonable
number of rigid bodies. For a big number of
particles and a small number of rigid bodies with a
small total line length, algorithm B is faster.
7 CONCLUSIONS AND
OUTLOOK
This paper has presented a modular approach
towards mixed fluid and rigid body systems. So far,
there are still some limitations. First of all, the
approach is based on the fluid library presented in
(Eisenbiegler, 2016b) and this fluid library is limited
to two dimensional simulations. Three dimensional
fluid simulations are challenging. It takes far bigger
numbers of particles to achieve the same precision
with a three dimensional model. This results in a far
bigger amount of computing time.
The rigid body physics used in the examples is
limited to some physical effects: static friction,
dynamic friction, and collision. The library is so far
restricted to these effects. More physical effects
could be added and should be added.
So far, there has been a focus on optimizing the
fluid simulations. The data structures and algorithms
are optimized to handle as many fluid particles as
possible. However, the FRB library is not yet
designed for big numbers of rigid bodies.
REFERENCES
Eisenbiegler, D., 2015a. The Software Architecture of the
Physolator – a Physical Simulation Framework. In
MSAM 2015, Conference on Modelling, Simulation
and Appled Mathematics, Atlantis Press, pp. 61-64.
Eisenbiegler, D., 2016a. Object Oriented Modeling and
Simulation with the Physolator – Getting Started,
Available at: https://opus.hs-furtwangen.de/frontdoor/
index/index/docId/614.
Eisenbiegler, D., 2016b. A Generic Particle Modeling
Library for Fluid Simulation. In AMSM 2016,
Conference on Applied Mathematics, Simulation and
Modelling, Atlantis Press.
Eisenbiegler, D., 2015b. Objektorientierte Modellierung
und Simulation physikalischer Systeme mit dem
Physolator, BoD Norderstedt.
Eisenbiegler, D., 2016c. An Object Oriented Library for
Acoustics Simulation Based on the Physolator
Simulation Framework, In CMSAM 2016, Conference
on Modeling, Simulation and Applied Mathematics,
DEStech Publications.
Greenspan, D., 1997. Particle Modeling, Birkhäuser
Boston, Basel, Berlin.
Greenspan, D., 2004. N-Body Problems and Models,
World Scientific Publishing Co. Pte. Ltd.
Greenspan, D., 1985. Computer Studies in Particle
Modeling of Fluid Phenomena, Mathematical
Modeling, Vol. 6, pp 273-294, Pergamon Press Ltd..
Nijmeijer, M. J. P., et al., 1992. Molecular Dynamics of
the Surface Tension of a Drop, The Journal of
Chemical Physics, vol. 96, no. 1, pp. 565-576.
Korlie, M. S., 1997. Particle Modeling of Liquid Drop
Formation on a Solid Surface in 3-D, Elsevier Science
Ltd, Computers Math. Applic. Vol. 33, No. 9, pp. 97-
114.
Korlie, M. S., 1999. Three-Dimensional Computer
Simulation of Liquid Drop Evaporation, Computers &
Mathematics with applications, Elsevier.
Bresenham, J. E., 1965. Algorithm for computer control of
a digial plotter, IBM Systems Journal, Vol. 4, p. 24.
Pozrikidis, C., 2017. Fluid Simulation – Theory,
Computation, and Numerical Simulation”, Springer.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
44
