Analysing Buyers’ Burstiness in E-Business: Parameter Estimation and

Practical Applications

Andreas Ahrens and Jelena Zaš

cerinska

Hochschule Wismar, University of Technology, Business and Design Philipp-Müller-Straße 14, 23966 Wismar, Germany

Keywords:

E-Business Process, Buyers’ Burstiness, Gap Processes, Binary Customer Behaviour.

Abstract:

Optimization of e-business process assists in earning proﬁts in e-business. For the success of the optimization

of e-business process, a simulation model based on gap processes for the analysis of buyers’ burstiness in

e-business process has been recently developed. However, the model has to be validated in terms of input

parameter values and distributions. The research question is as follows: What are practically relevant input

parameter values and distributions of the model based on gap processes for the analysis of buyers’ burstiness

in e-business process? The aim of the research is to validate the simulation model based on gap processes for

the analysis of buyers’ burstiness in e-business process in terms of input parameter values and distributions

underpinning elaboration of a new research question on the model validity. The meaning of the key concepts of

validation, model validation and model validation approach is studied. The results of the present research show

that the simulation model for analysis of buyers’ burstiness e-business process in terms of input parameter

values and distributions is valid. The novel contribution of the paper is revealed in the newly created research

question on the proposed model for evaluation of buyers’ burstiness in e-business process. Directions of

further research are formulated.

1 INTRODUCTION

Optimization of e-business process assists in earn-

ing proﬁts in e-business. Optimization of e-business

process implies choices about quantity of goods to

be delivered, number of the staff to be employed as

highlighted in (Ahrens et al., 2015), goods’ pricing,

goods discounts, computer software to be installed,

networking between a business company and its cus-

tomers to be established, etc. Additionally, such a re-

sult of business process as purchase and/or sale of a

good or service indicates the output of this process.

For the success of the optimization of e-business

process, a simulation model based on gap processes

for the analysis of buyers’ burstiness in e-business

process has been recently developed (Ahrens and Za-

cerinska, 2016). Existing models do not take into ac-

count the context of e-business process. E-business

process proceeds under certain conditions. One of

the conditions is bursty processes that are quite com-

mon in our daily live. Table 1 demonstrates the phe-

nomenon of burstiness in a range of scientiﬁc ﬁelds

(Ahrens and Zaš

cerinska, 2016).

Beginning in 1960 Gilbert presented the ﬁrst

model in telecommunications which emphasized that

bit errors occurred in bundles or, in other words,

bursts (Gilbert, 1960; Elliott, 1963). Since then, the

issues of a general procedure to evaluate the perfor-

mance or, in other words, e-business process in the

present research, as well as a basic set of parameters

or, in other words, criteria, are still relevant today.

In business including e-business, burstiness of

workload is traditionally analyzed (Heinrich, 2014).

However, the paradigm has changed from an input

based business process or, in other words, burstiness

of workload to an outcome based process or, in other

words, burstiness of buyers (Ahrens et al., 2015). The

shift from analysis of burstiness of workload to eval-

uation of burstiness of buyers allows increasing the

efﬁciency of e-business process and, consequently, e-

business proﬁt.

In e-Business, buyers’ burstiness has to be high-

lighted as such a condition. Buyers’ burstiness

in e-business reﬂects the real environment in e-

business. By phenomenon’s burstiness, intervals of

high-activity alternating with long low-activity peri-

ods are meant.

A new model for analyzing buyers burstiness in

e-business process was presented in (Ahrens and Za-

cerinska, 2016). For the design of a mathematical

Ahrens, A. and Zašcerinska, J.

Analysing Buyers’ Burstiness in E-Business: Parameter Estimation and Practical Applications.

DOI: 10.5220/0006407800710077

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 2: ICE-B, pages 71-77

ISBN: 978-989-758-257-8

Table 1: Burstiness in different scientiﬁc ﬁelds.

Scientiﬁc ﬁeld Phenomenon of burstiness

Telecommunications Burstiness of bit-errors in data transmission

Economics Burstiness of crises

Natural sciences Burstiness of disasters or earthquakes

Logistics Burstiness of trafﬁc

Social media Burstiness of hot topic, keyword or event

Business Burstiness of workload

E-Business Burstiness of buyers

model for evaluation of buyers’ burstiness in e-

business process, the synergy between e-business and

telecommunications is promoted as the phenomenon

of customers in the e-business process as well as bit-

errors in data transmission appear to be of a similar

nature, namely, the bursty nature. It should be noted

that the present research is not limited to only two

scientiﬁc disciplines, namely e-business and telecom-

munication, but is based on a number of scientiﬁc

disciplines such as business, social media, logistics,

literature, etc. Such mathematical models that con-

sider the bursty nature of bit-errors in data transmis-

sion have been successfully implemented in telecom-

munications for optimizing data communication pro-

tocols and will be adopted in this work to the buyers’

burstiness in e-business process. The proposed model

for analyzing buyers burstiness in e-business process

is able to take the buyers’ concentration into account

since the buyers’ concentration cannot be considered

when only analyzing the buyers’ probability (Ahrens

and Zaš

cerinska, 2016). Thus, this model is novel as

it offers two parameters, namely, the buyers’ prob-

ability and the buyers’ concentration, for analyzing

buyers burstiness in e-business process.

A comparison of the model of evaluation of bursti-

ness of hot topic, keyword, etc. in social media shown

by the group of Japanese researchers (Kotozaki et al.,

2015) with the model for evaluation of buyers’ bursti-

ness in e-business process is reﬂected in Table 2. The

comparative analysis of Table 2 reveals that Klein-

berg’s burst detection algorithm, which is based on

a queuing theory, is built on a sequence of phenom-

ena while gap distribution function is featured by se-

quential independence of gaps between two buyers.

The comparative analysis assists in concluding that

e-business process is characterized by sequential in-

dependence of gaps between two buyers.

However, the model has to be validated in terms

of input parameter values and distributions as the

model was already evaluated by experts (Ahrens

et al., 2016b). The novelty of this contribution is

that the model validity is checked by analyzing the

visitor/buyer relationship in two different e-shops.

Whereas the ﬁrst e-shop is focused on selling kitchen

furniture, the second e-shop is specialized in selling

everyday products.

The research question is as follows: What are

practically relevant input parameter values and distri-

butions of the model based on gap processes for the

analysis of buyers’ burstiness in e-business process?

The aim of the research is to validate the simulation

model based on gap processes for the analysis of buy-

ers’ burstiness in e-business process in terms of in-

put parameter values and distributions underpinning

elaboration of a new research question on the model

validity. The meaning of the key concepts of valida-

tion, model validation and model validation approach

is studied. Moreover, the analysis demonstrates how

the key concepts are related to the idea of e-business

process.

The remaining part of this paper is organized as

follows: Section 2 introduces buyers’ burstiness in

e-business process. Here, a mathematical model for

evaluation of buyers’ burstiness in e-business process

via gap processes is presented. In Section 3 the con-

ceptual framework on modal validation is introduced.

The associated results of an empirical study will be

discussed in Section 4. Finally, some concluding re-

marks are provided in Section 5.

2 MODEL DESCRIPTION

The present part of the paper reveals the simula-

tion model based on gap processes for the analysis

of buyers’ burstiness in e-business process with the

focus on the description of buyers’ burstiness in e-

business process and estimation of parameters of buy-

ers’ burstiness.

ICE-B 2017 - 14th International Conference on e-Business

Table 2: Comparison of models for evaluation of burstiness in social media and e-business process.

Model’s Element Social Media E-Business Process

Sequence of batched Sequential independence

Feature georeferenced of gaps

documents between two buyers

Kleinberg’s burst

detection algorithm Gap distribution

Approach based on queuing function

theory

2.1 Buyers’ Burstiness in E-Business

Process

By binary customer behaviour, to buy, or not to buy

is meant as depicted in Figure 1 (Ahrens et al., 2015;

Ahrens and Zaš

cerinska, 2016). It should be noted

that, in the present contribution, the terms customer

and buyer are used synonymously. Within the bi-

To buy

Not to buy

Binary customer behavior

Figure 1: Elements of customers’ binary option.

nary decision (to buy, or not to buy) paradigm, the

e-business process such as selling or buying is a suc-

cess if it ﬁnishes with a deal such as a sale or a pur-

chase (Ahrens et al., 2016c). Gap in the present con-

tribution means the buying process which ends with-

out a purchase (Ahrens et al., 2016c). Buyers’ bursti-

ness is a feature of e-business process. By buyers’

burstiness, intervals of buyers’ high-activity alternat-

ing with long low-activity periods within a fat-tailed

inter-event time distribution is meant (adopted from

(Karsai et al., 2012)).

An efﬁcient modelling of buyers’ burstiness in

e-business processes requires that the characteristic

variables are considered with a given precision. Mod-

els have to take both – the buyers’ probability p

well as the concentration of the buyers – into account

as pointed in Table 3.

Table 3: Characteristics of buyers’ burstiness.

Characteristics

Buyers’ probability Buyers’ concentration

(1− α)

Further on, the levels of buyers’ burstiness are sum-

marized in Table 4.

Models based on gap processes allow a realistic eval-

uation of buyers’ burstiness in e-business process.

Fig. 2 illustrates an e-business process between buy-

ers described by gaps. In (Ahrens et al., 2015; Ahrens

block interval n

buyer

sequence of people

visitor

Figure 2: Buyers’ gap for describing binary customer be-

havior.

and Zaš

cerinska, 2016), the e-business process was

deﬁned by a buyers-gap distribution function u(k)

deﬁning the probability of a gap larger than k, i.e.

u(k) = P(X ≥ k) . (1)

For the buyers-gap distribution function u(k) the

following expression was identiﬁed

u(k) = ((k + 1)

− k

) · e

−β·k

0 ≤ k ≤ ∞ (2)

with

lim

k→∞

−β·k

= 0 β > 0 (3)

and

β ≈ p

1/α

. (4)

The e-business process, i. e. the buyers’ character-

istics, is modeled by two parameters, namely buyers’

probability p

and the buyers’ concentration (1− α).

Re-writing of u(k) leads to the buyers-gap density

function v(k), i. e.

v(k) = P(X = k) , (5)

which describes the probability of a gap X equal to

k. Using (1), buyers-gap density function v(k) can be

calculated as follows

u(k) = v(k) + v(k + 1) + v(k + 2) + ···

u(k+ 1) = v(k+ 1) + v(k+ 2) + ··· .

Finally, by calculating the difference between u(k)

and u(k + 1) the buyers-gap density function v(k) =

P(X = k) can be obtained

v(k) = u(k) − u(k + 1) . (6)

Analysing Buyers’ Burstiness in E-Business: Parameter Estimation and Practical Applications

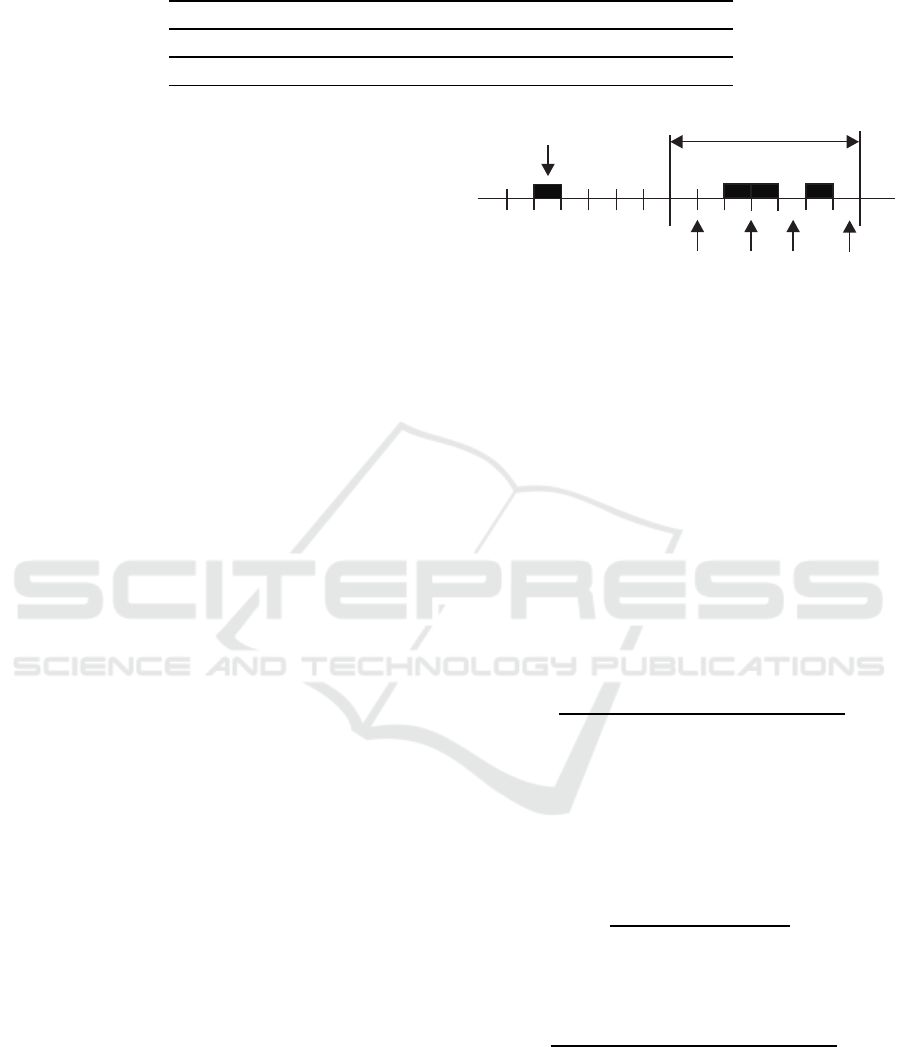
Table 4: Levels of buyers’ burstiness (1− α).

L1 L2 L3 L4 L5

very low low average high very high

0.00− 0.10 0.11− 0.20 0.21− 0.30 0.31− 0.40 > 0.41

The stochastic nature of the e-business process is de-

ﬁned by the buyers-gap density function v(k) or the

buyers-gap distribution function u(k), which depends

on the buyers’ probability p

and the buyers’ concen-

tration (1− α). Figure 3 illustrates the buyers’ bursti-

ness within a sequence of e-shop visitors, which can

be obtained by analyzing (1) for given parameters of

and (1− α).

x x - x x x - - x x x x x x - x x - - - - - - - - - - - -

- - - - - - - x x x x - x - - x x - - x x - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - x x x x

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - x x - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - x x x x - - - - - x - - x x -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - x x x - - - - x x x - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - x x x - - - - - - - - - - - - - - - x x - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

x x x x x - - - - - - - - - - - x x - - x x x x x x - x -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - x x x x x x - - - - - - - - - - - - - - - - - - - -

Figure 3: Buyers’ burstiness (represented by "x") within a

sequence of visitors (represented by "-").

2.2 Buyers’ Burstiness Parameter

Estimation

Next to the generation of data streams which describe

the bursty nature of buyers (see also Fig. 3), it is also

essential to be able to analyze a given set of data for

the buyers’ probability p

and buyers’ concentration

(1− α). In the following section the estimation of p

and (1 − α) are shown based on a given set of col-

lected data.

By analysing the probability P(E) of a pattern E

within an interval of n visitors, information about the

distribution of the buyers can be obtained. Assum-

ing that the gaps between buyers are statistically in-

dependent the probability P(E) of a pattern E in an

interval of n visitors with e buyers at the positions

,·· · ,n

can be obtained

P(E) = p

· u(n

− 1) · u(n− n

) ·

∏

ν=2

v(n

− n

ν−1

− 1) . (7)

block interval

n = 7

buyer

with p

position

1 2

5 6

u(2) v(0) v(1) u(1)

Figure 4: Calculation of the probability P(E) of a pattern E

within an interval of n = 7 visitor with e = 3 buyers at the

positions n

= 3, n

= 4 and n

= 6.

Figure 4 illustrates the calculation of the probability

P(E) of a pattern E within an interval of n = 7 visi-

tors. Here, the e = 3 buyers are at the positions n

= 3,

= 4 and n

= 6. The probability P(E) of such a

pattern E within an interval of n = 7 visitors is given

P(E) = p

· u(2) · v(0) · v(1) · u(1) . (8)

For n = 2 one gets:

P(E) = p

· v(0) (9)

By analysing a captured data stream it is possible

to determine the values P(E) and p

for n = 2. The

probability P(E) can be obtained as follows

P(E) =

E{number of neighbouring buyers}

E{number of visitors}

(10)

with the parameter E{·} denoting the expectation

functional. The number of neighbouring buyers are

counted when after a buyer immediately the next

buyer appears, i.e. the distance k between two buyers

is k = 0 (neighbouring buyers). The buyers’ probabil-

ity p

is given by

E{number of buyers}

E{number of visitors}

. (11)

Combining (9), (10) and (11) we get the probabil-

ity P(E) for n = 2:

P(E) =

E{number of neighbouring buyers}

E{number of buyers}

. (12)

Taking the buyers-gap distribution function u(k) into

consideration

u(k) = ((k+ 1)

− k

) · e

−β·k

0 ≤ k ≤ ∞ (13)

the buyers’ concentration (1 − α) can be calculated.

By analyzing the buyers-gap density function v(k) =

ICE-B 2017 - 14th International Conference on e-Business

P(X = k), which describes the probability of a gap X

equals to k we get

v(k) = u(k) − u(k + 1) . (14)

Analyzing the parameter v(0)

v(0) = u(0) − u(1) (15)

the buyers’ concentration (1 − α) can be estimated.

Analyzing

u(0) = 1 (16)

and

u(1) = (2

− 1)e

−β

. (17)

with the assumption

−β

≈ 1 for β ≪ 1 , (18)

we get

P(E)

= v(0) ≈ 2− 2

. (19)

From this equation, the buyers’ concentration (1− α)

is given as

(1− α) ≈ 1− log

[2− v(0)] . (20)

Practically, analysing a captured sequence for the

buyers’ concentration (1− α) requires the calculation

of the parameter v(0). Here, the equation

v(0) = 1− u(1) (21)

has to be analysed for a given data sequence. The

parameter u(1) describes the probability for buyers’

gaps larger than 1, i. e.

u(1) = P(X ≥ 1) . (22)

Let us assume that a given sequence contains 9807

buyers. After analysing the buyers’ gaps it was found

out that 8247 gaps with k ≥ 1 are within the se-

quence. Following, we have 1560 situations where

after a buyer in the distance of k = 0 another buyer

appears. Here we get

v(0) = 1−

8247

9807

= 0,159 . (23)

Finally, in this sequence we can expect a buyers’ con-

centration (1− α) of

(1− α) ≈ 1− log

[2− 0,159] = 0,1195 , (24)

concluding, that the calculated buyers’ concentration

(1− α) shows a low level of burstiness.

3 CONCEPTUAL FRAMEWORK

No model can be accepted unless it has passed the

tests of validation, since the procedure of validation is

vital to ascertain the credibility of the model (Martis,

2006).

Validation is the task of demonstrating that the

model is a reasonable representation of the actual sys-

tem: that it reproduces system behaviour with enough

ﬁdelity to satisfy analysis objectives (Govindarajan,

2014).

A model is usually developed to analyse a par-

ticular problem and may therefore represent differ-

ent parts of the system at different levels of abstrac-

tion (Govindarajan, 2014). As a result, the model

may have different levels of validity for different parts

of the system across the full spectrum of system be-

havior (Govindarajan, 2014). For most models there

are three separate aspects which should be considered

during model validation (Govindarajan, 2014):

• Assumptions,

• Input parameter values and distributions and

• Output values and conclusions.

The assumptions of the simulation model based

on gap processes for the analysis of buyers’ bursti-

ness in e-business process were validated (Ahrens

et al., 2016a). Experts positively evaluated the pre-

sented simulation model (Ahrens et al., 2016b). Con-

sequently, the present contribution will concentrate

on such a model validation as input parameter val-

ues and distributions. Real system measurements will

be carried out of three approaches to model validation

(Govindarajan, 2014):

• Expert intuition,

• Real system measurements and

• Theoretical results/analysis.

It should be noted that any combination of the

three approaches may be applied as appropriate to the

different aspects of a particular model (Govindarajan,

2014).

Real system measurements mean comparison with

a real system that is the most reliable and preferred

way to validate a simulation model (Govindarajan,

2014). In practice, however, this is often infeasible

because the measurements would be too expensive

to carry out as assumptions, input values, output val-

ues, workloads, conﬁgurations and system behaviour

should all be compared with those observed in the real

world (Govindarajan, 2014).

Analysing Buyers’ Burstiness in E-Business: Parameter Estimation and Practical Applications

4 PRACTICAL APPLICATIONS

For data analysis the visitor/buyer relationship was

captured in two e-shops as highlighted in Table 5.

Table 5: E-Shop’s characteristics for analysing visitor and

buyer relationship.

E-Shop Number Shops Specialization

1 selling kitchen furniture

2 selling everyday products

E-shop 1 is specialized in selling kitchen furniture.

Here a low level of buyers’ concentration (1 − α)

as well as a low buyers’ probability p

is expected.

Whereas e-shop 2 sells everyday products, here peo-

ple visit with a high wish to buy. That is why a higher

level of buyers’ concentration and buyers’ probability

is assumed. The data are captured within 10 minutes

intervals. A "x" appeared when at least one buyer

was registered within the 10 minutes interval as re-

vealed in Fig. 5 and 6. The data were collected for

two month.

x - --- - - xx - x- - - - - - - - - - - - - - xx - - - - - x - - -

- - ---x - - - - - - - - - - - -x - - - - - - x - - - - - - - xxx

- - --- - - - - - - - - - - - - - - - - - x- - - - - - - - - - - - -

- - --- - - - x - - - - - x -x- - - - - - - - - - - - - - - - x - -

x - --- - - - - - - - - - x-x- - - - x - - - - - xx- - - - - - -

- - --- - - - - - - - - - x- - - - - - x - - - - - - - - - - - - - -

- - --- - - xx - - -x - - - - -x - - - - - - - - - - - - - - - - -

- - --- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - --- - - - - - - - - - - - - - - - - x - - - - x - - - - - - - x -

- - --- - - xxx - - - - - - - - - x - - - - - - - - - - - - - - - -

- x---x - - - - - - - - - - - - - - - - - - - - x - - - - - - - - -

- - ---x - - - - - - - - - - - - - - x - - - - - x - - -x - xx - -

- - --- - x - - - - - - - - - - -x - x x - -xx - - - - - - - - - -

- - --- - - - - - - - - x - - - - - - - - - - - x - - - - - x - - - x

Figure 5: Buyers’ distribution (in parts) within E-Shop 1

(buyer represented by "x" and visitor represented by "-").

x - - - - x - - - - - - - - - - - - - - - - - - - - - - x - - xx - - x

- xx - - - - - - x - x - - - - - xx - - - - - - x- - - - - - - - - -

- - - - xxxxx - - - - - - - - - - x - x - - - - - x - x - x - - xx

- - - x - - xxxx - - - - - - - - - - - xxxx - - - - x - - - xxx

x - - - x - x - - - - xx - - x - - x - x - - - - x - - x - - xxxx -

- - - - - - x - - - - - x - x - - - - - - - - - - x - - - - x- x - - -

- - - - -xxx - x - - - - - - - xxx - - x - - - xx - - - - - - - -

- - - - -x - - - - x - - - - - - - - - - - xx - x - - xx - - - - - x

xx - - - - - - - -xx - - - - - - - - - - - - - - - - - - - - - - - -

- - x - - - - - - - - - - - - - - - - - - - - - - - - x - - xx - - x -

xx - - - - - xxxx - - - - - x - - - - - - - - - x - - xx - - - - -

x - - - - - - - x - - - - - x- - - x - - - - - - - xx - - x - - x - x

x - x - - x - - x -x - - - - xx - xx - - xx - x- - - - x - - - - -

- x - x - x - - - - xx - - - x - - x - x - - - - - - - - - - - - - - -

- - - - -x - - - - x - xx - - - xxx - - x - - - - - xx - - - x - -

Figure 6: Buyers’ distribution (in parts) within E-Shop 2

(buyer represented by "x" and visitor represented by "-").

With the estimated values for the buyers’ probability

and buyers’ concentration it is now possible to calcu-

late the averaged gap-length between two buyers. The

Table 6: Estimated levels of buyers’ probability and buyers’

concentration for the investigated E-Shops.

E-Shop Buyers’ probability Buyers’ concentration

(1− α)

1 0,091 0,039

2 0,252 0,187

averaged gap-length can be calculated as follows

E(k) =

∞

∑

k=0

k· v(k) =

∞

∑

k=0

u(k) − 1 (25)

and depends on the buyers’ probability and buyers’

concentration. The buyers’ probability is given by

E(k) + 1 =

. (26)

Data analysis presented in Tab. 6 allows estimating

the levels of buyers’ probability and buyers’ concen-

tration for the investigated e-shops based on Tab. 4.

Tab. 7 presents the levels of the buyers’ concentration

for the investigated e-shops: In e-shop 1 the buyers’

concentration refers to Level 1 or the very low level

of buyers’ burstiness and in e-shop 2 the buyers’ con-

centration indicates level 2 or the low level of buyers’

burstiness.

Table 7: Estimated levels of buyers’ concentration for the

investigated e-shops.

Shop Levels of buyers’ concentration

1 L1

2 L2

Summarizing content analysis (Mayring, 2004) of the

data reveals that the buyers’ burstiness in

• E-Shop 1 (the furniture shop) is of the very low

level and

• E-Shop 2 (the everyday product shop) is of the

low level.

5 CONCLUSIONS

The practical applications of the simulation model

based on gap processes for the analysis of buyers’

burstiness in e-business process allow drawing a con-

clusion that the model is valid.

The empirical ﬁndings of the research allow draw-

ing the conclusions on the levels of buyers’ probabil-

ity and buyers’ concentration for the two investigated

e-shops.

The following research question has been formu-

lated: Is the simulation model based on gap processes

ICE-B 2017 - 14th International Conference on e-Business

for the analysis of buyers’ burstiness in e-business

process valid in terms of output values?

The present research has limitations. The inter-

connections between e-business process, binary cus-

tomer behaviour, the buyers’ burstiness and gap pro-

cesses have been set. The study is also limited by

• Considering only one aspect of model validation

such as input parameter values and distributions

and

• Examining the model validation in terms of input

parameter values and distributions only through

one approach, namely real system measurements.

Another limitation is the empirical study based on

two cases only. Therein, the results of the study can-

not be representative for the whole area. Neverthe-

less, the results of the research, namely practical ap-

plication of the mathematical model for evaluation of

buyers’ burstiness in e-business process based on gap

processes and its results, may be used as a basis of

analysis of buyers’ burstiness in e-business process. If

the results of other cases had been available for anal-

ysis, different results could have been attained. There

is a possibility to continue the study.

Further research tends to facilitate the practical

applications of the validated simulation model for

evaluation of buyers’ burstiness in e-business process.

Despite that initial validation attempts will concen-

trate on the output of the model, and only if that val-

idation suggests a problem more detailed validation

will be undertaken (Govindarajan, 2014), the search

for relevant methods, tools and techniques for further

model validation is proposed. Consideration of output

values is planned. Use of the combination of the three

approaches is intended for application in order to val-

idate the simulation model (Govindarajan, 2014):

• Expert intuition,

• Real system measurements and

• Theoretical results/analysis.

A comparative research on validation of simula-

tion models for evaluation of burstiness in other sci-

entiﬁc ﬁelds could be carried out, too.

REFERENCES

Ahrens, A., Purvinis, O., Zaš

cerinska, J., and Andreeva,

N. (2015). Gap Processes for Modelling Binary Cus-

tomer Behavior. In 8th International Conference on

Engineering and Business Education, pages 8–13, Os-

tfold University College, Fredrikstad (Norway).

Ahrens, A., Purvinis, O., Zaš

cerinska, J., and Andreeva, N.

(2016a). Education for Health Society: Indicators of

Burstiness in Research. Education in a Changing So-

ciety, 1:28–40.

Ahrens, A., Purvinis, O., Zaš

cerinska, J., and Andreeva, N.

(2016b). Experts’ Evaluation of the Model for Analy-

sis of Buyers’ Burstiness in E-Business. In 4th Annual

International Scientiﬁc-Practical Application Confer-

ence Trends in Science and Higher Education Stud-

ies Under Conditions of Globalization., Panevezys

(Lithuania). (accepted for publication).

Ahrens, A. and Zaš

cerinska, J. (2016). Gap Processes for

Analysing Buyers Burstiness in E-Business Process.

In International Conference on e-Business (ICE-B),

Lisbon (Portugal).

Ahrens, A., Zaš

cerinska, J., Purvinis, O., and Andreeva, N.

(2016c). A Model for Simulation of Binary Customer

Behaviour in a Bursty Business Process. In Interna-

tional Forum on Innovative Technologies and Man-

agement for Sustainability., Panevezys (Lithuania).

Elliott, E. O. (1963). Estimates of Error Rates for Codes on

Burst-Noise Channels. Bell System Technical Journal,

42(5):1977–1997.

Gilbert, E. N. (1960). Capacity of a Burst-Noise Channel.

Bell System Technical Journal, 39:1253–1265.

Govindarajan, M. (2014). Decision Making Methods. IGI

Global, New York, wang, j.: encyclopedia of business

analytics and optimization edition.

Heinrich, R. (2014). Aligning Business Processes and In-

formation Systems: New Approaches to Continuous

Quality Engineering. Springer, New York, 1 edition.

Karsai, M., Kaski, K., Barabasi, A., and Kertesz, J. (2012).

Universal Features of correlated Bursty Behavior. Sci-

entiﬁc Reports.

Kotozaki, K., Tamura, K., and Kitakami, H. (2015). Identi-

fying Local Burstiness in a Sequence of Batched Geo-

referenced Documents. International Journal of Elec-

tronic Commerce Studies, 6(2):269–288.

Martis, M. S. (2006). Validation of Simulation Based Mod-

els: A Theoretical Outlook. Electronic Journal of

Business Research Methods, 4(1):39–46.

Mayring, P. (2004). Qualitative Content Analysis. In A

Companion to Qualitative Research, pages 266–269.

SAGE, Glasgow (UK).

Analysing Buyers’ Burstiness in E-Business: Parameter Estimation and Practical Applications