Not ACID, not BASE, but SALT

A Transaction Processing Perspective on Blockchains

Stefan Tai, Jacob Eberhardt and Markus Klems

Information Systems Engineering, Technische Universit

at Berlin, Germany

Keywords:

SALT, Blockchain, Decentralized, ACID, BASE, Transaction Processing.

Abstract:

Traditional ACID transactions, typically supported by relational database management systems, emphasize

database consistency. BASE provides a model that trades some consistency for availability, and is typically

favored by cloud systems and NoSQL data stores. With the increasing popularity of blockchain technology,

another alternative to both ACID and BASE is introduced: SALT. In this keynote paper, we present SALT

as a model to explain blockchains and their use in application architecture. We take both, a transaction and

a transaction processing systems perspective on the SALT model. From a transactions perspective, SALT is

about Sequential, Agreed-on, Ledgered, and Tamper-resistant transaction processing. From a systems perspec-

tive, SALT is about decentralized transaction processing systems being Symmetric, Admin-free, Ledgered and

Time-consensual. We discuss the importance of these dual perspectives, both, when comparing SALT with

ACID and BASE, and when engineering blockchain-based applications. We expect the next-generation of

decentralized transactional applications to leverage combinations of all three transaction models.

1 INTRODUCTION

There is a common belief that blockchains have the

potential to fundamentally disrupt entire industries.

Whether we are talking about ﬁnancial services, the

sharing economy, the Internet of Things, or future en-

ergy markets – any application where some form of

trade and agreement among different parties occurs is

deemed a candidate for blockchains. And when us-

ing blockchains, so the promise, trustless interactions

– in the sense that trust no longer must be managed

by some central or intermediating party – and hence

lowered transaction costs and other beneﬁts of decen-

tralization are introduced.

Is this considerable interest in blockchain technol-

ogy justiﬁed? What are blockchain-based transac-

tions? How do blockchain-based transactions com-

pare to traditional database and distributed systems

transactions? Do blockchains replace other database

technology and systems or should they be used as a

complement?

In this keynote paper, we take a transaction pro-

cessing perspective on blockchains. With relational

database management systems that implement ACID

transactions, and cloud systems and NoSQL stores

that favor the BASE model, we have two established

models to compare blockchain-based transactions

against. Using the admittedly contrived acronym of

SALT, we characterize blockchain-based transactions

– from a transactions perspective – as Sequential,

Agreed, Ledgered, and Tamper-resistant, and – from

a systems perspective – as Symmetric, Admin-free,

Ledgered, and Time-consensual.

Following either ACID, BASE, or SALT naturally

results in different notions of transactions and dif-

ferent transactional system architectures. Using two

real-world application examples that use blockchains

we illustrate how different business transactions map

to a combination of these three transaction models

and corresponding data management components.

2 BLOCKCHAINS

Since its inception in 2008 as the technology behind

Bitcoin (Nakamoto, 2008), blockchains are discussed

in a diversity of communities in research and practice.

These include cryptocurrency and security, databases

and distributed systems, IT law, entrepreneurship, and

many more. In addition, blockchain developer com-

munities exist, focusing on speciﬁc blockchain tech-

nologies such as Bitcoin, Ethereum, Hyperledger, and

other. Out of the many views on blockchains and cor-

responding deﬁnitions that exist, we like to emphasize

Tai S., Eberhardt J. and Klems M.

Not ACID, not BASE, but SALT - A Transaction Processing Perspective on Blockchains.

DOI: 10.5220/0006408207550764

In Proceedings of the 7th International Conference on Cloud Computing and Services Science (CLOSER 2017), pages 755-764

ISBN: 978-989-758-243-1

755

the following three:

1. A blockchain is a peer-to-peer protocol for trust-

less execution and recording of transactions se-

cured by asymmetric cryptography in a consistent

and immutable chain of blocks – the blockchain

developers and technology view.

2. A blockchain is a shared append-only distributed

database with full replication and a cryptographic

transaction permissioning model – the IT architect

and data management view.

3. A blockchain is a shared decentralized ledger, en-

abling business disintermediation and trustless in-

teractions, thereby lowering transaction costs –

the business executive and applications view.

With each of these three deﬁnitions, a different

emphasis is set, focusing either on the protocol aspect,

the data management aspect, or the decentralization

aspect of blockchains. Yet, all three deﬁnitions make

use of the term transaction. In the following, we thus

take a closer look at what a transaction is and how

such transactions traditionally have been supported by

transaction processing systems.

3 TRADITIONAL

TRANSACTIONS AND TP

SYSTEMS

A (business) transaction, in its most generic sense and

as used in commerce, is an instance of buying or sell-

ing something. In computer science, a transaction is

a logical unit of work performed within a transaction

processing system (TP system). A TP system, in turn,

refers to an information processing system that di-

vides all processing work into transactions, in a way

that each transaction can be guaranteed a set of prop-

erties by the system.

3.1 Understanding ACID

In the 1980s, relational database management sys-

tems (RDBMS) based on Codd’s relational model

were ﬁrst introduced. With the addition of TP tech-

nologies to RDBMS a few years later, originally pro-

posed by Jim Gray, the acronym “ACID transaction”

was born (Gray and Reuter, 1992). ACID refers to a

set of guarantees for each transaction to be processed

by the TP system: Atomicity, Consistency, Isolation,

and Durability.

ACID has since been understood as a very conve-

nient model:

• A transaction consisting of multiple operations is

executed as a whole or not at all (“all or nothing”).

• Each transaction transforms the database from

one consistent, valid state to another, adhering

to all validation rules and database integrity con-

straints.

• Concurrent transactions are executed by maintain-

ing isolation, that is, by executing them as if they

were sequential.

• Once a transaction has been committed, the re-

sults become permanent.

The responsibilities to achieve the ACID proper-

ties are spread across different components of a TP

system (Bernstein and Newcomer, 2009). A transac-

tion manager component typically is required to drive

coordination protocols among the resource managers,

for example, the 2PC completion protocol. Consis-

tency is a responsibility of components that perform

validation checks, for example, by using the rules

of the database itself. Isolation requires some con-

currency control, which typically relies upon locking

protocols such as the 2PL. And durability typically is

a responsibility of the database itself.

Figure 1 illustrates a TP system in support of

ACID transactions. An application interacts with

the transaction manager to begin (1) and end (3) a

transaction as a logical unit-of-work. Each transac-

tion groups a set of operations (2) on one or more

databases (resources). For each resource involved

in a transaction, a resource manager component ex-

ists. The resource managers must be registered with

the transaction manager and must understand proto-

cols and provide interfaces in support of transaction

processing, e.g., the X/Open XA interface, so that

the transaction manager can run completion protocols

when committing the transaction (4).

Resource

Manager

Resource

Manager

Transaction

Manager

Application

Resource Resource

1 3

interface

RM2

interface

RM1

interface

Figure 1: Architecture of a TP system supporting ACID

transactions.

Guaranteeing the ACID properties implies that

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

756

whenever things do go wrong, the TP system will

detect the failure and rollback any intermediate steps

taken, if necessary.

3.2 Understanding BASE

With the emergence of unprecedented scalability

needs of modern Web applications, an alternative to

the rather expensive and consistency-focused ACID

model was introduced: BASE – Basically Avail-

able, Soft state, Eventually consistent. The term was

coined around the year 2000, deliberately constructed

to describe a model that is diametrically opposed to

ACID (Brewer, 2000).

Today, BASE is a model commonly favored by

cloud systems and NoSQL stores. BASE captures the

following properties (Pritchett, 2008):

• A system is basically available when supporting

partial failures without total system failure.

• The state of the system is ‘soft’ in that it can

change over time even if no further updates are

made.

• The system will eventually become consistent, if

no new updates are made to the system.

Generally, BASE systems follow a peer-to-peer

architecture, where each peer is equally responsible

for a subset of the overall data, a so-called shard. An

incoming client request is forwarded to a responsible

node based on a sharding function, e.g., a distributed

hashtable. No notion of a transaction manager exists

with BASE systems; all nodes can instead process in-

coming requests, which dramatically increases scala-

bility and throughput. Shards themselves are usually

replicated for increased fault tolerance. Hence, not

only the data itself, but also the control over it is dis-

tributed.

BASE systems typically use optimistic replication

techniques and thereby trade some consistency for

availability. Instead of requiring availability of all

components that are participating in a logical transac-

tion (and thereby coupling all components when pro-

cessing the transaction), a BASE design encourages

interaction only with select nodes and components,

thereby tolerating partial failures (of other nodes and

components) and accepting that the overall consis-

tency will be in a state of ﬂux. Read and write oper-

ations by different clients can be performed by differ-

ent nodes in the system, thereby ensuring high avail-

ability. Updates written to a node typically are prop-

agated asynchronously to other required nodes after

returning to the client – the system therefore is in soft

state and, if no new updates are made to a given data

item, will only eventually converge to a consistent

state.

Figure 2 illustrates a system that follows the

BASE model. An application interacts either directly

with a resource managing component (1.b), or, more

typically, through some load balancer (1.a) that dis-

tributes incoming requests to peers of nodes with

symmetrical responsibilities and capabilities. Re-

quests are served by one or more resource managers

directly, and changes are propagated (2) to other re-

quired nodes subsequently. The number of resource

managers required depends on the sharding model

and the system conﬁguration chosen, ranging from a

single node (single replica) to a quorum of nodes to,

theoretically, all replicas of a given data record.

Resource

Manager

Resource

Manager

Load

Balancer

Application

Resource Resource

RM interface

sync

RM2

interface

RM1

interface

sync

Figure 2: Architecture of a System following the BASE

model.

Notice that BASE refers to properties of the TP

system more so than of an individual transaction, and

that BASE hardly describes any guarantee: being ba-

sically available, soft-state and eventually consistent

are very weak guarantees, if any. In comparison to

ACID, BASE does not address atomicity and does not

support isolation. BASE compromises consistency

to eventual consistency. Durability (persistence) of

changes to the system is the only property common to

both models.

In the context of BASE systems, the term trans-

action (and transaction processing, correspondingly)

is misleading. A “BASE transaction” – if at all –

probably is best understood as the unit of work com-

prising an initial client request to one system node

and all subsequent steps to propagate the effects of

that request to all other required nodes. However, we

prefer referring to “ACID transactions” (rather than

“ACID systems”) and to “BASE systems” (rather than

“BASE transactions”) instead, reﬂecting the focus of

each of the acronyms.

Not ACID, not BASE, but SALT

Not ACID, not BASE, but SALT - A Transaction Processing Perspective on Blockchains

757

4 SALT: THE BLOCKCHAIN

ALTERNATIVE TO ACID AND

BASE

While ACID transactions provide convenient consis-

tency guarantees and BASE systems scale to meet the

demands of the largest of applications, they both re-

quire the users’ trust. A blackbox to the clients, the

correct execution of transactions can rarely be con-

trolled. For example, when you send money to a bank

account, you cannot be sure that this account was ac-

tually credited. You rather trust your bank to play by

the rules and to keep balances correct.

Turning to blockchains now, an alternative to

ACID and BASE is introduced. Blockchains address

this trust concern and propose a system design that

enables transactions which do not involve trust in a

central party (therefore, the interactions become trust-

less). These transactions neither ﬁt the ACID nor the

BASE model, which is why we introduce SALT as

a new acronym to describe the unique properties of

blockchain-based transactions and systems.

Whereas ACID compromises availability in favor

of consistency, and BASE compromises consistency

in favor of availability, blockchains compromise scal-

ability in favor of trustless interactions (Tai, 2017).

As explained before, ACID focuses on properties

of transactions while BASE focuses on properties of

the system. Hence, we provide two SALT perspec-

tives: a transactions perspective, and a systems per-

spective.

4.1 SALT – The Transactions

Perspective

Blockchain-based transactions can be character-

ized as Sequential, Agreed, Ledgered, and Tamper-

resistant.

Notice that blockchains use two main types of data

records: transactions and blocks. A block groups a set

of transactions. The SALT transaction properties also

apply to blocks, however, for now, we will concen-

trate on transactions and discuss blocks in section 4.2

when deﬁning the SALT systems properties.

Sequential

All transactions are processed sequentially. Unlike

with ACID transactions, there is no parallel process-

ing of transactions in the SALT model. However, just

like the isolation property in ACID, all transactions

are processed in a sequential order.

Agreed

A transaction is accepted when the majority of the

network agrees on its validity. Essentially, commu-

nity consensus determines the system state – unlike

in ACID and BASE, where it is solely controlled by a

central authority.

Ledgered

All agreed-on transactions are added to an append-

only transaction ledger and cannot be revoked. State

changes cannot be undone; compensating transac-

tions can be processed, however.

Note, though, that the ledgered property is a bit

weaker than the durability property in ACID. Due to

the majority-based agreement process, a part of the

ledger may be overwritten by another, later version.

The likeliness of this happening for a given transac-

tion quickly diminishes with the number of transac-

tions succeeding said transaction.

Tamper-Resistant

A transaction cannot be manipulated or censored.

This has two dimensions: Pending and agreed-on

transactions.

Unlike with ACID and BASE, there is no cen-

tral access management. The access control model

is completely decentralized and tied to asymmetric

cryptography. Pending transactions contain a signa-

ture that only the original sender can create. There are

no privileged users which could alter or block pend-

ing transactions. Furthermore, the ledger data struc-

ture is designed in a way that any alteration to an

agreed-on transaction would invalidate the data struc-

tures. Hence, other nodes in the network could never

be convinced of such an invalid history.

4.2 SALT – The Systems Perspective

Blockchain-basesd systems supporting transactions

can be characterized as Symmetric, Admin-free,

Ledgered, and Time-consensual.

Symmetric

All nodes in the peer-to-peer network symmetrically

share their responsibilities. This does not only refer

to transaction processing, but also to state storage and

propagation of information.

Admin-free

As a fully peer-to-peer system, there is no concept of

a system administrator who is responsible for main-

tenance, infrastructure provisioning or access control.

Updates of peers happen on an individual basis and

by that are subject to community consensus.

Ledgered

All peers in the system maintain an append-only data

structure of transactions which we refer to as the

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

758

interface

Transaction

Manager

Resource

Manager

Resource

Block

interface

validation

Block

validation

Block

mining

Append

block

interface

Transaction

Manager

Resource

Manager

Resource

Block

interface

validation

Block

validation

Block

mining

Append

block

interface

Transaction

Manager

Resource

Manager

Resource

Block

interface

validation

Block

validation

Block

mining

Append

block

Application

Legend

internal

interface

external

interface

Miner

Figure 3: Transaction-oriented Architecture of the SALT system perspective.

ledger. Before transactions can be appended to that

ledger, all nodes in the network need to agree on an

order to maintain the ledgers consistency.

Since ﬁnding consensus is expensive, blockchains

introduce blocks, a data structure that groups a set of

transactions. Blocks are then used as the unit of con-

sensus, thus reducing the number of consensus rounds

relative to the number of transactions. When consen-

sus is found, the agreed-on block is appended to the

ledger and with it the contained transactions.

Time-consensual To ensure timely processing of

transactions while tolerating network latencies due to

geo-distribution of the networks’ peers, the consensus

algorithm targets a deﬁned average time between the

creation of two blocks. This is called the block inter-

val. Hence, while not guaranteed, a transaction is on

average processed and included into the ledger within

half the block interval.

4.3 Understanding SALT

Figure 3 illustrates a TP system in support of SALT

transactions. An application can begin a transaction

with any of the peers in the system (1). Each peer

maintains a local copy of the entire blockchain. The

transaction is validated locally at the chosen node and

– if valid – added to its list of ”pending transactions”

(2). Furthermore, the node propagates the validated

transaction to other nodes in the network (3). The

receiving nodes perform the same steps themselves

(4), which together leads to a gossip-like spread of

valid transactions and them being in pending state on

many nodes.

Some of the nodes – called the miners – group

their pending transactions into candidate blocks, the

unit of consensus. This happens in parallel on many

nodes and a consensus algorithm, (e.g., Proof-of-

Work, Proof-of-Stake) is used to decide which node’s

candidate block becomes a valid block accepted by

the network without communication between peers.

This is referred to as mining (5). This agreed-on block

is then appended to the miner’s blockchain (6) and

broadcast (7) so it spreads to all nodes in the network

in a gossip-like way. The receiving nodes check the

validity of the block (8) by validating all contained

transactions as well as the contained proof, that the

block was actually selected in the consensus process.

A valid block is then appended to the node’s local

blockchain. As this happens on all nodes in the net-

work, the contained transactions are now reﬂected in

the overall system state.

4.4 Comparing SALT, ACID and BASE

A SALT transaction conceptually is simpler than an

ACID transaction; there is no concept of grouping

multiple operations into an atomic unit-of-work from

a client perspective. Hence, no SALT property di-

rectly relates to the atomicity property of ACID. Note,

however, that grouping multiple operations is possible

inside a SALT system by creating stored procedures.

We expand on this idea in section 4.5. Neither of both

approaches is commonly supported in BASE systems.

The isolation property of ACID is closely related

to the sequential processing of transactions in the

Not ACID, not BASE, but SALT

Not ACID, not BASE, but SALT - A Transaction Processing Perspective on Blockchains

759

SALT model. In both models, transactions have a

well-deﬁned order that is consistent within the net-

work. In BASE systems, in contrast, a deﬁned global

order of transactions is not enforced by the system

and does not have to exist, which is why BASE sys-

tems are soft-state.

Both, the agreed-on property of SALT and the

consistency property of ACID, refer to the validity

of transactions and are thus closely related. While

essentially the same guarantee, the parties enforcing

the guraranee differ: In the ACID case, speciﬁc com-

ponents of the TP system check the post transaction

database state for integrity and reject transactions in

case of violations. In the SALT case, all nodes in the

network independently validate transactions based on

an agreed-on ruleset and acknowledge them depend-

ing on the result.

Note, that this notion of consistency in ACID and

SALT is different from the system-centric consistency

notion in BASE. With BASE systems, consistency

refers to (reaching) equivalence of state across repli-

cas. This notion of consistency is a pre-requisite for

distributed systems in support of ACID transactions,

also. Yet, ACID makes no direct statement about

replica consistency. In systems supporting BASE,

replicas can be in conﬂicting state because they each

process a different set of transactions. The same can

happen in systems supporting SALT, when two nodes

mine different blocks and hence temporarily maintain

different state. Whereas systems supporting BASE

are guaranteed to converge in the absence of new

transactions, in SALT systems the conﬂict is resolved

by deciding for exactly one block to be agreed-on by

all peers.

Another interesting relation exists between the

ledgered property of SALT and the durability prop-

erty of ACID, as already brieﬂy discussed in 4.1. Not

considering factors external to the system, a trans-

action written to a TP system supporting ACID or

BASE is guaranteed to be persistent and cannot be

lost. This guarantee is weakened to a probabilis-

tic version in the SALT model. It can happen, that

a transaction is no longer represented in the system

state although it has been processed successfully at

an earlier point in time. With the number of subse-

quent transactions, the probability of this happening

quickly diminishes (Nakamoto, 2008). While having

to rely on probabilistic state appears unreliable, it is

barely a problem in current networks (e.g., Bitcoin or

Ethereum). As a best practice, users wait for a cer-

tain number of blocks (based on their risk threshold)

succeeding the block containing their transaction until

they consider the transaction to be ﬁnal.

4.5 T for Turing Complete?

Traditional TP systems know the concepts of stored

procedures. These procedures group a sequence of

database operations and can be exposed to clients.

This reduces the permissions clients require and can

also improve usability.

With blockchains, the same concept becomes

much more powerful. The procedure is executed

on every node in the network and the resulting state

changes are applied. Hence, a stored procedure on

a blockchain is essentially a piece of software that is

executed in a fully decentralized way without anyone

being able to control it.

Applying the concept of stored procedures to

blockchains has two challenges, though. Because the

state changes caused by the stored procedures on ev-

ery node have to be consistent, the code needs to be

deterministic. Furthermore, for the network to make

progress and for block times to average the targeted

block interval, there can be no inﬁnite loops or long

running transactions.

Determinism can be achieved by not allowing any

non-deterministic operations in stored procedures.

External API calls, for example, cannot be allowed,

as they might yield different results when performed

on different nodes in the network.

The second problem, preventing inﬁnite loops,

theoretically reduces to the halting problem: Does

a given program terminate or will it run forever? It

is well known, that this problem is undecidable for

turing-complete languages, so another way of pre-

venting inﬁnite loops has to be found.

One approach is to write stored procedures in a

less powerful language so they are guaranteed to ter-

minate after a well-deﬁned number of steps. While

this constrains overall expressiveness, it enhances se-

curity by reducing potential vulnerabilities. A promi-

nent example of a blockchain following this approach

is Bitcoin, which provides a rather limited scripting

language mainly used for signature veriﬁcation.

Another approach is to introduce a cost model

to a turing-complete language: Every operation is

assigned a price and an initial endowment is speci-

ﬁed for a stored procedure when it is called. With

that, every stored procedure is guaranteed to halt, be-

cause even if it contains an inﬁnite loop, the endow-

ment will be used up at some point which causes ex-

ecution to stop. Although it involves additional risk

from a security perspective, this approach is certainly

more expressive and enables more powerful appli-

cations. However, the cost calculation and tracking

during execution involve considerable overhead. The

Ethereum blockchain adopts this approach and refers

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

760

to its stored procedures as Smart Contracts (Buterin,

2014), (Wood, 2014).

5 DESIGNING SALTy

APPLICATIONS

With an understanding of SALT transactions and

SALT systems, we now turn to the question of how

to design the next generation of decentralized trans-

actional applications that use blockchains. Innovative

companies are already building such applications to-

day, which allows us to discuss SALT in the context

of speciﬁc industry use cases. Besides ﬁnancial ap-

plications in the banking and insurance industry, there

are numerous examples of non-ﬁnancial, blockchain-

based applications, such as notary services, digital

content monetization, decentralized storage, decen-

tralized IoT, and so on (Crosby et al., 2015).

We propose to approach the design and analysis

of blockchain-based applications along the two SALT

perspectives: the transactions perspective, and the

systems (data management components) perspective.

We selected two non-ﬁnancial use cases to illustrate

the basic approach.

5.1 Monegraph Use Case

The ﬁrst use case, Monegraph, is a content distri-

bution and monetization platform that enables media

creators to transfer rights of digital artwork to media

owners (Monegraph, 2017). With the platform, me-

dia creators, such as photographers, videographers,

and musicians, can monetize their work, and media

owners can manage their media’s use rights, distribute

content, and share revenue with media creators, pub-

lishing partners, and afﬁliates.

5.1.1 The Transactions Perspective

The main business transactions from the point of view

of the two main stakeholders, the media creators and

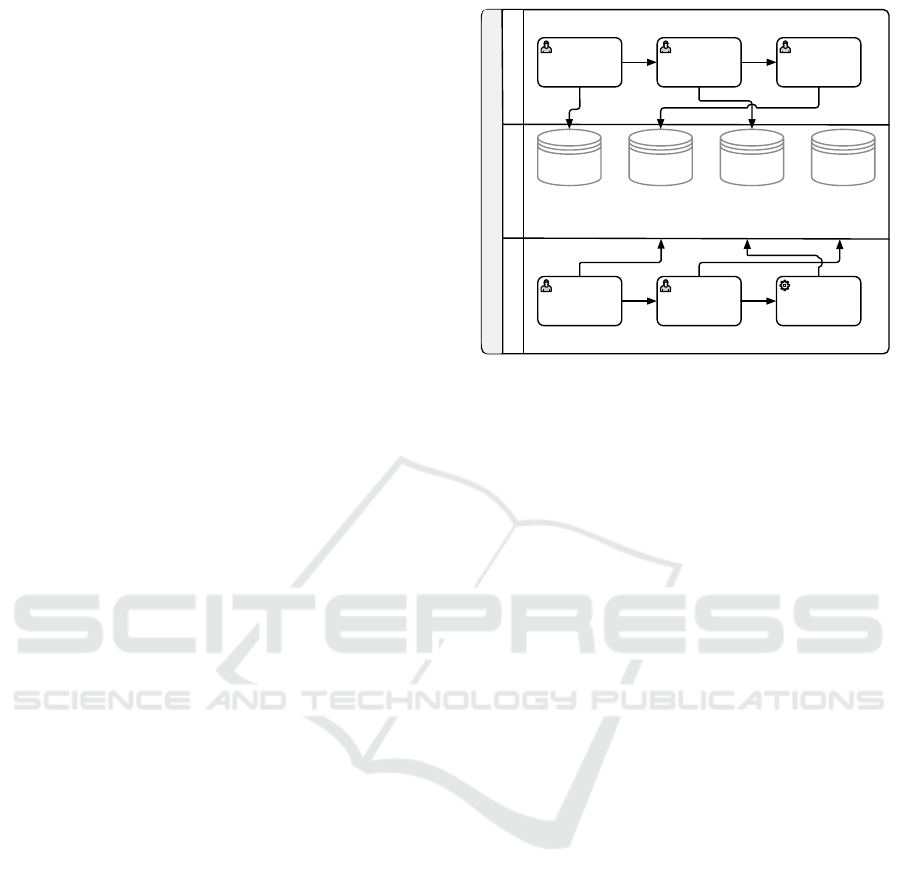
the media owners, are the following, as depicted in

ﬁgure 4.

• Media creators can, for example, create and up-

load digital artwork (as a ﬁle), register the artwork

as a public record, and list their artwork in a pri-

vate catalog.

• Media owners use the platform to agree to terms

(in the form of a Smart Contract), make payments

using Bitcoin or traditional payment transactions,

and transfer ownership of the public record.

Monegraph

Data Mgt. Media Creator

Create

digital artwork

artwork

List in

catalog

Media Owner

Agree

to terms

Make a

payment

Transfer of

ownership

File Store

(AWS S3)

Doc Store

(Couchbase)

Blockchain

(Ethereum)

Blockchain

(Bitcoin)

Art Portfolio

Binary Assets

Sales Contracts

& Catalogs

JSON Docs

Owner History

Crypto Hashes

Payments

Virtual Currency

Figure 4: Monegraph use case from a combined transac-

tions and data management systems perspective.

Using blockchain technology, Monegraph gains

the following SALT transaction properties.

Sequential

Transactions are guaranteed to be processed in a se-

quential order so that the transfer of media rights from

creators to owners is performed without “double sell-

ing”, i.e., selling the same rights to different media

owners.

Agreed

Since an agreement among the majority of the

blockchain network is required, it becomes more dif-

ﬁcult to illegitimately claim media rights ownership.

Once an agreement on a transaction has been reached

in the network, there is a certain level of trust that me-

dia rights that have been exchanged really belong to

the agreed-on media owner.

Ledgered

Appending all agreed-on transactions to a public

ledger asserts that media ownership records cannot

be revoked by a single party or a small part of the net-

work. Thereby, media owners gain trust that their dig-

ital rights ownership cannot be single-handedly an-

nulled by a seller.

Tamper-resistant

All transactions are tamper-resistant, making it difﬁ-

cult to forge transactions, e.g., by replacing the media

owner in a transaction through a man-in-the-middle

attack.

5.1.2 The Systems Perspective

Monegraph uses three different types of data stores

for enabling the business transactions described be-

Not ACID, not BASE, but SALT

Not ACID, not BASE, but SALT - A Transaction Processing Perspective on Blockchains

761

fore:

1. A blob store for digital artworks, which stores the

art portfolio as binary ﬁles (jpeg, mp4, mp3, etc.).

The blob store (using AWS S3) is suitable for stor-

ing multiple Petabytes of unstructured data in a

ﬂat namespace.

2. A NoSQL data store for storing sales contracts

and catalog data in JSON format. The NoSQL

document store (using Couchbase) is suitable for

storing Terabytes of semi-structured data.

3. Two blockchain data stores for storing Gigabytes

of data:

(a) One blockchain, Ethereum, is used for stor-

ing the ownership history of digital artworks as

crypto hashes.

(b) Another blockchain, the Bitcoin system, is used

for facilitating payments with the Bitcoin vir-

tual currency.

The two different NoSQL data stores (S3 and

Couchbase) that Monegraph uses are both BASE sys-

tems which enable scalable and highly-available data

storage of unstructured items in a blob store, and

semi-structured JSON items in a document store, re-

spectively. It would be prohibitively expensive to

use the Ethereum blockchain as a data store for these

items. Using the Ethereum blockchain as part of the

data management system, however, enables, in partic-

ular, the following SALT system properties that sim-

plify revenue sharing and payment distribution.

Ledgered

Transparently storing all agreed-on transactions in a

public ledger simpliﬁes revenue sharing between mul-

tiple parties, such as publishers, media creators, and

afﬁliates, without layers of intermediaries that use

their own complex accounting and rights management

processes. For example, a third-party that wants to li-

cense media can more easily verify media ownership

of the party that claims to be the media owner by look-

ing up the ownership record in the public blockchain.

Time-consensual

The time-consensual property implies that transac-

tions are appended to the ledger after a deﬁned av-

erage time period. Although this could be problem-

atic for some applications, a certain delay involved in

transferring media rights could still be acceptable in

this use case.

5.2 Provenance Use Case

The second use case, Provenance, is a supply chain

traceability application that provides insight into the

provenance of items across different supply chains

(Provenance, 2017). Thereby, Provenance makes it

possible for consumers to transparently retrace the

origin of products that they purchase. A pilot project

shows how blockchain technology can be used for

tracing yellowﬁn and skipjack tuna ﬁsh in Indonesia

from catch to consumer.

Provenance

FisherSupplierFactoryPOS

Data Mgt.

catch

Receive

catch

Receive

certiﬁcate

Consumer

scans tag

Display

provenance

data

Blockchain

(Ethereum)

ERP System

(Tally-O)

Provenance

(RDBMS)

Hand-over

catch

Tag products

Ship

products

Figure 5: Provenance use case from a combined transac-

tions and data management systems perspective.

5.2.1 The Transactions Perspective

Provenance uses blockchain technology to integrate

different stakeholders across the supply chain, en-

abling them to support the following business trans-

actions, as shown in ﬁgure 5.

1. Local ﬁshermen in Indonesia register their catch

(by sending an SMS message to a Provenance ap-

plication), which triggers the creation of a public

digital certiﬁcate that represents the physical good

in the blockchain.

2. Along with the physical transaction of the catch

from ﬁsher to supplier, suppliers receive the digi-

tal certiﬁcate from the blockchain.

3. In the factory that processes and packages the ﬁsh,

the products are tagged (e.g., using QR codes, bar-

codes, NFC tags, etc.), and can thereby be traced

along the supply chain by linking the tag to the

digital certiﬁcate.

4. At the Point of Sale, consumers scan the tag

on a product (e.g., a QR code) with their mo-

bile phones and retrieve information regarding the

product’s provenance.

In the tuna ﬁsh tracing pilot project of Provenance,

NGOs perform audits to validate compliance along

the supply chain. Therefore, the system is not com-

pletely trustless. However, audits are simpliﬁed by

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

762

using the blockchain as a shared data layer for certiﬁ-

cates.

Using blockchain technology for building the cer-

tiﬁcation system enables, in particular, the following

SALT transaction properties.

Agreed

There is no single party that governs the certiﬁcation

process. Instead, an agreement between all stakehold-

ers is automatically formed based on deﬁned conven-

tions of the blockchain consensus protocol. The cer-

tiﬁcation data is thereby not prone to arbitrary actions

of a single party.

Ledgered

The agreed-on transactions in a blockchain cannot be

revoked, thereby providing a perfectly auditable sys-

tem which is particularly important for NGOs who

are responsible for auditing the uninterrupted chain

of custody from raw ﬁsh to packaged products at the

point of sale. It is practically impossible for a sin-

gle party to modify transactions once they have been

appended to the blockchain.

5.2.2 The Systems Perspective

Provenance uses the Ethereum blockchain as a secure,

auditable, shared data layer, thereby avoiding data si-

los in heterogeneous systems with limited interoper-

ability. With the blockchain, data can be accessed and

veriﬁed by all involved parties, rather than solely by

the original certiﬁcatory.

By using a blockchain-based system in the tuna

tracing pilot project, Provenance gains two main ad-

vantages. First, the blockchain serves as an integra-

tion layer between different stakeholders with het-

erogeneous IT systems that range from the mobile

phones of ﬁshermen to complex ERP systems of man-

ufacturers. Second, the peer-to-peer setup and cryp-

tographic properties of the system make it impossi-

ble for a single governing party to manipulate data at

some point in the supply chain, thereby strengthen-

ing the conﬁdence of consumers into the provenance

information they retrieve at the point of sale.

The following SALT system properties are of par-

ticular importance in the Provenance use case.

Symmetric

Fragmentation along the chain of custody makes a

certiﬁcation system vulnerable to fraud. Furthermore,

no single organization can be trusted to broker all data

about every product’s supply chain. Relying on a

single party creates an inherent bias that eventually

could weaken trust of consumers regarding the certi-

ﬁed provenance information that they receive at the

point of sale. A blockchain-based peer-to-peer net-

working approach with symmetrically shared respon-

sibilities takes the role of an “honest broker” in such

a distributed certiﬁcation system.

Admin-free

The blockchain serves as an integration layer between

different stakeholders with heterogeneous IT systems

that are ranging from the mobile phones of local pro-

ducers to the ERP systems of manufacturers. Tra-

ditionally, a governing third-party, such as an NGO,

would have been required to integrate all IT systems

along the supply chain with their own auditing sys-

tem, thereby increasing cost of operations. Cost shar-

ing is difﬁcult and could weaken the trustworthiness

of the system due to adverse incentives of the govern-

ing third-party who might be more interested in pleas-

ing the sponsor rather than performing proper over-

sight.

Moreover, by using a blockchain, the authentica-

tion system is drastically simpliﬁed compared to cen-

trally managed public key infrastructure. This re-

moves a critical single-point-of-failure and security

risk from the certiﬁcation system.

6 SUMMARY AND OUTLOOK

Different notions of transactions and transaction pro-

cessing systems exist, most notably ACID transac-

tions and BASE systems. With the emergence of

blockchain technology, an alternative to ACID and

BASE is introduced: SALT. In this paper, we intro-

duced SALT along the two perspectives of transac-

tions and TP systems. We discussed the importance

of these dual perspectives.

When engineering blockchain-based applications,

the SALT model can be used to explain the

blockchains under consideration, that is, to study both

the business transactions and their supporting sys-

tems. While there are speciﬁc transactions that are

exclusively SALT, we expect the systems to always

encompass different data management components so

that SALT, ACID, and BASE can all be supported at

the same time. The two use cases discussed are ﬁrst

examples of such systems that beneﬁt from using mul-

tiple transactional models and systems.

This immediately raises two main research ques-

tions that require further exploration:

1. Given a combination of different transaction

models and systems, including SALT, are there

system-wide application properties that can be

guaranteed?

Not ACID, not BASE, but SALT

Not ACID, not BASE, but SALT - A Transaction Processing Perspective on Blockchains

763

2. With blockchain technology advancing at a rapid

pace, will ACID, BASE and SALT continue to co-

exist as alternatives, or can frameworks and solu-

tions stacks be designed that impose an integrated

data management using all three models?

Further, a number of related research challenges

emerge:

1. In this paper, we suggested a business transac-

tions and a systems perspective when engineering

blockchain-based applications. Other perspec-

tives – for example, a consensus-perspective, or a

blockchain technology (platforms and tools) per-

spective – may also be beneﬁcial.

2. Private and permissioned blockchains, as opposed

to the public blockchains discussed in this pa-

per, maintain some of the SALT properties, while

compromising others. Whenever closed networks

with different consensus algorithms and asym-

metric peers are suggested – is less SALT actually

healthy?

3. Scalability (of blockchains and blockchain-based

applications) is a major limitation of current

blockchain technology. Heterogeneous data man-

agement, as exempliﬁed with the two use cases

above, may help to improve scalability (and ad-

dress related concerns of data volume, distribu-

tion, and processing needs). How, and at what

costs, can scalability be improved?

The list above is by no means complete and ﬁ-

nal; our discussion in this paper is largely driven from

a data management and distributed systems interest,

while several other communities (including security,

privacy, legal, economics) also formulate a number

of open issues related to blockchains and blockchain-

based applications. As blockchain technology and

blockchain-based applications continue to evolve at

a rapid pace and more lessons are learned, we ex-

pect both a ﬁne-tuning of speciﬁc open issues and a

more integrated, inter-disciplinary big picture to be-

come important next steps.

REFERENCES

Bernstein, P. A. and Newcomer, E. (2009). Principles of

Transaction Processing. Morgan Kaufmann Publish-

ers Inc., San Francisco, CA, USA, 2nd edition.

Brewer, E. A. (2000). Towards robust distributed systems.

In PODC, volume 7.

Buterin, V. (2014). Ethereum: A next-generation smart con-

tract and decentralized application platform. https://

github.com/ethereum/wiki/wiki/%5BEnglish%5D-

White-Paper.

Crosby, M., Nachiappan, Pattanayak, P., Verma, S., and

Kalyanaraman, V. (2015). Blockchain technology:

Beyond bitcoin. Technical report, Sutardja Center for

Entrepreneurship & Technology, Berkeley, CA.

Gray, J. and Reuter, A. (1992). Transaction Processing:

Concepts and Techniques. Morgan Kaufmann Pub-

lishers Inc., San Francisco, CA, USA, 1st edition.

Monegraph (2017). https://monegraph.com/. Accessed:

2017-02-07.

Nakamoto, S. (2008). Bitcoin: A peer-to-peer electronic

cash system.

Pritchett, D. (2008). BASE: An acid alternative. ACM

Queue, 6(3):48–55.

Provenance (2017). https://www.provenance.org/. Ac-

cessed: 2017-02-07.

Tai, S. (2017). Continuous, trustless, and fair: Chang-

ing priorities in services computing. In Advances

in Service-Oriented and Cloud Computing (ASOCC).

Springer.

Wood, G. (2014). Ethereum: A secure decentralised gen-

eralised transaction ledger. Ethereum Project Yellow

Paper.

CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science

764