An Algebraic Collision Avoidance Approach for Unmanned Aerial

Vehicle

Adriana Dapena

, Mar

ıa Jos

e Souto-Salorio

, Ana Dorotea Tarr

ıo-Tobar

and Paula M. Castro

Department of Computer Engineering, Universidade da Coru

na, Coru

na, Spain

Department of Computer Science, Universidade da Coru

na, Coru

na, Spain

Department of Mathematics, Universidade da Coru

na, Coru

na, Spain

Keywords:

Collision Avoidance, Control and Supervision Systems, Characteristic Polynomial, Engineering Applications,

Hyperboloid Structure, Modelling and Simulation, Unmanned Aerial Vehicle.

Abstract:

In this paper we address the problem of avoidancing collisions between an Unmanned Aerial Vehicle (UAV)

and a rigid surface. The UAV is modelled as an unique sphere envolving the UAV or as multiple spheres only

envolving the motors. The UAV ﬂies inside a rigid hyperboloid structure typically used in architecture. The

collision is detected by means of the study of the characteristic polynomial associated to quadric surfaces.

Computer simulation results included in this paper will show both the accuracy and the low computational

cost exhibited by the proposed method.

1 INTRODUCTION

Collision detection between two or more rigid bodies

is based on determining whether any of the solids

makes contact at one or more points (Brozos-V

azquez

et al., 2016), (Choi et al., 2006). This problem has

a great interest in many ﬁelds such as robotics (Choi

et al., 2006), (Steinbach et al., 2006), computer graph-

ics (Jia et al., 2006), animation and computer simu-

lated environments (C. O’Sullivan, 1999), etc.

From a mathematical point of view, the contact

between rigid bodies can be determined by saying that

the surfaces are in contact when their intersection is

not an empty set of points. Then, given two surfaces,

the question is to know whether they intersect or not.

Most work in the literature devoted to the study

of collision detection only considers convex bodies

(Choi et al., 2006), (Jia et al., 2006). Moreover,

most of the proposed algorithms are indeed valid

only under that condition of convexity. Recently, in

(Brozos-V

azquez et al., 2016), the authors have pre-

sented a study in which one of the bodies was not

convex (in fact, that was a hyperboloid). Since hyper-

boloid structures are doubly ruled surfaces, this type

of architectural structures is very strong against buck-

ling and cheaper than other singly ruled surfaces, like

cylinders or cones. For this reason, the hyperboloid

structure is used in architecture to design cooling tow-

ers, water towers, cathedrals, air trafﬁc control towers,

and so on.

Because of its potential for commercial, military,

law-enforcement, research, and other purposes, Un-

manned Aerial Vehicles (UAVs) have received con-

siderable attention in recent years. The fast develop-

ment of this ﬁeld has required the design of robust

collision avoidance systems which are based, in gene-

ral, on the combination of information acquired from

several sensors, which implies processing latency and

complexity (Giancarmine et al., 2008). If the surface

shape changes in height (like occurs with the hyper-

boloid structure) those sensors must be used for the

registration of this information in all directions. Col-

lision avoidance methods based on computing the dis-

tance from the UAV to the surface are adequate in

most situations where that surface shape is similar for

all height positions.

The method presented in this paper is oriented to

predict collisions when an UAV is ﬂying inside a hy-

perboloid structure. We propose to model the UAV

using multiples spheres adapted to its shape. Using

the results presented in (Brozos-V

azquez et al., 2016),

we propose several algorithms for collision avoidance

by means of the study of the roots of a character-

istic polynomial associated to quadric surfaces. In

those algorithms, the conditions for collision detec-

tion are evaluated before any UAV movement so that

only valid movements are allowed thus avoiding such

262

Dapena, A., Souto-Salorio, M., Tarrío-Tobar, A. and Castro, P.

An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle.

DOI: 10.5220/0006410002620269

In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 262-269

ISBN: Not Available

collisions. We will show that this collision detection

can be performed using a reduced number of opera-

tions.

This paper is organized as follows. Section 2

brieﬂy introduces some ideas about the collision

avoidance systems in the literature similar to our pro-

posal. Section 3 contains the mathematical formula-

tion of the proposed method for collision avoidance,

which will be applied in Section 4 when an UAV is

ﬂying inside a hyperboloid structure for tasks of mo-

nitoring, maintenance or control. Section 5 includes

the simulation results and, ﬁnally, Section 6 contains

the main conclusions about this work.

2 COLLISION AVOIDANCE

SYSTEMS

Collision Avoidance Systems (CASs) for UAV con-

sist of two main functions: ﬁrstly, sensing and de-

tection, and secondly, collision avoidance/maneuver

approach. The ﬁrst one refers to the way of ac-

quiring useful information about its surrounding en-

vironment, as for example, the UAV position or its

speed/heading, environment conditions... This task

can be done using active and/or passive sensors and

communication equipments. The second function,

i.e. the collision avoidance/maneuver approach, in-

cludes mechanisms for trajectory calculation and dis-

tance estimation (Albaker and Rahim, 2009), (Pham

et al., 2015). In particular, the geometric approaches

perform this second function using geometry, usually

by means of the simulation of the UAV trajectories

and the calculation of the shortest distance to the sur-

rounding obstacles in a 2-D space (Park et al., 2018),

(Strobel and Schwarzbach, 2014). For this purpose,

such geometric approaches make use of information

such as location, speed or heading of the UAV with

respect to obstacles, which is frequently obtained by

Automatic Dependent Surveillance-Broadcast (ADS-

B). Geometric approaches are specially useful when

the UAV is inside simple surfaces as cylinders or

spheres, in which the surface shape remains un-

changed with height. However, for hyperboloid sur-

faces, on which we focus in this work, this property

can not be assumed.

In this paper, we will consider only the colli-

sion between the UAV and a rigid surface (the hy-

perboloid) which represents the structure walls. For

collision avoidance, an UAV could employ contour or

schematic maps specially useful for indoor environ-

ments (Krokowicz et al., 2010). For regular structures

(like squares or cylinders), this map is quite simple

since it remains unchanged for all height. However,

the hyperboloid surfaces are more complex because

they change with height. For this reason, we focus

on collision avoidance in the real scenario of an UAV

ﬂying inside a hyperboloid structure (like a cooling

tower in a power station). The information used by

the proposed method is minimal, since only requires

the knowledge of the UAV position, speed and turn

angle. We hope that the ideas presented in this work

can be extended to different surfaces for other real ap-

plications.

3 MATHEMATICAL

FORMULATION

We consider a circular hyperboloid of one sheet

centred at the origin and described by the following

equation

H :

−

= 1,for a,c > 0. (1)

Using the standard notation for projective spaces, we

can ﬁnd the matrix H associated to the surface H . Let

x = (x, y, z, 1)

be a generic vector in homogeneous

coordinates not placed at inﬁnity. Then, x

Hx = 0

deﬁnes the surface H , where H is given by

H =







−2

0 0 0

0 a

−2

0 0

0 0 −c

−2

0 0 0 −1







. (2)

Moreover, we also consider a spherical surface of

radius r > 0 whose centre is at (x

), deﬁned by

the following equation

S :(x −x

)

+ (y −y

)

+ (z −z

)

= r

. (3)

As above, we can express this equation in matrix

form using homogeneous coordinates in this way

S =







1 0 0 −x

0 1 0 −y

0 0 1 −z

−x

−y

−z

−r

+ x

+ y

+ z







(4)

The characteristic polynomial of both surfaces H

An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle

263

and S is a polynomial of degree 4 given by

f (λ) = det(λH + S) =

+ λ)g(λ)

(5)

where

g(λ) = −(a

+ λ)[(c

−λ)(r

+ λ) + z

λ]

+λ(c

−λ)(x

+ y

)

= λ

+ a

λ + a

(6)

where a

, a

, and a

are the real coefﬁcients of g(λ).

Therefore, we can directly conclude that one root of

f (λ) = 0 is λ

= −a

and that the other roots are also

roots of the cubic equation g(λ) = 0.

3.1 Calculation of g(λ) Roots

In this section we will show how to obtain the dis-

criminant ∆ from the cubic polynomial g(λ), which

will be used for detecting collision between the UAV

and the hyperboloid surface i.e., for determining if the

UAV movement is valid or not, instead of directly cal-

culating the roots of g(λ).

Cardano’s formulas can be applied to g(λ) for de-

tecting contacts between H and S employing simple

calculations, as described in the following.

Thus, based on the roots of g(λ), we can deter-

mine the position of the sphere with respect to the hy-

perboloid (Brozos-V

azquez et al., 2016). Considering

r < a, Table 1 shows all the cases deﬁning the relative

position between S and H .

In general, for a monotonic polynomial

+ a

λ + a

, the following real para-

meters can be deﬁned

Q =

−a

R =

−27a

−2a

∆ = Q

+ R

(7)

From Table 1, you can see that this parameter ∆

could be used as discriminant to cluster that relative

position between S and H into two groups (contact,

for ∆ ≥ 0, and non-contact, for ∆ < 0), although

it does not provide enough information about the

non-contact case since S can be interior or exterior

to H i.e., about if the scenario corresponds to the

ﬁrst row of Table 1 or to the second one. For only

this purpose, we will be forced to compute the roots

of g(λ) so that their sign will allow us to distinguish

both scenarios. Since all the roots are real-valued

when ∆ < 0, the following expressions will be used

for their computation

φ =

acos

−Q

= 2

−Qcos (φ) −

= 2

−Qcos



φ +

2π



−

= 2

−Qcos



φ +

4π



−

(8)

where R and Q are the parameters deﬁned in Equation

(7).

4 COLLISION AVOIDANCE

In this paper we consider UAVs with four motors, like

those shown in Figure 1, although this development

could be applied for any number of motors. As ﬁrst

approach, the UAV is modelled as one sphere with its

centre in the UAV centre (see Figure 1(a)). As second

approach, the UAV is modelled as multiple spheres,

four in our case, centred at each of its motors (see

Figure 1(b)).

4.1 UAV Model of One Sphere

Firstly, we will model the UAV according to the

representation of Figure 1(a). In this ﬁgure you

can see that the UAV is represented by means of

one sphere S with radius r centred at (x

Considering the deﬁnition of the characteristic

polynomial given in Equation (5) and the matrices of

Equations (2) and (4), we can obtain the coefﬁcients

of g(λ) of Equation (6). Thus, the coefﬁcients of this

characteristic polynomial are given by

= −a

= −(a

−a

+ c

−c

+ a

= a

−c

+ r

−z

−x

−y

(9)

Since we are interested in determining when the UAV

moves to a valid position (i.e. if the UAV moves in

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

264

Table 1: General relative position between S and H.

Description Roots of g(λ) ∆ UAV Movement

S interior to H All the roots are real and

different: two negative,

one positive

∆ < 0 Valid

S exterior to H All the roots are positive

real and different

∆ < 0 Non-valid

Centre of S interior to H . S tangent to H . All the roots are real,

and two equal: two

equal negative, one po-

sitive

∆ = 0 Non-valid

Centre of S exterior to H . S tangent to H . All the roots are positive

real, and two equal

∆ = 0 Non-valid

Intersection of S and H . One root is positive real

and two are complex

conjugate

∆ > 0 Non-valid

the interior of H ), and taking into account the clas-

siﬁcation of Table 1, we could detect collisions from

the study of the roots. Notice that the computational

complexity associated to the calculation of these roots

can be reduced considering that ∆ ≥ 0 corresponds to

non-valid movements. Moreover, if ∆ < 0 S could be

interior or exterior to H . However, with the root sign

we can determine if S is interior to H or not.

The following algorithm, termed Algorithm 1, de-

tails the procedure.

Algorithm 1: One sphere.

Compute ∆.

If ∆ < 0

Compute the root λ

If λ

< 0, then valid movement (interior),

otherwise

Compute the root λ

If λ

< 0, then valid movement (interior),

otherwise non-valid movement.

4.2 UAV Model of Four Spheres

We consider in this subsection the spheres S

and S

, all of them with radius r

, to model the

four motors of our UAV, as shown in Figure 1(b).

Considering that the UAV is centred at (x

), the

centre of each motor sphere, denoted by (x

can be mathematically expressed as follows

= x

√

(cos(g) −sin(g)) = x

√

= y

√

(cos(g) + sin(g)) = y

√

= z

(10)

where T

and T

are obviously given by

= cos(g) −sin(g),

= cos(g) + sin(g).

(11)

Notice that for the initial position given in Figure 1,

the spheres S

, S

, and S

respectively have an-

gles of −π/2, 0, π/2, and 3π/2. In general, the an-

gle of S

, S

, and S

can be computed from the angle

of S

, denoted by g

, by using g

+ (i −1)π/2, with

i = 2, 3,4, respectively.

Considering Equation (10), we have that

+ y

√

= x

+ l

√

+ y

+ l

√

= x

+ y

+ l

√

2(T

+ T

(12)

An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle

265

(a) (b)

Figure 1: UAV models: (a) one sphere; (b) four spheres.

where we have used T

+ T

= 2. Substituting

Equation (12) into Equation (9), we obtain

(g) = A

+ c

C(g),

(g) = A

−C(g),

(13)

where

= −(a

−a

+ c

−c

) + l

= a

−c

+ r

−z

−x

−y

−l

C(g) = l

√

2(T

+ T

(14)

with T

and T

as deﬁned in Equation (11). From

these expressions and considering the deﬁnition of

of Equation (9), we can compute ∆(g) for each

sphere by using the following expressions

Q(g) =

(g) −a

(g)

R(g) =

(g)a

(g) −27(

)

−2a

(g)

∆(g) = Q(g)

+ R(g)

(15)

For this UAV model, the collision detection can be

performed applying the Algorithm 1 for each sphere.

However, with the goal of reducing the computational

complexity, we propose a two-step algorithm. For

the ﬁrst step, we will analyse the position of the to-

tal sphere S . When ∆ < 0, we use the same procedure

as done in Algorithm 1 to determine if the movement

is valid or non-valid. Otherwise, when ∆ ≥ 0, we re-

ﬁne the decision by computing the discriminant ∆(g)

for the four spheres.

The resulting algorithm is summarized as detailed

below, and we will referred to as Algorithm 2.

Algorithm 2: Four spheres.

For the sphere S of radius r, compute ∆.

If ∆ < 0

Compute the root λ

If λ

< 0, then valid movement (interior),

otherwise

Compute the root λ

If λ

< 0, then valid movement (interior),

otherwise non-valid movement.

otherwise

Compute ∆(g

+ (i −1)π/2) for i = 2,3, 4, with g

being the S

angle,

If all ∆(g

+ (i −1)π/2) < 0, then valid movement

(interior),

otherwise non-valid movement.

5 EXPERIMENTAL RESULTS

We consider a computer simulated environment

where the hyperboloid models the cooling tower of

a power station. This tower has a height of 35.6 m

and a base diameter of 36.5m. The UAV has a radius

of 25 cm. Different motor radius have been consid-

ered in our simulations. Figure 2(a) shows the UAV

model. The UAV ﬂies inside the cooling tower fol-

lowing a random trajectory determined as follows:

• Straight UAV movement with probability 0.25.

• Down or up UAV movement with probability

0.25.

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

266

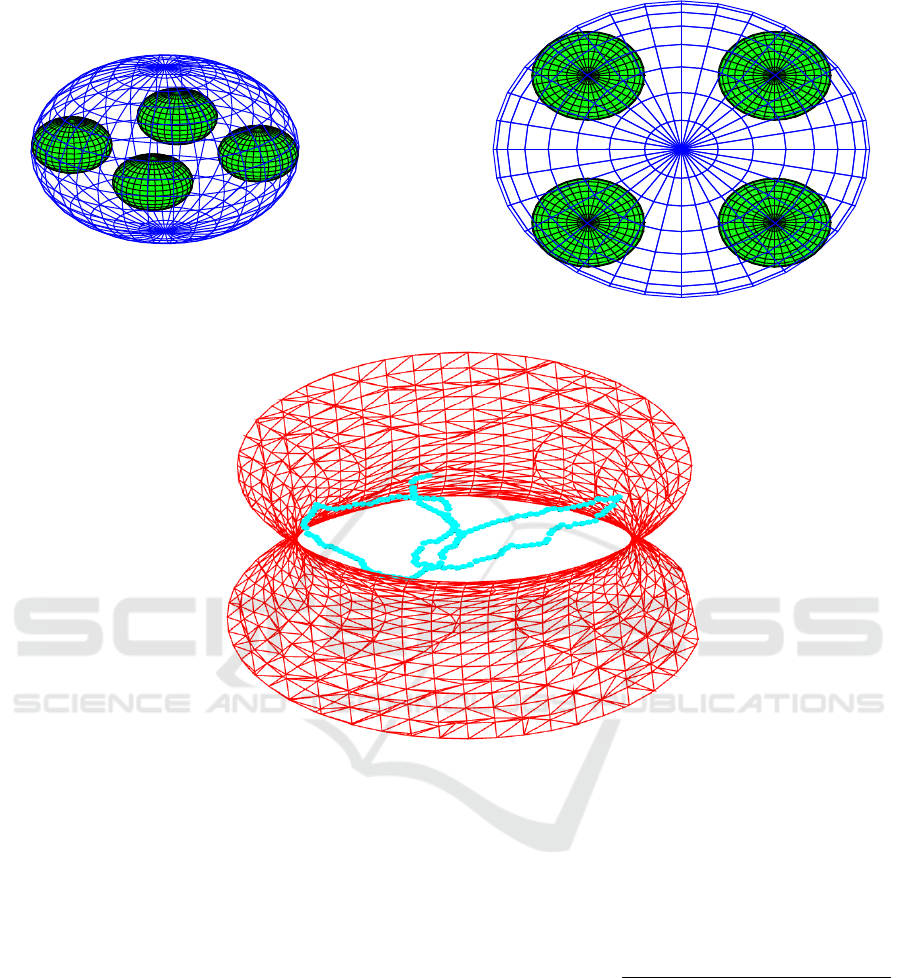
(a) UAV model: 3-D and 2-D views.

(b) Example of an UAV trajectory.

Figure 2: Computer simulations.

• UAV random turn with angle in [−π/4,π/4] with

probability 0.5.

• UAV turn of angle −π/2 or π/2 if a non-valid

movement is detected with Algorithm 1.

We consider that the UAV follows a trajectory of

D = 500 meters with a speed of v m/s. Before any

movement, the UAV evaluates the Algorithm 1 or the

Algorithm 2 to determine if the movement is valid.

This prediction is done considering the position of

the UAV in t seconds, i.e. its response time. For a

non-valid movement, the UAV turns and tries a new

movement. Figure 2(b) plots only one realization of

our simulations.

We are interested in comparing the performances

of both proposed algorithms for different motor

radius. We have considered 5, 7.5, and 10 cm of

radius. Table 2 shows the results obtained for this

comparison between the Algorithm 1 (model of one

sphere) and the Algorithm 2 (model of four spheres)

considering different speeds and response times. The

following expression has been evaluated

ε(%) = 100 ×

non-valid movements with Alg. 2

non-valid movements with Alg. 1

(16)

For all response times, we can see that there exists

a considerable difference between both algorithms for

a radius of r = 5cm. This difference reduces when the

radius increases since the volume of the small spheres

is similar to the volume of the big one. For instance,

the accuracy achieved with the Algorithm 1 is higher

than a 90% for all speeds with a radius of r = 10 cm.

An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle

267

Table 2: Comparison of the proposed algorithms in terms of ε(%) for three different UAV response times.

(a) t = 10 ms

Speed (m/s) 5 6 7 8 9

Precision (cm) 5 6 7 8 9

Radius 5 51.49 52.22 58.30 66.22 70.86

(cm) 7.5 79.20 82.92 88.09 91.05 92.15

10 91.01 93.82 94.91 94.07 96.61

(b) t = 50 ms

Speed (m/s) 5 6 7 8 9

Precision (cm) 25 30 35 40 45

Radius 5 68.18 68.29 69.42 70.49 81.81

(cm) 7.5 86.56 89.83 90.40 93.41 93.22

10 92.82 93.54 94.40 98.10 99.12

Speed (m/s) 5 6 7 8 9

Precision (cm) 50 60 70 80 90

Radius 5 68.42 71.42 75.90 80.00 83.33

(cm) 7.5 89.00 91.81 99.20 99.50 95.71

10 94.61 95.33 96.00 98.50 99.70

6 CONCLUSIONS

We have modelled the UAV as a spherical surface cen-

tred at the UAV centre or as four spherical surfaces re-

spectively centred at each one of the four motor cen-

tres. We have shown that the roots of a character-

istic polynomial can be used to decide if there is or

not contact between the UAV and a rigid surface. We

have considered a hyperboloid surface due its archi-

tectural properties and to its presence in real scenarios

that could require control or maintenance, although

the ideas here presented could be used for other sur-

face types. Both proposed algorithms have a very low

computational complexity since they are computing

the roots of that characteristic polynomial only a very

reduced number of times.

The results obtained from computer simulations

show that the algorithm for collision detection based

on a model of sphere per UAV motor is more adequate

when a high or medium distance precision or equiv-

alently, low response times, is needed. However, the

method based on only one sphere could be used for

requirements of low precision or, equivalently, high

response times.

ACKNOWLEDGEMENTS

This work has been funded by the Xunta de

Galicia (ED431C 2016-045, ED341D R2016/012),

the Agencia Estatal de Investigaci

on of Spain

(TEC2016-75067-C4-1-R) and ERDF funds of the

EU (AEI/FEDER, UE).

REFERENCES

Albaker, B. and Rahim, N. (2009). A survey of collision

avoidance approaches for unmanned aerial vehicles.

In IEEE International Conference for Technical Post-

graduates (TECHPOS), pages 1–7.

Brozos-V

azquez, M., Pereira-S

aez, M., Souto-Salorio, M.,

and Tarr

ıo-Tobar, A. D. (2016). Contact detection be-

tween a sphere and a hyperboloid by means of the

roots of a characteristic polynomial. arXiv preprint

arXiv:1602.06744.

C. O’Sullivan, J. D. (1999). Real-time collision detection

and response using sphere-trees. In 15th Spring Con-

ference on Computer Graphics, pages 83–92.

Choi, Y.-K., Wang, W., and Liu, Y. (2006). Continuous

collision detection for two moving elliptic disks. IEEE

Transactions on Robotics, 22:213–224.

Giancarmine, F., Accardo, D., Moccia, A., Carbone,

C., Ciniglio, U., Corraro, F., and Salvatore, L.

(2008). Multi-sensor-based fully autonomous non-

cooperative collision avoidance system for unmanned

ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics

268

air vehicles. Journal of aerospace computing, infor-

mation, and communication, 5(10):338–360.

Jia, X., Choi, Y.-K., Mourrain, B., and Wang, W. (2006).

An algebraic approach to continuous collision detec-

tion for ellipsoids. Computer Aided Geometric De-

sign, 28:164–176.

Krokowicz, T., Gasca, M., Voos, H., and Ucinski, D.

(2010). Indoor navigation for quadrotor uavs using

schematic environment maps. In Robotics in Alpe-

Adria-Danube Region (RAAD), 2010 IEEE 19th In-

ternational Workshop on, pages 457–462. IEEE.

Park, J.-W., Oh, H.-D., and Tahk, M.-J. (2018). UAV colli-

sion avoidance based on geometric approach. In IEEE

SICE Annual Conference, pages 2122 – 2126.

Pham, H., Smolka, S. A., Stoller, S. D., Phan, D., and

Yang, J. (2015). A survey on unmanned aerial ve-

hicle collision avoidance systems. arXiv preprint

arXiv:1508.07723.

Steinbach, K., Kuffner, J., Asfour, T., and Dillmann, R.

(2006). Efﬁcient collision and self-collision detec-

tion for humanoids based on sphere trees hierarchies.

In 6th IEEE-RAS International Conference on Hu-

manoid Robots.

Strobel, A. and Schwarzbach, M. (2014). Cooperative sense

and avoid: Implementation in simulation and real

world for small unmanned aerial vehicles. In IEEE

International Conference on Unmanned Aircraft Sys-

tems (ICUAS), pages 1253–1258.

An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle

269