
Track-to-track Fusion using Multiple Detection Linear Multitarget
Integrated Probabilistic Data Association
Yuan Huang, Sa Yong Chong and Taek Lyul Song
Department of Electronic Systems Engineering, Hanyang University, Ansan, Republic of Korea
Keywords:
Track-to-track Fusion, Centralized Fusion, Multiple Detection, LM-IPDA.
Abstract:
The multi-sensor multiple detection target tracking problem is considered in this paper. The probability of
target existence is used as the track quality measure and plays an important part in the fusion paradigm. The
multiple detection linear multi-target integrated probabilistic data association (MD-LM-IPDA) is utilized and
extended to the multi-sensor structure. Both centralized fusion MD-LM-IPDA and distributed track-to-track
fusion MD-LM-IPDA are proposed. The centralized fusion method utilizes the information from all local
sensors’ measurements to get the best tracking performance but suffers from the high communication load.
The distributed fusion method can control the communication load by adjusting the threshold for transmitting
local tracks to the fusion center. One can make a choice between these two structures based on the tracking
performance requirement and the computation resources.
1 INTRODUCTION
The multiple detection problem gained a substantial
amount of attention in recent years due to that many
kinds of high resolution sensors and radars are rou-
tinely used in many surveillance and tracking scenar-
ios (Vivone et al., 1999; Baum and Hanebeck, 2014;
Chen et al., 2014). In these multiple detection tar-
get tracking applications, the point target assumption,
which allows each target generate at most one detec-
tion at each scan, cannot remain valid (Bar-Shalom
et al., 2011). Instead, there can be more than one mea-
surements come from the same object, the data as-
sociation process need to enumerate the one-to-many
track-to-measurements assignments and evaluate the
corresponding posteriori data association probabili-
ties. Both random matrix (Lan and Li, 2016) and
measurement partition method (Mahler, 2009) are in-
troduced to cover this multiple detection problem.
In target tracking applications, the real targets ex-
istence information is not known prior. The tracks can
be initialized by both target measurements and clut-
ter measurements which leads to the existence of both
true tracks (tracking targets) and false tracks (tracking
clutter) in the surveillance area (Musicki et al., 1994).
The true track and false track states can be inter-
changed during tracking period based on the informa-
tion extracted from the measurements. The probabil-
ity of target existence is introduced as a judging stan-
dard of the existence of a target in order to solve the
false track discrimination (FTD) problem, which in-
volves true tracks confirmation and false track termi-
nation (Musicki and Evans, 2004; Musicki and Scala,
2008).
The multiple detection linear multitarget in-
tegrated probabilistic data association (MD-LM-
IPDA), which embedded the measurement partition
method into the LM-IPDA algorithm (Musicki and
Scala, 2008), is an efficient method designed for
multitarget multiple detection applications. In tra-
ditional MD structures (Habtemariam et al., 2013;
Habtemariam et al., 2011), the selected measure-
ments are partitioned into measurement cells, where
each cell contains one or some of the selected mea-
surements, and then these measurement cells are uti-
lized in the joint track-to-measurement cell assign-
ments. The MD-LM-IPDA bypass the joint track-
to-measurement cell assignments process by treating
the possible measurement cells of targets followed
by other tracks as additional clutter measurements to
modulate the clutter spatial density. This mechanism
makes MD-LM-IPDA work efficiently in the closely
spaced multitarget tracking applications but lose part
of the optimality.
In the centralized fusion structure, the local sen-
sors transmit measurements to the fusion center for
global tracks update. This approach is optimal but
usually not feasible due to the high communication
Huang, Y., Chong, S. and Song, T.
Track-to-track Fusion using Multiple Detection Linear Multitarget Integrated Probabilistic Data Association.
DOI: 10.5220/0006410104310439
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 1, pages 431-439
ISBN: 978-989-758-263-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
431

load or for the reason that the local sensors only out-
put the track information. The distributed track-to-
track fusion approach focus on fusing the local sensor
tracks with the global tracks at the fusion center. The
performance of this approach is usually worse com-
pared to centralized fusion method. However, the dis-
tributed track-to-track fusion approach requires only
a fraction of the computation time needed for the cen-
tralized fusion since the number of local tracks trans-
mitted to the fusion center is much less compared to
the number of local sensor measurements (Musicki
et al., 2015; Lee et al., 2014).
In this paper, both track-to-track fusion and cen-
tralized fusion are considered under the multiple de-
tection situation. The MD-LM-IPDA is implemented
in these two fusion structures. The probability of tar-
get existence is used as the track quality measure for
local tracks and global tracks and only the confirmed
local sensor tracks are sent to the fusion center for
track-to-track fusion. In both these two fusion struc-
tures, the fusion center generates global tracks and
uses local sensor output, tracks for track-to-track fu-
sion and measurements for centralized fusion, to up-
date global track states and probabilities of target ex-
istence.
In the track-to-track fusion structure, local sen-
sors use the original measurements to update the local
track states and the confirmed tracks (both true tracks
or false tracks) are transmitted to the fusion center.
Then, these confirmed tracks come form the local sen-
sors assume the role of measurements to update the
global track states at the fusion center. The probabil-
ity of target existence of the local tracks are used in
calculating the fusion probabilities. The fusion pro-
cess improves both FTD and tracking accuracy com-
pared to local sensor performance.
In the centralized fusion structure, all local sen-
sors send the measurements to the fusion center and
the global tracks are updated using these measure-
ments. Usually the measurements used by the global
tracks in centralized fusion is different from that of
the distributed fusion. This different is due to that
in the distributed fusion structure, each local sensor
processes the tracking algorithm to generate tracks
and confirmed local tracks are considered as measure-
ments at the fusion center. Usually the centralized fu-
sion obtains better performances than distributed fu-
sion but plagued by the high communication burden.
Section 2 depicts the target and measurement
models. Section 3 demonstrates the centralized fu-
sion structure. The distributed fusion process is given
in Section 4. In Section 5, the performances of the
two fusion structures are compared followed by the
conclusion in Section 6.
2 PROBLEM STATEMENT
The dynamic state for target τ propagates according
to a constant velocity model, given by
x
τ
k+1
= Fx
τ
k
+ v
k
(1)
where x
τ
k
stands for the target state at scan k, F is the
state propagation matrix. v
k
is the zero-mean Gaus-
sian process noise with covariance Q.
The target measurement detected by sensor “s” is
generated by
z
s
k
= H
s
x
τ
k
+ w
s
k
(2)
where H
s
is the measurement matrix and w
s
k
is the
zero-mean Gaussian measurement noise with covari-
ance R
s
. The process noise and measurement noise
are assumed independent. Since the multiple detec-
tion problem is considered, each target can generate
more than one measurements.
The clutter measurement follows the Pois-
son/uniform distribution which means that the num-
ber of clutter measurements at each scan followsPois-
son distribution and the spatial distribution of a clutter
measurement follows the uniform distribution in the
surveillance area.
Let Z
s
k
stand for the measurements obtained by
sensor “s” and z
s
k, j
is the j-th measurement of Z
s
k
. The
measurements gathered by sensor “s” from initial to
scan k is denoted by
Z
k,s
= {Z
s
1
,Z
s
2
,.. . ,Z
s
k
} (3)
so that all the measurement obtained by all the sensors
from initial to current scan k is given as
Z
k
=
n
Z
k,1
,Z
k,2
,.. . ,Z
k,L
o
(4)
where L is the number of sensors.
The probability of target existence event χ
k
and
not exist event
¯
χ
τ
k
satisfies
P
χ
τ
k
|Z
k
+ P
¯
χ
τ
k
|Z
k
= 1 (5)
For reasons of clarity, here we define that
ˆ
ψ
τ
k
= P
χ
τ
k
|Z
k,s
;
¯
ψ
τ
k
= P
χ
τ
k
|Z
k−1,s
(6)
and the prediction relation between these two param-
eters is given by
¯
ψ
τ
k
= p
11
ˆ
ψ
τ
k−1
(7)
where p
11
is the propagation probability that a target
exists at scan k− 1 and keeps existence at scan k.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
432
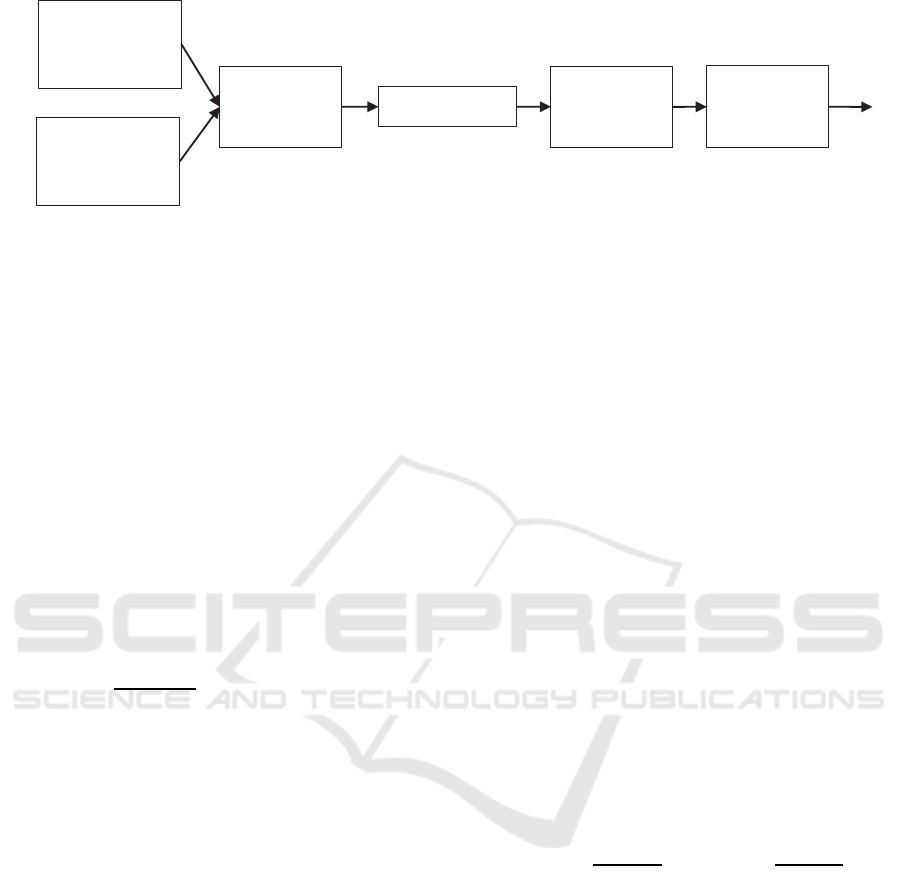
Signal
processing
Signal
processing
Fusion
center
Association
Filter
update
Global
tracks
Figure 1: The structure of centralized fusion.
m
s
k
The number of measurements selected
by sensor “s” at scan k
φ
τ,max
The predetermined maximum number
of target τ detections
ϕ
τ,max
The maximum number of tar-
get originated measurements in
the m
k
selected measurements,
ϕ
τ,max
= min(φ
τ,max
,m
k
)
z
s
ϕ
τ
,n
ϕ
t
(k) One measurement cell of track τ at
time k
ϕ
τ
The number of measurements origi-
nated from target τ such that 1 ≤ ϕ
τ
≤
ϕ
τ,max
n
ϕ
τ
An index that indicates if the measure-
ment cell z
ϕ
τ
,n
ϕ
t
(k) is one of the possi-
ble c
ϕ
τ
combinations, where there are
ϕ
τ
measurements originating from tar-
get τ; n
ϕ
τ
∈
1,2,.. .,c
ϕ
τ
and c
ϕ
τ
=
m
k
!
ϕ
τ
!(m
k
−ϕ
τ
)!
χ
τ
k,0
The event that none of the selected
measurementsoriginated from target τ
χ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
The event that measurement cell
z
s
ϕ
τ
,n
ϕ
τ
originated from target τ
3 CENTRALIZED FUSION
STRUCTURE
In the multiple detection centralized fusion structure,
each local sensor gathers measurements and sends
these measurements to the fusion center. Some no-
tations for algorithms derivation are given above and
the structure of centralized fusion is shown in Figure
1.
Here, we use a simple example to show the mea-
surement cells generated by the measurement parti-
tion method. Assuming that at scan k track τ se-
lects two measurements
n
z
s
k,1
,z
s
k,4
o
out of the total
n
z
s
k,1
,z
s
k,2
,z
s
k,3
,z
s
k,4
o
and the corresponding partition
events are:
• Only one of these two selected measurements is
target detection (ϕ
τ
= 1), the number of possi-
ble combinations c
ϕ
τ
= C
2
1
= 2 and the n
ϕ
τ
varies
from 1 to 2. The measurement cells are:
z
s
1,1
(k) = z
s
k,1
z
s
1,2
(k) = z
s
k,4
• Both these two selected measurements are target
detections (ϕ
τ
= 2), the number of possible com-
binations c
ϕ
τ
= C
2
2
= 1 and the n
ϕ
τ
is 1. The mea-
surement cell is:
z
s
2,1
(k) =
z
s
k,1
,z
s
k,4
At the fusion center, the MD-LM-IPDA algorithm
is used to update the global tracks using the local sen-
sors measurements sequentially. For the brevity of
notations, the time index k of the measurement cells
are omitted and a brief description of this algorithm is
given as follows:
P
τ
k,z
s
ϕ
τ
,n
ϕ
τ
is defined as the a priori probability that
target τ exists and measurement cell z
s
ϕ
τ
,n
ϕ
τ
is gener-
ated by target τ. This probability is given by
P
τ
k,z
s
ϕ
τ
,n
ϕ
τ
∆
=P
χ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
,χ
τ
k
|Z
k−1
≈
p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
ρ
τ
z
s
ϕ
τ
,n
ϕ
τ
,
ϕ
τ,max
∑
ϕ
τ
=1
c
ϕ
τ
∑
n
ϕ
τ
=1
p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
ρ
τ
z
s
ϕ
τ
,n
ϕ
τ
!
· P
τ
Dϕ
τ
(P
τ
G
)
ϕ
τ
¯
ψ
τ
k
(8)
where p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
is the measurement cell likelihood
calculated by the same method as given in [10]. P
τ
Dϕ
τ
is the probability that detected a target ϕ
τ
times. P
τ
G
is
the gating probability (Challa et al., 2011).
In (8), ρ
τ
z
s
ϕ
τ
,n
ϕ
τ
is calculated by
ρ
τ
z
s
ϕ
τ
,n
ϕ
τ
=
∏
z
j
∈z
s
ϕ
τ
,n
ϕ
τ
ρ
k, j
+
T
∑
σ=1
σ6=τ
P
σ
D1
(P
σ
G
)
1
¯
ψ
σ
k
p
σ
k, j
i
(9)
where p
σ
k, j
is the measurement likelihood function of
z
s
k, j
for track σ and ρ
k, j
stands for the clutter measure-
ment density at point z
s
k, j
.
Track-to-track Fusion using Multiple Detection Linear Multitarget Integrated Probabilistic Data Association
433

Here, define
˜
ρ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
as the modulated clutter
measurement density, satisfies
˜
ρ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
∆
= ρ
k,z
s
ϕ
τ
,n
ϕ
τ
+
T
∑
σ=1
σ6=τ
p
σ
k,z
s
ϕ
τ
,n
ϕ
τ
P
σ
k,z
s
ϕ
τ
,n
ϕ
τ
1− P
σ
k,z
s
ϕ
τ
,n
ϕ
τ
(10)
where ρ
k,z
s
ϕ
τ
,n
ϕ
τ
=
∏
z
s
k, j
∈z
s
ϕ
τ
,n
ϕ
τ
ρ
k, j
.
The measurement likelihood ratio Λ
τ
k
is defined by
Λ
τ
k
∆
=
p
z
k
|χ
τ
k
,Z
k−1
p
z
k
|
¯
χ
τ
k
,Z
k−1
≈1− P
τ
Dec
+
ϕ
τ,max
∑
ϕ
τ
=1
c
ϕ
τ
∑
n
ϕ
τ
=1
p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
˜
ρ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
ϕ
τ
!P
Dϕ
τ
(P
G
)
ϕ
τ
(11)
The a posteriori probability that target τ exists and
there is no measurement generated by target τ is
P
χ
τ
k,0
,χ
τ
k
|Z
k,s
=
(1− P
τ
Dec
)
¯
ψ
τ
k
1− P
τ
Dec
¯
ψ
τ
k
P
χ
τ
k,0
|Z
k,s
(12)
The a posteriori probability that target τ exists and
measurement cell z
s
ϕ
τ
,n
ϕ
τ
is the set of target τ detec-
tions satisfies
P
χ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
,χ
τ
k
|Z
k,s
≈
¯
ψ
τ
k
P
τ
Dϕ
τ
P
τ
G
ϕ
τ
1−
¯
ψ
τ
k
1− Λ
τ
k
p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
˜
ρ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
ϕ
τ
!
(13)
The probability of target existence of track τ is up-
dated by
P
χ
τ
k
|Z
k,s
=P
χ
τ
k,0
,χ
τ
k
|Z
k,s
+
ϕ
τ,max
∑
ϕ
τ
=1
c
ϕ
τ
∑
n
ϕ
τ
=1
P
χ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
,χ
τ
k
|Z
k,s
≈
Λ
τ
k
¯
ψ
τ
k
1− P
¯
ψ
τ
k
1− Λ
τ
k
(14)
The data association probabilities are given by
β
τ
k,0
=
P
χ
τ
k,0
,χ
τ
k
|Z
k,s
P
χ
τ
k
|Z
k,s
≈
1− P
τ
Dec
Λ
τ
k
(15)
and
β
τ
k,z
s
ϕ
τ
,n
ϕ
τ
=
P
χ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
,χ
τ
k
|Z
k,s
P
χ
τ
k
|Z
k,s
≈
P
τ
Dϕ
t
P
τ
G
ϕ
t
Λ
τ
k
p
τ
k,z
s
ϕ
τ
,n
ϕ
τ
˜
ρ
τ
k,z
s
ϕ
τ
,n
ϕ
τ
(ϕ
τ
!)
(16)
Each measurement cell updates the track state us-
ing a modified Kalman filter [10] and together with
the predicted state are used to generate the final track
state by a Gaussian Mixture.
4 DISTRIBUTED
TRACK-TO-TRACK FUSION
STRUCTURE
The LM-IPDA algorithm is a suboptimal method
for multitarget tracking/fusion problem in which the
computational load is linear with the number of
tracks. The confirmed local sensor tracks are used
to update the global track states at the fusion cen-
ter sequentially. Here we consider the situation that
updating track τ using tracks {ζ} comes from sensor
“s”. In the track-to-track fusion structure, the tracks
in {ζ} that follow other potential targets are treated as
‘clutter’ tracks with respect to τ. Then these ‘clutter’
tracks are used to modulate the clutter track density
and by doing so the single target tracking approach is
enabled to cover the multitarget tracking problem.
In the fusion center, the local tracks are treated as
measurements and the a priori probability that mea-
surement ζ comes from target τ is
P
τ
ζ
= P
T
¯
ψ
τ
k
¯
ψ
ζ
k
p
τ
ζ
.
ρ
ζ
∑
l∈{ζ}
¯
ψ
l
k
p
τ
l
ρ
l
(17)
where P
T
is the track detection probability and the
measurement likelihood p
τ
ζ
is given by
p
τ
ζ
= N
ˆx
ζ
k
; ˆx
τ
,S
τ
ζ
(18)
and the parameters used in (18) will be given latter.
The ρ
ζ
used in (17) is the clutter track density and
a simple way to calculate this value is
ρ
ζ
=
b
V
(19)
where b is the number of confirmed tracks transmitted
to the fusion center by sensor “s” andV is the volume
of the surveillance area.
The modulated clutter track density is defined as
˜
ρ
τ
ζ
∆
= ρ
ζ
+
∑
σ6=τ
P
σ
ζ
1− P
σ
ζ
¯
ψ
ζ
k
p
σ
ζ
(20)
where in this modulated clutter density, the possibil-
ity that track ζ is tracking another target is taken into
consideration. This clutter track density expression is
the core of the LM track-to-track fusion approach.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
434

Signal
processing
Signal
processing
Association
Filter
update
Tracks
Association
Filter
update
Tracks
Fusion center:
track
to track
association and
fusion
Global
tracks
Figure 2: The structure of distributed fusion.
Then, the measurement likelihood ratio is ex-
pressed by
Λ
τ
= 1− P
T
+ P
T
∑
ζ
¯
ψ
ζ
k
p
τ
ζ
˜
ρ
τ
ζ
(21)
The a posteriori probability of target existence of
track τ is updated by
ˆ
ψ
τ
k
=
Λ
τ
¯
ψ
τ
k
1− (1− Λ
τ
)
¯
ψ
τ
k
(22)
where
¯
ψ
τ
is the predicted target existence probability
given in (7).
The track fusion probabilities, where the modu-
lated clutter track density is used, can be obtained by
β
τ
ζ
=
1
Λ
τ
(
1− P
T
ζ = 0
P
T
¯
ψ
ζ
k
p
τ
ζ
.
ρ
ζ
ζ > 0
(23)
In the track-to-track fusion structure, even through
the measurement noises of different sensors can be
assumed independent there is still estimation errors
correlate between two track if these two tracks are
tracking the same targets (Bar-Shalom et al., 2011;
Bar-Shalom, 1981; Bar-Shalom and Campo, 1986;
Chen et al., 2003). So that the correlated Kalman filter
(CKF) is employed for track state update.
The innovation covariance is generated by
S
τ
ζ
= P
ζ
k
+ P
τ
− P
τ
ζ
−
P
τ
ζ
T
(24)
where the cross covarianceP
τ
ζ
considers the correlated
trajectory estimation errors between target ζ and τ,
calculated by
P
τ
ζ
= E
h
ˆx
ζ
k
− x
k
( ˆx
τ
− x
k
)
i
(25)
The Kalman gain is calculated by
K
τ
ζ
=
P
τ
− P
τ
ζ
S
τ
ζ
−1
(26)
The track state and corresponding covariance are
updated by
ˆx
τ
ζ
= ˆx
τ
+ K
τ
ζ
ˆx
ζ
k
− ˆx
τ
(27)
and
P
τ
ζ
=
I − K
τ
ζ
P
τ
I − K
τ
ζ
T
+ K
τ
ζ
P
ζ
k
K
τ
ζ
T
+
I − K
τ
ζ
P
τ
ζ
K
τ
ζ
T
+ K
τ
ζ
P
τ
ζ
T
I − K
τ
ζ
T
(28)
In the distributed track-to-track fusion structure,
the global tracks in the fusion center are updated by
the local sensor tracks sequentially. In all above equa-
tions, the state and state covariance for target τ are not
specified by a time index k. When track τ is fused
with the first sensor’s local tracks, the predicted infor-
mation ˆx
τ
k|k−1
and P
τ
k|k−1
are used as ˆx
τ
and P
τ
. Then,
in order to fuse with the second sensor’s local tracks,
the updated state ˆx
τ
ζ
and state covariance P
τ
ζ
are used
as ˆx
τ
and P
τ
. In the probability of target existence
update recursion, the predicted existence probability
¯
ψ
τ
k
is updated using the first sensor’s confirmed tracks
information. When this parameter is updated by the
second sensor, the updated existence probability
ˆ
ψ
τ
k
is
used as the predicted information for the second sen-
sor.
5 SIMULATION STUDIES
Two simulations are considered in this part, one is
used for comparing different fusion structures and the
other is used for comparing multiple detection struc-
ture with single detection structure.
Track-to-track Fusion using Multiple Detection Linear Multitarget Integrated Probabilistic Data Association
435

Table 1: Simulation parameters.
Centralized T2TF T2TF-2 Sensor1 Sensor2 Sensor3
Initial PTE 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
Confirmed threshold (local) – 0.001 0.1 0.999 0.999 0.999
Confirmed threshold (fusion center) 0.99 0.95 0.97 – – –
P
d
[0.4,0.3] – – [0.4,0.3] [0.4,0.3] [0.4,0.3]
P
T
– 0.7 0.7 – – –
Number of confirmed false tracks 1 1 1 1 2 2
Simulation time (per each run) 13.27s 0.31s 0.26s 0.27s 0.28s 0.28s
0 100 200 300 400 500
0
50
100
150
200
250
300
350
400
450
500
X (m)
Y (m)
Target 1
Target 1 Start Point
Target 2
Target 2 Start Point
Target 3
Target 3 Start Point
Figure 3: Simulation scenario.
5 10 15 20 25 30 35 40
0
100
200
300
400
500
600
700
800
900
scan
number of confirmed true tracks
Centralized
T2TF
T2TF−2
Sensor1
Sensor2
Sensor3
Figure 4: Confirmed true tracks for all the targets.
5.1 Simulation One
In this simulation scenario, three targets move in a
500m × 500m Cartesian coordinates with the con-
stant velocities. All of them reach the same location
[250m, 250m] at scan 20. Totally 300 Monte Carlo
simulation runs where each run contains 40 scans
with the scan interval equal to 1s. Three sensors are
used to detect targets, all these sensors are located at
the origin of the coordinates and each detects targets
independent from the others. In this simulation, the
multiple detection problem is considered where the
detection probability of the local sensors and central-
ized fusion structure is set as [0.4,0.3] which denotes
5 10 15 20 25 30 35 40
0
1
2
3
4
5
6
7
8
9
10
scan
root mean square position error (m)
Centralized
T2TF
T2TF−2
Sensor1
Sensor2
Sensor3
Figure 5: Root mean square position error of target 2.
that each sensor obtains one detection from a target
with probability 0.4 and two detections from a target
with probability 0.3. In the distributed fusion struc-
ture, the track detection probability P
T
at the fusion
center is set as 0.7. The average number of clutter
measurements occurs at each scan for each sensor is
25.
The target state propagation matrix and the pro-
cess noise covariance are given as
F =
1 0 T 0
0 1 0 T
0 0 1 0
0 0 0 1
(29)
and
Q = 0.75m
2
s
−3
T
3
3 0 T
2
2 0
0 T
3
3 0 T
2
2
T
2
2 0 T 0
0 T
2
2 0 T
(30)
The process noise covariance is given by
R =
25 0
0 25
(31)
The initial states of these three targets are
target 1 :
50m 250m 10m/ s 0m/s
target 2 :
90m 350m 8m/s −5m/s
target 3 :
170m 430m 4m/s −9m/s
(32)
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
436
Each local sensor utilizes the MD-LM-IPDA al-
gorithm for tracking targets. The probability of target
existence is used to solve the FTD problem. Once the
probability of a track exceeds the confirmed thresh-
old, it remains confirmed state. All the local sen-
sors’ performances are shown and compared with dis-
tributed and centralized fusion structures.
In the track-to-track fusion (T2TF) structure, af-
ter each sensor utilizes the MD-LM-IPDA algorithm,
the confirmed local tracks of each sensor are trans-
mitted to the fusion center and then the global tracks
are fused with local confirmed tracks sequentially us-
ing the method proposed in Section IV. The track
confirmed threshold used for selecting local tracks to
transmit to the fusion center can be adjusted to con-
trol the number of tracks transmitted. The influence of
this parameter can be seen from Figure 4 and Figure 5
where two different performances obtained by using
different values for the local track confirmed thresh-
old are demonstrated (T2TF and T2TF-2).
The centralized fusion implements tracking pro-
cess using each sensor’s measurements sequentially.
This optimal fusion framework immediately extracts
targets information from local sensor measurements,
which obtains the best performancecompared to other
fusion structures but not always feasible due to both
communication load and computational burden.
The simulation parameters for different algo-
rithms are shown in Table I. The initial probabilities
of target existence (PTE) for different algorithms are
set the same and the confirmed thresholds are adjusted
in order to obtain almost same number of confirmed
false tracks. The method for adjusting whether a track
is a confirmed true track or a confirmed false track is
the same as given in (Musicki et al., 2013).
The number of confirmed true tracks of different
algorithms are shown in Figure 4. The tracking per-
formance after using fusion paradigm is much better
compared to that of the single sensor. The fusion
process enhances the target existence information,
the centralized fusion method obtains the best per-
formance as expected. The performance of track-to-
track fusion process is worse than centralized method
but much more efficient in the sense of computational
expense. And the performance of track-to-track fu-
sion using a lower local track confirmed threshold is
better compared to the one uses higher value because
more information is transmitted to the fusion center.
In Figure 5, the root mean square position er-
rors are shown. The position estimates after fusion
are more accurate compared to single sensor perfor-
mances. Since both centralized and distributed fusion
take advantage of the information from all the sen-
sors, they obtain similar performances.
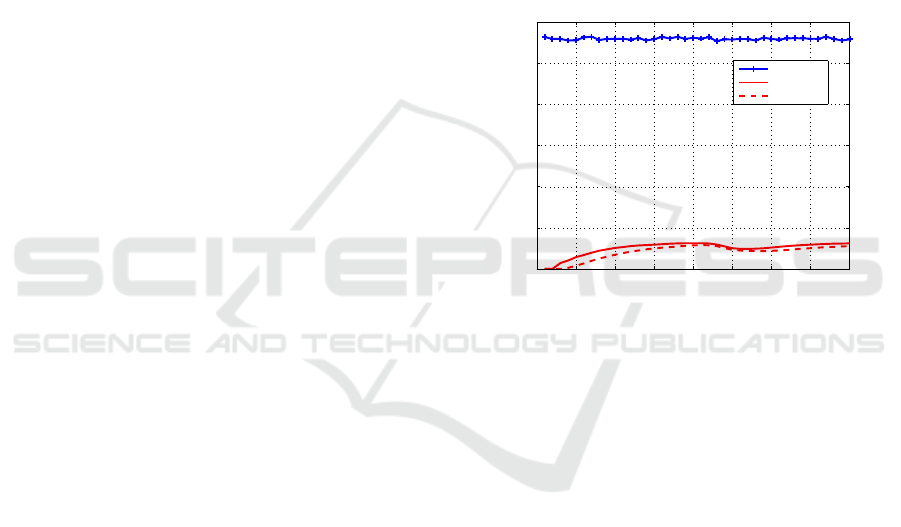
Here the average number of measurements ob-
tained by each sensor at each scan over 300 runs and
the average number of confirmed tracks (treated as
measurements at the fusion center) transmitted to the
fusion center of each sensor at each scan over 300
runs are shown in Figure 6. This figure indicates that
in the distributed fusion structure, local sensor trans-
mits much less information to the fusion center which
makes this structure more efficient compared to cen-
tralized fusion especially in high clutter environment.
When adjusting the confirmed threshold, the number
of tracks transmitter to the fusion center changed a lit-
tle bit, this is due to the fact that the tracks excluding
confirmed true tracks cannot survive for a long period
(they are merged or terminated).
0 5 10 15 20 25 30 35 40
0
5
10
15
20
25
30
scan
number of measurements at each scan
Local sensor
T2TF
T2TF−2
Figure 6: Number of measurements at each scan.
5.2 Simulation Two
The simulation scenario demonstrated in Figure 3 is
applied. Only distributed fusion structure is consid-
ered to compare MD-LM-IPDA and LM-IPDA in or-
der to show the difference between multiple detection
structure and single detection structure. The simu-
lation parameters used by these two algorithms are
shown in Table 2 and the other parameters about tar-
gets and environment background are the same as
those given in subsection 5.1.
Figure 7 demonstrates the number of confirmed
true tracks for all these three targets. It is obvious that
MD-LM-IPDA has a bitter performance compared to
LM-IPDA in the sense of true track confirmation. The
root mean square position errors for each of these
three targets are similar so that only the performance
for target 2 is shown in Figure 8. From this figure, we
can see that the target state estimation error of MD-
LM-IPDA is lower than that of LM-IPDA.
Track-to-track Fusion using Multiple Detection Linear Multitarget Integrated Probabilistic Data Association
437
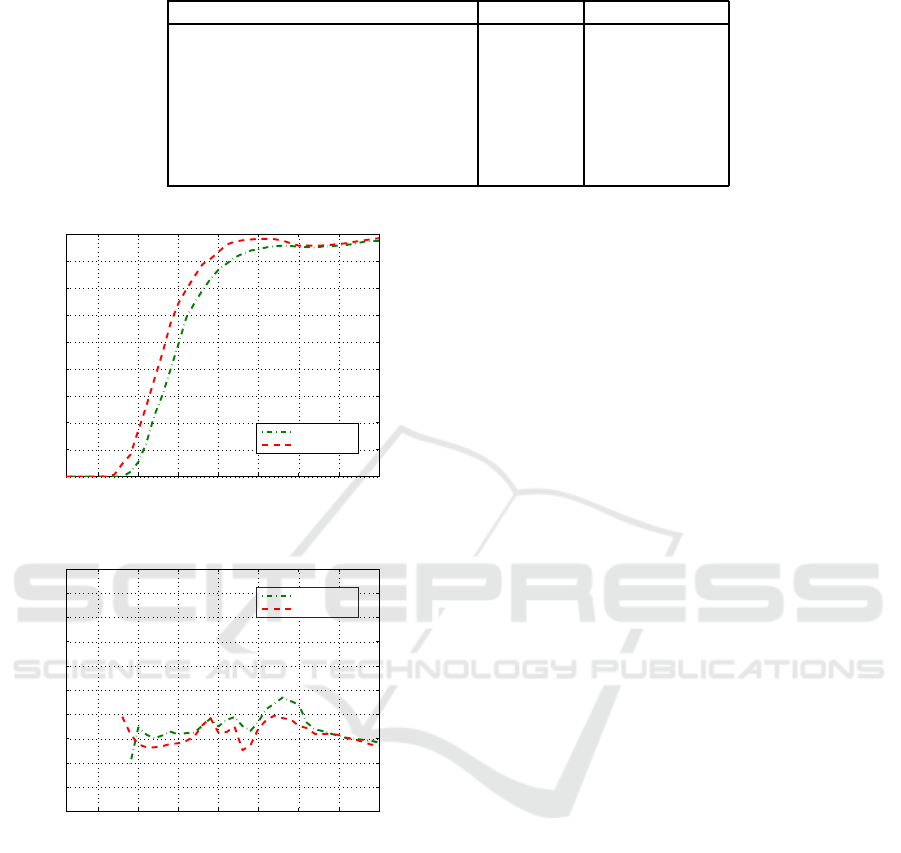
Table 2: Simulation parameters.
LM-IPDA MD-LM-IPDA
Initial PTE 0.0001 0.0001
Confirmed threshold (local) 0.1 0.1
Confirmed threshold (fusion center) 0.97 0.97
P
d
0.7 [0.4,0.3]
P
T
0.7 0.7
Number of confirmed false tracks 1 1
Simulation time (per each run) 0.24s 0.26s
5 10 15 20 25 30 35 40
0
100
200
300
400
500
600
700
800
900
scan
number of confirmed true tracks
number of CTTs at Each Scan for All Targets
LM−IPDA
MD−LM−IPDA
Figure 7: Confirmed true tracks for all the targets.
5 10 15 20 25 30 35 40
0
1
2
3
4
5
6
7
8
9
10
scan
root mean square position error (m)
RMSE for target2
LM−IPDA
MD−LM−IPDA
Figure 8: Root mean square position error of target 2.
6 CONCLUSIONS
In this paper, we propose both centralized and dis-
tributed fusion structures based on a suboptimal mul-
tiple detection multitarget tracking algorithm called
MD-LM-IPDA. These two structures utilize the prob-
ability of target existence to cover the true track con-
firmation and false track discrimination problem.
In the distributed fusion paradigm, local sen-
sor uses the target existence information to confirm
tracks. Only confirmed tracks are transmitted to the
fusion center and used as measurements to update
global tracks. By adjusting the local track confirmed
threshold, the amount of information (track states and
target existence probabilities) transmitted to the fu-
sion center can be controlled.
Since centralized fusion utilizes the information
from all the measurements, it obtains the best per-
formance with a high communication burden between
local sensors and fusion center. In distributed fusion
structure, local sensors process tracking algorithm to
generate tracks and send high quality tracks (with
high probability of target existence) to the fusion cen-
ter which makes this structure more feasible in many
practical applications.
When distributed fusion structure is considered,
MD-LM-IPDAoutperforms LM-IPDA in the sense of
true track confirmation and state estimation accuracy.
This performancesuperiority of MD-LM-IPDA is due
to that multiple detection structure helps to extract tar-
get state information contained in measurements by
considering more possible target oriented measure-
ment combinations.
ACKNOWLEDGEMENTS
This work was supported by LIGNEX1 under the con-
tract LIGNEX1-2017-0201(00).
REFERENCES
Bar-Shalom, Y. (1981). On the track-to-track correlation
problem. IEEE Trans. Automat. Contr., 26(2):571–
572.
Bar-Shalom, Y. and Campo, L. (1986). The effect of
the common process noise on the two-sensor fused-
track covariance. IEEE Trans. Aerosp. Electron. Syst.,
22(6):803–805.
Bar-Shalom, Y., Willett, P., and Tian, X. (2011). Tracking
and Data Fusion. YBS, Storrs, 1st edition.
Baum, M. and Hanebeck, U. D. (2014). Extended ob-
ject tracking with random hypersurface models. IEEE
Trans. Aerosp. Electron. Syst., 50(1):149–159.
Challa, S., Evans, R., Morelande, M., and Musicki, D.
(2011). Fundamentals of Object Tracking. Cambridge
University, United Kingdom., 1st edition.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
438

Chen, H., Kirubarajan, T., and Bar-Shalom, Y. (2003). Per-
formance limits of track-to-track fusion versus cen-
tralized estimation: Theory and applications. IEEE
Trans. Aerosp. Electron. Syst., 39(2):386–400.
Chen, J. F., Ma, H., Liang, C. G., and Zhang, Y. F. (2014).
OTHR multipath tracking using the bernoulli fil-
ter. IEEE Trans. Aerosp. Electron. Syst., 50(3):1974–
1990.
Habtemariam, B., Tharmarasa, R., Thayaparan, T., Grim-
mett, D., and Wakayama, C. (2011). Multiple detec-
tion probabilistic data association filter for multistatic
target tracking. In 4th Int. Conf. Information Fusion.
Habtemariam, B., Tharmarasa, R., Thayaparan, T., Mallick,
M., and Kirubarajan, T. (2013). A multiple-detection
joint probabilistic data association filter. IEEE Trans.
Aerosp. Electron. Syst., 7(3):461–471.
Lan, J. and Li, X. R. (2016). OTHR multipath tracking us-
ing the bernoulli filter. IEEE Trans. Aerosp. Electron.
Syst., 52(6):2973–2989.
Lee, E. H., Musicki, D., and Song, T. L. (2014). Multi-
sensor distributed fusion based on integrated proba-
bilistic data association. In 17th Int. Conf. Information
Fusion.
Mahler, R. (2009). PHD filters for nonstandard targets, I:
Extended targets. In 12th Int. Conf. Information Fu-
sion.
Musicki, D. and Evans, R. (2004). Joint integrated proba-
bilistic data association: JIPDA. IEEE Trans. Aerosp.
Electron. Syst., 40(3):1093–1099.
Musicki, D., Evans, R., and Stankovic, S. (1994). Integrated
probabilistic data association (IPDA). IEEE Trans.
Automat. Contr., 39(6):1237–1241.
Musicki, D. and Scala, B. L. (2008). Multi-target tracking in
clutter without measurement assignment. IEEE Trans.
Aerosp. Electron. Syst., 44(3):877–896.
Musicki, D., Song, T. L., and Kim, T. H. (2013). Smoothing
multi-scan target tracking in clutter. IEEE Trans. on
Signal Process., 61(19):4740–4752.
Musicki, D., Song, T. L., Lee, H. H., Chen, X., and
Kirubarajan, T. (2015). Track-to-track fusion with tar-
get existence. IET Radar, Sonar Navig., 9(3):241–248.
Vivone, G., Braca, P., Granstrom, K., and Willett, P. (1999).
Multistatic bayesian extended target tracking. IEEE
Trans. Aerosp. Electron. Syst., 25(6):2626–2643.
Track-to-track Fusion using Multiple Detection Linear Multitarget Integrated Probabilistic Data Association
439
