
Top-k Keyword Search over Wikipedia-based RDF Knowledge Graphs
Hrag Yoghourdjian, Shady Elbassuoni, Mohamad Jaber and Hiba Arnaout
Department of Computer Science, American University of Beirut, Beirut, Lebanon
Keywords:
RDF, Knowledge Graphs, Top-k Search, Keyword Search, Ranking, Wikipedia.
Abstract:
Effective keyword search over RDF knowledge graphs is still an ongoing endeavor. Most existing techniques
have their own limitations in terms of the unit of retrieval, the type of queries supported or the basis on
which the results are ranked. In this paper, we develop a novel retrieval model for general keyword queries
over Wikipedia-based RDF knowledge graphs. Our model retrieves the top-k scored subgraphs for a given
keyword query. To do this, we develop a scoring function for RDF subgraphs and then we deploy a graph
searching algorithm that only retrieves the top-k scored subgraphs for the given query based on our scoring
function. We evaluate our retrieval model and compare it to state-of-the-art approaches using YAGO, a large
Wikipedia-based RDF knowledge graph.
1 INTRODUCTION
Many large RDF knowledge graphs such as YAGO
(Suchanek et al., 2008), DBpedia (Auer et al., 2007),
and Google’s knowledge graph have been constructed
from Wikipedia. These graphs are labeled graphs
consisting of billions of edges where node labels are
either URIs representing resources or literals, and
edge labels are URIs representing predicates. For ex-
ample, Figure 1 shows a snippet of an RDF knowl-
edge graph about books. Such RDF knowledge
graphs can be typically queried using a graph-pattern
query language such as SPARQL. The results of a
SPARQL query are subgraphs from the knowledge
graph that are isomorphic to the graph pattern in the
query.
Even though graph-pattern query languages are
very powerful, they are also very restrictive. They
require some expertise as well as familiarity with
the underlying data (i.e., the exact URIs of resources
and predicates). Enabling keyword search over RDF
knowledge graphs can increase the usability of such
data sources. In addition, it enables adapting state-
of-the-art Information Retrieval searching and rank-
ing techniques.
In this paper, we propose a top-k retrieval model
for keyword queries over large Wikipedia-based RDF
knowledge graphs such as YAGO or DBpedia. Our
model takes as input a keyword query and retrieves
the top-k subgraphs that match the query. For exam-
ple, Table 1 shows the top-3 subgraphs for the query
“books by Pulitzer prize winners” from our exam-
ple knowledge graph in Figure 1, where the goal is
to find books by Pulitzer prize winners. In a nut-
shell, our approach works as follows. First, we create
inverted indices for the resources and the predicates
in the knowledge graph (i.e., node and edge labels).
We also associate each edge in our knowledge graph
with a weight reflecting the importance of the edge,
which is derived from the Wikipedia link structure as
well as the degrees of the nodes. We then develop a
novel scoring function for RDF subgraphs, which is
based on the edge weights. Finally, we develop a top-
k searching algorithm that explores the knowledge
graph starting from the query keywords and stops
once the top-k scored subgraphs are retrieved. Our
search algorithm is easily parallelizable and we use
the parallelized version in our experiments.
Our contributions can be summarized as follows:
1. We develop a novel scoring function for gen-
eral keyword queries over Wikipedia-based RDF
knowledge graphs.
2. We develop a graph search algorithm that retrieves
only the top-k scored subgraphs for a given key-
word query.
3. We prove that our search algorithm terminates
only when the top-k subgraphs are retrieved.
Yoghourdjian H., Elbassuoni S., Jaber M. and Arnaout H.
Top-k Keyword Search over Wikipedia-based RDF Knowledge Graphs.
DOI: 10.5220/0006411400170026
In Proceedings of the 9th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (KDIR 2017), pages 17-26
ISBN: 978-989-758-271-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
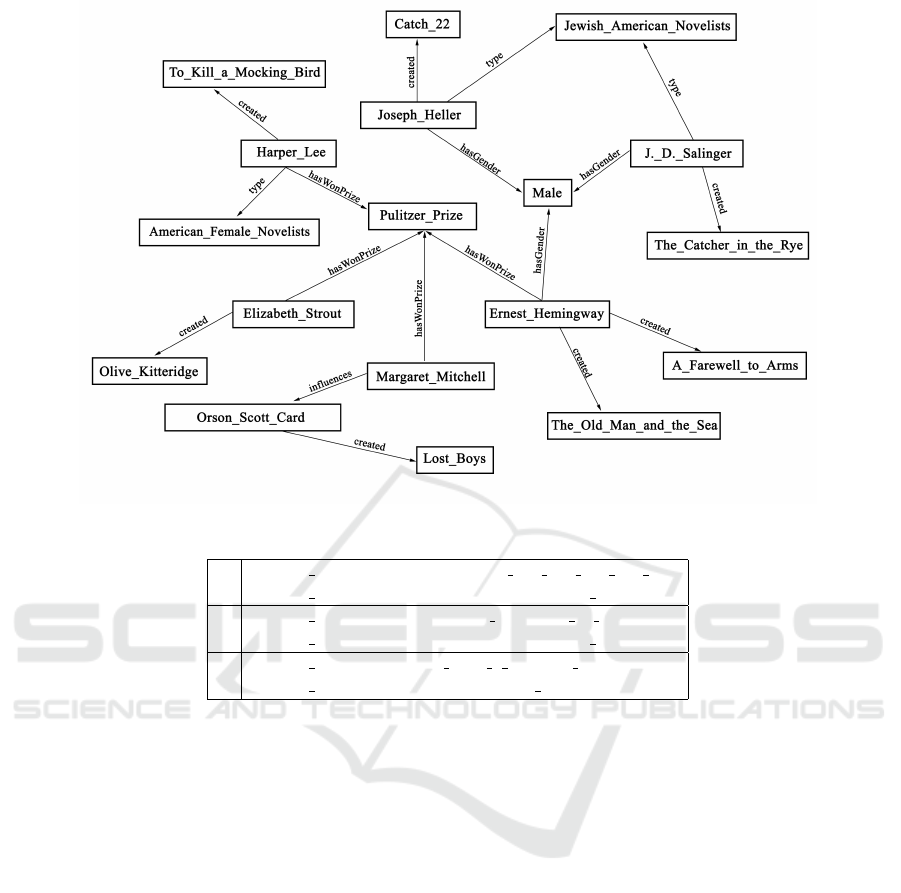
Figure 1: An example RDF knowledge graph about books.
Table 1: Top-3 subgraphs for the query “books by Pulitzer prize winners”.
1 Ernest Hemingway created The Old Man and the Sea
Ernest Hemingway hasWonPrize Pulitzer Prize
2 Ernest Hemingway created A Farewell to Arms
Ernest Hemingway hasWonPrize Pulitzer Prize
3 Harper Lee created To Kill a Mocking Bird
Harper Lee hasWonPrize Pulitzer Prize
2 RELATED WORK
Many techniques have been proposed for keyword
search over graphs (Sima and Li, 2016; He et al.,
2007; Kargar and An, 2011; Le et al., 2014; Dalvi
et al., 2008; Mass and Sagiv, 2016; Tran et al., 2009;
Li et al., 2008; Fu and Anyanwu, 2011; Golenberg
et al., 2008; Kasneci et al., 2009; Bhalotia et al.,
2002; Dass et al., 2016; Yuan et al., 2017). Most of
these techniques have their own limitations. For in-
stance, some techniques assume the unit of retrieval
to be (Steiner) trees (Golenberg et al., 2008; Kasneci
et al., 2009; Bhalotia et al., 2002; Sima and Li, 2016;
Mass and Sagiv, 2016), while in the case of search-
ing RDF knowledge graphs, the results should not
be restricted to only tree-shaped subgraphs. Others
assume the keyword queries to consist of references
to nodes only and completely ignore edge labels (He
et al., 2007; Kargar and An, 2011; Le et al., 2014;
Dalvi et al., 2008; Tran et al., 2009; Li et al., 2008;
Fu and Anyanwu, 2011; Kasneci et al., 2009). This is
a strong assumption in the case of labeled graphs such
as RDF knowledge graphs since user queries could
contain references to certain predicates (i.e., edge la-
bels)and these predicates should be taken into consid-
eration when searching the graph. In our approach,
we treat edge labels as first-class citizens and we can
handle the case when the user query consists of a ref-
erence to one or more predicates. Finally, many pre-
vious approaches do not provide any means for result
ranking, apart from the size of the results (Le et al.,
2014; Tran et al., 2009), degrees of nodes (Bhalotia
et al., 2002), which are both inadequate in the case of
RDF graphs as we show in our experiments. Other
works focused on other aspects of keyword search
such as the diversity of the results (Dass et al., 2016),
or distributed query processing (Yuan et al., 2017).
Keyword search on structured and semi-structured
data have been also studied (Nie et al., 2007; Blanco
et al., 2010; Kim et al., 2009; Xu and Papakonstanti-
nou, 2005; Schuhmacher and Ponzetto, 2014). Some
of these approaches have been adopted to the RDF
setting. For instance, the Web Object Retrieval ap-
proaches have been used to retrieve a set of resources

Figure 2: System Architecture.
(i.e., nodes) for a given keyword query, where re-
sults are typically ranked using IR techniques such
as BM25 (Blanco et al., 2010) or language models
(Nie et al., 2007). We compare our approach to one
of these techniques ((Nie et al., 2007)) in our experi-
ments.
Similar to our approach, the closely-related work
(Elbassuoni and Blanco, 2011) takes into considera-
tion both node and edge labels during the retrieval of
results and provides a model for result ranking. How-
ever, this approach is not applicable for large RDF
graphs such as Wikipedia-based ones as it does not in-
volve a top-k search algorithm and its ranking model
is not adequate as we show in our experiments.
Finally, there has been significant work on Natural
Language Question Answering over RDF Knowledge
graphs (for instance (Yahya et al., 2012; Lopez et al.,
2007; Bao et al., 2014)). Most of these techniques
utilize natural-language processing tools to translate
a user’s question into the most-likely SPARQL query.
This is an orthogonal problem to ours where we do
not want to rely heavily on the quality of the transla-
tion process.
3 APPROACH
Our system architecture is depicted in Figure 2. In
a nutshell, our approach works as follows. First, the
input keyword query is segmented and matched to a
set of resources and predicates (i.e., node and edge la-
bels or URIs). This is done by consulting the inverted
indices of the resources and predicates as the query
is being segmented. We explain how we build our in-
verted indices in Section 3.1 and how the segmenta-
tion and matching process works in Section 3.2. Next,
we explore the knowledge graph, to retrieve the top-k
scored subgraphs that connect all the nodes represent-
ing the resources mentioned in the query, and such
that these subgraphs contain for each predicate re-
ferred to in the query, a corresponding edge that is
labeled by this predicate. We describe the scoring
function that the algorithm uses in Section 3.3, and
describe the algorithm itself in Section 3.4. We then
prove the correctness of the algorithm’s termination
condition in Section 3.5.
3.1 Indexing
To be able to process keyword queries over an RDF
knowledge graph, we make use of two types of in-
verted indices. The first consists of resources or node
labels and their surface names, where surface names
are keywords that can be used to refer to a particular
resource. Resource surface names are readily avail-
able information in many RDF knowledge graphs
such as YAGO or DBpedia. For example, in YAGO,
the resource Ernest
Hemingway is associated with the
surface names “Ernest Hemingway”, “Ernest” and
“Hemingway”, where the first is typically referred
to as the preferred label. Similarly, Pulitzer Prize
is associated with the surface names “Pulitzer Prize”
and “Pulitzer Award”.
More precisely, for each resource in our knowl-
edge graph, we extract the preferred surface name and
then create an inverted index for the resources using
Apache Lucene
1
. This inverted index contains the
surface name and the corresponding resource it refers
to. Note that we only extract the preferred surface
1
https://lucene.apache.org/

name of each resource and hence each surface name
would be associated with only one resource. We also
do not tokenize the surface names and assume each
surface name (as a whole) is a key in the inverted in-
dex. This means that we assume that in the user query,
the user will use the whole preferred surface name to
refer to a resource. Alternatively, we could extract all
the surface names of the resources and tokenize them
before indexing. In that case, some changes should be
done to our segmentation and label matching proce-
dure described in the next section. Since, the main fo-
cus of the paper is on result ranking and top-k search,
we defer this to future work.
Similarly, for predicates (i.e., edge labels), we cre-
ate an inverted index that contains textual representa-
tions for predicates and the predicates they refer to,
again using Apache Lucene. To do this, we first ex-
tract for each predicate in the knowledge graph, the
possible textual representations that can be used to ex-
press that predicate. This can be done in various ways.
For example, for some knowledge graphs such as
YAGO, we can use existing sources of predicate tex-
tual representations such as PATTY (Nakashole et al.,
2012), which is a collection of semantically-typed re-
lational patterns mined from large corpora (Wikipedia
and the New York Times archive). Other knowledge
graphs, such as DBpedia, contain textual represen-
tations of their predicates just like surface names of
resources, which can be directly used. A third op-
tion is to let human experts manually suggest potential
textual representations for each predicate. A crowd-
sourcing activity would be helpful in this maneuver.
In our case, we opted for the third option and re-
trieved for each predicate, a list of textual represen-
tations using crowdsourcing. We then tokenized the
textual representations we obtained and ended up with
an inverted index that consists of single-words as keys
and lists of predicates as values. For example, one en-
try in this inverted index is the word “birth” and the
corresponding value is <wasBornIn, wasBornOn>.
3.2 Query Segmentation and Label
Matching
In this section, we describe in details the steps we per-
form for query segmentation and how the query seg-
ments are then matched to node and edge labels from
the knowledge graph (i.e., resources and predicates).
Given a keyword query, our segmentation and match-
ing process works as follows. First, we start by mark-
ing words that refer to predicates in the query. To do
this, we scan the query word by word from left to right
and for each word we consult the inverted index for
predicates and if a word matches one or more predi-
cates in the inverted index, it is marked as a predicate
word.
Next, for all phrases (consecutive words) that are
delimited by predicate words (i.e., before or after a
word marked as a predicate word), we consult the in-
verted index for resources to see if this phrase or the
longest substring of the phrase matches any resources
in the knowledge graph. Doing so will result in a set
of resources R.
Finally, to output the set of predicates P referred
to in the query, we try to resolve words marked as
predicate words to only one predicate. In case the
word was matched to only one predicate, we just add
this to P. In case the word matched more than one
predicate, we use the closest identified resource to the
predicate (i.e., immediately preceding or succeeding
the predicate in the query) and count the edges in the
knowledge graph that are labeled by the predicate and
contains the closest resource as a node. The predicate
word is then matched to the predicate with the highest
number of edges, and it is added to P. In this fashion,
we jointly resolve predicates and resources to identify
the most likely ones referred to in the user query.
For example, consider our example query “books
by Pulitzer prize winners”. Our segmentation
and matching process starts by marking the words
“books” and “winners” as two predicate words. Then
it tries to match the longest substring of the phrase “by
Pulitzer prize” to a resource in the knowledge graph,
which would result in a match to Pulitzer Prize. Fi-
nally, the predicate words “books” and “winners” are
matched to the predicates created and hasWonPrize,
respectively. Thus, P = {created,hasWonPrize} and
R = {Pulitzer Prize}.
We have described the general case for our seg-
mentation and matching process, where the user
query consists of words referring to both resources
and predicates. In the extreme cases, the user query
might refer to only predicates or only resources. In the
former, we again scan the query and mark any words
that match a predicate in the inverted index as a pred-
icate word. In case a predicate word match more than
one predicate, we pick the predicate which occurs the
most as an edge label in our knowledge graph.
In the latter, we try to match the longest substrings
of the query to resources in the knowledge graph by
scanning the query from left to right until a resource
is matched. Once a resource is matched, its matching
substring is removed from the query string and what-
ever is left in the query is again scanned from left to
right in an attempt to match other resources.
We acknowledge that our segmentation and
matching process is ad-hoc, however our focus in this
paper is mainly the top-k searching. In an orthogonal

work, we are currently developing more robust seg-
mentation and matching techniques that utilize deep
learning for this task. The results of this work can
then be adopted by our framework by replacing the
described segmentation and labeling process above.
3.3 Scoring Function
Once a keyword query is segmented and we have
identified a set of resources R and a set of predi-
cates P mentioned in the query, our goal is to find
all connected subgraphs such that each subgraph g
i
contains: (1) one and only one node for each resource
r
j
∈ R, and (2) one and only one edge whose label
corresponds to one of the predicate p
k
∈ P. For in-
stance, consider running our example query “books
by Pulitzer prize winners” on the example knowledge
graph in Figure 1. Table 2 shows some subgraphs
that satisfy the above two properties. Recall that our
segmentation and matching process will output the
resource Pulitzer Prize and the predicates created
and hasWonPrize for the example query.
For Wikipedia-based knowledge graphs such as
YAGO or DBpedia, the number of results returned for
many queries could be overwhelming and thus result
ranking is crucial. The most obvious aspect based on
which the subgraphs can be ranked is the size of the
subgraph (i.e., the number of nodes or edges). This
is the strategy adopted by most previous work (e.g.,
(Le et al., 2014)). We argue that this is not sufficient
as a basis for result ranking in Wikipedia-based RDF
knowledge graphs. Consider the first three subgraphs
in Table 2. They all have the same size, namely 2
edges. However, it is intuitive that when a user is
searching for “books by Pulitzer prize winners”, she
expects books by more famous authors such as Ernest
Hemingway to be ranked before books by those who
are less known such as Elizabeth Strout.
To be able to capture this, we associate each edge
e = (u, p,v), where u and v are the nodes connected
by e and p is the edge label, with a weight w(e) which
is computed as follows.
w(e) = inLinks(u,v) (1)
where inLinks(u,v) is the number of Wikipedia arti-
cles that link to both resources denoted by the nodes
u and v. The intuition behind this is that the more ar-
ticles that mention the resources in the edge, the more
important this edge is in the knowledge graph.
Moreover, our scoring function takes into con-
sideration the degrees of the nodes. This is mo-
tivated by the following example. Consider run-
ning the query “J. D. Salinger Joseph Heller”. This
query consists of no predicate phrases and will thus
be segmented into the following set of resources
R = {J. D. Salinger, Joseph Haller}. Running this
query over our example knowledge graph in Figure 1
will return the two subgraphs shown in Table 3.
Clearly, subgraph g
1
in Table 3 is more informa-
tive than subgraph g
2
, since it is very obvious that
both writers are males. However, both subgraphs
have the exact same size (2 edges) and moreover the
weights of the edges of the second subgraph will be
higher than those of the edges of the first subgraph
if we just rely on the number of Wikipedia links to
compute the edge weights (i.e., Equation 1). Con-
sequently, we take into consideration another aspect
when ranking the subgraphs, namely the degrees of
the nodes in the subgraph. To do this, we add for
each edge e = (u, p,v) in the knowledge graph another
weight computed as follows.
degree(e) = degree(u) + degree(v) (2)
where degree(x) is the number of edges in the knowl-
edge graph that contains x as a node. This way,
an edge such as e
1
=J. D. Salinger hasGender Male
would have a higher degree than e
2
=J. D. Salinger
type Jewish American Novelists, provided that the
degree of the node labeled Male is higher than that of
the node labeled Jewish American Novelists, which
is very well-expected.
Finally, given a subgraph g = (e
1
,e
2
,...,e
n
), its
total score is computed as follows.
s(g) =
n
∑
i=1
α
1−
w(e
i
)
∑
e∈E
w(e)
+(1−α)
degree(e
i
)
∑
e∈E
degree(e)
(3)
where E is the set of all edges and α is a weighting pa-
rameter that combines the weights of edges and their
degrees, which is set empirically to a value between 0
and 1 as we describe in the experiments section. The
denominators in Equation 3 are used for normaliza-
tion so that the weight and degree of each edge is a
value between 0 and 1.
Note that using scoring function above, a sub-
graph with a lower score will be ranked higher than a
subgraph with a higher score. This is intuitive since
we want subgraphs which have 1) smaller sizes, 2)
edges with higher weights w(e), and 3) edges with
lower degrees degree(e) to be ranked higher. Since
our scoring functions sums the scores of each individ-
ual edge in a subgraph g, then subgraphs with more
edges will have higher scores provided that the other
two factors (edge weights and degrees) are kept con-
stant. Similarly, since our scoring function subtracts
the normalized weight of an edge from 1 (first part of
Equation 3), the higher the weights of edges in g are,
the lower the score of the subgraph. Finally, the sec-
ond part in Equation 3 ensures that subgraphs whose
edges have higher degrees will have higher scores.

Table 2: Some subgraphs retrieved for the query “books by Pulitzer prize winners”.
g
1
Elizabeth Strout hasWonPrize Pulitzer Prize
Elizabeth Strout created Olive Kitteridge
g
2
Ernest Hemingway hasWonPrize Pulitzer Prize
Ernest Hemingway created The Old Man and the Sea
g
3
Harper Lee hasWonPrize Pulitzer Prize
Harper Lee created To Kill a Mocking Bird
g
4
Margaret Mitchell hasWonPrize Pulitzer Prize
Margaret Mitchell influences Orson Scott Card
Orson Scott Card created Lost Boys
Table 3: The subgraphs retrieved for the query “J. D. Salinger Joseph Heller”.
g
1
J. D. Salinger type Jewish American Novelists
Joseph Heller type Jewish American Novelists
g
2
J. D. Salinger hasGender Male
Joseph Heller hasGender Male
3.4 Top-k Search Algorithm
Our top-k search algorithm (Algorithm 1) is inspired
by the backward search algorithm proposed previ-
ously (Le et al., 2014). It takes as input a set of re-
sources R and a set of predicates P, which were iden-
tified in the user query using the segmentation and
matching process described in Section 3.2. It returns
the top-k lowest scored subgraphs that contain 1) a
node and only node for each resource r
i
∈ R, and 2)
for each predicate p
j
∈ P, an edge and only one edge
labeled with p
j
.
The algorithm maintains two main data structures,
which are necessary for book keeping. The first is
a set of minimum heaps L
1
,L
2
,. ..,L
n
, one for each
resource r
i
∈ R. The second is a look-up table M that
is used to keep track of information about each node
visited during the algorithm. Particularly, it contains
a row for each node u visited during the search and a
column for each resource r
i
. Both data structures are
empty in the beginning of the algorithm.
In the first loop of the algorithm, the node u repre-
senting each query resource r
i
is expanded by retriev-
ing all the edges that contain u and for each retrieved
edge e = (u, p,v) or e = (v, p,u), a single-edged sub-
graph g = (e) is inserted in the minimum heap L
i
along with its score as computed based on Equation
3. We also note in the minimum heap that the next
node to be expanded for the subgraph g is the node v.
Moreover, if the look-up table M does not contain
the node v, a new row is created for v and we insert g
and its score s(g) in the cell M[v][i] and nil in all the
other cells. In case M already consists of an entry for
v, we insert the pair (g,s(g)) in the cell M[v][i].
Finally, for each row in M which does not con-
tain any entries equal to nil and which contains ∀ j
∈ 1,2,.. .,m, an edge labeled p
j
∈ P, the concate-
nation of the subgraphs stored in the cells of this
row represent a candidate result. We then pick the
k lowest-scored candidates and add them to the topk
list using the procedure getTopK(M,P). Note that
this procedure takes P as input to ensure that candi-
date subgraphs which contain an edge for each predi-
cate p
j
∈ P are the only ones considered and the rest
of candidates are discarded.
In the second loop of Algorithm 1, we pop from
the minimum heaps the subgraph with the lowest
score and we further expand the next unexpanded
node of this subgraph. For instance, assume that the
subgraph with the lowest score g was popped from
L
i
, where the node to be expanded is u. We again re-
trieve all the edges e = (u, p,v) ∈ E or e = (v, p,u) ∈ E
and for each such edge, we append g to get a new
subgraph g
0
where s
0
(g) = s(g) + s(e). We then re-
insert each new subgraph g
0
back in L
i
. We also up-
date the look-up table M the same way as in the first
loop. Finally, we update the topk list as follows. For
any candidate subgraph c in M, we check its score
against the kth subgraph g
k
in the current topk list. If
s(c) < s(g
k
), we replace g
k
with c in the topk list. If
the topk list contains less than k candidates, we ap-
pend to it the candidates with the lowest scores until
we have exactly k subgraphs in the topk List.
In the next section, we explain our termination
condition which guarantees that we only stop explor-
ing the knowledge graph when the k lowest-scored
candidates are retrieved. However, before we do this,
we explain how the algorithm works in case there are
no resource mentions in the user queries. That is, if
R =
/
0. In that case, we modify Algorithm 1 so that it
contains a minimum heap for each predicate p
i
∈ P,
and the look-up table contains a column for each pred-

Algorithm 1: Top-k Search Algorithm.
Input: R = { r
1
,r
2
,. ..,r
n
}, P = { p
1
, p
2
,. .., p
m
},k
Output: Top-k lowest-scored subgraphs
Initialize n min-heaps L
1
,L
2
,. ..,L
n
; M ←
/
0 ;
topk ←
/
0
for i = 1 to n do
u = node denoting r
i
for e = (u, p,v) ∈ E or e = (v, p,u) ∈ E do
g ← e ; s (g) = α(1 −
w(e)
∑
e
0
∈E
w(e
0
)
) + (1 −
α)
degree(e)
∑
e
0
∈E
degree(e
0
)
L
i
.Insert(v, g,s(g));
if v /∈ M then
M[v] ← {nil, ..., (g,s(g)), . .., nil}
else
M[v][i] ← (g,s(g))
end if
end for
topk ← getTopK(M,P)
end for
while termination condition not met do
(u,g,s(g)) ← pop(argmin
n
i=1
{L
i
.top})
for v ∈ V and (e = (u, p, v) ∈ E or e = (v, p,u) ∈
E)and u /∈ g do
g ← g ∪ e ; s(g) = s(g) + α(1 −
w(e)
∑
e
0
∈E
w(e
0
)
) +
(1 − α)
degree(e)
∑
e
0
∈E
degree(e
0
)
L
i
.Insert(v, g,s(g));
if v /∈ M then
M[v] ← {nil, ..., (g,s(g)), . .., nil}
else
M[v][i] ← (g,s(g))
end if
end for
topk ← getTopK(M,P)
end while
return topk
icate p
i
. In the first loop of the algorithm, for each
predicate p
i
, we retrieve all edges e = (u, p
i
,v) ∈ E
and then we add the edges e to the minimum heaps
as described before. We also add both nodes u and v
to the look-up table M exactly as before. The rest of
the algorithm also behaves in the exact same way as
in the general case where we have both resources and
predicates.
Note that our algorithm can be efficiently paral-
lelized by creating multiple parallel threads for the
graph exploration steps. We use this parallelized ver-
sion in our experiments, where all the threads work in
parallel to expand the nodes but share the same data
structures, namely the look-up table M and the mini-
mum heaps L
1
,L
2
,. ..,L
n
.
3.5 Termination Condition
To guarantee that our top-k algorithm returns the k
lowest-scored subgraphs for a given user query, we
need to ensure two things:
1. For those rows in M with one or more nil value,
the subgraphs in these rows if concatenated with
subgraphs that contain the resource corresponding
to a nil value will never have a score lower than
those in the returned topk list.
2. There are no more rows that can be inserted in M
in the future and the concatenation of these sub-
graphs would have a score lower than those in the
returned topk list.
To guarantee that the first condition above holds, we
use the look-up table M as follows. For each row in M
where there is at least one cell with a nil value, let b(i)
be an indicator function that returns 0 if the ith cell of
the row is nil and 1 otherwise. Furthermore, let g
i
be
the subgraph stored in the ith cell, in case it does not
contain nil. Finally, let the score of the subgraph in
the top of the minimum heap L
i
be s(L
i
.top). The best
score of any subgraph g formed by concatenating the
subgraphs in the cells that do not contain nil values
can then be computed as follows.
bestscore(g) =
n
∑
i=1
s(g
i
) × b(i) + s(L
i
.top) × (1 − b
i
)
(4)
As for the second condition, to compute the best
score any subgraph g
0
in the knowledge graph can
have at a certain stage of the exploration, we use the
following equation.
τ =
n
∑
i=1
s(L
i
.top) (5)
Finally, to check if the k subgraphs in the cur-
rent topk list are indeed the k lowest-scored sub-
graphs possible and thus can successfully terminate
the graph exploration, we check if the following in-
equality holds:
s(g
k
) ≤ min
min
g∈NC
(bestscore(g)),τ
(6)
where NC is the set of (not necessarily connected)
subgraphs which are retrieved from the look-up ta-
ble M by going through the rows with nil values and
concatenating the subgraphs in those cells that do not
contain nil values, bestscore(g) is computed using
Equation 4, τ is the best score any candidate subgraph
that might be constructed later can have, which can be
computed using Equation 5, and s(g
k
) is the score of
the kth subgraph in the current topk list.

Table 4: Query Benchmark.
ron howard actor director woody allen actor director creator
woody allen wife birthday married albert einstein
woody allen acted judy davis woody allen
actor director woody allen scarlett johansson albert einstein isaac newton
boston university albert einstein frank b. morse albert einstein
judy davis woody allen taylor swift nicki minaj kendrick lamar
woody allen scarlett johansson actor director
actor wife birthday born wife actor director
germany population country london capital
elton john dogma and chasing amy
gone with the wind director doctor zhivago actors
jessica alba jennifer aniston jessica alba ioan gruffudd
meryl streep mamma mia! australia leader
russia leader wife birthplace england capital population
germany england pierce brosnan meryl streep
leader birthplace birth death dates actors
Table 5: Average NDCG values for different values of α.
α 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
NDCG 0.979 0.982 0.981 0.985 0.981 0.981 0.979 0.980 0.979 0.981 0.971
4 EVALUATION
We conducted two main experiments to evaluate our
top-k retrieval model. The first experiment was
used to tune the parameter α in our scoring func-
tion (which is used in Equation 3). Once this pa-
rameter was tuned, a second experiment was con-
ducted to compare our approach to state-of-the-art
approaches for keyword search over RDF data. In
all our experiments, we use YAGO (Suchanek et al.,
2008) as our knowledge graph. YAGO is a large-scale
general-purpose RDF knowledge graph derived from
Wikipedia and WordNet. It contains more than 120
million edges about 10 million resources (e.g., per-
sons, organizations, cities) and consists of 75 distinct
predicates.
4.1 Parameter Tuning
To be able to tune our single parameter α used in our
scoring function described in Section 3.3, we created
a benchmark composed of 32 keyword queries. Table
4 displays all the queries in the benchmark. We re-
sorted to creating our own benchmark since most of
the benchmarks available assume the results to be en-
tities rather than subgraphs. In addition, all the avail-
able benchmarks consider only binary relevance (i.e.,
result either correctly answer the query or not). In our
case, we want to assess the relevance of the results on
a multilevel scale.
For each query in our benchmark, we ran our top-
-k search algorithm to retrieve the top-10 subgraphs,
varying the value of α from 0 to 1 with a scale of 0.1.
We pooled the top-10 results for each value of α and
presented them in random order to five human judges
2
which were asked to assess the relevance of the results
with respect to the query on a four-point scale: 3 for
highly relevant and popular results, 2 for highly rel-
evant results, 1 for marginally relevant results, and 0
for non-relevant results
3
.
We calculated the Fleiss’ kappa coefficient (Fleiss,
1971) to measure the agreement between our human
judges and acquired a value of κ = 0.66, which is in
the range of substantial agreement. We also used three
gold queries during our assessment tasks and all hu-
man judges assessed all the results of the three gold
queries exactly as specified in the gold assessments.
Finally, we used a majority vote to aggregate the
assessments of the five judges and used these ag-
gregated assessments as a relevance level for the re-
sults. Next, we calculated the average Normalized
Discounted Cumulative Gain (NDCG) for each value
of α, which can be seen in Table 5. We conclude from
the table that the best value for α is 0.3, based on the
average NDCG. This indicates that relying solely on
the degrees of nodes for ranking as some previous ap-
proaches do is inadequate.
2
All judges were graduate computer science students
3
The guidelines and the relevance assessments will be made
publicly available

Table 6: Average NDCG values for our approach versus state-of-the-art approaches.
Our Approach Backward Search WOR KBR
0.985 0.898 0.141 0.157
4.2 Comparison to State-of-the-art
In this experiment, we compare our approach with the
value of α set to 0.3 to three different approaches. The
first approach is the backward search approach (Le
et al., 2014), which uses a very similar top-k search
algorithm to ours, however it does not take into con-
sideration predicates and only relies on the size of the
subgraphs for scoring.
The second approach we compared ours to is the
Web Object Retrieval (WOR)(Nie et al., 2007), which
retrieves a list of resources for a given keyword query
and ranks them based on statistical language models.
This approach represents the family of approaches
which retrieve a list of resources in response to a
keyword query. To be able to run this approach on
our knowledge graph, we first associate each edge
e = (u, p, v) in the knowledge graph with a set of key-
words which are the surface names of all resources
linked to by either u or v as well as the textual repre-
sentation of the predicate p. To be comparable to our
approach, we also associate each edge-keyword pair
(e,t) with a weight w(e,t) reflecting the importance
of the edge e with respect to the keyword t which is
computed as the number of Wikipedia pages that link
to both u and v and contain the keyword t.
Now, given a keyword query q = {q
1
,q
2
,. ..,q
n
}
where q
i
is a single keyword, we start by retrieving all
the edges which are associated with each keyword q
i
.
Next, we extract all the unique resources r
1
,r
2
,. ..,r
m
that are nodes in any of these edges. Finally, we score
each resource r using the below scoring function and
rank them descendingly based on their scores.
s(r) =
n
∏
i=1
∑
e∈E
P(q
i
|e) × P(e|r) (7)
where P(q
i
|e) is set to
w(e,q
i
)
∑
e
0
∈E
w(e
0
,q
i
)
and P(e|r) is equal
to 1 if e consists of a node representing resource r,
and 0 otherwise.
The third approach we compared against is the
keyword-based retrieval model over RDF graphs
(KBR) (Elbassuoni and Blanco, 2011). This ap-
proach first retrieves edges that contain any of the
keywords in the user query, and then proceed by join-
ing these edges to construct connected minimal sub-
graphs which are then ranked based on a hierarchical
language modeling approach.
For each of the above three approaches as well
as our approach (with α set to 0.3 for our approach),
we ran all the queries in our benchmark and retrieved
the top-10 results for each query. These results were
then pooled together and presented to the same five
human judges, which again assessed their relevance
with respect to the queries on the same 4-point scale.
Note that in the case of the Web Object Retrieval ap-
proach, we also provided the human judges with the
Wikipedia link to each resource retrieved in order to
help them assess the relevance of the resources with
the respect to the queries.
Similar to the previous experiment, our human
judges had a substantial agreement as measured by
Fleiss’ Kappa coefficient. We again aggregated the
assessments for each result using a majority vote and
then computed the average NDCG for each approach.
As can be seen from Table 6, our approach signifi-
cantly outperforms all other approaches based on the
average NDCG (with a p-value ≤ 0.026).
For the case of WOR and KBR, the average
NDCG is very low for the following reasons. WOR
assumes independence between the query keywords
and it treats each resource as a bag-of-words ignor-
ing the structure in the underlying data. KBR on the
other hand does not take into consideration the link-
structure or degrees when ranking subgraphs.
Finally, we report on the time it took to run our 35
queries and retrieve the top-10 results. The average
execution time for a non-parallelized version of our
search algorithm is 18.069 seconds and the average
execution time for the parallelized version is 13.17
seconds.
5 CONCLUSION
In this paper, we presented a top-k search algo-
rithm for keyword queries over Wikipedia-based RDF
knowledge graphs. Our approach utilizes a novel
scoring function to score a subgraph, which takes into
consideration the size of the subgraph as well as its
edge weights. The edge weights are computed using
a careful combination of the degrees of the nodes as
well as the number of Wikipedia articles that point
to them. Our top-k algorithm guarantees that for a
given k, the returned subgraphs are indeed the lowest-
scored. We have compared our approach to various
state-of-the-art approaches and it significantly outper-
formed all the other approaches based on the average
NDCG of a benchmark consisting of 32 queries.

In future work, we plan to use a more robust seg-
mentation and label matching process than the one we
used here, which will rely on deep learning to iden-
tify candidate resources and predicates referred to in
a given keyword query. Moreover, we plan to improve
the efficiency of our top-k search algorithm by mak-
ing use of graph summarization techniques as well as
developing a distributed version of our search algo-
rithm. We also plan to generalize our ranking model
to be applicable to a wider range of RDF knowledge
graphs, that are not necessarily based on Wikipedia.
REFERENCES
Auer, S., Bizer, C., Kobilarov, G., Lehmann, J., Cyganiak,
R., and Ives, Z. (2007). Dbpedia: A nucleus for a web
of open data. In ISWC/ASWC.
Bao, J., Duan, N., Zhou, M., and Zhao, T. (2014).
Knowledge-based question answering as machine
translation. Cell, 2(6).
Bhalotia, G., Hulgeri, A., Nakhe, C., Chakrabarti, S., and
Sudarshan, S. (2002). Keyword searching and brows-
ing in databases using banks. In ICDE.
Blanco, R., Mika, P., and Zaragoza, H. (2010). Entity search
track submission by yahoo! research barcelona. Sem-
Search.
Dalvi, B. B., Kshirsagar, M., and Sudarshan, S. (2008).
Keyword search on external memory data graphs.
Proceedings of the VLDB Endowment, 1(1).
Dass, A., Aksoy, C., Dimitriou, A., Theodoratos, D., and
Wu, X. (2016). Diversifying the results of keyword
queries on linked data. In International Conference
on Web Information Systems Engineering.
Elbassuoni, S. and Blanco, R. (2011). Keyword search over
rdf graphs. In CIKM.
Fleiss, J. L. (1971). Measuring nominal scale agreement
among many raters. Psychological bulletin, 76(5).
Fu, H. and Anyanwu, K. (2011). Effectively interpreting
keyword queries on rdf databases with a rear view. In
International Semantic Web Conference.
Golenberg, K., Kimelfeld, B., and Sagiv, Y. (2008). Key-
word proximity search in complex data graphs. In
Proceedings of the 2008 ACM SIGMOD international
conference on Management of data.
He, H., Wang, H., Yang, J., and Yu, P. S. (2007). Blinks:
ranked keyword searches on graphs. In Proceedings
of the 2007 ACM SIGMOD international conference
on Management of data.
Kargar, M. and An, A. (2011). Keyword search in graphs:
Finding r-cliques. Proceedings of the VLDB Endow-
ment, 4(10).
Kasneci, G., Ramanath, M., Sozio, M., Suchanek, F. M.,
and Weikum, G. (2009). Star: Steiner tree approxima-
tion in relationship-graphs. In ICDE.
Kim, J., Xue, X., and Croft, W. B. (2009). A probabilistic
retrieval model for semistructured data. In ECIR.
Le, W., Li, F., Kementsietsidis, A., and Duan, S. (2014).
Scalable keyword search on large rdf data. IEEE
Transactions on knowledge and data engineering,
26(11).
Li, G., Ooi, B. C., Feng, J., Wang, J., and Zhou, L. (2008).
Ease: an effective 3-in-1 keyword search method for
unstructured, semi-structured and structured data. In
Proceedings of the 2008 ACM SIGMOD international
conference on Management of data. ACM.
Lopez, V., Uren, V., Motta, E., and Pasin, M. (2007). Aqua-
log: An ontology-driven question answering system
for organizational semantic intranets. Web Semant.,
5(2).
Mass, Y. and Sagiv, Y. (2016). Virtual documents and an-
swer priors in keyword search over data graphs. In
EDBT/ICDT Workshops.
Nakashole, N., Weikum, G., and Suchanek, F. (2012). Patty:
a taxonomy of relational patterns with semantic types.
In Proceedings of the 2012 Joint Conference on Em-
pirical Methods in Natural Language Processing and
Computational Natural Language Learning.
Nie, Z., Ma, Y., Shi, S., Wen, J., and Ma, W. (2007). Web
object retrieval. In WWW.
Schuhmacher, M. and Ponzetto, S. P. (2014). Knowledge-
based graph document modeling. In Proceedings of
the 7th ACM international conference on Web search
and data mining.
Sima, Q. and Li, H. (2016). Keyword query approach over
rdf data based on tree template. In Big Data Analysis
(ICBDA), 2016 IEEE International Conference on.
Suchanek, F. M., Kasneci, G., and Weikum, G. (2008).
Yago: A large ontology from wikipedia and wordnet.
J. Web Sem., 6(3).
Tran, T., Wang, H., Rudolph, S., and Cimiano, P. (2009).
Top-k exploration of query candidates for efficient
keyword search on graph-shaped (rdf) data. In 2009
IEEE 25th International Conference on Data Engi-
neering.
Xu, Y. and Papakonstantinou, Y. (2005). Efficient keyword
search for smallest lcas in xml databases. In Proceed-
ings of the 2005 ACM SIGMOD international confer-
ence on Management of data.
Yahya, M., Berberich, K., Elbassuoni, S., Ramanath, M.,
Tresp, V., and Weikum, G. (2012). Natural language
questions for the web of data. In EMNLP.
Yuan, Y., Lian, X., Chen, L., Yu, J., Wang, G., and Sun, Y.
(2017). Keyword search over distributed graphs. IEEE
Transactions on Knowledge and Data Engineering.
