Differential and Rotational Cryptanalysis of Round-reduced MORUS

Ashutosh Dhar Dwivedi, Paweł Morawiecki and Sebastian W

ojtowicz

Institute of Computer Science, Polish Academy of Sciences, Warsaw, Poland

Keywords:

Authenticated Encryption, MORUS, Rotational Cryptanalysis, Internal Differential Cryptanalysis, CAESAR

Competition.

Abstract:

In this paper we investigate the security margin of MORUS — an authenticated cipher taking part in the CAE-

SAR competition. We propose a new key recovery approach, which can be seen as an accelerated exhaustive

search. We also verify the resistance of MORUS against internal differential and rotational cryptanalysis. Our

analysis reveals that the cipher has a solid security margin and a lack of round constants does not bring any

weakness. Our work helps to reliably evaluate this new, high-performance algorithm, which is particularly

important in the context of the ongoing CAESAR competition.

1 INTRODUCTION

A cryptographic algorithm which provides both con-

ﬁdentiality and authenticity, is called an authenticated

encryption (AE) or simply an authenticated cipher. It

encrypts and authenticates messages using both a se-

cret key (shared by the sender and the receiver) as well

as a public number (called a nonce). AE algorithms

are often built as various combinations of block ci-

phers, stream ciphers, message-authentication codes

and hash functions.

The great interest and importance of AE have

been manifested by the announcement of a new pub-

lic call for AE algorithms — the CAESAR competi-

tion (CAE, ). The contest has started in 2014 and has

received worldwide attention. In the ﬁrst round, 57

algorithms were submitted and now (January 2017),

in the third round, 16 ciphers are still in the race. Par-

ticularly MORUS (Wu and Huang, ) — the cipher we

focus on — has advanced to the third round of the

CAESAR competition. MORUS exhibits excellent

software performance and can be also a great choice

for hardware platforms. However, the problem is very

little third-party cryptanalysis of this algorithm (see

Related work below) as the third-party investigation

is essential to build trust towards new, promising ci-

phers.

MORUS has an interesting design feature, namely

a lack of round constants. Typically, the round

constants are introduced to break a symmetry be-

tween rounds and/or between parts of the state. The

MORUS designers, however, chose a different ap-

proach. A pseudorandom constant is introduced only

into the initial state and with a strong initialization

phase all possible state symmetries should be elim-

inated. In our work, we want to verify whether such

design decisions lead to a weakness exploitable by in-

ternal differentials or rotational cryptanalysis. These

two techniques were previously used to attack some

algorithms (or their reduced variants), where the state

symmetries were not fully disturbed by the round con-

stants (Dinur et al., 2013; Morawiecki et al., 2013).

Related Work

As mentioned, there are very few cryptanalytic works

on MORUS. Mileva et al. made some observations

and they described the distinguisher (in a nonce-reuse

scenario) (Mileva et al., 2015). However, the rele-

vance of this work to the cipher’s security was ques-

tioned by the MORUS designers (MORUSGoogle-

GroupDiscussin, ). Some concerns about MORUS

security is highlighted in (Saarinen, 2016), where the

author claims that MORUS represents signiﬁcantly

elevated adaptive-chosen-plaintext attack risk. Full

round SAT analysis was made by Dwivedi et al. on

MORUS-640 (Dwivedi et al., 2016).

In our work, besides the classic differential crypt-

analysis, we apply internal differentials and rotational

cryptanalysis. Internal differentials were ﬁrst pro-

posed by Peyrin (Peyrin, 2010) in the attack on the

Grøstl hash function. In (Dinur et al., 2013), Dinur

et al. showed that internal differentials could be also

used to produce collisions against the round-reduced

Dwivedi, A., Morawiecki, P. and Wójtowicz, S.

Differential and Rotational Cryptanalysis of Round-reduced MORUS.

DOI: 10.5220/0006411502750284

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 275-284

ISBN: 978-989-758-259-2

275

Keccak, exploiting the round constants and their re-

lation to the state symmetry. Most recently, internal

differentials were combined with the boomerang tech-

nique, which led to the 8-round practical distinguisher

of the Keccak-f permutation (Jean and Nikolic, 2015).

Rotational cryptanalysis was formally introduced

in (Khovratovich and Nikoli

c, 2010) but the technique

itself was mentioned and applied earlier (Bernstein,

2005; Knudsen et al., 2009; Standaert et al., 2006).

Rotational cryptanalysis was also combined with the

rebound attack and applied to the compression func-

tion of the SHA-3 candidate Skein and its underly-

ing cipher Threeﬁsh (Khovratovich et al., 2010). In

(Morawiecki et al., 2013), the preimage attack against

the round-reduced Keccak (Bertoni et al., b) is given

and the attack takes advantage of the low Hamming

weight round constants.

Our Contribution

The classic techniques for the key recovery (such as

so called R − 1 differential attack) cannot be directly

applied to MORUS due to a different structure of the

algorithm and limitations introduced by the nonce re-

quirement. We propose a new key recovery approach,

where differential characteristics are used in a differ-

ent manner than in typical attacks known for block

ciphers. Our approach can be viewed as the accel-

erated exhaustive search and can be combined with

other techniques such as rotational cryptanalysis.

To quantify the security margin and gain more in-

sight into the ciphers, we analyse reduced variants.

Speciﬁcally, we reduce a number of rounds (steps) in

the initialization phase, all the other parameters of the

algorithms are the same as in the full variants. Our

best result is the theoretical key recovery attack on

MORUS-1280-256, where the initialization phase is

reduced to 18 rounds. We also apply internal differen-

tial and rotational cryptanalysis to investigate whether

a lack of round constants could pose a threat to the

security of MORUS. The presented attacks respect

the nonce requirement and need very few plaintext-

ciphertext pairs. Table 1 shows our main ﬁndings.

With 80 rounds in the MORUS initialization, the

algorithm has a very solid security margin against ro-

tational and internal differential cryptanalysis. Our

analysis supports the designers’ claims on a strong

security level of the ciphers and offers some crypt-

analytic insight, which is very important for reliable

evaluation of this new promising design. We argue

that our ﬁndings, such as 18-round differential char-

acteristics with probability 1, could serve as a starting

point for other analysis, for example the differential-

linear attack.

2 MORUS DESCRIPTION

MORUS has been designed to achieve a great perfor-

mance on both software and hardware, across vari-

ous platforms. Actually, MORUS is a family of three

authenticated ciphers: MORUS-640-128, MORUS-

1280-128, and MORUS-1280-256.

The ﬁrst number in the cipher’s name is a size of

the state (in bits) and the second number stands for the

key size. The state consists of 5 registers (either 128-

or 256-bit) and each register is divided into 4 words.

The state update function consists of 5 very sim-

ilar rounds and it relies on four simple bitwise oper-

ations. These operations are: AND, XOR, and two

kinds of rotations. The symbol ≪ denotes the rota-

tion in the register by a given number of bits, whereas

Rotl(s,b) rotates words in the register s over b bits.

Figure 1 shows the state update function. In our anal-

ysis we focus on MORUS with a 1280-bit state, then

let us describe the initialization and encryption phase

for this variant.

Initialization

First, the key, initialization vector (IV) and the

constants are loaded into the ﬁve registers of the state.

= IV k0

128

= K

= 1

256

= 0

256

= constant

For MORUS-1280-256, K denotes the 256-bit

key, for MORUS-1280-128 K is built by the concate-

nation of the 128-bit key with itself. The constant

in the 5th register is the Fibonacci sequence modulo

256. After preparing the initial state, the state update

function is called 16 times. Each of these 16 steps

consists 5 rounds, so there are 5 × 16 = 80 rounds in

the initialization. Finally, the key is XORed with the

second register S

Encryption

Once the initialization is ﬁnished, the plaintext block

is encrypted.

= P

⊕ S

⊕ (S

≪ 192) ⊕ (S

)

Then, the plaintext P

is used to update the state.

Once the state is updated, the next plaintext block

i+1

can be encrypted.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

276

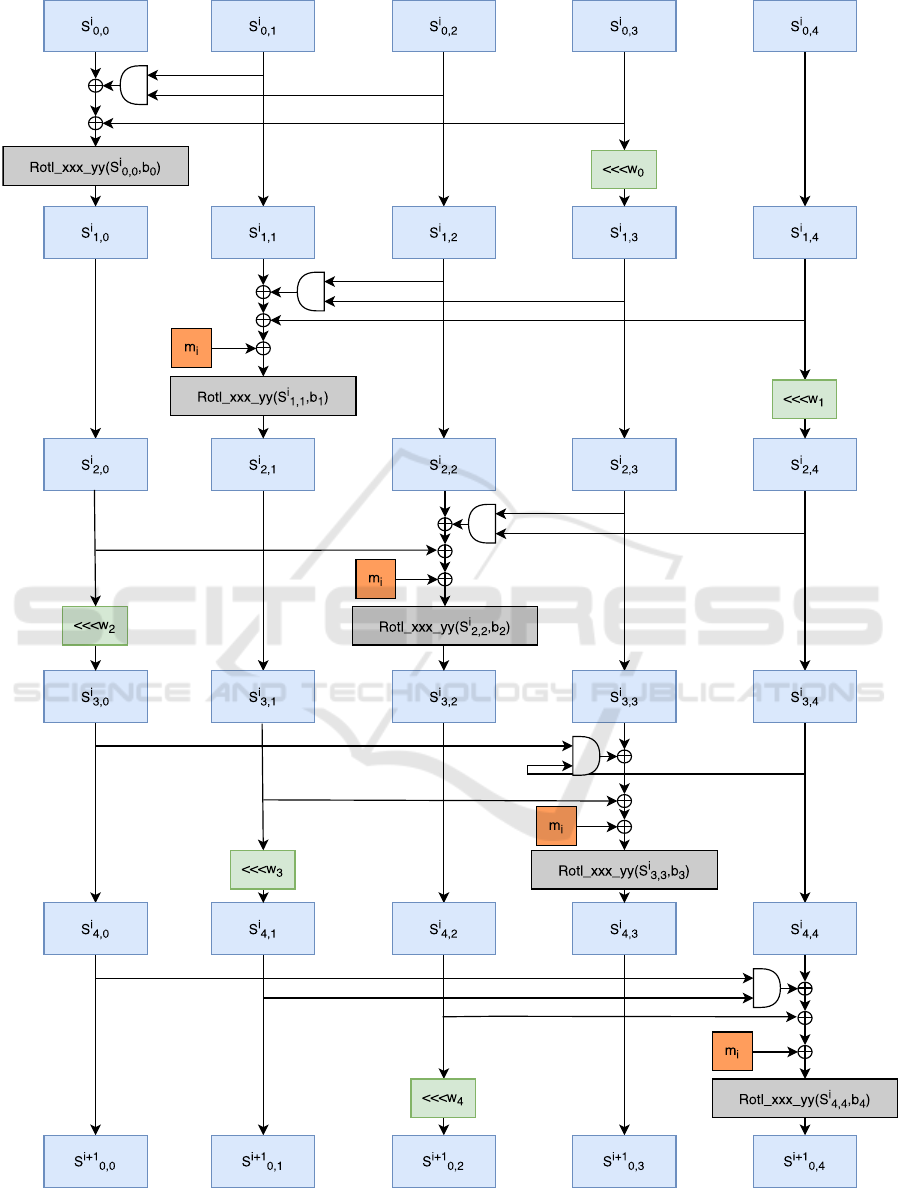
Figure 1: The state update function of MORUS.

Differential and Rotational Cryptanalysis of Round-reduced MORUS

277

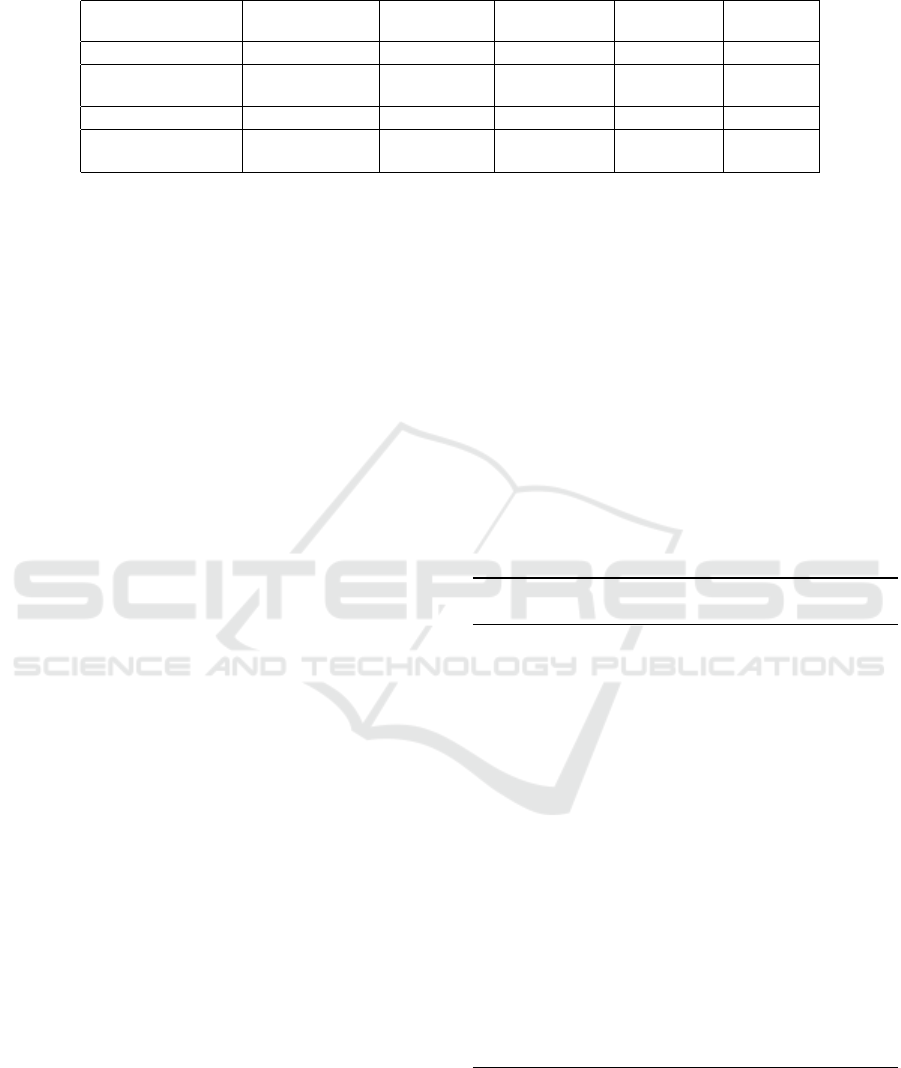
Table 1: Our attacks on reduced variants of MORUS.

Algorithm Intialization

rounds

Technique Attack type Complexity Reference

MORUS-1280-256 18 differential key recovery 2

253

Sect. 3

MORUS-1280-128 7 internal

differential

ciphertext

prediction

Sect. 4.1

MORUS-1280-256 8 rotational key recovery 2

251

Sect. 5.1

MORUS-1280-256 10 rotational ciphertext

prediction

Sect. 5.2

3 KEY RECOVERY ATTACK ON

MORUS WITH 18-ROUND

INITIALIZATION

A common approach for attacking block ciphers with

differential cryptanalysis is the so called R− 1 attack.

First, the attacker constructs a differential character-

istic which covers all but last round. Then, by guess-

ing a round key from the last round, she inverts the

last round from given ciphertexts. If the statistics of

‘new’ ciphertexts behaves accordingly to the differen-

tial characteristic, then the round key guess is correct.

However, MORUS has a completely different struc-

ture than a typical modern block cipher (such as AES)

and it is not clear how the classic key recovery at-

tacks could be used against MORUS. Also, applying

block-cipher-like differential cryptanalysis directly to

the encryption phase is not possible because of the

nonce requirement.

To circumvent these limitations, we propose a

new, different way for the key recovery. Our idea

can be viewed as an accelerated exhaustive search.

A general scheme of the attack is as follows. For a

given 256-bit key, there are 256 differential counter-

parts which differ from a given key on a single bit.

We try to guess/identify one of such counterparts and

then we argue that a total cost for this is lower than

the exhaustive search. Once the differential counter-

part is identiﬁed and the XOR difference with the key

is known, clearly the secret key itself is also revealed.

The attack below is described for MORUS-1280-

256, where the initialization phase is reduced to 18

rounds. For a 256-bit key, the probability that we

guess one of its 256 counterparts is 2

−256

× 256 =

−248

, so after 2

248

guesses we should hit the dif-

ferential counterpart of the key. Now the question is

how to check (cheaply) whether we guess the coun-

terpart. Here help comes from differential character-

istics, such as the one shown in Table 2. In the ta-

ble differences are given in the hexadecimal format.

When bits with a non-zero input difference are mul-

tiplied (bitwise AND), the output difference depends

on the actual values of these bits. Since we do not

know these actual values (only their differences), such

an output difference can not be determined with cer-

tainty. We denote a nibble with the undetermined dif-

ference by ‘?’. (To avoid heavy and unreadable no-

tation, the symbol ‘?’ captures both partly undeter-

mined nibbles and nibbles, where all 4 bits are under-

mined.)

In a precomputation phase, we construct 256 dif-

ferential characteristics, each with 1-bit difference

initial state. The 18-round characteristics end with a

ciphertext (256 bits), where differences for some bits

are still known. These characteristics are stored in

memory and then used to identify whether we guess

the counterpart of the key or not. Algorithm 1 shows

the pseudocode of the attack.

Algorithm 1 Key recovery attack on MORUS-1280-

256 with 18-round initialization.

1: P ← 0x00...0  Set plaintext to all-zero vector

2: IV ← 0x00...0  Set IV to all-zero vector

3: MORUS-1280-256(IV , key)  Initialization

4: C ← P ⊕ S

⊕ (S

≪ 192) ⊕ (S

) 

Calculate the ciphertext C

5: for i ← 0 to i < 2

248

6: MORUS-1280-256(IV , guessedKey) 

Initialization

7: C

← P ⊕ S

⊕ (S

≪ 192) ⊕ (S

) 

Calculate the ciphertext C

8: for n ← 1 to 256 do

9: if (C ⊕ C0 matches the characteristic

)

then

10: (guessedKey ⊕ characteristic

input)

is a candidate for the secret key

11: end if

12: end for

13: end for

After 2

248

guesses the attacker should hit one of

the 256 differential counterparts of the secret key.

Hence the main loop is iterated 2

248

times. In the in-

ner loop, the ciphertexts difference is calculated and

if it matches the output from one of the 256 character-

istics (generated in the precomputation phase), then

SECRYPT 2017 - 14th International Conference on Security and Cryptography

278

Table 2: The 18-round differential characteristic for MORUS-1280-256.

Initial state of differences

0000000000000000 0000000000000000 0000000000000000 0000000000000000

0000080000000000 0000000000000000 0000000000000000 0000000000000000

0000000000000000 0000000000000000 0000000000000000 0000000000000000

↓

Step 1 (Rounds 1–5)

↓

0000000000000000 0100000000000000 0000000000000000 0000000000000000

0000000000000000 0000000000000000 0000000002000000 0000000000000000

0000000000000000 0000000040000000 0000000000000000 0000000000000000

0000000100000000 0000000000000000 0000000000000000 0000000000000000

0000000400000000 ?000000000000000 00000000?0000000 0000000000000000

ciphertext: 254 known differences

↓

Step 2 (Rounds 6–10)

↓

0000000000000000 0000200000000000 00000?0000000020 000000?000000000

0000000000000?80 000000000000?000 0000000000010000 00000?000000?000

0000000?000000?0 000000000008000? 00000800000?0010 000000000000??00

000000?000800000 00??0000000?0000 000?0?00000??000 0000?08000?0000?

0000000?0080???0 000?800000??0100 0000?04000????00 0000???0000?0?0?

ciphertext: 229 known differences

↓

Step 3 (Rounds 11–15)

↓

0???000?0???0000 000??0100???0000 ?400000?0?0?000? ???00000??0?0000

????0000???0000? ???0?000????00?0 ???0000??00??02? ??4?000??0?0000?

?????00????00?00 ?????0000??0??00 0???0??10????0?? ???????0?00??0??

???0????????1??? 2??????0????0??? ???04????8?????? ???00?????00?0??

????04???????0?? ??????1????????? ?????????8?????? ????00?????0?0??

ciphertext: 101 known differences

↓

Step 4 (Rounds 16–18)

↓

???????????????? ?????????2?????? ???????????????? ?8??????????????

???????????????? ???????????????? ???????????????? ????????????????

2??????0????0??? ???04????8?????? ???00?????00?0?? ???0????????1???

?????????8?????? ????00?????0?0?? ????04???????0?? ??????1?????????

ciphertext: 2 known differences

the guessed key might be the counterpart of the se-

cret key. Please note that the cost of the inner loop is

very small. Basically, we need one bitwise XOR be-

tween C and C0 and then bitwise AND with the 256-

bit mask, which tells which bits should be taken into

account. For comparison, the 18-round initialization

requires 252 XOR operations on registers and 90 bit-

wise AND between registers. So, the total cost of the

inner loop is negligible as it is just a tiny fraction of a

single call to the 18-round MORUS-1280-256.

Outputs (ciphertexts) from the 18-round differ-

ential characteristics have, on average, 3 bits with

known differences. So, for 256-bit ciphertexts the ‘ﬁl-

ter’ is not very strong and we expect around 2

256

253

false alarms to check. Thus, checking false

alarms is a dominant factor of the time complexity

of the attack.

We could try to use more differential character-

istics which start with a 2- or 3-bit difference. This

would lead to fewer iterations in the main loop (lower

complexity of the attack), however, our experiments

show that we could penetrate fewer rounds in that

cases. Indeed, this is expected as more differences

in the initial state lead to faster propagation of differ-

ences and unknown differences start dominating the

state earlier.

Differential and Rotational Cryptanalysis of Round-reduced MORUS

279

4 INTERNAL DIFFERENTIAL

CRYPTANALYSIS OF MORUS

In internal differential cryptanalysis, the attacker fol-

lows differences between parts of the state. However,

it is not obvious which parts should be compared.

Thus, the ﬁrst step is to specify how we calculate an

internal difference. A hint for us is that a symmet-

ric state (zero internal difference) should be preserved

(ideally) by all the operations in the algorithm. If

some operations break the chosen symmetry, then we

should look for another symmetry. (Though it might

be the case that there is not such a symmetry.) For

MORUS there are three ‘natural’ choices how to de-

ﬁne the symmetry and calculate internal differences.

We could try a difference between two halves of a

state, between two halves of a register or between two

halves of a word. The symmetry between halves of

the state is broken by both ≪ and Rotl operations,

whereas the other two symmetries are preserved by all

the operations. In this analysis we focus on a symme-

try within the registers and the reason for this choice

is the following. MORUS-1280 operates on 256-bit

registers and the 128-bit secret key is concatenated

with its copy (keykkey), then loaded in the S

in the initial state. Thus, there is a symmetry in S

regardless of the actual value of the key. The other

choice of symmetry (within words) is discussed at the

end of this section.

4.1 Ciphertext Prediction for

MORUS-1280-128 with 7-round

Initialization

Let us ﬁrst analyse a propagation of internal differ-

ences for MORUS-1280-128. The IV has to be set to

all 0’s to have the ﬁrst register S

symmetric. As ex-

plained above, the S

of a key value. The subsequent registers S

and S

are

initialized with all 1’s and all 0’s, so they are clearly

symmetric. Finally, the ﬁfth register S

is ﬁlled with

a constant, which is the Fibonacci sequence modulo

256.

Clearly, this is not a symmetric constant, so the

initial state has some internal differences (the symme-

try is partly disturbed). Table 3 shows an evolution of

the internal differences up to 8 rounds. If the initial-

ization is reduced to 7 rounds, the attacker is able to

predict a ciphertext bit with probability 1. As shown

in Table 3, the ciphertext after 7 rounds still has one

known internal difference. Speciﬁcally, the difference

between bits number 29 and 157 is known. The at-

tacker initializes MORUS-1280-128 with the IV set to

all 0’s and obtains the 29th bit from a ciphertext block.

Knowing a plaintext and the difference between 29th

and 157th bit from a ciphertext, she can predict the

value of the unseen 157th ciphertext bit. The predic-

tion works for any key and any known plaintext.

We also investigate the internal differentials with

probabilistic transitions. However, we could not ﬁnd

any low-cost differential path, which leads to many

known ciphertext differences after 8 rounds.

Other Symmetry

The other symmetry, which is preserved by both ≪

and Rotl operations, is the symmetry between halves

of a word. Interestingly, in MORUS a rotation num-

ber in ≪ is always a multiple of a word size (due

to implementation efﬁciency) and it helps us to keep

the symmetry as ≪ moves the whole words ‘intact’

to a new position in the state. However, using the

symmetry within words for the ciphertext prediction

is more difﬁcult. To have the S

with 128-bit key) symmetric, we have to assume that

a key itself is symmetric. Therefore the analysis is

valid only against the weak key class of 2

symmet-

ric keys. We investigate how the internal differences

evolve for this symmetry and the result is very sim-

ilar to ﬁndings from Table 3, that is up to 7 rounds

there are known differences in the ciphertext (see Ap-

pendix).

5 ROTATIONAL

CRYPTANALYSIS OF MORUS

In this section we show how to use rotational crypt-

analysis to mount the key recovery attack and the

ciphertext prediction for MORUS with the round-

reduced initialization phase. We study how rotational

relations between two states change over the subse-

quent rounds and then try to use these observations

for the attacks.

First, we should specify what we mean by rota-

tional relation between two MORUS states. Having

two states S and S

, the state S

is rotated (with a ref-

erence to S) if all words in S

are copied from S and

rotated by a rotational number n. (In MORUS-1280,

a word size is 64 bits, so there are 64 possible values

of n.) With S

constructed like this, all the steps in

the algorithm preserve the rotational relation between

S and S

. Similarly to internal differentials, where

the constant breaks the symmetry, here the constants

breaks the desired rotational relation. The pseudoran-

dom constant (Fibonacci sequence) breaks the rota-

tional pattern regardless of a chosen value of n.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

280

Table 3: The 8-round internal differential characteristic for MORUS-1280-128.

Initial state of internal differences

00000000 00000000 00000000 00000000

db3c1957 6ec727fc 3533061b e35c51bf

↓

Round 1

↓

00000000 00000000 00000000 00000000

db3c1957 6ec727fc 3533061b e35c51bf

ciphertext: 128 known internal differences

↓

Round 2

↓

00000000 00000000 00000000 00000000

ed9e0cab 376393fe 9a99830d f1ae28df

00000000 00000000 00000000 00000000

3533061b e35c51bf db3c1957 6ec727fc

ciphertext: 128 known internal differences

↓

Round 3

↓

00000000 00000000 00000000 00000000

ed9e0cab 376393fe 9a99830d f1ae28df

00000000 00000000 00000000 00000000

3533061b e35c51bf db3c1957 6ec727fc

ciphertext: 128 known internal differences

↓

Round 4

↓

00000000 00000000 00000000 00000000

9a99830d f1ae28df ed9e0cab 376393fe

00000000 00000000 00000000 00000000

???????? ???????? ??????6? ????????

3533061b e35c51bf db3c1957 6ec727fc

ciphertext: 27 known internal differences

↓

Round 5

↓

00000000 00000000 00000000 00000000

9a99830d f1ae28df ed9e0cab 376393fe

00000000 00000000 00000000 00000000

???????? ???????? ??????6? ????????

?0?????? ???????? ???????? ????????

ciphertext: 27 known internal differences

↓

Round 6

↓

???????? ???????? ???????? ????????

9a99830d f1ae28df ed9e0cab 376393fe

00000000 00000000 00000000 00000000

???????? ??????6? ???????? ????????

?0?????? ???????? ???????? ????????

ciphertext: 4 known internal differences

↓

Round 7

↓

???????? ???????? ???????? ????????

00000000 00000000 00000000 00000000

???????? ??????6? ???????? ????????

???????? ???????? ?0?????? ????????

ciphertext: 1 known internal difference

↓

Round 8

↓

???????? ???????? ???????? ????????

???????? ??????6? ???????? ????????

???????? ???????? ?0?????? ????????

ciphertext: 0 known internal differences

Now, let us see an example of the rotational charac-

teristic for MORUS-1280-256. We use the same no-

tation as for internal differentials but this time a hex-

adecimal number means the difference between cor-

responding bits from the states S and S

. So, for exam-

ple, if we consider the 1st bit and rotational number

n = 8, then we calculate the XOR difference between

1st bit from S and 9th bit from S

(within a given

word). Table 4 shows the rotational characteristic

Please note that here we trace differences between two

states, so we need two times more symbols than in the case

of internal differences of a single state.

with n = 43. The registers S

...S

have a (rotational)

differences set to 0, whereas the 5th register is ini-

tialized with the Fibonacci constant, hence there are

differences and rotational relation is disturbed.

5.1 Key-recovery Attack on MORUS

with 8-round Initialization

In the following key recovery attack we use our

idea of accelerated exhaustive search from Section 3.

This time, however, we take advantage of rotational

characteristics rather than differential. The attack is

Differential and Rotational Cryptanalysis of Round-reduced MORUS

281

Table 4: The 9-round rotational characteristic (n = 43) for MORUS-1280-256.

Initial state

0000000000000000 0000000000000000

284169020b0d1815 5ee927f08153b5e5

ca42968c8500849f 8957d842fa3f3b40

↓

Round 1

↓

0000000000000000 0000000000000000

284169020b0d1815 5ee927f08153b5e5

ca42968c8500849f 8957d842fa3f3b40

ciphertext: 256 known differences

↓

Round 2

↓

0000000000000000 0000000000000000

46054a105a4082c3 ed7957ba49fc2054

2127f290a5a32140 ced02255f610be8f

0000000000000000 0000000000000000

ca42968c8500849f 8957d842fa3f3b40

284169020b0d1815 5ee927f08153b5e5

ciphertext: 256 known differences

↓

Round 3

↓

0000000000000000 0000000000000000

46054a105a4082c3 ed7957ba49fc2054

2127f290a5a32140 ced02255f610be8f

0000000000000000 0000000000000000

ca42968c8500849f 8957d842fa3f3b40

284169020b0d1815 5ee927f08153b5e5

ciphertext: 256 known differences

↓

Round 4

↓

0000000000000000 0000000000000000

2127f290a5a32140 ced02255f610be8f

46054a105a4082c3 ed7957ba49fc2054

0000000000000000 0000000000000000

02a5082d204161a3 bcabdd24fe102a76

93f94852d190a010 68112afb085f47e7

ca42968c8500849f 8957d842fa3f3b40

284169020b0d1815 5ee927f08153b5e5

ciphertext: 146 known differences

↓

Round 5

↓

0000000000000000 0000000000000000

2127f290a5a32140 ced02255f610be8f

46054a105a4082c3 ed7957ba49fc2054

0000000000000000 0000000000000000

02a5082d204161a3 bcabdd24fe102a76

93f94852d190a010 68112afb085f47e7

a42968c8500849fc 957d842fa3f3b408

84169020b0d18152 ee927f08153b5e55

ciphertext: 146 known differences

↓

Round 6

↓

????????????6??? 7???????????????

????5????4?????f ??????????f?????

2127f290a5a32140 ced02255f610be8f

46054a105a4082c3 ed7957ba49fc2054

0000000000000000 0000000000000000

bcabdd24fe102a76 93f94852d190a010

68112afb085f47e7 02a5082d204161a3

a42968c8500849fc 957d842fa3f3b408

84169020b0d18152 ee927f08153b5e55

ciphertext: 90 known differences

↓

Round 7

↓

????????????6??? 7???????????????

????5????4?????f ??????????f?????

d??????????????? ??a?????????????

??????8????????? ?????0????2????1

0000000000000000 0000000000000000

bcabdd24fe102a76 93f94852d190a010

68112afb085f47e7 02a5082d204161a3

84169020b0d18152 ee927f08153b5e55

a42968c8500849fc 957d842fa3f3b408

ciphertext: 48 known differences

↓

Round 8

↓

??????????f????? ????????????6???

7??????????????? ????5????4?????f

d??????????????? ??a?????????????

??????8????????? ?????0????2????1

???????????????? ????????????????

bcabdd24fe102a76 93f94852d190a010

68112afb085f47e7 02a5082d204161a3

84169020b0d18152 ee927f08153b5e55

a42968c8500849fc 957d842fa3f3b408

ciphertext: 20 known differences

↓

Round 9

↓

??????????f????? ????????????6???

7??????????????? ????5????4?????f

??????8????????? ?????0????2????1

d??????????????? ??a?????????????

???????????????? ????????????????

84169020b0d18152 ee927f08153b5e55

a42968c8500849fc 957d842fa3f3b408

ciphertext: 1 known difference

SECRYPT 2017 - 14th International Conference on Security and Cryptography

282

applied to MORUS-1280-256 with the initialization

phase reduced to 8 rounds. The general scheme of the

attack is similar to the differential one, yet some de-

tails speciﬁc rotational analysis need to be explained.

The main idea behind the attack is that we can

ﬁnd the rotational counterpart of the secret key with

an effort lower than the exhaustive search. Once the

rotational counterpart is found, we rotate it back to

get the key. The attack description given below is for

MORUS-1280-256 but the attack works in the same

way for MORUS-1280-128.

A register in MORUS-1280 has 64-bit words.

Therefore, there are 64 possible values of the rota-

tional number n, including the identity transforma-

tion. For 256-bit key, the probability that we guess

one of its rotational counterparts is 2

−256

× 64 =

−250

, so after 2

250

guesses we should hit the rota-

tional counterpart of the key

. Now the question is

how to check (cheaply) whether we guess the rota-

tional counterpart. Here the rotational characteristics

(such as the one shown in Table 4) come in handy. In

Precomputation, we generate 64 rotational character-

istics, each corresponds to a different rotational num-

ber. The 8-round characteristics end with a ciphertext

(256 bits), where rotational relations for some bits are

still known. These characteristics are stored in mem-

ory and then used to identify whether we guess the

rotational counterpart of the key or not. Algorithm 2

shows the pseudocode of the attack.

As explained above, after 2

250

the attacker should

guess one of the 64 rotational counterparts of the se-

cret key. Hence the main loop is iterated 2

250

times. In

the inner loop, the ciphertexts difference is calculated

and if it matches one of the 64 characteristics (gener-

ated in Precomputation), then the guessed key (rotated

by n) might be the secret key. Please note that the cost

of the inner loop is very small. Basically, we need one

bitwise XOR between C and C0 and then bitwise AND

with the 256-bit mask, which tells which bits should

be taken into account. For comparison, the 8-round

initialization requires 112 XOR operations on regis-

ters and 40 bitwise AND between registers. So, the

total cost of the inner loop is not more than a single

call to the 8-round MORUS-1280.

Outputs (ciphertexts) from the 8-round rotational

characteristics have, on average, 11 bits with known

differences. So, for 256-bit ciphertexts the ‘ﬁlter’ is

not very strong and there will be many false alarms.

There is a class of symmetric keys, where both halves

of a word is the same. For such keys, rotations act as the

identity function hence there are not any rotational counter-

parts. However, 2

128

such keys is only a tiny fraction of all

256

possible keys and checking the whole class before the

actual attack does not affect the total complexity of our key

recovery attack.

Algorithm 2 Key recovery attack on MORUS-1280-

256 with 8-round initialization.

1: P ← 0x00...0  Set plaintext to all-zero vector

2: IV ← 0x00...0  Set IV to all-zero vector

3: MORUS-1280-256(IV , key)  Initialization

4: C ← P ⊕ S

⊕ (S

≪ 192) ⊕ (S

) 

Calculate the ciphertext C

5: for i ← 0 to i < 2

250

6: MORUS-1280-256(IV , guessedKey) 

Initialization

7: C

← P ⊕ S

⊕ (S

≪ 192) ⊕ (S

) 

Calculate the ciphertext C

8: for n ← 0 to 64 do

9: if (C ⊕ C0 matches the characteristic

)

then

10: (guessedKey ≪ n) is a candidate for

the secret key

11: end if

12: end for

13: end for

For example, when the rotational number n is 43,

there are 20 known differences in the ciphertext,

hence we expect around 2

250

= 2

230

false pos-

itives. We calculate an expected number of false

alarms for all 64 values of n and the total number

of false alarms (candidates for one of the rotational

counterpart of the secret key) is about 2

248

. There-

fore, the time complexity of the attack is dominated

by calls to MORUS in the main loop (2

250

iterations).

Adding false alarms (2

248

) plus a small cost of bitwise

operations in the inner loop make the total cost of the

attack equal to around 2

251

More Rounds

There are rotational characteristics (such as the one

shown in Table 4), which cover 9 or even 10 rounds.

However, a number of known differences in the ci-

phertexts (for 9 or 10 rounds) is, on average, less than

1. This means that a number of false alarms would

be very close to 2

256

and it would be difﬁcult to ar-

gue that the total cost of the attack is lower than the

exhaustive search for the 256-bit key.

5.2 Ciphertext Prediction in Weak Key

Scenario for 10-round MORUS

When we assume that the 256-bit secret key is one

of 2

128

symmetric keys (for which halves of a given

word are the same), then we could use the rotational

characteristics to predict the ciphertext, similarly to

the attack described in Section 4.1. For the 10-round

Differential and Rotational Cryptanalysis of Round-reduced MORUS

283

rotational characteristic, where n = 18, there are 4

known differences between the ciphertext and its rota-

tional counterpart. The attacker initializes MORUS-

1280-256 with an arbitrarily chosen IV and obtains

the ciphertext block. Now the attacker can predict the

ciphertext (4 bits), which would be generated from

MORUS initialized with the rotated IV (each word of

the IV rotated by 18). So, using rotational characteris-

tics the prediction is possible up to 10 rounds, yet we

need a stronger assumption — a key from the weak

key class.

6 CONCLUSION

We have proposed a new approach for the theoret-

ical key recovery attack against the round-reduced

MORUS. The technique can be seen as an accelerated

exhaustive search and it works not only with differen-

tial cryptanalysis but also with other types of distin-

guishers. The technique could be particularly useful

for ciphers, which have completely different struc-

ture than typical block ciphers such as AES, for ex-

ample for the sponge-based cryptographic primitives

(Bertoni et al., a).

We have also analysed the resistance of MORUS

against internal differentials and rotational cryptanal-

ysis. Our ﬁndings have revealed that the cipher offers

solid security margin against these techniques. As

MORUS has some unorthodox design features (such

as a lack of round constants) we think it is essential to

analyse such new, promising algorithms with a possi-

bly wide range of cryptanalytic tools and techniques.

All performed test are applicable for old and new ver-

sion of submitted cipher. Our work helps to realize

this goal.

REFERENCES

CAESAR: Competition for Authenticated Encryp-

tion: Security, Applicability, and Robustness.

http://competitions.cr.yp.to/caesar.html.

Bernstein, D. J. (2005). Salsa20. Technical re-

port, eSTREAM, ECRYPT Stream Cipher Project.

http://cr.yp.to/snufﬂe.html.

Bertoni, G., Daemen, J., Peeters, M., and Van Assche, G.

Cryptographic Sponges. http://sponge.noekeon.org/

CSF-0.1.pdf.

Bertoni, G., Daemen, J., Peeters, M., and Van Assche,

G. Keccak Sponge Function Family Main Document.

http://keccak.noekeon.org/Keccak-main-2.1.pdf.

Dinur, I., Dunkelman, O., and Shamir, A. (2013). Collision

Attacks on Up to 5 Rounds of SHA-3 Using General-

ized Internal Differentials. In Fast Software Encryp-

tion - 20th International Workshop, FSE 2013, Sin-

gapore, March 11-13, 2013. Revised Selected Papers,

pages 219–240.

Dwivedi, A. D., Kloucek, M., Morawiecki, P., Nikolic, I.,

Pieprzyk, J., and W

ojtowicz, S. (2016). Sat-based

cryptanalysis of authenticated ciphers from the CAE-

SAR competition. IACR Cryptology ePrint Archive,

2016:1053.

Jean, J. and Nikolic, I. (2015). Internal differen-

tial boomerangs: Practical analysis of the round-

reduced keccak-f permutation. In Leander, G., edi-

tor, FSE 2015, volume 9054 of LNCS, pages 537–556.

Springer, Heidelberg.

Khovratovich, D. and Nikoli

c, I. (2010). Rotational crypt-

analysis of ARX. In Proceedings of the 17th interna-

tional conference on Fast software encryption, LNCS,

pages 333–346. Springer-Verlag.

Khovratovich, D., Nikolic, I., and Rechberger, C. (2010).

Rotational Rebound Attacks on Reduced Skein. In

ASIACRYPT’10, volume 6477 of LNCS, pages 1–19.

Knudsen, L. R., Matusiewicz, K., and Thomsen, S. S.

(2009). Observations on the Shabal keyed permuta-

tion. Available online. http://www.mat.dtu.dk/people/

S.Thomsen/shabal/shabal.pdf.

Mileva, A., Dimitrova, V., and Velichkov, V. (2015). Analy-

sis of the authenticated cipher MORUS (v1). In Cryp-

tography and Information Security in the Balkans

- Second International Conference, BalkanCryptSec

2015, Koper, Slovenia, September 3-4, 2015, Revised

Selected Papers, pages 45–59.

Morawiecki, P., Pieprzyk, J., and Srebrny, M. (2013). Rota-

tional cryptanalysis of round-reduced Keccak. In Fast

Software Encryption, LNCS. Springer.

MORUSGoogleGroupDiscussin. https://groups.google.com/

forum/#!msg/crypto-competitions/p1TQVraGkrU/

C0bpcrLxMQAJ/.

Peyrin, T. (2010). Improved Differential Attacks for ECHO

and Grøstl. In Advances in Cryptology - CRYPTO

2010, 30th Annual Cryptology Conference, Santa Bar-

bara, CA, USA, August 15-19, 2010. Proceedings,

pages 370–392.

Saarinen, M. O. (2016). The BRUTUS automatic cryptana-

lytic framework - testing CAESAR authenticated en-

cryption candidates for weaknesses. J. Cryptographic

Engineering, 6(1):75–82.

Standaert, F.-X., Piret, G., Gershenfeld, N., and Quisquater.,

J.-J. (2006). SEA: A Scalable Encryption Algorithm

for Small Embedded Applications. In CARDIS’06,

volume 3928 of LNCS, pages 222–236.

Wu, H. and Huang, T. The Authenticated Ci-

pher MORUS. https://competitions.cr.yp.to/

caesar-submissions.html.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

284