GLITCH: A Discrete Gaussian Testing Suite for

Lattice-based Cryptography

James Howe and M

aire O’Neill

Centre for Secure Information Technologies (CSIT), Queen’s University Belfast, U.K.

Keywords:

Post-quantum Cryptography, Lattice-based Cryptography, Discrete Gaussian Samplers, Discrete Gaussian

Distribution, Random Number Generators, Statistical Analysis.

Abstract:

Lattice-based cryptography is one of the most promising areas within post-quantum cryptography, and offers

versatile, efﬁcient, and high performance security services. The aim of this paper is to verify the correctness of

the discrete Gaussian sampling component, one of the most important modules within lattice-based cryptog-

raphy. In this paper, the GLITCH software test suite is proposed, which performs statistical tests on discrete

Gaussian sampler outputs. An incorrectly operating sampler, for example due to hardware or software errors,

has the potential to leak secret-key information and could thus be a potential attack vector for an adversary.

Moreover, statistical test suites are already common for use in pseudo-random number generators (PRNGs),

and as lattice-based cryptography becomes more prevalent, it is important to develop a method to test the

correctness and randomness for discrete Gaussian sampler designs. Additionally, due to the theoretical re-

quirements for the discrete Gaussian distribution within lattice-based cryptography, certain statistical tests for

distribution correctness become unsuitable, therefore a number of tests are surveyed. The ﬁnal GLITCH test

suite provides 11 adaptable statistical analysis tests that assess the exactness of a discrete Gaussian sampler,

and which can be used to verify any software or hardware sampler design.

1 INTRODUCTION

Post-quantum cryptography as a research ﬁeld has

grown substantially recently, essentially due to the

growing concerns posed by quantum computers. The

proviso being to provide long-term and highly secure

cryptography, practical in comparison to RSA/ECC,

but more importantly being adequately safe from

quantum computers. This requirement is also has-

tened by the need for “future prooﬁng” currently

secure data, ensuring current IT infrastructures are

quantum-safe before large-scale quantum computers

are realised (Campagna et al., 2015).

As such, government agencies, companies, and

standards agencies are planning transitions towards

quantum-safe algorithms. The Committee on Na-

tional Security Systems (CNSS) (CNSS, 2015) and

the National Technical Authority for Information As-

surance (CESG/NCSC) (CESG, 2016) are now plan-

ning drop-in quantum-safe replacements for current

cryptosystems. The ETSI Quantum-Safe Cryptogra-

phy (QSC) Industry Speciﬁcation Group (ISG) (Cam-

pagna et al., 2015) is also highly active in researching

industrial requirements for quantum-safe real-world

deployments. NIST (Moody, 2016) have also called

for quantum-resistant cryptographic algorithms for

new public-key cryptography standards, similar to

previous AES and SHA-3 competitions.

Lattice-based cryptography (Ajtai, 1996; Regev,

2005) is a very promising candidate for quantum-safe

cryptography. Lattice-based cryptography bases its

hardness on ﬁnding the shortest (or closest) vector in a

lattice, which is currently resilient to all known quan-

tum reductions and hence attacks by a quantum com-

puter. Furthermore, lattice-based cryptography also

offers extended functionality whilst being more efﬁ-

cient than ECC and RSA based primitives of public-

key encryption (P

oppelmann and G

uneysu, 2014) and

digital signature schemes (Howe et al., 2015).

Lattice-based cryptoschemes are usually founded

on either the learning with errors problem (LWE)

(Regev, 2005) or the short integer solution problem

(SIS) (Ajtai, 1996) or variants of these over ideal

lattices. The general idea within lattice-based cryp-

tosystems is to hide computations on secret-data with

noise, usually discrete Gaussian noise, which would

otherwise be retrievable via Gaussian elimination.

The rationale for using discrete Gaussian noise (as

Howe, J. and O’Neill, M.

GLITCH: A Discrete Gaussian Testing Suite for Lattice-based Cryptography.

DOI: 10.5220/0006412604130419

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 413-419

ISBN: 978-989-758-259-2

413

opposed to another probability distribution) is that

it allows for more efﬁcient lattice-based algorithms,

with smaller output sizes such as ciphertexts or sig-

natures. Background on discrete Gaussian sampling

techniques is provided by Dwarakanath and Galbraith

(Dwarakanath and Galbraith, 2014) and Howe et al.

(Howe et al., 2016).

The speciﬁcations for the discrete Gaussian noise

within lattice-based cryptography are very precise.

The statistical distance between the theoretical dis-

crete Gaussian distribution and the one observed

in practice should be overwhelmingly small (Peik-

ert, 2010), usually at least as small as 2

−λ

for λ ∈

{64,... ,128}. Providing guidelines to test implemen-

tations of discrete Gaussian samplers is therefore nec-

essary for real-world applications in order to prevent

attacks exploiting biased samplers. Moreover, an er-

roneously operating sampler could affect the target se-

curity level of the overall lattice-based cryptoscheme.

Additionally, the test suite is applicable for lattice-

based cryptoschemes whose outputs are also dis-

tributed via the discrete Gaussian distribution, such as

lattice-based encryption schemes (Lindner and Peik-

ert, 2011; Lyubashevsky et al., 2013) and digital sig-

natures (Gentry et al., 2008; Ducas et al., 2013).

Indeed, a biased sampler or cryptoscheme could

be a potential attack vector for an adversary. Opera-

tional errors or bugs within sampler software or hard-

ware designs, could signiﬁcantly effect the theoretical

security of the lattice-based cryptoscheme. To combat

these issues for PRNGs, the DIEHARD (Marsaglia,

1985; Marsaglia, 1993; Marsaglia, 1996) and NIST

SP 800-22 Rev. 1a (Bassham III et al., 2010) test

suites were created. This is therefore clearly needed

for discrete Gaussian random number generators.

This research investigates and proposes a discrete

Gaussian testing suite for lattice-based cryptography,

named GLITCH, which tests the correctness of a

generic discrete Gaussian sampler (or lattice-based

cryptoscheme) design. GLITCH takes as input his-

togram data, thus being able to test any discrete Gaus-

sian sampling design, either in hardware or software.

This paper surveys statistical tests that could be used

for this purpose, proposing 11 tests appropriate for

use within lattice-based cryptography. These test the

main parameters and the shape of the distribution, and

include normality and graphical tests.

The next section provides prerequisites on the dis-

crete Gaussian distribution. Section 3 details a survey

of the tests considered for the discrete Gaussian test

suite, and is furthered by the 11 tests considered in

GLITCH. The results are then analysed in Section 4.

2 THE DISCRETE GAUSSIAN

DISTRIBUTION

The discrete Gaussian distribution or discrete normal

distribution (D

Z,σ

) over Z with mean µ = 0 and pa-

rameter σ is deﬁned to have a weight proportional to

(x) = exp(−(x −µ)

/(2σ

)) for all integers x. The

variable S

= ρ

(Z) =

∑

∞

k=−∞

(k) ≈

√

2πσ is then

deﬁned so that the probability of sampling x ∈Z from

the distribution D

Z,σ

is ρ

(x)/S

. For applications

within lattice-based cryptography, it is assumed that

these parameters are ﬁxed and known in advanced.

Theoretically, the discrete Gaussian distribution

has inﬁnitely long tails and inﬁnitely high precision,

therefore in practice compromises have to be made

which do not hinder the integrity of the scheme. The

discrete Gaussian parameters needed are (µ, σ,λ, τ);

representing the sampler’s centre, standard deviation,

precision, and tail-cut, respectively.

The mean (µ) is the centre of a normalised distri-

bution. Within lattice-based cryptography, the mean

is usually set to µ = 0.

The standard deviation (σ) controls the distribu-

tion’s shape by quantifying the dispersion of data

from the mean. The standard deviation depends on

the modulus used within LWE or SIS. For instance in

LWE, should σ be too small the hardness assumption

may become easier than expected, and if σ is too large

the problem may not be as well-deﬁned as required.

The precision parameter (λ) governs the level of

precision required for an implementation, exacting

the statistical distance between the “perfect” theoret-

ical discrete Gaussian distribution and the “practical”

to be no greater than 2

−λ

, corresponding directly to

the scheme’s security level.

The tail-cut parameter (τ) administers the exclu-

sion point on the x-axis, for a particular security level.

That is, given a target security level of b-bits, the tar-

get distance from “perfect” need be no less than 2

−b

Thus, instead of considering |x| ∈ {0,∞}, it is instead

considered as |x|∈{0,στ}. Applying the reduction in

precision also affects the tail-cut parameter, which is

calculated as τ =

λ ×2 ×ln(2).

These parameters are chosen via the scheme’s

security proofs. For example, the Lindner-Peikert

lattice-based encryption scheme (Lindner and Peik-

ert, 2011) requires parameters (µ = 0, σ = 3.33,λ =

128,τ = 13.3) and the BLISS lattice-based signature

scheme (Ducas et al., 2013) requires much larger pa-

rameters (µ = 0,σ = 215,λ = 128,τ = 13.3). The

next section presents a variety of statistical tests to

check these parameters from observed data outputs

from a generic discrete Gaussian sampler.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

414

3 A DISCRETE GAUSSIAN

TESTING SUITE

This section describes the GLITCH discrete Gaussian

testing suite for use within lattice-based cryptogra-

phy. To the best of the authors’ knowledge, this is

the ﬁrst proposal for testing the outputs of discrete

Gaussian samplers for use within lattice-based cryp-

tography. That is, if the samplers are actually pro-

ducing the distribution required for speciﬁc values for

µ,σ, τ, and λ. GLITCH can also be applied to outputs

of cryptoschemes which follow the discrete Gaussian

distribution, such as the BLISS signature scheme.

3.1 Statistical Testing Within

Cryptography

Statistical testing is used to estimate the likelihood

of a hypothesis given a set of data. For example,

in cryptanalysis, statistical testing is commonly used

to detect non-randomness in data, that is to distin-

guish the output of a PRNG from a truly random bit-

stream or to ﬁnd the correctly decrypted message.

The need for random and pseudorandom numbers

arises in many cryptographic applications. For exam-

ple, common cryptosystems employ keys that must be

generated in a random fashion. Many cryptographic

protocols also require random or pseudorandom in-

puts at various points, for example, for auxiliary quan-

tities used in generating digital signatures, or for gen-

erating challenges in authentication protocols.

Moreover, the inclusion of statistical tests is

paramount when implementing cryptography in prac-

tice. For example, to test a PRNG for cryp-

tographically adequate randomness, the test suites

DIEHARD (Marsaglia, 1985; Marsaglia, 1993;

Marsaglia, 1996) and NIST SP 800-22 Rev. 1a

(Bassham III et al., 2010) were proposed to check

for insecure randomness, that is, to test a PRNG for

weaknesses that an adversary could exploit.

3.2 Statistical Testing for Lattice-based

Cryptography

To exploit or attack a PRNG, an algorithm could de-

termine the deviation of its output from that of a truly

uniformly random deviation. This is especially im-

portant for the discrete Gaussian distribution within

lattice-based cryptography, since these values hide se-

cret information. Normality tests can be used to deter-

mine if, and how well, a data set follows the required

normally structured distribution. More speciﬁcally,

statistical hypothesis testing is used, which under the

null hypothesis (H

), states that the data is normally

distributed. The alternative hypothesis (H

), states

that the data is not normally distributed. All of the

methods proposed for testing the correctness of a dis-

crete Gaussian sampler design only require an input

of histogram values output from the sampler.

For the test suite, two normality tests are adopted,

each using the same statistics of the discrete Gaussian

samples, by producing two important (and somewhat

distinct) results. Both also follow the same hypothe-

ses; the null hypothesis that the sample data is nor-

mally distributed, and the alternative hypothesis that

they are not normally distributed.

The ﬁrst test considered is the Jarque-Bera (Jar-

que and Bera, 1987) goodness-of-ﬁt test, which takes

the skewness and kurtosis from the sample data, and

matches it with the discrete Gaussian distribution. It

tests the shape of the sampled distribution, rather than

dealing with expected values, which makes the test

signiﬁcantly simpler than, say, a χ

test. Interest-

ingly, if the sample data is normally distributed, the

test statistic from the Jarque-Bera test asymptotically

follows a χ

distribution with two degrees of freedom,

which is then used in the hypothesis test.

The second test is the D’Agostino-Pearson K

om-

nibus test (D’Agostino et al., 1990), and is another

goodness-of-ﬁt test using the sample skewness and

kurtosis. This test however is an omnibus test, which

tests whether the explained deviation in the sample

data is signiﬁcantly greater than the overall unex-

plained deviation. The test also has the same asymp-

totic property as the Jarque-Bera test.

D’Agostino et al. (D’Agostino et al., 1990) anal-

yse the asymptotic performances of more commonly

used normality tests; those being the χ

test, Kol-

mogorov test (Kolmogorov, 1956), and the Shapiro-

Wilk W-test (Shapiro and Wilk, 1965). These are

important results, since the sample sizes required are

far beyond those used in typical applications, in say,

medicine or econometrics. Additionally it is recom-

mended not to use the χ

test and Kolmogorov test,

due to their poor power properties. That is, for a large

sample size, the probability of making a Type II error

(that is, incorrectly retaining a false null hypothesis)

signiﬁcantly increases. Furthermore, for sample sizes

N > 50, D’Agostino et al. state the Shapiro-Wilk W-

test is no longer available, and even with the test ex-

tended (N ≤ 2000) (Royston, 1982), it still falls be-

low the required sample size. The ﬁnal major test for

normality is the Anderson-Darling test (Anderson and

Darling, 1952; Anderson and Darling, 1954). How-

ever, the D’Agostino-Pearson K

omnibus test is pre-

ferred since the Anderson-Darling test is biased to-

wards the tails of the distribution (Razali et al., 2011).

GLITCH: A Discrete Gaussian Testing Suite for Lattice-based Cryptography

415

The ﬁnal tests are graphical. The ﬁrst simply

plots the observed histogram data versus the expected

data. The second graphic is a quantile-quantile (QQ)

plot. This test illustrates how strongly the histogram

data follows a discrete Gaussian distribution, pro-

viding a QQ-plot and coefﬁcient of determination

). The QQ-plot is supplementary to the numeri-

cal assessment of normality and is a graphical method

for comparing two probability distributions. In this

case, these two probability distributions are the ob-

served and expected quantiles of the discrete Gaus-

sian distribution. This test is essentially the same

as a probability-probability (PP) plot, wherein a data

set is plotted against its target theoretical distribu-

tion. However, QQ-plots have the ability to arbitrarily

choose the precision (to equal that of λ, say 128-bits)

as well as being easier to interpret in the case of large

sample sizes, hence its inclusion over PP-plots.

The R

value complements this plot, analysing

how well the linear reference line approximates the

expected data. The output R

∈ [0, 1] is a measure

of the proportion of total variance of the outcomes,

which is explained by the model. Therefore, the

higher the R

value, the better the model ﬁts the data.

3.3 The GLITCH Test Suite

The GLITCH test suite is provided in Python and is

made publicly available online

. Additionally, dis-

crete Gaussian data sets are provided. GLITCH is

designed to take, as input, a histogram of discrete

Gaussian samples. This is seen as advantageous over

an input of listed samples, as calculations are signiﬁ-

cantly simpliﬁed, are signiﬁcantly faster, and decrease

storage. The suite of tests are speciﬁcally chosen so

that each parameter in the discrete Gaussian sampling

stage is tested. The main parameters under test are

the mean and standard deviation of the discrete Gaus-

sian (µ,σ), with additional tests included to check the

shape of the distribution, and ﬁnally normality tests.

Precision is also adaptable and set to 128-bits as per

most lattice-based cryptoschemes.

3.3.1 Tests (1-3): Testing Parameters

The ﬁrst set of tests are to approximate the main

statistical parameters µ and σ, producing values for

sample mean (¯x) and sample standard deviation (s).

This is done by using adapted formulas for the

ﬁrst (m

) and second (m

) moments, taking as in-

put a histogram of values (x

), where m

= ¯x =

(

∑

i=1

)/N corresponding to the sample mean, and

GLITCH software test suite available at

https://github.com/jameshoweee/glitch

= s

= (

∑

i=1

− ¯x)

)/N corresponding to the

sample variance, for a sample size N. The subsequent

moments are then m

= (

∑

i=1

− ¯x)

/N)/σ

, us-

ing sample standard deviation s =

√

Next, the standard error (SE) is calculated for the

sampling distribution. This statistic measures the re-

liability of a given sample’s descriptive statistics with

respect to the population’s target values, that is, the

mean and standard deviation. Additionally, the stan-

dard error is used in measuring the conﬁdence in the

sample mean and sample standard deviation. For this,

a two-tail t-test is constructed, given the null hypoth-

esis µ = 0 (similarly for σ), with the alternate hypoth-

esis that they are not equal. So, if the null hypothesis

is accepted, it is concluded that a 100(1 −α)% conﬁ-

dence interval (C.I.) is ¯x ±ε

¯x

and s ±ε

, where ε

¯x

α/2

¯x

and ε

= t

α/2

. Since the aim of these tests

if for the highest conﬁdence (99.9%), t

α/2

= 3.29.

3.3.2 Tests (4-7): Testing the Distribution’s

Shape

The next set of tests deal with statistical descriptors of

the shape of the probability distribution. The ﬁrst de-

scriptor is the skewness; which is a measure of sym-

metry of the probability distribution and is adapted

from the third moment. The skewness for a normally

shaped distribution, or any symmetric distribution,

is zero. Moreover, a negative skewness implies the

left-tail is long, relative to the right-tail, and a posi-

tive skewness implies a long right-tail, relative to the

left-tail. The population skewness is simply m

however the sample skewness must be adapted to

ω = m

N(N −1)/N −2 to account for bias (Joanes

and Gill, 1998). Also SE

is calculated, to show the

relationship between the expected skewness and ω.

The forth moment is kurtosis; and describes the

peakedness of a distribution. For a normally shaped

distribution, the target sampled kurtosis is three, and

is calculated as m

. More commonly, the sam-

pled excess kurtosis is used and is deﬁned as κ =

) −3. A positive kurtosis indicates a peaked

distribution, similarly a negative kurtosis indicates a

ﬂat distribution. It can also be seen, given an increase

in kurtosis, that probability mass has moved from the

shoulders of the distribution, to its centre and tails

(Balanda and MacGillivray, 1988). Similarly, SE

calculated to show the relationship between the ex-

pected excess kurtosis and κ.

An appropriate test for these statistical descriptors

would be a z-test, where conﬁdence intervals could

also be calculated for some conﬁdence level α. How-

ever, under a null hypothesis of normality, z-tests tend

to be easily rejected for larger samples (N > 300)

SECRYPT 2017 - 14th International Conference on Security and Cryptography

416

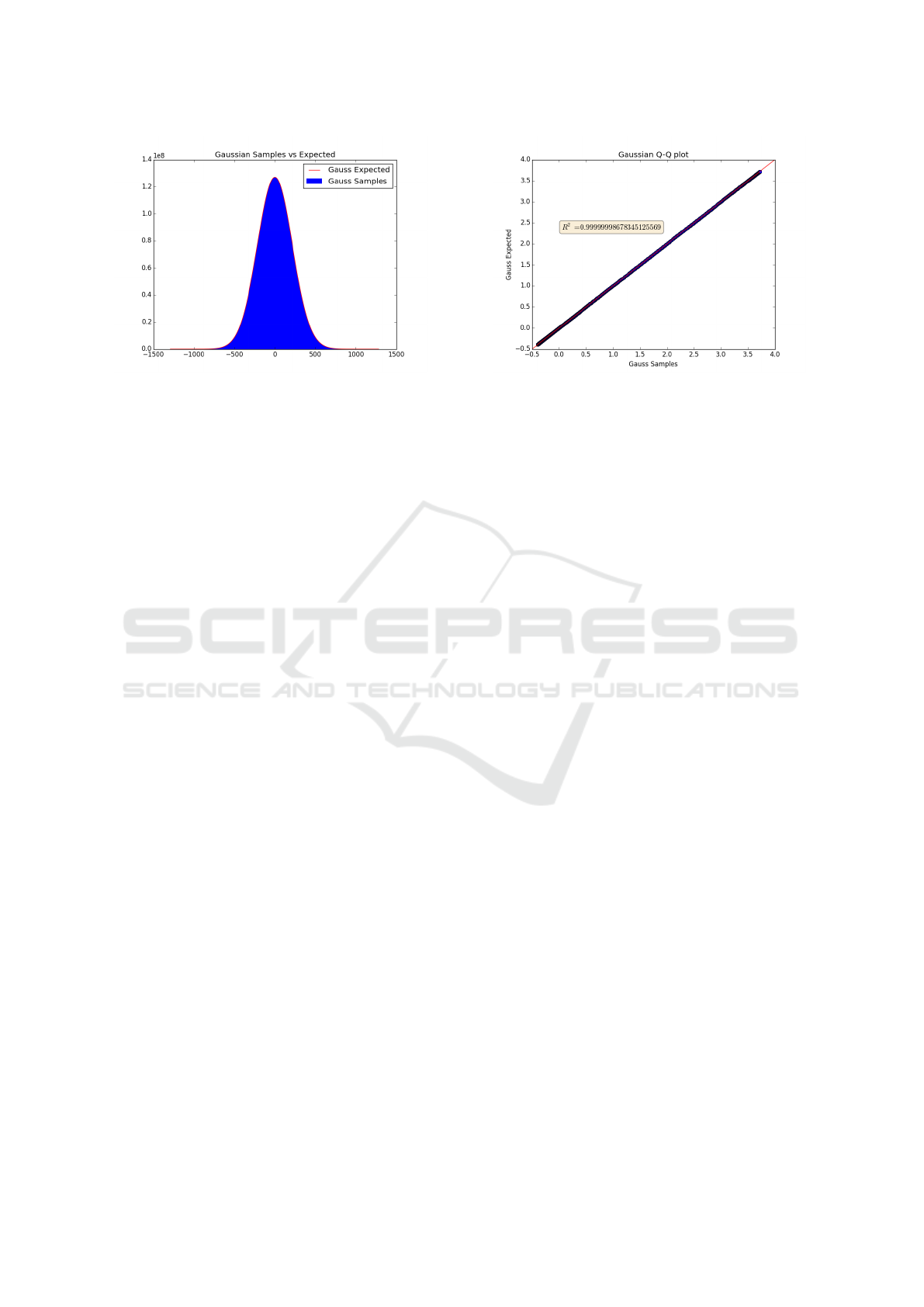
Figure 1: Histogram of observed (blue) discrete Gaus-

sian samples versus expected (red).

Figure 2: QQ-plot of the observed discrete Gaussian

samples with the coefﬁcient of determination (R

) value.

taken from a not substantially different normal dis-

tribution (Kim, 2013).

Higher-order moments, speciﬁcally the ﬁfth and

sixth, are used in the last two tests on the distribu-

tion’s shape. The ﬁrst of these tests hyper-skewness

∗

= m

, which still measures symmetry but is

more sensitive to extreme values (Hinton, 2014, p.97).

Likewise, the second of these tests is for excess hyper-

kurtosis κ

∗

= m

, which tests for peakedness

with greater sensitivity towards more-than-expected

weight in the tails (Hinton, 2014, p.100).

3.3.3 Tests (8-9): Normality Testing

These tests calculate the test statistic and p-value

for the two normality tests described in Section 3,

these are the Jarque-Bera (Jarque and Bera, 1987) and

D’Agostino-Pearson (D’Agostino et al., 1990) om-

nibus tests. The Jarque-Bera test statistic is calculated

as JB = (N/6)(ω

+ ((κ −3)

/4)), where its p-value

is taken from a χ

distribution with two degrees of

freedom. The null hypothesis (of normality) is re-

jected if the test statistic is greater than the χ

p-value.

The D’Agostino-Pearson omnibus test is based on

transformations of the sample skewness (Z

(ω)) and

sample kurtosis (Z

(κ)), which are combined to pro-

duce an omnibus test. This statistic detects deviations

from normality due to either skewness or kurtosis and

is deﬁned as K

= Z

(ω)

+ Z

(κ)

3.3.4 Tests (10-11): Illustrating Normality

D’Agostino et al. (D’Agostino et al., 1990) recom-

mend, as well as test statistics for normality, graph-

ical representations of normality are also provided.

Hence, the ﬁnal two tests are illustrative tests on the

discrete Gaussian samples. The ﬁrst graphic, shown

in Figure 1, plots the histogram of the observed values

(in blue) alongside the expected values (in red).

The second graphic is a quantile-quantile (QQ)

plot, shown in Figure 2. For this test, the cal-

culated z-scores are plotted against the expected z-

scores, where if the data is normally distributed, the

result will be a straight diagonal line (Field, 2009,

p.145-148). A 45-degree reference line is plotted,

which will overlap with the QQ-plot if the distribu-

tions match. The coefﬁcient of determination (R

)

value is calculated as R

= 1 −(SS

res

/SS

tot

), where

res

∑

− f

)

is the residual sum of squares and

tot

∑

− ¯x)

is the total sum of squares, y

is the

observed data set and f

is the expected values.

4 CONCLUSION

The research on statistical testing for discrete Gaus-

sian samples reapplies well established statistical test-

ing techniques to lattice-based cryptography, taking

into consideration the stringent requirements within

the area. This was completed by conducting a full

survey on a number of different testing techniques,

collating the relevant tests to form the adaptable

GLITCH software statistical test suite.

The ﬁrst number of tests are for analysing the

main discrete Gaussian parameters from the observed

data; giving standard error, conﬁdence intervals, and

hypothesis tests with the highest level of conﬁdence

(99.9%). The next set of tests veriﬁes the shape of

the distribution, analysing whether there is any bias

towards the positive or negative side of the distribu-

tion, and whether the distribution has a bias towards

the peak of the distribution. For these tests and for the

following tests on normality, the tests which allow for

samples sizes large enough for lattice-based cryptog-

raphy constraints are chosen. The last tests illustrate

the difference between the observed data’s distribu-

tion and the expected distribution’s shape.

GLITCH: A Discrete Gaussian Testing Suite for Lattice-based Cryptography

417

The tests chosen are powerful and operate well on

large sample sizes, with each analysing different as-

pects within the discrete Gaussian distribution. Fail-

ure in any of these tests indicates a deviation from

the target distribution, which is therefore evidence of

an incorrectly performing discrete Gaussian sampler.

The software for GLITCH is made available online

(https://github.com/jameshoweee/glitch), which also

provides sample data for discrete Gaussian samplers;

which are able to be tested upon.

The full version of this paper is available at (Howe

and O’Neill, 2017), which includes more concise de-

tails on the statistical formulae used as well as exam-

ple results discussions.

REFERENCES

Ajtai, M. (1996). Generating hard instances of lattice prob-

lems (extended abstract). In STOC, pages 99–108.

Anderson, T. W. and Darling, D. A. (1952). Asymptotic

theory of certain ”goodness of ﬁt” criteria based on

stochastic processes. The Annals of Mathematical

Statistics, 23(2):193–212.

Anderson, T. W. and Darling, D. A. (1954). A test of good-

ness of ﬁt. Journal of the American Statistical Associ-

ation, 49(268):765–769.

Balanda, K. P. and MacGillivray, H. (1988). Kurtosis: a

critical review. The American Statistician, 42(2):111–

119.

Bassham III, L. E., Rukhin, A. L., Soto, J., Nechvatal, J. R.,

Smid, M. E., Barker, E. B., Leigh, S. D., Levenson,

M., Vangel, M., Banks, D. L., Heckert, N. A., Dray,

J. F., and Vo, S. (2010). SP 800-22 Rev. 1a. A Statisti-

cal Test Suite for Random and Pseudorandom Number

Generators for Cryptographic Applications. Technical

report, Gaithersburg, MD, United States.

Campagna, M., Chen, L., Dagdelen,

O., Ding, J., Fernick,

J., Gisin, N., Hayford, D., Jennewein, T., L

utkenhaus,

N., Mosca, M., et al. (2015). Quantum safe cryptog-

raphy and security. ETSI White Paper, (8).

CESG (2016). Quantum key distribution: A CESG white

paper.

CNSS (2015). Use of public standards for the secure shar-

ing of information among national security systems.

Committee on National Security Systems: CNSS Ad-

visory Memorandum, Information Assurance 02-15.

D’Agostino, R. B., Belanger, A., and D’Agostino Jr, R. B.

(1990). A suggestion for using powerful and infor-

mative tests of normality. The American Statistician,

44(4):316–321.

Ducas, L., Durmus, A., Lepoint, T., and Lyubashevsky, V.

(2013). Lattice signatures and bimodal Gaussians. In

CRYPTO (1), pages 40–56. Full version: https://

eprint.iacr.org/2013/383.pdf.

Dwarakanath, N. C. and Galbraith, S. D. (2014). Sampling

from discrete Gaussians for lattice-based cryptogra-

phy on a constrained device. Appl. Algebra Eng. Com-

mun. Comput., pages 159–180.

Field, A. (2009). Discovering statistics using SPSS. Sage

publications.

Gentry, C., Peikert, C., and Vaikuntanathan, V. (2008).

Trapdoors for hard lattices and new cryptographic

constructions. In STOC, pages 197–206.

Hinton, P. R. (2014). Statistics explained. Routledge.

Howe, J., Khalid, A., Rafferty, C., Regazzoni, F., and

O’Neill, M. (2016). On Practical Discrete Gaus-

sian Samplers For Lattice-Based Cryptography. IEEE

Transactions on Computers.

Howe, J. and O’Neill, M. (2017). GLITCH: A Discrete

Gaussian Testing Suite For Lattice-Based Cryptogra-

phy. Cryptology ePrint Archive, Report 2017/438.

http://eprint.iacr.org/2017/438.

Howe, J., P

oppelmann, T., O’Neill, M., O’Sullivan, E.,

and G

uneysu, T. (2015). Practical lattice-based digital

signature schemes. ACM Transactions on Embedded

Computing Systems, 14(3):24.

Jarque, C. M. and Bera, A. K. (1987). A test for normality

of observations and regression residuals. International

Statistical Review, pages 163–172.

Joanes, D. N. and Gill, C. A. (1998). Comparing measures

of sample skewness and kurtosis. Journal of the Royal

Statistical Society: Series D (The Statistician), 47(1).

Kim, H.-Y. (2013). Statistical notes for clinical re-

searchers: assessing normal distribution (2) using

skewness and kurtosis. Restorative dentistry & en-

dodontics, 38(1):52–54.

Kolmogorov, A. N. (1956). Foundations of the theory of

probability (2nd ed.). Chelsea Publishing Co., New

York.

Lindner, R. and Peikert, C. (2011). Better key sizes (and

attacks) for LWE-based encryption. In CT-RSA, pages

319–339.

Lyubashevsky, V., Peikert, C., and Regev, O. (2013). On

ideal lattices and learning with errors over rings. J.

ACM, 60(6):43.

Marsaglia, G. (1985). A current view of random number

generators. In Computer Science and Statistics, Six-

teenth Symposium on the Interface. Elsevier Science

Publishers, North-Holland, Amsterdam, pages 3–10.

Marsaglia, G. (1993). A current view of random numbers.

In Billard, L., editor, Computer Science and Statistics:

Proceedings of the 16th Symposium on the Interface,

volume 36, pages 105–110. Elsevier Science Publish-

ers B. V.

Marsaglia, G. (1996). DIEHARD: A battery of tests

of randomness. http://www.stat.fsu.edu/pub/

diehard/.

Moody, D. (2016). Post-quantum cryptography: NIST’s

plan for the future. Talk given at PQCrypto ’16 Con-

ference, 23-26 February 2016, Fukuoka, Japan.

Peikert, C. (2010). An efﬁcient and parallel Gaussian sam-

pler for lattices. In CRYPTO, pages 80–97.

oppelmann, T. and G

uneysu, T. (2014). Area optimiza-

tion of lightweight lattice-based encryption on recon-

ﬁgurable hardware. In ISCAS, pages 2796–2799.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

418

Razali, N. M., Wah, Y. B., et al. (2011). Power comparisons

of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and

Anderson-Darling tests. Journal of statistical model-

ing and analytics, 2(1):21–33.

Regev, O. (2005). On lattices, learning with errors, random

linear codes, and cryptography. In STOC, pages 84–

93.

Royston, J. P. (1982). An extension of Shapiro and Wilk’s

W test for normality to large samples. Applied Statis-

tics, pages 115–124.

Shapiro, S. S. and Wilk, M. B. (1965). An analysis

of variance test for normality (complete samples).

Biometrika, pages 591–611.

GLITCH: A Discrete Gaussian Testing Suite for Lattice-based Cryptography

419