Using Physical Modeling and RGB-D Registration for Contact Force
Sensing on Deformable Objects
Antoine Petit, Fanny Ficuciello, Giuseppe Andrea Fontanelli, Luigi Villani and Bruno Siciliano
Dipartimento di Ingegneria Elettrica e Tecnologie dell’Informazione, Universit
`
a degli Studi di Napoli,
via Claudio 21, 80125 Napoli, Italy
Keywords:
Force Estimation, Physical Modelling, Deformable Objects.
Abstract:
In this paper we propose a method to estimate the force applied to a manipulated deformable object by process-
ing information provided by an external vision sensor, in this case a consumer RGB-D camera. By measuring
the deformations undergone by the object through a registration technique, the idea is to retrieve the contact
force which minimises the deviation between the measured and the simulated deformations, given a simple
interaction model and by employing a fitting process. The system resorts to a realistic mesh-based Finite
Element Method model to accurately model deformations, whose elastic parameters are estimated in advance
using the vision system and a force sensor. Experimental results are presented for the case of a compressive
point-wise contact force applied, at static equilibrium, on a deformable object.
1 INTRODUCTION
The measure of contact forces is a key requirement in
various applications such as capturing and synthesis-
ing human manipulation tasks or controlling robotic
hands. Force sensing for robotics or virtual reality
applications is typically based on mechatronic trans-
ducers (Siciliano and Khatib, 2008; Fazioli et al.,
2016). These devices can be placed on the object to be
manipulated, or on the operator, embedded on skins
or gloves (Wettels et al., 2009; Dahiya et al., 2010;
Yousef et al., 2011; Cirillo et al., 2015). Force can
be also estimated through sensing devices mounted
on the joints of the robot manipulator. However, in
applications as minimally invasive surgery, these sen-
sors cannot be easily installed on surgical instruments,
due to the need of sterilisation or electrification.
Capturing the interactions in manipulation based
on computer vision has aroused considerable inter-
est recently and may represent a convenient, mini-
mally invasive and cheap sensing set-up. Some efforts
have been focused on sensing the interactions be-
tween rigid objects, but the field remains open when
considering deformations.
The main contribution of this paper is to propose
a method enabling to measure contact forces between
the operator and a deformable object, using an RGB-
D camera. The task is very challenging, since a given
deformation can be gendered by a multiplicity of in-
teractions. Here we demonstrate that, by confronting
a physical deformation model for the object with de-
formations measured through vision, it is possible to
retrieve a single point-wise contact force exerted by
an operator (a human hand, a robot end-effector) on
the considered object. The material properties of the
object, consisting in elastic parameters, are estimated
in a preliminary step by using a force sensor and an
optimisation technique. Then, assuming that the ob-
ject lies on a flat surface and that the tool/object inter-
action consists in a known single contact point, a sim-
ilar optimisation technique is used to infer the value
of the 3D force exerted on that point. This is achieved
by fitting the simulated deformations with those mea-
sured by the vision system. The proposed approach
is based on the techniques suggested in (Petit et al.,
2015b; Petit et al., 2017).
1.1 Related Works
Approaches using visual information as a cue to mea-
sure contact force have recently appeared. For in-
stance in (Hristu et al., 2000; Mascaro and Asada,
2001; Sun et al., 2008; Sun et al., 2009; Urban et al.,
2013; Grieve et al., 2013; Essahbi et al., 2015), the
changes in the appearance of the fingertip are mea-
sured through photodetectors or an external camera,
and are processed to estimate contact forces using
statistical models. These techniques are limited to
measure the normal force and cannot simultaneously
24
Petit, A., Ficuciello, F., Fontanelli, G., Villani, L. and Siciliano, B.
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects.
DOI: 10.5220/0006415900240033
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 24-33
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

consider shear or slip. A promising approach (Yuan
et al., 2015), also based on visual observations, re-
lies on the GelSight sensor (Sato et al., 2010). In this
case the deformations, measured by marker-based vi-
sual tracking techniques on an embedded elastomer
medium, are interpreted as known responses to the
external load exerted on the sensor.
All the above force sensing methods require in-
strumenting the interacting tool/hand and/or the ma-
nipulated object with cumbersome and expensive
equipment which can also limit the range of motion.
Often they are tailored to particular objects and hard
to generalise, whereas we wish to design a generic
data-driven system. Force sensing based on an exter-
nal sensing device represent an appealing alternative
and vision sensors appear as the most simple, cheap,
convenient technology to propose.
Several works in the literature have suggested the
use of an external vision system to capture the in-
teractions and to sense contact forces in the case
of object manipulation by a human or any manip-
ulation tool. In the motion capture field, this ap-
proach has been investigated by some systems using
marker-based or markerless vision tracking to cap-
ture and synthesise hand/object interaction (Oikono-
midis et al., 2011; Ballan et al., 2012; Kyriazis and
Argyros, 2013). A kinematic analysis of the interac-
tions through discriminative or generative processes
is performed and some physics-based constraints are
introduced to deal with occlusions or collision detec-
tion. Some other approaches (Wang et al., 2013; Zhao
et al., 2013) propose to bridge the gap between the
kinematics provided by the motion capture systems
and the contact forces by linking physical constraints
to visual observations.
The techniques proposed in (Brubaker et al., 2009;
Pham et al., 2015) go further by employing rigid body
and contact dynamics to fully model interactions, and
to link these models with the kinematics provided by
an external vision systems. In this way the contact
forces between a human and the ground (Brubaker
et al., 2009) or between a hand and a manipulated ob-
ject (Pham et al., 2015; Ficuciello et al., 2010) can be
estimated in a physically realistic manner. To the best
of our knowledge, these are the only works proposed
in the literature where external visual tracking is used
as a cue for contact force estimation, in the case of
rigid and articulated bodies interactions.
1.2 Contribution
In this paper we propose to use an external vision
system to infer contact forces deriving from the ma-
nipulation of deformable objects, by confronting the
physical properties of the object and its deformation
model with the output of the vision system. Our ap-
proach is close to the idea in (Yuan et al., 2015) of re-
lating measured deformations to forces. The method
presented in (Yuan et al., 2015), however, relies on
an embedded sensing device and addresses force es-
timation through empirical relationships between de-
formations and forces.
In our approach, as major contribution, we pro-
pose to use realistic physical modeling of a de-
formable object to infer interaction forces exerted on
it, by processing external vision data. We focus here
on a static case. The general idea is to estimate a
point-wise contact force for which the resulting de-
formations best fit the deformations measured by the
vision system. We assume the contact point to be
known and the deformable object to be isotropic.
Relying on a physical model implies knowing the
mechanical properties of the object. Here we employ
the Finite Element Method (FEM) to model the object
and its elasticity, which is described by two parame-
ters, the Young Modulus and the Poisson ratio. As a
second contribution, we suggest to estimate these two
parameters during a preliminary step. Conversely to
the force estimation process, a force sensor is used in
order to fit the simulated deformations based on the
measured contact force with the vision data.
2 DEFORMATION AND
INTERACTION MODELS
A key issue of this work is to rely on a realistic physi-
cal deformation model of the considered elastic and
isotropic object. A FEM model provides accurate
physical realism, by relying on continuum mechanics,
instead of finite differences for mass-spring systems
for instance. For an exhaustive description of FEM,
the reader can refer to (Cook, 1994). The method
consists in tessellating the deformable object into a
mesh made of elements connecting a set X = {x
j
}
n
X
j=1
of 3D vertices. The deformation fields over the ele-
ments are approximated as continuous interpolations
of the displacements of the vertices. We rely here on
a volumetric linear FEM approach with tetrahedral el-
ements.
2.1 Modeling Elastic Deformations
In order to model elasticity for a continuous isotropic
material, we follow the method proposed in (Petit
et al., 2015a), by resorting to the linear elasticity, with
Hooke’s law, and to the infinitesimal strain theory
(Cook, 1994), modified by adopting a co-rotational
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects
25

approach (Etzmuß et al., 2003; M
¨
uller and Gross,
2004; Nesme et al., ), so as to accommodate to ro-
tation transformations. The infinitesimal strain tensor
ε
e
and stress tensor σ
e
within a tetrahedron e can be
written using the Voigt notation in terms of 6 ×1 vec-
tors as:
ε
e
= L
e
ˆ
u
r
e
= L
e
(R
−1
e
x
e
− x
e,0
) (1)
σ
e
= C
e
(E, ν)ε
e
.
If the deformations
ˆ
u
e
can be written as
ˆ
u
e
= x
e
−
x
e,0
, we define here
ˆ
u
r
e
= R
−1
e
x
e
−x
e,0
, with R
−1
e
x
e
the
back rotated deformed coordinates of the four vertices
of e, stacked into the 12 × 1 vector x
e
. R
e
is a 12 ×
12 block diagonal matrix containing four copies of
the 3 × 3 rotation matrix corresponding the rotational
component of the deformations of the element. L
e
is
the constant 6 × 12 matrix related to the interpolation
function, C
e
is a 6 × 6 symmetric matrix depending
on two elastic parameters of the material, the Young
modulus E and the Poisson ratio ν.
The internal elastic forces f
e
exerted on the ver-
tices of e can then be related to
ˆ
u
r
e
through:
f
e
= R
e
K
e
ˆ
u
r
e
(2)
being K
e
= V
e
L
T
e
C
e
L
e
the stiffness matrix of the el-
ement of volume V
e
. In this way, the overall forces
on the whole mesh can be summed to zero, while
computational efficiency is ensured since K
e
can be
computed in advance, in contrast to non-linear FEM
approaches.
2.2 Modeling Interaction
We consider the case of a manipulated object lying
on a known flat rigid surface. The object is then de-
formed by a single contact force which acts verti-
cally, so that the contact between the object and the
plane remains constant. In the experiments (see Sec-
tion 6), this force is applied by a tool mounted on
a robotic arm. We assume a pointwise contact on a
point of known position lying on the surface of the ob-
ject. Considering for the simulation model the mesh
X = {x
j
}
n
X
j=1
, and using the co-rotated deformation
model described in Section 2.1, the Lagrangian dy-
namics is described by the equations:
M
¨
x + C
˙
x + f = f
sim
ext
(3)
with f
sim
ext
= MG + f
ground
+ f
op
where G is the vector of the gravity forces applied to
the vertices, f
op
is the pointwise external force exerted
by the operator, and f
ground
is the vector of the contact
forces of the flat rigid surface or ground, exerted on
the vertices in contact with it. These forces act on ver-
tices of the mesh for which the signed distance is neg-
ative (below the plane), attracting them thus towards
the plane. We simply model them as damped linear
springs according to the signed distance between the
vertices of mesh and the known plane representing the
surface. We assume an inelastic surface, meaning that
the stiffness of the springs is set high. For simplicity
and since we deal with a vertical compressing effort
on the object, we neglect adhesive sticky effects, as
well as tangential friction.
3 ESTIMATION OF THE
DEFORMATIONS WITH RGB-D
DATA
In this section the external vision data is used to es-
timate, in a physically realistic manner, the deforma-
tions undergone by the object which will then drive
the estimation of the force exerted by an operator (see
Section 5). The registration problem we tackle con-
sists in fitting the point cloud data, provided by an
RGB-D sensor, with the tetrahedral mesh, in terms of
both rigid and non-rigid transformations. We directly
employ the approach proposed in (Petit et al., 2015a),
for which the main steps are recalled hereafter:
Preliminary Visual Segmentation. The visual seg-
mentation step presented in (Petit et al., 2015a) is car-
ried out in order to restrict the acquired point cloud
to the considered object, so as to avoid ambiguities
in the matching process with the background or with
occluding shapes. This phase provides us with the set
Y of the 3D points of the target point cloud. We limit
the size of Y by sampling D
k
on a regular grid in the
image plane.
Rigid Iterative Closest Point. The observed seg-
mented point cloud Y is registered in terms of rigid
translation and rotation transformations, initially con-
sidering the mesh of the object as rigid. We employ a
classical rigid Iterative Closest Point (ICP) algorithm
(Chen and Medioni, 1992) between Y and the vertices
of the visible surface X
V
of the mesh, transformed
with respect to the previous RGB-D data. Through
this procedure a fair initialization for the non-rigid
process can be obtained.
Deformable Registration Process. Following the
approaches in (Petit et al., 2015a; Petit et al., 2015b),
the basic idea is to derive external forces exerted by
the point cloud on the mesh, and to balance them with
the internal forces based on the deformation model
presented in Section 2, with respect to the displace-
ments of the vertices of the mesh. In this work, we
use external forces f
g
ext
related to geometrical informa-
tion as introduced in (Petit et al., 2015a). The method
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
26

Figure 1: External forces based on nearest neighbours
searches.
consists first in determining nearest neighbors corre-
spondences, both from the segmented point cloud to
the mesh and from the mesh to the segmented point
cloud, as shown in Figure 1.
Based on the two sets of mesh-to-point cloud and
point cloud-to-mesh correspondences, an external
elastic force f
g
ext
exerted on each x
j
in X
V
, can be com-
puted as follows:
f
g
ext
(x
j
) = k
g
ext
(x
j
− y
f
j
) (4)
where, as described in (Petit et al., 2015a), y
f
j
is a lin-
ear combination of points in the point clouds which
are matched to x
j
, either from mesh-to-point cloud
and from point cloud-to-mesh correspondence sets.
k
g
ext
is the stiffness of these external elastic forces.
Estimation. Estimating the deformations of the mesh
consists in solving a dynamic system of linear ordi-
nary differential equations involving the internal and
external forces, based on the Lagrangian dynamics:
M
¨
x + C
˙
x + f = f
g
ext
(5)
with f = Kx + f
0
where x is a 3n
X
× 1 vector containing the posi-
tions to estimate of the vertices in X, M and C
are the 3n
X
× 3n
X
mass and damping matrices, K
the 3n
X
× 3n
X
global stiffness matrix which sums
the 3n
X
× 3n
X
element-wise rotated stiffness matri-
ces K
r
e
= R
e
K
e
R
−1
e
, written with respect to whole
set of vertices, and f
0
the corresponding global off-
set summing the element-wise ones R
e
K
e
x
e,0
. f
g
ext
is
a 3n
X
×1 vector containing the external forces defined
in equation (4).
An Euler implicit integration scheme is used
in (Petit et al., 2015a) to solve the system with re-
spect to x, along with a conjugate gradient method.
Notice that here we consider the static case, with
the static equilibrium of the deformations assumed
to be reached, so the transient and the dynamic
terms of equation (5) could be neglected, leading to
simply solving the equality between internal elastic
forces and external forces with the conjugate gradient
method.
4 ESTIMATION OF ELASTIC
PARAMETERS
The elastic parameters of the object are estimated us-
ing the point cloud data on the basis of the deforma-
tions observed using an RGB-D sensor, and of the
force measurements provided by a force sensor. No-
tice that this force sensor is used only for this prelim-
inary step, and can be unmounted for the second step
where, conversely, the estimation of the contact force
is made using vision.
Here we follow the data-driven approaches de-
scribed in (Frank et al., 2010; Wang et al., 2015).
They consist in minimizing a fitting error between the
simulated deformations, actuated by the input oper-
ator force provided by the sensor, and the deforma-
tions captured by the RGB-D sensor. These two meth-
ods also employ finite elements for the deformation
model. The work (Wang et al., 2015) goes further
by proposing a framework that sequentially tracks the
shape and estimates both material and dynamic pa-
rameters (damping). A dynamic deformation model
is used and the vision capture set-up consists in vari-
ous RGB-D sensors around the scene.
Here we consider a static model and limit this pre-
liminary process to the estimation of the Young mod-
ulus and the Poisson ratio of the material. We use a
single RGB-D sensor and a force sensor mounted on a
robotic arm, with a set-up similar to the one proposed
in (Frank et al., 2010). The deformations are indeed
generated by applying an effort, in our case compres-
sion, on the deformable object and we observe the de-
formations with the vision sensor once static equilib-
rium is reached.
These deformations can be simulated, starting
from the same initial rest shape, by using the defor-
mation and interaction model presented above and the
input measured contact force. Our problem is then ad-
dressed by minimizing, with respect to the elasticity
parameters, the deviation between these simulated de-
formations, and the observed ones. This deviation is
defined by a fitting function e
param
accounting for the
sum of squared distances between the point cloud ac-
quired on the object, and the simulated deformations,
defined as:
e
param
(E, ν) = dist(sim(E, ν, f
op
(x
i
c
)),Y ) (6)
where E and ν are respectively the Young modulus
and the Poisson ratio, f
op
is the measured contact
force exerted by the operator on the object, on the
contact point x
i
c
, Y is the acquired point cloud. We
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects
27

use the point cloud segmented on the considered ob-
ject by running the segmentation phase described in
Sect. 3. For a relevant significant error function, we
employ the matching technique presented in Sect. 3
between the segmented point cloud and the visible
part of the deformed mesh, and conversely. Based on
the two sets of mesh-to-point cloud and point cloud-
to-mesh correspondences, the error function is calcu-
lated as:
e
param
(E, ν) =
1
n
X
V
n
X
V
∑
i=0
(x
sim
i
− NN
Y
(x
sim
i
))
2
+
1
n
Y
n
Y
∑
j=0
(y
j
− NN
X
V
(y
j
))
2
(7)
where X
V
= {x
sim
i
}
n
X
V
i=0
are the vertices of the visible
part of the mesh which is deformed by simulation.
Y = {y
j
}
n
Y
j=0
are the vertices of the segmented point
cloud. NN
Y
(x
sim
i
) and NN
X
V
(y
j
) define the corre-
spondences between x
sim
i
and y
j
, using nearest neigh-
bour searches respectively within the sets Y and X
V
.
This optimization problem with respect to (E, ν) is
non-linear and the evaluation of the objective function
is expensive and its gradients are non-trivial to com-
pute making gradient-based optimization methods
prohibitive. We thus employ the gradient-free Nelder-
Mead method (Nelder and Mead, 1965), which is an
extension of the downhill simplex method to the non-
linear case. For each evaluation of the objective func-
tion in the Nelder-Mead process, the mesh is initially
reset to its rest shape. We then apply the measured
contact force f
op
on the known vertex of the mesh,
given the elasticity parameters (E, ν) to evaluate. A
simulation is then started until a static equilibrium is
reached. From this static equilibrium, the matching
process that leads to equation (7) is handled.
5 ESTIMATION OF THE
CONTACT FORCE
The problem of computing the contact force exerted
on the manipulated object also consists in a fitting
procedure between the simulated and the observed de-
formations. Knowing the material parameters, we can
use the deformation model and the registration tech-
nique described in Sect. 3, providing a regularized and
complete observation of the deformations.
The idea is to determine the force for which the
resulting simulated deformations best fit the mesh de-
formed by the vision data. More formally, we mini-
mize, we respect to f
op
, the least square error e
f orce
between the deformations sensed through registration
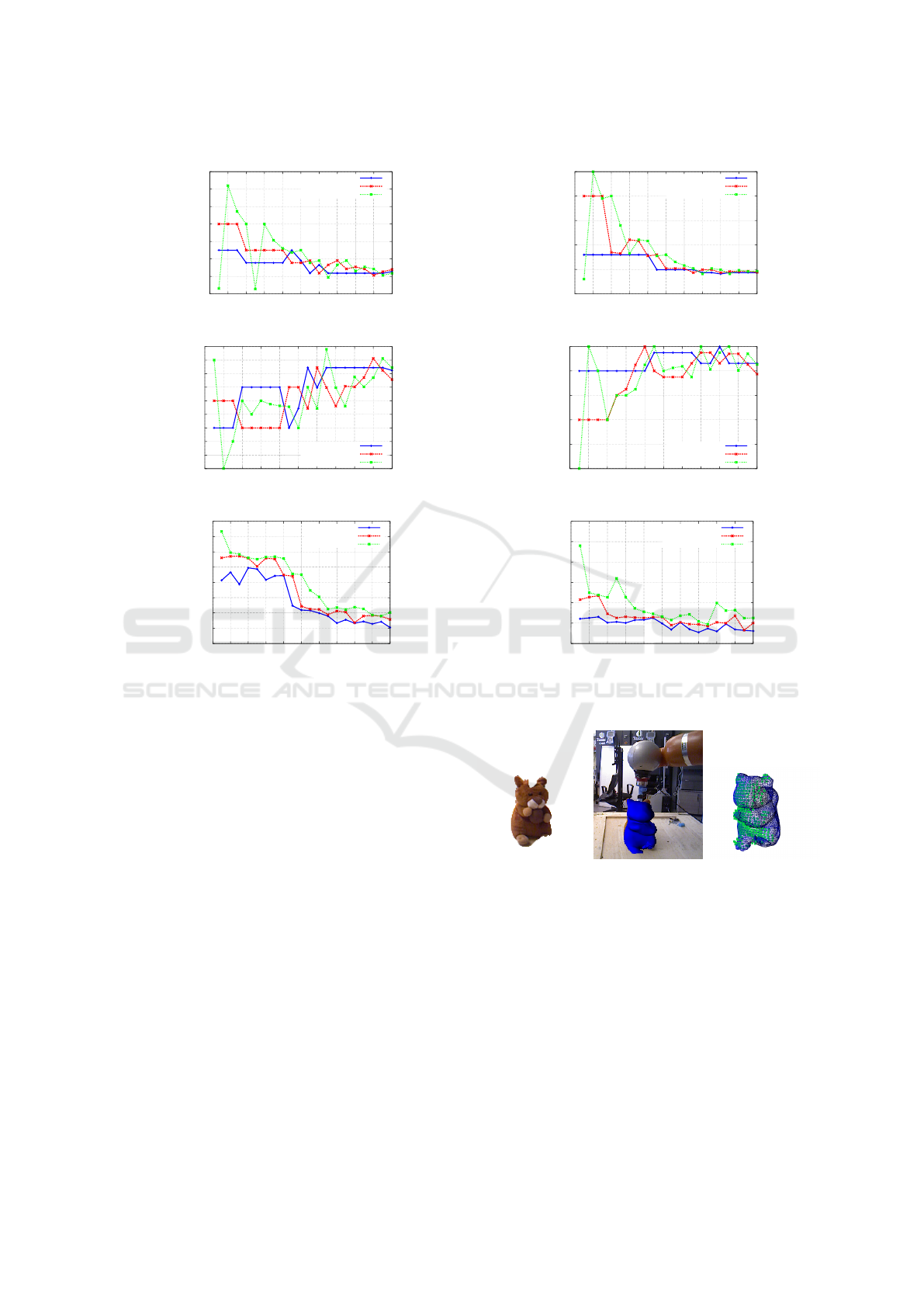
Figure 2: Left: The experimental set-up, with the tool
mounted on the robotic arm equipped with a force sensor,
compressing the object. Right: Surface triangular (in red)
and volumetric tetrahedral mesh (in blue) of the stuffed toy.
{x
vision
i
}
n
X
i=1
and the simulated deformations {x
sim
i
}
n
X
i=1
,
based on the interaction model.
e
f orce
(f
op
) =
n
X
∑
i
(x
vision
i
− x
sim
i
(f
op
))
2
(8)
The derivation of e
f orce
given the full interaction
model is a non-trivial task which requires the inver-
sion of the model. Instead, since we aim at per-
forming a quite global process without any strong
guess on this force, we use a Nelder-Mead optimiza-
tion framework to minimize e
f orce
with respect to
f
op
=

f
op
x
f
op
y
f
op
z

T
. In practice, in order to com-
pute e
f orce
for a given force f
op
, we start from the de-
formed state of the mesh, following registration. We
then substitute all the external forces due to the point
cloud data by f
op
on the known vertex in contact with
the operator. A simulation is evolved based on this
force and the interaction model. After a few iterations
in the simulation process, e
f orce
is computed. It mea-
sures the ability of f
op
to reproduce the actions of the
forces on the object provided by vision.
6 EXPERIMENTAL RESULTS
The results presented here involve a deformable ob-
ject, a stuffed toy undergoing a compression deforma-
tion effort applied by a tool fixed on the end-effector
of a Kuka LWR arm, equipped with a force sensor at
the wrist (see Figure 2). The point clouds of the inves-
tigated scenes are acquired using a calibrated RGB-D
camera Asus Xtion, 320×240 RGB and depth images
being processed. For both the estimation of the elas-
ticity parameters and the applied contact compression
force, we process the data of a single RGB-D camera,
taken at static equilibrium.
To build the deformation model of the stuffed toy,
a surface mesh of the undeformed object was recon-
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
28

structed offline using an RGB-D based dense 3D re-
construction technique (Newcombe et al., 2011), by
flying around the object with the Xtion sensor. We
then manually segment the part of scene featuring the
object. Finally, some remeshing and smoothing pro-
cedures are performed with a modeling engine in or-
der to get a fair, closed and clean surface mesh of the
object.
The volumetric tetrahedral mesh was generated by
carrying out a 3D Delaunay triangulation on the sur-
face mesh, with the CGAL library
2
. As a compro-
mise between modeling accuracy and real-time con-
straints, we have generated a volumetric mesh with
951 vertices and 5015 tetrahedral elements (see Fig-
ure 2). As an approximation, we assume the isotropy
of the material of the stuffed toy to apply the defor-
mation model described in Sect. 2.1.
For modeling, we have employed the Simula-
tion Open Framework Architecture (SOFA) simula-
tor (Faure et al., 2012), which enables to deal with
various physical models and to evolve simulations
in real-time. In terms of hardware, a standard lap-
top with an NVIDIA GeForce 720M graphic card has
been used, along with a 2.4GHz Intel Core i7 CPU.
0
5000
10000
15000
20000
25000
30000
35000
0
0.1
0.2
0.3
0.4
0.5
0.012
0.013
0.014
0.015
0.016
0.017
0.018
0.019
0.02
0.021
Error (m)
Fitting error
Young modulus (Pa)
Poisson ratio
Error (m)
0.012
0.013
0.014
0.015
0.016
0.017
0.018
0.019
0.02
0.021
3000
4000
5000
6000
7000
8000
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.0125
0.013
0.0135
0.014
0.0145
0.015
0.0155
0.016
0.0165
0.017
Error (m)
Fitting error
Young modulus (Pa)
Poisson ratio
Error (m)
0.0125
0.013
0.0135
0.014
0.0145
0.015
0.0155
0.016
0.0165
0.017
Figure 3: Top: Fitting error with respect to the elasticity
parameters. Bottom: Closer view around the global mini-
mum.
2
http://www.cgal.org
6.1 Elastic Parameters Estimation
For the estimation of the elastic parameters, we first
measure the contact force exerted by the tool mounted
on the robotic arm to compress the object, giving a
value of f
op
mech
= [0.17 1.125 4.006]
T
. Due to the par-
ticular shape of the considered object, the application
of this pointwise contact force in simulation may re-
sult in the loss of the static equilibrium. For this rea-
son, we constrain the system by fixing the position
of some vertices on the lower part of the shape, close
to the contact area with the flat surface. In this way
the object may not get bent excessively or turned over
and its base remains quite rigidly attached to the flat
contact surface.
Following the Nelder-Mead algorithm basic im-
plementation and the parameter space for (E, ν) being
of dimension 2, 3 candidate samples will be sorted af-
ter each iteration of the optimization, while perform-
ing the reflection, expansion, contraction and shrink-
ing steps, providing a best, a good and a worst can-
didate. We also integrate the specific boundaries for
both E and ν in the process, in the sense that inequali-
ties E > 0 and 0 < ν < 0.5 should be preserved during
the different steps. If an inequality is violated, E or ν
is reset slightly below or above.
We have tested our parameters estimation technique
with two different initial configurations. In Figure 4
and 5 we can observe for these two configurations the
trajectories of the 3 sorted candidates, along E and
ν throughout the iterations of the Nelder-Mead pro-
cess. The figures show also the fitting errors for the 3
candidates after each iteration. In the first case the ini-
tial values are quite far from the actual estimated one,
stressing out the robustness of the estimation with re-
spect to coarse initial guesses, while, in the second
configuration, the process starts closer to the solution.
For both configurations convergence is achieved
respectively towards (E, ν) = (4268.65Pa, 0.412031)
and (E, ν) = (4328.12Pa, 0.415625). The fitting er-
ror being prone to local minima, convergence may be
reached after a certain number of iterations, around 8
in the first case and around 11, despite its closer ini-
tial values. On the plot of the fitting error in Figure 3,
it can be noticed that the non-convexity can be espe-
cially observable for the ν parameter, along which the
error is quite flat, resulting in some local minima.
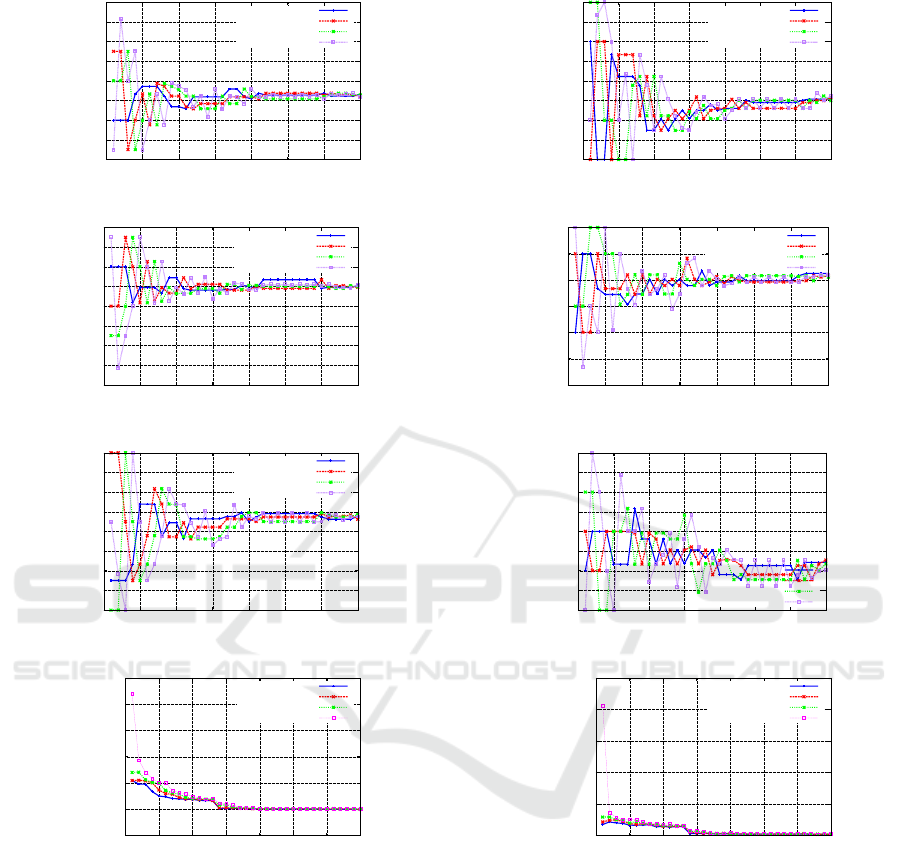
6.2 Contact Force Estimation
With the aim of testing the operator contact force es-
timation based on the vision tracking system, we first
proceed by setting the material parameters of the de-
formation models used in the vision system (here we
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects
29

3000
4000
5000
6000
7000
8000
9000
10000
0 2 4 6 8 10 12 14 16 18 20
Young Modulus (N)
Iteration
Trajectory along the Young Modulus
best point
good point
worst point
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0 2 4 6 8 10 12 14 16 18 20
Poisson ratio
Iteration
Trajectory along the Poisson ratio
best point
good point
worst point
0.012
0.0125
0.013
0.0135
0.014
0.0145
0.015
0.0155
0.016
0 2 4 6 8 10 12 14 16 18 20
Error (m)
Iteration
Fitting errors
best point
good point
worst poin
Figure 4: Nelder-Mead process for elasticity parameters es-
timation for the first initial configuration.
use (E, ν) = (4268.65Pa, 0.412031)). The result of
the registration process can be observed in Figure 6.
Let us remind that for each evaluation of the er-
ror function, the registered mesh is relaxed from the
forces exerted by vision while applying the point wise
contact force to evaluate on the known vertex. Fix-
ing vertices as boundary conditions to constraint the
simulation is not necessary since we measure here
the ability of this force to keep the static equilibrium
already reached by the action of the vision forces.
The parameter space being of dimension 3, there will
be 4 samples to sort after each iteration, the best,
the worst and two intermediate ones. Two differ-
ent initial configurations are tested here, starting re-
spectively quite far, without any particular guess on
the intensity and direction of the force, and close
to the actual value of the force given by the sen-
sor f
op
mech
= [0.17 1.125 4.006]
T
. Figures 7 and 8
show in both cases the trajectories of the four can-
didates for the estimate of the contact force f
op
, along
X, Y and Z, and the corresponding fitting errors. In
both cases, the algorithm converges respectively to-
0
5000
10000
15000
20000
25000
0 2 4 6 8 10 12 14 16 18 20
Young Modulus (N)
Iteration
Trajectory along the Young Modulus
best point
good point
worst point
0.2
0.25
0.3
0.35
0.4
0.45
0 2 4 6 8 10 12 14 16 18 20
Poisson ratio
Iteration
Trajectory along the Poisson ratio
best point
good point
worst point
0.012
0.013
0.014
0.015
0.016
0.017
0.018
0 2 4 6 8 10 12 14 16 18 20
Error (m)
Iteration
Fitting errors
best point
good point
worst point
Figure 5: Nelder-Mead process for elasticity parameters es-
timation for the second initial configuration.
(a) (b) (c)
Figure 6: Registration process, with: (a) Preliminary seg-
mentation, (b) Fitting result between the mesh and the seg-
mented point cloud, (c) Registered mesh reprojected in the
image.
wards a force f
op
= [0.618 0.0687929 3.54801]
T
and
f
op
= [−0.462414 0.247626 3.71292]
T
, which are
relatively close to the value sensed by the force sen-
sor mounted on the robot, thus validating our whole
model. Convergence is of course reached much faster
in the second case.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
30

-6
-4
-2
0
2
4
6
8
10
0 5 10 15 20 25 30 35
ForceX (N)
Iteration
Trajectory along x
best point
good point 1
good point 2
worst point
-10
-8
-6
-4
-2
0
2
4
6
0 5 10 15 20 25 30 35
ForceY (N)
Iteration
Trajectory along y
best point
good point 1
good point 2
worst point
-6
-4
-2
0
2
4
6
8
10
0 5 10 15 20 25 30 35
ForceZ (N)
Iteration
Trajectory along z
best point
good point 1
good point 2
worst point
0
0.005
0.01
0.015
0.02
0.025
0.03
0 5 10 15 20 25 30 35
Error (m)
Iteration
Fitting errors
best point
good point 1
good point 2
worst point
Figure 7: Nelder-Mead process for force estimation, for the
first initial configuration.
7 DISCUSSION
The proposed framework consists in: 1) estimating
the material parameters based on a known exerted
force, in order to develop a deformation model; 2)
estimating the force based on the known deformation
model and on a registration technique that allows to
measure deformations. The results presented in this
paper are promising, but several issues shall be dis-
cussed.
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0 5 10 15 20 25 30 35
ForceX (N)
Iteration
Trajectory along x
best point
good point 1
good point 2
worst point
-4
-3
-2
-1
0
1
2
0 5 10 15 20 25 30 35
ForceY (N)
Iteration
Trajectory along y
best point
good point 1
good point 2
worst point
2.5
3
3.5
4
4.5
5
5.5
6
6.5
0 5 10 15 20 25 30 35
ForceZ (N)
Iteration
Trajectory along z
best point
good point 1
good point 2
worst point
0.005
0.01
0.015
0.02
0.025
0.03
0 5 10 15 20 25 30 35
Error (m)
Iteration
Fitting errors
best point
good point 1
good point 2
worst point
Figure 8: Nelder-Mead process for force estimation, for the
second initial configuration.
7.1 Deformation Capture Set-up
Our imaging set-up is based on a single Asus Xtion
RGB-D sensor, providing in quite low resolution, par-
tial and noisy point cloud data around the object. It re-
sults in a non-convex shapes for the fitting error func-
tion in the elasticity estimation process, especially
with respect to ν, or in registration errors.
A more sophisticated set-up to capture deformations,
such as the one proposed in (Wang et al., 2015), with
a set of RGB-D sensors at different viewpoint, would
give more accurate results for the estimation of both
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects
31

the mechanical parameters and the contact force.
7.2 Interaction Capture
In this work we assume the contact point between the
object and the operator to be known, as well as the
contact between the object and the underlying flat sur-
face. A further development of our approach would
be the design of a vision system able to capture the
interaction between the object and its interacting en-
vironment: the manipulation tool, the table etc... en-
abling the detection of contact points, some useful pri-
ors for the segmentation and registration of the differ-
ent entities.
7.3 Efficient Inversion of the FEM
In the estimation of the force exerted by the opera-
tor, we use a gradient-free Nelder-Mead optimization
method. It has the advantage of being quite easy to
implement and robust to a coarse initialization, it is
however quite slow to run. Indeed for force estima-
tion, each evaluation of the error function requires
at least 5 successive simulations to obtain a reliable
error with respect to deformations of the registration
process. An iteration in the Nelder-Mead algorithm
requires in this case 7 evaluations, so around 350ms,
given that one simulation takes around 10ms, making
the process quite far from being real-time if consid-
ering a stream a successive RGB-D data. A possible
improvement would be to investigate an efficient in-
version of the full interaction model and some local
optimization techniques such as quadratic program-
ming, as proposed by (Largilliere et al., 2015).
7.4 Using Dynamics Towards
Deformation and Force Tracking
Our system is designed for the static case, for which
deformations have reached a static equilibrium. It
could be adapted to a dynamic case by benefiting
from a measure, through vision, of the kinematics of
the object or of interacting entities. Hence, based on
Lagrangian dynamics, the system could track on-line
both the deformations and the force.
8 CONCLUSION
In this work we have designed a system able to re-
cover a single contact force exerted on a deformable
object by resorting to an external vision and regis-
tration system and by fitting simulated deformations
with the observed ones. This is achieved by taking
advantage of a physically realistic deformation model
based on an FEM approach, and by employing a basic
interaction model with the manipulator and the envi-
ronment, proposing here a simple manipulation sce-
nario. The deformation model requires two mechan-
ical parameters, the Young Modulus and the Poisson
ratio, which we initially estimate, also by fitting sim-
ulated deformations with the point cloud given by an
RGB-D sensor. The fully determined elastic model
then feeds the registration system and the simulator,
which are matched with respect to the contact force.
We address these two optimization problems using
gradient-free Nelder-Mead methods. Some promising
results have been obtained on a simple case of single
applied compression force on a known contact point,
at static equilibrium. Future works would aim at ex-
tending the proposed approach to the dynamic case,
and to benefit from the vision-based capture of the in-
teractions.
ACKNOWLEDGEMENTS
This research has been partially funded by the
EC Seventh Framework Programme (FP7) within
RoDyMan project 320992 and by the national grant
MUSHA.
REFERENCES
Ballan, L., Taneja, A., Gall, J., Van Gool, L., and Pollefeys,
M. (2012). Motion capture of hands in action using
discriminative salient points. In European Conference
on Computer Vision, pages 640–653.
Brubaker, M. A., Sigal, L., and Fleet, D. J. (2009). Estimat-
ing contact dynamics. In IEEE International Confer-
ence on Computer Vision, pages 2389–2396.
Chen, Y. and Medioni, G. (1992). Object modelling by reg-
istration of multiple range images. Image and vision
computing, 10(3):145–155.
Cirillo, A., Ficuciello, F., Natale, C., and Pirozzi, S., V. L.
(2015). A conformable force/tactile skin for physical
human/robot interaction. IEEE Robotics and Automa-
tion Letters, 1:41–48.
Cook, R. D. (1994). Finite element modeling for stress anal-
ysis. Wiley.
Dahiya, R. S., Metta, G., Valle, M., and Sandini, G. (2010).
Tactile sensing–from humans to humanoids. IEEE
Transactions on Robotics, 26:1–20.
Essahbi, N., Bouzgarrou, B., and Gogu, G. (2015). Soft ma-
terial modeling for robotic task formulation and con-
trol in the muscle separation process. Robotics and
Computer-Integrated Manufacturing, 32:37–53.
Etzmuß, O., Keckeisen, M., and Straßer, W. (2003). A fast
finite element solution for cloth modelling. In IEEE
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
32

Pacific Conference on Computer Graphics and Appli-
cations, pages 244–251.
Faure, F., Duriez, C., Delingette, H., Allard, J., Gilles, B.,
Marchesseau, S., Talbot, H., Courtecuisse, H., Bous-
quet, G., Peterlik, I., et al. (2012). Sofa: A multi-
model framework for interactive physical simulation.
In Soft Tissue Biomechanical Modeling for Computer
Assisted Surgery, pages 283–321. Springer.
Fazioli, F., Ficuciello, F., Fontanelli, G., Siciliano, B., and
Villani, V. (2016). Implementation of a soft-rigid col-
lision detection algorithm in an open-source engine
for surgical realistic simulation. In IEEE Int. Conf. on
Robotics and Biomimetics, ROBIO’2016, pages 2204–
2208.
Ficuciello, F., Carloni, R., Visser, L., and Stramigioli, S.
(2010). Port-hamiltonian modeling for soft-finger ma-
nipulation. In IEEE Int. Conf. on Intelligent Robots
and Systems, IROS’2010, page 42814286.
Frank, B., Schmedding, R., Stachniss, C., Teschner, M., and
Burgard, W. (2010). Learning the elasticity parame-
ters of deformable objects with a manipulation robot.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 1877–1883.
Grieve, T. R., Hollerbach, J. M., and Mascaro, S. A. (2013).
Force prediction by fingernail imaging using active
appearance models. In World Haptics Conference,
pages 181–186.
Hristu, D., Ferrier, N., and Brockett, R. W. (2000). The
performance of a deformable-membrane tactile sen-
sor: basic results on geometrically-defined tasks. In
IEEE International Conference on Robotics and Au-
tomation, pages 508–513.
Kyriazis, N. and Argyros, A. (2013). Physically plausi-
ble 3d scene tracking: The single actor hypothesis.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 9–16.
Largilliere, F., Verona, V., Coevoet, E., Sanz-Lopez, M.,
Dequidt, J., and Duriez, C. (2015). Real-time control
of soft-robots using asynchronous finite element mod-
eling. In IEEE International Conference on Robotics
and Automation, pages 2550–2555.
Mascaro, S. A. and Asada, H. H. (2001). Photoplethysmo-
graph fingernail sensors for measuring finger forces
without haptic obstruction. IEEE Transactions on
Robotics and Automation, 17:698–708.
M
¨
uller, M. and Gross, M. (2004). Interactive virtual mate-
rials. In Graphics Interface, pages 239–246.
Nelder, J. and Mead, R. (1965). A simplex method for func-
tion minimization. The Computer Journal, 7(4):308–
313.
Nesme, M., Payan, Y., and Faure, F. Efficient, physically
plausible finite elements. In Eurographics, pages 77–
80.
Newcombe, R. A., Davison, A. J., Izadi, S., Kohli, P.,
Hilliges, O., Shotton, J., Molyneaux, D., Hodges, S.,
Kim, D., and Fitzgibbon, A. (2011). Kinectfusion:
Real-time dense surface mapping and tracking. In
IEEE International Symposium on Mixed and Aug-
mented Reality, pages 127–136.
Oikonomidis, I., Kyriazis, N., and Argyros, A. A. (2011).
Full dof tracking of a hand interacting with an object
by modeling occlusions and physical constraints. In
IEEE International Conference on Computer Vision,
pages 2088–2095.
Petit, A., Lippiello, V., Fontanelli, G. A., and Siciliano, B.
(2017). Tracking elastic deformable objects with an
RGB-D sensor for a pizza chef robot. Robotics and
Autonomous Systems, 88:187–201.
Petit, A., Lippiello, V., and Siciliano, B. (2015a). Real-time
tracking of 3D elastic objects with an RGB-D sensor.
In IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 3914–3921.
Petit, A., Lippiello, V., and Siciliano, B. (2015b). Tracking
fractures of deformable objects in real-time with an
RGB-D sensor. In IEEE International Conference on
3D Vision, pages 632–639.
Pham, T.-H., Kheddar, A., Qammaz, A., and Argyros, A. A.
(2015). Towards force sensing from vision: Observing
hand-object interactions to infer manipulation forces.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 2810–2819.
Sato, K., Kamiyama, K., Kawakami, N., and Tachi, S.
(2010). Finger-shaped gelforce: sensor for measuring
surface traction fields for robotic hand. IEEE Trans-
actions on Haptics, 3:37–47.
Siciliano, B. and Khatib, O. (2008). Springer handbook of
robotics. Springer Science & Business Media.
Sun, M., Su, H., Savarese, S., and Fei-Fei, L. (2009). A
multi-view probabilistic model for 3d object classes.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 1247–1254.
Sun, Y., Hollerbach, J. M., and Mascaro, S. A. (2008). Pre-
dicting fingertip forces by imaging coloration changes
in the fingernail and surrounding skin. IEEE Transac-
tions on Biomedical Engineering, 55:2363–2371.
Urban, S., Bayer, J., Osendorfer, C., Westling, G., Edin,
B. B., and Van Der Smagt, P. (2013). Computing grip
force and torque from finger nail images using gaus-
sian processes. In IEEE/RSJ International Conference
on Intelligent Robots and Systems, pages 4034–4039.
Wang, B., Wu, L., Yin, K., Ascher, U., Liu, L., and Huang,
H. (2015). Deformation capture and modeling of soft
objects. ACM Transactions on Graphics, 34:94.
Wang, Y., Min, J., Zhang, J., Liu, Y., Xu, F., Dai, Q., and
Chai, J. (2013). Video-based hand manipulation cap-
ture through composite motion control. ACM Trans-
actions on Graphics, 32:43.
Wettels, N., Fishel, J., Su, Z., Lin, C., and Loeb, G. (2009).
Multi-modal synergistic tactile sensing. In Workshop
on Tactile Sensing in Humanoids, Tactile Sensors and
Beyond, 9th IEEE-RAS International Conference on
Humanoid Robots.
Yousef, H., Boukallel, M., and Althoefer, K. (2011). Tac-
tile sensing for dexterous in-hand manipulation in
robotics. A review. Sensors and Actuators A: Phys-
ical, 167:171–187.
Yuan, W., Li, R., Srinivasan, M. A., and Adelson, E. H.
(2015). Measurement of shear and slip with a gelsight
tactile sensor. In IEEE International Conference on
Robotics and Automation, pages 304–311.
Zhao, W., Zhang, J., Min, J., and Chai, J. (2013). Robust re-
altime physics-based motion control for human grasp-
ing. ACM Transactions on Graphics, 32:207.
Using Physical Modeling and RGB-D Registration for Contact Force Sensing on Deformable Objects
33