
Learning from Simulated World - Surrogates Construction with Deep
Neural Network
Zong-De Jian
1
, Hung-Jui Chang
1,2
, Tsan-sheng Hsu
1
and Da-Wei Wang
1
1
Institute of Information Science, Academia Sinica, Taipei, Taiwan
2
Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan
Keywords:
Deep Learning, Surrogate, Disease Simulator.
Abstract:
The deep learning approach has been applied to many domains with success. We use deep learning to construct
the surrogate function to speed up simulation based optimization in epidemiology. The simulator is an agent-
based stochastic model for influenza and the optimization problem is to find vaccination strategy to minimize
the number of infected cases. The optimizer is a genetic algorithm and the fitness function is the simulation
program. The simulation is the bottleneck of the optimization process. An attempt to use the surrogate function
with table lookup and interpolation was reported before. The preliminary results show that the surrogate
constructed by deep learning approach outperforms the interpolation based one, as long as similar cases of the
testing set have been available in the training set. The average of the absolute value of relative error is less
than 0.7 percent, which is quite close to the intrinsic limitation of the stochastic variation of the simulation
software 0.2 percent, and the rank coefficients are all above 0.99 for cases we studied. The vaccination strategy
recommended is still to vaccine the school age children first which is consistent with the previous studies. The
preliminary results are encouraging and it should be a worthy effort to use machine learning approach to
explore the vast parameter space of simulation models in epidemiology.
1 INTRODUCTION
Simulation models are built so that we can experiment
with them to gain insight about subjects investigated.
With the current success of machine learning, espe-
cially deep learning, it is worth exploring about using
machine learning technique to learn from the simula-
tion models. We explore the possibility by using the
deep neural network to construct a surrogate function
as the cost function instead of running real simulation
when applying the genetic algorithm to search for ef-
fective vaccination strategy in the domain of public
health.
Agent-based stochastic simulations have been ap-
plied widely for the study of infectious diseases (Ger-
mann et al., 2006)(Chao et al., 2010). Comparing to
the mathematical models, the flexibility to easily in-
corporate detailed disease control strategies into sim-
ulation model is one of its strength. However, it still
needs a significant amount of computing resources.
Epidemiologists usually have to carefully craft the
scenarios to demonstrate their points. Vaccination
can effectively mitigate the impact of the pandemic
flu with an appropriate vaccinating strategy which
might depend on an amount of available vaccines. In-
stead of comparing a few strategies selected by do-
main experts, we formulate it as an optimization prob-
lem and employ genetic algorithms to search for the
best vaccination priority. The search space can po-
tentially contain many dimensions, for example, the
house-hold structure is one of the important dimen-
sions (Chang et al., 2015). In this paper, we focus on
the dimension of vaccination allocation.
The supply of the vaccine is usually limited, the
disease control agency has to decide the amount of
vaccine allocated to various groups. Without a doubt,
the health care professionals should get the highest
priority. Then the agency determined how much to
distribute to different age groups. How to determine
the number of doses to each age group is an impor-
tant issue. The objective can also be complicated, for
example, one can search for a strategy to minimize
economic impact, or to minimize the total number of
infected cases. In this paper, the goal is to minimize
the total number of infected cases.
For a given scenario, that is the setting of our sim-
ulation module, the gene encodes the vaccine distribu-
tion among age groups and the fitness function is the
Jian, Z-D., Chang, H-J., Hsu, T-s. and Wang, D-W.
Learning from Simulated World - Surrogates Construction with Deep Neural Network.
DOI: 10.5220/0006418100830092
In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2017), pages 83-92
ISBN: 978-989-758-265-3
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
83

total number of infected cases. The fitness evaluation
is done by running the simulation module.
Each simulation run takes about 3 minutes, thus
the fitness evaluation becomes the bottleneck of the
optimization process. Using a faster approximation
in place of the true fitness function, in our case the
simulation program, is called surrogated-assisted evo-
lutionary computation (Jin, 2011). The idea was first
suggested in the mid-1980s (J.J. Grefenstette, 1985).
A surrogate function combines table lookups and lin-
ear interpolation was suggested in (Jian et al., 2016).
In this study, we use the deep neural network to con-
struct the surrogate function and compare it with the
previous interpolation based one.
The accuracy is measured by the relative error,
that is the difference between the output of surrogate
function and the simulation divided by the output of
the simulation. The average of the absolute value
of the relative errors of the surrogate functions con-
structed by the deep neural network approach range
from 0.18 percent to 0.68 percent for different train-
ing sets and testing sets. When the training sets have
cases similar to the testing sets, the surrogate con-
structed by deep neural network usually performs bet-
ter than the interpolation based one. The search re-
sults with the surrogate in place of the simulation sys-
tem have error margin less than one percent. The
rank correlation coefficients of the surrogates are bet-
ter than 99 percent.
2 MATERIAL AND METHOD
Our approach to search for the optimal vaccina-
tion strategy belongs to the general category of
simulation-based optimization (Gosavi, 2015). We
first introduce our simulation software, followed by
a description of our optimization procedure.
We use the simulation software developed in our
laboratory (Tsai et al., 2010). Below is a brief de-
scription of how the simulation works. It is a stochas-
tic discrete time agent-based model. The mock pop-
ulation of the model is constructed according to na-
tional demographics from Taiwan Census 2000 data
(http://eng.stat.gov.tw/). The connection between any
two individuals indicates the possibility of daily and
relatively close contact which could result in a suc-
cessful transmission of the flu virus. An important
virus-dependent parameter is the transmission proba-
bility, denoted by p
trans
. It is the probability that an
effective contact results in an infection. An individ-
ual can be in one of the following four states, suscep-
tible(S), exposed(E), infectious(I), and recovered(R).
when an effective contact happens between an indi-
vidual in the state S and an individual in the state I,
the susceptible individual will become exposed with
probability p
trans
. According to the disease natural
history, an exposed individual becomes infectious and
an infectious individual becomes recovered, in our
setting the average incubation period is 1.9 days and
the average infectious period is 4.1 days (Germann
et al., 2006). A contact group is a daily close associ-
ation of individuals, where every member has a con-
tact probability to have effective contact with all other
members in the same group. There are eleven such
contact groups in the model, they are communities,
neighborhood, household cluster, household, work-
group, high school, middle school, elementary school,
daycare center, kindergarten, and playgroup (Chang
et al., 2015). The population size of Taiwan is about
22.12 million. There are about 1.72 million
preschool
children
(0-5 years old), about 2.36 million
elemen-
tary school children
(6-12 years old), about 0.99 mil-
lion
middle school children
(13-15 years old), about
0.97 million
high school children
(16-18 years old),
about 3.86 million
young adults
(19-29 years old),
about 10.28 million
adults
(30-64 years old), and
about 1.94 million
elders
(65+ years old).
Each individual can belong to several contact
groups simultaneously at any time. The duration of
a simulation run is set at 365 days. Each day has
two 12-hour periods, daytime and nighttime respec-
tively. Behaviors of individuals are depicted in Fig-
ure 1. During daytime, contact occurs in all contact
group. School aged children go to schools. There
are around 7.8% school aged children do not go to
school in Taiwan. They stay home in our simulation.
Preschool children go to a daycare center, kinder-
garten or playgroup. Young adults and adults go to
workgroup. In the nighttime, contact occurs only in
communities, neighborhoods,household clusters, and
household.
The model parameters are similar to ones in a
study by (Germann et al., 2006), with modifications to
fit Taiwan situation better with the help of study out-
come in contact diary study (Fu et al., 2012). We re-
call that the stochastic variation of the simulation sys-
tem is reported to be around 0.2 percent (Tsai et al.,
2010).
In this paper, our setting is similar to our previous
study about surrogates functions(Jian et al., 2016):the
p
t
rans is set at 0.1, the vaccine is available 30 days af-
ter the index case occurred, total 2.5 million of doses
are applied to different age groups according to the
priority.. However, we only focus on the case that the
vaccine efficacy,VEi and VEs, are fixed at 0.9 (Basta
et al., 2008). The vaccine is available 30 days after
the index case occurred, total available vaccine are all
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
84

Community
Working
group
School
neighborhood
Household cluster
r
r
Household
r
Working
group
r
r
r
(a) Contact behavior in daytime.
Community
Working
group
School
neighborhood
Household cluster
r
r
Household
r
Working
group
r
r
r
(b) Contact behavior in nighttime.
Figure 1: Contact behavior.
Simulated annealing
Selection
Crossover
Mutation
ܲܽݎ݁݊ݐݏ
= { Ƹ, Ƹ, … , Ƹ }
ܲܽݎ݁݊ݐݏ
ାଵ
= { Ƹ, Ƹ, … , Ƹ}
ܥ݄݈݅݀ݎ݁݊
= { Ƹ, Ƹ, … , Ƹ }
Copy the best Ƹ
Copy the first nine Ƹ
Check the
stopping criteria
Figure 2: Process of HSAGA.
administered to individuals.
A vaccination priority is denoted by p =
(x
1
,x
2
,...,x
7
), where x
i
is the amount of vaccine for
the age group i and it is less than the population of age
group i. We use p
α
to denote vectors with only those
value of x
α
are nonzero and α is a set with numberings
of each age group. For example p
2,3
denote the set
of vaccination priority with non-zero entries for age
group 2 and age group 3 and p
i, j,k
to denote the set of
vectors with 3 non-zero entries. Let p =
~
0 denote the
baseline case with no vaccination. We use Sim(p) to
denote the number of infected cases reported by the
simulation program with vaccination priority p.
Ƹ
= ( 30, 70, 91, 103, 205, 240, 250 )
Ƹ
= ( 10, 20,
40, 77, 121, 210, 250 )
Ƹ
ᇲ
= ( 30,
40, 77, 121, 205, 240, 250 )
Ƹ
ᇲ
= ( 10, 20,
70, 91, 103, 210, 250 )
Random select two numbers: [ , ]
Figure 3: Crossover of HSAGA.
Ƹ = ( 3, 25, 70, 90, 150, 200, 250 )
Random select a index, change a random number [83],
and re-sort the chromosome.
Ƹ’ = ( 3, 25, 70, 83, 90, 200, 250 )
Figure 4: Mutation of HSAGA.
We use the genetic algorithm to search for the
optimal vaccine strategy. A simulated annealing
step is introduced to speedup the process. In
the hybrid simulated annealing genetic algorithm
(HSAGA), the population is consists of vaccine al-
locations represented in prefix sum format. That
is p = (20, 50,50, 70,20, 30,10) can be rewritten as
ˆp = (20, 70,120,190, 210,240,250), since the total
amount of vaccine is always 2.5 millions the last co-
ordinate can be dropped. The population size is ten,
and each iteration begins with simulated annealing
step to perturb each candidate, followed by the se-
lection, crossover, and mutation steps. Figure 2 is the
flow-chart of the process. For a given allocation, we
carried out 5 simulation runs, and the fitness score is
the average of the values of the objective function of
each run. The best solution of the previous generation
and the first nine solutions for this generation become
the candidates of next generation. At the beginning
of each iteration, we carry out a simulated annealing
step for each candidate. It is a temperature controlled
mutation, i.e., we mutate each candidate according to
the temperature (that is the number of iterations up to
the point in our case). The process stops at 200 itera-
tions and the early stop condition is that five consec-
utive iterations consist of the same candidates. Given
two genes (vaccine priorities), the crossover operation
is the following: Randomly generate a pair of num-
bers g
1
,g
2
where 0 ≤ g
1
≤ g
2
≤ 250, if the interval
[g
1
,g
2
] covers the same number of chromosomes in
both genes, then we exchange the covered part. The
segment of chromosomes x
i
,x
j
is covered by interval
[g
1
,g
2
] if and only if x
i−1
≤ g
2
≤ x
i
and x
j
≤ g
2
≤
x
j+1
. Figure 3 is an example of the crossover oper-
ation. We randomly increase g
1
or decrease g
2
if a
direct exchange is invalid, that is the length of cov-
ered segments differ. A more detailed description can
be found in (Jian et al., 2016).
The mutation operation is defined as following:
Randomly pick index i and randomly generate a num-
ber x, replace x
i
with x and sort the resultant sequence.
Figure 4 is an illustration of the mutation operation.
Learning from Simulated World - Surrogates Construction with Deep Neural Network
85
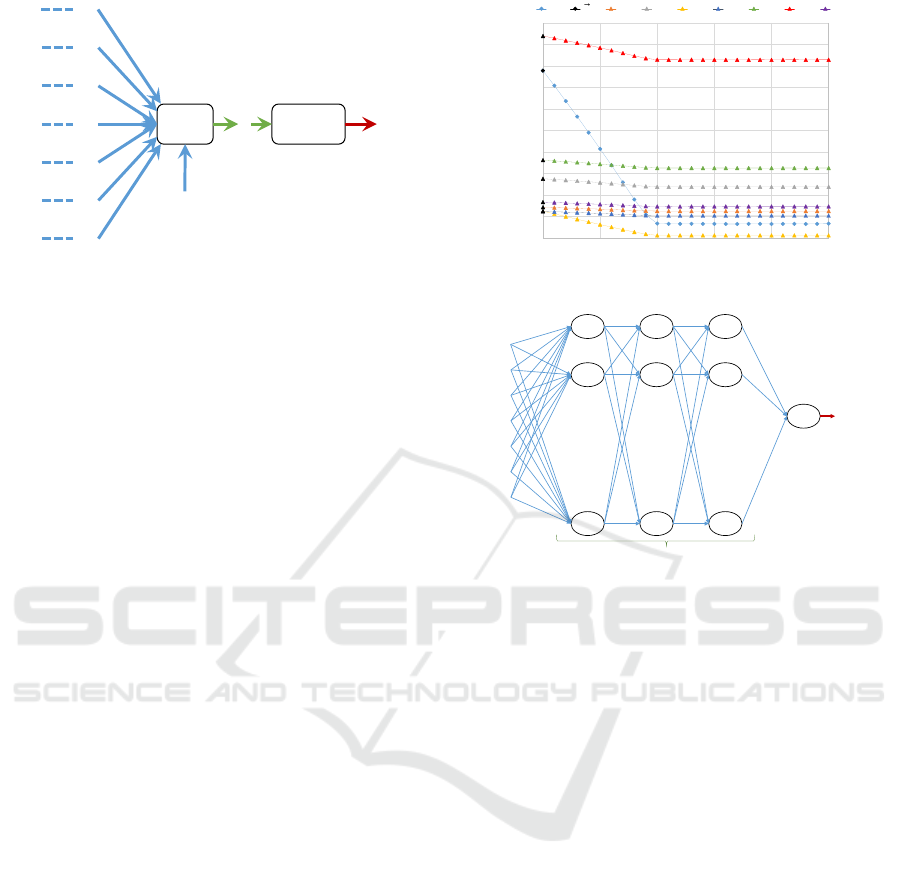
ݔ
ଵ
ݔ
ଶ
ݔ
ଷ
ݔ
ସ
ݔ
ହ
ݔ
ݔ
Sum Function
ݓ
ଶ
ݓ
ଷ
ݓ
ସ
ݓ
ହ
ݓ
ݓ
ݓ
ଵ
ܾ
ݖ ݂(ݖ)
Figure 5: The model of Sur
D
1
(p).
2.1 Surrogates with Deep Learning
Deep learning gained a lot of attention with a few
highly publicized success. It is a branch of machine
learning, and one of its basic ingredients is the ar-
tificial neural network. The word deep referring to
the fact that the model is built with multilayer per-
ceptrons(MLP). Each perceptron has a transformation
function to produce output to next perceptrons with
the inputs from connected perceptrons at the previous
stage. During the training phase, the prediction er-
ror is determined by the loss function, and the error
triggering a weight adjustment procedure, backprop-
agation is the most commonly applied method.
In our research, we use deep neuron networks
(DNN) as the model of the surrogate function. In
this study, we use Keras on Theano running on Nvidia
GeForce GTX 1080 Graphics Card (Keras, 2015).
The surrogate function takes the vaccine alloca-
tion of seven age groups, p, as the input and the output
is the total number of infected cases.
We first applied single perceptron model with the
linear function to check if there exist good linear sur-
rogates. The single perceptron model is shown in Fig-
ure 5, in which w
i
denotes the weight, and b is the
bias. We let the activation function to be a linear func-
tion, i.e., f(z) = z and the output of the single percep-
tron model is denoted by Sur
D
1
Sur
D
1
(p) = f(z) = z =
7
∑
i=1
(w
i
x
i
) + b (1)
As shown in Figure 6, the slope approaching zero
when the vaccine allocation is approaching the size
of the population of that age group. As expected, we
can see that the number of infected cases of other age
groups is also affected by the amount allocated to one
specific age group.
We next move on to the deep neural network
with nonlinear activation function. The architecture
is shown in Figure 7. The output of the deep neural
0
500,000
1,000,000
1,500,000
2,000,000
2,500,000
3,000,000
3,500,000
4,000,000
7,000,000
7,200,000
7,400,000
7,600,000
7,800,000
8,000,000
8,200,000
8,400,000
8,600,000
8,800,000
9,000,000
0 500,000 1,000,000 1,500,000 2,000,000 2,500,000
cases for each age group
total cases
doses
t 0 1 2 3 4 5 6 7
ଷ
0
ܿ
ଵ
య
ܿ
ଶ
య
ܿ
ଷ
య
ܿ
ସ
య
ܿ
ହ
య
ܿ
య
ܿ
య
Figure 6: Sim(p
3
) with p
3
∈ P
t
.
ݔ
ଵ
ݔ
ଶ
ݔ
ଷ
ݔ
ସ
ݔ
ହ
ݔ
ݔ
ܮ
ଵ
ଵ
ܮ
ଶ
ଵ
ܮ
ଵଶ
ଵ
. . . . . .
ܮ
ଵ
ଶ
ܮ
ଶ
ଶ
ܮ
ଵଶ
ଶ
. . . . . .
ܮ
ଵ
ଷ
ܮ
ଶ
ଷ
ܮ
ଵଶ
ଷ
. . . . . .
ܮ
ଵ
ସ
ܵݑݎ
ଶ
()
Hidden layers Output layerInput layer
Figure 7: The model of Sur
D
2
(p).
network is denoted by Sur
D
2
(p). It is a fully connected
architecture, that is the outputs of every neuron in this
layer are inputs for every neuron in next layer. We add
three hidden layers, and each layer has
∑
7
i=1
C
7
i
= 127
perceptrons, which corresponding to the number of
all the combinations of the seven age groups. The ac-
tivation function is exponential linear units (ELUs),
it can handle non-linear relations and outperform the
traditional rectified linear unit(ReLU)(Clevert et al.,
2015).
2.2 Surrogates with Interpolation
We compare the surrogates learnt by neural networks
with the interpolation based ones we constructed be-
fore. We first give a brief description of the previ-
ous work, and the details can be found in (Jian et al.,
2016).
To apply interpolation, we need a set of reference
points, denoted by P
t
, the values of these points are
the simulation results. In other words, points in p
t
are
entries of the lookup table. If p ∈ P
t
the result, Sim(p),
is the total number of infected cases by simulation. If
p /∈ P
t
, then Sim(p) denote the estimated total number
of infected cases by interpolation. We first sampled
26 points for each age group, there are 182 points in
total. The 26 points are evenly spaced up to 2.5 mil-
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
86
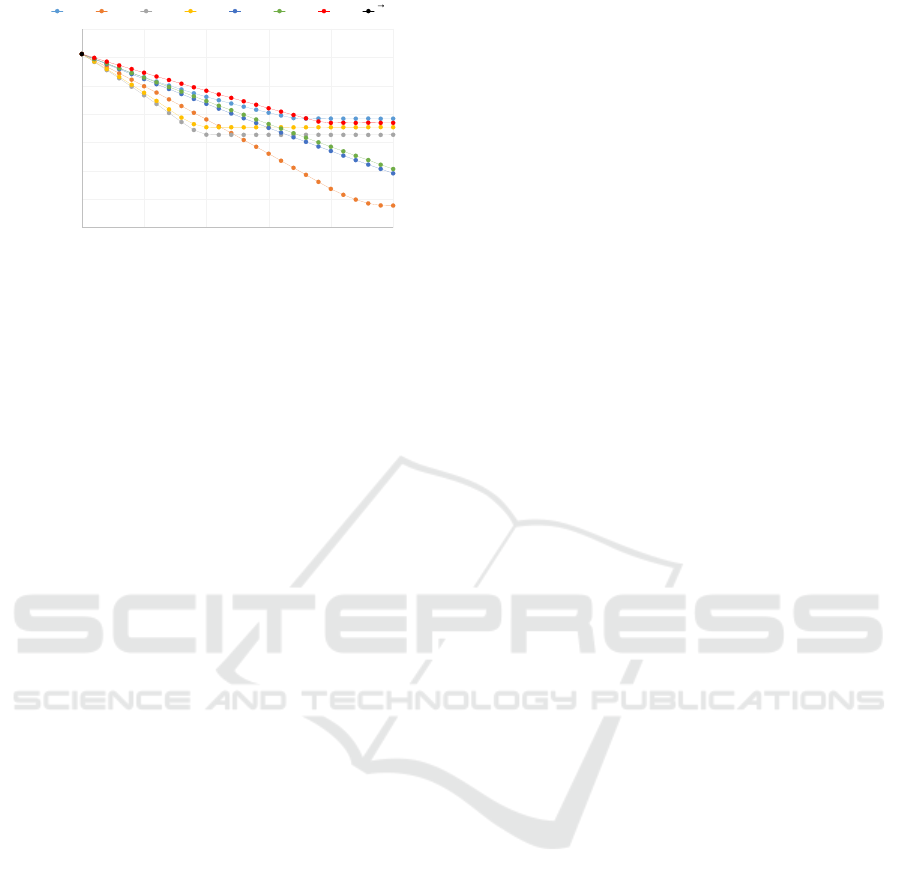
5,500,000
6,000,000
6,500,000
7,000,000
7,500,000
8,000,000
8,500,000
9,000,000
0 500,000 1,000,000 1,500,000 2,000,000 2,500,000
total cases
doses
p1 p2 p3 p4 p5 p6 p7 0
ଵ
ଶ
ଷ
ସ
ହ
0
Figure 8: Sim(p
i
) with p
i
∈ P
t
.
lion doses of vaccine. Figure 8 shows the value of
each point. We then define the effect of introducing
strategy p
i
, denoted by ∆(p
i
) as following:
∆(p
i
) = Sim(p
i
) − Sim(
~
0) (2)
To approximate the effect of a point p, we add the
effect of each component and denote it by Sur
I
1
(p):
Sur
I
1
(p) = Sim(
~
0) +
7
∑
i=1
∆(p
i
) (3)
If the value of p
i
is not sampled, the linear interpo-
lation is applied to estimate ∆(p
i
). As expected, this
simple surrogate does not capture the interaction be-
tween age groups well. We build a lookup table with
entries in the form of p
i, j
to capture the interactions
between age groups. For each age group i, five evenly
spaced values are determined. Given two age groups,
we take one value from each group to form a vacci-
nation strategy and carry out the simulation. There
are total 21× 5 × 5 = 525 such points. For a point
p = (x
1
,x
2
,...,x
7
), we slightly abuse the notation and
use p
j,k
denote the point with the same value as p
in j
th
and k
th
dimensions and all other dimensions are
zero. The adjustment term for the interaction between
dimension j and k, denoted by δ(p
j,k
), is defined as
following:
δ(p
j,k
) = Sim(p
j,k
) − Sur
I
1
(p
j,k
) (4)
When p
j,k
is not sampled, a bilinear interpolation
is applied. The surrogate with the two age group in-
teraction adjustment, denoted by Sur
I
2
(p), is defined
as following:
Sur
I
2
(p) = Sim(
~
0)+
7
∑
i=1
∆(p
i
) +
6
∑
j=1
7
∑
k= j+1
δ(p
j,k
) (5)
3 RESULTS
We collected two sets of points in our previous study.
First, the set of base points, p
t
, which are the points
serve as the sampled points while developing interpo-
lation based surrogate. Second, the set of points eval-
uated during the execution of HSAGA and we denote
the set by P
h
. For this study, we further evaluate a
set of points, denoted by P
q
, which are points have
3 age groups assigned none zero entries. There are
C
7
3
= 36 combinations and for each dimension, we
evenly sampled 4 points up to the population size of
that age group. In other words, the increment is 1/4
of the size of the age group. We also limit the total
amount is no more than 4 million doses and each age
group gets at most 2.5 million. We note that because
of the choice of increment P
t
T
P
q
=
/
0. There size of
P
t
is 707, P
h
is 988, and P
q
is 1557. Our training and
testing data are drawn from these three sets. We set
epoch to be 10 thousand, mini-batch to be 10 and we
use mean absolute error (MAE) as our loss function
and Nadam as optimizer (Dozat, 2015).
We compare surrogates learnt by DNN with inter-
polation based surrogates. There are several settings.
We always use D
a
to denote the training set and D
b
to denote the testing set. The interpolation based sur-
rogate does not have the training phase, only testing
set matters for their evaluation. We use the relative er-
ror between the output of surrogate and the simulation
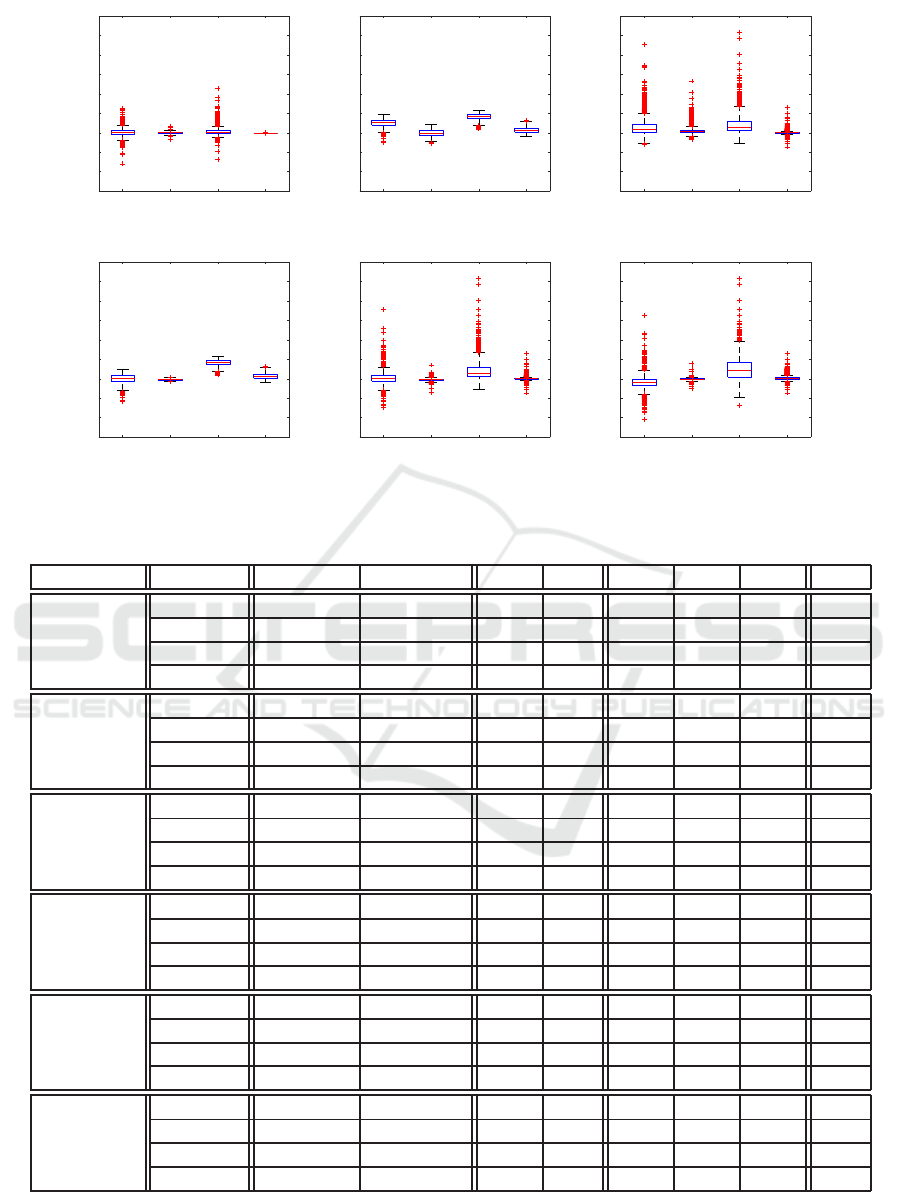
result and use box plot to visualize the results.
In Figure 9(a), there is no error for Sur
I
2
(p) be-
cause the testing data is P
t
which are the reference
base for interpolation. Similarly, the error for Sur
I
1
(p)
is from points with pattern p
j,k
. From the fact that
Sur
D
1
(p) is the result of a thorough training phase and
that it has much larger error comparing with Sur
D
2
(p),
it is safe to say that the relation between vaccine allo-
cation and the total number of infected case reduced
is not a simple linear one.
In Figure 9(b), we note that P
h
contains points
with many non-zero dimensions because the ge-
netic algorithm starts with random points and grad-
ually converge to points concentrating on vaccinat-
ing school children. We can see that Sur
D
1
(p) and
Sur
I
1
(p) obviously over-estimate the value, although
the spreading patterns are more or less similar in all
four cases.
In Figure 9(c), the testing data P
q
contains points
with 3 non-zero entries. Compared with Figure 9(a)
the over-estimating phenomenon is even more obvi-
ous, even Sur
I
2
(p) can not remedy the fact that the
interaction among three age groups is not captured.
We can see that Sur
I
2
(p) is outperformed by
Sur
D
2
(P) in Figure 9(a) and 9(c) . The reason is that
Learning from Simulated World - Surrogates Construction with Deep Neural Network
87
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(a) D
a
= P
t
, D
b
= P
t
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(b) D
a
= P
t
, D
b
= P
h
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(c) D
a
= P
t
, D
b
= P
q
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(d) D
a
= P
t
S
P
h
, D
b
= P
h
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(e) D
a
= P
t
S
P
q
, D
b
= P
q
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(f) D
a
= D
b
= P
t
S
P
h
S
P
q
Figure 9: Box plot with different surrogates.
Table 1: Detail data of Figure 9.
surrogate avg of abs max of abs avg SD Q
1
Q
2
Q
3
IQR
Figure 9(a)
Sur
D
1
(p) 0.80 8.00 0.11 1.25 -0.38 0.09 0.57 0.95
Sur
D
2
(p) 0.23 1.71 0.05 0.31 -0.14 0.08 0.21 0.34
Sur
I
1
(p) 0.77 11.32 0.48 1.43 0.00 0.08 0.70 0.70
Sur
I
2
(p) 0.00 0.04 0.00 0.00 0.00 0.00 0.00 0.00
Figure 9(b)
Sur
D
1
(p) 2.65 4.69 2.61 1.06 2.04 2.82 3.35 1.30
Sur
D
2
(p) 0.68 2.79 0.01 0.88 -0.52 -0.01 0.60 1.11
Sur
I
1
(p) 4.16 5.87 4.16 0.84 3.62 4.23 4.75 1.13
Sur
I
2
(p) 0.86 3.28 0.80 0.83 0.20 0.58 1.29 1.09
Figure 9(c)
Sur
D
1
(p) 1.76 22.77 1.43 2.28 0.15 0.96 2.11 1.96
Sur
D
2
(p) 0.66 13.30 0.56 1.00 0.09 0.36 0.73 0.64
Sur
I
1
(p) 2.42 25.77 2.23 2.84 0.54 1.52 3.04 2.50
Sur
I
2
(p) 0.22 6.48 0.15 0.44 -0.01 0.08 0.19 0.20
Figure 9(d)
Sur
D
1
(p) 1.00 5.81 0.02 1.30 -0.66 0.17 0.97 1.63
Sur
D
2
(p) 0.19 0.73 -0.14 0.19 -0.27 -0.14 -0.02 0.25
Sur
I
1
(p) 4.16 5.87 4.16 0.84 3.62 4.23 4.75 1.13
Sur
I
2
(p) 0.86 3.28 0.80 0.83 0.20 0.58 1.29 1.09
Figure 9(e)
Sur
D
1
(p) 1.20 17.81 0.21 1.85 -0.62 0.13 0.88 1.50
Sur
D
2
(p) 0.29 3.56 -0.24 0.30 -0.37 -0.24 -0.11 0.26
Sur
I
1
(p) 2.42 25.77 2.23 2.84 0.54 1.52 3.04 2.50
Sur
I
2
(p) 0.22 6.48 0.15 0.44 -0.01 0.08 0.19 0.20
Figure 9(f)
Sur
D
1
(p) 1.30 16.21 -0.85 1.60 -1.58 -0.77 -0.04 1.54
Sur
D
2
(p) 0.18 3.88 -0.10 0.25 -0.21 -0.08 0.04 0.24
Sur
I
1
(p) 2.59 25.77 2.44 2.50 0.44 2.09 4.15 3.72
Sur
I
2
(p) 0.37 6.48 0.31 0.64 0.00 0.07 0.38 0.38
the training data and testing data are in a different cat-
egory and Sur
I
2
(P) is designed to work with those spe-
cial categories well. In Figure 9(b) the testing set con-
tains more randomly sampled data, we see Sur
D
2
(p)
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
88
Sur
D
1
(p) S ur
D
2
(p) S ur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(a) 20%, 80%
Sur
D
1
(p) S ur
D
2
(p) S ur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(b) 40%, 60%
Sur
D
1
(p) S ur
D
2
(p) S ur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(c) 60%, 40%
Sur
D
1
(p) S ur
D
2
(p) S ur
I
1
(p) Sur
I
2
(p)
-15
-10
-5
0
5
10
15
20
25
30
Relative Error (%)
(d) 80%, 20%
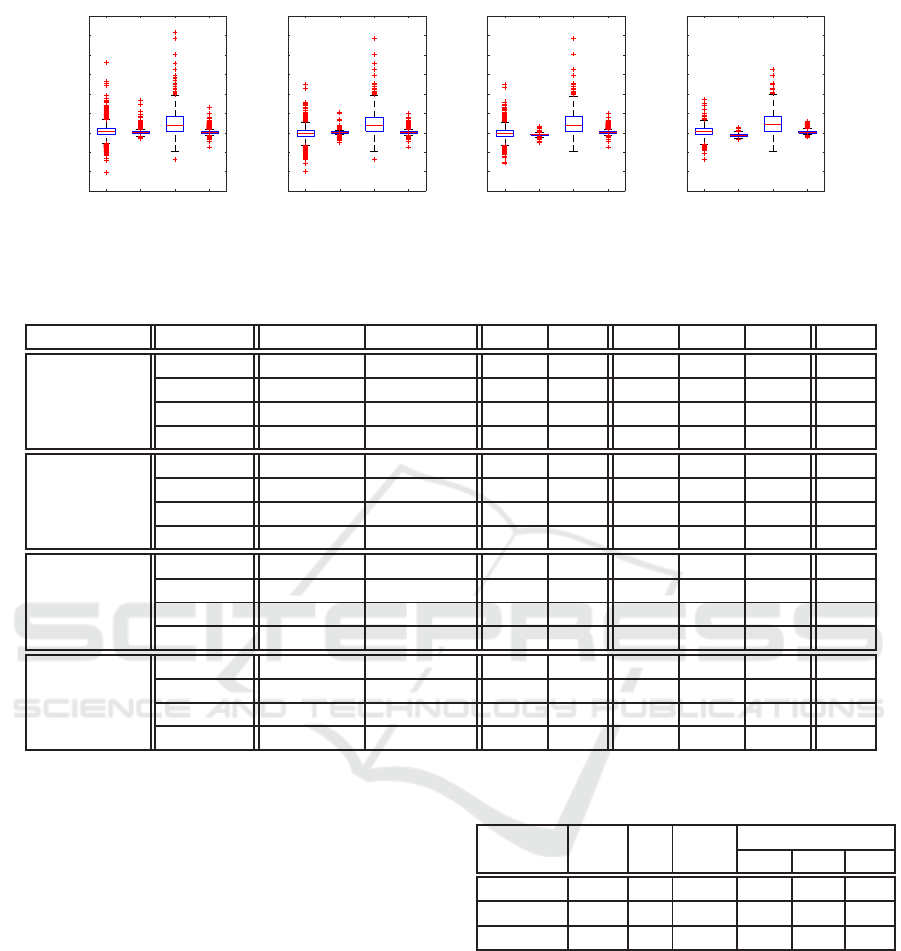
Figure 10: Box plot which cutting sample data P
t
S
P
h
S
P
q
by different percentage for D
a
and D
b
.
Table 2: Detail data of Figure 10.
surrogate avg of abs max of abs avg SD Q
1
Q
2
Q
3
IQR
Figure 10(a)
Sur
D
1
(p) 1.14 18.00 0.30 1.64 -0.46 0.30 1.10 1.57
Sur
D
2
(p) 0.30 8.29 0.09 0.49 -0.18 0.04 0.82 0.46
Sur
I
1
(p) 2.60 25.77 2.45 2.55 0.43 2.05 4.15 3.72
Sur
I
2
(p) 0.38 6.48 0.32 0.65 0.00 0.07 0.39 0.39
Figure 10(b)
Sur
D
1
(p) 1.06 12.48 -0.21 1.57 -0.92 -0.15 0.59 1.51
Sur
D
2
(p) 0.26 5.20 0.12 0.39 -0.02 0.14 0.30 0.32
Sur
I
1
(p) 2.54 24.22 2.39 2.49 0.39 1.99 4.11 3.72
Sur
I
2
(p) 0.38 5.07 0.32 0.65 0.00 0.06 0.38 0.38
Figure 10(c)
Sur
D
1
(p) 1.08 12.44 -0.22 1.60 -0.93 -0.18 0.57 1.50
Sur
D
2
(p) 0.44 2.40 -0.43 0.27 -0.57 -0.42 -0.27 0.30
Sur
I
1
(p) 2.62 24.22 2.47 2.58 0.46 2.01 4.18 3.72
Sur
I
2
(p) 0.39 5.07 0.33 0.66 0.00 0.07 0.40 0.40
Figure 10(d)
Sur
D
1
(p) 1.13 8.51 0.24 1.55 -0.50 0.30 1.07 1.57
Sur
D
2
(p) 0.59 1.73 -0.57 0.33 -0.81 -0.58 -0.35 0.46
Sur
I
1
(p) 2.70 16.24 2.55 2.53 0.47 2.14 4.31 3.84
Sur
I
2
(p) 0.38 3.00 0.33 0.61 0.00 0.08 0.44 0.44
performs better. In the next few experiments, we al-
low training set to contain the testing set. We are fully
aware that training set and testing set should be dis-
joint in general. But here we want to demonstrate
the advantage of the machine learning approach, that
is by providing proper training set the performance
can be enhanced greatly. As expected, in Figure 9(d)
and Figure 9(f) we can see Sur
D
2
(p) learned a better
approximation function and outperforms Sur
I
2
(p). In
Figure 9(e), Sur
I
2
(p) performs better and we suspect
that the testing set, points with three non-zero ele-
ments, is very close to the table lookup entries, points
with two non-zero elements. And this particular phe-
nomenon deserve further investigation.
A proper evaluation should have the disjoint train-
ing set and testing set. We take the union of P
t
, P
h
and
P
q
as the sample set. And then partition the whole
set into training and testing set. The result is shown
in Figure 10, the percentage on the left is the portion
of the training set and left is the testing set. Observ-
ing the quartile,Q
1
andQ
3
, of Sur
D
2
(p) and Sur
I
2
(p),
Table 3: The best allocation of HSAGA with each fitness
function.
F C I N
p (×10
4
doses)
ES MS HS
Sim(p) 4.99 72 988 97 79 74
Sur
D
2
(p) 4.98 75 1020 100 81 69
Sur
I
2
(p) 4.99 87 1135 96 78 76
’ F ’: fitness function
’ C ’: total cases (×10
6
)
’ I ’: total iterations
’ N ’: total allocations
’ ES ’:
elementary school children
’ MS ’:
middle school children
’ HS ’:
high school children
we can see the effect of learning. Also, the width of
the spreading pattern decreases as the training data in-
creases. We include all the numerical data for the plot
in Table 2. There are two columns ”avg” and ”avg
of abs”, the former is the average of the relative error
and the latter is the average of the absolute value of
Learning from Simulated World - Surrogates Construction with Deep Neural Network
89
relative error.
We then put Sur
D
2
(p) to the application test, and
use it as the fitness function in HSAGA to search for
the appropriate vaccine strategy. The training set for
the function is P
t
S
P
h
S
P
q
. The result is shown in
Table 3. Three methods produce similar results and
the conclusion confirms to previously reported stud-
ies: that the best strategy is to vaccinate school chil-
dren.
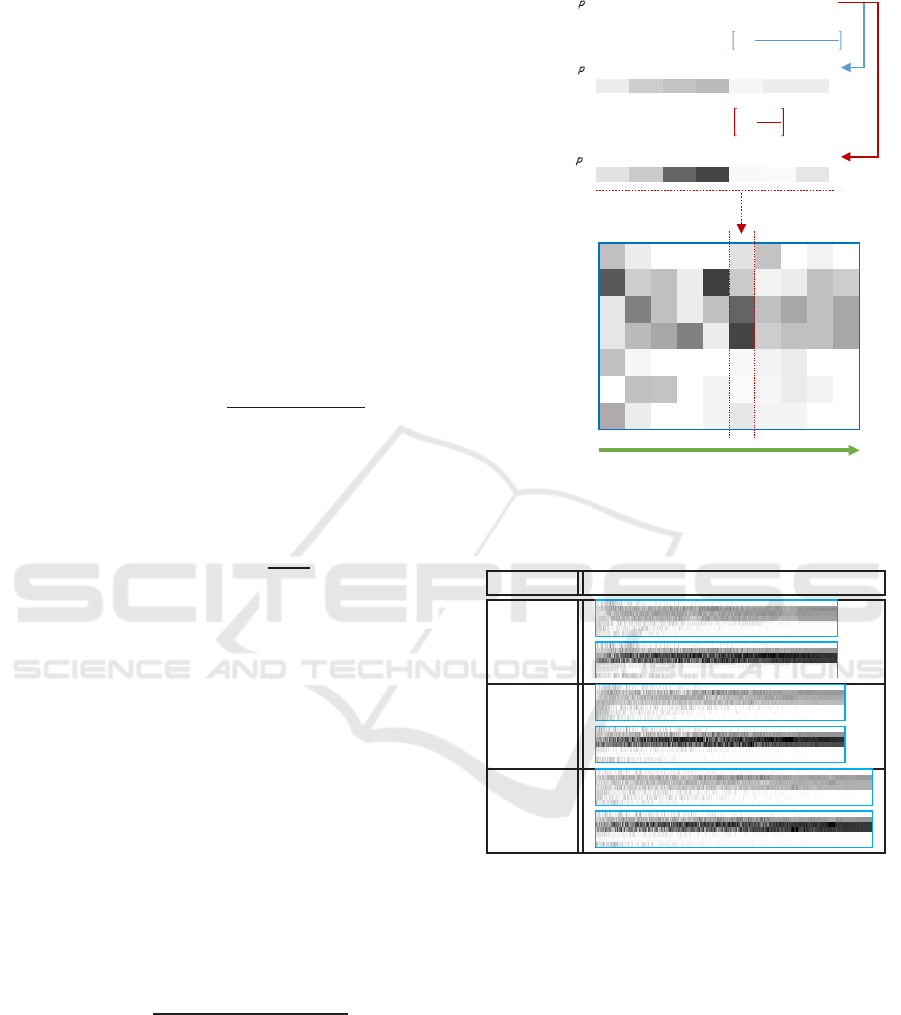
To visualize the vaccine allocations and to facil-
itate further exploration, a method to encode the al-
location by gray level was developed in (Jian et al.,
2016). We briefly recap the method. There are two
encoding schemes,volume scheme and ratio scheme.
For volume scheme, the color white is to denote zero
doses and black for 2.5 million doses. Let x
i
be the
number of doses for age group i, the gray level is com-
puted by the following equation:
g
volume
i
= 255× [1−
x
i
2.5 million doses
] (6)
For the ratio scheme, the color white to denote
zero percent of the age group i vaccinated and black
hundred percent and we used #AG
i
to denote the pop-
ulation of age group i. The gray level is computed by
following equation:
g
ratio
i
= 255× [1 −
x
i
#AG
i
] (7)
After each age group is assigned a gray level accord-
ing to the equation above, we use a line segment with
that gray level to represent vaccination level of each
age group, as shown in the top half of Figure 11. The
allocation is then represented by stacking the seven
line segment vertically (in the middle part of Figure
11, we put the line segment horizontally).
For a set of ordered allocations, the line segment
for each allocation is stitched together according to
the ordering. The sequence of allocations is sorted
from left to right where the better allocations are on
the right hand side. As shown in Table 4, the visual
effect of concentration on school children is obvious.
For genetic algorithms, the rank preserving sur-
rogates are preferred. One metric to measure the fi-
delity of surrogates is rank correlation coefficient (r
s
)
(Loshchilov et al., 2010):
r
s
= 1−
6×
∑
N
i=1
(R
A
[i] − R
B
[i])
2
N(N
2
− 1)
(8)
We compute the rank correlation coefficient for all
surrogates with all sampled points in the list. The
coefficients of Sur
D
2
(p) are all above 99 percentage
and the numbers are shown in Table 5, the left col-
umn indicate the domain of elements and the Sur
D
2
(p)
is trained with P
a
= P
t
S
P
h
S
P
q
. Sur
D
2
(p) has the
best coefficient except the case where all elements are
from P
t
.
DOORFDWLRQ
S
YROXPHVFKHPHRI
S
Ɲ
UDWLRVFKHPHRI
S
Ɲ
0-5 6-12 13-15
16-18
19-29 30-64 65+
235 204 194
184
245 235 235
225 201 100
71
248 250 229
݃
௩௨
= 255 × 1 െ
ݔ
2.5 ݈݈݉݅݅݊ ݀ݏ݁ݏ
݃
௧
= 255 × 1 െ
ݔ
#ܣܩ
7KHJUD\OHYHOUDWLRVFKHPHRIDOORFDWLRQV濣
ݎݐܽݐ݁ െ 90°
0-5
6-12
13-15
16-18
19-29
30-64
65+
Sorting by the number of infected cases
larger smaller
Figure 11: The gray level(Jian et al., 2016).
Table 4: The gray level of total allocations of HSAGA with
each fitness function.
function allocations
Sim(p)
Sur
D
2
(p)
Sur
I
2
(p)
4 CONCLUSION AND
DISCUSSION
We explore the feasibility of using machine learning
approach to constructing surrogates as the cost func-
tion for optimization schemes. The training data is
generated by simulation system. It is natural to sus-
pect that the cost of generating enough training points
would be higher than using simulation as the cost
function during the optimization process. We thus try
to utilize the data points recorded by previous study
and discover that those data points can be reused to
produce good surrogate by the deep neural network.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
90

Table 5: Rank correlation coefficient.
r
s
Sur
D
1
(p) Sur
D
2
(p) Sur
I
1
(p) Sur
I
2
(p)
P
t
0.9974 0.9999 0.9990 0.9999
P
h
0.9155 0.9972 0.9516 0.9611
P
q
0.9958 0.9999 0.9999 0.9999
P
a
0.9913 0.9998 0.9902 0.9976
’ P
a
’: P
t
S
P
h
S
P
q
It is clearly demonstrated that linear
approximations,Sur
I
1
(p) and Sur
D
1
(p), are much
less accurate than more complicated approximations,
Sur
I
2
(p) and Sur
D
2
(p). It illustrated that there are
interesting interactions among age groups. We also
confirmed that if the training set and testing set are
very different, the performance of Sur
D
2
(p) is less
impressive than Sur
I
2
(p). However, when the training
set does contain similar points as testing set, Sur
D
2
(p)
outperforms Sur
I
2
(p). It is more accurate and has
higher rank coefficient correlation.
Our results confirm the finding of previous studies
that school children should be vaccinated with high
priority. One obvious future direction is to use ma-
chine learning to explore the vast landscape of scenar-
ios with various objective functions and constraints.
For example, the infectiousness of the virus strand
might vary, the available date of vaccine may not
be known in advance, and other mitigation strategies
such as antiviral treatment and school closure might
vary. The objective function can vary too. Instead of
minimizing infected cases, one might want to mini-
mize economic cost (Meltzer et al., 1999). Currently,
we the only variables are the amounts of vaccine al-
located to different age groups. More parameters will
be included as input and we plan to try the convo-
lutional neural network and the recurrent neural net-
work in the future. We hope not only we can con-
struct accurate surrogates with more parameters, but
also can gain insight about the delicate interaction be-
tween model parameters and outcome by studying the
neural networks.
Finally, we envision that an autonomous software
searches through the huge scenario space with the
help of surrogate function and adaptively executes
simulation program to revise the surrogate function
to produce higher fidelity surrogate and better search
results by applying reinforcement learning methods.
ACKNOWLEDGEMENTS
We thank anonymous reviewers for their sugges-
tions. The research is partially funded by the grant of
”MOST105-2221-E-001-034”, ”MOST104-2221-E-
001-021-MY3”, and ”Multidisciplinary Health Cloud
Research Program: Technology Development and
Application of Big Health Data. Academia Sinica,
Taipei, Taiwan”.
REFERENCES
Basta, N. E., Halloran, M. E., Matrajt, L., and Longini, I. M.
(2008). Estimating influenza vaccine efficacy from
challenge and community-based study data. Ameri-
can Jourmal of Epidemiology, 168(12):1343–1352.
Chang, H.-J., Chuang, J.-H., Fu, Y.-C., Hsu, T.-S., Hsueh,
C.-W., Tsai, S.-C., and Wang, D.-W. (2015). The im-
pact of household structures on pandemic influenza
vaccination priority. In Proceedings of the 5th In-
ternational Conference on Simulation and Modeling
Methodologies, Technologies and Applications - Vol-
ume 1: SIMULTECH,, pages 482–487.
Chao, D. L., Halloran, M. E., Obenchain, V. J., and Longini,
Jr, I. M. (2010). Flute, a publicly available stochastic
influenza epidemic simulation model. PLOS Compu-
tational Biology, 6(1):1–8.
Clevert, D., Unterthiner, T., and Hochreiter, S. (2015). Fast
and accurate deep network learning by exponential
linear units (elus). CoRR, abs/1511.07289.
Dozat, T. (2015). Incorporating nesterov momen-
tum into adam. http://cs229.stanford.edu/proj2015/
054
report.pdf.
Fu, Y.-c., Wang, D.-W., and Chuang, J.-H. (2012). Rep-
resentative contact diaries for modeling the spread of
infectious diseases in taiwan. PLoS ONE, 7(10):1–7.
Germann, T. C., Kadau, K., Longini, I. M., and Macken,
C. A. (2006). Mitigation strategies for pandemic in-
fluenza in the United States. Proceedings of the Na-
tional Academy of Sciences, 103(15):5935–5940.
Gosavi, A. (2015). Simulation-based optimization. para-
metric optimization techniques and reinforcement
learning.
Jian, Z.-D., Hsu, T.-S., and Wang, D.-W. (2016). Search-
ing vaccination strategy with surrogate-assisted evo-
lutionary computing. In Proceedings of the 6th In-
ternational Conference on Simulation and Modeling
Methodologies, Technologies and Applications - Vol-
ume 1: SIMULTECH,, pages 56–63.
Jin, Y. (2011). Surrogate-assisted evolutionary computa-
tion: Recent advances and future challenges. Swarm
and Evolutionary Computation, 2(1):61–70.
J.J. Grefenstette, J. F. (1985). Genetic search with approxi-
mate fitness evaluations. In International Conference
on Genetic Algorithms and Their Applications, pages
112–120.
Keras (2015). Keras documentation. https://keras.io/.
Loshchilov, I., Schoenauer, M., and Sebag, M. (2010).
Parallel Problem Solving from Nature, PPSN XI:
11th International Conference, Krak´ow, Poland,
Learning from Simulated World - Surrogates Construction with Deep Neural Network
91

September 11-15, 2010, Proceedings, Part I, chap-
ter Comparison-Based Optimizers Need Comparison-
Based Surrogates, pages 364–373. Springer Berlin
Heidelberg, Berlin, Heidelberg.
Meltzer, M. I., Cox, N. J., and Fukuda, K. (1999). The
economic impact of pandemic influenza in the United
States: priorities for intervention. Emerging Infect.
Dis., 5(5):659–671.
Tsai, M.-T., Chern, T.-C., Chuang, J.-H., Hsueh, C.-W.,
Kuo, H.-S., Liau, C.-J., Riley, S., Shen, B.-J., Shen,
C.-H., Wang, D.-W., and Hsu, T.-S. (2010). Efficient
simulation of the spatial transmission dynamics of in-
fluenza. PLOS ONE, 5(11):1–8.
SIMULTECH 2017 - 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
92
