One Random Jump and One Permutation: Sufﬁcient Conditions to

Chaotic, Statistically Faultless, and Large Throughput PRNG for FPGA

Mohammed Bakiri

1,2∗

, Jean-Franc¸ois Couchot

and Christophe Guyeux

FEMTO-ST Institute, UMR 6174 CNRS, Universit´e of Bourgogne Franche, Comt´e, France

Centre de D´eveloppement des Technologies Avanc´ees, ASM-IPLS Team, Algeria

Keywords:

Random Number Generators, Chaotic Circuits, Discrete Dynamical Systems, Statistical Tests, Cryptography

Hardware and Implementation, Applied Cryptography, FPGA.

Abstract:

Sub-categories of mathematical topology, like the mathematical theory of chaos, offer interesting applications

devoted to information security. In this research work, we have introduced a new chaos-based pseudorandom

number generator implemented in FPGA, which is mainly based on the deletion of a Hamilton cycle within

the n-cube (or on the vectorial negation), plus one single permutation. By doing so, we produce a kind of post-

treatment on hardware pseudorandom generators, but the obtained generator has usually a better statistical

proﬁle than its input, while running at a similar speed. We tested 6 combinations of Boolean functions and

strategies that all achieve to pass the most stringent TestU01 battery of tests. This generation can reach

a throughput/latency ratio equal to 6.7 Gbps, being thus the second fastest FPGA generator that can pass

TestU01.

1 INTRODUCTION

The theory of chaos, which refers here to a sub-

category of the mathematical topology discipline,

proposes attractive applications in computer science,

as in the information security ﬁeld. For instance, var-

ious authors propose to use chaos for pseudorandom

numbers generation (PRNGs, which are not true ran-

dom number TRNGs, the former being deterministic

algorithms based on iterative processes like recurrent

sequences, while the latter use a physical or mechan-

ical phenomenon as sources of randomness), leading

to the notion of chaotic pseudorandom number gen-

erators (CPRNGs). Rigorously speaking, CPRNGs

are non-linear algorithms of the form x

∈ R: x

t+1

f(x

), where f is a chaotic continuous map on a given

topological space, and x

is the t-th term of a sequence

x. In practice, and unfortunately, this acronym often

improperly refers to any attempt to use an element of

chaos (logistic map, etc.) within an algorithm, and for

pseudorandom generation purpose.

Reasons explaining the use of chaos for random-

ness generation encompass their sensitivity to ini-

tial conditions, their unpredictability, and their abil-

ity of reciprocal synchronization (Pecora and Carroll,

∗

Authors in alphabetic order

1990). However, due to ﬁnite precision and quan-

tization of ﬂoating point numbers, a CPRNG may

exhibit both deﬂated periods and non uniformly dis-

tributed outputs when designing it on ﬁnite state ma-

chines. Additionally, from a security point of view,

these chaotic PRNGs have most of the times ma-

jor drawbacks that are frequently reported (Wiggins,

2003). To face these drawbacks, an original work

was ﬁrstly introduced in (Bahi et al., 2009; Guyeux,

2010), in which the authors present a new way to gen-

erate pseudorandom numbers that rigorously satisﬁes

the mathematical properties of chaos, as deﬁned by

Devaney (Devaney, 2003), Li-Yorke (Li and Yorke,

1975), and so on. The main idea is to only manipulate

bounded integers, while iterating on an inﬁnite count-

able set. By doing so, what is designed on computers

is exactly what is studied theoretically, the whole al-

gorithm is mathematically proven as chaotic, and they

do not deal with ﬂoating point numbers.

Following this approach, this article investigates

the hardware point of view, and targets to reach speed

generation with good statistical proﬁle, while being

chaotic. Contributions can be summarized as follows.

A new pseudorandom number generator, speciﬁcally

designed for FPGA, is proposed. At each iteration,

it receives a new input from another given generator,

called the strategy. Thanks to an embedded Boolean

Bakiri, M., Couchot, J-F. and Guyeux, C.

One Random Jump and One Permutation: Sufﬁcient Conditions to Chaotic, Statistically Faultless, and Large Throughput PRNG for FPGA.

DOI: 10.5220/0006418502950302

In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 295-302

ISBN: 978-989-758-259-2

295

function and a permutation, our generator, which can

be considered as a post-treatment on the inputted one,

has usually a better statistical proﬁle than its input,

while running at a similar speed. With more details,

we tested 6 combinations of functions and strategies

that all achieve to pass the whole TestU01, which

is the most stringent battery of tests currently avail-

able. This generation can be achieved with a through-

put/latency ratio equal to 6.7 Gbps, which is close

to the fastest existing FPGA generator (that can pass

TestU01 as XOR-CIPRNG). The proposal has been

fully deployed on a FPGA, it runs completely in par-

allel while consuming as low resources as possible.

The remainder of this article is organized as fol-

lows. The next section recalls various proposals in

the use of chaos for hardware pseudorandom num-

ber generation. Their FPGA implementation is pre-

sented, explaining how to compare them in terms

of hardware resources and statistical behavior. Sec-

tion 3 describes our proposed design for a new chaotic

PRNG, targeting a FPGA implementation. Then, in

Section 4, the hardware platform used to evaluate all

evoked chaotic PRNGs is presented. Statistical com-

parisons are provided in the same section, using the

well-known TestU01 battery of tests. Finally, this ar-

ticle ends by a conclusion section, in which the con-

tribution is recalled and intended future work is out-

lined.

2 CHAOTIC RANDOM NUMBER

GENERATORS

This section ﬁrst presents an exhaustivelist of PRNGs

that are linked to a chaotic behavior in one way or

another. It next presents their FPGA implementation

to compare them in terms of hardware resources and

statistical behavior.

2.1 Chaotic PRNGs

Chaotic Mapping PRNG. Most of these generators

are based on the Logistic Chaotic Map, also called

the “LCG” map (May et al., 1976), deﬁned as fol-

lows: x

t+1

= r × x

(1 − x

), where 0 < x

< 1 and

r is the biotic potential (3.57 < r < 4.0). The lo-

gistic map mainly depends on the parameter r: its

chaotic behavior is lost when r is out of the range pro-

vided above. The second most frequently used func-

tion is the H

enon chaotic map (H´enon, 1976), which

takes a point (x

) within the plan square unit and

maps it into a new point (x

t+1

, y

t+1

). This map is

deﬁned by these equations: x

t+1

= (1− a(x

)

) + y

and y

t+1

= bx

t+1

, where a and b are called canonical

parameters.

In (Dabal and Pelka, 2011), the authors have

used ﬁxed point representation (Padgett and Ander-

son, 2009) to implement the logistic map using Mat-

lab DSP System Toolbox software. They gener-

ate many designs with different lengths from 16 to

64 bits, where the resources are depending on the

precision (24 to 53 bits). Authors of (Dabal and

Pelka, 2012) compare this implementation with an-

other chaotic PRNG based on the H´enon map. Un-

like the logistic map, the 64 bits multiplication in

H´enon map cannot be implemented with a left shift

operation, which leads to the use of DSPs blocks of

the FPGA for all multiplications needed to imple-

ment a(x

)

. Two optimized versionsof PRNGs based

on chaotic logistic map are proposed in (Dabal and

Pelka, 2014), which aim to reduce resources and in-

crease frequency. The objective of these two PRNGs

is to pipeline the multiplication operations and syn-

chronize them while adding some delays into each

stage, in order to ensure a parallel execution of se-

quences.

In (Pande and Zambreno, 2010), the authors vary

the biotic potential r and observe the divergence of

random for almost all initial values. Accordingly,

they propose a range of the form [α, 1 − α], where

α < 0.5. Another way to select the parameter r is

presented in (Liu et al., 2008). They propose a cou-

ple of two logistic map PRNGs, each having different

seed and parameter (x

, r

and y

, r

respectively),

where both generates pseudorandom numbers syn-

chronously. The main idea is to recycle the pseudo-

random number generated by the ﬁrst chaotic map,

namely x

t+1

, as the biotic potential r

for the second

one (y

t+1

) when either 3.57 < x

t+1

< 4 is satisﬁed or

the sequence output is divergent.

Finally, in (Giard et al., 2012) four different

chaotic maps are implemented in FPGA, namely,

the so-called Bernoulli, Chebychev, Tent, and Cubic

chaotic maps. The implementation is done with and

without FPGA’s DSP blocks for the multiplication op-

erations. The results show that the Bernoulli chaotic

map gives a higher ratio of area/power compared to

the other chaotic proposed generators.

Chaotic based Timing Reseeding (CTR). Authors

of (

Cern´ak, 1996) address the short period problem

due to the quantization error from a nonlinear chaotic

map PRNG. Instead of initializing the chaotic PRNG

with a new seed, the seed can be selected by mask-

ing the current state x

t+1

at a speciﬁc time. More

precisely, the reseeding unit compares the two reg-

ister states to check whether a ﬁxed point has been

reached. This main concept of CTR was ﬁrst imple-

SECRYPT 2017 - 14th International Conference on Security and Cryptography

296

mented in FPGA (Li et al., 2006), in which the Carry

Lookahead Adder has been used to optimise the crit-

ical path of the partial products of the multiplication

operation. Authors of (Li et al., 2012) present more

hardware details for reducing multiplication operation

resources. They also mix the output from the PRNG

with an auxiliary generator y

t+1

to improve statisti-

cal tests. Finally, they suggest to choose a reseeding

period that must be not only prime, but also not a mul-

tiple of the nonlinear chaotic map PRNG.

Differential Chaotic PRNG. This is a digitized im-

plementation of a nonlinear chaotic oscillator system

in R¨ossler format (Rossler, 1976). It uses an approx-

imated numerical solution to solve a generalization

of the L¨orenz hyperchaos equation. The resolution

was the main study done in (Zidan et al., 2011a) with

other differential systems as the Chen and Elwakil

ones. The authors design various numerical methods

for each system. They show that obtained results with

the Euler numerical approach are the best regarding

area and throughput perspectives.

More details regarding implementation and opti-

mization of this L¨orenz Equation are given in (Zidan

et al., 2011b). In this article, authors proposed to use

again an Euler approximation with less area but same

range of throughput. Authors of (Dabal and Pelka,

2012), for their part, have implemented the so-called

Oscillator Frequency Dependent Negative Resistors

(OFDNR) (Elwakil and Kennedy, 2000), and use the

same Euler approximation.

Chaotic Iteration based PRNG (CIPRNG). For-

mally speaking, this is a random walk in the graph of

iterations of a speciﬁc binary function. The direction

to take and the path length are deﬁned by the embed-

ded generator(s). Practically, it can be seen as post

processing treatment which adds chaos (as deﬁned by

Devaney) to the embedded PRNG (Guyeux and Bahi,

2010). A ﬁrst application of such an approach was

presented in the PRNG framework, leading to the so-

called chaotic iterations based pseudorandom number

generators (CIPRNG, (Fang et al., 2014; Bahi et al.,

2013)). Since then, various improved versions have

been proposed, one of them being designed speciﬁ-

cally for FPGAs. This latter has been recently up-

dated, in which two CIPRNG variants for FPGA have

been designed, namely the XOR-CIPRNG and the

CIPRNG-MultiCycle, see (Bakiri et al., 2016).

Meanwhile, in (Couchot et al., 2014), the authors

have proposed to removea Hamilton Cycle, satisfying

some balance properties, from the Markov chain on

the n-cube, while in (Contassot-Vivier et al., 2017),

authors proposed new functions without a Hamilton

Cycle, and studied the length of the walk in their cube,

until having an associated Markov graph close enough

to the uniform distribution. In these ﬁrst studies, the

minimum length of the chain between two uniform

outputs is larger than 109, which id prohibitive.

2.2 FPGA Performance Analysis

In this section, Table 1 and Table 2 resume the im-

plementation results of different chaotic PRNG pre-

sented in previousSection 2.1 and recall results of lin-

ear PRNGs (already presented in (Bakiri et al., 2016)

which pass TestU01).

In order to compare the considered generators,

we thus have computed throughput (rate), latency,

and the ratio throughput/latency of both. Obtained

results on FPGAs are provided in Tables 1 and 2.

We can conclude that the three best chaotic gen-

erators for FPGA are, namely, the one from (Da-

bal and Pelka, 2014) that uses the logistic map with

Matlab simulink macros, the chaotic iterations based

PRNG (Bakiri et al., 2016), and the one based on the

chaotic Bernoulli map (Giard et al., 2012). If we con-

sider the linear PRNGs who pass TestU01 (see section

below), they have the worst throughput due to their

use of multiplications and their various dependencies.

However, to have a large throughput does not mean

to produce an uniform distribution of numbers, which

leads to the investigation of statistical results.

2.3 Statistical Tests

Statistical tests are fast methods to study in practice

the randomness of generated numbers, by the mean

of software batteries. They are based on various

mathematical and physical approaches, and are thus

used as generator benchmarks. To perform compar-

isons, in this study, we considered the reputed NIST

SP800−22 (NIST, 2010) and TestU01 (L’Ecuyer and

Simard, 2007) batteries of tests. On the one hand,

the NIST battery, considers 15 tests to evaluate the

randomness of a sequence of ﬁxed length 10

, where

each test is passed if its p-value is larger than 0.0001.

On the other hand, TestU01 (L’Ecuyer and Simard,

2007) is the most complete and stringent battery to

pass, which embeds 7 big batteries that test more than

pseudorandom values for each inputted genera-

tor. TestU01 consider passing tests if the p-value is

∈ [0.001, 0.999].

From our ﬁrst experiments, it can already be no-

ticed that almost all chaotic PRNGs can pass the NIST

batteries, but they fail on TestU01, with the exception

of XOR-CIPRNG. Conversely, some linear PRNGs

like PCG32, xorshift64*, or MRG32, chosen for com-

parison in this study, can also pass the TestU01. This

is why the work in (Dabal and Pelka, 2014) and

One Random Jump and One Permutation: Sufﬁcient Conditions to Chaotic, Statistically Faultless, and Large Throughput PRNG for FPGA

297

in (Giard et al., 2012), based on the logistic map and

the Bernoulli one, will be used for throughput com-

parison, while linear PRNGs will be considered for

statistical tests. We can however already conclude

that only XOR-CIPRNG satisﬁes both low hardware

resources and a success against the TestU01 battery,

which has already been stated in (Bakiri et al., 2016).

3 THE PROPOSAL

The previous section ends with the idea that it is hard

to have together the three properties of: chaos, hard-

ware efﬁciency, and a random-like statistical proﬁle.

3.1 General Idea

Let us ﬁrst discuss on how we tackle this problem.

The ﬁrst key idea is to have a short internal state, pos-

sibly split into parallel blocs. This divide and con-

quer approach aims at ensuring hardware efﬁciency

but is in conﬂict with statistical quality. Chaotic it-

erations (Bahi et al., 2013; Fang et al., 2014) can

be used to achieve chaos objectives. However, the

general formulation of the chaotic iterations (Bahi

et al., 2015) should be preferred than the original one

when efﬁciency is needed. Finally, permutation tech-

niques (O’Neill, 2016) have presented a convenient

way to ensure statistical faultless, in a fast manner.

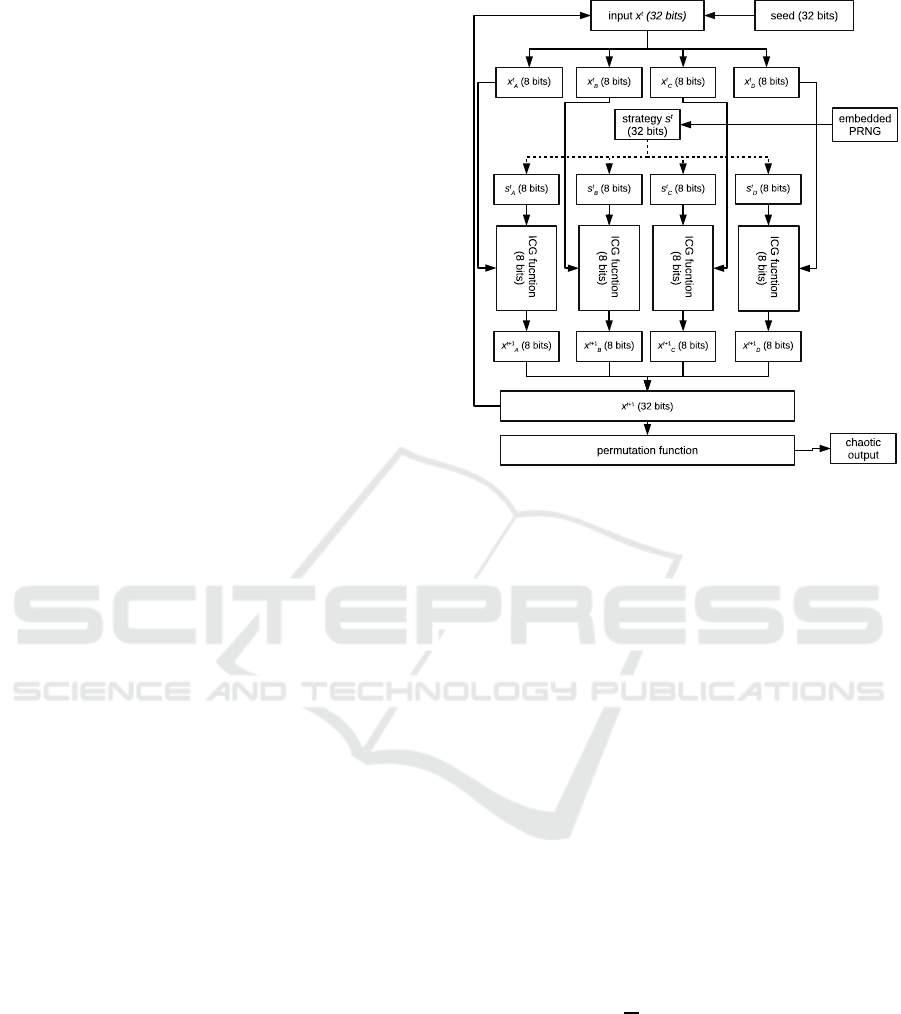
Our proposal is based on these three main ideas and

is summarized in Figure 1.

At ﬁrst, it can be seen that the seed x

, the in-

ternal state x

, and the output x

t+1

are all expressed

with the same number N of bits. Without loss of

generality, we consider hereafter that N = 32. Let

us show how to produce a new output x

t+1

for a

given input x

. This one is ﬁrst split into n blocs of

equal length. We consider here that n = 4 and we

thus have x

= (x

, x

) where x

is of size 8

for l ∈ {A, B,C, D}. The next step consists in ob-

taining a N-bits number s

from another embedded

PRNG, which is called the strategy. Similarly to x

the vector s

is split into n blocs. Here we thus ob-

tain s

= (s

, s

). Each s

, l ∈ {A, B,C, D}, can

be interpreted as a set of elements in {1, 2, . . . , 8}.

Each bloc x

is modiﬁed separately as the result of the

general formulation of the Chaotic Iterations (Bahi

et al., 2015) applied on x

, s

and a speciﬁc function

f : B

→ B

, as described hereafter. The i-th compo-

nent of x

t+1

is the i-th one of f(x

) if i is within the set

, else this component is the i-th one of x

(i.e., only

the components indicated by the set s

are updated).

This results x

t+1

. All the x

t+1

are concatenated here-

after, producing the new internal state x

t+1

. Finally, a

Figure 1: The proposal.

permutation over the N bits is applied on x

t+1

to pro-

duce the new output.

The choice of the function f executed inside the

ICG iteration, of the embedded PRNG, and of the

chosen ﬁnal permutation function has a great inﬂu-

ence on the quality of the generator. It is discussed in

the next sections.

3.2 Iterated Function

Let s ∈ (B

)

be a sequence of subests of {1, . . . N},

be a vector in B

, and f be a function from B

. The sequence (x

)

t∈N

of vectors in B

deﬁned

according the general formulation of the Chaotic Iter-

ations (Bahi et al., 2015) is

t+1

= (x

t+1

, . . . , x

t+1

) where x

t+1



) if i ∈ s

otherwise.

Two functions from B

to B

are mainly studied

in this article. The former is the negation function,

further denoted as NEG. In this one, each f

is de-

ﬁned with f

(x) =

. For instance, the image of 5 =

00000101 is 250 = 11111010. The latter, denoted as

F1, is a function whose graph of generalized iterations

is strongly connected and which has been obtained by

removing a balanced Hamiltonian cycle in a N-cube

following the method suggested in (Contassot-Vivier

et al., 2017). These two functions are recalled in Ta-

ble 3. The choice of these two functions is motivated

by the objective to make the iterations chaotic.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

298

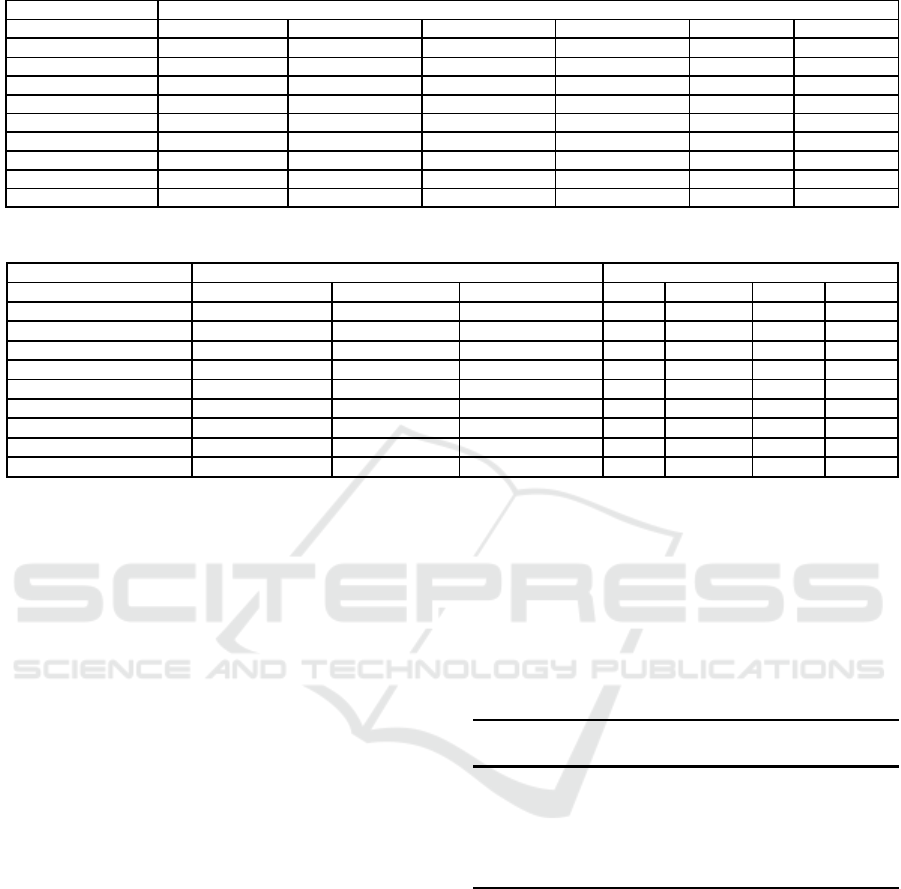
Table 1: FPGA implementations of chaotic PRNGs.

PRNG 32 Bit Chaotic

(Bakiri et al., 2016) (Dabal and Pelka, 2011) (Dabal and Pelka, 2012) (Dabal and Pelka, 2014) (Li et al., 2006) (Li et al., 2012)

Function XOR-CIPRNG [A,B,2] LCGM

LCG- H´enon- FNDR

LCG

Timing Reseeding Timing Reseeding

Frequency (Mhz) 258 76.1 151.1 - 58.2 - 183 233 200 200

DSP 0 4 4-4-0 16 0 0

Area 7568 784 640 - 4568 - 4568 9240 *** 11903

Design Latency 2 *** *** 8 to 16 *** ***

Output Latency 1 1 1 1 1 1

Throughput/Latency (Gbps) 8.30 2.435 4.835 - 1.862 - 5.856 7.5 6.4 6.4

NIST Test PASS PASS PASS PASS PASS PASS

TestU01 (BigCrush) PASS NO NO NO NO NO

Table 2: FPGA implementation of chaotic (continuation of Table 1) and linear PRNGs.

PRNG 32 Bit Chaotic Linear

(Zidan et al., 2011a) (Fang et al., 2014) (Giard et al., 2012) PCG32 xorshift64* KISS32 MRG32

Function LRZ - Chen - ELW ICPRNG B - CH - T LCG xorshift Combine Combine

Frequency (Mhz) 53.53 - 122 - 126.7 200 265.9 - 118.7 - 111.8 112 113 100 106

DSP 8 - 0- 0 *** 0 0 0 0 0

Area 3064 - 13968 3652 *** 27632 27968 26520 33456

Design Latency *** *** *** 17 21 9 14

Output Latency 1 1 1 17 21 9 14

Throughput/Latency (Gbps) 1.71 - 3.9 - 4.06 6.4 8.5 - 3.798 - 3.577 0.189 0.34 0.8 0.24

NIST Test NO PASS PASS PASS PASS PASS PASS

TestU01 (BigCrush) NO PASS NO PASS PASS NO PASS

3.3 Permutation Function

First of all, our proposal is a parallel execution of 4

blocks, each one producing 8 bits. The internal state

x is next produced as the concatenation of the results

of the 4 blocks. This design is guided by the goal of

reducing the required resources. However, such an

approach suffers from decreasing the statistical com-

plexity of the PRNG: without any post treatment it

would be dramatic, because it is equivalent to deal

with 8 bits only. A ﬁnal step which scrambles the in-

ternal state is thus necessary to tackle this problem.

This can be practically implemented with a per-

mutation function (which allows to obtain a uniform

output) provided it does not break the chaos prop-

erty (as proven in the next section). Among the

large choice of permutation functions (such as rota-

tion, dropping, xoring...), we inspire from one de-

tailed in (O’Neill, 2016). This work indeed proposes

a bench of permutation functions allowing to succeed

statistical tests.

This permutation function is implemented as in

Algorithms 1. It is not hard to see that it is mainly

a composition of three subfunctions. Let In32 be the

internal state. The ﬁrst function scrambles between

17 and 28 rightmost bits (i.e. middle bits) with a xor

function. The number of selected elements depends

on the value of In32. Then, the second function ap-

plies a modular multiplication in the cyclic group of

elements in {1, . . . , 2

− 2}. The chosen multiplier

b is a primitive root of the modulus 2

− 1. How-

ever, in (O’Neill, 2016) they need more than 36 bits

of internal state to pass TestU01, which is equiva-

lent of a modulus of 2

− 25. Therefore, b is set to

277803737, but any primitive root of 2

− 25 is con-

venient for their work in (O’Neill, 2016). The latter

function is a simple right xorshift on the lowest bits to

scramble them.

Algorithm 1: Random Xorshift Permutation

Function.

Input: In32 32-bit word)

Output: Out32 (a 32-bit word)

word1 ← (In32 ≫ ((In32 ≫ 28u) + 4u))⊗ In32

word2 ← word1∗b

word3 ← (word2 ≫ 22u) ⊗ word2

return Out32 ← word3

3.4 Chaotic Behavior of Our Generator

Let us recall or specify ﬁrst some notations and def-

initions in use in this section. In what follows, B is

the Boolean set, while N is the usual sets of integer

numbers. For a, b ∈ N , Ja, bK is the set of integers:

{a, a+1, . . . , b}, X

is the set of sequences belonging

in X and s

is the k-th term of a sequence s =





k∈N

which may be a vector (thus explaining the use of an

exponent). Finally, f

means the n-th composition of

the function f (i.e., f

= f ◦ f ◦ . . . ◦ f).

In the proposal, the internal function h

is iter-

ated on the current internal state, and with a new

One Random Jump and One Permutation: Sufﬁcient Conditions to Chaotic, Statistically Faultless, and Large Throughput PRNG for FPGA

299

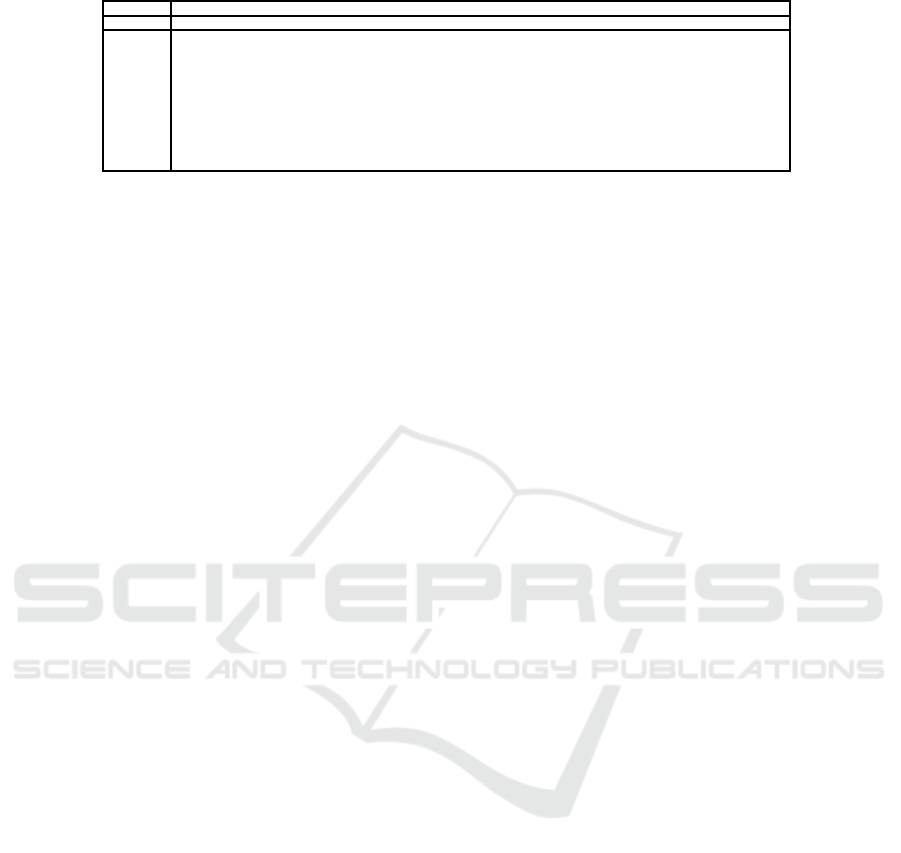
Table 3: Boolean functions.

Function f(x) for x ∈ [0, 1, 2, 3, 4, 5. . ., 2

− 1]

NEG

[255, 254, 253, 252, 251, 250 ..., 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]

[223, 190, 249, 236, 243, 234, 241, 252, 183, 244, 229, 245, 179, 178, 225, 248, 237, 254, 173, 232, 171, 202, 201, 200,

247, 198, 228, 230, 195, 242, 233, 160, 215, 220, 205, 216, 218, 154, 221, 208, 213, 210, 212, 148, 147, 211, 217, 209,

239, 238, 141, 140, 235, 203, 193, 204, 135, 134, 199, 197, 131, 226, 129, 224, 63, 174, 253, 184, 251, 250, 189, 176,

191, 246, 180, 182, 51, 50, 185, 240, 47, 46, 175, 188, 139, 42, 161, 172, 231, 164, 181, 165, 227, 130, 33, 32, 31, 222, 153,

158, 219, 26, 25, 156, 159, 214, 151, 149, 146, 18, 144, 152, 207, 206, 157, 136, 138, 170, 169, 8, 133, 6, 5, 196, 3, 194,

137, 192, 255, 110, 109, 120, 107, 126, 125, 112, 103, 114, 116, 118, 123, 98, 121, 96, 79, 78, 111, 124, 75, 122, 97,

108, 71, 100, 117, 101, 115, 66, 113, 64, 127, 90, 89, 94, 83, 91, 81, 92, 95, 84, 87, 85, 82, 86, 80, 88, 77, 76, 93, 72, 74,

106, 105, 104, 69, 102, 68, 70, 99, 67, 73, 65, 55, 58, 57, 44, 187, 186, 49, 60, 119, 52, 37, 53, 35, 54, 177, 56, 45, 62, 61,

40, 59, 10, 9, 168, 167, 166, 36, 38, 163, 162, 41, 48, 23, 28, 13, 24, 155, 30, 29, 16, 21, 150, 20, 22, 27, 19, 145,

17, 143, 142, 15, 14, 43, 11, 1, 12, 39, 4, 7, 132, 2, 34, 0, 128]

term taken from the outer strategy. Then, the out-

put is a permutation p of the internal state, which is

not internally modiﬁed. The topological framework

proposed in (Bakiri et al., 2016) for the CIPRNG-

XOR and in (Contassot-Vivier et al., 2017) can be

applied, mutatis mutandis, to this generator. It is

then possible to state that iterations of the internal

function are chaotic on its iteration space, denoted

as X

= B

× J0, 31K

. And, using a topological

semi-conjugacy, that the permutation does not alter

such an unpredictable behavior. After having estab-

lished that the 8-bits ICG function, denoted as g

is strongly transitive on its iteration space X

, we

can ﬁrst deduce that the discrete dynamical system

∈ X

, x

n+1

= g

) is chaotic, and then that h

chaotic according to Devaney.

Finally, the whole generator with the permutation

p must be integrated inside the iterations, to see if the

output has a chaotic behavior when modifying the in-

put (internal state or strategy). To write the generator

as a discrete dynamical system, we need to introduce

the reverse permutation p

−1

. To do so, let us deﬁne

p : X

−→ X

(e, s) 7−→ (p(e), s),

its inverse being

−1

: X

−→ X

(e, s) 7−→ (p

−1

(e), s).

We can now introduce the following diagram:

−−−−→ X



−1



−−−−→ X

−1

and p are obviously continuous on (X

, d

which can be directly deduced by the sequential char-

acterization of the continuity. So the commutative di-

agram depicted above is a topological conjugacy, and

the generator

= p

−1

◦ h

◦ p

thus inherits the chaotic behavior of h

on (X

, d

4 PLATFORM AND HARDWARE

IMPLEMENTATION ON FPGA

In this section, the hardware implementation of the

PRNG described in this article is executed the test

platform presented in (Bakiri et al., 2016). It uses

a Xilinx Zynq-7000 (EPP) (Rajagopalan et al., 2011)

and an AXI core selector deployed as a wrapper for

PRNGs. The main methodology of comparison be-

tween PRNGs is based on Xilinx Vivado tool 16.4

and Zybo Board 125Mhz. For area comparison, we

only considered LUT and FF as follows:

(LUT + FF) × 8,

Rate, for its part, is the number of bits that are treated

or transferred in each delay unit (Bps).

Table 4 presents the results of six different im-

plementations of our proposal on FPGA with their

TestU01 statistical test evaluations. During these im-

plementations, we considered two distinct Boolean

functions, namely the negation and F1 as mentioned

in Section 3. Three PRNGs are used as strategies (in-

putted generators), which are LFSR113, Taus88, and

xorshift128. Obtained results are described hereafter.

Negation Function. Three implementations have

been realized and evaluated, see Table 4. Notice that

in these 3 evaluations the value of the minimum mod-

ular multiplication operand b used in the permutation

(see Section 3) function is not the same. To pass

TestU01, it must be equal to 95 for all strategies as

LFSR113, Tauss88, and xorshift128 (as a compari-

son, we found 277803737 for PCG32). We have ob-

tained that the negation function outperforms F1 in

terms of throughput and area. Additionally, it is obvi-

ously more efﬁcient than its best competitors recalled

in this paper, as its throughput is between 1.0 and 4

times larger than the other chaotic PRNGs (that can-

not pass TestU01), while it is 8 times faster than the

linear PRNGs... with the exception of (Dabal and

Pelka, 2014) using the logistic map: it is true that

the latter has a throughput of 7.5 Gbps for 32bits, but

with 2 times less area (we discarded (Dabal and Pelka,

2014), as this latter is fully dependent on Matlab

SECRYPT 2017 - 14th International Conference on Security and Cryptography

300

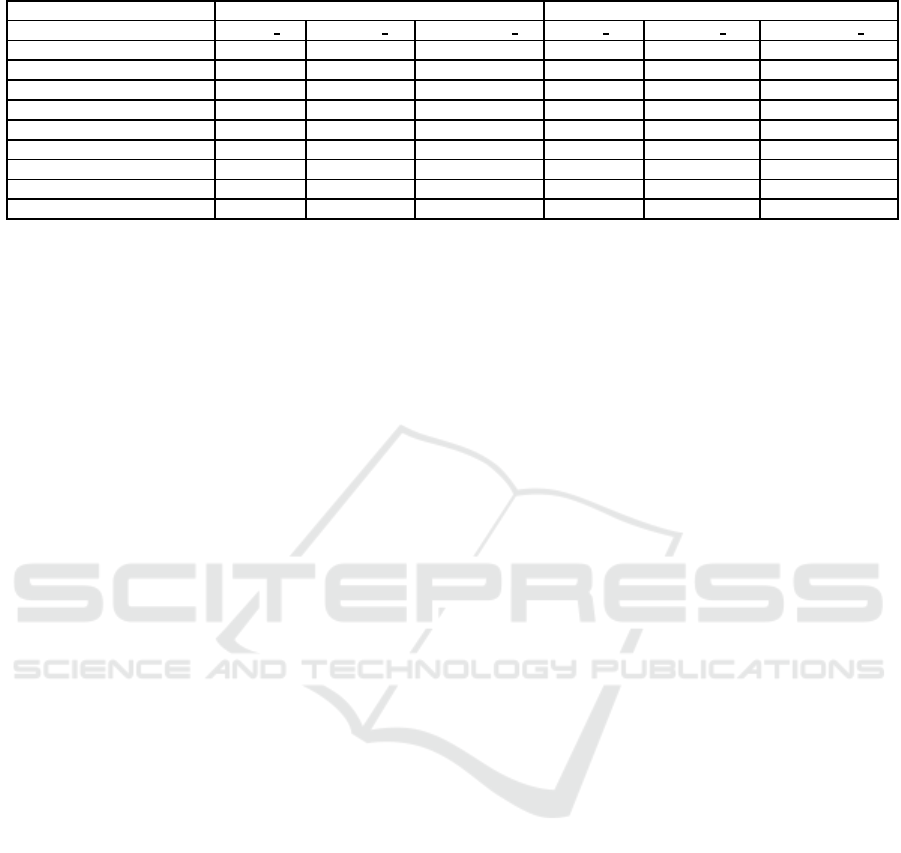
Table 4: FPGA Implementation Results.

Function Negation F1

PRNG Taus88 95 LFSR113 95 xorshiftP128 95 Taus88 811 LFSR113 811 xorshiftP128 811

LUT 222 250 224 426 431 420

FF 274 306 306 336 368 368

DSP 0 0 0 0 0 0

RAM 0 0 0 0 0 0

Frequency (Mhz) 200 202 210.7 162 165 167.5

Area 3968 4448 4240 6096 6392 6304

Design Latency 3 3 3 3 3 3

Output Latency 1 1 1 1 1 1

Throughput/Latency (Gbps) 6.4 6.5 6.7 5.2 5.3 5.4

Simulink macros, which is not relevant for ASIC im-

plementation). Similarly, our three implementations

using the negation function exhibit less robust results

compared to XOR-CIPRNG (Bakiri et al., 2016) for

throughput compared to the area. Finally, compared

to the linear PRNGs that can pass TestU01 too, our

three proposals with the negation function use less

area and are faster. To conclude this part, and when

considering the negation, our proposal using xor-

shift128 as strategy is our best candidate for FPGA,

and with a throughput/latency equal to 6.7Gbps.

F1 function. We performed similar experiments

than for the negation function. But, in these cases,

the minimum modular multiplication operand b is al-

ways set to 811 for all strategies. We obtained a lower

performance in terms of throughout when compared

with the negation function, which is due to the mul-

tiplication operation in the permutation, and because

in the negation we iterate a very simple logical opera-

tion (see Algorithm 1 to compare). However, despite

its use of a bigger constant, which leads to a longer

data path, the proposal with F1 does not consume any

DSP block of FPGA: logic operators are sufﬁcient.

Additionally, results show that the three implemen-

tations with F1 function perform better than all the

other chaotic PRNGs that can pass the TestU01, if

we except both our proposal with the negation and

the XOR-CIPRNGTheir performances are close to

what has been obtained with the negation function, or

to (Bakiri et al., 2016) with Taus88 as strategy, while

F1 makes harder to reverse the process without know-

ing the internal transition function.

To conclude this experiment section, all what we

proposed can pass all statistical tests of TestU01, from

SmallCruh to BigCrush. Let us recall that the permu-

tation function (O’Neill, 2016) does not pass Crush

and BigCrush when the space is lower than 36 bits,

while in our case it does with only 32 bits and a lower

modular multiplicative constant. These results can be

improved with 64 or 128 bit outputted for a better

throughput. Finally, compared to the other CPRNG

evoked in this article, we presented the only ones who

can pass the stringent TestU01 battery.

5 CONCLUSION

In this research work, we have introduced a new

chaotic PRNG implemented in FPGA, which is

based on the combination of parallel executions of

generalized chaotic iterations and of an efﬁcient

permutation scheme. Two Boolean functions have

been iterated: the vectorial negation and one issued

from removing a Hamilton cycle in the N-cube Three

interesting strategy builders have been evaluated

for each of them. These six variations lead to an

hardware generator with one of the best throughput

of the literature, and that can pass the most stringent

statistical batteries of tests. If we consider the two

conditions of throughput and statistics, we thus have

obtained one of the best existing hardware generator.

This work is partially funded by the Labex ACTION

program (contract ANR-11-LABX-01-01).

REFERENCES

Bahi, J., Guyeux, C., and Wang, Q. (2009). A novel pseudo-

random generator based on discrete chaotic iterations.

In INTERNET’09, 1-st Int. Conf. on Evolving Internet,

pages 71–76, Cannes, France.

Bahi, J. M., Couturier, R., Guyeux, C., and Heam, P.-C.

(2015). Efﬁcient and cryptographically secure gener-

ation of chaotic pseudorandom numbers on gpu. The

journal of Supercomputing, 71(10):3877–3903.

Bahi, J. M., Fang, X., Guyeux, C., and Larger, L. (2013).

Fpga design for pseudorandom number generator

based on chaotic iteration used in information hiding

application. Appl. Math, 7(6):2175–2188.

Bakiri, M., Couchot, J.-F., and Guyeux, C. (2016). Fpga

implementation of f2-linear pseudorandom number

generators based on zynq mpsoc: A chaotic itera-

tions post processing case study. In Proceedings of

the 13th International Joint Conference on e-Business

One Random Jump and One Permutation: Sufﬁcient Conditions to Chaotic, Statistically Faultless, and Large Throughput PRNG for FPGA

301

and Telecommunications - Volume 4: SECRYPT,,

pages 302–309.

Cern´ak, J. (1996). Digital generators of chaos. Physics

letters A, 214(3):151–160.

Contassot-Vivier, S., Couchot, J.-F., Guyeux, C., and

Heam, P.-C. (2017). Random walk in a n-cube with-

out hamiltonian cycle to chaotic pseudorandom num-

ber generation: Theoretical and practical considera-

tions. International Journal of Bifurcation and Chaos,

27(01):1750014.

Couchot, J.-F., Heam, P.-C., Guyeux, C., Wang, Q., and

Bahi, J. M. (2014). Pseudorandom number generators

with balanced gray codes. In Security and Cryptogra-

phy (SECRYPT), 2014 11th International Conference

on, pages 1–7. IEEE.

Dabal, P. and Pelka, R. (2011). A chaos-based pseudo-

random bit generator implemented in fpga device. In

Design and Diagnostics of Electronic Circuits & Sys-

tems (DDECS), 2011 IEEE 14th International Sympo-

sium on, pages 151–154. IEEE.

Dabal, P. and Pelka, R. (2012). Fpga implementation of

chaotic pseudo-random bit generators. In Mixed De-

sign of Integrated Circuits and Systems (MIXDES),

2012 Proceedings of the 19th International Confer-

ence, pages 260–264. IEEE.

Dabal, P. and Pelka, R. (2014). A study on fast pipelined

pseudo-random number generator based on chaotic lo-

gistic map. In Design and Diagnostics of Electronic

Circuits Systems, 17th International Symposium on,

pages 195–200.

Devaney, R. L. (2003). An Introduction to Chaotic Dynam-

ical Systems, 2nd Edition. Westview Pr.

Elwakil, A. and Kennedy, M. (2000). Chaotic oscillator

conﬁguration using a frequency dependent negative

resistor. International journal of circuit theory and

applications, 28(1):69–76.

Fang, X., Wang, Q., Guyeux, C., and Bahi, J. M. (2014).

Fpga acceleration of a pseudorandom number genera-

tor based on chaotic iterations. Journal of Information

Security and Applications, 19(1):78–87.

Giard, P., Kaddoum, G., Gagnon, F., and Thibeault, C.

(2012). Fpga implementation and evaluation of

discrete-time chaotic generators circuits. In IECON

2012-38th Annual Conference on IEEE Industrial

Electronics Society, pages 3221–3224. IEEE.

Guyeux, C. (2010). Le d´esordre des it´erations chaotiques

et leur utilit´e en s´ecurit´e informatique. Theses, Uni-

versit´e de Franche-Comt´e.

Guyeux, C. and Bahi, J. (2010). An improved watermark-

ing algorithm for internet applications. In INTER-

NET’2010. The 2nd Int. Conf. on Evolving Internet,

pages 119 – 124, Valencia, Spain.

H´enon, M. (1976). A two-dimensional mapping with a

strange attractor. Communications in Mathematical

Physics, 50(1):69–77.

L’Ecuyer, P. and Simard, R. (2007). Testu01: Ac li-

brary for empirical testing of random number gener-

ators. ACM Transactions on Mathematical Software

(TOMS), 33(4):22.

Li, C.-Y., Chen, J.-S., and Chang, T.-Y. (2006). A chaos-

based pseudo random number generator using timing-

based reseeding method. In Circuits and Systems,

2006. ISCAS 2006. Proceedings. 2006 IEEE Interna-

tional Symposium on, pages 4–pp. IEEE.

Li, C.-Y., Chen, Y.-H., Chang, T.-Y., Deng, L.-Y., and To,

K. (2012). Period extension and randomness enhance-

ment using high-throughput reseeding-mixing prng.

Very Large Scale Integration (VLSI) Systems, IEEE

Transactions on, 20(2):385–389.

Li, T. Y. and Yorke, J. A. (1975). Period three implies chaos.

Amer. Math. Monthly, 82(10):985–992.

Liu, S., Sun, J., Xu, Z., and Cai, Z. (2008). An im-

proved chaos-based stream cipher algorithm and its

vlsi implementation. In Networked Computing and

Advanced Information Management, 2008. NCM’08.

Fourth International Conference on, volume 2, pages

191–197. IEEE.

May, R. M. et al. (1976). Simple mathematical models with

very complicated dynamics. Nature, 261(5560):459–

467.

NIST (2010). National institute of standards and technology

(nist): A statistical test suite for random and pseudo-

random number generators for cryptographic applica-

tions @ONLINE.

O’Neill, M. E. (2016). PCG: A family of simple fast

space-efﬁcient statistically good algorithms for ran-

dom number generation. submitted to ACM Transac-

tions on Mathematical Software (47 pages).

Padgett, W. and Anderson, D. (2009). Fixed-Point Signal

Processing. Synthesis lectures on signal processing.

Morgan & Claypool.

Pande, A. and Zambreno, J. (2010). Design and hardware

implementation of a chaotic encryption scheme for

real-time embedded systems. In Signal Processing

and Communications (SPCOM), 2010 International

Conference on, pages 1–5. IEEE.

Pecora, L. M. and Carroll, T. L. (1990). Synchronization in

chaotic systems. Physical review letters, 64(8):821.

Rajagopalan, V., Boppana, V., Dutta, S., Taylor, B., and

Wittig, R. (2011). Xilinx zynq-7000 epp–an exten-

sible processing platform family. In 23rd Hot Chips

Symposium, pages 1352–1357.

Rossler, O. (1976). An equation for continuous chaos.

Physics Letters A, 57(5):397 – 398.

Wiggins, S. (2003). Introduction to applied nonlinear dy-

namical systems and chaos, volume 2. Springer Sci-

ence & Business Media.

Zidan, M. A., Radwan, A. G., and Salama, K. N. (2011a).

The effect of numerical techniques on differential

equation based chaotic generators. In Microelectron-

ics (ICM), 2011 International Conference on, pages

1–4. IEEE.

Zidan, M. A., Radwan, A. G., and Salama, K. N. (2011b).

Random number generation based on digital differ-

ential chaos. In Circuits and Systems (MWSCAS),

2011 IEEE 54th International Midwest Symposium

on, pages 1–4. IEEE.

SECRYPT 2017 - 14th International Conference on Security and Cryptography

302